В алгебраической топологии, разделе математики, сингулярной гомологии относится к изучению определенного набора алгебраических инвариантов топологического пространства X, так называемых групп гомологии  Интуитивно, сингулярная гомология считает для каждого измерения n n-мерные дыры в пространстве. Сингулярные гомологии - это частный пример теории гомологий, которая теперь превратилась в довольно обширное собрание теорий. Из различных теорий это, пожалуй, одна из самых простых для понимания, поскольку она построена на довольно конкретных конструкциях.
Интуитивно, сингулярная гомология считает для каждого измерения n n-мерные дыры в пространстве. Сингулярные гомологии - это частный пример теории гомологий, которая теперь превратилась в довольно обширное собрание теорий. Из различных теорий это, пожалуй, одна из самых простых для понимания, поскольку она построена на довольно конкретных конструкциях.
Вкратце, сингулярные гомологии строятся путем преобразования отображений стандартного n-симплекса в топологическое пространство и их компоновки в формальные суммы, называемые особые цепи . Граничная операция - отображение каждого n-мерного симплекса на его (n − 1) -мерную границу - индуцирует сингулярный цепной комплекс . Тогда особые гомологии - это гомологии цепного комплекса. Полученные группы гомологий одинаковы для всех гомотопически эквивалентных пространств, что и является причиной их изучения. Эти конструкции могут применяться ко всем топологическим пространствам, и поэтому особые гомологии могут быть выражены в терминах теории категорий, где гомологии выражаются в виде функтора из категории топологических пространства в категорию градуированных абелевых групп.
Содержание
- 1 Сингулярные симплексы
- 2 Сингулярный цепной комплекс
- 3 Гомотопическая инвариантность
- 4 Функториальность
- 5 Коэффициенты в R
- 6 Относительные гомологии
- 7 Когомологии
- 8 Гомологии и когомологии Бетти
- 9 Экстраординарные гомологии
- 10 См. Также
- 11 Ссылки
Особые симплексы
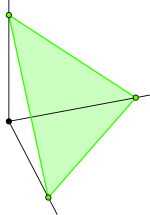
Стандартные 2-симплексы Δ в R
A сингулярный n-симплекс в топологическом пространстве X - это непрерывная функция (также называемая картой)  из стандарта n- симплекс
из стандарта n- симплекс  до X, записывается
до X, записывается  Эта карта не обязательно должна быть инъективной, и могут быть неэквивалентные сингулярные симплексы с тем же изображением в X.
Эта карта не обязательно должна быть инъективной, и могут быть неэквивалентные сингулярные симплексы с тем же изображением в X.
Граница  обозначается как
обозначается как  определяется как формальная сумма сингулярных (n - 1) -симплексов, представленных ограничением
определяется как формальная сумма сингулярных (n - 1) -симплексов, представленных ограничением  к граням стандартного n-симплекса с чередованием знака для учета ориентации. (Формальная сумма - это элемент свободной абелевой группы на симплексах. Основой группы является бесконечное множество всех возможных сингулярных симплексов. Групповая операция - это «сложение», а сумма симплекса a с симплексом b обычно обозначается просто как a + b, но a + a = 2a и т. д. Каждый симплекс a имеет отрицательный −a.) Таким образом, если мы обозначим
к граням стандартного n-симплекса с чередованием знака для учета ориентации. (Формальная сумма - это элемент свободной абелевой группы на симплексах. Основой группы является бесконечное множество всех возможных сингулярных симплексов. Групповая операция - это «сложение», а сумма симплекса a с симплексом b обычно обозначается просто как a + b, но a + a = 2a и т. д. Каждый симплекс a имеет отрицательный −a.) Таким образом, если мы обозначим  вершинами
вершинами
![{\ displaystyle [p_ {0}, p_ {1}, \ ldots, p_ {n}] = [\ sigma (e_ {0}), \ sigma (e_ {1}), \ ldots, \ sigma (e_ {n})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a156a535bec090583a12c0f6122ab3b0fb1fd132)
соответствующий вершины  стандартного n-симплекса
стандартного n-симплекса  (какой из конечно, не полностью определяет сингулярный симплекс, полученный с помощью
(какой из конечно, не полностью определяет сингулярный симплекс, полученный с помощью  ), тогда
), тогда
![{\ displaystyle \ partial _ {n} \ sigma = \ sum _ {k = 0} ^ {n} (- 1) ^ {k} \ sigma \ mid _ { [p_ {0}, \ ldots, p_ {k-1}, p_ {k + 1}, \ ldots, p_ {n}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0708e00793307183ecdaa1d74808957624df68f4)
- формальная сумма из определенным образом обозначенные лица симплексного изображения. (То есть конкретное лицо должно быть ограничено  лицом
лицом  , который зависит от порядка, в котором перечислены его вершины.) Таким образом, например, граница
, который зависит от порядка, в котором перечислены его вершины.) Таким образом, например, граница ![\ sigma = [p_0, p_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/15e0502186b53d6fa17c4ffc0dcf18b4a72fed6a) (кривая, идущая от
(кривая, идущая от  до
до  ) - формальная сумма (или «формальная разница»)
) - формальная сумма (или «формальная разница») ![[p_1] - [p_0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/729957f5d060a9c7bdbe6d5e1b4c69b6e6ffdecd) .
.
Сингулярная цепочка комплекс
Обычное построение сингулярных гомологий продолжается путем определения формальных сумм симплексов, которые можно понимать как элементы свободной абелевой группы, а затем показа, что мы можем определить некоторую группу, группа гомологий топологического пространства, включающая граничный оператор.
Сначала рассмотрим множество всех возможных сингулярных n-симплексов  на топологическом пространстве X. Этот набор может использоваться в качестве основы свободной абелевой группы, так что каждый сингулярный n-симплекс является генератором группы. Этот набор генераторов, конечно, обычно бесконечен, часто несчетный, так как существует много способов отображения симплекса в типичное топологическое пространство. Свободная абелева группа, порожденная этим базисом, обычно обозначается как
на топологическом пространстве X. Этот набор может использоваться в качестве основы свободной абелевой группы, так что каждый сингулярный n-симплекс является генератором группы. Этот набор генераторов, конечно, обычно бесконечен, часто несчетный, так как существует много способов отображения симплекса в типичное топологическое пространство. Свободная абелева группа, порожденная этим базисом, обычно обозначается как  . Элементы
. Элементы  называются сингулярными n-цепями ; они представляют собой формальные суммы сингулярных симплексов с целыми коэффициентами.
называются сингулярными n-цепями ; они представляют собой формальные суммы сингулярных симплексов с целыми коэффициентами.
граница  легко расширяется для воздействия на сингулярные n-цепи. Расширение, называемое граничным оператором, записывается как
легко расширяется для воздействия на сингулярные n-цепи. Расширение, называемое граничным оператором, записывается как

является гомоморфизмом групп. Граничный оператор вместе с  образуют цепной комплекс абелевых групп, называемый сингулярным комплексом . Его часто обозначают как
образуют цепной комплекс абелевых групп, называемый сингулярным комплексом . Его часто обозначают как  или проще
или проще  .
.
Ядро граничного оператора:  , и называется группой особых n-циклов . Образ граничного оператора:
, и называется группой особых n-циклов . Образ граничного оператора:  и называется группой сингулярных n-границ .
и называется группой сингулярных n-границ .
. Также можно показать, что  .
.  -я группа гомологии
-я группа гомологии  затем определяется как факторная группа
затем определяется как факторная группа

Элементы  называются классами гомологии .
называются классами гомологии .
Гомотопическая инвариантность
Если X и Y - два топологических пространства с одним и тем же гомотопическим типом (т. Е. гомотопический эквивалент ), тогда

для все n ≥ 0. Это означает, что группы гомологий являются топологическими инвариантами.
В частности, если X - связное стягиваемое пространство, то все его группы гомологий равны 0, кроме  .
.
Доказательство гомотопической инвариантности сингулярных групп гомологий можно набросать следующим образом. Непрерывное отображение f: X → Y индуцирует гомоморфизм

Сразу можно проверить, что

т.е. f # - это цепное отображение , которое спускается до гомоморфизмов на гомологиях

Теперь мы покажем, что если f и g гомотопически эквивалентны, то f * = г *. Отсюда следует, что если f - гомотопическая эквивалентность, то f * - изоморфизм.
Пусть F: X × [0, 1] → Y - гомотопия, переводящая f в g. На уровне цепочек определите гомоморфизм

который, говоря геометрически, переводит базисный элемент σ: Δ → X в C n (X) в «призму» P (σ): Δ × I → Y. Граница P (σ) можно выразить как

Итак, если α в C n (X) является n-циклом, тогда f # (α) и g # (α) отличаются границей:

т.е. они гомологичны. Это доказывает утверждение.
Функториальность
Вышеупомянутая конструкция может быть определена для любого топологического пространства и сохраняется за счет действия непрерывных отображений. Эта общность подразумевает, что теорию сингулярных гомологий можно переформулировать на языке теории категорий. В частности, группу гомологий можно понимать как функтор из категории топологических пространств Top в категорию абелевых групп Ab.
Сначала рассмотрим, что  - это отображение топологических пространств на свободные абелевы группы. Это говорит о том, что
- это отображение топологических пространств на свободные абелевы группы. Это говорит о том, что  можно рассматривать как функтор, если можно понять его действие на морфизмы из Верх . Теперь морфизмы Top являются непрерывными функциями, поэтому, если
можно рассматривать как функтор, если можно понять его действие на морфизмы из Верх . Теперь морфизмы Top являются непрерывными функциями, поэтому, если  является непрерывной картой топологических пространств, его можно расширить до гомоморфизма групп
является непрерывной картой топологических пространств, его можно расширить до гомоморфизма групп

путем определения

где  - симплекс в единственном числе, а
- симплекс в единственном числе, а  является сингулярной n-цепочкой, то есть элементом
является сингулярной n-цепочкой, то есть элементом  . Это показывает, что
. Это показывает, что  является функтором
является функтором

из категории топологических пространств в категорию абелевых групп.
Граничный оператор коммутирует с непрерывными отображениями, так что  . Это позволяет рассматривать весь цепной комплекс как функтор. В частности, это показывает, что карта
. Это позволяет рассматривать весь цепной комплекс как функтор. В частности, это показывает, что карта  является функтором
является функтором

из категории топологических пространств в категорию абелевых групп. Согласно аксиоме гомотопии,  также является функтором, называемым функтором гомологии, действующим на hTop, фактор гомотопическая категория :
также является функтором, называемым функтором гомологии, действующим на hTop, фактор гомотопическая категория :

Это отличает сингулярную гомологию от других теорий гомологии, где  по-прежнему является функтором, но не обязательно определен на всем Top . В некотором смысле, особые гомологии являются «наибольшей» теорией гомологий, поскольку каждая теория гомологий в подкатегории из Top согласуется с сингулярными гомологиями в этой подкатегории. С другой стороны, особые гомологии не обладают чистейшими категориальными свойствами; такая очистка мотивирует развитие других теорий гомологии, таких как клеточная гомология.
по-прежнему является функтором, но не обязательно определен на всем Top . В некотором смысле, особые гомологии являются «наибольшей» теорией гомологий, поскольку каждая теория гомологий в подкатегории из Top согласуется с сингулярными гомологиями в этой подкатегории. С другой стороны, особые гомологии не обладают чистейшими категориальными свойствами; такая очистка мотивирует развитие других теорий гомологии, таких как клеточная гомология.
В более общем смысле, функтор гомологии определяется аксиоматически, как функтор на абелевой категории или, альтернативно, как функтор на цепных комплексах, удовлетворяющий аксиомам, требующим граничного морфизма, который превращает короткие точные последовательности в длинные точные последовательности. В случае особых гомологий функтор гомологии может быть разложен на две части: топологический и алгебраический. Топологическая часть задается формулой

, которая отображает топологические пространства как  и непрерывные функции как
и непрерывные функции как  . Итак, здесь
. Итак, здесь  понимается как сингулярный цепной функтор, который отображает топологические пространства в категорию цепных комплексов Comp (или Kom ). Категория цепных комплексов имеет цепные комплексы в качестве объектов, а отображает как свои морфизмы.
понимается как сингулярный цепной функтор, который отображает топологические пространства в категорию цепных комплексов Comp (или Kom ). Категория цепных комплексов имеет цепные комплексы в качестве объектов, а отображает как свои морфизмы.
Вторая, алгебраическая часть - это функтор гомологии

, который отображает

и переводит цепные отображения в отображения абелевых групп. Именно этот функтор гомологии может быть определен аксиоматически, так что он стоит сам по себе как функтор в категории цепных комплексов.
Гомотопические карты снова входят в картину, определяя гомотопически эквивалентные цепные карты. Таким образом, можно определить факторную категорию hComp или K, гомотопическую категорию цепных комплексов.
Коэффициенты в R
Для любого кольца с единицей R множество сингулярных n-симплексов на топологическом пространстве можно взять в качестве генераторов свободного R-модуля. То есть вместо того, чтобы выполнять вышеупомянутые конструкции с начальной точки свободных абелевых групп, вместо них используются свободные R-модули. Все конструкции проходят практически без изменений. Результатом этого является

, который теперь является R-модулем. Конечно, обычно это не бесплатный модуль. Обычная группа гомологий восстанавливается, если заметить, что

если принять кольцо за кольцо целых чисел. Обозначение H n (X, R) не следует путать с почти идентичным обозначением H n (X, A), которое обозначает относительную гомологию (ниже).
Относительная гомология
Для подпространства  , относительная гомология Hn(X, A) понимается как гомология частного цепных комплексов, то есть
, относительная гомология Hn(X, A) понимается как гомология частного цепных комплексов, то есть

где фактор цепных комплексов задается короткой точной последовательностью

Когомологии
Путем дуализации гомологии цепного комплекса ( т.е. применяя функтор Hom (-, R), R - любое кольцо), мы получаем комплекс коцепей с кограничным отображением  . Группы когомологий комплекса X определяются как группы гомологий этого комплекса; в шутку, «когомологии - это гомологии ко [двойственного комплекса]».
. Группы когомологий комплекса X определяются как группы гомологий этого комплекса; в шутку, «когомологии - это гомологии ко [двойственного комплекса]».
Группы когомологий имеют более богатую или, по крайней мере, более знакомую алгебраическую структуру, чем группы гомологий. Во-первых, они образуют дифференциальную градуированную алгебру следующим образом:
- градуированный набор групп формирует градуированный R- модуль ;
- , которому может быть придана структура градуированного R- алгебра с использованием чашечного произведения ;
- гомоморфизм Бокштейна β дает дифференциал.
Существуют дополнительные операции когомологий, а алгебра когомологий имеет сложение структура mod p (как и раньше, когомологии mod p являются когомологиями коцепного комплекса mod p, а не редукцией когомологий mod p), в частности структура алгебры Стинрода.
Гомологии и когомологии Бетти
Поскольку количество теорий гомологии стало большим (см. Категория: теория гомологий ), термины Гомологии Бетти и когомологии Бетти иногда применяются (в частности, авторами, пишущими по алгебраической геометрии ) к сингулярной теории, поскольку они приводят к числам Бетти наиболее известных пространств, таких как симплициальные комплексы и замкнутые многообразия.
Экстраординарные гомологии
Если определить теорию гомологий аксиоматически (через аксиомы Эйленберга – Стинрода ), а затем ослабляет одну из аксиом (аксиому размерности), получается обобщенная теория, называемая теорией экстраординарной гомологии. Первоначально они возникли в форме необычных теорий когомологий, а именно K-теории и теории кобордизмов. В этом контексте сингулярная гомология называется обычной гомологией.
См. Также
Ссылки
- Аллен Хэтчер, Алгебраическая топология. Cambridge University Press, ISBN 0-521-79160-X и ISBN 0-521-79540-0
- JP Мэй, Краткий курс алгебраической топологии, Издательство Чикагского университета ISBN 0-226-51183-9
- Джозеф Дж. Ротман, Введение в алгебраическую топологию, Springer-Verlag, ISBN 0-387-96678-1

 Стандартные 2-симплексы Δ в R
Стандартные 2-симплексы Δ в R






![{\ displaystyle [p_ {0}, p_ {1}, \ ldots, p_ {n}] = [\ sigma (e_ {0}), \ sigma (e_ {1}), \ ldots, \ sigma (e_ {n})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a156a535bec090583a12c0f6122ab3b0fb1fd132)



![{\ displaystyle \ partial _ {n} \ sigma = \ sum _ {k = 0} ^ {n} (- 1) ^ {k} \ sigma \ mid _ { [p_ {0}, \ ldots, p_ {k-1}, p_ {k + 1}, \ ldots, p_ {n}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0708e00793307183ecdaa1d74808957624df68f4)


![\ sigma = [p_0, p_1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/15e0502186b53d6fa17c4ffc0dcf18b4a72fed6a)


![[p_1] - [p_0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/729957f5d060a9c7bdbe6d5e1b4c69b6e6ffdecd)


















































