Цепной комплекс

редактировать

Инструмент в гомологической алгебре

В математике, цепной комплекс - это алгебраическая структура, которая состоит из последовательности абелевых групп (или модулей ) и последовательности гомоморфизмов между последовательными группами, такими как что образ каждого гомоморфизма включен в ядро следующего. С цепным комплексом связана его гомология, которая описывает, как изображения включаются в ядра.

A Коцепной комплекс похож на цепной комплекс, за исключением того, что его гомоморфизмы следуют другому соглашению. Гомологии коцепного комплекса называются его когомологиями.

В алгебраической топологии сингулярный цепной комплекс топологического пространства X строится с использованием непрерывных отображений из симплекса в X, а гомоморфизмы цепного комплекса показывают, как эти отображения ограничиваются границей симплекса. Гомология этого цепного комплекса называется сингулярной гомологией пространства X и является обычно используемым инвариантом топологического пространства.

Цепные комплексы изучаются в гомологической алгебре, но используются в нескольких областях математики, включая абстрактную алгебру, теорию Галуа, дифференциальная геометрия и алгебраическая геометрия. Они могут быть определены более широко в абелевых категориях.

Содержание

1 Определения
- 1.1 Точные последовательности
- 1.2 Цепные отображения
- 1.3 Цепная гомотопия
2 Примеры
- 2.1 Сингулярная гомология
- 2.2 Когомология де Рама
3 Категория цепных комплексов
4 Дополнительные примеры
5 См. Также
6 Ссылки

Определения

A цепной комплекс $(A ∙, d ∙) {\ displaystyle (A _ {\ bullet}, d _ {\ bullet})}$ $(A _ {\ bullet}, d _ {\ bullet})$ - последовательность абелевых групп или модулей..., A 0, A 1, A 2, A 3, A 4,... связанные гомоморфизмами (называемые граничными операторами или дифференциалы ) d n : A n → A n − 1, так что композиция любых двух последовательных отображений равна нулю карта. Явно, дифференциалы удовлетворяют условию d n ∘ d n + 1 = 0 или с подавленными индексами d = 0. Комплекс можно записать следующим образом.

⋯ ← d 0 A 0 ← d 1 A 1 ← d 2 A 2 ← d 3 A 3 ← d 4 A 4 ← d 5 ⋯ {\ displaystyle \ cdots {\ xleftarrow {d_ {0}}} A_ { 0} {\ xleftarrow {d_ {1}}} A_ {1} {\ xleftarrow {d_ {2}}} A_ {2} {\ xleftarrow {d_ {3}}} A_ {3} {\ xleftarrow {d_ { 4}}} A_ {4} {\ xleftarrow {d_ {5}}} \ cdots}

{\ displaystyle \ cdots {\ xleftarrow {d_ {0}}} A_ {0} {\ xleftarrow {d_ { 1}}} A_ {1} {\ xleftarrow {d_ {2}}} A_ {2} {\ xleftarrow {d_ {3}}} A_ {3} {\ xleftarrow {d_ {4}}} A_ {4} {\ xleftarrow {d_ {5}}} \ cdots}

комплекс коцепей $(A ∙, d ∙) {\ displaystyle (A ^ { \ bullet}, d ^ {\ bullet})}$ $(A ^ {\ bullet}, d ^ {\ bullet})$ - это двойственное понятие цепного комплекса. Он состоит из последовательности абелевых групп или модулей..., A, A, A, A, A,..., связанных гомоморфизмами d: A → A, удовлетворяющими d ∘ d = 0. Коцепной комплекс может быть записан в аналогично цепному комплексу.

⋯ → d - 1 A 0 → d 0 A 1 → d 1 A 2 → d 2 A 3 → d 3 A 4 → d 4 ⋯ {\ displaystyle \ cdots {\ xrightarrow {d ^ {- 1}} } A ^ {0} {\ xrightarrow {d ^ {0}}} A ^ {1} {\ xrightarrow {d ^ {1}}} A ^ {2} {\ xrightarrow {d ^ {2}}} A ^ {3} {\ xrightarrow {d ^ {3}}} A ^ {4} {\ xrightarrow {d ^ {4}}} \ cdots}

{\ displaystyle \ cdots {\ xrightarrow {d ^ {- 1}}} A ^ {0} { \ xrightarrow {d ^ {0}}} A ^ {1} {\ xrightarrow {d ^ {1}}} A ^ {2} {\ xrightarrow {d ^ {2}}} A ^ {3} {\ xrightarrow {d ^ {3}}} A ^ {4} {\ xrightarrow {d ^ {4}}} \ cdots}

Индекс n в любом A n или A обозначается как градус (или размер ). Разница между цепными и коцепными комплексами состоит в том, что в цепных комплексах дифференциалы уменьшают размерность, тогда как в коцепных комплексах они увеличивают размерность. Все концепции и определения цепных комплексов применимы к коцепным комплексам, за исключением того, что они будут следовать этому другому соглашению для измерения, и часто термины будут иметь префикс co-. В этой статье будут даны определения для цепных комплексов, когда различение не требуется.

A комплекс с ограниченной цепью - это комплекс, в котором почти все A n равны 0; то есть конечный комплекс, расширенный влево и вправо на 0. Примером является цепной комплекс, определяющий симплициальную гомологию конечного симплициального комплекса. Цепной комплекс ограничен выше, если все модули выше некоторой фиксированной степени N равны 0, и ограничен ниже, если все модули ниже некоторой фиксированной степени равны 0. Ясно, что комплекс ограничен и сверху и снизу тогда и только тогда, когда комплекс ограничен.

Элементы отдельных групп (со) цепного комплекса называются (со) цепями . Элементы в ядре d называются (со) циклами (или закрытыми элементами), а элементы в образе d называются (со) границами (или точные элементы). Согласно определению дифференциала, все границы являются циклами. n-я (со) группа гомологий Hn(H) - это группа (со) циклов по модулю (со) границ в степени n, то есть

H n = ker ⁡ dn им dn + 1 (ЧАС N = ker ⁡ dn им dn - 1) {\ displaystyle H_ {n} = {\ frac {\ ker d_ {n}} {{\ t_dv {im}} d_ {n + 1}}} \ quad \ left (H ^ {n} = {\ frac {\ ker d ^ {n}} {{\ t_dv {im}} d ^ {n-1}}} \ right)}

{\ displaystyle H_ {n} = {\ frac {\ ker d_ {n}} {{\ t_dv {im}} d_ {n + 1}}} \ quad \ left ( H ^ {n} = {\ frac {\ ker d ^ {n}} {{\ t_dv {im}} d ^ {n-1}}} \ right)}

Точные последовательности

точная последовательность (или точный комплекс) - это цепной комплекс, все группы гомологии которого равны нулю. Это означает, что все замкнутые элементы в комплексе точны. Короткая точная последовательность - это ограниченная точная последовательность, в которой только группы A k, A k + 1, A k + 2 может быть ненулевым. Например, следующий цепной комплекс представляет собой короткую точную последовательность.

⋯ → 0 → Z → × p Z ↠ Z / p Z → 0 → ⋯ {\ displaystyle \ cdots {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \; \ mathbf {Z} \; {\ xrightarrow {\ times p}} \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / p \ mathbf {Z} \; {\ xrightarrow {}} \; 0 \; {\ xrightarrow {} } \ cdots}

{\ displaystyle \ cdots {\ xrightarrow {}} \; 0 \; {\ xrightarrow {}} \; \ mathbf {Z } \; {\ xrightarrow {\ times p}} \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / p \ mathbf {Z} \; {\ xrightarrow {}} \; 0 \; {\ xrightarrow { }} \ cdots}

В средней группе закрытые элементы - это элементы p Z ; это явно точные элементы в этой группе.

Цепочка отображает

A карту цепочки f между двумя цепными комплексами $(A ∙, d A, ∙) {\ displaystyle (A _ {\ bullet}, d_ {A, \ bullet})}$ $(A _ {\ bullet}, d_ {A, \ bullet})$ и $(B ∙, d B, ∙) {\ displaystyle (B _ {\ bullet}, d_ {B, \ bullet})}$ $(B _ {\ bullet}, d_ {B, \ bullet})$ - последовательность $е ∙ {\ displaystyle f _ {\ bullet}}$ $f _ {\ bullet}$ гомоморфизмов $fn: A n → B n {\ displaystyle f_ {n}: A_ {n} \ rightarrow B_ {n}}$ $f_ {n}: A_ {n} \ rightarrow B_ {n}$ для каждого n, который коммутирует с граничными операторами в двух цепных комплексах, поэтому $d B, n ∘ fn = fn - 1 ∘ d A, n {\ displaystyle d_ {B, n} \ круг f_ {n} = f_ {n-1} \ circ d_ {A, n}}$ $d_ {B, n} \ circ f_ {n} = f_ {n-1} \ circ d_ {A, n}$ . Это записано в следующей коммутативной диаграмме.

Цепное отображение отправляет циклы в циклы и границы в границы, и, таким образом, индуцирует отображение на гомологии $(f ∙) ∗: H ∙ (A ∙, d A, ∙) → H ∙ (B ∙, d B, ∙) {\ displaystyle (f _ {\ bullet}) _ {*}: H _ {\ bullet} (A _ {\ bullet}, d_ {A, \ bullet}) \ rightarrow H _ {\ bullet} (B _ {\ bullet}, d_ {B, \ bullet})}$ $(f _ {\ bullet}) _ {*}: H _ {\ bullet } (A _ {\ bullet}, d_ {A, \ bullet}) \ rightarrow H _ {\ bullet} (B _ {\ bulle t}, d_ {B, \ bullet})$ .

Непрерывное отображение f между топологическими пространствами X и Y индуцирует цепное отображение между сингулярными цепными комплексами X и Y, а значит, индуцирует отображение f * между сингулярными гомологиями X и Y. Когда X и Y оба равны n-сфере, отображение, индуцированное на гомологии, определяет степень отображения f.

Концепция карты цепочки сводится к концепции границы посредством построения конуса карты цепочки.

Цепная гомотопия

Цепная гомотопия предлагает способ связать две цепные карты, которые индуцируют одно и то же отображение на группах гомологий, даже если карты могут быть разными. Для двух цепных комплексов A и B и двух цепных отображений f, g: A → B цепная гомотопия представляет собой последовательность гомоморфизмов h n : A n → B n + 1 такое, что hd A + d B h = f - g. Карты могут быть записаны на диаграмме следующим образом, но эта диаграмма не коммутативна.

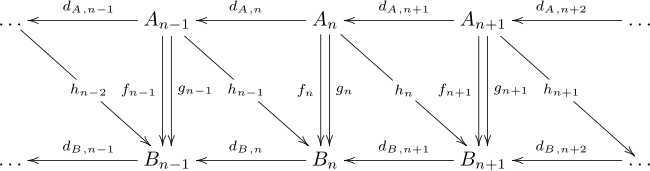
Отображение hd A + d B h легко проверяется и индуцирует нулевое отображение на гомологии для любого h. Отсюда сразу следует, что f и g индуцируют одно и то же отображение на гомологиях. Говорят, что f и g являются цепными гомотопическими (или просто гомотопическими ), и это свойство определяет отношение эквивалентности между цепными отображениями.

Пусть X и Y - топологические пространства. В случае особых гомологий гомотопия между непрерывными отображениями f, g: X → Y индуцирует цепную гомотопию между цепными отображениями, соответствующими f и g. Это показывает, что два гомотопических отображения индуцируют одно и то же отображение на особых гомологиях. Название «цепная гомотопия» мотивировано этим примером.

Примеры

Особые гомологии

Пусть X - топологическое пространство. Определите C n (X) для natural n как свободную абелеву группу, формально порожденную сингулярными n-симплексами в X, и определить граничную карту $∂ N: C n (X) → C n - 1 (X) {\ displaystyle \ partial _ {n}: C_ {n} (X) \ to C_ {n-1} (X)}$ ${\ displaystyle \ partial _ {n}: C_ {n} (X) \ to C_ {n-1} (X)}$ быть

∂ n: (σ: [v 0,…, vn] → X) ↦ ∑ i = 0 n (- 1) i (σ: [v 0,…, v ^ я,…, vn] → Икс) {\ Displaystyle \ partial _ {n}: \, (\ sigma: [v_ {0}, \ ldots, v_ {n}] \ к X) \ mapsto \ sum _ {i = 0} ^ {n} (- 1) ^ {i} (\ sigma: [v_ {0}, \ ldots, {\ hat {v}} _ {i}, \ ldots, v_ {n}] \ to X)}

{\ displaystyle \ partial _ {n}: \, (\ sigma: [v_ {0 }, \ ldots, v_ {n}] \ to X) \ mapsto \ sum _ {i = 0} ^ {n} (- 1) ^ {i} (\ sigma: [v_ {0}, \ ldots, { \ hat {v}} _ {i}, \ ldots, v_ {n}] \ to X)}

, где шляпа означает пропуск вершины . То есть граница особого симплекса - это знакопеременная сумма ограничений на его грани. Можно показать, что ∂ = 0, поэтому $(C ∙, ∂ ∙) {\ displaystyle (C _ {\ bullet}, \ partial _ {\ bullet})}$ $(C _ {\ bullet}, \ partial _ {\ bullet})$ представляет собой цепной комплекс; сингулярная гомология $H ∙ (X) {\ displaystyle H _ {\ bullet} (X)}$ $H _ {\ bullet} (X)$ является гомологией этого комплекса.

Сингулярные гомологии - полезный инвариант топологических пространств с точностью до гомотопической эквивалентности. Группа гомологий нулевой степени является свободной абелевой группой на компонентах пути X.

Когомологии де Рама

Дифференциальные k-формы на любом гладком многообразии M образуют вещественное векторное пространство, называемое Ω (M) при сложении. Внешняя производная d отображает Ω (M) в Ω (M), а d = 0 по существу следует из симметрии вторых производных, поэтому векторные пространства k-форм вместе с внешние производные представляют собой коцепной комплекс.

Ω 0 (M) → d Ω 1 (M) → Ω 2 (M) → Ω 3 (M) → ⋯ {\ displaystyle \ Omega ^ {0} (M) \ {\ stackrel {d} {\ to}} \ \ Omega ^ {1} (M) \ to \ Omega ^ {2} (M) \ to \ Omega ^ {3} (M) \ to \ cdots}

{\ displaystyle \ Omega ^ {0} (M) \ {\ stackrel {d} {\ to}} \ \ Omega ^ {1} (M) \ to \ Omega ^ {2} (M) \ to \ Omega ^ {3} (M) \ to \ cdots}

Когомологиями этого комплекса называется когомологии де Рама пространства X. Группа гомологий в размерности ноль изоморфна векторному пространству локально постоянных функций от M до R . Таким образом, для компактного многообразия это вещественное векторное пространство, размерность которого равна количеству компонент связности M.

Гладкие отображения между многообразиями индуцируют цепные отображения, а гладкие гомотопии между отображениями индуцируют цепные гомотопии.

Категория цепных комплексов

Цепные комплексы K-модулей с цепными отображениями образуют категорию ChK, где K - коммутативное кольцо.

Если V = V $∗ {\ displaystyle {} _ {*}}$ ${\ displaystyle {} _ {*}}$ и W = W $∗ {\ displaystyle {} _ {*}}$ ${\ displaystyle {} _ {*}}$ представляют собой цепные комплексы, их тензорное произведение $V ⊗ W {\ displaystyle V \ otimes W}$ $V \ otimes W$ представляет собой цепной комплекс с элементами степени n, заданными как

(V ⊗ W) n = ⨁ {i, j | я + J знак равно N} В я ⊗ W J {\ Displaystyle (V \ otimes W) _ {n} = \ bigoplus _ {\ {i, j | i + j = n \}} V_ {i} \ otimes W_ {j}}

{\ displaystyle (V \ otimes W) _ {n} = \ bigoplus _ {\ {i, j | i + j = n \}} V_ { i} \ otimes W_ {j}}

и дифференциал, равный

∂ (a ⊗ b) = ∂ a ⊗ b + (- 1) | а | a ⊗ ∂ b {\ displaystyle \ partial (a \ otimes b) = \ partial a \ otimes b + (- 1) ^ {\ left | a \ right |} a \ otimes \ partial b}

{\ displaystyle \ partial (a \ otimes b) = \ partial a \ otimes b + (- 1) ^ {\ left | a \ right |} a \ otimes \ partial b}

где a и b - любые два однородных вектора из V и W соответственно, а $| а | {\ displaystyle \ left | a \ right |}$ ${\ displaystyle \ left | a \ right |}$ обозначает степень a.

Этот тензорный продукт превращает категорию Ch K в симметричную моноидальную категорию. Тождественным объектом по отношению к этому моноидальному произведению является базовое кольцо K, рассматриваемое как цепной комплекс степени 0. Сплетение задается на простых тензорах однородных элементов как

a ⊗ b ↦ (- 1) | а | | б | b ⊗ a {\ displaystyle a \ otimes b \ mapsto (-1) ^ {\ left | a \ right | \ left | b \ right |} b \ otimes a}

{\ displaystyle a \ otimes b \ mapsto (-1) ^ {\ left | a \ right | \ left | b \ right |} b \ otimes a}

Знак необходим для плетения цепная карта.

Более того, категория цепных комплексов K-модулей также имеет внутреннее Hom : для заданных цепных комплексов V и W внутренняя Hom модулей V и W обозначается Hom (V, W), представляет собой цепной комплекс со степенью n элементов, заданных формулой $Π i Hom K (V i, W i + n) {\ displaystyle \ Pi _ {i} {\ text {Hom}} _ {K} (V_ { i}, W_ {i + n})}$ $\ Pi _ {i} {\ text {Hom}} _ {K} (V_ {i}, W_ {i + n})$ и дифференциал, заданный как

(∂ f) (v) = ∂ (f (v)) - (- 1) | f | е (∂ (v)) {\ Displaystyle (\ partial f) (v) = \ partial (f (v)) - (- 1) ^ {\ left | f \ right |} f (\ partial (v)) }

{\ Displaystyle (\ partial f) (v) = \ partial (f (v)) - (- 1) ^ {\ left | f \ right |} f (\ partial (v))}

У нас есть естественный изоморфизм

Hom (A ⊗ B, C) ≅ Hom (A, Hom (B, C)) {\ displaystyle {\ text {Hom}} (A \ otimes B, C) \ cong {\ text {Hom}} (A, {\ text {Hom}} (B, C))}

{\ text {Hom}} (A \ otimes B, C) \ cong {\ text {Hom}} (A, {\ text {Hom}} (B, C))

Дополнительные примеры

Комплекс Амицура
Комплекс, используемый для определения Высшие группы Чжоу Блоха
Комплекс Чеха
Комплекс Кошуля
Комплекс Мура

См. Также

Дифференциальная градуированная алгебра
Дифференциальная градуированная алгебра Ли
Соответствие Дольда – Кана говорит о наличии эквивалентность категории цепных комплексов и категории симплициальных абелевых групп.
Дифференциальный градуированный модуль

Литература

Ботт, Рауль ; Ту, Лоринг В. (1982), Дифференциальные формы в алгебраической топологии, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-90613-3
Хэтчер, Аллен (2002). Алгебраическая топология. Кембридж: Издательство Кембриджского университета. ISBN 0-521-79540-0.