Точная последовательность

редактировать

Последовательность гомоморфизмов такая, что каждое ядро равно предыдущему изображению

точная последовательность понятие в математике, особенно в теории групп, кольце и модульной теории, гомологической алгебре, а также как в дифференциальная геометрия. Точная последовательность - это последовательность, конечная или бесконечная, объектов и морфизмов между ними такая, что изображение одного морфизма равно ядру из следующего.

Содержание

1 Определение
- 1.1 Простые случаи
- 1.2 Короткая точная последовательность
- 1.3 Длинная точная последовательность
2 Примеры
- 2.1 Целые числа по модулю два
- 2.2 Пересечение и сумма модулей
- 2.3 Grad, curl и div в дифференциальной геометрии
3 Свойства
4 Приложения точных последовательностей
5 Ссылки
6 Внешние ссылки

Определение

В контексте теория групп, последовательность

G 0 → f 1 G 1 → f 2 G 2 → f 3 ⋯ → fn G n {\ displaystyle G_ {0} \; {\ xrightarrow {\ f_ { 1} \}} \; G_ {1} \; {\ xrightarrow {\ f_ {2} \}} \; G_ {2} \; {\ xrightarrow {\ f_ {3} \}} \; \ cdots \ ; {\ xrightarrow {\ f_ {n} \}} \; G_ {n}}

{\ displaystyle G_ {0} \; {\ xrightarrow {\ f_ {1} \}} \; G_ {1} \; {\ xrightarrow { \ f_ {2} \}} \; G_ {2} \; {\ xrightarrow {\ f_ {3} \}} \; \ cdots \; {\ xrightarrow {\ f_ {n} \}} \; G_ { n}}

из групп и групповых гомоморфизмов называется точным, если изображение каждого гомоморфизма равно ядру следующего:

im ⁡ (fk) = ker ⁡ (fk + 1) {\ displaystyle \ operatorname {im} (f_ {k}) = \ ker (f_ {k + 1})}

{\ displaystyle \ operatorname {im} ( f_ {k}) = \ ker (f_ {k + 1})}

Последовательность групп и гомоморфизмов может быть конечной или бесконечной.

Аналогичное определение может быть сделано для других алгебраических структур. Например, можно иметь точную последовательность векторных пространств и линейных отображений или модулей и гомоморфизмов модулей. В более общем плане понятие точной последовательности имеет смысл в любой категории с ядрами и cokernels.

Простыми случаями

Чтобы понять определение, нужно полезно для рассмотрения относительно простых случаев, когда последовательность конечна и начинается или заканчивается тривиальной группой. Традиционно, это, наряду с единственным единичным элементом, обозначается 0 (аддитивная запись, обычно, когда группы абелевы), или обозначается 1 (мультипликативная запись).

Рассмотрим последовательность 0 → A → B. Образ крайнего левого отображения равен 0. Следовательно, последовательность точна тогда и только тогда, когда крайнее правое отображение (от A до B) имеет ядро {0}; т.е. если и только если это отображение является мономорфизмом (инъективным или взаимно однозначным).
Рассмотрим двойственную последовательность B → C → 0. Ядро самого правого отображения есть C. Следовательно, последовательность точна тогда и только тогда, когда изображение крайнего левого отображения (от B до C) полностью совпадает с C; т.е., если и только если это отображение является эпиморфизмом (сюръективным или на).
Следовательно, последовательность 0 → X → Y → 0 точна тогда и только тогда, когда отображение из X в Y является одновременно мономорфизмом и эпиморфизмом (то есть биморфизмом ) и, таким образом, во многих случаях, изоморфизмом из X в Y.

Краткая точная последовательность

Важными являются короткие точные последовательности, которые представляют собой точные последовательности вида

0 → A → f B → g C → 0 {\ displaystyle 0 \ to A \; {\ xrightarrow {\ f \}} \; B \; {\ xrightarrow {\ g \}} \; C \ to 0}

{\ displaystyle 0 \ к A \; {\ xrightarrow {\ f \}} \; B \; {\ xrightarrow {\ g \}} \; C \ to 0}

Как установлено выше, для любой такой короткой точной последовательности f является мономорфизмом и g - эпиморфизм. Кроме того, образ f равен ядру g. Полезно думать об A как о подобъекте объекта B с f, встраивающем A в B, и о C как о соответствующем факторном объекте (или частном ), B / A, с g индуцирует изоморфизм

C ≅ B / im ⁡ (f) {\ displaystyle C \ cong B / \ operatorname {im} (f)}

{\ displaystyle C \ cong B / \ operatorname {im} (f)}

Короткая точная последовательность

0 → A → f B → g C → 0 {\ displaystyle 0 \ to A \; {\ xrightarrow {\ f \}} \; B \; {\ xrightarrow {\ g \}} \; C \ to 0}

{\ displaystyle 0 \ к A \; {\ xrightarrow {\ f \}} \; B \; {\ xrightarrow {\ g \}} \; C \ to 0}

называется разделите, если существует гомоморфизм h: C → B такой, что композиция g ∘ h является тождественным отображением на C. Отсюда следует, что если это абелевы группы, B изоморфна прямой сумме из A и C (см. лемму о расщеплении ):

B ≅ A ⊕ C. {\ displaystyle B \ cong A \ oplus C.}

B\cong A\oplus C.

Длинная точная последовательность

A длинная точная последовательность - это точная последовательность, состоящая из более чем трех ненулевых членов, часто бесконечная точная последовательность.

Длинная точная последовательность

A 0 → f 1 A 1 → f 2 A 2 → f 3 ⋯ → fn A n {\ displaystyle A_ {0} \; {\ xrightarrow {\ f_ {1 } \}} \; A_ {1} \; {\ xrightarrow {\ f_ {2} \}} \; A_ {2} \; {\ xrightarrow {\ f_ {3} \}} \; \ cdots \; {\ xrightarrow {\ f_ {n} \}} \; A_ {n}}

{\ displaystyle A_ {0} \; {\ xrightarrow {\ f_ {1} \}} \; A_ {1} \; {\ xrightarrow {\ f_ {2} \}} \; A_ {2} \; {\ xrightarrow {\ f_ {3} \}} \ ; \ cdots \; {\ xrightarrow {\ f_ {n} \}} \; A_ {n}}

эквивалентно последовательности коротких точных последовательностей

A 0 → K 1 → 0, 0 → K 1 → A 1 → К 2 → 0, ⋮ 0 → К n - 1 → A n - 1 → К n → 0, 0 → К n → A n {\ displaystyle {\ begin {align} A_ {0} \; \ rightarrow \; K_ {1} \; \ rightarrow \; 0 \;, \\ 0 \; \ rightarrow \; K_ {1} \ rightarrow {} A_ {1} \; \ rightarrow \; K_ {2} \; \ rightarrow \; 0 \;, \\\ vdots \, \, \, \, \\ 0 \; \ rightarrow \; K_ {n-1} \ rightarrow {} A_ {n-1} \ rightarrow \; K_ {n} \ ; \ rightarrow \; 0 \;, \\ 0 \; \ rightarrow K_ {n} \ rightarrow {} A_ {n} \ end {align}}}

{\ displaystyle {\ begin {align} A_ {0} \; \ rightarrow \; K_ {1} \; \ rightarrow \; 0 \;, \\ 0 \; \ rightarrow \; K_ {1} \ rightarrow {} A_ {1} \; \ rightarrow \; K_ {2} \; \ rightarrow \; 0 \;, \\\ vdots \, \, \, \, \\ 0 \; \ rightarrow \; K_ {n-1} \ rightarrow {} A_ {n-1} \ rightarrow \; K_ {n} \; \ rightarrow \; 0 \;, \\ 0 \; \ rightarrow K_ {n} \ rightarrow {} A_ {n} \ end {align}}}

где $K i = im ⁡ (fi) = ker ⁡ (fi + 1) {\ displaystyle K_ {i} = \ operatorname {im} (f_ {i}) = \ ker (f_ {i + 1})}$ ${\ displaystyle K_ {i} = \ operatorname { im} (е_ {я}) = \ ker (f_ {я + 1})}$ для каждого $i {\ displaystyle i}$ $i$ .

Примеры

Целые числа по модулю два

Рассмотрим следующую последовательность абелевых групп :

Z ↪ 2 × Z ↠ Z / 2 Z {\ displaystyle \ mathbf {Z} \; \; {\ overset {2 \ times} {\ hookrightarrow}} \; \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / 2 \ mathbf {Z}}

{\ displaystyle \ mathbf {Z} \; \; {\ overset {2 \ times} {\ hookrightarrow}} \; \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / 2 \ mathbf {Z}}

Первый гомоморфизм отображает каждый элемент i в наборе целых чисел Z на элемент 2i в Z . Второй гомоморфизм отображает каждый элемент i в Z на элемент j в фактор-группе, т. Е. J = i mod 2. Здесь стрелка-крючок $↪ {\ displaystyle \ hookrightarrow}$ $\ hookrightarrow$ указывает, что карта 2 × от Z до Z является мономорфизмом, а двунаправленная стрелка $↠ {\ displaystyle \ twoheadrightarrow}$ $\ twoheadrightarrow$ указывает на эпиморфизм (мод 2 карты). Это точная последовательность, потому что образ 2 Z мономорфизма является ядром эпиморфизма. По сути, «ту же» последовательность можно записать как

2 Z ↪ Z ↠ Z / 2 Z {\ displaystyle 2 \ mathbf {Z} \; \; {\ hookrightarrow} \; \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / 2 \ mathbf {Z}}

{\ displaystyle 2 \ mathbf {Z } \; \; {\ hookrightarrow} \; \; \ mathbf {Z} \ twoheadrightarrow \ mathbf {Z} / 2 \ mathbf {Z}}

В этом случае мономорфизм равен 2n ↦ 2n, и, хотя он выглядит как тождественная функция, он не включен (то есть не эпиморфизм), потому что нечетные числа не Не принадлежит 2 Z . Однако изображение 2 Z посредством этого мономорфизма является точно таким же подмножеством Z, что и изображение от Z до n ↦ 2n, использованное в предыдущей последовательности. Эта последняя последовательность действительно отличается конкретной природой своего первого объекта от предыдущей, поскольку 2 Z не то же самое, что и Z, даже несмотря на то, что эти два изоморфны как группы.

Первая последовательность также может быть записана без использования специальных символов для мономорфизма и эпиморфизма:

0 → Z ⟶ 2 × Z ⟶ Z / 2 Z → 0 {\ displaystyle 0 \; \ to \; \ mathbf {Z} \; \; {\ overset {2 \ times} {\ longrightarrow}} \; \; \ mathbf {Z} \; \ longrightarrow \; \ mathbf {Z} / 2 \ mathbf {Z} \; \ to \; \ 0}

{\ displaystyle 0 \; \ to \; \ mathbf {Z} \; \; {\ overset {2 \ times} {\longrightarrow }}\;\;\mathbf {Z} \;\longrightarrow \;\mathbf {Z} /2\mathbf {Z} \;\to \;\ 0}

Здесь 0 обозначает тривиальную группу, отображение из Z в Z - это умножение на 2, а отображение из Z к группе факторов Z/2Zдается путем уменьшения целых чисел по модулю 2. Это действительно точная последовательность:

изображение карты 0 → Z - это {0}, и ядро умножения на 2 также {0}, поэтому последовательность точна с первого Z.
изображение умножения на 2 равно 2 Z, и ядро уменьшения по модулю 2 также равно 2 Z, поэтому последовательность точна на втором Z.
изображении приведения по модулю 2 составляет Z/2Z, и ядро нулевого отображения также Z/2Z, поэтому последовательность точна в позиции Z/2Z.

Первая и третья последовательности являются своего рода частным случаем из-за бесконечной природы Z . Конечная группа не может быть отображена включением (т. Е. Мономорфизмом) как собственная подгруппа. Вместо этого последовательность, которая вытекает из первой теоремы об изоморфизме, следующая:

1 → N → G → G / N → 1 {\ displaystyle 1 \ to N \ to G \ to G / N \ to 1}

1 \ to N \ to G \ to G / N \ to 1

В качестве более конкретного примера точной последовательности на конечных группах:

1 → C n → D 2 n → C 2 → 1 {\ displaystyle 1 \ to C_ {n} \ to D_ {2n} \ to C_ {2} \ to 1}

1 \ на C _ {n} \ к D_ {2n} \ к C_ {2} \ to 1

где $C n {\ displaystyle C_ {n}}$ $C_ {n}$ - это циклическая группа порядка n и $D 2 n {\ displaystyle D_ {2n}}$ $D _ {{2n}}$ - это группа диэдра порядка 2n, которая является неабелевой группой.

Пересечение и сумма модулей

Пусть I и J два идеала кольца R. Тогда

0 → I ∩ J → I ⊕ J → I + J → 0 {\ displaystyle 0 \ to I \ cap J \ to I \ oplus J \ to I + J \ to 0}

{\ displaystyle 0 \ to I \ cap J \ to I \ oplus J \ to I + J \ to 0}

- точная последовательность R-модулей, где гомоморфизм модулей $I ∩ J → I ⊕ J {\ displaystyle I \ cap J \ to I \ oplus J}$ ${\ displaystyle I \ cap J \ to I \ oplus J}$ отображает каждый элемент x из $I ∩ J {\ displaystyle I \ cap J}$ $I \ cap J$ к элементу $(x, x) {\ displaystyle (x, x)}$ ${\ displaystyle (x, x)}$ из прямой суммы $I ⊕ J {\ displaystyle I \ oplus J}$ ${\ displaystyle I \ oplus J}$ , а homomorphsim $I ⊕ J → I + J {\ displaystyle I \ oplus J \ to I + J}$ ${\ displaystyle I \ oplus J \ to I + J}$ отображает каждый элемент $(x, y) {\ displaystyle (x, y)}$ $(x, y)$ из $I ⊕ J {\ displaystyle I \ oplus J}$ ${\ displaystyle I \ oplus J}$ до $x - y {\ displaystyle xy}$ $xy$ .

Эти гомоморфизмы являются ограничениями гомоморфизмов, определенных аналогичным образом, которые образуют короткую точную последовательность

0 → R → R ⊕ R → R → 0 {\ displaystyle 0 \ на R \ на R \ oplus R \ на R \ на 0}

{\ displaystyle 0 \ to R \ to R \ oplus R \ to R \ to 0}

Переход к модулям коэффициентов yield другая точная последовательность

0 → R / (I ∩ J) → R / I ⊕ R / J → R / (I + J) → 0 {\ displaystyle 0 \ to R / (I \ cap J) \ to R / I \ oplus R / J \ to R / (I + J) \ to 0}

{\ displaystyle 0 \ к R / (I \ cap J) \ к R / I \ oplus R / J \ к R / (I + J) \ to 0}

Grad, curl и div в дифференциальной геометрии

Другой пример может быть получен из дифференциальной геометрии, особенно актуально для работы над уравнениями Максвелла.

Рассмотрим гильбертово пространство $L 2 {\ displaystyle L ^ {2}}$ $L ^ {2}$ скалярнозначных интегрируемые с квадратом функции в трех измерениях ${f: R 3 → R} {\ displaystyle \ left \ lbrace f: \ mathbb {R} ^ {3} \ to \ mathbb {R} \ right \ rbrace}$ ${\ displaystyle \ left \ lbrace f: \ mathbb {R} ^ {3} \ to \ mathbb {R} \ right \ rbrace}$ . Принятие градиента функции $f ∈ H 1 {\ displaystyle f \ in \ mathbb {H} _ {1}}$ ${\ displaystyle f \ in \ mathbb {H} _ {1}}$ перемещает нас к подмножеству $H 3 {\ displaystyle \ mathbb {H} _ {3}}$ ${\ displaystyle \ mathbb {H} _ {3}}$ , пространство векторнозначных, все еще интегрируемых с квадратом функций в той же области ${f: R 3 → R 3} { \ displaystyle \ left \ lbrace f: \ mathbb {R} ^ {3} \ to \ mathbb {R} ^ {3} \ right \ rbrace}$ ${\ displaystyle \ left \ lbrace f: \ mathbb {R} ^ {3} \ to \ mathbb {R} ^ {3} \ right \ rbrace}$ - в частности, набор таких функций, которые представляют консервативные векторные поля. (Обобщенная теорема Стокса сохранила интегрируемость.)

Во-первых, обратите внимание, что curl всех таких полей равен нулю - поскольку

curl ⁡ (grad ⁡ е) ≡ ∇ × (∇ е) знак равно 0 {\ Displaystyle {\ begin {выровнено} \ operatorname {curl} (\ operatorname {grad} f) \ эквив \ набла \ раз (\ набла f) = 0 \ конец {выровнено}}}

{\ displaystyle {\ begin {align} \ operatorname {curl} (\ operatorname {grad} f) \ Equiv \ nabla \ times ( \ набла f) = 0 \ конец {выровнено}}}

для всех таких f. Однако это только доказывает, что изображение градиента является подмножеством ядра локона. Чтобы доказать, что они на самом деле являются одним и тем же множеством, докажите обратное: если ротор векторного поля $F → {\ displaystyle {\ vec {F}}}$ ${\ vec {F}}$ равен 0, то $F → {\ displaystyle {\ vec {F}}}$ ${\ vec {F}}$ - градиент некоторой скалярной функции. Это почти сразу следует из теоремы Стокса (см. Доказательство в консервативная сила.) Тогда изображение градиента является в точности ядром локона, и так что затем мы можем принять локон в качестве нашего следующего морфизма, снова возвращая нас к (другому) подмножеству $H 3 {\ displaystyle \ mathbb {H} _ {3}}$ ${\ displaystyle \ mathbb {H} _ {3}}$ .

Аналогично, мы отмечаем, что

div ⁡ (curl ⁡ v →) ≡ ∇ ⋅ ∇ × v → знак равно 0, {\ displaystyle {\ begin {align} \ operatorname {div} (\ operatorname {curl} {\ vec {v}}) \ Equiv \ nabla \ cdot \ nabla \ times {\ vec {v}} = 0, \ end {align}}}

{\begin{aligned}\operatorname {div} (\operatorname {curl} {\vec {v}})\equiv \nabla \cdot \nabla \times {\vec {v} }=0,\end{aligned}}

, поэтому изображение завитка является подмножеством ядра дивергенции . Обратное довольно сложно:

Доказательство того, что $div ⁡ F → {\ displaystyle \ operatorname {div} {\ vec {F}}}$ ${\ displaystyle \ operatorname {div} { \ vec {F}}}$ = 0 подразумевает $F → = curl ⁡ A → {\ displaystyle {\ vec {F}} = \ operatorname {curl} {\ vec {A}}}$ ${\ displaystyle {\ vec { F}} = \ operatorname {curl} {\ vec {A}}}$ для некоторых $A → {\ displaystyle {\ vec {A}} }$ ${\ vec {A}}$
Мы продолжим построение: дано векторное поле $F → = F xi ^ + F yj ^ + F zk ^ {\ displaystyle {\ vec {F}} = F_ {x} {\ hat { i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}}}$ ${\ displaystyle {\ vec {F}} = F_ {x} {\ hat { i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}}}$ такой, что $∇ ⋅ F → = 0 {\ displaystyle \ nabla \ cdot {\ vec {F}} = 0}$ ${\ displaystyle \ nabla \ cdot {\ vec {F}} = 0}$ , мы создаем поле $A → {\ displaystyle {\ vec {A}}}$ ${\ vec {A}}$ такое, что $∇ × A → = (∂ y A z - ∂ z A y) i ^ + (∂ z A x - ∂ x A z) j ^ + (∂ x A y - ∂ y A x) k ^ = F xi ^ + F yj ^ + F zk ^ = F → {\ displaystyle {\ begin {align} \ nabla \ times {\ vec {A}} = \ left (\ partial _ {y} A_ {z} - \ partial _ {z} A_ {y} \ right) {\ hat {i}} + \ left (\ partial _ {z} A_ {x} - \ partial _ {x} A_ {z} \ right) {\ hat {j }} + \ left (\ partial _ {x} A_ {y} - \ partial _ {y} A_ {x} \ right) {\ hat {k}} \\ = F_ {x} {\ hat {i } } + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}} = {\ vec {F}} \ end {align}}}$ ${\ displaystyle {\ begin {align} \ nabla \ times { \ vec {A}} = \ left (\ partial _ {y} A_ {z} - \ partial _ {z} A_ {y} \ right) {\ hat {i}} + \ left (\ partial _ { z} A_ {x} - \ partial _ {x} A_ {z} \ right) {\ hat {j}} + \ left (\ partial _ {x} A_ {y} - \ partial _ {y} A_ { x} \ right) {\ hat {k}} \\ = F_ {x} {\ hat {i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k} } = {\ vec {F}} \ end {align}}}$ Во-первых, обратите внимание, что, поскольку, как доказано выше $curl ⁡ (grad ⁡ f) = 0 {\ displaystyle \ operatorname {curl} (\ operatorname {grad} f) = 0}$ ${\ displaystyle \ operatorname {curl} (\ operatorname {grad} f) = 0}$ , мы можем добавить градиент любой скалярной функции к $A → {\ displaystyle {\ vec {A}}}$ ${\ vec {A}}$ без изменения завитка. Мы можем использовать эту свободу калибровки, чтобы установить любой компонент $A → {\ displaystyle {\ vec {A}}}$ ${\ vec {A}}$ на ноль без изменения его локона; выбирая произвольно z-компоненту, мы, таким образом, просто требуем, чтобы $- ∂ z A yi ^ + ∂ z A xj ^ + (∂ x A y - ∂ y A x) k ^ = F xi ^ + F yj ^ + F zk ^ {\ displaystyle - \ partial _ {z} A_ {y} {\ hat {i}} + \ partial _ {z} A_ {x} {\ hat {j}} + \ left (\ partial _ { x} A_ {y} - \ partial _ {y} A_ {x} \ right) {\ hat {k}} = F_ {x} {\ hat {i}} + F_ {y} {\ hat {j} } + F_ {z} {\ hat {k}}}$ ${\ displaystyle - \ partial _ {z} A_ { y} {\ hat {i}} + \ partial _ {z} A_ {x} {\ hat {j}} + \ left (\ partial _ {x} A_ {y} - \ partial _ {y} A_ { x} \ right) {\ hat {k}} = F_ {x} {\ hat {i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}}}$ Затем, просто интегрировав первые два компонента и отметив, что «константа» интегрирования все еще может зависеть от любой переменной, не интегрированной, мы находим, что $A x знак равно ∫ F ydz + C 1 → (x, y) A y = - ∫ F xdz + C 2 → (x, y) {\ displaystyle {\ begin {align} A_ {x} = \ int F_ {y} dz + {\ vec {C_ {1}}} (x, y) \\ A_ {y} = - \ int F_ {x} dz + {\ vec {C_ {2}}} (x, y) \ end {align}}}$ ${\ displaystyle {\ begin {align} A_ {x} = \ int F_ {y} dz + {\ vec { C_ {1}}} (x, y) \\ A_ {y} = - \ int F_ {x} dz + {\ vec {C_ {2}}} (x, y) \ end {align}}}$ Обратите внимание, что, поскольку два члена интеграции $C 1 →, C 2 → {\ displaystyle {\ vec {C_ {1}}}, {\ vec {C_ {2}} }}$ ${\ displaystyle {\ vec {C_ {1}}}, {\ vec {C_ {2}}}}$ оба зависят только от x и y, а не от z, тогда мы можем добавить еще один градиент некоторой функции $f (x, y) {\ displaystyle f (x, y)}$ $f (x, y)$ , что также не зависит от конец на z. Это позволяет нам исключить один из терминов в пользу другого, не нарушая нашу предыдущую работу, которая установила $A z {\ displaystyle A_ {z}}$ $A_z$ равным нулю. Выбирая для удаления $C 2 → {\ displaystyle {\ vec {C_ {2}}}}$ ${\ displaystyle {\ vec {C_ {2}}}}$ и применяя последний компонент в качестве ограничения, мы имеем $- ∂ x ∫ F xdz + ∂ Икс C 1 → (x, y) - ∂ Y ∫ F ydz = F Z - ∫ (∂ x F x + ∂ y F y) dz + ∂ x C 1 → (x, y) = F z {\ displaystyle {\ begin {align} - \ partial _ {x} \ int F_ {x} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) - \ partial _ {y} \ int F_ {y} dz = F_ {z} \\ - \ int \ left (\ partial _ {x} F_ {x} + \ partial _ {y} F_ {y} \ right) dz + \ partial _ {x} { \ vec {C_ {1}}} (x, y) = F_ {z} \ end {align}}}$ ${\ displaystyle {\ begin {align} - \ partial _ {x} \ int F_ {x} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) - \ partial _ {y} \ int F_ {y} dz = F_ {z} \\ - \ int \ left (\ partial _ {x} F_ {x} + \ partial _ {y} F_ {y} \ right) dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) = F_ {z} \ end {align}}}$ По предположению, $div ⁡ F → = ∂ x F x + ∂ y F y + ∂ Z F Z знак равно 0 {\ displaystyle \ operatorname {div} {\ vec {F}} = \ partial _ {x} F_ {x} + \ partial _ {y} F_ {y} + \ partial _ {z } F_ {z} = 0}$ ${\ displaystyle \ operatorname {div} {\ vec {F}} = \ partial _ { x} F_ {x} + \ partial _ {y} F_ {y} + \ partial _ {z} F_ {z} = 0}$ , и поэтому $∫ ∂ z F zdz + ∂ x C 1 → (x, y) = F z {\ displaystyle \ int \ partial _ {z} F_ {z} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) = F_ {z}}$ ${\ displaystyle \ int \ частичный _ {z} F_ {z} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) = F_ {z}}$ Поскольку основная теорема исчисления требует, чтобы первый член выше должен быть в точности $F z {\ displaystyle F_ {z}}$ $F_ {z}$ плюс константа в z, решение Приведенная выше система уравнений гарантированно существует.

Доказательство того, что

div ⁡ F → {\ displaystyle \ operatorname {div} {\ vec {F}}}

{\ displaystyle \ operatorname {div} { \ vec {F}}}

= 0 подразумевает

F → = curl ⁡ A → {\ displaystyle {\ vec {F}} = \ operatorname {curl} {\ vec {A}}}

{\ displaystyle {\ vec { F}} = \ operatorname {curl} {\ vec {A}}}

для некоторых

A → {\ displaystyle {\ vec {A}} }

{\ vec {A}}

Мы продолжим построение: дано векторное поле

F → = F xi ^ + F yj ^ + F zk ^ {\ displaystyle {\ vec {F}} = F_ {x} {\ hat { i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}}}

{\ displaystyle {\ vec {F}} = F_ {x} {\ hat { i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}}}

такой, что

∇ ⋅ F → = 0 {\ displaystyle \ nabla \ cdot {\ vec {F}} = 0}

{\ displaystyle \ nabla \ cdot {\ vec {F}} = 0}

, мы создаем поле

A → {\ displaystyle {\ vec {A}}}

{\ vec {A}}

такое, что

∇ × A → = (∂ y A z - ∂ z A y) i ^ + (∂ z A x - ∂ x A z) j ^ + (∂ x A y - ∂ y A x) k ^ = F xi ^ + F yj ^ + F zk ^ = F → {\ displaystyle {\ begin {align} \ nabla \ times {\ vec {A}} = \ left (\ partial _ {y} A_ {z} - \ partial _ {z} A_ {y} \ right) {\ hat {i}} + \ left (\ partial _ {z} A_ {x} - \ partial _ {x} A_ {z} \ right) {\ hat {j }} + \ left (\ partial _ {x} A_ {y} - \ partial _ {y} A_ {x} \ right) {\ hat {k}} \\ = F_ {x} {\ hat {i } } + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}} = {\ vec {F}} \ end {align}}}

{\ displaystyle {\ begin {align} \ nabla \ times { \ vec {A}} = \ left (\ partial _ {y} A_ {z} - \ partial _ {z} A_ {y} \ right) {\ hat {i}} + \ left (\ partial _ { z} A_ {x} - \ partial _ {x} A_ {z} \ right) {\ hat {j}} + \ left (\ partial _ {x} A_ {y} - \ partial _ {y} A_ { x} \ right) {\ hat {k}} \\ = F_ {x} {\ hat {i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k} } = {\ vec {F}} \ end {align}}}

Во-первых, обратите внимание, что, поскольку, как доказано выше $curl ⁡ (grad ⁡ f) = 0 {\ displaystyle \ operatorname {curl} (\ operatorname {grad} f) = 0}$ ${\ displaystyle \ operatorname {curl} (\ operatorname {grad} f) = 0}$ , мы можем добавить градиент любой скалярной функции к $A → {\ displaystyle {\ vec {A}}}$ ${\ vec {A}}$ без изменения завитка. Мы можем использовать эту свободу калибровки, чтобы установить любой компонент $A → {\ displaystyle {\ vec {A}}}$ ${\ vec {A}}$ на ноль без изменения его локона; выбирая произвольно z-компоненту, мы, таким образом, просто требуем, чтобы

- ∂ z A yi ^ + ∂ z A xj ^ + (∂ x A y - ∂ y A x) k ^ = F xi ^ + F yj ^ + F zk ^ {\ displaystyle - \ partial _ {z} A_ {y} {\ hat {i}} + \ partial _ {z} A_ {x} {\ hat {j}} + \ left (\ partial _ { x} A_ {y} - \ partial _ {y} A_ {x} \ right) {\ hat {k}} = F_ {x} {\ hat {i}} + F_ {y} {\ hat {j} } + F_ {z} {\ hat {k}}}

{\ displaystyle - \ partial _ {z} A_ { y} {\ hat {i}} + \ partial _ {z} A_ {x} {\ hat {j}} + \ left (\ partial _ {x} A_ {y} - \ partial _ {y} A_ { x} \ right) {\ hat {k}} = F_ {x} {\ hat {i}} + F_ {y} {\ hat {j}} + F_ {z} {\ hat {k}}}

Затем, просто интегрировав первые два компонента и отметив, что «константа» интегрирования все еще может зависеть от любой переменной, не интегрированной, мы находим, что

A x знак равно ∫ F ydz + C 1 → (x, y) A y = - ∫ F xdz + C 2 → (x, y) {\ displaystyle {\ begin {align} A_ {x} = \ int F_ {y} dz + {\ vec {C_ {1}}} (x, y) \\ A_ {y} = - \ int F_ {x} dz + {\ vec {C_ {2}}} (x, y) \ end {align}}}

{\ displaystyle {\ begin {align} A_ {x} = \ int F_ {y} dz + {\ vec { C_ {1}}} (x, y) \\ A_ {y} = - \ int F_ {x} dz + {\ vec {C_ {2}}} (x, y) \ end {align}}}

Обратите внимание, что, поскольку два члена интеграции $C 1 →, C 2 → {\ displaystyle {\ vec {C_ {1}}}, {\ vec {C_ {2}} }}$ ${\ displaystyle {\ vec {C_ {1}}}, {\ vec {C_ {2}}}}$ оба зависят только от x и y, а не от z, тогда мы можем добавить еще один градиент некоторой функции $f (x, y) {\ displaystyle f (x, y)}$ $f (x, y)$ , что также не зависит от конец на z. Это позволяет нам исключить один из терминов в пользу другого, не нарушая нашу предыдущую работу, которая установила $A z {\ displaystyle A_ {z}}$ $A_z$ равным нулю. Выбирая для удаления $C 2 → {\ displaystyle {\ vec {C_ {2}}}}$ ${\ displaystyle {\ vec {C_ {2}}}}$ и применяя последний компонент в качестве ограничения, мы имеем

- ∂ x ∫ F xdz + ∂ Икс C 1 → (x, y) - ∂ Y ∫ F ydz = F Z - ∫ (∂ x F x + ∂ y F y) dz + ∂ x C 1 → (x, y) = F z {\ displaystyle {\ begin {align} - \ partial _ {x} \ int F_ {x} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) - \ partial _ {y} \ int F_ {y} dz = F_ {z} \\ - \ int \ left (\ partial _ {x} F_ {x} + \ partial _ {y} F_ {y} \ right) dz + \ partial _ {x} { \ vec {C_ {1}}} (x, y) = F_ {z} \ end {align}}}

{\ displaystyle {\ begin {align} - \ partial _ {x} \ int F_ {x} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) - \ partial _ {y} \ int F_ {y} dz = F_ {z} \\ - \ int \ left (\ partial _ {x} F_ {x} + \ partial _ {y} F_ {y} \ right) dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) = F_ {z} \ end {align}}}

По предположению, $div ⁡ F → = ∂ x F x + ∂ y F y + ∂ Z F Z знак равно 0 {\ displaystyle \ operatorname {div} {\ vec {F}} = \ partial _ {x} F_ {x} + \ partial _ {y} F_ {y} + \ partial _ {z } F_ {z} = 0}$ ${\ displaystyle \ operatorname {div} {\ vec {F}} = \ partial _ { x} F_ {x} + \ partial _ {y} F_ {y} + \ partial _ {z} F_ {z} = 0}$ , и поэтому

∫ ∂ z F zdz + ∂ x C 1 → (x, y) = F z {\ displaystyle \ int \ partial _ {z} F_ {z} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) = F_ {z}}

{\ displaystyle \ int \ частичный _ {z} F_ {z} dz + \ partial _ {x} {\ vec {C_ {1}}} (x, y) = F_ {z}}

Поскольку основная теорема исчисления требует, чтобы первый член выше должен быть в точности $F z {\ displaystyle F_ {z}}$ $F_ {z}$ плюс константа в z, решение Приведенная выше система уравнений гарантированно существует.

Доказав таким образом, что образ завитка и есть ядро дивергенции, этот морфизм, в свою очередь, возвращает нас в пространство, которое мы начали с $L 2 {\ displaystyle L ^ {2}}$ $L ^ {2}$ . Поскольку по определению мы попали в пространство интегрируемых функций, любую такую функцию можно (по крайней мере формально) интегрировать, чтобы создать векторное поле, дивергенция которого и является этой функцией - так что образ дивергенции - это все $L 2 {\ displaystyle L ^ {2}}$ $L ^ {2}$ , и мы можем завершить нашу последовательность:

0 → L 2 → grad H 3 → curl H 3 → div L 2 → 0 {\ displaystyle 0 \ to L ^ {2} \; \; {\ xrightarrow {\ operatorname {grad}}} \; \; \ mathbb {H} _ {3} \; \; {\ xrightarrow {\ operatorname {curl}}} \; \; \ mathbb {H} _ {3} \; \; {\ xrightarrow {\ operatorname {div}}} \; \; L ^ {2} \ to 0}

{\ displaystyle 0 \ to L ^ {2} \; \; {\ xrightarrow {\ operatorname {grad}}} \; \; \ mathbb {H} _ {3} \; \; {\ xrightarrow {\ operatorname {curl}}} \; \; \ mathbb {H} _ {3} \; \; {\ xrightarrow {\ operatorname {div}}} \; \; L ^ {2} \ to 0}

Аналогично, мы могли бы рассуждать наоборот: в односвязном пространстве векторное поле без завитков (поле в ядре завитка) всегда может быть записано как градиент скалярной функции (и таким образом находится в изображении градиента). Точно так же поле без дивергенции может быть записано как ротор другого поля. (Рассуждения в этом направлении, таким образом, используют тот факт, что трехмерное пространство топологически тривиально.)

Эта короткая точная последовательность также позволяет гораздо более короткое доказательство справедливости разложения Гельмгольца который не полагается на векторное исчисление методом перебора. Рассмотрим подпоследовательность

0 → L 2 → grad H 3 → curl im ⁡ (curl) → 0. {\ displaystyle 0 \ to L ^ {2} \; \; {\ xrightarrow {\ operatorname {grad}}} \; \; \ mathbb {H} _ {3} \; \; {\ xrightarrow {\ operatorname {curl}}} \; \; \ operatorname {im} (\ operatorname {curl}) \ to 0.}

{\ displaystyle 0 \ к L ^ {2} \; \; {\ xrightarrow {\ operatorname {grad}}} \; \; \ mathbb {H} _ {3} \; \; { \ xrightarrow {\ operatorname {cur l}}} \; \; \ operatorname {im} (\ operatorname {curl}) \ to 0.}

Поскольку дивергенция градиента является лапласианом, и поскольку гильбертово пространство квадратично интегрируемых функций может быть охвачено собственными функциями лапласиана, мы уже видим, что некоторое обратное отображение $∇ - 1: H 3 → L 2 {\ displaystyle \ nabla ^ {- 1}: \ mathbb {H} _ {3} \ to L ^ {2}}$ ${\ displaystyle \ nabla ^ {- 1}: \ mathbb {H} _ {3 } \ к L ^ {2}}$ должен существовать. Чтобы явно построить такой обратный, мы можем начать с определения векторного лапласиана

∇ 2 A → = ∇ (∇ ⋅ A →) + ∇ × (∇ × A →) {\ displaystyle \ nabla ^ {2} {\ vec {A}} = \ nabla (\ nabla \ cdot {\ vec {A}}) + \ nabla \ times (\ nabla \ times {\ vec {A}})}

{\ displaystyle \ nabla ^ {2} {\ vec {A}} = \ nabla (\ nabla \ cdot {\ vec {A}}) + \ nabla \ times (\ nabla \ times {\ vec {A}})}

Поскольку мы пытаемся построить тождественное отображение, составив некоторую функцию с градиентом, мы знаем, что в нашем случае $∇ × A → = curl ⁡ (A →) = 0 {\ displaystyle \ nabla \ times {\ vec {A}} = \ имя оператора {curl} ({\ vec {A}}) = 0}$ ${\ displaystyle \ nabla \ times {\ vec {A}} = \ operatorname {curl} ({\ vec {A}}) = 0}$ . Тогда, если мы возьмем расхождение обеих сторон,

∇ ⋅ ∇ 2 A → = ∇ ⋅ ∇ (∇ ⋅ A →) = ∇ 2 (∇ ⋅ A →) {\ displaystyle {\ begin {align} \ nabla \ cdot \ nabla ^ {2} {\ vec {A}} = \ nabla \ cdot \ nabla (\ nabla \ cdot {\ vec {A}}) \\ = \ nabla ^ {2} (\ nabla \ cdot { \ vec {A}}) \\\ end {align}}}

{\ Displaystyle {\ begin {выровнено} \ набла \ cdot \ наб la ^ {2} {\ vec {A}} = \ nabla \ cdot \ nabla (\ nabla \ cdot {\ vec {A}}) \\ = \ nabla ^ {2} (\ nabla \ cdot {\ vec {A}}) \\\ конец {выровнено}}}

мы видим, что если функция является собственной функцией векторного лапласиана, ее дивергенция должна быть собственной функцией скалярного лапласиана с тем же собственным значением. Затем мы можем построить нашу обратную функцию $∇ - 1 {\ displaystyle \ nabla ^ {- 1}}$ ${\ displaystyle \ nabla ^ {- 1}}$ , просто сломав любую функцию в $H 3 {\ displaystyle \ mathbb {H} _ {3}}$ ${\ displaystyle \ mathbb {H} _ {3}}$ в векторно-лапласовский собственный базис, масштабируя каждое значение, обратное их собственному значению, и принимая дивергенцию; действие $∇ - 1 ∘ ∇ {\ displaystyle \ nabla ^ {- 1} \ circ \ nabla}$ ${\ displaystyle \ nabla ^ {- 1} \ circ \ nabla}$ , таким образом, явно является тождеством. Таким образом, по лемме о расщеплении,

H 3 ≅ L 2 ⊕ im ⁡ (curl) {\ displaystyle \ mathbb {H} _ {3} \ cong L ^ {2} \ oplus \ operatorname {im} (\ operatorname {curl})}

{\ displaystyle \ mathbb {H} _ {3} \ cong L ^ {2} \ oplus \ operatorname {im} (\ operatorname {curl})}

или, что эквивалентно, любое интегрируемое с квадратом векторное поле на $R 3 {\ displaystyle \ mathbb {R} ^ {3}}$ $\ mathbb {R} ^ {3}$ можно разбить на сумму градиент и завиток - вот что мы намеревались доказать.

Свойства

Лемма о расщеплении утверждает, что если короткая точная последовательность

0 → A → f B → g C → 0 {\ displaystyle 0 \ to A \; {\ xrightarrow {\ f \}} \; B \; {\ xrightarrow {\ g \}} \; C \ to 0}

{\ displaystyle 0 \ к A \; {\ xrightarrow {\ f \}} \; B \; {\ xrightarrow {\ g \}} \; C \ to 0}

допускает морфизм t: B → A такой, что t ∘ f является тождество на A или морфизм u: C → B такой, что g ∘ u является тождеством на C, то B является прямой суммой A и C (для некоммутативных групп, это полупрямой продукт ). Говорят, что такая короткая точная последовательность расщепляется.

Лемма змейка показывает, как коммутативная диаграмма с двумя точными строками приводит к более длинной точной последовательности. Лемма девяти - частный случай.

лемма пяти дает условия, при которых среднее отображение в коммутативной диаграмме с точными строками длины 5 является изоморфизмом; лемма краткая пятерка является частным случаем ее применения к коротким точным последовательностям.

Важность коротких точных последовательностей подчеркивается тем фактом, что каждая точная последовательность является результатом «сплетения вместе» нескольких перекрывающихся коротких точных последовательностей. Рассмотрим, например, точную последовательность

A 1 → A 2 → A 3 → A 4 → A 5 → A 6 {\ displaystyle A_ {1} \ to A_ {2} \ to A_ {3} \ to A_ {4 } \ to A_ {5} \ to A_ {6}}

A_{1}\to A_{2}\to A_{3}\to A_{4}\to A_{5}\to A_{6}

, что означает, что существуют объекты C k в категории такие, что

C k ≅ ker ⁡ (A k → A k + 1) ≅ им ⁡ (A k - 1 → A k) {\ displaystyle C_ {k} \ cong \ ker (A_ {k} \ to A_ {k + 1}) \ cong \ operatorname {im} (A_ { k-1} \ to A_ {k})}

C_ {k} \ cong \ ker (A_ {k} \ to A_ {k + 1}) \ cong \ operatorname {im} (A_ {k-1} \ to A_ {k})

Предположим дополнительно, что коядро каждого морфизма существует и изоморфно образу следующего морфизма в последовательности:

C к ≅ коксование ⁡ (A k - 2 → A k - 1) {\ displaystyle C_ {k} \ cong \ operatorname {coker} (A_ {k-2} \ to A_ {k-1})}

C_ {k} \ cong \ operatorname {coker} (A_ {k-2} \ to A_ {k-1})

( Это верно для ряда интересных категорий, включая любую абелеву категорию, такую как абелевы группы ; но это не верно для всех категорий, допускающих точные последовательности, и, в частности, неверно для категория групп, в которой coker (f): G → H не является H / im (f), а $H / ⟨im ⁡ f⟩ H {\ displaystyle H / {\ left \ langle \ operatorname {im} f \ right \ rangle} ^ {H}}$ $H / {\ left \ langle \ operatorname {im } f \ right \ rangle} ^ {H}$ , частное H по сопряженному замыканию функции im (f).) Тогда мы получаем коммутативную диаграмму в все диагонали представляют собой короткие точные последовательности:

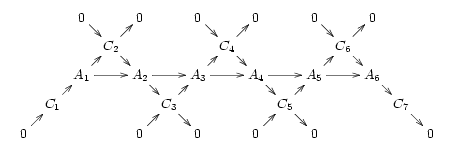
Длинные короткие точные последовательности.png

Единственная часть этой диаграммы, которая зависит от состояния коядра, - это объект $C 7 {\ textstyle C_ {7}}$ ${\ textstyle C_ {7}}$ и последняя пара морфизмов $A 6 → C 7 → 0 {\ textstyle A_ {6} \ to C_ {7} \ to 0}$ ${\ textstyle A_ {6} \ to C_ {7} \ to 0}$ . Если существует какой-либо объект $A k + 1 {\ displaystyle A_ {k + 1}}$ $A _ {{k + 1}}$ и морфизм $A k → A k + 1 {\ displaystyle A_ {k} \ to A_ {k + 1}}$ ${\ displaystyle A_ {k} \ к A_ {k + 1}}$ такой, что $A k - 1 → A k → A k + 1 {\ displaystyle A_ {k-1} \ to A_ {k} \ to A_ {k + 1}}$ ${\ displaystyle A_ {k-1} \ to A_ {k} \ to A_ {k + 1}}$ является точным, тогда точность $0 → C k → A k → C k + 1 → 0 {\ displaystyle 0 \ to C_ {k} \ to A_ {k} \ to C_ {k + 1} \ to 0}$ ${\ displaystyle 0 \ к C_ {k} \ к A_ {k} \ к C_ {k + 1} \ к 0}$ обеспечивается. Снова возьмем пример категории групп: тот факт, что im (f) является ядром некоторого гомоморфизма на H, означает, что это нормальная подгруппа, что совпадает с ее сопряженным замыканием; таким образом, coker (f) изоморфен образу H / im (f) следующего морфизма.

И наоборот, учитывая любой список перекрывающихся коротких точных последовательностей, их средние члены образуют точную последовательность таким же образом.

Приложения точных последовательностей

В теории абелевых категорий короткие точные последовательности часто используются как удобный язык для разговоров о суб- и факторных объектах.

Проблема расширения по сути является вопросом «Учитывая конечные члены A и C короткой точной последовательности, какие возможности существуют для среднего члена B?» В категории групп это эквивалентно вопросу, какие группы B имеют A как нормальную подгруппу и C как соответствующую фактор-группу? Эта проблема важна в классификации групп. См. Также Группа внешних автоморфизмов.

Обратите внимание, что в точной последовательности композиция f i + 1 ∘ f i отображает A i в 0 в A i + 2, поэтому каждая точная последовательность представляет собой цепной комплекс . Кроме того, только f i -изображения элементов A i отображаются в 0 посредством f i + 1, поэтому гомология этот цепной комплекс тривиален. Более кратко:

Точные последовательности - это в точности те цепные комплексы, которые являются ациклическими.

Для любого цепного комплекса его гомология, следовательно, может рассматриваться как мера степени, в которой он не может быть точным.

Если мы возьмем серию коротких точных последовательностей, связанных цепными комплексами (то есть короткую точную последовательность цепных комплексов или, с другой точки зрения, цепной комплекс коротких точных последовательностей), то мы можем получить из этого длинную точную последовательность (т. е. точную последовательность, индексированную натуральными числами) на гомологии, применяя зигзагообразную лемму. Он возникает в алгебраической топологии при изучении относительной гомологии ; последовательность Майера – Виеториса является другим примером. Длинные точные последовательности, индуцированные короткими точными последовательностями, также характерны для производных от функторов.

Точные функторы - это функторы, которые преобразуют точные последовательности в точные последовательности.

Ссылки

Генерал

Спаниер, Эдвин Генри (1995). Алгебраическая топология. Берлин: Springer. п. 179. ISBN 0-387-94426-5.
Эйзенбуд, Дэвид (1995). Коммутативная алгебра: взгляд на алгебраическую геометрию. Springer-Verlag New York. п. 785. ISBN 0-387-94269-6.

Цитаты

Внешние ссылки

«Точная последовательность». PlanetMath.