0,999 ... - 0.999...

Альтернативное десятичное расширение числа 1

Повторяющееся десятичное число продолжается бесконечно.

В математике, 0,999... (также записывается как 0,9, среди других способов ) обозначает повторяющееся десятичное число, состоящее из бесконечно много девяток после десятичной точки (и один 0 перед ней). Это повторяющееся десятичное число представляет наименьшее число не менее через каждое десятичное число в последовательности (0,9, 0,99, 0,999,...). Это число равно 1. Другими словами, «0,999...» и «1» представляют собой одно и то же число. Есть много способов показать это равенство, от интуитивных аргументов до математически строгих доказательств. Используемый метод зависит от целевой аудитории, исходных предположений, исторического контекста и предпочтительного развития вещественных чисел, системы, в которой обычно определяется 0,999... (В других системах 0,999... может иметь то же значение, другое определение или быть неопределенным.)

В более общем смысле, каждое ненулевое завершающее десятичное число имеет два равных представления (например,, 8.32 и 8.31999...), что является свойством всех базовых представлений. Утилитарное предпочтение завершающего десятичного представления способствует неправильному представлению о том, что это единственное представление. По этой и другим причинам - таким как строгие доказательства, основанные на неэлементарных методах, свойствах или дисциплинах - некоторые люди могут найти равенство достаточно противоречащим интуиции, чтобы подвергнуть его сомнению или отвергнуть. Это было предметом нескольких исследований в математическом образовании.

• 1 Элементарное доказательство
  • 1.1 Интуитивное объяснение
  • 1.2 Обсуждение полноты
  • 1.3 Формальное доказательство
• 2 Алгебраические аргументы
• 3 Аналитические доказательства
  • 3.1 Бесконечные ряды и последовательности
  • 3.2 Вложенные интервалы и наименьшие верхние границы
• 4 Доказательства построения действительных чисел
  • 4.1 Дедекиндовы разрезы
  • 4.2 Последовательности Коши
  • 4.3 Бесконечное десятичное представление
• 5 Обобщения
  • 5.1 Невозможность уникального представления
• 6 Приложения
• 7 Скептицизм в образовании
• 8 Культурный феномен
• 9 В альтернативных системах счисления
  • 9.1 Бесконечно малые
  • 9.2 Хакенбуш
  • 9.3 Возвращение к вычитанию
  • 9.4 p-адические числа
  • 9.5 Ультрафинитизм
• 10 Связанные вопросы
• 11 См. Также
• 12 Примечания
• 13 Ссылки
• 14 Дополнительная литература
• 15 Внешние ссылки

Архимедово свойство : любая точка x перед финишной чертой лежит между двумя точек $P\; n\; \{\backslash \; displaystyle\; P\_\; \{n\}\}$(включительно).

Существует элементарное доказательство уравнения 0.999... = 1, который использует только математические инструменты сравнения и сложения (конечных) десятичных чисел, без каких-либо ссылок на более сложные темы, такие как series, limits, формальные построение действительных чисел и т. Д. Доказательство, упражнение, данное Стиллвеллом (1994, стр. 42), является прямой формализацией интуитивного факта, что если нарисовать 0,9, 0,99, 0,999 и т. Д. На числовой строке , не останется места для размещения числа между ними и 1. Смысл обозначения 0,999... это наименьшая точка на числовой прямой, лежащая справа от всех чисел 0,9, 0,99, 0,999 и т. д. Поскольку в конечном итоге между 1 и этими числами нет места, точка 1 должна быть этой наименьшая точка, и поэтому 0,999... = 1.

Интуитивное объяснение

Если поместить 0,9, 0,99, 0,999 и т. д. на числовую строку, вы увидите сразу видно, что все эти точки находятся слева от 1 и становятся все ближе и ближе к 1.

Точнее, расстояние от 0,9 до 1 составляет 0,1 = 1/10, расстояние от 0,99 до 1 0,01 = 1/10 и так далее. Расстояние до 1 от n-й точки (то есть с n 9s после десятичной точки) составляет 1/10.

Следовательно, если бы 1 не было наименьшим числом больше 0,9, 0,99, 0,999 и т. Д., То на числовой прямой была бы точка, которая находится между 1 и всеми этими точками. Эта точка будет на положительном расстоянии от 1, которое меньше 1/10 для каждого целого числа n. В стандартной системе счисления (рациональные числа и действительные числа ) не существует положительного числа, которое меньше 1/10 для всех n. Это (одна из версий) архимедова свойства, которое можно доказать в системе рациональных чисел. Следовательно, 1 - это наименьшее число, которое больше всех 0,9, 0,99, 0,999 и т. Д., И поэтому 1 = 0,999....

Обсуждение полноты

Часть того, что этот аргумент показывает, что существует наименьшая верхняя граница последовательности 0,9, 0,99, 0,999 и т.д.: наименьшее число, которое больше всех членов последовательности. Одной из аксиом системы действительных чисел является аксиома полноты, которая утверждает, что каждая ограниченная последовательность имеет наименьшую верхнюю границу. Эта точная верхняя граница является одним из способов определения бесконечных десятичных разложений: действительное число, представленное бесконечным десятичным числом, является наименьшей верхней границей его конечных усечений. Аргумент здесь не должен предполагать, что полнота действительна, потому что он показывает, что эта конкретная последовательность рациональных чисел фактически имеет наименьшую верхнюю границу и что эта наименьшая верхняя граница равна единице.

Формальное доказательство

Предыдущее объяснение не является доказательством, так как невозможно правильно определить отношения между числом и его представлением в виде точки на числовой прямой. Для точности доказательства число 0,999... 9 с n девятками после десятичной точки обозначается 0. (9) n. Таким образом, 0. (9) 1 = 0,9, 0. (9) 2 = 0,99, 0. (9) 3 = 0,999 и т. Д. Поскольку 1/10 = 0,0... 01 с n цифрами после десятичной точки, правило сложения десятичных чисел подразумевает

$0.\; (9)\; n\; +\; 1/10\; n\; =\; 1,\; \{\backslash \; displaystyle\; 0.\; (9)\; \_\; \{n\}\; +\; 1/10\; ^\; \{n\}\; =\; 1,\}$

и

для каждого натурального числа n.

Нужно показать, что 1 - это наименьшее число, которое не меньше всех 0. (9) n. Для этого достаточно доказать, что если число x не больше 1 и не меньше всех 0. (9) n, то x = 1. Итак, пусть x такое, что

$0.\; (9)\; n\; \le \; x\; \le \; 1,\; \{\backslash \; displaystyle\; 0.\; (9)\; \_\; \{n\}\; \backslash \; leq\; x\; \backslash \; leq\; 1,\}$

для каждого положительного целого числа n. Следовательно,

$0\; \le \; 1\; -\; x\; \le \; 1\; -\; 0.\; (9)\; n\; =\; 1/10\; n.\; \{\backslash \; displaystyle\; 0\; \backslash \; leq\; 1-x\; \backslash \; leq\; 1-0.\; (9)\; \_\; \{n\}\; =\; 1/10\; ^\; \{n\}.\}$

Это означает, что разница между 1 и x меньше, чем величина, обратная любое положительное целое число. Таким образом, эта разница должна быть равна нулю, и, следовательно, x = 1; то есть

$0,999\dots \; =\; 1.\; \{\backslash \; displaystyle\; 0.999\; \backslash \; ldots\; =\; 1.\}$

Это доказательство основано на том факте, что ноль - единственное неотрицательное число, которое меньше всех обратных целых чисел, или, что то же самое, нет числа, превышающего любое целое число. Это свойство Архимеда, которое проверяется для рациональных чисел и вещественных чисел. Действительные числа могут быть увеличены до систем счисления, таких как гиперреальные числа, с бесконечно малыми числами (бесконечно малыми ) и бесконечно большими числами (бесконечными числами ). При использовании таких систем обозначение 0,999... обычно не используется, так как не существует наименьшего числа, которое было бы не меньше всех 0. (9) n. (Это подразумевается тем фактом, что 0. (9) n ≤ x < 1 implies 0.(9)n – 1 ≤ 2x - 1 < x < 1).

Дело в чрезмерной Упрощенные иллюстрации равенства являются предметом педагогических дискуссий и критики. Байерс (2007, стр. 39) обсуждает аргумент о том, что в начальной школе человека учат, что ⁄ 3 = 0,333..., поэтому, игнорируя все существенные тонкости, "умножение" этой идентичности на 3 дает 1 = 0,999.... Далее он говорит, что этот аргумент неубедителен из-за нерешенной двусмысленности в значении знак равенства ; ученик может подумать: «Это, конечно, не означает, что число 1 идентично тому, что обозначается обозначением 0,999...». Большинство студентов математических специальностей, с которыми сталкивается Байерс, считают, что 0,999... "очень близко" к 1 на основании этого аргумента, при этом некоторые даже говорят, что оно "бесконечно близко", они не готовы сказать, что оно равно 1. Richman (1999) обсуждает, как "этот аргумент его сила объясняется тем фактом, что большинству людей внушают принять первое уравнение, не задумываясь », но также предполагает, что этот аргумент может заставить скептиков усомниться в этом предположении.

Байерс также приводит следующий аргумент. Пусть

$x\; =\; 0,999\dots \; 10\; x\; =\; 9,999\dots \; путем\; «умножения»\; на\; 10\; 10\; x\; =\; 9\; +\; 0,999\dots \; путем\; «разделения»\; целой\; части\; 10\; x\; =\; 9\; +\; x\; по\; определению\; x\; 9\; x\; =\; 9\; путем\; вычитания\; xx\; =\; 1\; делением\; на\; 9\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; x\; =\; 0,999\; \backslash \; ldots\; \backslash \backslash \; 10x\; =\; 9,999\; \backslash \; ldots\; \{\backslash \; text\; \{путем\; «умножения»\; на\}\}\; 10\; \backslash \backslash \; 10x\; =\; 9\; +\; 0,999\; \backslash \; ldots\; \{\backslash \; text\; \{путем\; «отделения»\; от\; целой\; части\}\}\; \backslash \backslash \; 10x\; =\; 9\; +\; x\; \{\backslash \; text\; \{по\; определению\}\}\; x\; \backslash \backslash \; 9x\; =\; 9\; \{\backslash \; text\; \{путем\; вычитания\}\}\; x\; \backslash \backslash \; x\; =\; 1\; \{\; \backslash \; text\; \{путем\; деления\; на\}\}\; 9\; \backslash \; end\; \{align\}\}\}$

Студенты, которые не приняли первый аргумент, иногда принимают второй аргумент, но, по мнению Байерса, все еще не разрешили двусмысленность и, следовательно, принимают не понимаю представления для бесконечных десятичных знаков. Peressini Peressini (2007), представляя тот же аргумент, также заявляют, что он не объясняет равенство, указывая, что такое объяснение, вероятно, будет включать концепции бесконечности и полноты. Baldwin Norton (2012), цитируя Katz Katz (2010a), также пришли к выводу, что обращение с личностью, основанное на таких аргументах, как эти, без формальной концепции ограничения, преждевременно.

Тот же аргумент также приводится Richman (1999), который отмечает, что скептики могут сомневаться в том, отменяемо, то есть имеет ли смысл вычитать x с обеих сторон.

Поскольку вопрос о 0,999... не влияет на формальное развитие математики, его можно отложить до тех пор, пока не будут доказаны стандартные теоремы реального анализа. Одно из требований состоит в том, чтобы характеризовать действительные числа, которые могут быть записаны в десятичной системе счисления, состоящей из необязательного знака, конечной последовательности из одной или нескольких цифр, образующих целую часть, десятичного разделителя и последовательности цифр, образующих дробную часть. В целях обсуждения 0,999... целую часть можно резюмировать как b 0, а отрицательными можно пренебречь, поэтому десятичное разложение имеет форму

$b\; 0.\; б\; 1\; б\; 2\; б\; 3\; б\; 4\; б\; 5\dots .\; \{\backslash \; displaystyle\; b\_\; \{0\}.b\_\; \{1\}\; b\_\; \{2\}\; b\_\; \{3\}\; b\_\; \{4\}\; b\_\; \{5\}\; \backslash \; dots.\}$

Дробная часть, в отличие от целой, не ограничивается конечным числом цифры. Это позиционное обозначение , поэтому, например, цифра 5 из 500 дает в десять раз больше, чем 5 из 50, а 5 из 0,05 вносит вклад в одну десятую больше, чем 5 из 0,5.

Бесконечные ряды и последовательности

Возможно, наиболее распространенной разработкой десятичных разложений является определение их как сумм бесконечных рядов. В общем:

$b\; 0.\; б\; 1\; б\; 2\; б\; 3\; б\; 4\dots \; =\; б\; 0\; +\; б\; 1\; (1\; 10)\; +\; б\; 2\; (1\; 10)\; 2\; +\; б\; 3\; (1\; 10)\; 3\; +\; б\; 4\; (1\; 10)\; 4\; +\; \cdots .\; \{\backslash \; displaystyle\; b\_\; \{0\}.b\_\; \{1\}\; b\_\; \{2\}\; b\_\; \{3\}\; b\_\; \{4\}\; \backslash \; ldots\; =\; b\_\; \{0\}\; +\; b\_\; \{1\}\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; right)\; +\; b\_\; \{2\}\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; right)\; ^\; \{2\}\; +\; b\_\; \{3\}\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; right)\; ^\; \{\; 3\}\; +\; b\_\; \{4\}\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; right)\; ^\; \{4\}\; +\; \backslash \; cdots.\}$

Для 0.999... можно применить сходимость теорема о геометрическом ряду :

Если , затем $a\; r\; +\; a\; r\; 2\; +\; a\; r\; 3\; +\; \cdots \; =\; a\; r\; 1\; -\; r.\; \{\backslash \; displaystyle\; ar\; +\; ar\; ^\; \{2\}\; +\; ar\; ^\; \{3\}\; +\; \backslash \; cdots\; =\; \{\backslash \; frac\; \{ar\}\; \{1-r\}\}.\}$

Поскольку 0,999... это такая сумма с a = 9 и знаменатель r = ⁄ 10, теорема упрощает ответ на вопрос:

$0,999\dots \; =\; 9\; (1\; 10)\; +\; 9\; (1\; 10)\; 2\; +\; 9\; (1\; 10)\; 3\; +\; \cdots \; знак\; равно\; 9\; (1\; 10)\; 1–1\; 10\; =\; 1.\; \{\backslash \; displaystyle\; 0.999\; \backslash \; ldots\; =\; 9\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; right)\; +9\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{\; 10\}\}\; \backslash \; right)\; ^\; \{2\}\; +9\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; right)\; ^\; \{3\}\; +\; \backslash \; cdots\; =\; \{\backslash \; frac\; \{9\; \backslash \; left\; (\{\backslash \; tfrac\; \{1\}\; \{10\}\}\; \backslash \; right)\}\; \{1\; -\; \{\backslash \; tfrac\; \{1\}\; \{10\}\}\}\}\; =\; 1.\}$

Это доказательство появляется уже в 1770 году в статье Леонарда Эйлера Элементы алгебры.

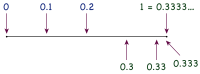Пределы: Единичный интервал, включая последовательность дробей по основанию 4 (.3,.33,.333,...), сходящуюся к 1.

Сумма геометрический ряд сам по себе является результатом даже старше Эйлера. В типичном выводе 18-го века использовались пословные манипуляции, подобные приведенному выше алгебраическому доказательству, и уже в 1811 году в учебнике Бонникасла «Введение в алгебру» такой аргумент для геометрических рядов используется для обоснования тот же маневр на 0,999... Реакция 19 века против таких либеральных методов суммирования привела к определению, которое все еще доминирует сегодня: сумма ряда определяется как предел последовательности его частичных сумм. Соответствующее доказательство теоремы явно вычисляет эту последовательность; его можно найти в любом основанном на доказательствах введении в исчисление или анализ.

A последовательность (x0, x 1, x 2,...) имеет limit x, если расстояние | x - x n | становится сколь угодно малым с увеличением n. Утверждение, что 0,999... = 1 само по себе может быть интерпретировано и доказано как предел:

$0,999\dots \; =\; def\; lim\; n\; \to \; \infty \; 0.\; 99\dots \; 9\; ⏟\; n\; =\; def\; lim\; n\; \to \; \infty \; \sum \; k\; =\; 1\; n\; 9\; 10\; к\; =\; lim\; n\; \to \; \infty \; (1\; -\; 1\; 10\; n)\; =\; 1\; -\; lim\; n\; \to \; \infty \; 1\; 10\; n\; =\; 1\; -\; 0\; =\; 1.\; \{\backslash \; displaystyle\; 0.999\; \backslash \; ldots\; \backslash \; \{\backslash \; overset\; \{\backslash \; underset\; \{\backslash \; mathrm\; \{def\}\}\; \{\}\}\; \{=\}\}\; \backslash \; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; 0.\; \backslash \; underbrace\; \{99\; \backslash \; ldots\; 9\}\; \_\; \{n\}\; \backslash \; \{\backslash \; overset\; \{\backslash \; underset\; \{\backslash \; mathrm\; \{def\}\}\; \{\}\}\; \{\; =\}\}\; \backslash \; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{9\}\; \{10\; ^\; \{k\}\}\}\; \backslash \; =\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{1\}\; \{10\; ^\; \{n\}\}\}\; \backslash \; right)\; =\; 1-\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{10\; ^\; \{n\}\}\; \}\; =\; 1\; \backslash ,\; -\; \backslash ,\; 0\; =\; 1.\}$

Первые два равенства можно интерпретировать как сокращенные определения символов. Остальные равенства доказываются. Последний шаг, ⁄ 10 → 0 при n → ∞, часто оправдывается свойством архимеда действительных чисел. Это основанное на ограничении отношение к 0,999... часто выражается в более запоминающихся, но менее точных терминах. Например, в учебнике 1846 года «Университетская арифметика» объясняется, что «0,999 + продолжается до бесконечности = 1, потому что каждое присоединение 9 приближает значение к 1»; арифметика для школ 1895 года гласит: «Когда берется большое количество девяток, разница между 1 и 0,99999... становится невероятно малой». Такая эвристика часто неправильно интерпретируется студентами как подразумевающая, что 0,999... само по себе меньше 1.

Вложенные интервалы и наименьшие верхние границы

Вложенные интервалы: по основанию 3, 1 = 1.000... = 0.222...

Приведенное выше определение ряда - это простой способ определить действительное число, названное десятичным разложением. Дополнительный подход адаптирован к противоположному процессу: для данного действительного числа определите десятичное расширение (я), чтобы назвать его.

Если известно, что действительное число x лежит в закрытом интервале [0, 10] (т. Е. Оно больше или равно 0 и меньше или равно 10), можно представить себе разделение этого интервала на десять частей, которые перекрываются только в своих конечных точках: [0, 1], [1, 2], [2, 3], и так далее до [9, 10]. Число x должно принадлежать к одному из них; если он принадлежит [2, 3], то записывается цифра «2» и этот интервал делится на [2, 2.1], [2.1, 2.2],..., [2.8, 2.9], [2.9, 3]. Продолжение этого процесса дает бесконечную последовательность вложенных интервалов, помеченных бесконечной последовательностью цифр b 0, b 1, b 2, b 3,..., и записывается

$x\; =\; b\; 0.\; b\; 1\; b\; 2\; b\; 3\dots \; \{\backslash \; displaystyle\; x\; =\; b\_\; \{0\}.b\_\; \{1\}\; b\_\; \{2\}\; b\_\; \{3\}\; \backslash \; ldots\}$

В этом формализме тождества 1 = 0,999... и 1 = 1.000... отражают, соответственно, тот факт, что 1 лежит как в [0, 1], так и в [1, 2], поэтому можно выбрать любой подинтервал при нахождении его цифр. Чтобы гарантировать, что это обозначение не злоупотребляет знаком «=», нужен способ восстановления уникального действительного числа для каждого десятичного знака. Это может быть сделано с ограничениями, но другие конструкции продолжают тему упорядочивания.

Одним из простых вариантов является теорема о вложенных интервалах, которая гарантирует, что задана последовательность вложенных, закрытых интервалов, длина которых становятся сколь угодно малыми, интервалы содержат ровно одно действительное число в их пересечении. Итак, b 0.b1b2b3... определяется как уникальный номер, содержащийся во всех интервалах [b 0, b 0 + 1], [b 0.b1, b 0.b1+ 0,1] и так далее. 0,999... тогда единственное действительное число, которое лежит во всех интервалах [0, 1], [0,9, 1], [0,99, 1] и [0,99... 9, 1] для каждой конечной строки 9с. Поскольку 1 является элементом каждого из этих интервалов, 0,999... = 1.

Теорема о вложенных интервалах обычно основана на более фундаментальной характеристике действительных чисел: существовании наименьших верхних границ или suprema. Чтобы напрямую использовать эти объекты, можно определить b 0.b1b2b3... как наименьшую верхнюю границу набора аппроксимаций {b 0, b 0.b1, b 0.b1b2,... }. Затем можно показать, что это определение (или определение вложенных интервалов) согласуется с процедурой подразделения, подразумевая снова 0,999... = 1. Том Апостол заключает:

Тот факт, что действительное число может иметь два различных десятичных представления, является просто отражением того факта, что два разных набора действительных чисел могут иметь одну и ту же верхнюю грань.

Некоторые подходы явно определяют действительные числа как определенные структуры, построенные на рациональных числах, используя аксиоматическую теорию множеств. Натуральные числа - 0, 1, 2, 3 и так далее - начинаются с 0 и продолжаются вверх, так что у каждого числа есть преемник. Можно расширить натуральные числа с их отрицательными числами, чтобы получить все целые числа, и расширить до соотношений, получив рациональные числа. Эти системы счисления сопровождаются арифметикой сложения, вычитания, умножения и деления. Более тонко, они включают упорядочивание, так что одно число можно сравнить с другим и найти, что оно меньше, больше или равно другому числу.

Шаг от рациональных чисел к действительным - серьезное расширение. Есть по крайней мере два популярных способа достижения этого шага, оба опубликованные в 1872 году: Дедекинд сокращает и последовательности Коши. Доказательства того, что 0,999... = 1, которые напрямую используют эти конструкции, не встречаются в учебниках по реальному анализу, где современной тенденцией последних нескольких десятилетий является использование аксиоматического анализа. Даже когда предлагается конструкция, она обычно применяется для доказательства аксиом действительных чисел, которые затем подтверждают приведенные выше доказательства. Тем не менее, некоторые авторы высказывают идею, что начало конструкции более логично, а полученные доказательства более самодостаточны.

Дедекинд сокращает

В вырезке Дедекинда, каждое действительное число x определяется как бесконечный набор всех рациональных чисел, меньших x. В частности, действительное число 1 - это набор всех рациональных чисел, которые меньше 1. Каждое положительное десятичное разложение легко определяет разрез Дедекинда: набор рациональных чисел, которые меньше некоторой стадии разложения. Итак, действительное число 0,999... - это набор рациональных чисел r таких, что r < 0, or r < 0.9, or r < 0.99, or r is less than some other number of the form

$1\; -\; 1\; 10\; n\; =\; 0.\; (9)\; n\; =\; 0.\; 99\dots \; 9\; ⏟\; n\; девяток.\; \{\backslash \; displaystyle\; 1\; -\; \{\backslash \; frac\; \{1\}\; \{10\; ^\; \{n\}\}\}\; =\; 0.\; (9)\; \_\; \{n\}\; =\; 0.\; \backslash \; underbrace\; \{99\; \backslash \; ldots\; 9\}\; \_\; \{n\; \{\backslash \; text\; \{nines\}\}\; \}.\}$

Каждый элемент 0,999... меньше 1, поэтому он является элементом действительного числа 1. И наоборот, все элементы 1 являются рациональными числами, которые можно записать как

с b>0 и b>a. Отсюда следует

$1\; -\; ab\; =\; b\; -\; ab\; \ge \; 1\; b>1\; 10\; b,\; \{\backslash \; displaystyle\; 1\; -\; \{\backslash \; frac\; \{a\}\; \{b\}\}\; =\; \{\backslash \; frac\; \{ba\}\; \{b\}\}\; \backslash \; geq\; \{\backslash \; frac\; \{1\}\; \{b\}\}>\{\backslash \; frac\; \{1\}\; \{10\; ^\; \{b\}\}\},\}$

и, следовательно,

и поскольку

по определению выше, каждый элемент 1 также является элементом 0,999..., и, в сочетании с доказательством выше, каждый элемент 0,999... также является элементом 1, наборы 0,999... и 1 содержат одинаковые рациональные числа и, следовательно, являются одним и тем же набором, то есть 0,999... = 1.

Определение действительных чисел как сокращений Дедекинда было впервые опубликовано Ричардом Дедекиндом в 1872 году. Вышеупомянутый подход к присвоению действительного числа каждому десятичному расширению обусловлен пояснительной статьей под названием «Is 0.999... = 1? »Фреда Ричмана в журнале Mathematics Magazine, предназначенном для учителей. университетской математики, особенно на младшем / старшем уровне, и их ученики. Ричман отмечает, что использование Дедекинда сокращений в любом плотном подмножестве рациональных чисел дает те же результаты; в частности, он использует десятичные дроби, для которых доказательство является более непосредственным. Он также отмечает, что обычно определения позволяют {x: x < 1 } to be a cut but not { x : x ≤ 1 } (or vice versa) "Why do that? Precisely to rule out the existence of distinct numbers 0.9* and 1. [...] So we see that in the traditional definition of the real numbers, the equation 0.9* = 1 is built in at the beginning." A further modification of the procedure leads to a different structure where the two are not equal. Although it is consistent, many of the common rules of decimal arithmetic no longer hold, for example the fraction ​⁄3не иметь представления; см. «Альтернативные системы счисления » ниже.

Последовательности Коши

Другой подход - определить действительное число как предел последовательности Коши рациональных чисел . Эта конструкция действительных чисел использует упорядочение рациональных чисел менее прямо. Во-первых, расстояние между x и y определяется как абсолютное значение | x - y |, где абсолютное значение | z | определяется как максимум z и -z, поэтому никогда не бывает отрицательным. Затем действительные числа определяются как последовательности рациональных чисел, которые имеют свойство последовательность Коши, использующее это расстояние. То есть в последовательности (x 0, x 1, x 2,...) отображение натуральных чисел в рациональные числа для любых положительных рационального δ существует такое N, что | x m - x n | ≤ δ для всех m, n>N. (Расстояние между членами становится меньше любого положительного рационального числа.)

Если (x n) и (y n) - две последовательности Коши, то они определены быть равным действительным числам, если последовательность (x n - y n) имеет предел 0. Усечения десятичного числа b 0.b1b2b3... генерируют последовательность рациональных чисел который является Коши; это используется для определения действительного значения числа. Таким образом, в этом формализме задача состоит в том, чтобы показать, что последовательность рациональных чисел

$(1\; -\; 0,\; 1\; -\; 9\; 10,\; 1\; -\; 99\; 100,\dots )\; =\; (1,\; 1\; 10,\; 1\; 100,\dots )\; \{\backslash \; displaystyle\; \backslash \; left\; (1-0,1-\; \{9\; \backslash \; over\; 10\},\; 1-\; \{99\; \backslash \; over\; 100\},\; \backslash \; dots\; \backslash \; right)\; =\; \backslash \; left\; (1,\; \{1\; \backslash \; over\; 10\},\; \{1\; \backslash \; over\; 100\},\; \backslash \; dots\; \backslash \; right)\}$

имеет предел 0. Таким образом, учитывая n-й член последовательности для n ∈ ℕ, нужно показать, что

$lim\; n\; \to \; \infty \; 1\; 10\; n\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{n\; \backslash \; rightarrow\; \backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{10\; ^\; \{n\}\}\}\; =\; 0.\}$

Этот предел очевиден, если кто-то понимает определение для limit. Итак, снова 0,999... = 1.

Определение действительных чисел как последовательностей Коши было впервые опубликовано отдельно Эдуардом Гейне и Георгом Кантором, также в 1872 году. Вышеупомянутый подход к десятичным разложениям, включая доказательство того, что 0,999... = 1, во многом повторяет работу Гриффитса и Хилтона 1970 г. «Всеобъемлющий учебник классической математики: современная интерпретация». Книга написана специально, чтобы предложить второй взгляд на знакомые концепции в современном свете.

Бесконечное десятичное представление

Обычно в средних школах математическое образование вещественные числа создаются путем определения числа с использованием целого числа, за которым следует точка счисления и бесконечная последовательность, записанная в виде строки, представляющей дробную часть любого заданного действительного числа. В этой конструкции набор любой комбинации целого числа и цифр после десятичной точки (или десятичной системы счисления в системах с основанием не 10) является набором действительных чисел. Можно строго показать, что эта конструкция удовлетворяет всем действительным аксиомам после определения отношения эквивалентности на множестве, которое определяет 1 = eq 0,999... а также для любых других ненулевых десятичных знаков с конечным числом ненулевых членов в десятичной строке с ее завершающей 9-й версией. При такой конструкции вещественных чисел все доказательства утверждения «1 = 0,999...» можно рассматривать как неявно предполагающие равенство, когда какие-либо операции выполняются с действительными числами.

Результат 0,999... = 1 легко обобщается двумя способами. Во-первых, каждое ненулевое число с конечной десятичной записью (эквивалентно бесконечным завершающим нулем) имеет аналог с конечными девятками. Например, 0,24999... равно 0,25, как и в рассматриваемом частном случае. Эти числа являются в точности десятичными дробями, и они плотные.

Во-вторых, сопоставимая теорема применяется к каждому основанию системы счисления или основанию. Например, в системе счисления по основанию 2 (двоичная система счисления ) 0,111... равно 1, а по основанию 3 (троичная система счисления ) 0,222... равно 1. В общем случае, любое завершающее выражение с основанием b имеет аналог с повторяющимися конечными цифрами, равными b - 1. Учебники реального анализа, вероятно, пропустят пример 0,999... и представят одно или оба этих обобщения с самого начала.

Альтернативные представления 1 также встречаются в нецелочисленных основаниях. Например, в базе золотого сечения два стандартных представления - это 1.000... и 0.101010..., и существует бесконечно много других представлений, которые включают смежные единицы. Как правило, для почти всех q между 1 и 2 существует несчетное количество разложений по основанию q для 1. С другой стороны, все еще существует несчетное количество q (включая все натуральные числа больше 1), для которых есть только одно разложение 1 по основанию q, кроме тривиального 1.000.... Этот результат был впервые получен Полем Эрдёшем, Миклошом Хорватом и Иштваном Джо примерно в 1990 году. В 1998 году Вилмос Коморник и Паола Лорети определила наименьшую такую ​​базу, постоянную Коморника – Лорети q = 1,787231650.... В этой базе 1 = 0,11010011001011010010110011010011...; цифры задаются последовательностью Туэ – Морзе, которая не повторяется.

Более далеко идущее обобщение обращается к наиболее общим позиционным системам счисления. У них тоже есть множественные представления, и в некотором смысле трудности еще хуже. Например:

• В сбалансированной тройной системе, ⁄ 2 = 0,111... = 1. 111....
• В обратной факториальной системе счисления (с использованием оснований 2!, 3!, 4!,... для позиций после десятичной точки), 1 = 1.000... = 0.1234....

Невозможность уникального представления

То, что все эти разные системы счисления страдают от множественных представлений некоторых действительных чисел, можно объяснить фундаментальным различием между действительными числами как упорядоченным набором и наборами бесконечных строк символов, упорядоченных лексикографически. Действительно, следующие два свойства объясняют сложность:

• Если интервал из действительных чисел разделен на две непустые части L, R, так что каждый элемент L (строго) меньше, чем каждый элемент R, то либо L содержит наибольший элемент, либо R содержит наименьший элемент, но не оба.
• Набор бесконечных строк символов, взятых из любого конечного «алфавита», лексикографически упорядоченного, можно разделить на две непустые части L, R, так что каждый элемент L меньше, чем каждый элемент R, в то время как L содержит наибольший элемент и R содержит наименьший элемент. Действительно, достаточно взять два конечных префикса (начальные подстроки) p 1, p 2 элементов из коллекции, которые отличаются только своим конечным символом, для какого символа они имеют последовательные значения и принимают в качестве L набор всех строк в коллекции, чей соответствующий префикс не превышает p 1, а для R остаток - строки в коллекции, чей соответствующий префикс не меньше p 2. Тогда L имеет наибольший элемент, начиная с p 1 и выбирая наибольший доступный символ во всех следующих позициях, в то время как R имеет наименьший элемент, полученный путем следования p 2 наименьшим символом в все позиции.

Первый пункт следует из основных свойств действительных чисел: L имеет верхнюю грань, а R имеет нижнюю грань, которые, как легко заметить, равны; будучи действительным числом, оно либо лежит в R, либо в L, но не в обоих, поскольку предполагается, что L и R не пересекаются. Вторая точка обобщает пару 0,999... / 1 ​​000..., полученную для p 1 = "0", p 2 = "1". Фактически нет необходимости использовать один и тот же алфавит для всех позиций (так, чтобы, например, можно было включить смешанные системы счисления ) или рассматривать полный набор возможных строк; единственные важные моменты заключаются в том, что в каждой позиции можно выбрать конечный набор символов (который может даже зависеть от предыдущих символов) (это необходимо для обеспечения максимального и минимального выбора), и что выполнение правильный выбор для любой позиции должен привести к действительной бесконечной строке (поэтому нельзя допускать «9» в каждой позиции, запрещая бесконечную последовательность «9» с). При этих предположениях приведенный выше аргумент показывает, что отображение , сохраняющее из набора строк в интервал действительных чисел, не может быть биекцией : либо некоторые числа не соответствуют никаким строка, или некоторые из них соответствуют более чем одной строке.

Марко Петковшек доказал, что для любой позиционной системы, которая называет все действительные числа, множество действительных чисел с несколькими представлениями всегда плотно. Он называет доказательство «поучительным упражнением в элементарной точечной топологии »; он включает в себя просмотр наборов позиционных значений как Каменные пространства и замечание, что их реальные представления задаются непрерывными функциями.

Одно приложение 0.999... как представление из 1 встречается в элементарной теории чисел. В 1802 году Х. Гудвин опубликовал наблюдение о появлении девяток в повторяющемся десятичном представлении дробей, знаменателями которых являются некоторые простые числа. Примеры включают:

• ​⁄7= 0,142857 и 142 + 857 = 999.
• ​⁄73= 0,01369863 и 0136 + 9863 = 9999.

E. Миди доказал общий результат о таких дробях, который теперь называется теоремой Миди, в 1836 году. Публикация была неясной, и неясно, связано ли его доказательство напрямую с 0,999..., но по крайней мере одно современное доказательство WG Ливитт знает. Если можно доказать, что если десятичное число вида 0.b 1b2b3... является положительным целым числом, то оно должно быть 0,999..., что в таком случае является источником девяток в теореме. Исследования в этом направлении могут мотивировать такие понятия, как наибольшие общие делители, модульная арифметика, простые числа Ферма, порядок группы элементов и квадратичная взаимность.

Позиции ⁄ 4, ⁄ 3 и 1 в наборе Кантора

Возвращение к реальному Анализ, аналог base-3 0,222... = 1 играет ключевую роль в характеристике одного из простейших фракталов, средних третей множества Кантора :

• Точка в единичный интервал лежит в наборе Кантора тогда и только тогда, когда он может быть представлен в троичном виде, используя только цифры 0 и 2.

n-я цифра представления отражает положение точки на n-м этапе конструкция. Например, точке ⁄ 3 дается обычное представление 0,2 или 0,2000..., так как она находится справа от первого удаления и слева от каждого последующего удаления. Точка ⁄ 3 представлена ​​не как 0,1, а как 0,0222..., поскольку она находится слева от первого удаления и справа от каждого последующего удаления.

Повторяющиеся девятки также появляются в еще одной работе Георга Кантора. Они должны быть приняты во внимание для построения действительного доказательства, применяя его диагональный аргумент 1891 года к десятичным разложениям, несчетности единичного интервала. Такое доказательство должно иметь возможность объявлять определенные пары действительных чисел разными на основе их десятичных разложений, поэтому нужно избегать пар, таких как 0,2 и 0,1999... Простой метод представляет все числа с неограничивающими расширениями; противоположный метод исключает повторение девяток. Вариант, который может быть ближе к исходному аргументу Кантора, на самом деле использует основание 2, и, превратив расширения с основанием 3 в расширения с основанием 2, можно также доказать несчетность множества Кантора.

Студенты-математики часто отвергают равенство 0,999... и 1 по причинам, варьирующимся от их несопоставимого внешнего вида до глубоких опасений по поводу концепции limit и разногласий по поводу природы бесконечно малых. Есть много общих факторов, способствующих путанице:

• Студенты часто «мысленно привержены представлению о том, что число может быть представлено одним и только одним способом с помощью десятичной дроби». Увидеть два явно разных десятичных знака, представляющих одно и то же число, кажется парадоксом, который усиливается появлением, казалось бы, хорошо понятного числа 1.
• Некоторые ученики интерпретируют «0,999... "(или аналогичное обозначение) как большая, но конечная строка из девяток, возможно, переменной, неопределенной длины. Если они примут бесконечную последовательность девяток, они все равно могут ожидать последних 9 «на бесконечности».
• Интуиция и неоднозначное обучение заставляют студентов думать о пределе последовательности как о некоем бесконечном процессе, а не о фиксированное значение, так как последовательность не должна достигать своего предела. Если учащиеся принимают разницу между последовательностью чисел и ее пределом, они могут читать «0,999...» как означающее последовательность, а не ее предел.

Эти идеи ошибочны в контексте стандартных действительных чисел, хотя некоторые могут быть действительными в других системах счисления, изобретенных для их общей математической полезности или в качестве поучительных контрпримеров для лучшего понимания 0,999...

Многие из этих объяснений были найдены Дэвидом Толл, изучивший особенности обучения и познания, которые привели к некоторым недопониманиям, с которыми он столкнулся у студентов своего колледжа. Опрашивая своих студентов, чтобы определить, почему подавляющее большинство изначально отвергало равенство, он обнаружил, что «студенты продолжали воспринимать 0,999... как последовательность чисел, приближающихся к единице, а не фиксированное значение, потому что« у вас нет » указывает, сколько там знаков 'или' это ближайшее возможное десятичное число ниже 1 '".

Элементарный аргумент умножения 0,333... = ⁄ 3 на 3 может убедить неохотно студенты, что 0,999... = 1. Тем не менее, столкнувшись с конфликтом между своей верой в первое уравнение и неверием во второе, некоторые студенты либо начинают не верить в первое уравнение, либо просто разочаровываются. Не являются надежными и более сложные методы: студенты, полностью способные применять строгие определенные ионы могут по-прежнему прибегать к интуитивным изображениям, когда их удивляет результат продвинутой математики, включая 0,999.... Например, один настоящий студент-аналитик смог доказать, что 0,333... = ⁄ 3 используя определение supremum, но затем настаивал на том, что 0,999... < 1 based on her earlier understanding of long division. Others still are able to prove that ​⁄3 = 0,333..., но, столкнувшись с дробным доказательством, настаивал эта «логика» заменяет математические вычисления.

Джозеф Мазур рассказывает историю о своем блестящем ученике по математике, который «подвергал сомнению почти все, что я сказал в классе, но никогда не подвергал сомнению свой калькулятор», и который пришел к выводу, что девять цифр - это все, что нужно сделать математики, включая вычисление квадратного корня из 23. Студент по-прежнему недоволен ограничивающим аргументом, что 9,99... = 10, называя это «дико воображаемым бесконечным процессом роста».

Как часть математической работы Эда Дубинского обучения, он и его сотрудники (2005) предполагают, что студенты, которые представляют 0,999... как конечную неопределенную строку с бесконечно малым расстоянием от 1, «еще не построили полную концепцию процесса бесконечной десятичной дроби». Другие студенты, у которых есть полная концепция процесса 0,999... могут еще не быть в состоянии «инкапсулировать» этот процесс в «концепцию объекта», например, концепцию объекта 1, и поэтому они видят процесс 0,999... и объект 1 как несовместимый. Дубинский и др. также связывают эту умственную способность инкапсуляции с рассмотрением ⁄ 3 как самостоятельного числа и с работой с множеством натуральных чисел в целом.

С появлением Интернета дебаты о 0,999... стали обычным явлением в группах новостей и досках сообщений, в том числе многим, у которых номинально мало общего с математикой. В группе новостей sci.math споры по поводу 0,999... описываются как «популярный вид спорта», и это один из вопросов, на который дан ответ в FAQ. В FAQ кратко рассматриваются ⁄ 3, умножение на 10 и ограничения, а также упоминаются последовательности Коши.

Выпущенная в 2003 году газетная колонка The Straight Dope обсуждает 0,999... через ⁄ 3 и ограничения, говоря о заблуждениях,

Низший примат в нас все еще сопротивляется, говоря:.999 ~ на самом деле не число, а процесс. Чтобы найти число, мы должны остановить процесс, и тогда 0,999 ~ = 1 развалится. Вздор.

A В статье Slate сообщается, что концепция 0.999... "горячо оспаривается на веб-сайтах, от досок объявлений World of Warcraft до форумов Айн Рэнд ". Точно так же вопрос о 0,999... оказался такой популярной темой в первые семь лет форумов Blizzard Entertainment Battle.net, которые компания выпустила в "прессу". release »в День дураков 2004, что 1:

Мы очень рады закрыть книгу на эту тему раз и навсегда. Мы стали свидетелями душевной боли и беспокойства по поводу того, равно ли.999 ~ 1 или нет, и мы гордимся тем, что следующее доказательство окончательно и окончательно решает проблему для наших клиентов.

Затем предлагаются два доказательства, основанные на ограничения и умножение на 10.

0,999... также присутствует в математических анекдотах, например:

Q: Сколько математиков нужно, чтобы вкрутить лампочку ?

A: 0,999999....

Хотя действительные числа образуют чрезвычайно полезную систему счисления, решение интерпретировать обозначение «0,999... ", поскольку наименование действительного числа в конечном итоге является условием, и Тимоти Гауэрс утверждает в« Математике: очень краткое введение », что полученное в результате тождество 0,999... = 1 также является условным:

Однако, это ни в коем случае не произвольное соглашение, потому что его непринятие вынуждает либо изобретать новые странные объекты, либо отказываться от некоторых из знакомых правил арифметики.

Можно определить использовать другие системы счисления, используя другие правила или новые объекты; в некоторых таких системах счисления приведенные выше доказательства нужно будет переосмыслить, и можно будет обнаружить, что в данной системе счисления 0,999... и 1 могут не совпадать. Однако многие системы счисления являются расширениями, а не независимыми альтернативами действительной системе счисления, поэтому 0,999... = 1 остается в силе. Однако даже в таких системах счисления стоит изучить альтернативные системы счисления не только на предмет того, как ведет себя 0,999... (если, действительно, число, выраженное как «0,999...», является значимым и однозначным), но и для поведения связанных явлений. Если такие явления отличаются от явлений в действительной системе счисления, то по крайней мере одно из допущений, встроенных в систему, должно быть нарушено.

Бесконечно малые

Некоторые доказательства того, что 0,999... = 1 основаны на свойстве Архимеда действительных чисел: нет ненулевых бесконечно малых. В частности, разность 1 - 0,999... должна быть меньше любого положительного рационального числа, поэтому она должна быть бесконечно малой; но поскольку действительные числа не содержат ненулевых бесконечно малых чисел, разница, следовательно, равна нулю, и, следовательно, два значения совпадают.

Однако существуют математически согласованные упорядоченные алгебраические структуры, включая различные альтернативы действительным числам, которые не являются архимедовыми. Нестандартный анализ предоставляет систему счисления с полным набором бесконечно малых (и их обратных). A. Х. Лайтстон разработал десятичное разложение для гиперреальных чисел в (0, 1). Lightstone показывает, как связать с каждым числом последовательность цифр,

$0.\; d\; 1\; d\; 2\; d\; 3\dots ;\; \dots \; D\; \infty \; -\; 1\; d\; \infty \; d\; \infty \; +\; 1\dots ,\; \{\backslash \; displaystyle\; 0.d\_\; \{1\}\; d\_\; \{2\}\; d\_\; \{3\}\; \backslash \; dots;\; \backslash \; dots\; d\; \_\; \{\backslash \; infty\; -1\}\; d\; \_\; \{\backslash \; infty\}\; d\; \_\; \{\backslash \; infty\; +1\}\; \backslash \; dots,\}$

проиндексировано сверхъестественными числами. Хотя он прямо не обсуждает 0,999..., он показывает, что действительное число ⁄ 3 представлено 0,333...;... 333... что является следствием переноса принцип. Как следствие, число 0,999...;... 999... = 1. В этом типе десятичного представления не каждое раскрытие представляет собой число. В частности, «0,333...;... 000...» и «0,999...;... 000...» не соответствуют никаким числам.

Стандартное определение числа 0,999... это предел последовательности 0,9, 0,99, 0,999,... Другое определение включает то, что Терри Тао называется сверхпределом, то есть классом эквивалентности [(0.9, 0.99, 0.999,...)] этой последовательности в сверхмощной конструкции, которая является числом, которое на бесконечно малую величину меньше 1. В более общем смысле, гиперреалистическое число u H = 0,999...;... 999000... с последней цифрой 9 с бесконечным сверхъестественным рангом H удовлетворяет строгому неравенству u H< 1. Accordingly, an alternative interpretation for "zero followed by infinitely many 9s" could be

$0.\; 999\dots \; ⏟\; H\; =\; 1\; -\; 1\; 10\; H.\; \{\backslash \; displaystyle\; \{\backslash \; underset\; \{H\}\; \{0.\; \backslash \; underbrace\; \{999\; \backslash \; ldots\}\}\}\; \backslash ;\; =\; 1\; \backslash ;\; -\; \backslash ;\; \{\backslash \; frac\; \{1\}\; \{10\; ^\; \{H\}\}\}.\}$

Все такие интерпретации «0,999...» бесконечно близки к 1. Ян Стюарт характеризует эту интерпретацию как «вполне разумный» способ строго оправдать интуицию о том, что «немного не хватает» от 1 из 0,999..... Наряду с Katz Katz, Роберт Эли также подвергает сомнению предположение, что представления студентов о 0,999... < 1 are erroneous intuitions about the real numbers, interpreting them rather as nonstandard intuitions that could be valuable in the learning of calculus. Jose Benardete in his book Infinity: An essay in metaphysics argues that some natural pre-mathematical intuitions cannot be expressed if one is limited to an overly restrictive number system:

Разборчивость континуума была обнаружена - много раз - чтобы требовать, чтобы область действительных чисел была увеличены, чтобы включать бесконечно малые. Эту расширенную область можно назвать областью континуальных чисел. Теперь будет очевидно, что.9999... не равно 1, но бесконечно меньше его. Я думаю, что.9999... действительно следует принять как число... хотя и не как действительное число.

Хакенбуш

Комбинаторная теория игр также предлагает альтернативные действительные числа с бесконечным сине-красным Хакенбуш в качестве одного особенно подходящего примера. В 1974 году Элвин Берлекамп описал соответствие между строками Хакенбуша и двоичными разложениями действительных чисел, мотивированными идеей сжатия данных. Например, значение строки Hackenbush LRRLRLRL... равно 0,010101 2... = ⁄ 3. Однако значение LRLLL... (соответствующее 0,111... 2) бесконечно меньше 1. Разница между ними - сюрреалистическое число ​⁄ω, где ω - это первый бесконечный порядковый номер ; соответствующая игра - LRRRR... или 0,000... 2.

Фактически это верно для двоичных разложений многих рациональных чисел, где значения чисел равны, но соответствующие пути двоичного дерева различны. Например, 0.10111... 2 = 0.11000... 2, которые оба равны 3/4, но первое представление соответствует пути двоичного дерева LRLRLLL... в то время как второй соответствует другому пути LRLLRRR....

Возвращение к вычитанию

Другой способ, которым доказательства могут быть подорваны, - если 1 - 0,999... просто не существует, потому что вычитание не всегда возможно. Математические структуры с операцией сложения, но не операцией вычитания, включают коммутативные полугруппы, коммутативные моноиды и полукольца. Ричман рассматривает две такие системы, разработанные так, что 0,999... < 1.

Во-первых, Ричман определяет неотрицательное десятичное число как буквальное десятичное расширение. Он определяет лексикографический порядок и операцию сложения, отмечая, что 0,999... < 1 simply because 0 < 1 in the ones place, but for any nonterminating x, one has 0.999... + x = 1 + x. So one peculiarity of the decimal numbers is that addition cannot always be cancelled; another is that no decimal number corresponds to ​⁄3. После определения умножения десятичные числа образуют положительное, полностью упорядоченное коммутативное полукольцо.

В процессе определения умножения Ричман также определяет другую систему, которую он называет «вырезать D», которая представляет собой набор Дедекинд отсекает десятичных дробей. Обычно это определение приводит к действительным числам, но для десятичной дроби d он допускает как сокращение (−∞, d), так и «основное сокращение» (−∞, d]. В результате действительные числа «живут нелегко. вместе с «десятичными дробями. Снова 0,999... < 1. There are no positive infinitesimals in cut D, but there is "a sort of negative infinitesimal," 0, which has no decimal expansion. He concludes that 0.999... = 1 + 0, while the equation "0.999... + x = 1" has no solution.

p-адические числа

На вопрос о 0,999... новички часто полагают, что должно быть« конечное число 9 », полагая, что 1 - 0,999... быть положительным числом, которое они записывают как "0,000... 1". Независимо от того, имеет ли это смысл, интуитивная цель ясна: добавление 1 к последним 9 в 0,999... 9 на 0 и оставьте 1 на месте. Среди других причин эта идея не срабатывает, потому что в 0,999 нет "последней 9".... Однако есть система, которая содержит бесконечную строку 9, включая последнюю 9.

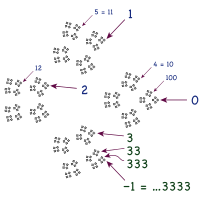4-адические целые числа (черные точки), включая последовательность (3, 33, 333,...), сходящуюся к -1. 10-адический аналог... 999 = -1.

p-адические числа - это альтернативная система счисления, представляющая интерес в n умбра теория. Как и действительные числа, p-адические числа могут быть построены из рациональных чисел с помощью последовательностей Коши ; конструкция использует другую метрику, в которой 0 ближе к p и намного ближе к p, чем к 1. p-адические числа образуют поле для простого p и кольцо для других p, включая 10. Значит, арифметика может выполняться в p-адиках, и бесконечно малых нет.

В 10-адических числах аналоги десятичных разложений идут влево. 10-адическое расширение... 999 имеет последние 9 и не имеет первых 9. Можно добавить 1 к разряду единиц, и после переноса останется только 0: 1 +... 999 =... 000 = 0, а значит... 999 = −1. Другой вывод использует геометрический ряд. Бесконечный ряд, подразумеваемый «... 999», не сходится в действительных числах, но он сходится в 10-адиках, поэтому можно повторно использовать знакомую формулу:

$\dots \; 999\; =\; 9\; +\; 9\; (10)\; +\; 9\; (10)\; 2\; +\; 9\; (10)\; 3\; +\; \cdots \; =\; 9\; 1\; -\; 10\; =\; -\; 1.\; \{\backslash \; displaystyle\; \backslash \; ldots\; 999\; =\; 9\; +\; 9\; (10)\; +9\; (10)\; ^\; \{2\}\; +9\; (10)\; ^\; \{3\}\; +\; \backslash \; cdots\; =\; \{\backslash \; frac\; \{9\}\; \{1-10\}\}\; =\; -\; 1.\}$

(Сравните с серией выше.) Третий вывод был изобретен семиклассница, которая сомневалась в ограничивающем аргументе своего учителя о том, что 0,999... = 1, но была вдохновлена ​​принять доказательство умножения на 10 выше в противоположном направлении: если x =... 999, то 10x =... 990, поэтому 10x = x - 9, следовательно, x = -1 снова.

В качестве окончательного расширения, поскольку 0,999... = 1 (в вещественных числах) и... 999 = −1 (в 10-адиках), то «слепая вера и беззастенчивое жонглирование символами» можно сложить два уравнения и прийти к... 999.999... = 0. Это уравнение не имеет смысла ни как 10 -адическое разложение или обычное десятичное разложение, но оно оказывается значимым и истинно в дважды бесконечном десятичном разложении 10-адического соленоида, с повторением левых концов для представления действительных чисел и в конечном итоге повторением правых концов для представления 10-адические числа.

Ультрафинитизм

Философия ультрафинитизма отвергает как бессмысленные концепции, имеющие дело с бесконечными множествами, такие как идея о том, что запись $0,999\dots \; \{\backslash \; displaystyle\; 0.999\; \backslash \; ldots\}$может означать десятичное число с бесконечной последовательностью девяток, а также суммирование бесконечного числа чисел $9/10\; +\; 9/100\; +\; \cdots \; \{\backslash \; displaystyle\; 9/10\; +\; 9/100\; +\; \backslash \; cdots\}$, соответствующие позиционным значениям десятичных цифр в этой бесконечной строке. В этом подходе к математике имеет смысл только определенное (фиксированное) количество конечных десятичных цифр. Вместо «равенства» используется «приблизительное равенство», то есть равенство до количества десятичных цифр, которое разрешено вычислять. Хотя Кац и Кац утверждают, что ультрафинитизм может уловить интуицию студента о том, что 0,999... должно быть меньше 1, идеи ультрафинитизма не получили широкого признания в математическом сообществе, а философия не имеет общепризнанного формального математического основания..

• Парадоксы Зенона, особенно парадокс бегуна, напоминают очевидный парадокс, что 0,999... и 1 равны. Парадокс бегуна можно смоделировать математически, а затем, например, 0,999..., разрешить с помощью геометрического ряда. Однако неясно, решает ли этот математический подход основные метафизические проблемы, которые исследовал Зенон.
• Деление на ноль встречается в некоторых популярных дискуссиях о 0,999..., и это также вызывает споры. В то время как большинство авторов предпочитают определять 0,999..., почти все современные методы оставляют деление на ноль неопределенным, поскольку оно не может иметь никакого значения в стандартных действительных числах. Однако деление на ноль определено в некоторых других системах, таких как комплексный анализ, где расширенная комплексная плоскость, то есть сфера Римана, имеет символ "бесконечно удаленная ". Здесь имеет смысл определить ⁄ 0 как бесконечность; и, по сути, результаты являются глубокими и применимы ко многим задачам техники и физики. Некоторые выдающиеся математики выступали за такое определение задолго до того, как была разработана какая-либо система счисления.
• Отрицательный ноль - еще одна избыточная особенность многих способов записи чисел. В системах счисления, таких как действительные числа, где «0» обозначает аддитивное тождество и не является ни положительным, ни отрицательным, обычная интерпретация «-0» заключается в том, что он должен обозначать аддитивный инверсный к 0, что вынуждает -0 = 0 Тем не менее, в некоторых научных приложениях используются отдельные положительные и отрицательные нули, как и в некоторых вычислительных двоичных системах счисления (например, целые числа, хранящиеся в формате знака , и величины или с дополнением до единиц, или плавающие числа в соответствии со стандартом IEEE для чисел с плавающей запятой ).

• Предел (математика)
• Серия (математика)
• Наивная математика
• Конечность

Слушайте эту статью Этот аудиофайл был создан на основе редакции этой статьи от 19 октября 2006 г. и не отражать последующие правки. (

• Аудиопомощь
• Другие устные статьи

)

Викискладе есть средства массовой информации, связанные с 0,999….

• .999999... = 1? из у.е. t-the-knot
• Почему 0,9999... = 1?
• Доказательство равенства на основе арифметики
• Исследование Дэвида Толла о познании математики
• Что плохого в том, чтобы считать действительные числа бесконечными? десятичные дроби?
• Теорема 0.999... о Metamath