Свойство Архимеда

редактировать

Отсутствие бесконечно малых величин в математической системе

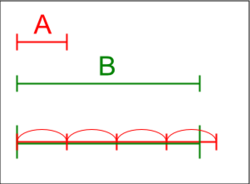
Иллюстрация свойства Архимеда.

В абстрактной алгебре и анализе, Архимедова свойство, названное в честь древнегреческого математика Архимеда из Сиракуз, является свойством некоторых алгебраических структур, таких как упорядоченные или нормированные группы и поля. Грубо говоря, это свойство не иметь бесконечно больших или бесконечно меньших элементов. Именно Отто Штольц дал название аксиоме Архимеда, потому что она появляется как Аксиома V Архимеда О сфере и цилиндре.

. Это понятие возникло из теории величин Древней Греции; он по-прежнему играет важную роль в современной математике, такой как аксиомы Дэвида Гильберта для геометрии и теории упорядоченных групп, упорядоченных полей и локальные поля.

Алгебраическая структура, в которой любые два ненулевых элемента сопоставимы в том смысле, что ни один из них не является бесконечно малым по отношению к другому, называется быть Архимедом . Структура, которая имеет пару ненулевых элементов, один из которых бесконечно мал по отношению к другому, называется неархимедовой . Например, линейно упорядоченная группа, которая является архимедовой группой, является архимедовой группой.

. Это может быть уточнено в различных контекстах с немного разными формулировками. Например, в контексте упорядоченных полей существует аксиома Архимеда, которая формулирует это свойство, где поле вещественных чисел является Архимедовым, но это рациональных функций в вещественных коэффициентах нет.

Содержание

1 История и происхождение названия архимедова свойства
2 Определение для линейно упорядоченных групп
- 2.1 Упорядоченные поля
3 Определение для нормированных полей
4 Примеры и не примеры
- 4.1 Архимедово свойство действительных чисел
- 4.2 Неархимедово упорядоченное поле
- 4.3 Поля с неархимедовым значением
- 4.4 Эквивалентные определения архимедова упорядоченного поля
5 См. Также
6 Примечания
7 Ссылки

История и происхождение названия архимедовой собственности

Концепция была названа Отто Штольцем (в 1880-х гг.) В честь древнегреческого геометр и физик Архимед из Сиракузы.

Архимедово свойство появляется в Книге V Элементов Евклида как Определение 4:

Величины, как говорят, имеют отношение к друг друга, которые при умножении могут превосходить друг друга.

Поскольку Архимед приписал это Евдоксу Книдскому, это также известно как «Теорема Евдокса» или аксиома Евдокса.

Архим des использовал бесконечно малые в эвристических аргументах, хотя он отрицал, что они были закончены математические доказательства.

Определение для линейно упорядоченных групп

Пусть x и y равны положительные элементы из линейно упорядоченной группы G. Тогда x бесконечно мал по отношению к y (или, что эквивалентно, y бесконечно мал по отношению к x ), если для каждого натурального числа n кратное nx равно меньше y, то есть выполняется следующее неравенство:

x + ⋯ + x ⏟ n терминов < y. {\displaystyle \underbrace {x+\cdots +x} _{n{\text{ terms}}}

\ underbrace {x + \ cdots + x} _ {n \ text {terms}} <y. \,

Это определение можно распространить на всю группу, взяв абсолютные значения.

Группа G является архимедовой, если не существует пары (x, y) такой, что x бесконечно мал по отношению к y.

Кроме того, если K является алгебраической структурой с единицей (1) - например, кольцо - аналогичное определение применяется к K. Если x бесконечно малая относительно 1, то x является бесконечно малым элементом . Аналогично, если y бесконечно относительно 1, то y является бесконечным элементом . Алгебраическая структура K является архимедовой, если в ней нет бесконечных элементов и бесконечно малых элементов.

Упорядоченные поля

Упорядоченные поля имеют некоторые дополнительные свойства:

Рациональные числа встроены в любое упорядоченное поле. То есть любое упорядоченное поле имеет характеристику ноль.
Если x бесконечно мал, то 1 / x бесконечно, и наоборот. Следовательно, чтобы убедиться, что поле архимедово, достаточно проверить только отсутствие бесконечно малых элементов или отсутствие бесконечных элементов.
Если x бесконечно мало и r- рациональное число, то rx также бесконечно мал. В результате, учитывая общий элемент c, три числа c / 2, c и 2c либо все бесконечно малы, либо все не бесконечно малы.

В этой настройке упорядоченное поле K является архимедовым именно тогда, когда следующее утверждение, называется аксиомой Архимеда, выполняется:

«Пусть x будет любым элементом K. Тогда существует натуральное число n такое, что n>x».

В качестве альтернативы можно использовать следующую характеристику :

∀ ε ∈ K (ε>0 ⟹ ∃ n ∈ N: 1 / n < ε). {\displaystyle \forall \,\varepsilon \in K{\big (}\varepsilon>0 \ подразумевает \ существует \ n \ in N: 1 / n <\varepsilon {\big)}.}

\forall \,\varepsilon \in K{\big (}\varepsilon>0 \ подразумевает \ существует \ n \ in N: 1 / n <\varepsilon {\big)}.

Определение для нормированных полей

Квалификатор «Архимедово» также сформулирован в теории однозначных полей и нормированных пространств над однозначными полями следующим образом. Пусть F будет полем, наделенным функцией абсолютного значения, т. Е. Функцией, которая связывает действительное число 0 с элементом поля 0 и связывает положительное действительное число $| x | {\ displaystyle | x |}$ $| x |$ с каждым ненулевым x ∈ F и удовлетворяет $| xy | = | x | | y | { \ displaystyle | xy | = | x || y |}$ $| xy | = | x | | Y |$ и $| х + у | ≤ | х | + | y | {\ displaystyle | x + y | \ leq | x | + | y |}$ $| x + y | \ le | x | + | y |$ . Тогда F называется архимедовым, если для любого ненулевого x ∈ F существует натуральное число n такое, что

| x + ⋯ + x ⏟ n терминов |>1. {\ displaystyle | \ underbrace {x + \ cdots + x} _ {n {\ text {terms}}} |>1. \,}

| \ underbrace {x + \ cdots + x} _ {n \ text {terms}} |>1. \,

Аналогично нормированный пространство архимедово, если сумма из n членов, каждое из которых равно ненулевому вектору x, имеет норму больше единицы для достаточно большого n. Поле с абсолютным значением или нормированное пространство либо архимедово, либо удовлетворяет более сильному условию, обозначенному как ультраметрическое неравенство треугольника,

| x + y | ≤ max (| x |, | y |) {\ displaystyle | x + y | \ leq \ max (| x |, | y |)}

| x + y | \ le \ max (| x |, | y |)

соответственно. Поле или нормированное пространство, удовлетворяющее ультраметрическому неравенству треугольника, называется неархимедовым .

Концепция неархимедова нормированного линейного пространства была введена А.Ф. Монной.

Примеры и непримеры

Архимедово свойство действительных чисел

Поле рациональных чисел может быть присвоено одной из ряда функций абсолютного значения, включая тривиальную функцию $| х | = 1, {\ displ aystyle | x | = 1,}$ $| x | = 1,$ когда x ≠ 0, более обычный $| х | = x 2 {\ displaystyle | x | = {\ sqrt {x ^ {2}}}}$ $| x | = \ sqrt {x ^ 2}$ , и функции p-адического абсолютного значения . Согласно теореме Островского, любое нетривиальное абсолютное значение рациональных чисел эквивалентно либо обычному абсолютному значению, либо некоторому p-адическому абсолютному значению. Поле рациональных значений не является полным относительно нетривиальных абсолютных значений; по отношению к тривиальному модулю рациональное поле является дискретным топологическим пространством, поэтому полным. Завершением относительно обычного абсолютного значения (из порядка) является поле действительных чисел. По этой конструкции поле действительных чисел архимедово и как упорядоченное, и как нормированное поле. С другой стороны, пополнения относительно других нетривиальных абсолютных значений дают поля p-адических чисел, где p - простое целое число (см. Ниже); поскольку p-адические абсолютные значения удовлетворяют свойству ultrametric, тогда поля p-адических чисел не являются архимедовыми как нормированные поля (их нельзя преобразовать в упорядоченные поля).

В аксиоматической теории действительных чисел несуществование ненулевых бесконечно малых действительных чисел подразумевается свойством наименьшей верхней границы следующим образом. Обозначим через Z множество, состоящее из всех положительных бесконечно малых. Сверху это множество ограничено 1. Теперь предположим от противоречия, что Z непусто. Тогда он имеет наименьшую верхнюю границу c, которая также положительна, поэтому c / 2 < c < 2c. Since c is an верхняя граница Z и 2c строго больше, чем c, 2c не является положительной бесконечно малой. То есть существует некоторое натуральное число n, для которого 1 / n < 2c. On the other hand, c/2 is a positive infinitesimal, since by the definition of least upper bound there must be an infinitesimal x between c/2 and c, and if 1/k < c/2 ≤ x then x is not infinitesimal. But 1/(4n) < c/2, so c/2 is not infinitesimal, and this is a contradiction. This means that Z is empty after all: there are no positive, infinitesimal real numbers.

Архимедово свойство действительных чисел сохраняется также в конструктивном анализе, даже если свойство наименьшей верхней границы может не работать в этом контексте.

Неархимедово упорядоченное поле

В качестве примера упорядоченного поля, которое не является архимедовым, возьмите поле рациональных функций с действительными коэффициентами. (Рациональная функция - это любая функция, которая может быть выражена как один полином , разделенный на другой полином; далее мы будем предполагать, что это было сделано таким образом, что старший коэффициент знаменателя положительно.) Чтобы сделать это поле упорядоченным, нужно назначить порядок, совместимый с операциями сложения и умножения. Теперь f>g тогда и только тогда, когда f - g>0, поэтому нам нужно только сказать, какие рациональные функции считаются положительными. Назовите функцию положительной, если старший коэффициент числителя положителен. (Необходимо проверить, что этот порядок правильно определен и совместим со сложением и умножением.) По этому определению рациональная функция 1 / x положительна, но меньше рациональной функции 1. Фактически, если n - любое натуральное число, то n (1 / x) = n / x положительно, но все же меньше 1, независимо от того, насколько велико n. Следовательно, 1 / x бесконечно малая величина в этом поле.

Этот пример обобщается на другие коэффициенты. Принятие рациональных функций с рациональными коэффициентами вместо действительных дает счетное неархимедово упорядоченное поле. Принимая коэффициенты как рациональные функции в другой переменной, например y, дает пример с другим типом порядка.

неархимедовозначными полями

Поле рациональных чисел, наделенных p-адическая метрика и поля p-адического числа, которые являются дополнениями, не имеют свойства Архимеда как поля с абсолютными значениями. Все поля с архимедовыми значениями изометрически изоморфны подполю комплексных чисел со степенью обычного абсолютного значения.

Эквивалентные определения упорядоченного архимедова поля

Каждое линейно упорядоченное поле K содержит (изоморфное копия) рациональных чисел как упорядоченного подполя, а именно подполя, порожденного мультипликативной единицей 1 поля K, которая, в свою очередь, содержит целые числа как упорядоченную подгруппу, которая содержит натуральные числа как упорядоченный моноид. Вложение рациональных чисел затем дает возможность говорить о рациональных числах, целых и натуральных числах в K. Ниже приведены эквивалентные характеристики архимедовых полей в терминах этих подструктур.

1. Натуральные числа - это cofinal в K. То есть каждый элемент K меньше некоторого натурального числа. (Это не тот случай, когда существует бесконечное количество элементов.) Таким образом, архимедово поле - это такое поле, натуральные числа которого неограниченно растут.

2. Ноль - это инфимум в K набора {1/2, 1/3, 1/4,...}. (Если бы K содержало положительную бесконечно малую величину, это была бы нижняя граница для множества, откуда ноль не был бы наибольшей нижней границей.)

3. Множество элементов K между положительными и отрицательными рациональными числами закрыто. Это связано с тем, что набор состоит из всех бесконечно малых, который является просто набором {0}, когда нет ненулевых бесконечно малых, и в противном случае является открытым, поскольку нет ни наименьшего, ни наибольшего ненулевых бесконечно малых. Заметим, что в обоих случаях множество бесконечно малых замкнуто. В последнем случае: (i) каждая бесконечно малая меньше любого положительного рационального, (ii) не существует ни наибольшего бесконечно малого, ни наименее положительного рационального числа, и (iii) между ними нет ничего другого. Следовательно, любое неархимедово упорядоченное поле является неполным и несвязным.

4. Для любого x в K множество целых чисел больше x имеет наименьший элемент. (Если бы x было отрицательной бесконечной величиной, каждое целое число было бы больше его.)

5. Каждый непустой открытый интервал K содержит рациональное число. (Если x является положительным бесконечно малым, открытый интервал (x, 2x) содержит бесконечно много бесконечно малых, но ни одного рационального числа.)

6. Рациональные числа плотны в K как по sup, так и по inf. (То есть каждый элемент K является sup некоторого набора рациональных чисел и inf некоторого другого набора рациональных чисел.) Таким образом, архимедово поле - это любое плотное упорядоченное расширение рациональных чисел в смысле любого упорядоченного поля, которое плотно вмещает свои рациональные элементы.

См. Также

0.999... - Альтернативное десятичное разложение числа 1
Архимедово упорядоченное векторное пространство
Построение действительных чисел - Аксиоматические определения действительного числа