 Иллюстрация диагонального аргумента Кантора (в основании 2) для существования несчетных множеств. Последовательность внизу не может встречаться в перечисленных выше последовательностях.
Иллюстрация диагонального аргумента Кантора (в основании 2) для существования несчетных множеств. Последовательность внизу не может встречаться в перечисленных выше последовательностях.  Бесконечное множество может иметь такую же мощность, как надлежащее подмножество самого по себе, как изображенным биекциям е ( х) = 2 х из натуральных к четным числам демонстрирует. Тем не менее, как показывает диагональный аргумент Кантора, существуют бесконечные множества различной мощности.
Бесконечное множество может иметь такую же мощность, как надлежащее подмножество самого по себе, как изображенным биекциям е ( х) = 2 х из натуральных к четным числам демонстрирует. Тем не менее, как показывает диагональный аргумент Кантора, существуют бесконечные множества различной мощности. В теории множеств, диагональ Кантора, также называемый диагонализация аргумент, то диагональная слэш аргумент, то анти-диагональный аргумент, то диагональный метод, и диагонализация доказательство Кантора, был опубликован в 1891 году Георгом Кантором как математическое доказательство, что существуют бесконечные множества которое нельзя поставить во взаимно однозначное соответствие с бесконечным множеством натуральных чисел. Такие множества теперь известны как несчетные множества, и размер бесконечных множеств теперь рассматривается в рамках теории кардинальных чисел, которую начал Кантор.
Диагональный аргумент не был первым доказательством Кантора несчетности действительных чисел, которое появилось в 1874 году. Однако он демонстрирует общую технику, которая с тех пор использовалась в широком диапазоне доказательств, включая первую теорему Геделя о неполноте и ответ Тьюринга. к Entscheidungsproblem. Аргументы Диагонализация часто также является источником противоречий, как парадокс Рассела и парадокс Ричарда.
В своей статье 1891 года, Кантор рассмотрел множество T всех бесконечных последовательностей из двоичных цифр (т.е. каждая цифра равна нулю или один). Он начинает с конструктивного доказательства следующей теоремы:
Доказательство начинается с перечисления элементов из T, например:
| s 1 = | (0, | 0, | 0, | 0, | 0, | 0, | 0, | ...) |
| s 2 = | (1, | 1, | 1, | 1, | 1, | 1, | 1, | ...) |
| s 3 = | (0, | 1, | 0, | 1, | 0, | 1, | 0, | ...) |
| s 4 = | (1, | 0, | 1, | 0, | 1, | 0, | 1, | ...) |
| s 5 = | (1, | 1, | 0, | 1, | 0, | 1, | 1, | ...) |
| s 6 = | (0, | 0, | 1, | 1, | 0, | 1, | 1, | ...) |
| s 7 = | (1, | 0, | 0, | 0, | 1, | 0, | 0, | ...) |
| ... |
Затем создается последовательность s, выбирая 1-ю цифру как дополнительную к 1-й цифре s 1 (заменяя 0 s на 1 с и наоборот), 2-ю цифру как дополнительную ко 2-й цифре s 2, 3-ю цифру как комплементарная 3 цифры с 3 -х, и в целом для каждого п, то п - й цифра в качестве дополнения к п й цифре с п. В приведенном выше примере это дает:
| с 1 | знак равно | ( 0, | 0, | 0, | 0, | 0, | 0, | 0, | ...) |
| с 2 | знак равно | (1, | 1, | 1, | 1, | 1, | 1, | 1, | ...) |
| с 3 | знак равно | (0, | 1, | 0, | 1, | 0, | 1, | 0, | ...) |
| с 4 | знак равно | (1, | 0, | 1, | 0, | 1, | 0, | 1, | ...) |
| с 5 | знак равно | (1, | 1, | 0, | 1, | 0, | 1, | 1, | ...) |
| с 6 | знак равно | (0, | 0, | 1, | 1, | 0, | 1, | 1, | ...) |
| с 7 | знак равно | (1, | 0, | 0, | 0, | 1, | 0, | 0, | ...) |
| ... | |||||||||
| s | знак равно | ( 1, | 0, | 1, | 1, | 1, | 0, | 1, | ...) |
По построению s отличается от каждого s n, поскольку их n- е цифры различаются (выделено в примере). Следовательно, s не может встречаться в перечислении.
Основываясь на этой теореме, Кантор затем использует доказательство от противного, чтобы показать, что:
Доказательство начинается в предположении, что T является счетным. Тогда все его элементы можно записать в виде перечисления s 1, s 2,..., s n,.... Применение предыдущей теоремы к этому перечислению дает последовательность s, не принадлежащую перечислению. Однако это противоречит тому, что s является элементом T и, следовательно, принадлежит перечислению. Это противоречие означает, что исходное предположение неверно. Следовательно, T несчетно.
Несчетность действительных чисел уже была установлена первым доказательством несчетности Кантора, но это также следует из приведенного выше результата. Чтобы доказать это, будет построена инъекция из множества T бесконечных двоичных строк в множество R действительных чисел. Поскольку T неисчислимо, образ этой функции, которая является подмножеством R, неисчислим. Следовательно, R несчетно. Кроме того, при использовании способа строительства, разработанного Cantor, A биекция будет построен между Т и R. Следовательно, T и R имеют одинаковую мощность, которая называется « мощностью континуума » и обычно обозначается или.
Инъекция из T в R осуществляется путем преобразования двоичных строк в T в десятичные дроби, например преобразования t = 0111... в десятичную дробь 0,0111.... Эта функция, определяемая как f ( t) = 0. t, является инъекция, потому что она сопоставляет разные строки с разными числами.
Построить биекцию между T и R немного сложнее. Вместо преобразования 0111... в десятичное число 0,0111... его можно преобразовать в число с основанием b: 0,0111... b. Это приводит к семейству функций: f b ( t) = 0. t b. Функции f b ( t) являются инъекционными, за исключением f 2 ( t) . Эта функция будет изменена, чтобы произвести взаимно однозначное соответствие между Т и R.
| Построение биекции между T и R |
|---|
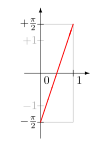 Функция h: (0,1) → (−π / 2, π / 2) Функция h: (0,1) → (−π / 2, π / 2) 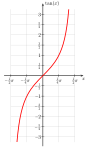 Функция tan: (−π / 2, π / 2) → R Функция tan: (−π / 2, π / 2) → R Эта конструкция использует метод, разработанный Кантором, который был опубликован в 1878 году. Он использовал его для построения взаимно однозначного соответствия между закрытым интервалом [0, 1] и иррациональными числами в открытом интервале (0, 1). Сначала он удалил счетное бесконечное подмножество из каждого из этих множеств, так что между оставшимися несчетными множествами существует взаимно однозначное соответствие. Поскольку существует взаимное соответствие между счетно бесконечными подмножествами, которые были удалены, объединение двух взаимно однозначно приводит к взаимному соответствию между исходными наборами. Метод Кантора можно использовать для изменения функции f 2 ( t) = 0. t 2 для создания взаимно однозначного соответствия от T до (0, 1). Поскольку некоторые числа имеют два двоичных разложения, f 2 ( t) даже не инъективен. Например, f 2 (1000…) = 0,1000... 2 = 1/2 и f 2 (0111…) = 0,0111... 2 = 1/4 + 1/8 + 1/16 +… = 1/2, поэтому и 1000... и 0111... отображаются на одно и то же число 1/2. Для того, чтобы изменить е 2 ( т), заметим, что это биекция для счетного подмножества (0, 1) и счетного подмножества, кроме Т. Это не биекция для чисел в (0, 1), которые имеют два двоичных разложения. Они называются двоичными числами и имеют вид m / 2 n, где m - нечетное целое число, а n - натуральное число. Поместите эти числа в последовательность: r = (1/2, 1/4, 3/4, 1/8, 3/8, 5/8, 7/8,...). Кроме того, f 2 ( t) не является взаимно однозначным соответствием (0, 1) для строк в T, появляющихся после двоичной точки в двоичных разложениях 0, 1 и чисел в последовательности r. Поместите эти окончательно константные строки в последовательность: s = ( 000..., 111..., 1 000..., 0 111..., 01 000..., 00 111..., 11 000..., 10 111...,...). Определите биекцию g ( t) от T до (0, 1): если t - n- я строка в последовательности s, пусть g ( t) будет n- м числом в последовательности r ; в противном случае g ( t) = 0. t 2. Чтобы построить биекцию от T к R, начните с касательной функции tan ( x), которая является биекцией от (−π / 2, π / 2) к R (см. Рисунок справа). Затем заметьте, что линейная функция h ( x) = π x - π / 2 является биекцией из (0, 1) в (−π / 2, π / 2) (см. Рисунок слева). Сложная функция тангенс ( ч ( х)) = тангенс (π х - π / 2) является биекцией из (0, 1) в R. Компоновка этой функции с г ( т) производит функция тангенса ( ч ( г ( т))) = тангенс (π г ( т) - π / 2), который представляет собой взаимно однозначное соответствие от Т до R. |
 Иллюстрация обобщенного диагонального аргумента: множество T = { n ∈ℕ: n ∉ f ( n)} внизу не может находиться где-либо в диапазоне f: ℕ → P (ℕ). Пример отображения f соответствует примеру перечисления s на рисунке выше.
Иллюстрация обобщенного диагонального аргумента: множество T = { n ∈ℕ: n ∉ f ( n)} внизу не может находиться где-либо в диапазоне f: ℕ → P (ℕ). Пример отображения f соответствует примеру перечисления s на рисунке выше. Обобщенная форма диагонального аргумента был использован Кантором, чтобы доказать теорему Кантора : для каждого множества S, то силовой агрегат из S, то есть, множество всех подмножеств из S (здесь записывается в виде P ( S)) - не может быть в биекция с самой S. Это доказательство происходит следующим образом:
Пусть f - любая функция из S в P ( S). Достаточно доказать, что f не может быть сюръективным. Это означает, что некоторые члены Т из Р ( S), то есть некоторое подмножество S, не является в изображении из F. В качестве кандидата рассмотрим набор:
Для каждого s в S либо s находится в T, либо нет. Если ы в Т, то по определению T, ев не в е ( ы), так что Т не равна F ( ов). С другой стороны, если s не находится в T, то по определению T, s находится в f ( s), так что снова T не равно f ( s); ср. рисунок. Более полное изложение этого доказательства см. В теореме Кантора.
Кантор определяет отношение порядка мощностей, например, и, в терминах существования инъекций между базовыми множествами, и. Аргумент в предыдущем абзаце затем доказал, что такие множества несчетны, то есть, и мы можем встроить натуральные числа в функциональное пространство, чтобы оно у нас было. В контексте классической математики, это исчерпывает возможности и диагональное аргумент, таким образом, может быть использовано для установления, что, к примеру, хотя оба рассматриваемых множества являются бесконечными, существует на самом деле более бесконечные последовательности единиц и нули, чем есть натуральные числа. Регенты результат, то также следует, что понятие множества всех множеств противоречиво: Если S были множеством всех множеств, то P ( S) будет в то же время быть больше, чем S и подмножество S.
Принимая во внимание закон исключенного среднего, каждое подсчетное множество (свойство с точки зрения сюръекций) также уже является счетным.
В конструктивной математике сложнее или невозможно упорядочить порядковые числа, а также кардиналы. Например, теорема Шредера – Бернштейна требует закона исключенной середины. Следовательно, интуиционисты не принимают теорему о кардинальном порядке. Порядок вещественных чисел (стандартный порядок, расширяющий порядок рациональных чисел) также не обязательно разрешим. Большинство свойств интересных классов функций также не являются разрешимыми по теореме Райса, т. Е. Правильный набор подсчетных чисел для подсчетных множеств может не быть рекурсивным. В теории множеств моделируются математические теории. Например, в теории множеств «набор» действительных чисел идентифицируется как набор, удовлетворяющий некоторым аксиомам действительных чисел. Были изучены различные модели, такие как реалы Дедекинда или реалы Коши. Более слабые аксиомы означают меньше ограничений и, таким образом, позволяют использовать более богатый класс моделей. Следовательно, в конструктивном контексте (закон исключенного третьего не принимается в качестве аксиомы) целесообразно принимать неклассические аксиомы, которые противоречат следствиям закона исключенного третьего. Например, можно утверждать, что несчетное пространство функций является подсчетным, понятие размера ортогонально заявлению. В таком контексте возможен подсчет всех наборов или инъекции из в.
Мотивированный пониманием того, что набор действительных чисел «больше», чем набор натуральных чисел, можно спросить, существует ли набор, мощность которого находится «между» числом целых и действительных чисел. Этот вопрос приводит к известной гипотезе континуума. Точно так же вопрос о том, существует ли множество, мощность которого находится между | S | и | P ( S) | для некоторого бесконечного S приводит к гипотезе обобщенного континуума.
Парадокс Рассела показал, что наивная теория множеств, основанная на схеме неограниченного понимания, противоречива. Обратите внимание, что есть сходство между построением T и множеством в парадоксе Рассела. Следовательно, в зависимости от того, как мы модифицируем схему понимания аксиом, чтобы избежать парадокса Рассела, такие аргументы, как несуществование набора всех наборов, могут или не могут оставаться действительными.
Аналоги диагонального аргумента широко используются в математике для доказательства существования или отсутствия определенных объектов. Например, обычное доказательство неразрешимости проблемы остановки - это, по сути, диагональный аргумент. Кроме того, диагонализация изначально использовалась, чтобы показать существование классов произвольной сложности, и сыграла ключевую роль в первых попытках доказать, что P не равно NP.
Приведенное выше доказательство не соответствует теории множеств " Новые основы " У. В. Куайна. В NF схема понимания наивных аксиом модифицируется, чтобы избежать парадоксов, вводя своего рода "локальную" теорию типов. В этой схеме аксиом
это не набор - то есть, не удовлетворяет схему аксиом. С другой стороны, мы могли бы попытаться создать модифицированный диагональный аргумент, заметив, что
это множество в NF. В этом случае, если P 1 ( S) - это множество одноэлементных подмножеств S, а f - предполагаемая биекция из P 1 ( S) в P ( S), можно использовать доказательство от противного, чтобы доказать, что | P 1 ( S) | lt;| P ( S) |.
Доказательство следует из того факта, что если бы f действительно было отображением на P ( S), то мы могли бы найти r в S, такое, что f ({ r }) совпадает с модифицированным диагональным множеством, указанным выше. Мы могли бы заключить, что если r не входит в f ({ r }), то r находится в f ({ r }), и наоборот.
Это не возможно поставить P 1 ( S) в отношении один к одному с S, как два имеют разные типы, и поэтому любой функции, определенной таким образом будут нарушать правила типизации для схемы понимания.