Отношения Максвелла

Для электромагнитных уравнений см. Уравнения Максвелла.

Термодинамика
Классическая тепловая машина Карно
ветви Классический Статистическая Химическая Квантовая термодинамика Равновесие  / Неравновесие
Законы Zeroth Первый Второй В третьих
Системы Закрытая система Изолированная система Состояние Уравнение состояния Идеальный газ Настоящий газ Состояние вопроса Фаза (материя) Равновесие Контрольный объем Инструменты Процессы Изобарический Изохорический Изотермический Адиабатический Изэнтропический Изентальпический Квазистатический Политропный Бесплатное расширение Обратимость Необратимость Необратимость Циклы Тепловые двигатели Тепловые насосы Термический КПД
Свойства системы Примечание: Сопряженные переменные в курсивом Диаграммы свойств Интенсивные и обширные свойства Функции процесса Работа Нагревать Функции государства Температура  / энтропия  ( введение ) Давление  / Объем Химический потенциал  / число частиц Качество пара Сниженные свойства
Свойства материала Базы данных недвижимости Удельная теплоемкость   ${\ displaystyle c =}$ ${\ displaystyle T}$ ${\ displaystyle \ partial S}$ ${\ displaystyle N}$ ${\ displaystyle \ partial T}$ Сжимаемость   ${\ displaystyle \ beta = -}$ ${\ displaystyle 1}$ ${\ displaystyle \ partial V}$ ${\ displaystyle V}$ ${\ displaystyle \ partial p}$ Тепловое расширение   ${\ Displaystyle \ альфа =}$ ${\ displaystyle 1}$ ${\ displaystyle \ partial V}$ ${\ displaystyle V}$ ${\ displaystyle \ partial T}$
Уравнения Теорема Карно Теорема Клаузиуса Фундаментальное отношение Закон идеального газа Максвелл отношения Взаимные отношения Онзагера Уравнения Бриджмена Таблица термодинамических уравнений
Возможности Свободная энергия Свободная энтропия
История Культура История Общий Энтропия Газовые законы Машины "вечный двигатель" Философия Энтропия и время Энтропия и жизнь Броуновская трещотка Демон Максвелла Парадокс тепловой смерти Парадокс лошмидта Синергетика Теории Теория калорийности Vis viva («живая сила») Механический эквивалент тепла Сила мотивации Ключевые публикации " Экспериментальное исследование... тепла " « О равновесии неоднородных веществ » « Размышления о движущей силе огня » Сроки Термодинамика Тепловые двигатели Изобразительное искусство Образование Термодинамическая поверхность Максвелла Энтропия как рассеивание энергии
Ученые Бернулли Больцман Карно Клапейрон Клаузиус Каратеодори Duhem Гиббс фон Гельмгольц Джоуль Максвелл фон Майер Онсагер Ренкин Смитон Шталь Томпсон Томсон ван дер Ваальс Waterston
Другой Зарождение Самостоятельная сборка Самоорганизация Порядок и беспорядок
Категория
v т е

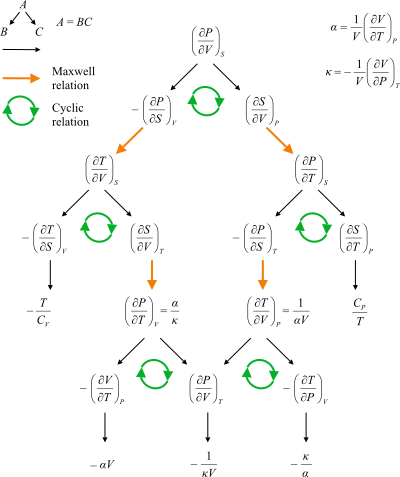
Блок-схема, показывающая пути между отношениями Максвелла. - давление, температура, объем, энтропия, коэффициент теплового расширения, сжимаемость, теплоемкость при постоянном объеме, теплоемкость при постоянном давлении.${\ displaystyle P}$${\ displaystyle T}$${\ displaystyle V}$${\ displaystyle S}$${\ displaystyle \ alpha}$ ${\ displaystyle \ kappa}$ ${\ displaystyle C_ {V}}$ ${\ displaystyle C_ {P}}$

Отношения Максвелла представляют собой набор уравнений термодинамики, которые выводятся из симметрии вторых производных и из определений термодинамических потенциалов. Эти отношения названы в честь физика девятнадцатого века Джеймса Клерка Максвелла.

• 1 Уравнения
• 2 Четыре наиболее распространенных отношения Максвелла
  • 2.1 Вывод
• 3 Вывод на основе якобианов
• 4 Общие отношения Максвелла
• 5 См. Также
• 6 Ссылки

См. Также: симметрия вторых производных

Структура соотношений Максвелла - это утверждение равенства вторых производных для непрерывных функций. Это непосредственно следует из того, что порядок дифференцирования аналитической функции двух переменных не имеет значения ( теорема Шварца ). В случае отношений Максвелла функция рассмотрен термодинамический потенциал и и являются двумя различными естественными переменными для этого потенциала, мы ${\ displaystyle x_ {i}}$${\ displaystyle x_ {j}}$

Теорема Шварца (общая)

${\ displaystyle {\ frac {\ partial} {\ partial x_ {j}}} \ left ({\ frac {\ partial \ Phi} {\ partial x_ {i}}} \ right) = {\ frac {\ partial } {\ partial x_ {i}}} \ left ({\ frac {\ partial \ Phi} {\ partial x_ {j}}} \ right)}$

где частные производные берутся с постоянными значениями всех других естественных переменных. Для каждого термодинамического потенциала существуют возможные соотношения Максвелла, где - число натуральных переменных для этого потенциала. Существенное увеличение энтропии будет проверяться согласно соотношениям, удовлетворяющим законам термодинамики. ${\ Displaystyle {\ гидроразрыва {п (п-1)} {2}}}$${\ displaystyle n}$

Четыре наиболее распространенных соотношения Максвелла - это равенства вторых производных каждого из четырех термодинамических потенциалов относительно их естественной тепловой переменной ( температуры или энтропии ) и их естественной механической переменной ( давления или объема ): ${\ displaystyle T}$ ${\ displaystyle S}$ ${\ displaystyle P}$ ${\ displaystyle V}$

Отношения Максвелла (общие)

${\ displaystyle {\ begin {align} + \ left ({\ frac {\ partial T} {\ partial V}} \ right) _ {S} amp; = amp; - \ left ({\ frac {\ partial P} { \ partial S}} \ right) _ {V} amp; = amp; {\ frac {\ partial ^ {2} U} {\ partial S \ partial V}} \\ + \ left ({\ frac {\ partial T} {\ partial P}} \ right) _ {S} amp; = amp; + \ left ({\ frac {\ partial V} {\ partial S}} \ right) _ {P} amp; = amp; {\ frac {\ partial ^ {2} H} {\ partial S \ partial P}} \\ + \ left ({\ frac {\ partial S} {\ partial V}} \ right) _ {T} amp; = amp; + \ left ({ \ frac {\ partial P} {\ partial T}} \ right) _ {V} amp; = amp; - {\ frac {\ partial ^ {2} F} {\ partial T \ partial V}} \\ - \ left ({\ frac {\ partial S} {\ partial P}} \ right) _ {T} amp; = amp; + \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {P} amp; = amp; {\ frac {\ partial ^ {2} G} {\ partial T \ partial P}} \ end {align}} \, \!}$

где потенциалы как функции их естественных тепловых и механических переменных являются внутренняя энергия, энтальпия, свободная энергия Гельмгольца, а свободная энергия Гиббса. Термодинамический квадрат может быть использован в качестве мнемонические вспомнить и вывести эти отношения. Полезность этих соотношений заключается в их количественной оценке изменений энтропии, которые нельзя измерить напрямую, с точки зрения измеримых величин, таких как температура, объем и давление. ${\ Displaystyle U (S, V)}$ ${\ Displaystyle H (S, P)}$ ${\ Displaystyle F (Т, В)}$ ${\ Displaystyle G (T, P)}$

Каждое уравнение можно переформулировать с помощью соотношения

${\ displaystyle \ left ({\ frac {\ partial y} {\ partial x}} \ right) _ {z} = 1 \ left / \ left ({\ frac {\ partial x} {\ partial y}} \ вправо) _ {z} \ right.}$

которые иногда также называют отношениями Максвелла.

Вывод

Отношения Максвелла основаны на простых правилах частичного дифференцирования, в частности, на полном дифференциале функции и симметрии вычисления частных производных второго порядка.

Вывод

Вывод соотношения Максвелла можно вывести из дифференциальных форм термодинамических потенциалов : Дифференциальная форма внутренней энергии U есть ${\ Displaystyle {\ begin {выровнено} dU amp; = TdS-PdV \\\ конец {выровнено}} \, \!}$ Это уравнение напоминает полные дифференциалы вида ${\ displaystyle dz = \ left ({\ frac {\ partial z} {\ partial x}} \ right) _ {y} \! dx + \ left ({\ frac {\ partial z} {\ partial y}} \ справа) _ {x} \! dy}$ Для любого уравнения вида можно показать, что ${\ Displaystyle dz = Mdx + Ndy \,}$ что ${\ displaystyle M = \ left ({\ frac {\ partial z} {\ partial x}} \ right) _ {y}, \ quad N = \ left ({\ frac {\ partial z} {\ partial y} } \ right) _ {x}}$ Рассмотрим уравнение. Теперь мы можем сразу увидеть, что ${\ Displaystyle dU = TdS-PdV \,}$ ${\ displaystyle T = \ left ({\ frac {\ partial U} {\ partial S}} \ right) _ {V}, \ quad -P = \ left ({\ frac {\ partial U} {\ partial V }} \ right) _ {S}}$ Поскольку мы также знаем, что для функций с непрерывными вторыми производными смешанные частные производные идентичны ( симметрия вторых производных ), то есть ${\ displaystyle {\ frac {\ partial} {\ partial y}} \ left ({\ frac {\ partial z} {\ partial x}} \ right) _ {y} = {\ frac {\ partial} {\ частичный x}} \ left ({\ frac {\ partial z} {\ partial y}} \ right) _ {x} = {\ frac {\ partial ^ {2} z} {\ partial y \ partial x}} = {\ frac {\ partial ^ {2} z} {\ partial x \ partial y}}}$ поэтому мы можем видеть, что ${\ displaystyle {\ frac {\ partial} {\ partial V}} \ left ({\ frac {\ partial U} {\ partial S}} \ right) _ {V} = {\ frac {\ partial} {\ частичное S}} \ left ({\ frac {\ partial U} {\ partial V}} \ right) _ {S}}$ и поэтому ${\ displaystyle \ left ({\ frac {\ partial T} {\ partial V}} \ right) _ {S} = - \ left ({\ frac {\ partial P} {\ partial S}} \ right) _ {V}}$ Вывод соотношения Максвелла из свободной энергии Гельмгольца. Дифференциальная форма свободной энергии Гельмгольца есть ${\ displaystyle {\ begin {align} dF amp; = - SdT-PdV \\\ конец {выровнено}} \, \!}$ ${\ displaystyle -S = \ left ({\ frac {\ partial F} {\ partial T}} \ right) _ {V}, \ quad -P = \ left ({\ frac {\ partial F} {\ partial V}} \ right) _ {T}}$ Из симметрии вторых производных ${\ displaystyle {\ frac {\ partial} {\ partial V}} \ left ({\ frac {\ partial F} {\ partial T}} \ right) _ {V} = {\ frac {\ partial} {\ частичное T}} \ left ({\ frac {\ partial F} {\ partial V}} \ right) _ {T}}$ и поэтому ${\ displaystyle \ left ({\ frac {\ partial S} {\ partial V}} \ right) _ {T} = \ left ({\ frac {\ partial P} {\ partial T}} \ right) _ { V}}$ Два других соотношения Максвелла могут быть получены из дифференциальной формы энтальпии и дифференциальной формы свободной энергии Гиббса аналогичным образом. Таким образом, все вышеупомянутые соотношения Максвелла вытекают из одного из уравнений Гиббса. ${\ Displaystyle {\ begin {выровнено} dH amp; = TdS + VdP \\\ конец {выровнено}} \, \!}$${\ Displaystyle {\ begin {выровнено} dG amp; = VdP-SdT \\\ конец {выровнено}} \, \!}$

Расширенное происхождение

Комбинированная форма первого и второго начала термодинамики, ${\ Displaystyle TdS = dU + PdV}$ (Уравнение 1) U, S и V - это функции состояния. Позволять, ${\ Displaystyle U = U (x, y)}$ ${\ Displaystyle S = S (х, у)}$ ${\ Displaystyle V = V (х, у)}$ ${\ displaystyle dU = \ left ({\ frac {\ partial U} {\ partial x}} \ right) _ {y} \! dx + \ left ({\ frac {\ partial U} {\ partial y}} \ справа) _ {x} \! dy}$ ${\ displaystyle dS = \ left ({\ frac {\ partial S} {\ partial x}} \ right) _ {y} \! dx + \ left ({\ frac {\ partial S} {\ partial y}} \ справа) _ {x} \! dy}$ ${\ displaystyle dV = \ left ({\ frac {\ partial V} {\ partial x}} \ right) _ {y} \! dx + \ left ({\ frac {\ partial V} {\ partial y}} \ справа) _ {x} \! dy}$ Подставляем их в уравнение 1, и получаем, ${\ displaystyle T \ left ({\ frac {\ partial S} {\ partial x}} \ right) _ {y} \! dx + T \ left ({\ frac {\ partial S} {\ partial y}} \ right) _ {x} \! dy = \ left ({\ frac {\ partial U} {\ partial x}} \ right) _ {y} \! dx + \ left ({\ frac {\ partial U} { \ partial y}} \ right) _ {x} \! dy + P \ left ({\ frac {\ partial V} {\ partial x}} \ right) _ {y} \! dx + P \ left ({ \ frac {\ partial V} {\ partial y}} \ right) _ {x} \! dy}$ А также написано как, ${\ displaystyle \ left ({\ frac {\ partial U} {\ partial x}} \ right) _ {y} \! dx + \ left ({\ frac {\ partial U} {\ partial y}} \ right) _ {x} \! dy = T \ left ({\ frac {\ partial S} {\ partial x}} \ right) _ {y} \! dx + T \ left ({\ frac {\ partial S} { \ partial y}} \ right) _ {x} \! dy-P \ left ({\ frac {\ partial V} {\ partial x}} \ right) _ {y} \! dx-P \ left ({ \ frac {\ partial V} {\ partial y}} \ right) _ {x} \! dy}$ сравнивая коэффициенты при dx и dy, получаем ${\ displaystyle \ left ({\ frac {\ partial U} {\ partial x}} \ right) _ {y} = T \ left ({\ frac {\ partial S} {\ partial x}} \ right) _ {y} -P \ left ({\ frac {\ partial V} {\ partial x}} \ right) _ {y}}$ ${\ displaystyle \ left ({\ frac {\ partial U} {\ partial y}} \ right) _ {x} = T \ left ({\ frac {\ partial S} {\ partial y}} \ right) _ {x} -P \ left ({\ frac {\ partial V} {\ partial y}} \ right) _ {x}}$ Дифференцируя приведенные выше уравнения по y, x соответственно ${\ displaystyle \ left ({\ frac {\ partial ^ {2} U} {\ partial y \ partial x}} \ right) = \ left ({\ frac {\ partial T} {\ partial y}} \ right) _ {x} \ left ({\ frac {\ partial S} {\ partial x}} \ right) _ {y} + T \ left ({\ frac {\ partial ^ {2} S} {\ partial y \ partial x}} \ right) - \ left ({\ frac {\ partial P} {\ partial y}} \ right) _ {x} \ left ({\ frac {\ partial V} {\ partial x}} \ right) _ {y} -P \ left ({\ frac {\ partial ^ {2} V} {\ partial y \ partial x}} \ right)}$ (Уравнение 2) а также ${\ displaystyle \ left ({\ frac {\ partial ^ {2} U} {\ partial x \ partial y}} \ right) = \ left ({\ frac {\ partial T} {\ partial x}} \ right) _ {y} \ left ({\ frac {\ partial S} {\ partial y}} \ right) _ {x} + T \ left ({\ frac {\ partial ^ {2} S} {\ partial x \ partial y}} \ right) - \ left ({\ frac {\ partial P} {\ partial x}} \ right) _ {y} \ left ({\ frac {\ partial V} {\ partial y}} \ right) _ {x} -P \ left ({\ frac {\ partial ^ {2} V} {\ partial x \ partial y}} \ right)}$ (Уравнение 3) U, S и V - точные дифференциалы, поэтому ${\ displaystyle \ left ({\ frac {\ partial ^ {2} U} {\ partial y \ partial x}} \ right) = \ left ({\ frac {\ partial ^ {2} U} {\ partial x \ partial y}} \ right)}$ ${\ displaystyle \ left ({\ frac {\ partial ^ {2} S} {\ partial y \ partial x}} \ right) = \ left ({\ frac {\ partial ^ {2} S} {\ partial x \ partial y}} \ right)}$ ${\ displaystyle \ left ({\ frac {\ partial ^ {2} V} {\ partial y \ partial x}} \ right) = \ left ({\ frac {\ partial ^ {2} V} {\ partial x \ partial y}} \ right)}$ Вычтем уравнения (2) и (3), и получим ${\ displaystyle \ left ({\ frac {\ partial T} {\ partial y}} \ right) _ {x} \ left ({\ frac {\ partial S} {\ partial x}} \ right) _ {y } - \ left ({\ frac {\ partial P} {\ partial y}} \ right) _ {x} \ left ({\ frac {\ partial V} {\ partial x}} \ right) _ {y} = \ left ({\ frac {\ partial T} {\ partial x}} \ right) _ {y} \ left ({\ frac {\ partial S} {\ partial y}} \ right) _ {x} - \ left ({\ frac {\ partial P} {\ partial x}} \ right) _ {y} \ left ({\ frac {\ partial V} {\ partial y}} \ right) _ {x}}$ Примечание. Вышеизложенное называется общим выражением термодинамического соотношения Максвелла. Первое отношение Максвелла Допустим, что x = S и y = V, и получится ${\ displaystyle \ left ({\ frac {\ partial T} {\ partial V}} \ right) _ {S} = - \ left ({\ frac {\ partial P} {\ partial S}} \ right) _ {V}}$ Второе отношение Максвелла Допустим, что x = T и y = V, и получится ${\ displaystyle \ left ({\ frac {\ partial S} {\ partial V}} \ right) _ {T} = \ left ({\ frac {\ partial P} {\ partial T}} \ right) _ { V}}$ Третье отношение Максвелла Допустим, что x = S и y = P, и получится ${\ displaystyle \ left ({\ frac {\ partial T} {\ partial P}} \ right) _ {S} = \ left ({\ frac {\ partial V} {\ partial S}} \ right) _ { П}}$ Четвертое отношение Максвелла Допустим, что x = T и y = P, и получится ${\ displaystyle \ left ({\ frac {\ partial S} {\ partial P}} \ right) _ {T} = - \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {П}}$ Пятое отношение Максвелла Разрешить x = P и y = V ${\ displaystyle \ left ({\ frac {\ partial T} {\ partial P}} \ right) _ {V} \ left ({\ frac {\ partial S} {\ partial V}} \ right) _ {P }}$${\ displaystyle - \ left ({\ frac {\ partial T} {\ partial V}} \ right) _ {P} \ left ({\ frac {\ partial S} {\ partial P}} \ right) _ { V}}$ = 1 Шестое отношение Максвелла Допустим, что x = T и y = S, и получится ${\ displaystyle \ left ({\ frac {\ partial P} {\ partial T}} \ right) _ {S} \ left ({\ frac {\ partial V} {\ partial S}} \ right) _ {T } - \ left ({\ frac {\ partial P} {\ partial S}} \ right) _ {T} \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {S} }$ = 1

Если мы рассмотрим первый закон термодинамики,

${\ Displaystyle {\ begin {выровнено} dU amp; = TdS-PdV \\\ конец {выровнено}} \, \!}$

в качестве утверждения о дифференциальных формах и возьмем внешнюю производную этого уравнения, получим

${\ displaystyle 0 = dTdS-dPdV}$

с тех пор. Это приводит к фундаментальной идентичности ${\ displaystyle d (dU) = 0}$

${\ displaystyle dPdV = dTdS.}$

Физический смысл этого тождества можно увидеть, отметив, что две стороны являются эквивалентными способами записи работы, выполненной в бесконечно малом цикле Карно. Эквивалентный способ записи идентичности:

${\ displaystyle {\ frac {\ partial (T, S)} {\ partial (P, V)}} = 1.}$

Отношения Максвелла теперь следуют напрямую. Например,

${\ Displaystyle {\ Bigl (} {\ frac {\ partial S} {\ partial V}} {\ Bigr)} _ {T} = {\ frac {\ partial (T, S)} {\ partial (T, V)}} = {\ frac {\ partial (P, V)} {\ partial (T, V)}} = {\ Bigl (} {\ frac {\ partial P} {\ partial T}} {\ Bigr)} _ {V},}$

Критический шаг - предпоследний. Остальные отношения Максвелла следуют аналогичным образом. Например,

${\ Displaystyle {\ Bigl (} {\ frac {\ partial T} {\ partial V}} {\ Bigr)} _ {S} = {\ frac {\ partial (T, S)} {\ partial (V, S)}} = {\ frac {\ partial (P, V)} {\ partial (V, S)}} = - {\ Bigl (} {\ frac {\ partial P} {\ partial S}} {\ Bigr)} _ {V}.}$

Вышесказанное - не единственные отношения Максвелла. Когда рассматриваются другие рабочие условия, включающие другие естественные переменные, помимо объемной работы, или когда число частиц включается в качестве естественной переменной, становятся очевидными другие соотношения Максвелла. Например, если у нас есть однокомпонентный газ, то количество частиц N   также является естественной переменной четырех вышеуказанных термодинамических потенциалов. Тогда соотношение Максвелла для энтальпии по отношению к давлению и количеству частиц будет следующим:

${\ displaystyle \ left ({\ frac {\ partial \ mu} {\ partial P}} \ right) _ {S, N} = \ left ({\ frac {\ partial V} {\ partial N}} \ right) _ {S, P} \ qquad = {\ frac {\ partial ^ {2} H} {\ partial P \ partial N}}}$

где μ - химический потенциал. Кроме того, существуют другие термодинамические потенциалы помимо четырех, которые обычно используются, и каждый из этих потенциалов дает набор соотношений Максвелла. Например, грандиозный потенциал дает: ${\ displaystyle \ Omega (\ mu, V, T)}$

${\ displaystyle {\ begin {align} \ left ({\ frac {\ partial N} {\ partial V}} \ right) _ {\ mu, T} amp; = amp; \ left ({\ frac {\ partial P} {\ partial \ mu}} \ right) _ {V, T} amp; = amp; - {\ frac {\ partial ^ {2} \ Omega} {\ partial \ mu \ partial V}} \\\ left ({\ frac {\ partial N} {\ partial T}} \ right) _ {\ mu, V} amp; = amp; \ left ({\ frac {\ partial S} {\ partial \ mu}} \ right) _ {V, T} amp; = amp; - {\ frac {\ partial ^ {2} \ Omega} {\ partial \ mu \ partial T}} \\\ left ({\ frac {\ partial P} {\ partial T}} \ right) _ {\ mu, V} amp; = amp; \ left ({\ frac {\ partial S} {\ partial V}} \ right) _ {\ mu, T} amp; = amp; - {\ frac {\ partial ^ { 2} \ Omega} {\ partial V \ partial T}} \ end {align}} \, \!}$

• Таблица термодинамических уравнений
• Термодинамические уравнения