Тепловое расширение

редактировать

Тенденция вещества к изменению объема ответа на изменение температуры

Деформационный шов в автомобильный мост, Использование для предотвращения повреждений от теплового расширения.

Тепловое расширение - это тенденция материи к изменению своей формы, площади, объема и плотности в ответ на изменение температуры, обычно не включая фазовые переходы.

Температура - это монотонная функция средняя молекулярная кинетическая энергия вещества. Когда вещество нагревается, молекулы начинают больше вибрировать и двигаться, обычно увеличивая расстояние между собой. Вещества, сокращаются при температуре, необычны и повышаются только в ограниченном диапазоне температур (см. Примеры ниже). Относительное расширение (также называемое деформацией ), деленное на изменение температуры, называется коэффициентом линейного теплового расширения материала и обычно изменяется в зависимости от температуры.

Содержание

1 Обзор
- 1.1 Прогнозирование расширения
- 1.2 Эффекты сжатия (отрицательное тепловое расширение)
- 1.3 Факторы, влияющие на тепловое расширение
- 1.4 Влияние на плотность
2 Коэффициент теплового расширения
- 2.1 Общий коэффициент теплового расширения
3 Расширение в твердых телах
- 3.1 Линейное расширение
  - 3.1.1 Влияние на деформацию
- 3.2 Расширение площади
- 3.3 Объемное расширение
  - 3.3.1 Изотропные материалы
  - 3.3.2 Анизотропные материалы
4 Изобарное расширение в газах
5 Расширение в жидкостях
- 5.1 Кажущееся и абсолютное расширение жидкости
6 Примеры и применения
7 факторов теплового расширения для различных материалов
8 См. Также
9 Ссылки
10 Внешние ссылки

Обзор

Прогнозирование расширения

Если доступно уравнение состояния, оно может быть для прогнозирования теплового расширения при всех требуемых температур и давлениях вместе со многими другими функциями состояния.

Эффект сжатия (отрицательное тепловое расширение)

Ряд материалов сжимаются при нагревании в определенных диапазонах температур; это обычно называется отрицательным тепловым расширением, а не «тепловым сжатием». Например, коэффициент теплового расширения воды до нуля, когда она охлаждается до 3,983 ° C, а затем становится отрицательным при этой температуре; Это означает, что вода имеет максимальную плотность при этой температуре, и это показывает, что водоемы этой температуры на более низкой плотности в течение длительных периодов отрицательной погоды. Кроме того, чистый кремний имеет отрицательный коэффициент теплового расширения при температуре от 18 до 120 кельвинов.

Факторы, влияющие на тепловое расширение

В отличие от газов или жидкостей. при воздействии термическое расширение.

Тепловое расширение обычно влияет на энергию связи , что также влияет на точку плавления твердые вещества, поэтому материалы с высокой температурой плавления с большей вероятностью будут иметь меньшее тепловое расширение. Как правило, жидкости расширяются немного больше, чем твердые тела. Тепловое расширение стекол выше, чем у кристаллов. При температуре стеклования перегруппировки, происходящие в аморфном материале, приводят к характерным скачкам коэффициента теплового расширения и удельной теплоемкости. Эти неоднородности определяют температуру стеклования, при которой переохлажденная жидкость превращается в стекло.

Поглощение или десорбция воды (или других растворителей) может изменить размер обычных материалов; многие органические материалы изменяют размер намного больше из-за этого эффекта, чем из-за теплового расширения. Обычные пластмассы, подвергающиеся воздействию воды, в долгосрочной перспективе расширяться на многие проценты.

Влияние на плотность

Тепловое расширение изменяет пространство между частями вещества, что приводит к изменению объема вещества при изменении его массы (ничтожно малая величина исходит от энергия-эквивалентность ), таким образом изменяет его любую плотность, что влияет на выталкивающие силы, действующие на него. Это играет решающую роль в конвекции неравномерно нагретых жидких масс, в частности тепловое расширение частично ответственным за ветер и океанские течения.

Коэффициент теплового расширения

Коэффициент теплового расширения представлен, как размер объекта изменяется при изменении температуры. В частности, он измеряет частичное изменение размера на градус изменения температуры при постоянном давлении, так что более низкие коэффициенты описывают меньшую склонность к изменению размера. Разработано несколько типов коэффициентов: объемные, площадные и линейные. Выбор коэффициента зависит от конкретного применения и от того, какие размеры считаются важными. Для твердых тел можно беспокоиться только об изменении по длине или по некоторой области.

Объемный коэффициент теплового расширения является самым основным коэффициентом теплового расширения и наиболее актуален для жидкостей. В общем, расширяются или сжимаются при изменении их температуры. Вещества, которые расширяются с одинаковой скоростью во всех направлениях, называются изотропными. Коэффициент линейного теплового расширения примерно в два и три раза больше.

Математические определения этих характеристик ниже для твердых тел, жидкостей и газов.

Общий коэффициент теплового расширения

В общем случае газа, жидкости или твердого тела объемный коэффициент теплового расширения определяется как

α = α V = 1 В (∂ В ∂ T) п {\ displaystyle \ alpha = \ alpha _ {\ text {V}} = {\ frac {1} {V}} \, \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {\ mathrm {p}}}

{\ displaystyle \ alpha = \ alpha _ {\ text {V}} = {\ frac {1} {V}} \, \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {\ mathrm {p} }}

Нижний индекс «p» у производной указывает, что это объемное (линейное) расширение входит в это общее определение. В случае газа важен тот факт, что давление поддерживается постоянным, поскольку объем газа будет заметно меняться в зависимости от давления, а также температуры. Для газа низкой плотности это видно из закона идеального газа.

Расширение в твердых телах

При расчете теплового расширения необходимо учитывать, может ли тело расширяться свободно или ограничено. Используя коэффициент теплового расширения, можно просто использовать коэффициент теплового расширения.

Если тело ограничено так, что оно не может расширяться, то внутреннее напряжение будет вызвано (или изменено) изменением температуры. Это напряжение может быть вычислено с учетом деформации, возникло бы, если бы тело могло свободно расширяться, и этого напряжения, необходимого для уменьшения напряжения до нуля, через напряжение / деформацию, характеризующуюся упругостью или модулем Юнга. В особом твердых материалов внешнее давление окружающей среды обычно не оказывает заметного влияния на размер объекта, и обычно нет необходимости влиять на изменение давления.

Обычные технические твердые обычно имеют коэффициенты теплового расширения, которые предназначены для использования в диапазоне температур, в котором они предназначены для использования, поэтому там, где не требуется высокая точность, практические расчеты должны быть основаны на постоянном, среднем, значении. коэффициента расширения.

Линейное расширение

Изменение длины стержня из-за теплового расширения.

Линейное расширение означает изменение размера (длины) в отличие от изменения объема (объемное расширение). В первом приближении изменения размера объекта из-за теплового расширения изменением температуры с помощью коэффициента линейного теплового расширения (CLTE). Это частичное изменение длины на градус изменения температуры. Предполагаемое незначительное влияние давления, мы можем написать:

α L = 1 L d L d T {\ displaystyle \ alpha _ {L} = {\ frac {1} {L}} \, {\ frac {dL} { dT}}}

\ alpha_L = \ frac {1} {L} \, \ frac {dL} {dT}

где $L {\ displaystyle L}$ $L$ - конкретное значение длины, а $d L / d T {\ displaystyle dL / dT}$ $dL / dT$ - скорость изменения этого линейного размера на единицу изменения температуры.

Изменение линейного размера можно оценить следующим образом:

Δ LL = α L Δ T {\ displaystyle {\ frac {\ Delta L} {L}} = \ alpha _ {L} \ Delta T}

\ frac {\ Delta L} {L} = \ alpha_L \ Delta T

Эта оценка работает хорошо, пока коэффициент линейного расширения не сильно меняется при изменении температуры $Δ T {\ displaystyle \ Delta T}$ $\ Delta T$ , дробное изменение длины небольшое $Δ L / L ≪ 1 {\ Displaystyle \ Delta L / L \ ll 1}$ $\ Delta L / L \ ll 1$ . Если какое-либо из этих условий не выполнено, необходимо интегрировать точное дифференциальное уравнение (с использованием $d L / d T {\ displaystyle dL / dT}$ $dL / dT$ ).

Влияние на деформацию

Для твердого увеличения длины, таких как стержни или кабели, степени теплового расширения может быть описана с помощью <материала107>деформация, задается как $ϵ термический { \ displaystyle \ epsilon _ {\ mathrm {термический}}}$ $\ epsilon_ \ mathrm {термический}$ и определяется как:

ϵ термический = (L конечный - L начальный) L начальный {\ displaystyle \ epsilon _ {\ mathrm {Thermal} } = {\ frac {(L _ {\ mathrm {final}} -L _ {\ mathrm {initial}})} {L _ {\ mathrm {initial}}}}}

\ epsilon_ \ mathrm {Thermal} = \ frac {(L_ \ mathrm {final} - L_ \ mathrm {initial})} {L_ \ mathrm { начальный}}

где $L начальное {\ displaystyle L _ {\ mathrm {initial}}}$ $L_ \ mathrm {initial}$ - длина до изменений температуры, а $L final {\ displaystyle L _ {\ mathrm {final}}}$ $L_ \ mathrm {final}$ - длина после изменения температуры.

Для широкого тела тепловое расширение измено температуры:

ϵ термическое ∝ Δ T {\ displaystyle \ epsilon _ {\ mathrm {Thermal}} \ propto \ Delta T}

\ epsilon_ \ mathrm {Thermal} \ propto \ Delta T

Таким образом, изменение либо деформации, либо температуру можно определить следующим образом:

ϵ термический = α L Δ T {\ displaystyle \ epsilon _ {\ mathrm {Thermal}} = \ alpha _ {L} \ Delta T}

\ epsilon_ \ mathrm {Thermal} = \ alpha_L \ Delta T

где

Δ T = (T final - T начальный) {\ displaystyle \ Delta T = (T _ {\ mathrm {final}} -T _ {\ mathrm {initial}})}

\ De l ta T = (T_ \ mathrm {fina l} - T_ \ mathrm {initial})

- это разница температура между двумя зарегистрированными деформациями, измеренная в градусах Фаренгейта, градусах Ренкина, градусах Цельсия или кельвинах <75.>и $α L {\ displaystyle \ alpha _ {L}}$ $\ alpha_L$ - линейный коэффициент теплового расширения в «на градус Фаренгейта», «на градус Ренкина», «на градус Цельсия», или «на кельвин », обозначаемые как ° F, R, ° C или K соответственно. В области механики сплошных сред тепловое расширение и его эффекты как собственная деформация и собственное напряжение.

Расширение площади

Коэффициент теплового расширения площади связывает изменение размеров материала с изменением температуры. Это относительное изменение площади на градус изменения температуры. Игнорируя давление, мы можем написать:

α A = 1 A d A d T {\ displaystyle \ alpha _ {A} = {\ frac {1} {A}} \, {\ frac {dA} {dT} }}

\ alph a_A = \ frac {1 } {A} \, \ frac {dA} {dT}

где $A {\ displaystyle A}$ $A$ - некоторая интересующая область объекта, а $d A / d T {\ displaystyle dA / dT}$ $dA / dT$ - скорость изменения этой площади на единицу изменения температуры.

Изменение площади можно оценить как:

Δ AA = α A Δ T {\ displaystyle {\ frac {\ Delta A} {A}} = \ alpha _ {A} \ Delta T}

\ frac {\ Delta A} {A} = \ alpha_A \ Delta T

Это уравнение работает хорошо до тех пор, пока коэффициент расширения площади не изменился при изменении температуры $Δ T {\ displaystyle \ Delta T}$ $\ Delta T$ , а также при частичном изменении площади маленький $Δ A / А ≪ 1 {\ Displaystyle \ Delta A / A \ ll 1}$ $\ Delta A / A \ ll 1$ . Если любое из этих условий не выполняется, уравнение необходимо проинтегрировать.

Объемное расширение

Для твердого тела мы можем игнорировать влияние давления на материал, и коэффициент объемного теплового расширения можно записать:

α V = 1 V d V d T {\ displaystyle \ alpha _ {V} = {\ frac {1} {V}} \, {\ frac {dV} {dT}}}

\ alpha_V = \ frac {1} {V} \, \ frac {dV } {dT}

где $V {\ displaystyle V}$ $V$ - это объем материала, а $d V / d T {\ displaystyle dV / dT}$ $dV / dT$ - изменение скорости этого объема с температурой.

Это означает, что объем материала изменяется на некоторую фиксированную дробную величину. Например, стальной блок объемом 1 кубический метр может расшириться до 1 002 кубометра при повышении температуры на 50 К. Это расширение составляет 0,2%. Если бы у нас был стальной блок объемом 2 кубометра, то при тех же условиях он расширился бы до 2 004 кубических метра, опять же на 0,2%. Коэффициент объемного расширения будет 0,2% для 50 К или 0,004% К.

Если мы уже знаем, что мы можем изменить размер

Δ VV = α V Δ T {\ displaystyle {\ frac {\ Delta V} {V}} = \ alpha _ {V} \ Delta T}

\ frac {\ Delta V} {V} = \ alpha_V \ Delta T

где $Δ V / V {\ displaystyle \ Delta V / V}$ $\ Delta V / V$ - это относительное изменение объема (например, 0,002), а $Δ T {\ displaystyle \ Delta T}$ $\ Delta T$ - изменение температуры (50 ° C).

В приведенном выше приведенном выше судебном постановлении указано выше, что коэффициент увеличения не изменился при изменении температуры и уменьшении размера по сравнению с исходным объемом. Это не всегда верно, но для небольших изменений температуры это хорошее приближение. Если коэффициент объемного увеличения действительно изменился с температурой или размером площади, то приведенное выше уравнение необходимо интегрировать:

ln n (V + Δ VV) = ∫ T i T f α V (T) d T {\ displaystyle \ ln \ left ({\ frac {V + \ Delta V} {V}} \ right) = \ int _ {T_ {i}} ^ {T_ {f}} \ alpha _ {V} (T) \, dT}

\ ln \ left (\ frac {V + \ Del та V} {V} \ right) = \ int_ {T_i} ^ {T_f} \ alpha_V (T) \, dT

Δ VV знак равно ехр ⁡ (∫ T я T е α V (T) d T) - 1 {\ displaystyle {\ frac {\ Delta V} {V}} = \ exp \ left (\ int _ {T_ { i}} ^ {T_ {f}} \ alpha _ {V} (T) \, dT \ right) -1}

\ frac {\ Delta V} {V} = \ exp \ left (\ int_ {T_i} ^ {T_f} \ alpha_V (T) \, dT \ right) - 1

где $α V (T) {\ displaystyle \ alpha _ {V} ( T)}$ $\ alpha_V (T)$ - коэффициент объемного расширения как функция температуры T, а $T i {\ displaystyle T_ {i}}$ $T_ {i}$ , $T f {\ displaystyle T_ {f}}$ $T_ {f}$ - начальная и конечная температура соответственно.

Изотропные материалы

Для изотропных материалов коэффициент объемного теплового расширения в три раза увеличенный линейный коэффициент:

α V = 3 α L {\ displaystyle \ alpha _ {V} = 3 \ alpha _ {L}}

\ alpha_V = 3 \ alpha_L

Это соотношение из трех взаимно ортогональных области. Таким образом, в изотропном материале при различных отклонениях одна треть объемного расширения на одну ось. В качестве примера возьмем стальной куб стороны длины L. Исходный объем будет $V = L 3 {\ displaystyle V = L ^ {3}}$ $V = L ^ 3$ , а новый объем будет иметь вид после повышения температуры будет

V + Δ V = (L + Δ L) 3 = L 3 + 3 L 2 Δ L + 3 L Δ L 2 + Δ L 3 ≈ L 3 + 3 L 2 Δ L = V + 3 В Δ LL. {\ Displaystyle V + \ Delta V = (L + \ Delta L) ^ {3} = L ^ {3} + 3L ^ {2} \ Delta L + 3L \ Delta L ^ {2} + \ Delta L ^ { 3} \ приблизительно L ^ {3} + 3L ^ {2} \ Delta L = V + 3V {\ Delta L \ over L}.}

{\ displaystyle V + \ Delta V = (L + \ Delta L) ^ {3} = L ^ {3} + 3L ^ {2} \ Delta L + 3L \ Delta L ^ {2} + \ Delta L ^ {3} \ приблизительно L ^ {3} + 3L ^ {2 } \ Delta L = V + 3V {\ Delta L \ over L}.}

Мы можем легко проигрывать членов, поскольку изменение L является небольшой величиной, которая при возведении в квадрат становится намного меньше.

Итак

Δ VV = 3 Δ LL = 3 α L Δ T. {\ displaystyle {\ frac {\ Delta V} {V}} = 3 {\ Delta L \ over L} = 3 \ alpha _ {L} \ Delta T.}

{\ displaystyle {\ frac {\ Delta V} {V}} = 3 {\ Delta L \ over L} = 3 \ alpha _ {L} \ Delta T.}

Приведенное выше приближение справедливо для малых температур и размеров (то есть, когда $Δ T {\ displaystyle \ Delta T}$ $\ Delta T$ и $Δ L {\ displaystyle \ Delta L}$ $\ Delta L$ маленькие); но это не выполняется, если мы пытаемся перемещаться между объемными и линейными коэффициентами, используя большие $Δ T {\ displaystyle \ Delta T}$ $\ Delta T$ . В этом случае необходимо привести третий член (а иногда даже четвертый член) в приведенном выше выражении.

Аналогично, коэффициент теплового увеличения площади в два раза больше линейного коэффициента:

α A = 2 α L {\ displaystyle \ alpha _ {A} = 2 \ alpha _ {L}}

\ alpha_A = 2 \ alpha_L

Это соотношение можно найти аналогично, как в приведенном выше линейном примере, что площадь грани на кубе составляет всего $L 2 {\ displaystyle L ^ {2}}$ $L ^ {2}$ . Кроме того, те же соображения необходимо учитывать при работе с большими значениями $Δ T {\ displaystyle \ Delta T}$ $\ Delta T$ .

Анизотропные материалы

Материалы с анизотропной структурой, например кристаллы (с менее чем кубической симметрией, например мартенситные фазы) и многие композиты, как правило, будут иметь разные коэффициенты линейного расширения $α L {\ displaystyle \ альфа _ {L}}$ $\ alpha_L$ в разные стороны. В результате общего объемного расширения распределяется по трем осям неравномерно. Если симметрия кристалла моноклинная или триклинная, даже углы между этими осями подвержены тепловым изменениям. В таких рассматривает коэффициент теплового расширения тензор с максимум шестью независимыми элементами. Хороший способ определить элементы тензора - изучить расширение с помощью дифракции рентгеновских лучей на порошке. Тензор коэффициента теплового расширения для материалов, обладающих кубической симметрией (например, FCC, BCC), является изотропным.

Изобарное расширение в газах

Для идеального газа объемное тепловое расширение (т. Е. Относительное изменение объема из-за изменения температуры) зависит от типа процесса, в котором изменяется температура. Два простых случая - постоянное давление (изобарический процесс ) и постоянный объем (изохорный процесс ).

Производная закона идеального газа, $p V = T {\ displaystyle pV = T}$ ${\ displaystyle pV = T}$ , равна

pd V + V dp = d T {\ displaystyle pdV + Vdp = dT}

{\ displaystyle pdV + Vdp = dT}

, где $p {\ displaystyle p}$ $p$ - давление, $V {\ displaystyle V}$ $V$ - удельный объем, а $T {\ displaystyle T}$ $T$ - температура, измеренная в единицах энергии.

По определению изобарического теплового расширения мы имеем $dp = 0 {\ displaystyle dp = 0}$ ${\ displaystyle dp = 0}$ , так что $pd V = d T {\ displaystyle pdV = dT}$ ${\ displaystyle pdV = dT}$ , коэффициент изобарного теплового расширения равен:

α p ≡ 1 V (d V d T) = 1 V (1 p) = 1 p V = 1 T {\ displaystyle \ alpha _ {p} \ Equiv {\ frac {1} {V}} \ left ({\ frac {dV} {dT}} \ right) = {\ frac {1} {V}} \ left ({\ frac {1} {p }} \ right) = {\ frac {1} {pV}} = {\ frac {1} {T}}}

{\ displaystyle \ alpha _ {p} \ Equiv {\ frac {1} {V}} \ left ({\ frac {dV} {dT}} \ right) = {\ frac {1} {V}} \ left ({\ frac { 1} {p}} \ right) = {\ frac {1} {pV}} = {\ frac {1} {T}}}

Аналогично, если объем поддерживается постоянным, то есть если $d V = 0 {\ displaystyle dV = 0}$ ${\ displaystyle dV = 0}$ , мы имеем $V dp = d T {\ displaystyle Vdp = dT}$ ${\ displaystyle Vdp = dT}$ , так что изохорическое тепловое расширение коэффициент равенства

α V ≡ 1 п (dpd T) = 1 п (1 V) = 1 p V = 1 T {\ displaystyle \ alpha _ {V} \ Equiv {\ frac {1} {p}} \ left ({\ frac {dp} { dT}} \ right) = {\ frac {1} {p}} \ left ({\ frac {1} {V}} \ right) = {\ frac {1} {pV}} = {\ frac {1 } {T}}}

{\ displaystyle \ alpha _ {V} \ Equiv {\ frac {1} {p}} \ left ({\ frac {dp} {dT}} \ right) = {\ frac {1} {p}} \ left ({\ frac {1} {V}} \ right) = {\ frac {1} {pV}} = {\ frac {1} {T}}}

Расширение в жидкостях

Теоретически коэффи ц ие нт линейного расширения можно определить из показателей объемного расширения (α V ≈ 3α L). Для жидкостей α L рассчитывается экспериментального определения α V. Жидкости, отличие от твердого тела, не имеют формы и формы емкости. Следовательно, жидкости не имеют стандартной толщины и площади.

Жидкости обычно расширяются при нагревании. Однако вода является исключением из этого общего поведения: ниже 4 ° C она сжимается при нагревании. При более высокой температуре он показывает нормальное положительное тепловое расширение. Тепловое расширение жидкостей обычно выше, чем у твердых тел из-за слабых межмолекулярных сил, присутствующих в жидкостях.

Тепловое расширение твердых тел обычно мало зависит от температуры, за низкие температуры, тогда как жидкости расширяются с разной скоростью при разных температурах.

Кажся и абсолютное расширение жидкости

Расширение жидкости обычно измеряется в контейнерах. Когда жидкость расширяется в сосуде, сосуд расширяется вместе с жидкостью. Следовательно, наблюдаемое увеличение объема жидкости. Расширение жидкости называется ее кажущимся расширением, фактическое расширение жидкости называется реальным расширением или абсолютным расширением. Отношение видимого увеличения жидкости на единицу повышения к исходному объему.

При небольшом и одинаковом повышении температуры увеличения объема жидкости (реальное расширение) жидкости равно сумме видимого увеличения (кажущегося расширения) жидкости и увеличения объема жидкости. вмещающий сосуд. Таким образом, жидкость имеет два коэффициента расширения.

Измерение расширения жидкости также должно быть расширение емкости. Например, когда колба с длинным узким стержнем, помещается в тепловую баню, высота столба жидкости в стержне сначала падает, а сразу же помещается на эту высоту. пока вся система колба, жидкость и тепловая баня не прогреется. Первоначальное падение высоты столба жидкости происходит не из-за начального сжатия жидкости, а скорее из-за расширения колбы, когда она первой соприкасается с термостатом. Вскоре после этого жидкость в колберевается самой колбой и начинает расширяться. Увеличение объема жидкости в колбе приводит к повышению уровня жидкости в колбе. Прямое измерение высоты столба жидкости - это измерение кажущегося расширения жидкости. Абсолютное расширение жидкости - это кажущееся расширение с поправкой на расширение вмещающего резервуара.

Примеры и применения

Тепловое расширение длинных непрерывных участков рельсовых путей является движущей силой для продольного изгиба рельсов. Это явление привело к сходу с рельсов 190 в течение 1998–2002 годов поездов только в США.

Расширение и сжатие материалов для измерения расстояния для геодезических изысканий, при проектировании литейных форм для литья. горячий материал и в других инженерных приложениях, когда ожидаются большие изменения размеров из-за температуры.

Тепловое расширение также используется в механических приложениях для прилегания деталей друг к другу, например, втулку можно установить на вал, сделав ее внутренний диаметр немного меньше диаметра вала, нагревая ее до тех пор, пока она не войдет на вал, и позволяя ей остыть после того, как она была надета на вал, таким образом достигла термоусадочная посадка ». Индукционная термоусадочная муфта - это общепринятый промышленный метод ввода металлических компонентов от 150 ° C до 300 ° C, что приводит к их расширению и вставке или удалению другого компонента.

Существуют сплавы с очень малым коэффициентом линейного расширения, используемые в приложениях, требующие очень малых изменений размеров в диапазоне температур. Один из них - инвар 36, с расширением равным 0,6 × 10 К. Эти сплавыны в аэрокосмической отрасли, где могут быть большие колебания температуры.

используется для определения линейного расширения металлического стержня в лаборатории. Аппарат состоит из закрытого с обоих концов металлического цилиндра (называемого паровой рубашкой). Он снабжен входом и выходом для пара. Для стержня ввода от бойлера, который соединен резиновой трубкой с входом. В центре цилиндра есть отверстие для термометра. Исследуемый стержень заключен в паровую рубашку. Один его конец свободен, а другой конец прижат к неподвижному винту. Положение стержня определяется с помощью винтового калибра микрометра или сферометра.

. Чтобы определить коэффициент линейного теплового расширения металла, труба, сделанная из этого металла, нагревается путем пропускания пара через Это. Один конец трубы надежно закреплен, а другой опирается на вращающийся вал, движение которого указывается стрелкой. Подходящий термометр регистрирует температуру трубы. Это позволяет рассчитать относительное изменение длины на градус изменения температуры.

Стакан для питья с изломом из-за неравномерного теплового расширения после заливки горячей жидкости в стакан, который был иначе был бы холодным.

Контроль теплового расширения в хрупких материалах является ключевой задачей по целому ряду причину. Например, стекло и керамика предлагает новое термическое напряжение, которое может привести к разрушению. Керамику необходимо соединить или сочетать с широким спектром материалов, поэтому их расширение должно соответствовать области применения. Телефону-глазури должны быть прочно прикреплены к подстилающему фарфору (или другому типу корпуса), их тепловое расширение должно быть настроено так, чтобы «соответствовать» корпусу, чтобы не формуло трещин или дрожания. Хорошими примерами продуктов, тепловое расширение которых является ключом к успеху, являются CorningWare и свечи зажигания. Тепловым расширением керамических тел можно управлять путем обжига крупных кристаллических частиц, которые могут влиять на общее расширение материала в желаемом направлении. В дополнение или этого в Сообщении тела вместо друг них, доставляющие частицы с желаемым расширением в матрицу. Тепловое расширение глазурей контролируется их химическим составом и режимом обжига. В большинстве случаев есть сложные вопросы, связанные с контролем над расширением массы и глазури, корректировка теплового расширения должна быть с учетом других свойств, которые должны быть включены в правила, необходимые компромиссы.

Тепловое расширение может быть заметное влияние на бензин, хранящийся в подземных резервуарах мощным, который может быть более значительным, чем бензин, хранящийся в подземных резервуарах зимой, чем бензин летом хранится в подземных резервуарах.

Контур расширения на трубопроводе

Расширение, вызванное нагревом, необходимо в области применения техники. Вот несколько примеров:

Окна с металлическим каркасом нуждаются в резиновых прокладках.
Резиновые шины должны хорошо работать в широком диапазоне температур, пассивно нагреваясь или охлаждаясь дорожным покрытием и погодой, а также активно нагреваясь механическими изгиб и трение.
Металлические трубы для горячего водоснабжения не предлагать на больших прямых участках.
Большие конструкции, такие как железные дороги и мосты, нуждаются в компенсаторах в конструкциях, чтобы избегайте загиба на солнце.
Одной из плохой работы двигателей холодных автомобилей то, что имеют Неэффективно большие расстояния до тех деталей пор, пока не достигнута нормальная рабочая температура.
A маятник с решеткой <7575>использует различных металлов для поддержания более стабильной температуры маятника.
Линия электропередачи в жаркий день провисает, но в холодный день она натянута. Это происходит потому, что металлы расширяются при нагревании.
Компенсирующие швы поглощают тепловое расширение в системе трубопроводов.
Точное проектирование почти всегда требует, чтобы инженер обращал внимание на тепловое расширение продукта. Например, при использовании сканирующего электронного электронного микроскопа небольшие изменения температуры, например, на 1 градус, может привести к изменению положения образца относительно точки фокусировки.
Жидкостные термометры содержат жидкость (обычно ртуть или спирт) в трубке, которая заставляет ее течь только в одном направлении, когда ее объем увеличивается из-за изменений температуры.
В биметаллическом механическом термометре используется биметаллическая полоса и изгибается из-за разного теплового расширения двух металлов.

Коэффициент теплового расширения для различных материалов

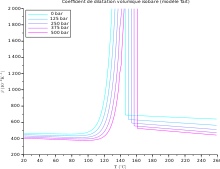Объемный коэффициент теплового расширения для полукристаллического полипропилена.

Коэффициент линейного теплового расширения для некоторых марок стали.

В этом разделе приведены коэффициенты для некоторых распространенных материалов.

Для изотропных материалов коэффициенты линейного теплового расширения α и объемного теплового расширения α V связано с использованием α V = 3α. Для жидкости обычно указывается коэффициент объемного расширения.

Коэффициент теплового расширения обратно пропорционален температура плавления. В частности, для металлов это соотношение:

α ≈ 0,020 T m {\ displaystyle \ alpha \ приблизительно {\ frac {0,020} {T_ {m}}}}

{\ displaystyle \ alpha \ приблизительно {\ frac {0,020} {T_ {m}}}}

для галогенидов и оксиды

α ≈ 0,038 Т м - 7,0 ⋅ 10-6 К - 1 {\ displaystyle \ alpha \ приблизительно {\ frac {0,038} {T_ {m}}} - 7,0 \ cdot 10 ^ {- 6} \, \ mathrm {K} ^ {- 1}}

{\ displaystyle \ альфа \ примерно {\ гидроразрыва {0,038} {T_ {m}}} - 7,0 \ cdot 10 ^ {- 6} \, \ mathrm {K} ^ {- 1}}

В таблице ниже диапазон для α составляет от 10 К для твердого тел до 10 К для медицинского. Коэффициент α меняется в зависимости от температуры, и некоторые материалы могут сильно отличаться; см., например, изменение в зависимости от температуры объемного коэффициента для полукристаллического полипропилена (ПП) при разном давлении, а также изменение линейного коэффициента в зависимости от температуры для некоторых марок (снизу вверх: ферритная нержавеющая сталь, мартенситная нержавеющая сталь, углеродистая сталь, дуплексная) нержавеющая сталь, аустенитная сталь). Самый высокий линейный коэффициент в твердом теле был зарегистрирован для сплава Ti-Nb.

(Для твердых тел обычно используется формула α V ≈ 3α.)

Материал	Линейный. коэффициент CLTE α. при 20 ° C. (x10 K)	Объемный. коэффициент α V. при 20 ° C. (x10 K)	Примечания
Алюминий	23,1	69
Латунь	19	57
Углеродистая сталь	10,8	32,4
Углепластик	- 0, 8	Анизотропный	Направление волокон
Бетон	12	36
Медь	17	51
Алмаз	1	3
Этанол	250	750
Бензин	317	950
Стекло	8,5	25,5
Стекло, боросиликат	3,3	9,9	подходящий уплотнительный компонент для вольфрама, молибдена и ковар.
Глицерин		485
Золото	14	42
Лед	51
Инвар	1,2	3, 6
Железо	11,8	35,4
Каптон	20	60	DuPont Kapton 200EN
Свинец	29	87
Macor	9.3
Никель	13	39
Дуб	54		Перпендикулярно волокнам
Дугласская ель	27	75	радиальный
пихта Дугласа	45	75	тангенциальная
пихта Дугласа	3,5	75	параллельно волокну
Платина	9	27
Полипропилен (ПП)	150	450
ПВХ	52	156
Плавленый кварц	0,59	1,77
	12-16 / 6-9		Параллельно оси A / оси C T = от -50 до 150 C
Резина	спорная	оспаривается	см. Обсуждение
Сапфир	5,3		Параллельно оси C, или [001]
Карбид кремния	2,77	8,31
Кремний	2,56	9
Серебро	18	54
Стеклокерамика «Ситалл "	0 ± 0,15	0 ± 0,45	в среднем для от -60 ° C до 60 ° C
Нержавеющая сталь	10,1 ~ 17,3	30,3 ~ 51,9
Сталь	11,0 ~ 13,0	33,0 ~ 39,0	Зависит от состава
Титан	8,6	26
Вольфрам	4,5	13,5
Вода	69	207
Стеклокерамика «Церодур "	≈0,007-0,1		при 0... 50 ° C

См. Также

Отрицательное тепловое расширение
Уравнение состояния Ми – Грюнайзена
Autovent
Параметр Грюнайзена
Видимое молярное свойство
Теплоемкость - Физическое свойство, описывающее энергию, необходимую для изменения температуры материала
Термодинамические базы данных для чистых веществ - Список термодинамических свойств
Свойства материала (термодинамика)
Закон Чарльза - Связь между объемом и температурой газа при постоянном давлении

Ссылки

Внешние ссылки

Викискладе есть материалы, связанные с Тепловое расширение.