• 1 История
• 2 Несжимаемые уравнения Эйлера с постоянной и равномерной плотностью
  • 2.1 Свойства
  • 2.2Обезразмерение
  • 2.3 Форма сохранения
  • 2.4 Пространственные размеры
• 3 Несжимаемые уравнения Эйлера <
  • 3.1 Форма сохранения
  • 3.2 Переменные сохранение
• 4 уравнения Эйлера
  • 4.1 Несжимаемое ограничение (пересмотрено)
  • 4.2 Сохранение энтальпии
  • 4.3. Термодинамика идеальных жидкостей
  • 4.4 Форма сохранения
• 5 Квазилинейная форма и характерные уравнения
  • 5.1 Характеристика ики уравнения
  • 5.2 Волны в одномерной невязкой непроводящейтермодинамической жидкости
  • 5.3 Сжимаемость и скорость звука
    • 5.3. 1 Идеальный газ
• 6 Теорема Бернулли для стабильного невязкого потока
  • 6.1 Несжимаемый случай и форма Лэмба
  • 6.2 Сжимаемый случай
  • 6.3 Форма Фридмана и форма Крокко
• 7 Разрывы
  • 7.1 Уравнения Ренкина - Гюгонио
  • 7.2 Форма конечного объема
• 8 Ограничения
  • 8.1 Идеальный политропный газ
  • 8.2 Устойчивый поток в материальных координатах
    • 8.2.1 Теорема обтекаемой кривизны
• 9Точные решения
• 10 См. также
• 11 Ссылки
  • 11.1 Примечания
  • 11.2 Цитаты
  • 11.3 Источники
  • 11.4 Дополнительная литература

Уравнения Эйлера впервые появились в опубликованной форме в статье Эйлера «Principes généraux du mouvement des fluides », опубликованной в Mémoires de l'Académie des Sciences de Berlin в 1757 году (в этой статье Эйлер фактически опубликован только общий вид уравнения неразрывности и уравнения; уравнение баланса энергии будетполучено столетием позже). Они были первых дифференциальных среди частных производных, которые были записаны. В то время, когда Эйлер опубликовал свою работу, система состояла из количества движения и неразрывности и поэтому была недоопределена, за исключением случая несжимаемой жидкости. Дополнительное уравнение, которое позже было названо условием адиабаты, было предоставлено Пьером-Симоном Лапласом в 1816 году.

Во второй половине XIX века.Установлено, что уравнение, связанное с балансом энергии, должно быть всегда соблюдаться. С открытием относительности концепции плотности энергии, импульса и напряжения были объединены в концепцию тензора энергии-импульса, энергия и импульс были объединены. аналогично объединенный в единое понятие, вектор энергии-импульса

В постоянной конвективной форме (то есть есть форма с конвективным оператором явное выражение в уравнении импульса ), несжимаемые уравнения Эйлера в случае постоянной плотности во времени и однородной в пространстве:

Несжимаемые уравнения Эйлера с постоянной плотностью (конвективная или лагранжева форма)

$\{DUDT\; знак\; равно\; -\; \nabla \; вес\; +\; г\; \nabla \; \cdot \; U\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{D\; \backslash \; mathbf\; \{u\}\; \backslash \; over\; Dt\}\; =\; -\; \backslash \; nabla\; w\; +\; \backslash \; mathbf\; \{g\}\; \backslash \; \backslash \backslash \; набла\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

где:

• $u\; \{\backslash \; displ\; aystyle\; \backslash \; mathbf\; \{u\}\}$- это вектор скорости потока , с комп. элементы в N-мерном пространстве $u\; 1,\; u\; 2,\dots ,\; u\; N\; \{\backslash \; displaystyle\; u\_\; \{1\},\; u\_\; \{2\},\; \backslash \; dots,\; u\_\; \{N\}\}$,
• $D\; v\; D\; t\; =\; \partial \; v\; \partial \; T\; +\; U\; \cdot \; \nabla \; v\; \{\backslash \; Displaystyle\; \{D\; \backslash \; mathbf\; \{v\}\; \backslash \; over\; Dt\}\; =\; \{\backslash \; partial\; \backslash \; mathbf\; \{v\}\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; mathbf\; \{v\; \}\}$для общей функции (или поля) $v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\}$обозначает ее материальную производную вовремени с относительно адвективного поля $u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\}$и
• $\nabla \; \{\backslash \; displaystyle\; \backslash \; nabla\}$обозначает градиент относительно пространства,
• $\cdot \; \{\backslash \; displaystyle\; \backslash \; cdot\; \}$обозначает скалярное произведение,
• $\nabla \; \{\backslash \; displaystyle\; \backslash \; nabla\}$- это оператор набла, здесь используется для представления настоящей термодинамической работы градиент (первое уравнение), а
• $\nabla \; \cdot \; u\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; math\; bf\; \{u\}\}$- скорость потока , дивергенция (второе уравнение),
• $ш\; \{\backslash \; д\; я\; splaystyle\; w\}$- конкретное (со смыслом для u масса) термодинамическая работа, внутренний исходный член.
• $g\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{g\}\}$представляет ускорения тела (на единицу массы), действующую на континуум, например гравитация, электрическое поле ускорение и т. д.

Первое уравнение - это уравнение импульсаса Эйлера с однородной плотностью (для этого уравнения также может быть постоянной во времени). Расширяя материальную производную, уравнения становятся:

$\{\partial \; u\; \partial \; t\; +\; (u\; \cdot \; \nabla )\; u\; =\; -\; \nabla \; w\; +\; g\; \nabla \; \cdot \; u\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{\; выровняйте\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\; \backslash \; over\; \backslash \; partial\; t\}\; +\; (\backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla)\; \backslash \; mathbf\; \{u\}\; =\; -\; \backslash \; nabla\; w\; +\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Фактически для потока с однородной плотностью $\rho \; 0\; \{\backslash displaystyle\; \backslash \; rho\; \_\; \{0\}\}$выполнено следующее тождество:

$\nabla \; вес\; \equiv \; \nabla \; (p\; \rho \; 0)\; =\; 1\; \rho \; 0\; \nabla \; p\; \{\backslash \; displaystyle\; \backslash \; nabla\; w\; \backslash \; Equiv\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{p\}\; \{\backslash \; rho\; \_\; \{0\}\}\}\; \backslash \; справа)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\; \_\; \{0\}\}\}\; \backslash \; nabla\; p\}$

где $p\; \{\backslash \; displaystyle\; p\}$- механика давление. Второе уравнение - это несжимаемая формула, утверждающая, что скорость потока соленоидальным полем (порядок не является определяющим, но подчеркивает тот факт, чтонесжимаемая не является вырожденной формулой уравнения неразрывности, а скорее уравнение энергии, как это станет ясно из дальнейшего). Примечательно, что уравнение неразрывности потребуется также в этом случае несжимаемой жидкости в качестве третьего уравнения в случае изменения плотности во времени или изменения в пространстве. Например, при однородной плотности, но меняющейся во времени, уравнение неразрывности, которое будет добавлено к приведенному выше набору, будетсоответствовать:

$\partial \; \rho \; \partial \; t\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; rho\}\; \{\backslash \; partial\; t\; \}\}\; =\; 0\}$

Таким образом, случай постоянной и однородной плотности единственной, не требуя уравнения неразрывности в дополнительных условиях независимо от наличия или отсутствия ограничения несжимаемости. Фактически, анализируемый случай удобных соотношений Эйлера с однородной плотностью - это игрушечная модель, содержащая только два упрощенных уравнения, поэтому она идеально подходитдля дидактических целей, даже если имеет ограниченную физическую релевантность.

Таким образом, приведенные выше уравнения сравнить соответственно Сохранение массы (1 скалярное уравнение) и импульса (1 уравнение, содержащее $N\; \{\backslash \; displaystyle\; N\}$скалярные компоненты, где $N\; \{\backslash \; displaystyle\; N\}$- физический размер интересующего пространства). Скорость потока и давление - это так называемые физические переменные.

В системекоординат, заданной как $(x\; 1,\dots ,\; x\; N)\; \{\backslash \; displaystyle\; \backslash \; left\; (x\_\; \{1\},\; \backslash \; dots,\; x\_\; \{N\}\; \backslash \; right)\}$Дизайн скорости и внешней силы $u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\}$и $g\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{g\}\}$иметь компоненты $(u\; 1,\dots ,\; u\; N)\; \{\backslash \; displaystyle\; (u\_\; \{1\},\; \backslash \; dots,\; u\_\; \{N\})\}$и $(g\; 1,\dots ,\; g\; N)\; \{\backslash \; displaystyle\; \backslash \; left\; (g\_\; \{1\},\; \backslash \; dots,\; g\_\; \{N\}\; \backslash \; right)\}$соответственно. Тогда уравнения могут быть записаны в нижних индексах как:

Особенности $\{\partial \; ui\; \partial \; t\; +\; \sum \; j\; =\; 1\; N\; \partial \; (uiuj\; +\; w\; \delta \; ij)\; \partial \; xj\; =\; gi\; \sum \; i\; =\; 1\; N\; \partial \; ui\; \partial \; xi\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{\backslash \; partial\; u\_\; \{i\}\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; partial\; \backslash \; left\; (\; u\_\; \{i\}\; u\_\; \{j\}\; +\; w\; \backslash \; delta\; \_\; \{ij\}\; \backslash \; right)\; \backslash \; over\; \backslash \; partial\; x\_\; \{j\}\}\; =\; g\_\; \{i\}\; \backslash \backslash \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; частичное\; u\_\; \{i\}\; \backslash \; over\; \backslash \; partial\; x\_\; \{i\}\}\; =\; 0\; \backslash \; end\; \{выравнивается\}\}\; \backslash \; right.\}$

, где $i\; \{\backslash \; displaystyle\; i\}$и $j\; \{\backslash \; displaystyle\; j\}$ нижние индексы обозначают компоненты N-мерного пространства, а $\delta \; ij\; \{\backslash \; displaystyle\; \backslash \; delta\; \_\; \{ij\}\}$- это Kroenecker дельта. Также часто используется нотация Эйнштейна (где сумма вместо подразумевается повторяющимся индексами сигма-нотации ).

Свойства

Хотя Эйлер впервые представил эти уравнения в 1755 году, многие фундаментальные вопросы о них остаются без ответа.

В трех измеренийх пространства, в некоторых упрощенныхсценариях, уравнения Эйлера системы сингулярности.

Гладкие решения свободных (в смысле без источника: g = 0) удовлетворяют закону сохранение удельной кинетической энергии:

$\partial \; \partial \; t\; (1\; 2\; u\; 2)\; +\; \nabla \; \cdot \; (u\; 2\; U\; +\; вес\; I)\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; partial\; \backslash \; over\; \backslash \; partial\; t\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; \backslash \; right)\; +\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; left\; (u\; ^\; \{2\}\; \backslash \; mathbf\; \{u\}\; +\; w\; \backslash \; mathbf\; \{I\}\; \backslash \; right)\; =\; 0\}$

В одномерном случае без источника (как градиента давления, так и внешней силы) уравнениеимпульса становится невязким уравнение Бюргерса :

$\partial \; u\; \partial \; t\; +\; u\; \partial \; u\; \partial \; x\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; partial\; u\; \backslash \; over\; \backslash \; partial\; t\}\; +\; u\; \{\backslash \; partial\; u\; \backslash \; over\; \backslash \; partial\; x\}\; =\; 0\}$

Это модельное уравнение дает много формул уравнений Эйлера.

обезразмеривание

Чтобы уравнения были безразмерными, характерная длина $r\; 0\; \{\backslash \; displaystyle\; r\_\; \{0\}\}$и характерная скорость $u\; 0\; \{\backslash \; displaystyle\; u\_\; \{0\}\}$, необходимо определить. Их следует выбирать так, чтобы всебезразмерные переменные были первого порядка. Таким образом получаются следующие безразмерные переменные:

$u\; \ast \; \equiv \; uu\; 0,\; r\; \ast \; \equiv \; rr\; 0,\; t\; \ast \; \equiv \; u\; 0\; r\; 0\; t,\; p\; \ast \; \equiv \; wu\; 0\; 2,\; \nabla \; \ast \; \equiv \; r\; 0\; \nabla \; \{\backslash \; displaystyle\; \{\backslash \; начало\; \{выровнено\}\; u\; ^\; \{*\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{u\}\; \{u\_\; \{0\}\}\},\; \backslash \backslash \; [5pt]\; r\; ^\; \{*\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{r\}\; \{r\_\; \{0\}\}\; \},\; \backslash \backslash \; [5pt]\; t\; ^\; \{*\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{u\_\; \{0\}\}\; \{r\_\; \{0\}\}\}\; t,\; \backslash \backslash \; [5pt]\; p\; ^\; \{*\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{\; w\}\; \{u\_\; \{0\}\; ^\; \{2\}\}\},\; \backslash \backslash \; [5pt]\; \backslash \; nabla\; ^\; \{*\}\; \backslash \; Equiv\; r\_\; \{0\}\; \backslash \; nabla\; \backslash \; end\; \{align\}\}\}$

и поляединичный вектор :

$g\; ^\; \equiv \; gg,\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; mathbf\; \{g\}\}\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{g\}\}\; \{g\}\},\}$

Замена этих Обратных соотношения в уравнениях Эйлера, определяющие число Фруда, дают (без * в apix):

Несжимаемые уравнения Эйлера с равномерной плотностью (безразмерная форма)

$\{DUDT\; знак\; равно\; -\; \nabla \; вес\; +\; 1\; F\; rg\; ^\; \nabla \; \cdot \; U\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{D\; \backslash \; mathbf\; \{u\}\; \backslash \; over\; Dt\}\; =\; -\; \backslash \; nabla\; w\; +\; \{\backslash \; frac\; \{1\}\; \{\backslash \; mathrm\; \{\; Fr\}\}\}\; \{\backslash \; hat\; \{\backslash mathbf\; \{g\}\}\}\; \backslash \backslash \backslash \; набла\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Уравнения Эйлера в пределе Фруда это (отсутствие поля) называются свободными уравнениями и являются консервативными. Предел больших чисел Фруда (низкое внешнее поле), таким образом, примечателен и может быть изучен с помощью оценки сохранения.

сохранения формы

Форма подчеркивает математические свойства Эйлера. наиболее удобной для вычислительной гидродинамики моделирования. Ввычислительном отношении сохраняемых чисел дает некоторые преимущества. Это приводит к появлению большого класса численных методов, называемых консервативными методами.

Свободные уравнения Эйлера консервативны в том смысле, что эквивалентны уравнению сохранения:

$\partial \; y\; \partial \; t\; +\; \nabla \; \cdot \; F\; =\; 0,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf)\; \{y\}\}\; \{\backslash \; partial\; t\}\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\; =\; \{\backslash \; mathbf\; \{0\}\},\}$

или просто в обозначениях Эйнштейна:

$\partial \; yj\; \partial \; t\; +\; \partial \; fij\; \partial \; R\; =\; 0\; я,\; \{\backslash displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; y\_\; \{j\}\}\; \{\backslash \; partial\; t\}\}\; +\; \{\backslash \; frac\; \{\backslash \; частичный\; f\_\; \{ij\}\}\; \{\backslash \; partial\; r\_\; \{i\}\}\}\; =\; 0\_\; \{i\; \},\}$

где величина $y\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\}$, в этом случае - вектор, а $F\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\}$- матрица поток. Это можно просто доказать.

Демонстрация формы сохранения

Во-первых, выполняются следующие тождества:

$\nabla \; \cdot \; (w\; I)\; =\; I\; \cdot \; \nabla \; w\; +\; w\; \nabla \; \cdot \; I\; =\; \nabla \; w\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; (w\; \backslash \; mathbf\; \{I\})\; =\; \backslash \; mathbf\{I\}\; \backslash \; cdot\; \backslash \; nabla\; w\; +\; w\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{I\}\; =\; \backslash \; nabla\; w\}$

$u\; \cdot \; \nabla \; \cdot \; u\; =\; \nabla \; \cdot \; (u\; \otimes \; u)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; \backslash \; nabla\; \backslash \; cdot\; (\backslash \; mathbf\; \{u\}\; \backslash \; otimes\; \backslash \; mathbf\; \{u\})\}$

где $\otimes \; \{\backslash \; displaystyle\; \backslash \; otimes\}$обозначает внешний продукт. Те же самые тождества, выраженные в нотации Эйнштейна, следующие:

$\partial \; i\; (w\; \delta \; ij)\; =\; \delta \; ij\; \partial \; iw\; +\; w\; \partial \; i\; \delta \; ij\; =\; \delta \; ij\; \partial \; iw\; =\; \partial \; jw\; \{\backslash \; displaystyle\; \backslash \; partial\; \_\; \{i\}\; \backslash \; left\; (w\; \backslash \; delta\; \_\; \{ij\}\backslash \; right)\; =\; \backslash \; delta\; \_\; \{ij\}\; \backslash \; partial\; \_\; \{i\}\; w\; +\; w\; \backslash \; partial\; \_\; \{i\}\; \backslash \; delta\; \_\; \{ij\}\; =\; \backslash \; delta\; \_\; \{ij\}\; \backslash \; partial\; \_\; \{i\}\; w\; =\; \backslash \; partial\; \_\; \{j\}\; w\}$

$uj\; \partial \; iui\; =\; \partial \; я\; (uiuj)\; \{\backslash \; displaystyle\; u\_\; \{j\}\; \backslash \; partial\; \_\; \{i\}\; u\_\; \{i\}\; =\; \backslash \; partial\; \_\; \{i\}\; \backslash \; left\; (u\_\; \{i\}\; u\_\; \{j\}\; \backslash \; right)\}$

где I - это единичная матрица с размерностью N, а δ ij - ее общий элемент, Дельта Кренекера.

Благодаря этому векторному тождеству уравнения Эйлера несжимаемая жидкость с постоянной плотностью и без внешнейформы, представленной в так называемой дифференциальной форме сохранения (или эйлерове) с векторной записью:

$\{\partial \; U\; \partial \; T\; +\; \nabla \; \cdot \; (U\; \otimes \; U\; +\; вес\; I)\; знак\; равно\; 0\; \partial \; 0\; \partial \; T\; +\; \nabla \; \cdot \; U\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; left\; (\backslash \; mathbf\; \{u\}\; \backslash \; otimes\; \backslash \; mathbf\; \{u\}\; +\; w\; \backslash \; mathbf\; \{I\}\; \backslash \; right)\; =\; \backslash \; mathbf\; \{0\}\; \backslash \backslash \; \{\backslash \; partial\; 0\; \backslash \; over\; \backslash \; частичное\; t\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; 0,\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

или в нотации Эйнштейна:

$\{\partial \; tuj\; +\; \partial \; i\; (uiuj\; +\; w\; \delta \; ij)\; Знак\; равно\; 0\; \partial \; T\; 0\; +\; \partial \; juj\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \backslash \; partial\; \_\; \{t\}\; u\_\; \{j\}\; +\; \backslash \; partial\; \_\; \{i\}\; \backslash \; left\; (u\_\; \{i\}\; u\_\; \{j\})\; +\; w\; \backslash \; delta\; \_\; \{ij\}\; \backslash \; right)\; =\; 0\; \backslash \backslash \backslash \; partial\; \_\; \{t\}\; 0+\; \backslash \; partial\; \_\; \{j\}\; u\_\; \{j\}\; =\; 0,\; \backslash \; end\; \{align\}\}\; \backslash \; right.\; \}$

Тогда несжимаемая уравнения Эйлера с равномерной плотностью переменные:

$y\; =\; (u\; 0);\; F\; =\; (u\; \otimes \; u\; +\; w\; I\; u).\; \{\backslash \; Displaystyle\; \{\backslash \; mathbf\; \{y\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\};\; \backslash qquad\; \{\backslash \; mathbf\; \{F\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{u\}\; \backslash \; otimes\; \backslash \; mathbf\; \{u\}\; +\; w\; \backslash \; mathbf\; \{I\}\; \backslash \backslash \backslash \; mathbf\; \{u\}\; \backslash \; end\; \{pmatrix\}\}.\}$

Обратите внимание, что во втором компоненте u сам по себе является вектором длины N, поэтому y имеет длину N + 1, а F - размер N (N + 1). В 3D, например, y имеет длину 4, I - размер 3 × 3, а F - размер 4 × 3, поэтому явные следующие формы:

$y\; =\; (u\; 1\; u\; 2\; u\; 3\; 0);\; F\; =\; (u\; 1\; 2\; +\; w\; u\; 1\; u\; 2\; u\; 1\; u\; 3\; u\; 2\; u\; 1\; u\; 2\; 2\; +\; w\; u\; 2\; u\; 3\; u\; 3\; u\; 1\; u\; 3\; u\; 2\; u\; 3\; 2\; +\; w\; u\; 1\; u\; 2\; u\; 3).\; \{\backslash Displaystyle\; \{\backslash \; mathbf\; \{y\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; u\_\; \{1\}\; \backslash \; u\_\; \{2\}\; \backslash \; u\_\; \{3\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\};\; \backslash \; quad\; \{\backslash \; mathbf\; \{F\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; u\_\; \{1\}\; ^\; \{2\}\; +\; w\; u\_\; \{1\}\; u\_\; \{2\}\; u\_\; \{1\}\; u\_\; \{3\}\; \backslash \backslash \; u\_\; \{2\}\; u\_\; \{1\}\; u\_\; \{2\}\; ^\; \{2\}\; +\; w\; u\_\; \{2\}\; u\_\; \{3\}\; \backslash \backslash \; u\_\; \{3\}\; u\_\; \{1\}\; u\_\; \{3\}\; u\_\; \{2\}\; u\_\; \{3\}\; ^\; \{\; 2\}\; +\; w\; \backslash \backslash \; u\_\; \{1\}\; u\_\; \{2\}\; u\_\; \{3\}\; \backslash \; end\; \{pmatrix\}\}.\}$

Наконец, уравнения Эйлера можно преобразовать в конкретное уравнение:

Несжимаемое уравнение (я) Эйлера с постоянной и равномерной плотностью ( Сохранение или форма Эйлера)

$\partial \; \partial \; T\; (u\; 0)\; +\; \nabla \; \cdot \; (u\; \otimes \; u\; +\; w\; I\; u)\; =\; (g\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{u\}\; \backslash \; otimes\; \backslash \; mathbf\; \{u\}\; +\; w\; \backslash \; mathbf\; \{I\}\; \backslash \backslash \backslash \; mathbf\; \{u\}\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\}$

Пространственные измерения

Для определенных проблем, особенно при анализе данных потока в воздуховоде или в случае, еслипоток цилиндрический или сферически симметричен, одномерные уравнения Эйлера самым п олезным приближением. Как правило, уравнения Эйлера решаются с помощью методов методов Римана характеристики. Это включает поиск кривых в плоскости независимых переменных (т. Е. $x\; \{\backslash \; displaystyle\; x\}$и $t\; \{\backslash \; displaystyle\; t\}$), вдоль которых частично дифференциальные уравнения (PDE) вырождаются в обыкновенные дифференциальные уравнения (ODE).Численное решение уравнения Эйлера в степени зависит от метода.

В конвективной форме несжимаемые уравнения Эйлера в случае проведения плотности в пространстве:

Несжимаемые уравнения Эйлера (конвективная или лагранжева форма)

$\{\; D\; \rho \; DT\; знак\; равно\; 0\; DUDT\; знак\; равно\; -\; \nabla \; п\; \rho \; +\; g\; \nabla \; \cdot \; U\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{D\; \backslash \; rho\; \backslash \; over\; Dt\}\; =\; 0\; \backslash \; \backslash \; \{D\; \backslash \; mathbf\; \{u\}\; \backslash \; over\; Dt\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; nabla\; p\}\; \{\backslash \; rho\}\}+\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; 0\; \backslash \; end\; \{выровнено\}\}\; \backslash \; справа.\}$

где дополнительные переменные:

• $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$- это жидкость массовая плотность,
• $p\; \{\backslash \; displaystyle\; p\}$- давление, $p\; =\; \rho \; w\; \{\backslash \; displaystyle\; p\; =\; \backslash \; rho\; w\}$.

Первое уравнение, которое является новым, - это уравнение для несжимаемой жидкости уравнение неразрывности. Фактически, общее уравнение неразрывности будет выглядеть следующим образом:

$\partial \; \rho \; \partial \; t\; +\; u\; \cdot \; \nabla \; \rho \; +\; \rho \; \nabla \; \cdot \; u\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; partial\; \backslash \; rho\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; rho\; +\; \backslash \; rho\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; 0\}$

, но здесь последний член тождественно равенство нулю для ограничения несжимаемости.

Форма сохранения

Несжимаемые уравнения Эйлера в пределе Фруда эквивалентны уравнению с сохраняющейся величиной и соответствующим потоком соответственно:

$y\; =\; (\rho \; \rho \; u\; 0);\; F\; =\; (\rho \; u\; \rho \; u\; \otimes \; u\; +\; p\; I\; u).\; \{\backslash \; Displaystyle\; \{\backslash \; math\; bf\; \{y\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; rho\; \backslash \backslash \backslash \; rho\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\};\; \backslash \; qquad\; \{\backslash \; mathbf\; \{F\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; rho\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \backslash \; rho\; \backslash \; mathbf\; \{u\}\; \backslash \; otimes\; \backslash \; mathbf\; \{u\}\; +\; p\; \backslash \; mathbf\; \{I\}\; \backslash \backslash \backslash \; mathbf\; \{u\}\; \backslash \; end\; \{pmatrix\}\}.\}$

Здесь $y\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\}$имеет длину $N\; +\; 2\; \{\backslash \; displaystyle\; N\; +\; 2\}$и $F\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\}$имеет размер $(N\; +\; 2)\; N\; \{\backslash \; displaystyle\; (N\; +\; 2)\; N\}$. В общем случае (не только впределе Фруда) уравнения Эйлера выражаются как:

$\partial \; \partial \; t\; (\rho \; \rho \; u\; 0)\; +\; \nabla \; \cdot \; (\rho \; u\; \rho \; u\; \otimes \; u\; +\; p\; I\; u)\; =\; (0\; \rho \; g\; 0)\; \{\; \backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; rho\; \backslash \backslash \backslash \; rho\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \{\backslash \; begin\; \{\; pmatrix\}\; \backslash \; rho\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \backslash \; rho\; \backslash \; mathbf\; \{u\}\; \backslash \; otimes\; \backslash \; mathbf\; \{u\}\; +\; p\; \backslash \; mathbf\; \{I\}\; \backslash \backslash \backslash \; mathbf\; \{u\}\; \backslash \; end\; \{pmatrix\}\}\; =\; \{\backslash \; begin\; \{\; pmatrix\}\; 0\; \backslash \backslash \backslash \; rho\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\}$

Переменные сохранение

Переменные дляуравнений в форме сохранения еще не оптимизированы. Фактически мы могли бы определить:

$y\; =\; (\rho \; j\; 0);\; F\; =\; (j\; 1\; \rho \; j\; j\; +\; p\; I\; j\; \rho ).\; \{\backslash \; displaystyle\; \{\backslash \; mathbf\; \{y\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; rho\; \backslash \backslash \backslash \; mathbf\; \{j\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\};\; \backslash \; qquad\; \{\backslash \; mathbf\; \{F\}\}\; =\; \{\backslash \; begin\; \{\; pmatrix\}\; \backslash \; mathbf\; \{j\}\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \backslash ,\; \backslash \; mathbf\; \{j\}\; \backslash \; otimes\; \backslash \; mathbf\; \{j\}\; +\; p\; \backslash \; mathbf\; \{I\}\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; mathbf\; \{\; j\}\}\; \{\backslash \; rho\}\}\; \backslash \; end\; \{pmatrix\}\}.\}$

где:

• $j\; =\; \rho \; u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{j\}\; =\; \backslash \; rho\; \backslash \; mathbf\; \{u\}\}$ - импульс плотность, переменная сохранения.

Несжимаемое уравнение (я) Эйлера (сохранение или эйлерова форма)

$\partial \; \partial \; t\; (\rho \; j\; 0)\; +\; \nabla \; \cdot \; (J\; 1\; \rho \; J\; \otimes \; J\; +\; п\; я\; J\; \rho )\; знак\; равно\; (0\; е\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; rho\; \backslash \backslash \backslash \; mathbf\; \{j\; \}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{j\}\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \backslash ,\; \backslash \; mathbf\; \{j\}\; \backslash \; otimes\; \backslash \; mathbf\; \{j\}\; +\; p\; \backslash \; mathbf\; \{I\}\; \backslash \backslash \; \{\backslash \; frac\; \{\backslash \; mathbf\; \{j\}\}\; \{\backslash \; rho\}\}\; \backslash \; end\; \{pmat\; rix\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; 0\; \backslash \backslash \backslash \; mathbf\; \{f\}\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\}$

где:

• $f\; =\; \rho \; g\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{f\}\; =\; \backslash \; rho\; \backslash \; mathbf\; \{g\}\}$- плотность силы, переменная сохранения.

В дифференциально-конвективной форме сжимаемые (и наиболее общие) уравнения Эйлера можно быстро записать с помощью материальной производной обозначения:

уравнения Эйлера (конвективная форма)

$\{D\; \rho \; D\; T\; знак\; равно\; -\; \rho \; \nabla \; \cdot \; U\; D\; u\; D\; Tзнак\; равно\; -\; \nabla \; (p\; \rho )\; +\; g\; D\; e\; D\; t\; =\; -\; p\; \rho \; \nabla \; \cdot \; u\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{\; выровнено\}\; \{D\; \backslash \; rho\; \backslash \; over\; Dt\}\; =\; -\; \backslash \; rho\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \; [1.2ex]\; \{\backslash \; frac\; \{D\; \backslash \; mathbf\; \{u\}\}\; \{Dt\}\}\; =\; -\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; +\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \; [1.2ex]\; \{De\; \backslash \; over\; Dt\}\; =\; -\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

где дополнительные переменные здесь:

• $e\; \{\backslash \; displaystyle\; e\}$это конкретный внутренний энергия ( внутренняя энергия на единицу массы).

Таким образом, приведенные выше уравнения представляют собой сохранение массы, импульса и энергии : уравнение энергии Выражение в переменной внутренней энергии позволяет понять связь с несжимаемым корпусом, но не в простейшей форме. Массовая плотность, скорость потока и давление - это так называемые конвективные переменные (или физические переменные, или лагранжевые переменные), в то время как массовая плотность,плотность количества движения и общая плотность энергии являются так называемыми (также называемыми эйлеровыми или математическими переменными).

Если указать материальную производную в явном виде, приведенные выше уравнения будут следующими:

$\{\partial \; \rho \; \partial \; t\; +\; u\; \cdot \; \nabla \; \rho \; +\; \rho \; \nabla \; \cdot \; u\; =\; 0\; \partial \; u\; \partial \; t\; +\; u\; \cdot \; \nabla \; u\; +\; p\; \rho \; =\; г\; \partial \; е\; \partial \; T\; +\; U\; \cdot \; \nabla \; е\; +\; п\; \rho \; \nabla \; \cdot \; U\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{\backslash \; partial\; \backslash \; rho\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; rho\; +\; \backslash \; rho\; \backslash \; nabla\; \backslash \; cdot\backslash \; mathbf\; \{u\}\; =\; 0\; \backslash \backslash \; [1.2ex]\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\}\; \{\backslash \; partial\; t\}\}\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; mathbf\; \{u\}\; +\; \{\backslash \; frac\; \{\backslash \; nabla\; p\}\; \{\backslash \; rho\}\}\; =\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \; [1.2ex]\; \{\backslash \; partial\; e\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; mathbf\; \{u\; \}\; \backslash \; cdot\; \backslash \; nabla\; e\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Несжимаемое ограничение (пересмотрено)

Возвращаясь к случаю несжимаемой жидкости, теперь становится очевидным, что типичное ограничение несжимаемости l изпервых случаев на самом деле является частной формой, действующей для несжимаемых потоков уравнения энергии, а не уравнения массы. В частности, несжимаемое ограничение соответствует следующему очень простому уравнению энергии:

$D\; e\; D\; t\; =\; 0\; \{\backslash \; displaystyle\; \{De\; \backslash \; over\; Dt\}\; =\; 0\}$

Таким образом, для несжимаемой невязкой жидкости удельный внутренняя энергия постоянна вдоль линий потока, а также в потоке, зависящем от времени. Давление в потоке несжимаемой жидкости действует какмножитель Лагранжа, будучи множителем ограничения несжимаемой жидкости в уравнении энергии, и, следовательно, в потоках несжимаемой жидкости оно не имеет термодинамического значения. Фактически, термодинамика типична для сжимаемых течений и вырождается в несжимаемых.

Основываясь на уравнении сохранения массы, это уравнение можно записать в форме сохранения:

$\partial \; \rho \; e\; \partial \; t\; +\; \nabla \; \cdot \; (\; \rho \; eu)\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; partial\; \backslash \; rho\; e\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; nabla\; \backslash \; cdot\; (\backslash \; rho\; e\; \backslash \; math\; bf\; \{u\})\; =\; 0\}$

означает, что для несжимаемого невязкого непроводящего потока a уравнение неразрывности выполняется для внутренней энергии.

Сохранение энтальпии

Поскольку по определению удельная энтальпия равна:

$h\; =\; e\; +\; p\; \rho \; \{\backslash \; displaystyle\; h\; =\; e\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\}$

Материальная производная удельной внутренней энергии может быть выражена как:

$D\; e\; D\; t\; =\; D\; h\; D\; t\; -\; 1\; \rho \; (D\; p\; D\; t\; -\; p\; \rho \; D\; \rho \; D\; t)\; \{\backslash \; displaystyle\; \{De\; \backslash \; over\; Dt\}\; =\; \{Dh\; \backslash \; over\; Dt\}\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rh\; o\}\}\; \backslash \; left\; (\{Dp\; \backslash \; over\; Dt\}\; -\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \{D\; \backslash \; rho\; \backslash \; over\; Dt\}\; \backslash \; right)\}$

Затем, подставляя уравнение импульса в это выражение, получаем:

$D\; e\; D\; t\; =\; D\; h\; D\; t\; -\; 1\; \rho \; (p\; \nabla \; \cdot \; u\; +\; D\; p\; D\; t)\; \{\backslash \; displaystyle\; \{\; De\; \backslash \; over\; Dt\}\; =\; \{Dh\; \backslash \; over\; Dt\}\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \backslash \; left\; (p\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; +\; \{Dp\; \backslash \; over\; Dt\}\; \backslash \; right)\}$

И, подставляя последнее в уравнение энергии, получаем, что выражение энтальпии для уравнения энергии Эйлера:

$D\; h\; D\; t\; =\; 1\; \rho \; D\; p\; D\; t\; \{\backslash \; displaystyle\; \{Dh\; \backslash over\; Dt\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \{Dp\; \backslash \; over\; Dt\}\}$

В системе отсчета, движущейся с невязким и непроводящим потоком, изменение энтальпии напр ямую соответствует изменение давления.

Термодинамика идеальных жидкостей

В термодинамике независимыми переменными являются удельный объем и удельная энтропия, в то время как удельная энергия является функцией состояния этих двух переменных.

Выведение формы, действующей длятермодинамических систем

Рассматривая первое уравнение, переменная должна быть изменена с плотности на удельный объем. По определению:

$v\; \equiv \; 1\; \rho \; \{\backslash \; displaystyle\; v\; \backslash \; Equiv\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\}$

Таким образом, выполняются следующие тождества:

$\nabla \; \rho \; =\; \nabla \; (1\; v)\; =\; -\; 1\; v\; 2\; \nabla \; v\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; rho\; =\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{v\}\}\; \backslash \; right)\; =\; -\; \{\backslash \; frac\; \{1\}\; \{v\; ^\; \{2\}\}\}\; \backslash \; nabla\; v\; \}$

$\partial \; \rho \; \partial \; T\; =\; \partial \; \partial \; T\; (1\; v)\; =\; -\; 1\; v\; 2\; \partial \; v\; \partial \; t\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; rho\}\; \{\backslash \; partial\; t\; \}\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \}\; \{\backslash \; partial\; t\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{v\}\}\; \backslash \; right)\; =\; -\; \{\backslash \; frac\; \{1\}\; \{v\; ^\; \{2\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; v\}\; \{\backslash \; partial\; t\}\}\}$

Затем, подставив эти выражения в уравнение сохранения массы:

$-\; uv\; 2\; \cdot \; \nabla \; v\; -\; 1\; v\; 2\; \partial \; v\; \partial \; t\; =\; -\; 1\; v\; \nabla \; \cdot \; u\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{\; \backslash \; mathbf\; \{u\}\}\; \{v\; ^\; \{2\}\}\}\; \backslash \; cdot\; \backslash \; nabla\; v\; -\; \{\backslash \; frac\; \{1\}\; \{v\; ^\; \{2\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; v\}\; \{\backslash \; partial\; t\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{v\}\}\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\}$

и умножением:

$\partial \; v\; \partial \; t\; +\; u\; \cdot \; \nabla \; v\; =\; v\; \nabla \; \cdot \; u\; \{\backslash \; displayst\; yle\; \{\backslash \; partial\; v\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; v\; =\; v\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\}$

Это уравнение явля ется единственным, принадлежащим общим уравнениям континуума, поэтому только это уравнение имеет тем же форма, например, также в уравнениях Навье-Стокса.

С другой стороны, давление в термодинамике противоположно частной производной удельной внутренней энергии по удельному объему:

$p\; (v,\; s)\; =\; -\; \partial \; e\; (v,\; s)\; \partial \; v\; \{\backslash \; displaystyle\; p\; (v,\; s)\; =\; -\; \{\backslash \; partial\; e\; (v,\; s)\; \backslash over\; \backslash \; partial\; v\}\}$

, поскольку внутренняя энергия в термодинамике является функцией двух упомянутых выше переменных, градиент давления, содержащийся в уравнении импульса, должен быть выражен как:

$-\; \nabla \; p\; (v,\; s)\; =\; -\; \partial \; p\; \partial \; v\; \nabla \; v\; -\; \partial \; p\; \partial \; s\; \nabla \; s\; =\; \partial \; 2\; e\; \partial \; v\; 2\; \nabla \; v\; +\; \partial \; 2\; е\; \partial \; v\; \partial \; s\; \nabla \; s\; \{\backslash \; displaystyle\; -\; \backslash \; nabla\; p\; (v,\; s)\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; v\}\}\; \backslash \; nabla\; v\; -\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; s\}\}\; \backslash \; nabla\; s\; =\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; e\}\; \{\backslash \; partial\; v\; ^\; \{2\}\}\}\; \backslash \; nabla\; v\; +\; \{\backslash \; frac\; \{\backslash \; part\; ial\; ^\; \{2\}\; e\}\; \{\backslash \; partial\; v\; \backslash \; partial\; s\}\}\; \backslash \; nabla\; s\}$

Для краткости удобно изменить обозначение для производных второго порядка:

$-\; \nabla \; p\; (v,\; s)\; =\; evv\; \nabla \; v\; +\; evs\; \nabla \; s\; \{\backslash \; displaystyle\; -\; \backslash \; nabla\; p\; (v,\; s)\; =\; e\_\; \{vv\}\; \backslash \; nabla\; v\; +\; e\_\; \{vs\}\; \backslash \; nabla\; s\}$

Наконец, уравнение энергии:

$D\; e\; D\; t\; =\; -\; pv\; \nabla \; \cdot \; u\; \{\backslash \; displaystyle\; \{De\; \backslash \; over\; Dt\}\; =\; -\; pv\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\}$

можно дополнительно упростить в конвективной форме, изменив переменную с удельной энергии на удельную энтропию : фактическипервый закон термодинамики в локальной форме может быть записан:

$D\; e\; D\; t\; =\; TD\; s\; D\; t\; -\; p\; D\; v\; D\; t\; \{\backslash \; displaystyle\; \{De\; \backslash \; over\; Dt\}\; =\; T\; \{Ds\; \backslash \; over\; Dt\}\; -p\; \{Dv\; \backslash \; over\; Dt\}\}$

путем подстановки материальной производной внутренней энергии уравнение энергии принимает следующий вид:

$TD\; s\; D\; t\; +\; p\; \rho \; 2\; (D\; \rho \; D\; t\; +\; \rho \; \nabla \; \cdot \; U)\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; T\; \{Ds\; \backslash \; over\; Dt\}\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\; ^\; \{2\}\}\}\; \backslash \; left\; (\{D\; \backslash \; rho\; \backslash \; over\; Dt\}\; +\; \backslash \; rho\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; \backslash \; right)\; =\; 0\}$

теперьчлен в скобках идентично нулю согласно закону сохранения массы, тогда уравнение энергии Эйлера становится просто:

$D\; s\; D\; t\; =\; 0\; \{\backslash \; displaystyle\; \{Ds\; \backslash \; over\; Dt\}\; =\; 0\}$

Следовательно, для термодинамической жидкости уравнения Эйлера сжимаемой жидкости лучше всего записывать как:

уравнения Эйлера (конвективная форма для термодинамической системы)

$\{D\; v\; D\; t\; знак\; равно\; v\; \nabla \; \cdot \; U\; D\; u\; D\; t\; =\; vevv\; \nabla \; v\; +\; vevs\; \nabla \; s\; +\; g\; D\; s\; D\; t\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{\; Dv\; \backslash \; overDt\}\; =\; v\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \; [1.2ex]\; \{\backslash \; frac\; \{D\; \backslash \; mathbf\; \{u\}\}\; \{Dt\}\}\; =\; ve\_\; \{vv\}\; \backslash \; nabla\; v\; +\; ve\_\; \{\; vs\}\; \backslash \; nabla\; s\; +\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \; [1.2ex]\; \{Ds\; \backslash \; over\; Dt\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

где:

• $v\; \{\backslash \; displaystyle\; v\}$- удельный объем
• $u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\}$- вектор скорости потока
• $s\; \{\backslash \; displaystyle\; s\}$- удельная энтропия

В общем случае, а не только в случае несжимаемой жидкости, уравнение энергии означает, что дляневязкой термодинамической жидкости удельная энтропия постоянна вдоль линий потока , а также в потоке, зависящем от времени. Основываясь на уравнении сохранения массы, это уравнение можно записать в виде сохранения:

$\partial \; \rho \; s\; \partial \; t\; +\; \nabla \; \cdot \; (\rho \; su)\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; partial\; \backslash \; rho\; s\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; nabla\; \backslash \; cdot\; (\backslash \; rho\; s\; \backslash \; mathbf\; \{u\})\; =\; 0\}$

означает, что для невязкого непроводящего потока выполняется уравнение неразрывности для энтропии.

С другой стороны, двечастные производные второго порядка удельной внутренней энергии в уравнении количества движения требуют указания рассматриваемого материала, то есть удельной внутренней энергии как функции двух переменных, специфичных для объем и удельная энтропия:

$e\; =\; e\; (v,\; s)\; \{\backslash \; displaystyle\; e\; =\; e\; (v,\; s)\}$

Основное уравнение состояния содержит всю термодинамическую информацию о системе (Callen, 1985), точно так же, как пара теплового уравнения состояния вместе с калорическим уравнением состояния.

Форма сохранения

Уравнения Эйлера в пределе Фруда эквивалентны одному уравнению сохранения с сохраняющейся величиной и соответствующим потоком соответственно:

$y\; =\; (\rho \; j\; E\; t);\; F\; =\; (j\; 1\; \rho \; j\; \otimes \; j\; +\; p\; I\; (E\; t\; +\; p)\; 1\; \rho \; j).\; \{\backslash \; displaystyle\; \{\backslash \; mathbf\; \{y\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; rho\; \backslash \backslash \backslash \; mathbf\; \{j\}\; \backslash \backslash \; E\; ^\; \{t\}\; \backslash \; end\; \{pmatrix\}\};\; \backslash \; qquad\; \{\backslash \; mathbf\; \{F\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{j\}\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \backslash \; mathbf\; \{j\}\; \backslash \; otimes\; \backslash \; mathbf\; \{j\}\; +\; p\; \backslash \; mathbf\; \{I\}\; \backslash \backslash \backslash \; left\; (E\; ^\; \{t\}\; +\; p\; \backslash \; right)\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \backslash \; mathbf\; \{j\}\; \backslash end\{pmatrix\}\}.\}$

where:

• $j\; =\; \rho \; u\; \{\backslash displaystyle\; \backslash mathbf\; \{j\}\; =\backslash rho\; \backslash mathbf\; \{u\}\; \}$is the momentum density, a conservation variable.
• $E\; t\; =\; \rho \; e\; +\; 1\; 2\; \rho \; u\; 2\; \{\backslash textstyle\; E^\{t\}=\backslash rho\; e+\{\backslash frac\; \{1\}\{2\}\}\backslash rho\; u^\{2\}\}$is the total energy density (total energy per unit volume).

Here $y\; \{\backslash displaystyle\; \backslash mathbf\; \{y\}\; \}$has length N + 2 and $F\; \{\backslash displaystyle\; \backslash mathbf\; \{F\}\; \}$has size N(N + 2). In general (not only in the Froude lim it) Euler equations are expressible as:

Euler equation(s)(original conservation or Eulerian form)

$\partial \; \partial \; t\; (\; \rho \; j\; E\; t)\; +\; \nabla \; \cdot \; (\; j\; 1\; \rho \; j\; \otimes \; j\; +\; p\; I\; (\; E\; t\; +\; p)\; 1\; \rho \; j)\; =\; (\; 0\; f\; 1\; \rho \; j\; \cdot \; f)\; \{\backslash displaystyle\; \{\backslash frac\; \{\backslash partial\; \}\{\backslash partial\; t\}\}\{\backslash begin\{pmatrix\}\backslash rho\; \backslash \backslash \backslash mathbf\; \{j\}\; \backslash \backslash E^\{t\}\backslash end\{pmatrix\}\}+\backslash nabla\; \backslash cdot\; \{\backslash begin\{pmatrix\}\backslash mathbf\; \{j\}\; \backslash \backslash \{\backslash frac\; \{1\}\{\backslash rho\; \}\}\backslash mathbf\; \{j\}\; \backslash otimes\; \backslash mathbf\; \{j\}\; +p\backslash mathbf\; \{I\}\; \backslash \backslash \backslash left(E^\{t\}+p\backslash right)\{\backslash frac\; \{1\}\{\backslash rho\; \}\}\backslash mathbf\; \{j\}\; \backslash end\{pmatrix\}\}=\{\backslash begin\{pmatrix\}0\backslash \backslash \backslash m\; athbf\; \{f\}\; \backslash \backslash \; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \backslash \; mathbf\; \{j\}\; \backslash \; cdot\; \backslash \; mathbf\; \{f\}\; \backslash \; end\; \{pmatrix\}\}\}$

где:

• $f\; =\; \rho \; g\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{f\}\; =\; \backslash \; rho\; \backslash \; mathbf\; \{g\}\}$- плотность силы, переменная сохранения.

Заметим, что уравнение Эйлера, даже если оно консервативно ( нет внешнего поля, предел Фруда) имеют нет инварианты Римана вообще. Требуются некоторые дополнительные предположения

Однако мы уже упоминали, что для термодинамической жидкости уравнение для полная плотность энергии эквивалентна уравнению сохранения:

$\partial \; \partial \; t\; (\rho \; s)\; +\; \nabla \; \cdot \; (\rho \; su)\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; partial\; \backslash \; over\; \backslash \; partial\; t\}\; (\backslash \; rho\; s)\; +\; \backslash \; nabla\; \backslash \; cdot\; (\backslash \; rho\; s\; \backslash \; mathbf\; \{u\})\; =\; 0\}$

Тогда уравнения сохранения в случае термодинамической жидкости проще выразить как:

уравнение (я) Эйлера (форма сохранения, для термодинамических жидкостей)

$\partial \; \partial \; t\; (\rho \; j\; S)\; +\; \nabla \; \cdot \; (j\; 1\; \rho \; j\; \otimes \; j\; +\; p\; IS\; j\; \rho )\; =\; (0\; f\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\; \}\}\{\backslash begin\{pmatrix\}\backslash rho\; \backslash \backslash \backslash mathbf\; \{j\}\; \backslash \backslash S\backslash end\{pmatrix\}\}+\backslash nabla\; \backslash cdot\; \{\backslash begin\{pmatrix\}\backslash mathbf\; \{j\}\; \backslash \backslash \{\backslash frac\; \{1\}\{\backslash rho\; \}\}\backslash mathbf\; \{j\}\; \backslash otimes\; \backslash mathbf\; \{j\}\; +p\backslash mathbf\; \{I\}\; \backslash \backslash S\{\backslash frac\; \{\backslash mathbf\; \{j\}\; \}\{\backslash rho\; \}\}\backslash end\{pmatrix\}\}=\{\backslash begin\{pmatrix\}0\backslash \backslash \backslash mathbf\; \{f\}\; \backslash \backslash 0\backslash end\{pmatrix\}\}\}$

where:

• $S\; =\; \rho \; s\; \{\backslash displaystyle\; S=\backslash rho\; s\}$is the entropy density, a thermodynamic conservation variable.

Another possible form for the energy equation, being particularly useful for isobarics, is:

$\partial \; H\; t\partial \; t\; +\; \nabla \; \cdot \; (\; H\; t\; u)\; =\; u\; \cdot \; f\; -\; \partial \; p\; \partial \; t\; \{\backslash displaystyle\; \{\backslash frac\; \{\backslash partial\; H^\{t\}\}\{\backslash partial\; t\}\}+\backslash nabla\; \backslash cdot\; \backslash left(H^\{t\}\backslash mathbf\; \{u\}\; \backslash right)=\backslash mathbf\; \{u\}\; \backslash cdot\; \backslash mathbf\; \{f\}\; -\{\backslash frac\; \{\backslash partial\; p\}\{\backslash partial\; t\}\}\}$

where:

• $H\; t\; =\; E\; t\; +\; p\; =\; \rho \; e\; +\; p\; +\; 1\; 2\; \rho \; u\; 2\; \{\backslash textstyle\; H^\{t\}=E^\{t\}+p=\backslash rho\; e+p+\{\backslash frac\; \{1\}\{2\}\}\backslash rho\; u^\{2\}\}$is the total enthalpy density.

Expanding the fluxes can be an important part of constructingnumerical solvers, for example by exploiting (approximate ) solutions to the Riemann problem. In regions where the state vector yvaries smoothly, the equations in conservative form can be put in quasilinear form :

$\partial \; y\; \partial \; t\; +\; A\; i\; \partial \; y\; \partial \; r\; i\; =\; 0.\; \{\backslash displaystyle\; \{\backslash frac\; \{\backslash partial\; \backslash mathbf\; \{y\}\; \}\{\backslash partial\; t\}\}+\backslash mathbf\; \{A\}\; \_\{i\}\{\backslash frac\; \{\backslash partial\; \backslash mathbf\; \{y\}\; \}\{\backslash partial\; r\_\{i\}\}\}=\{\backslash mathbf\; \{0\}\; \}.\}$

where $A\; i\; \{\backslash displaystyle\; \backslash mathbf\; \{A\}\; \_\{i\}\}$are call ed the flux Jacobians defined as the matrices :

$A\; i\; (\; y)\; =\; \partial \; f\; i\; (\; y)\; \partial \; y.\; \{\backslash displaystyle\; \backslash mathbf\; \{A\}\; \_\{i\}(\backslash mathbf\; \{y\})=\{\backslash frac\; \{\backslash partial\; \backslash mathbf\; \{f\}\; \_\{i\}(\backslash mathbf\; \{y\})\}\{\backslash partial\; \backslash mathbf\; \{y\}\; \}\}.\}$

Obviously this Jacobian does not exist in discontinuity regions (e.g. contact discontinuities, shock waves in inviscid nonconductive flows). If the flux Jacobians $A\; i\; \{\backslash displaystyle\; \backslash mathbf\; \{A\}\; \_\{i\}\}$are not functions of the state vector $y\; \{\backslash displaystyle\; \backslash math\; bf\; \{y\}\; \}$, the equations reveals linear.

Characteristic equations

The compressible Euler equations can be decoupled into a set N + 2 волновых уравнений, описывающих звук в континууме Эйлера, если они выражены в характеристических переменных вместо сохраняемых переменных.

Фактически тензор A всегда диагонализуемый. Если все собственные значения (случай уравнений Эйлера) являются действительными,система определяется гиперболической, а физически собственные значения представляют собой скорости распространения информации. Если все они выделены, система определяется строго гиперболической (это будет доказано для одномерных уравнений Эйлера). Кроме того, диагонализация сжимаемого уравнения Эйлера проще, когда уравнение энергии выражается в переменной энтропии (то есть уравнениями для термодинамических жидкостей), чем в других переменных энергии. Это станет ясно при рассмотрении одномерногослучая.

Если $pi\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; \_\; \{i\}\}$- это правый собственный вектор матрицы $A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\}$, соответствующий собственному значению $\lambda \; i\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{i\}\}$, путем построения матрица проекции :

$P\; =\; [p\; 1,\; p\; 2,...,\; pn]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{P\}\; =\; \backslash \; left\; [\backslash \; mathbf\; \{p\}\; \_\; \{1\},\; \backslash \; mathbf\; \{p\}\; \_\; \{2\},...,\; \backslash \; mathbf\; \{p\}\; \_\; \{n\}\; \backslash \; right\; ]\}$

Наконец, можно найтихарактеристические переменные как:

$w\; =\; P\; -\; 1\; y,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{w\}\; =\; \backslash \; mathbf\; \{P\}\; ^\; \{-\; 1\}\; \backslash \; mathbf\; \{y\},\}$

Поскольку A является константой, умножение исходного одномерного уравнения в потоково-якобианской форме на P дает характеристические уравнения:

$\partial \; wi\; \partial \; t\; +\; \lambda \; j\; \partial \; wi\; \partial \; rj\; знак\; равно\; 0\; я\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; w\_\; \{i\}\}\; \{\backslash \; partial\; t\}\}\; +\; \backslash \; lambda\; \_\; \{j\}\; \{\backslash \; frac\; \{\backslash \; partial\; w\_\; \{i\}\}\; \{\backslash \; partial\; r\_\; \{j\; \}\}\}\; =\; 0\_\; \{i\}\}$

Исходные уравнения были разделены на N + 2 характеристических уравнения, каждое из которых описывает простую волну, причем собственными значениями являются скорости волн. Переменные w i называются характеристическими переменными и являются подмножеством консервативных переменных. Наконец, решение задачи начального значения в терминах характеристических переменных оказывается очень простым. В одном пространственном измерении это:

$wi\; (x,\; t)\; =\; wi\; (x\; -\; \lambda \; it,\; 0)\; \{\backslash \; displaystyle\; w\_\; \{i\}\; (x,\; t)\; =\; w\_\; \{i\}\; \backslash \; l\; eft\; (x-\; \backslash \; lambda\; \_\; \{i\}\; t,\; 0\; \backslash \; right)\}$

Тогда решение в терминах исходных консервативных переменных получается обратным преобразованием:

$y\; =\; P\; w,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\; =\; \backslash \; mathbf\; \{\; P\}\; \backslash \; mathbf\; \{w\},\}$

это вычисление может быть выражено как линейная комбинация собственных векторов:

$y\; (x,\; t)\; =\; \sum \; i\; =\; 1\; mwi\; (x\; -\; \lambda \; it,\; 0)\; pi,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\; (x,\; t)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{m\}\; w\_\; \{i\}\; \backslash \; left\; (x-\; \backslash \; lambda\; \_\; \{i\}\; t,\; 0\; \backslash \; right)\; \backslash \; mathbf\; \{\; p\}\; \_\; \{i\},\}$

Теперь становитсяочевидным, что характеристические переменные действуют как веса в линейной комбинации собственных векторов якобиана. Решение можно рассматривать как суперпозицию волн, каждая из которых переносится независимо без изменения формы. Каждая i-я волна имеет форму w ipiи скорость распространения λ i. Ниже мы покажем очень простой пример этой процедуры решения.

Волны в одномерной невязкой непроводящей термодинамической жидкости

Если рассматривать уравнения Эйлера длятермодинамической жидкости с двумя дополнительными предположениями об одном пространственном измерении и свободном (без внешнего поля: g = 0):

$\{\partial \; v\; \partial \; t\; +\; u\; \partial \; v\; \partial \; x\; -\; v\; \partial \; u\; \partial \; x\; =\; 0\; \partial \; u\; \partial \; t\; +\; u\; \partial \; u\; \partial \; x\; -\; evvv\; \partial \; v\; \partial \; x\; -\; evsv\; \partial \; s\; \partial \; x\; =\; 0\; \partial \; s\; \partial \; t\; +\; U\; \partial \; s\; \partial \; Икс\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{\backslash \; partial\; v\; \backslash \; over\; \backslash \; partial\; t\}\; +\; u\; \{\backslash \; partial\; v\; \backslash \; over\; \backslash \; partial\; x\}\; -v\; \{\backslash \; partial\; u\; \backslash \; над\; \backslash \; partial\; x\}\; =\; 0\; \backslash \backslash \; [1.2ex]\; \{\backslash \; partial\; u\; \backslash \; over\; \backslash \; partial\; t\}\; +\; u\; \{\backslash \; partial\; u\; \backslash \; over\; \backslash partial\; x\}\; -e\_\; \{vv\}\; v\; \{\backslash \; partial\; v\; \backslash \; over\; \backslash \; partial\; x\}\; -e\_\; \{vs\}\; v\; \{\backslash \; partial\; s\; \backslash \; over\; \backslash \; partial\; x\}\; =\; 0\; \backslash \backslash \; [1.2ex]\; \{\backslash \; partial\; s\; \backslash \; over\; \backslash \; partial\; t\}\; +\; u\; \{\backslash \; partial\; s\; \backslash \; over\; \backslash \; partial\; x\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Если определить вектор переменных:

$y\; =\; (vus)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; v\; \backslash \backslash \; u\; \backslash \backslash \; s\; \backslash \; end\; \{pmatrix\}\}\}$

напоминая, что $v\; \{\backslash \; displaystyle\; v\}$- это удельный объем, $u\; \{\backslash \; displaystyle\; u\}$скорость потока, $с\; \{\; \backslash \; displ\; aystyle\; s\}$удельной энтропии, соответствующая матрица якоби имеет вид:

$A\; =\; (u\; -\; v\; 0\; -\; e\; v\; v\; v\; u\; -\; e\; v\; s\; v\; 0\; 0\; u).\; \{\backslash \; displaystyle\; \{\backslash \; mathbf\; \{A\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; u\; -v\; 0\; \backslash \backslash \; -\; e\_\; \{vv\}\; v\; u\; -e\_\; \{vs\}\; v\; \backslash \backslash \; 0\; 0\; u\; \backslash \; end\; \{pmatrix\}\}.\}$

Сначала необходимо найти собственные значения этой матрицы, решив характеристическое уравнение :

$det\; (A\; (y)\; -\; \lambda \; (y)\; I)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; det\; (\backslash \; mathbf\; \{A\}\; (\backslash \; mathbf\; \{y)\; \})\; -\; \backslash \; lambda\; (\backslash \; mathbf\; \{y\})\; \backslash \; mathbf\; \{I\})\; =\; 0\}$

, чтоявно:

$det\; [u\; -\; \lambda \; -\; v\; 0\; -\; evvvu\; -\; \lambda \; -\; evsv\; 0\; 0\; u\; -\; \lambda \; ]\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; u-\; \backslash \; lambda\; -v\; 0\; \backslash \backslash \; -\; e\_\; \{vv\}\; v\; u-\; \backslash \; lambda\; -e\_\; \{vs\}\; v\; \backslash \backslash \; 0\; 0\; u-\; \backslash \; lambda\; \backslash \; end\; \{bmatrix\}\; \}\; =\; 0\}$

Этот детерминант очень прост: самое быстрое вычисление начинается с последней строки, поскольку она имеет наибольшее количество нулевых элементов.

$(u\; -\; \lambda )\; det\; [u\; -\; \lambda \; -\; v\; -\; evvvu\; -\; \lambda ]\; =\; 0\; \{\backslash \; displaystyle\; (u-\; \backslash \; lambda)\; \backslash \; det\; \{\backslash \; begin\; \{bmatrix\}\; u-\; \backslash \; lambda\; -v\; \backslash \backslash \; -\; e\_\{vv\}\; v\; u-\; \backslash \; lambda\; \backslash \; end\; \{bmatrix\}\}\; =\; 0\}$

Теперь, вычислив определитель 2 × 2:

$(u\; -\; \lambda )\; ((u\; -\; \lambda )\; 2\; -\; evvv\; 2)\; =\; 0\; \{\; \backslash \; displaystyle\; (u-\; \backslash \; lambda)\; \backslash \; left\; ((u-\; \backslash \; lambda)\; ^\; \{2\}\; -e\_\; \{vv\}\; v\; ^\; \{2\}\; \backslash \; right)\; =\; 0\}$

путем определения параметра:

$a\; (\; v,\; s)\; \equiv \; vevv\; \{\backslash \; displaystyle\; a\; (v,\; s)\; \backslash \; Equiv\; v\; \{\backslash \; sqrt\; \{e\_\; \{vv\}\}\}\}$

или эквивалентно в механических переменных, как:

$a\; (\rho ,\; p)\; \equiv \; \partial \; p\; \partial \; \rho \; \{\backslash \; displaystyle\; a\; (\backslash \; rho,\; p)\; \backslash \; Equiv\; \{\backslash \; sqrt\; \{\backslash \; partial\; p\; \backslash \; over\; \backslash \; partial\; \backslash \; rho\}\}\}$

Этотпараметр всегда действителен согласно второму закону термодинамики. На самом деле второй закон термодинамики можно выразить несколькими постулатами. Наиболее элементарным из них с математической точки зрения является утверждение о выпуклости основного уравнения состояния, то есть матрицы Гесса удельной энергии, выраженной как функция удельного объема и удельной энтропии:

$(evvevsevsess)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{pmatrix\}\; e\_\; \{vv\}\; e\_\; \{vs\}\; \backslash \backslash \; e\_\; \{vs\}\; e\_\; \{ss\}\; \backslash \; end\; \{pmat\; rix\}\}\}$

определяется положительно. Этот оператор соответствует двум условиям:

$\{evv>0\; evvess\; -\; evs\; 2>0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; e\_\; \{vv\}>0\; \backslash \backslash \; [1.2ex]\; e\_\; \{vv\; \}\; e\_\; \{ss\}\; -e\_\; \{vs\}\; ^\; \{2\}>0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Первое условиегарантирует, что параметр a определен как действительный.

В конечном итоге получается характеристическое уравнение:

$(u\; -\; \lambda )\; ((\; u\; -\; \lambda )\; 2\; -\; a\; 2)\; знак\; равно\; 0\; \{\backslash \; displaystyle\; (u-\; \backslash \; lambda)\; \backslash \; left\; ((u-\; \backslash \; lambda)\; ^\; \{2\}\; -a\; ^\; \{2\}\; \backslash \; right)\; =\; 0\}$

Имеющий три действительных решения:

$\lambda \; 1\; (v,\; u,\; s)\; =\; u\; -\; a\; (v,\; s)\; \lambda \; 2\; (u)\; =\; u,\; \lambda \; 3\; (v,\; u,\; s)\; =\; u\; +\; a\; (v,\; s)\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{1\}\; (v,\; u,\; s)\; =\; ua\; (v,\; s)\; \backslash \; quad\; \backslash \; lambda\; \_\; \{2\}\; (u)\; =\; u,\; \backslash \; quad\; \backslash \; lambda\; \_\; \{3\}\; (v,\; u,\; s)\; =\; u\; +\; a\; (v,\; s)\; \}$

Тогда матрица имеет три выделенных действительных собственных значения: одномерные уравнения Эйлера являются строго гиперболой ic system .

На этом этапе следует определить три собственных вектора: каждый получается путем подстановки одного собственного значения в уравнение собственных значений и последующего его решения. Подставляя первое собственное значение λ 1, получаем:

$(a\; -\; v\; 0\; -\; evvva\; -\; evsv\; 0\; 0\; a)\; (v\; 1\; u\; 1\; s\; 1)\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{pmatrix\; \}\; a\; -v0\; \backslash \backslash \; -\; e\_\; \{vv\}\; v\; a\; -e\_\; \{vs\}\; v\; \backslash \backslash \; 0\; 0\; a\; \backslash \; end\; \{pmatrix\}\}\; \{\backslash \; begin\; \{pmatrix\}\; v\_\; \{1\}\; \backslash \backslash \; u\_\; \{1\}\; \backslash \backslash \; s\_\; \{1\}\; \backslash \; end\; \{pmatrix\}\}\; =\; 0\}$

На основе третьего уравнения, которое просто имеет решение s 1 = 0, система сводится к:

$(a\; -\; v\; -\; a\; 2\; /\; va)\; (\; v\; 1\; и\; 1)\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{pmatrix\}\; a\; -v\; \backslash \backslash \; -\; a\; ^\; \{2\}\; /\; v\; a\; \backslash \; end\; \{pmatrix\}\}\; \{\backslash \; begin\; \{pmatrix\}\; v\_\; \{1\}\; \backslash \backslash \; u\_\; \{1\; \}\; \backslash \; end\; \{pmatrix\}\}\; =\; 0\}$

Два уравнения, как обычно, избыточны, тогда собственный векторопределяется с помощью константы умножения. Мы выбираем правильный собственный вектор:

$p\; 1\; =\; (va\; 0)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; \_\; \{1\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; v\; \backslash \backslash \; a\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\}$

Два других собственных вектора можно найти с помощью аналогичной процедуры:

$p\; 2\; =\; (evs\; 0\; -\; (av)\; 2),\; p\; 3\; =\; (v\; -\; a\; 0)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; \_\; \{2\; \}\; =\; \{\backslash \; begin\; \{pmatrix\}\; e\_\; \{vs\}\; \backslash \backslash \; 0\; \backslash \backslash \; -\; \backslash \; left\; (\{\backslash \; frac\; \{a\}\; \{v\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; end\; \{pmatrix\}\},\; \backslash \; qquad\; \backslash \; mathbf\; \{\; p\}\; \_\; \{3\}\; =\; \{\backslash \; begin\; \{pmatrix\}v\; \backslash \backslash \; -\; a\; \backslash \backslash \; 0\; \backslash \; end\; \{pmatrix\}\}\}$

Тогда матрица проекции может быть построена:

$P\; (v,\; u,\; s)\; знак\; равно\; (п\; 1,\; п\; 2,\; п\; 3)\; =\; (vevsva\; 0\; -\; a\; 0\; -\; (av)\; 2\; 0)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{P\}\; (v,\; u,\; s)\; =\; (\backslash \; mathbf\; \{p\}\; \_\; \{1\; \},\; \backslash \; mathbf\; \{p\}\; \_\; \{2\},\; \backslash \; mathbf\; \{p\}\; \_\; \{3\})\; =\; \{\backslash \; begin\; \{pmatrix\}\; v\; e\_\; \{vs\}\; v\; \backslash \backslash \; a\; 0\; -a\; \backslash \backslash \; 0\; -\; \backslash \; left\; (\{\backslash \; frac\; \{\; a\}\; \{v\}\}\; \backslash \; right)\; ^\; \{2\}\; 0\; \backslash \; end\; \{pmatrix\}\}\}$

Наконец, становится очевидным, что реальный параметр a, ранее определенный, является скоростью распространенияинформации, характерной для гиперболической системы, состоящей из Уравнения Эйлера, т.е. это скорость волны. Остается показать, что скорость звука соответствует частному случаю:

$as\; \equiv \; (\partial \; p\; \partial \; \rho )\; s\; \{\backslash \; displaystyle\; a\_\; \{s\}\; \backslash \; Equiv\; \{\backslash \; sqrt\; \{\backslash \; left\; (\{\backslash \; partial\; p\; \backslash \; over\; \backslash \; partial\; \backslash \; rho\}\; \backslash \; right)\; \_\; \{s\}\}\}\}$

Сжимаемость и скорость звука

Скорость звука определяется как скорость волны изоэнтропического преобразования:

$как\; (\rho ,\; p)\; \equiv \; (\partial \; п\; \partial \; \rho )\; s\; \{\backslash \; displaystyle\; a\_\; \{s\}\; (\backslash \; rho,p)\; \backslash \; Equiv\; \{\backslash \; sqrt\; \{\backslash \; left\; (\{\backslash \; partial\; p\; \backslash \; over\; \backslash \; partial\; \backslash \; rho\}\; \backslash \; right)\; \_\; \{s\}\}\}\; \}$

по определению изоэнтропической сжимаемости:

$K\; s\; (\rho ,\; p)\; \equiv \; 1\; \rho \; (\partial \; p\; \partial \; \rho )\; s\; \{\backslash \; displaystyle\; K\_\; \{s\}\; (\backslash \; rho,\; p)\; \backslash \; Equiv\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \backslash \; left\; (\{\backslash \; partial\; p\; \backslash \; over\; \backslash \; partial\; \backslash \; rho\}\; \backslash \; right)\; \_\; \{s\}\}$

скорость звука всегда вычисляется как квадратный корень из отношения между изоэнтропической сжимаемостью и плотностью:

$как\; \equiv \; K\; s\; \rho \; \{\backslash \; displaystyle\; a\_\; \{s\}\; \backslash \; Equiv\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{K\_\; \{s\}\}\; \{\backslash \; rho\}\}\}\}$

Идеальный газ

Скорость звука в идеальном газе зависит только от его температуры:

$as\; (T)\; =\; \gamma \; T\; m\; \{\backslash \; displaystyle\; a\_\; \{s\}\; (T)\; =\; \{\backslash \; sqrt\; \{\backslash \; gam\; ma\; \{\backslash \; frac\; \{T\}\; \{m\}\}\}\}\}$

Вывод формы, действительный для идеальных газов

В идеальном газе изоэнтропическое преобразование описывается следующим образом:

$d\; (p\; \rho \; -\; \gamma )\; s\; =\; 0\; \{\backslash \; displaystyle\; d\; \backslash \; left\; (p\; \backslash \; rho\; ^\; \{-\; \backslash \; gamma\}\; \backslash \; right)\; \_\; \{s\}\; =\; 0\}$

, где γ - коэффициент теплоемкости, константа для материал. Путемявного указания дифференциалов:

$\rho \; -\; \gamma \; (dp)\; s\; +\; \gamma \; p\; \rho \; -\; \gamma \; -\; 1\; (d\; \rho )\; s\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; rho\; ^\; \{-\; \backslash \; gamma\}\; (dp)\; \_\; \{s\}\; +\; \backslash \; gamma\; p\; \backslash \; rho\; ^\; \{-\; \backslash \; gamma\; -1\}\; (d\; \backslash \; rho)\; \_\; \{s\}\; =\; 0\}$

и делением на ρ dρ:

$(\partial \; p\; \partial \; \rho )\; s\; =\; \gamma \; p\; \rho \; \{\backslash \; displaystyle\; \backslash \; left\; (\{\backslash \; partial\; p\; \backslash \; over\; \backslash \; partial\; \backslash \; rho\}\; \backslash \; right)\; \_\; \{s\}\; =\; \backslash \; gamma\; p\; \backslash \; rho\}$

Тогда при подстановке в общих определениях для идеального газа изоэнтропическая сжимаемость просто пропорциональна давление:

$K\; s\; (p)\; =\; \gamma \; p\; \{\backslash \; displaystyle\; K\_\; \{s\}\; (p)=\; \backslash \; gamma\; p\}$

и результаты скорости звука (закон Ньютона – Лапласа ):

$как\; (\rho ,\; p)\; =\; \gamma \; p\; \rho \; \{\backslash \; displaystyle\; a\_\; \{s\}\; (\backslash \; rho,\; p)\; =\; \{\backslash \; sqrt\; \{\backslash \; gamma\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\}\}\}$

Примечательно, что для идеального газа выполняется закон идеального газа, который в математической форме выглядит просто:

$p\; =\; n\; T\; \{\backslash \; displaystyle\; p\; =\; nT\}$

, где n - число . плотность, а T - абсолютная температура, при условии, что она измеряется в энергетическихединицах (то есть в джоулях ) путем умножения на Bol постоянная Цмана. Поскольку массовая плотность пропорциональна числовой плотности через среднюю молекулярную массу m материала:

$\rho \; =\; mn\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; mn\}$

Закон идеального газа может быть изменен в формулу:

$p\; \rho \; =\; T\; m\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; =\; \{\backslash \; frac\; \{T\}\; \{m\}\}\}$

Подставляя это соотношение в уравнение Ньютона – Лапласа По закону, наконец, достигается выражение скорости звукав идеальном газе как функции температуры.

Поскольку удельная энтальпия в идеальном газе пропорциональна его температуре:

$h\; =\; cp\; T\; =\; \gamma \; \gamma \; -\; 1\; T\; m\; \{\backslash \; displaystyle\; h\; =\; c\_\; \{p\}\; T\; =\; \{\backslash \; frac\; \{\backslash \; gamma\}\; \{\; \backslash \; gamma\; -1\}\}\; \{\backslash \; frac\; \{T\}\; \{m\}\}\}$

скорость звука в идеальном газе также может зависеть только от его удельной энтальпии:

$as\; (h)\; =\; (\gamma \; -\; 1)\; h\; \{\backslash \; displaystyle\; a\_\; \{s\}\; (h)\; =\; \{\backslash \; sqrt\; \{(\backslash \; gamma\; -1)\; h\}\}\}$

Теорема Бернулли является прямым следствием Уравнения Эйлера.

Несжимаемый регистр и форма Лэмба

Справедливо тождество векторного исчисления перекрестного произведения ротации :

$v\; \times \; (\nabla \; \times \; F)\; знак\; равно\; \nabla \; F\; (v\; \cdot \; F)\; -\; v\; \cdot \; \nabla \; F,\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{v\; \backslash \; \backslash \; times\}\; \backslash \; left\; (\backslash \; mathbf\; \{\backslash \; nabla\; \backslash \; times\; F\}\; \backslash \; right)\; =\; \backslash \; nabla\; \_\; \{F\}\; \backslash \; left\; (\backslash \; mathbf\; \{v\; \backslash \; cdot\; F\}\; \backslash \; right)\; -\; \backslash \; mathbf\; \{v\; \backslash \; cdot\; \backslash \; nabla\}\; \backslash \; mathbf\; \{F\}\; \backslash ,\}$

, где обозначение индекса Фейнмана $\nabla \; F\; \{\backslash \; displaystyl\; e\; \backslash \; nabla\; \_\; Используется\; \{F\}\}$, что означает, что индексированный градиент действует только на множитель $F\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\}$.

Лэмба в его знаменитой классической книге «Гидродинамика» ( 1895), все еще находящийся в печати, использовал это тождество для изменения конвективного члена скорости потока во вращательной форме:

$u\; \cdot \; \nabla \; u\; =\; 1\; 2\; \nabla \; (u\; 2)\; +\; (\nabla \; \times \; u)\; \times \; u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; mathbf\; \{u\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; nabla\; \backslash \; left\; (u\; ^\; \{2\}\backslash \; right)\; +\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\; \backslash \; раз\; \backslash \; mathbf\; \{u\}\}$

уравнение импульса Эйлера в форме Лэмба принимает следующий вид:

$\partial \; u\; \partial \; t\; +\; 1\; 2\; \nabla \; (u\; 2)\; +\; (\nabla \; \times \; u)\; \times \; u\; +\; \nabla \; p\; \rho \; знак\; равно\; g\; =\; \partial \; u\; \partial \; T\; +\; 1\; 2\; \nabla \; (u\; 2)\; -\; u\; \times \; (\nabla \; \times \; u)\; +\; \nabla \; p\; \rho \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\}\; \{\backslash \; partial\; t\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; nabla\; \backslash \; left\; (u\; ^\; \{2\}\; \backslash \; right)\; +\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\; \backslash \; times\; \backslash \; mathbf\; \{u\}\; +\; \{\backslash \; frac\; \{\backslash \; nabla\; p\}\; \{\backslash \; rho\}\}\; =\; \backslash \; mathbf\; \{g\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\}\; \{\backslash \; part\; ial\; t\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; nabla\; \backslash \; left\; (u\; ^\; \{2\}\; \backslash \; right)\; -\; \backslash \; mathbf\; \{u\}\; \backslash \; times\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\; +\; \{\backslash \; frac\; \{\backslash \; nabla\; p\}\; \{\backslash \; rho\}\}\}$

Сейчас, исходя из другого тождества:

$\nabla \; (p\; \rho )\; =\; \nabla \; p\; \rho \; -\; p\; \rho \; 2\; \nabla \; \rho \; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{\backslash \; nabla\; p\}\; \{\backslash \; rho\}\}\; -\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\; ^\; \{2\}\}\}\; \backslash \; nabla\; \backslash \; rho\}$

уравнение импульса Эйлера принимает форму, оптимальную для демонстрации Теорема Бернулли для установившихся потоков:

$\nabla \; (12\; u\; 2\; +\; p\; \rho )\; -\; g\; =\; -\; p\; \rho \; 2\; \nabla \; \rho \; +\; u\; \times \; (\nabla \; \times \; u)\; -\; \partial \; u\; \partial \; t\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; -\; \backslash \; mathbf\; \{g\}\; =\; -\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\; ^\; \{2\}\}\}\; \backslash \; nabla\; \backslash \; rho\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; times\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\; \}\; \{\backslash \; partial\; t\}\}\}$

Фактически, в случае внешнего консервативного поля, определяя его потенциал φ:

$\nabla \; (1\; 2\; u\; 2\; +\; \varphi \; +\; p\; \rho )\; =\; -\; п\; \rho \; 2\; \nabla \; \rho \; +\; U\; \times \; (\nabla \; \times \; U)\; -\; \partial \; U\; \partial \; T\; \{\backslash \; Displaystyle\; \backslash \; nabla\; \backslash \; left(\{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; \backslash \; phi\; +\; \{\backslash \; frac\; \{\; p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; =\; -\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\; ^\; \{2\}\}\}\; \backslash \; nabla\; \backslash \; rho\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; times\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\}\; \{\backslash \; partial\; t\}\}\}$

В случае установившегося потока производная скорости потока по времени исчезает, поэтому уравнение количества движения принимает вид:

$\nabla \; (1\; 2\; U\; 2\; +\; \varphi \; +\; p\; \rho )\; знак\; равно\; -\; п\; \rho \; 2\; \nabla \; \rho \; +\; U\; \times \; (\nabla \; \times \; u)\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; \backslash \; phi\; +\; \{\backslash \; frac\; \{p\}\{\backslash \; rho\}\}\; \backslash \; right)\; =\; -\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\; ^\; \{2\}\}\}\; \backslash \; nabla\; \backslash \; rho\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; times\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\}$

И при проецировании уравнения импульса на направление потока, то есть вдоль линии тока , перекрестное произведение исчезает, потому что его результат всегда перпендикулярен скорости:

$u\; \cdot \; \nabla \; (1\; 2\; U\; 2\; +\; \varphi \; +\; p\; \rho )\; знак\; равно\; -\; p\; \rho \; 2\; U\; \cdot \; \nabla \; \rho \; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{u\; \}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; \backslash \; phi\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; =\; -\; \{\backslash frac\; \{p\}\; \{\; \backslash \; rho\; ^\; \{2\}\}\}\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; rho\}$

В случае установившейся несжимаемой жидкости уравнение массы просто:

$u\; \cdot \; \nabla \; \rho \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\; \}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; rho\; =\; 0\}$,

то есть закон сохранения массы для установившегося потока несжимаемой жидкости утверждает, что плотность вдоль линии тока постоянна . Тогда уравнение количества движения Эйлера в случае установившейся несжимаемой жидкости принимает следующий вид:

$u\; \cdot \; \nabla \; (1\; 2\; u\; 2\; +\; \varphi \; +\; p\; \rho )=\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{\; 1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; \backslash \; phi\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; =\; 0\}$

Удобство определения общего напора для поток невязкой жидкости теперь очевиден:

$bl\; \equiv \; 1\; 2\; u\; 2\; +\; \varphi \; +\; p\; \rho ,\; \{\backslash \; displaystyle\; b\_\; \{l\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; \backslash \; phi\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\},\}$

который может быть просто записан как:

$u\; \cdot \; \nabla \; bl\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; b\_\; \{l\}\; =\; 0\; \}$

То есть баланс количествадвижения для устойчивого невязкого и несжимаемого потока во внешнем консервативном поле утверждает, что общий напор вдоль линии тока постоянен .

Сжимаемый случай

В самом общем в устойчивом (сжимаемом) случае уравнение массы в форме сохранения:

$\nabla \; \cdot \; j\; =\; \rho \; \nabla \; \cdot \; u\; +\; u\; \cdot \; \nabla \; \rho \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{j\}\; =\; \backslash \; rho\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; +\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; rho\; =\; 0\}$.

Следовательно, предыдущий пример давление скорее

$u\; \cdot \; \nabla \; (1\; 2\; u\; 2\; +\; \varphi \; +\; p\; \rho )\; =p\; \rho \; \nabla \; \cdot \; u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{2\}\; \}\; u\; ^\; \{2\}\; +\; \backslash \; phi\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\}$

правая часть появляется в уравнении энергии в конвективной форме, которая в установившемся состоянии выглядит так:

$u\; \cdot \; \nabla \; e\; =\; -\; p\; \rho \; \nabla \; \cdot \; u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; e\; =\; -\; \{\; \backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\}$

Таким образом, уравнение энергии принимает следующий вид:

$u\; \cdot \nabla \; (e\; +\; p\; \rho \; +\; 1\; 2\; u\; 2\; +\; \varphi )\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; left\; (е\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; \backslash \; phi\; \backslash \; right)\; =\; 0,\}$

, так что внутренняя удельная энергия теперь присутствует в голове.

Поскольку потенциал внешнего поля обычно мал по сравнению с другими членами, удобно сгруппировать последние в полной энтальпии :

$ht\; \equiv \; e\; +\; p\; \rho \; +\; 1\; 2\; u\; 2\; \{\; \backslash \; displaystyle\; h\; ^\; \{t\}\; \backslash \; Equiv\; e\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\}$

, а дляпотока невязкого газа равен:

$bg\; \equiv \; ht\; +\; \varphi \; =\; bl\; +\; e,\; \{\backslash \; displaystyle\; b\_\; \{g\}\; \backslash \; Equiv\; h\; ^\; \{t\}\; +\; \backslash \; phi\; =\; b\_\; \{l\}\; +\; e,\}$

что можно записать как

$U\; \cdot \; \nabla \; bg\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; b\_\; \{g\}\; =\; 0\}$

То есть, баланс энергии для устойчивого невязкого потока во внешнем консервативном поле утверждает, что сумма полной энтальпии и внешнего потенциала постоянна вдоль линии тока .

В обычном случае малого потенциального поля просто:

$u\; \cdot \; \nabla \; ht\; \sim \; 0\; \{\backslash \; displaystyle\; \backslash mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; h\; ^\; \{t\}\; \backslash \; sim\; 0\}$

Форма Фридмана и форма Крокко

Путем замены градиента давления на градиент энтропии и энтальпии в соответствии с первым законом термодинамики в форме энтальпии:

$v\; \nabla \; p\; =\; -\; T\; \nabla \; s\; +\; \nabla \; h\; \{\backslash \; displaystyle\; v\; \backslash \; nabla\; p\; =\; -T\; \backslash \; nabla\; s\; +\; \backslash \; nabla\; h\}$

в конвективной форме уравнения импульса Эйлера, мы получаем:

$D\; u\; D\; t\; =\; T\; \nabla \; s\; -\; \nabla \; h\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{D\; \backslash \; mathbf\; \{u\}\}\; \{Dt\}\}\; =\; T\; \backslash \; nabla\; \backslash ,\; s-\; \backslash \; nabla\; \backslash ,\; h\}$

Фридман вывелэто уравнение для частного случая идеального газа и опубликовано в 1922 году. Однако это уравнение является общим для невязкой непроводящей жидкости, и никакое уравнение состояния в нем не подразумевается.

С другой стороны, подставляя энтальпийную форму первого закона термодинамики во вращательную форму уравнения импульса Эйлера, получаем:

$\partial \; u\; \partial \; t\; +\; 1\; 2\; \nabla \; (u\; 2)\; +\; (\nabla \; \times \; U)\; \times \; U\; +\; \nabla \; п\; \rho \; знак\; равно\; g\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\}\; \{\backslash \; partial\; t\}\}\; +\; \{\backslash \; frac\{1\}\; \{2\}\}\; \backslash \; nabla\; \backslash \; left\; (\; u\; ^\; \{2\}\; \backslash \; right)\; +\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\; \backslash \; times\; \backslash \; mathbf\; \{u\}\; +\; \{\backslash \; frac\; \{\backslash \; nabla\; p\}\; \{\backslash \; rho\}\}\; =\; \backslash \; mathbf\; \{g\}\}$

и определив удельную общую энтальпию:

$ht\; =\; h\; +\; 1\; 2\; u\; 2\; \{\backslash \; displaystyle\; h\; ^\; \{t\}\; =\; h\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\}$

один приходит к форме Крокко – Вазсоньи (Crocco, 1937) уравнения импульса Эйлера:

$\partial \; u\; \partial \; t\; +\; (\nabla \; \times \; u)\; \times \; u\; -\; T\; \nabla \; s\; +\; \nabla \; ht\; знак\; равно\; г\; \{\backslash \; Displaystyle\; \{\backslash \; гидроразрыва\; \{\backslash \; partial\; \backslash \; mathbf\; \{u\}\}\; \{\backslash \; partial\; t\; \}\}\; +\; (\backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\})\; \backslash \; times\; \backslash \; mathbf\; \{u\}\; -T\; \backslash \; nabla\; s\; +\; \backslash \; nabla\; h\; ^\; \{t\}\; =\; \backslash \; mathbf\; \{g\}\}$

В стационарном случае две переменные энтропия и полная энтальпия особенно полезны, поскольку уравнения Эйлера можно преобразовать в форму Крокко:

$\{u\; \times \; \nabla \; \times \; u\; +\; Т\; \nabla \; s\; -\; \nabla \; ht\; =\; гу\; \cdot \; \nabla \; s\; знак\; равно\; 0\; U\; \cdot \; \nabla \; ht\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{u\}\; \backslash \; times\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\}\; +\; T\; \backslash \; nabla\; s-\; \backslash \; nabla\; h\; ^\; \{t\}\; =\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; s\; =0\; \backslash \backslash \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; h\; ^\; \{t\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Наконец, если поток также изотермический:

$T\; \nabla \; s\; =\; \nabla \; (T\; s)\; \{\backslash \; displaystyle\; T\; \backslash \; nabla\; s\; =\; \backslash \; nabla\; (Ts)\}$

путем определения удельной полной свободной энергии Гиббса :

$gt\; \equiv \; ht\; +\; T\; s\; \{\backslash \; displaystyle\; g\; ^\; \{t\}\; \backslash \; Equiv\; h\; ^\; \{t\}\; +\; Ts\}$

форма Крокко может быть уменьшена до:

$\{u\; \times \; \nabla \; \times \; u\; -\; \nabla \; gt\; =\; gu\; \cdot \; \nabla \; gt\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{u\}\; \backslash \; times\; \backslash \; nabla\; \backslash \; times\; \backslash \; mathbf\; \{u\}\; -\; \backslash \; nabl\; a\; g\; ^\; \{t\}\; =\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \backslash \; mathbf\; \{u\}\; \backslash \; cdot\; \backslash \; nabla\; g\; ^\; \{t\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

Из этих соотношений можно сделать вывод, что удельная полная свободная энергия однородна в установившемся безвихревом изотермическом изоэнтропическом невязком потоке.

Уравнения Эйлера - это квазилинейные гиперболические уравнения, а их общие решения - волны. При определенных предположениях их можно упростить, что приведет к уравнениюБюргерса. Подобно знакомым океанским волнам, волны, описываемые уравнениями Эйлера , «разбиваются» и образуются так называемые ударные волны ; это нелинейный эффект и представляет решение, которое становится многозначным. Физически это представляет собой нарушение предположений, которые привели к формулировке дифференциальных уравнений, и для извлечения дополнительной информации из уравнений мы должны вернуться к более фундаментальной интегральнойформе. Затем слабые решения формулируются путем работы «скачками» (разрывами) в величинах потока - плотности, скорости, давлении, энтропии - с использованием уравнений Ренкина – Гюгонио. Физические величины редко бывают прерывистыми; в реальных потоках эти неоднородности сглаживаются за счет вязкости и за счет теплопередачи. (См. уравнения Навье – Стокса )

Распространение ударной волны изучается - среди многих других областей - в аэродинамике и ракетном двигателе, где возникают достаточно быстрые потоки.

Для правильного вычисления величин континуума в разрывных зонах (например, ударных волнах или пограничных слоях) из локальных форм (все указанные выше формы являются локальными формами, поскольку описываемые переменные типичны для одной точки в рассматриваемом пространстве, т. Е. Они являются локальными переменными) уравнений Эйлера с помощью методов конечных разностей, как правило,для памяти компьютеров сейчас и в ближайшем будущем потребуется слишком много пространственных точек и временных шагов. В этих случаях обязательно избегать локальных формы уравнений сохранения, передающие некоторые слабые формы, такие как конечный объем 1.

уравнения Ренкина – Гюгонио

Начиная с простейшего случая, рассматривается устойчивое свободное сохранение уравнение в форме сохранения в пространственной области:

$\nabla \; \cdot \; F\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; m\; athbf\; \{F\}\; =\; \backslash \; mathbf\; \{0\}\}$

, где, как правило, F - это матрица потока. Интегрируя это локальное уравнение по фиксированному объему V m, получаем:

$\int \; V\; m\; \nabla \; \cdot \; F\; d\; V\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{V\_\; \{m\}\}\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\; dV\; =\; \backslash \; mathbf\; \{0\}.\}$

Затем, основываясь на теореме расходимости, мы можем преобразовать этот интеграл в граничном интеграле потока:

$\oint \; \partial \; V\; m\; F\; ds\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; oint\; \_\; \{\backslash \; partial\; V\_\; \{m\}\}\; \backslash \; mathbf\; \{F\}\; ds\; =\; \backslash \; mathbf\{0\}.\}$

Эта глобальная форма просто утверждает, что нет чистого потока сохраняемой величины, проходящей через регион. в корпусе устойчивый и без источника. В 1D объем сокращается до интервала, его границами являются его экстремумы, тогда теорема о расходимости сводится к основной теореме исчисления :

$\int \; xmxm\; +\; 1\; F\; (x\; \prime )\; dx\; \prime \; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{x\_\; \{m\}\}\; ^\; \{x\_\; \{m\; +\; 1\}\}\; \backslash \; mathbf\; \{F\}\; \backslash \; left\; (x\; \text{'}\backslash \; right)\; dx\text{'}\; =\; \backslash \; mathbf\; \{0\},\}$

что представляет собой простое уравнение конечных разностей, известное как соотношение скачков:

$\Delta \; F\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; mathbf\; \{0\}.\}$

Это можно сделать явным образом:

$F\; m\; +\; 1\; -\; F\; m\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{\; m\; +\; 1\}\; -\; \backslash \; mathbf\; \{F\}\; \_\; \{m\}\; =\; \backslash \; mathbf\; \{0\}\}$

где используются следующие обозначения:

$F\; m\; =\; F\; (xm).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; \_\; \{m\}\; =\; \backslash \; mathbf\; \{F\}\; (x\_\; \{m\}).\}$

Или, если выполняется неопределенный интеграл:

$F\; -\; F\; 0\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}-\; \backslash \; mathbf\; \{F\}\; \_\; \{0\}\; =\; \backslash \; mathbf\; \{0\}.\}$

С другой стороны, временное уравнение сохранения:

$\partial \; y\; \partial \; t\; +\; \nabla \; \cdot \; F\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; partial\; y\; \backslash \; over\; \backslash \; partial\; t\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; mathbf\; \{0\}\}$

приводит к соотношению скачка:

$dxdt\; \Delta \; u\; =\; \Delta \; F.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; \backslash ,\; \backslash \; Delta\; u\; =\; \backslash \; Delta\; \backslash \; mathbf\; \{F\}.\}$

Для одномерных уравнений Эйлера переменные сохранения и поток являются векторами:

$y\; =\; (1\; vj\; E\; t),\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\; =\; \{\backslash \; begin\; \{pmat\; rix\}\; \{\backslash \; frac\; \{1\}\; \{v\}\}\; \backslash \backslash \; j\; \backslash \backslash \; E\; ^\; \{t\}\; \backslash \; end\; \{pmatrix\}\},\}$

$F\; =\; (jvj\; 2\; +\; pvj\; (E\; t\; +\; p)),\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; j\; \backslash \backslash \; vj\; ^\; \{2\}\; +\; p\; \backslash \backslash \; vj\; \backslash \; left\; (E\; ^\; \{t\}\; +\; p\; \backslash \; right)\; \backslash \; end\; \{pmatrix\}\},\}$

где:

• $v\; \{\backslash \; displaystyle\; v\}$- удельный объем,
• $j\; \{\backslash \; displaystyle\; j\}$- поток массы.

В одномерном случае соответствующие соотношения скачков, называемые уравнениями Ренкина – Гюгонио, следующие: <

$\{dxdt\; \Delta \; (1\; v)\; =\; \Delta \; jdxdt\; \Delta \; j\; =\; \Delta \; (vj2\; +\; p)\; dxdt\; \Delta \; E\; t\; =\; \Delta \; (jv\; (E\; t\; +\; p)).\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; \backslash \; Delta\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{v\}\}\; \backslash \; right)\; =\; \backslash \; Delta\; j\; \backslash \backslash \; [1.2\; пример]\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; \backslash \; Delta\; j\; =\; \backslash \; Delta\; \backslash \; left\; (vj\; ^\; \{2\}\; +\; p\; \backslash \; right)\; \backslash \backslash \; [1.2ex]\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; \backslash \; Delta\; E\; ^\; \{t\}\; =\; \backslash \; Delta\; \backslash \; left\; (jv\; \backslash \; left\; (E\; ^\; \{t\}\; +\; p\; \backslash \; right)\; \backslash \; right)\; \backslash \; end\; \{align\}\}\; \backslash \; right..\}$

В устойчивом одномерном случае просто:

$\{\Delta \; j\; =\; 0\; \Delta \; (vj\; 2\; +\; p)\; =\; 0\; \Delta \; (j\; (E\; t\; \rho \; +\; p\; \rho ))\; =\; 0.\; \{\backslash \; Displaystyle\; \backslash \; left\backslash \; \{\{\backslash \; begin\; \{выровнено\}\; \backslash \; Delta\; j\; =\; 0\; \backslash \backslash \; [1.2ex]\; \backslash \; Delta\; \backslash \; left\; (vj\; ^\; \{2\}\; +\; p\; \backslash \; right)\; =\; 0\; \backslash \backslash \; [1.2ex]\; \backslash \; Delta\; \backslash \; left\; (j\; \backslash \; left\; (\{\backslash \; frac\; \{E\; ^\; \{t\}\}\; \{\backslash \; rho\}\}\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; \backslash \; right)\; \backslash \; right)\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right..\}$

Благодаря уравнению разности масс уравнение разности энергий можно упростить без каких-либо ограничений:

$\{\Delta \; j\; =\; 0\; \Delta \; (vj\; 2\; +\; p)\; =\; 0\; \Delta \; ht\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \backslash \; Delta\; j\; =\; 0\; \backslash \backslash \; [1.2ex]\; \backslash \; Delta\; \backslash \; left\; (vj\; ^\; \{2\}\; +\; p\; \backslash \; right)=\; 0\; \backslash \backslash \; [1.2ex]\; \backslash \; Delta\; h\; ^\; \{\; t\}\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.,\}$

где $ht\; \{\backslash \; displaystyle\; h\; ^\; \{t\}\}$- удельная общая энтальпия.

Обычно они выражаются в конвективных переменных:

$\{\Delta \; j\; =\; 0\; \Delta \; (u\; 2\; v\; +\; p)\; =\; 0\; \Delta \; (e\; +\; 1\; 2\; u\; 2\; +\; pv)\; =\; 0,\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \backslash \; Delta\; j\; =\; 0\; \backslash \backslash \; [1.2ex]\; \backslash \; Delta\; \backslash \; left\; (\{\backslash \; frac\; \{u\; ^\; \{2\}\}\; \{v\}\}\; +\; p\; \backslash \; right)\; =\; 0\; \backslash \; \backslash \; [1.2ex]\; \backslash \; Delta\; \backslash \; left\; (e\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\; \{2\}\; +\; pv\; \backslash \; right)\; =\; 0\; \backslash \; end\; \{align\}\}\; \backslash \; right.,\}$

где:

• $u\; \{\backslash \; displaystyle\; u\}$- скорость потока
• $e\; \{\backslash \; displaystyle\; e\}$- удельная внутренняя энергия.

Уравнение энергии представляет собой интегральную форму уравнения Бернулли в сжимаемом случае. Прежние уравнения массы и импульса путем подстановки приводят к уравнению Рэлея:

$\Delta \; p\; \Delta \; v\; =\; -\; u\; 0\; 2\; v\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; Delta\; p\}\; \{\backslash \; Delta\; v\}\}\; =\; -\; \{\backslash \; frac\; \{u\_\; \{0\}\; ^\; \{2\}\}\; \{v\_\; \{0\}\}\}.\}$

Поскольку второй член является константа, уравнение Рэлеявсегда описывает простую линию в плоскости давления и объема, независимо от какого-либо уравнения состояния, т.е. Путем подстановки в уравнения Ренкина – Гюгонио это также можно сделать явным как:

$\{\rho \; u\; =\; \rho \; 0\; u\; 0\; \rho \; u\; 2\; +\; p\; =\; \rho \; 0\; u\; 0\; 2\; +\; p\; 0\; e\; +\; 1\; 2\; u\; 2\; +\; p\; р\; знак\; равно\; е\; 0\; +\; 1\; 2\; и\; 0\; 2\; +\; р\; 0\; р\; 0.\; \{\backslash \; Displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \backslash \; rho\; u\; =\; \backslash \; rho\; \_\; \{0\}\; u\_\; \{0\}\; \backslash \backslash \; [1.2ex]\; \backslash \; rho\; u\; ^\; \{2\}\; +\; p\; =\; \backslash \; rho\; \_\; \{0\}\; u\_\; \{0\}\; ^\; \{2\}\; +\; p\_\; \{0\}\; \backslash \backslash \; [1.2ex]\; e\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\; ^\{2\}\; +\; \{\backslash \; frac\; \{p\}\; \{\backslash \; rho\}\}\; =\; e\_\; \{\; 0\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\_\; \{0\}\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{p\_\; \{0\}\}\; \{\backslash \; rho\; \_\; \{0\}\}\}\; \backslash \; end\; \{align\}\}\; \backslash \; right..\; \}$

Можно также получить кинетическое уравнение и уравнение Гюгонио. Аналитические отрывки здесь для краткости не показаны.

Это соответственно:

$\{u\; 2\; (v,\; p)\; =\; u\; 0\; 2\; +\; (p\; -\; p\; 0)\; (v\; 0\; +\; v)\; e\; (v,\; p)\; =\; e\; 0\; +\; 1\; 2\; (р\; +\; р\; 0)\; (v\; 0\; -\; v).\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; u\; ^\; \{2\}\; (v,\; p)\; =\; u\_\; \{0\}\; ^\; \{2\}\; +\; \backslash \; left\; (p-p\_\; \{0\}\; \backslash \; right)\; \backslash \; left\; (v\_\; \{0\}\; +\; v\; \backslash right)\; \backslash \backslash \; [1.2ex]\; e\; (v,\; p)\; =\; e\_\; \{0\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (p\; +\; p\_\; \{0\}\; \backslash \; right)\; \backslash \; left\; (v\_\; \{0\}\; -v\; \backslash \; right)\; \backslash \; end\; \{align\}\}\; \backslash \; right..\}$

Уравнение Гюгонио в сочетании с фундаментальным уравнением состояния материала:

$e\; =\; e\; (v,\; p)\; \{\backslash \; displaystyle\; e\; =\; e\; (v,\; p)\}$

описывает в общем случае в плоскости объема давления кривую, проходящую при условиях (v 0, p 0), то есть, форма которого сильно зависит от типа рассматриваемого материала.

Также принятоопределять функцию Гюгонио:

$h\; (v,\; s)\; \equiv \; e\; (v,\; s)\; -\; e\; 0\; +\; 1\; 2\; (p\; (v,\; s)\; +\; p\; 0)\; (\; v\; -\; v\; 0)\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{h\}\}\; (v,\; s)\; \backslash \; Equiv\; e\; (v,\; s)\; -e\_\; \{0\}\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (p\; (v,\; s)\; +\; p\_\; \{0\}\; \backslash \; right)\; \backslash \; left\; (v-v\_\; \{0\}\; \backslash \; right)\}$

, позволяющий количественно определять отклонения от уравнения Гюгонио, аналогично предыдущему определению гидравлического напора, полезного для отклонений из уравнения Бернулли.

Форма конечного объема

С другой стороны, интегрированиемобщего уравнения сохранения:

$\partial \; y\; \partial \; t\; +\; \nabla \; \cdot \; F\; =\; s\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{y\}\}\; \{\backslash \; partial\; t\}\}\; +\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; mathbf\; \{s\}\}$

на фиксированном объеме V m, а затем на основе теорема о расходимости, получается:

$ddt\; \int \; V\; myd\; V\; +\; \oint \; \partial \; V\; m\; F\; \cdot \; n\; ^\; ds\; =\; S.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{d\}\; \{dt\}\}\; \backslash \; int\; \_\; \{V\_\; \{m\}\}\; \backslash \; mathbf\; \{y\}\; dV\; +\; \backslash \; oint\; \_\; \{\backslash \; partial\; V\_\; \{m\}\}\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; \{\backslash \; hat\; \{\; n\}\}\; ds\; =\; \backslash \; mathbf\; \{S\}.\}$

Путем интегрированияэтого уравнения также по временному интервалу:

$\int \; V\; my\; (r,\; tn\; +\; 1)\; d\; V\; -\; \int \; V\; my\; (r,\; tn)\; d\; V\; +\; \int \; tntn\; +\; 1\; \oint \; \partial \; V\; m\; F\; \cdot \; n\; ^\; dsdt\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{V\_\; \{m\}\}\; \backslash \; mathbf\; \{y\}\; (\backslash \; mathbf\; \{r\},\; t\_\; \{n\; +\; 1\})\; \backslash ,\; dV-\; \backslash \; int\; \_\; \{V\_\; \{m\}\}\; \backslash \; mathbf\; \{y\}\; (\; \backslash \; mathbf\; \{r\},\; t\_\; \{n\})\; \backslash ,\; dV\; +\; \backslash \; int\; \_\; \{t\_\; \{n\}\}\; ^\; \{t\_\; \{n\; +\; 1\}\}\; \backslash \; oint\; \_\; \{\backslash \; partial\; V\_\; \{m\}\}\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; \{\backslash \; hat\; \{n\}\}\; \backslash ,\; ds\; \backslash ,\; dt\; =\; \backslash \; mathbf\; \{0\}.\}$

Теперь, определив количество сохраняемых узлов:

$ym,\; n\; \equiv \; 1\; V\; m\; \int \; V\; my\; (r,\; tn)\; d\; V,\; \{\backslash \; displ\; aystyle\; \backslash \; mathbf\; \{y\}\; \_\; \{m,\; n\}\; \backslash \; Equiv\; \{\backslash \; frac\; \{1\}\; \{V\_\; \{m\}\}\}\; \backslash \; int\; \_\; \{V\_\; \{m\}\}\; \backslash \; mathbf\; \{y\}\; (\backslash \; mathbf\; \{\; r\},\; t\_\; \{n\})\; \backslash ,\; dV,\}$

выводим форму конечного объема:

$ym,\; n\; +\; 1\; =\; ym,\; n\; -\; 1\; V\; m\; \int \; tntn\; +\; 1\; \oint \; \partial \; V\; m\; F\; \cdot \; n\; ^\; dsdt.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{y\}\; \_\; \{m,\; n\; +\; 1\}\; =\; \backslash \; mathbf\; \{y\}\; \_\; \{m,\; n\}\; -\; \{\backslash \; frac\; \{1\}\; \{V\_\; \{m\}\}\}\; \backslash \; int\; \_\; \{t\_\; \{n\}\; \}\; ^\; \{t\_\; \{n\; +\; 1\}\}\; \backslash \; oint\; \_\; \{\backslash \; partial\; V\_\; \{m\}\}\; \backslash \; mathbf\; \{F\}\; \backslash \; cdot\; \{\backslash \; hat\; \{n\}\}\; \backslash ,\; ds\; \backslash ,\; dt.\}$

В частности, для Уравнения Эйлера, после определения сохраняющихся величин,конвективные переменные выводятся обратной подстановкой:

$\{um,\; n\; =\; jm,\; n\; \rho \; m,\; nem,\; n\; =\; E\; m,\; nt\; \rho \; m,\; n\; -\; 1\; 2\; um,\; п\; 2.\; \{\backslash \; Displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{u\}\; \_\; \{m,\; n\}\; =\; \{\backslash \; frac\; \{\backslash \; mathbf\; \{j\}\; \_\; \{m,\; n\}\}\; \{\backslash \; rho\; \_\; \{m,\; n\; \}\}\}\; \backslash \backslash \; [1.2ex]\; e\_\; \{m,\; n\}\; =\; \{\backslash \; frac\; \{E\_\; \{m,\; n\}\; ^\; \{t\}\}\; \{\backslash \; rho\; \_\; \{m,\; n\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; u\_\; \{m,\; n\}\; ^\; \{2\}\; \backslash \backslash \; [1.2ex]\; \backslash \; end\; \{выравнивается\}\}\; \backslash \; right..\}$

Тогда явные выражения конечного объема исходных конвективных переменных: <

Euler equations( Finite volume form)

${ ρ m, n + 1 = ρ m, n − 1 V m ∫ tntn + 1 ∮ ∂ V m ⁡ ρ u ⋅ n ^ dsdtum, n + 1 = um, n − 1 ρ m, n V m ∫ tntn + 1 ∮ ∂ V m ⁡ ( ρ u ⊗ u − p I) ⋅ n ^ dsdtem, n + 1 = em, n − 1 2 ( um, n + 1 2 − um, n 2) − 1 ρ m, n V m ∫ tntn + 1 ∮ ∂ V m ⁡ ( ρ e + 1 2 ρ u 2 + p) u ⋅ n ^ dsdt. {\displ aystyle \ left \ {{\ begin {выровнено} \ rho _ {m, n + 1} = \ rho _ {m, n} - {\ frac {1} {V_ {m}}} \ int _ {t_ {n}} ^ {t_ {n + 1}} \ oint _ {\ partial V_ {m}} \ rho \ mathbf {u}\ cdot {\ hat {n}} \, ds \, dt \\ [1.2 пример] \ mathbf {u} _ {m, n + 1} = \ mathbf {u} _ {m, n} - {\ frac {1} {\ rho _ {m, n} V_ {m}}} \ int _ {t_ {n}} ^ {t_ {n + 1}} \ oint _ {\ partial V_ {m}} (\ rho \ mathbf {u} \ otimes \ mathbf {u} -p \ mathbf {I }) \ cdot {\ hat {n}} \, ds \, dt \\ [1.2ex] \ mathbf {e} _ {m, n + 1} = \ mathbf {e} _ {m, n} - {\ frac {1} {2}} \ left (u_ {m, n + 1} ^ {2} -u_ {m, n} ^ {2} \ right) - {\ frac {1} {\ rho _ {m, n} V_ {m}}} \ int _ {t_ {n}} ^ {t_ {n + 1}} \oint _ {\ partial V_ {m}} \ left (\ rho e + {\ frac { 1} {2}} \ rho u ^ {2} + p \ right) \ mathbf {u} \ cdot {\ hat {n}} \, ds \, dt \\ [1.2ex] \ end {выровнено}} \ right..}$

Было показано, что уравнения Эйлера не являются полным набором уравнений, но они требуют некоторых дополнительных ограничений для получения единственного решения: это уравнение состояние рассматриваемого материала. Чтобы соответствовать термодинамике, эти уравнения состояниядолжны удовлетворять двум законам термодинамики. С другой стороны, по определению неравновесные системы описываются законами, лежащими вне этих законов. Ниже мы перечисляем некоторые очень простые уравнения состояния и соответствующее влияние на уравнения Эйлера.

Идеальный политропный газ

Для идеального политропного газа основное уравнение состояния :

$e\; (v,\; s)\; =\; e\; 0\; e\; (\gamma \; -\; 1)\; м\; (s\; -\; s\; 0)\; (v\; 0\; v)\; \gamma \; -\; 1\; \{\backslash \; displaystyle\; e\; (v,\; s)\; =\; e\_\; \{0\}\; e\; ^\; \{(\backslash \; gamma\; -1)\; m\; \backslash \; left(s-s\_\; \{0\}\; \backslash \; right)\}\; \backslash \; left\; (\{v\_\; \{0\}\; \backslash \; over\; v\}\; \backslash \; right)\; ^\; \{\backslash \; gamma\; -1\}\}$

где $e\; \{\backslash \; displaystyle\; e\}$- удельная энергия, $v\; \{\backslash \; displaystyle\; v\}$- удельный объем, $s\; \{\backslash \; displaystyle\; s\}$- удельная энтропия, $m\; \{\backslash \; displaystyle\; m\}$- молекулярная масса, $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$здесь считается константой (политропный процесс ), и можно показать, что она соответствует коэффициент теплоемкости. Можнопоказать, что это уравнение согласуется с обычными уравнениями состояния, используемыми в термодинамике.

Демонстрация соответствия термодинамике идеального газа

По термодинамическому определению температуры:

$T\; (e)\; \equiv \; \partial \; e\; \partial \; s\; =\; (\gamma \; -\; 1)\; me\; \{\backslash \; displaystyle\; T\; (e)\; \backslash \; Equiv\; \{\backslash \; partial\; e\; \backslash \; over\; \backslash \; partial\; s\}\; =\; (\backslash \; gamma\; -1)\; me\}$

Где температура измеряется в единицах энергии. Сначала обратите внимание, что, объединив эти два уравнения, можно вывести закон идеального газа :

$pv\; =\; m\; T\; \{\backslash \; displaystyle\; pv\; =\; mT\}$

или, в обычной форме:

$p\; =\; n\; T\; \{\backslash \; displaystyle\; p\; =\; nT\}$

где: $n\; \equiv \; mv\; \{\backslash \; displaystyle\; n\; \backslash \; Equiv\; \{\backslash \; frac\; \{m\}\; \{v\}\}\}$- числовая плотность материал. С другой стороны, закон идеального газа менее строг, чем рассматриваемое исходное фундаментальное уравнение состояния.

Теперь рассмотрим молярную теплоемкость, связанную с процессом x:

$cx\; =\; (m\; T\; \partial \; s\; \partial \; T)\; x\; \{\backslash \; displaystyle\; c\_\; \{x\}\; =\; \backslash \; left\; (mT\; \{\backslash \; partial\; s\; \backslash \; over\; \backslash \; partial\; T\}\; \backslash \; righ\; t)\; \_\; \{x\}\}$

согласно первому закону термодинамики:

$de\; (v,\; s)\; =\; -\; pdv\; +\; T\; ds\; \{\backslash \; displaystyle\; de\; (v,\; s)\; =\; -\; pdv\; +\; T\; \backslash ,\; ds\}$

это может быть просто выражено как:

$cx\; \equiv \; m\; (\partial \; e\; \partial \; T)\; x\; +\; mp\; (\partial \; v\; \partial \; T)\; x\; \{\backslash \; displaystyle\; c\_\; \{x\}\; \backslash \; Equiv\; m\; \backslash \; left\; (\{\backslash \; partial\; e\; \backslash \; over\; \backslash \; partial\; T\}\; \backslash \; right)\; \_\; \{x\}\; +\; mp\; \backslash \; left\; (\{\backslash \; partial\; v\; \backslash \; over\; \backslash \; partial\; T\}\; \backslash \; right)\; \_\; \{x\}\}$

Теперь обращаем уравнение для температуры T (e) мы заключаем, что для идеального политропного газа изохорная теплоемкость являетсяпостоянной:

$cv\; \equiv \; m\; (\partial \; e\; \partial \; T)\; v\; =\; mded\; T\; =\; 1\; (\gamma \; -\; 1)\; \{\backslash \; displaystyle\; c\_\; \{v\}\; \backslash \; Equiv\; m\; \backslash \; left\; (\{\backslash \; partial\; e\; \backslash \; over\; \backslash \; partial\; T\}\; \backslash \; right)\; \_\; \{v\}\; =\; m\; \{de\; \backslash \; over\; dT\}\; =\; \{\backslash \; frac\; \{1\}\; \{(\backslash \; gamma\; -1)\}\}\}$

и аналогично для идеального политропного газа изобарная теплоемкость получается постоянной:

$cp\; \equiv \; m\; (\partial \; e\; \partial \; T)\; p\; +\; mp\; (\partial \; v\; \partial \; T)\; p\; =\; mded\; T\; +\; p\; (\partial \; v\; \partial \; T)\; p\; =\; 1\; (\gamma \; -\; 1)\; +\; 1\; \{\backslash \; Displaystyle\; c\_\; \{p\}\; \backslash \; Equiv\; m\; \backslash \; left\; (\{\backslash \; partial\; e\; \backslash \; over\; \backslash \; partial\; T\}\; \backslash \; right)\; \_\; \{p\}\; +\; mp\; \backslash \; left\; (\{\backslash \; partial\; v\; \backslash \; over\; \backslash partial\; T\}\; \backslash \; right)\; \_\; \{\; p\}\; =\; m\; \{de\; \backslash \; over\; dT\}\; +\; p\; \backslash \; left\; (\{\backslash \; partial\; v\; \backslash \; over\; \backslash \; partial\; T\}\; \backslash \; right)\; \_\; \{p\}\; =\; \{\backslash \; frac\; \{1\}\; \{(\backslash \; gamma\; -1)\}\}\; +\; 1\; \}$

Это приводит к двум важным отношениям между теплоемкостями : постоянная гамма фактически представляет коэффициент теплоемкости в идеальном политропном газе:

$cpcv\; =\; \gamma \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{c\_\; \{p\}\}\; \{c\_\; \{v\}\}\}\; =\; \backslash \; gamma\}$

и еще один приходит к игре Мейера :

$cp\; =\; cv\; +\; 1\; \{\backslash \; displaystyle\; c\_\; \{p\}\; =\; c\_\; \{v\}\; +1\}$

Тогда удельная энергия, инвертируя отношение T (e):

$e\; (T)\; =\; m\; T\; \gamma \; -\; 1\; =\; cvm\; T\; \{\backslash \; displaystyle\; e\; (T)\; =\; \{\backslash \; frac\; \{mT\}\; \{\backslash \; gamma\; -1\}\}\; =\; c\_\; \{v\}\; mT\}$

Удельная энтальпия результат замены и последнего закона идеального газа:

$h\; (T)\; \equiv \; e\; (T)\; +\; (pv)\; (\; T)\; =\; cvm\; T\; +\; m\; T\; =\; cpm\; T\; \{\backslash \; displaystyle\; h\; (T)\; \backslash \; Equiv\; e\; (T)\; +\; (pv)\; (T)\; =\; c\_\; \{v\}\; mT\; +\; mT\; =\; c\_\; \{p\}\; mT\}$

Из этого уравнения можно вывести уравнение для давления по е го термодинамическому определению:

$p\; (v\; е)\; \equiv \; -\; \partial \; е\; \partial \; v\; знак\; равно\; (\gamma -\; 1)\; ev\; \{\backslash \; displaystyle\; p\; (v,\; e)\; \backslash \; Equiv\; -\; \{\backslash \; partial\; e\; \backslash \; over\; \backslash \; partial\; v\}\; =\; (\; \backslash \; gamma\; -1)\; \{\backslash \; frac\; \{e\}\; \{v\}\}\}$

Инвертируя его, можно прийти к механическому уравнению состояния:

$e\; (v,\; p)\; =\; pv\; \gamma \; -\; 1\; \{\backslash \; displaystyle\; e\; (v,\; p)\; =\; \{\backslash \; frac\; \{pv\}\; \{\backslash \; gamma\; -1\}\}\}$

Тогда для идеального уравнения газа Эйлера сжимаемого газа могут быть просто выражены в механических или примитивных величинах: удельный объем, скорость потока и давление. re, взяв систему термодинамической системы и уравнение энергиив уравнение давления через это механическое уравнение состояния. Наконец, в конвективной форме они приводят:

уравнения Эйлера для идеального политропного газа (конвективная форма)

$\{D\; v\; D\; t\; =\; v\; \nabla \; u\; D\; u\; D\; t\; =\; v\; \nabla \; p\; +\; г\; D\; п\; DT\; знак\; равно\; -\; \gamma \; п\; \nabla \; \cdot \; U\; \{\backslash \; Displaystyle\; \backslash \; left\; \backslash \; \{\{\backslash \; begin\; \{align\}\; \{Dv\; \backslash \; over\; Dt\}\; =\; v\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{u\}\; \backslash \backslash \; [1.2ex]\; \{\backslash \; frac\; \{D\; \backslash \; mathbf\; \{u\}\}\; \{Dt\}\}\; =\; v\; \backslash \; nabla\; p\; +\; \backslash \; mathbf\; \{g\}\; \backslash \backslash \; [1.2ex]\; \{Dp\; \backslash \; over\; Dt\}\; =\; -\; \backslash \; gamma\; p\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\{u\; \}\; \backslash \; end\; \{align\}\}\; \backslash \; right.\}$

и в одномерной квазилинейной форме они дают:

$\partial \; y\; \partial \; t\; +\; A\; \partial \; y\; \partial \; x\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{\; y\}\}\; \{\backslash \; partial\; t\}\}\; +\; \backslash \; mathbf\; \{A\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{y\}\}\; \{\backslash \; partial\; x\}\}\; =\; \{\backslash \; mathbf\; \{0\}\}.\}$

где консервативная переменная :

$y\; =\; (vup)\; \{\backslash \; displaystyle\; \{\backslash \; mathbf\; \{y\}\}\; =\; \{\backslash \; begin\; \{pmatrix\}\; v\; \backslash \backslash \; u\; \backslash \backslash \; p\; \backslash \; end\; \{pmatrix\}\}\}$

и соответствующая матрица якобиана:

$A\; =\; (u\; -\; v\; 0\; 0\; uv\; 0\; \gamma \; pu).\; \{\backslash \; displaystyle\; \{\backslash \; mathbf\; \{A\}\}\; =\; \{\backslash begin\; \{pmatrix\}\; u\; -v\; 0\; \backslash \backslash \; 0\; u\; v\; \backslash \backslash \; 0\; \backslash \; gamma\; p\; u\; \backslash \; end\; \{pmatrix\}\}.\}$

Устойчивый поток в координатах материала

В случае установившегося потока удобно выбрать кадр Френе - Серре вдоль линии тока в качестве системы координат для описания установившегося импульс уравнение Эйлера:

$u\; \cdot \; \nabla \; u\; =\; -\; 1\; \rho \; \nabla \; p,\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{u\}\}\; \backslash \; cdot\; \backslash \; nabla\; \{\backslash \; boldsymbol\; \{u\}\}\; =\; -\; \{\backslash \; frac\; \{\; 1\}\; \{\backslash \; rho\}\}\; \backslash \; nabla\; p,\}$

где $u\; \{\backslash \; displ\; aystyle\; \backslash \; mathbf\; \{u\}\}$, $p\; \{\backslash \; displaystyle\; p\}$и $\rho \; \{\; \backslash \; displaystyle\; \backslash \; rho\}$обозначают скорость потока, давление и плотность, соответственно.

Пусть $\{es,\; en,\; eb\}\; \{\backslash \; displaystyle\; \backslash \; left\; \backslash \; \{\backslash \; mathbf\; \{e\}\; \_\; \{s\},\; \backslash \; mathbf\; \{e\}\; \_\; \{n\},\; \backslash \; mathbf\; \{e\}\; \_\; \{b\}\; \backslash \; right\; \backslash \}\}$быть ортонормированным базисом Френе - Серре , который состоит из тангенциального единичного события, нормального единичного события и бинормальногоединичного случая к линии тока соответственно. Линия тока показывает собой кривую, касательную к вектору скорости потока, левая часть приведенного выше уравнения, описана следующим образом:

$u\; \cdot \; \nabla \; u\; знак\; равно\; u\; \partial \; \partial \; s\; (ues)\; (u\; =\; ues,\; \partial \; /\; \partial \; s\; \equiv \; es\; \cdot \; \nabla )\; =\; u\; \partial \; u\; \partial \; ses\; +\; u\; 2\; R\; en\; (\because \; \partial \; es\; \partial \; s\; =\; 1\; R\; en),\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; boldsymbol\; \{u\}\}\; \backslash \; cdot\; \backslash \; nabla\; \{\backslash \; boldsymbol\; \{u\}\}\; \backslash \backslash \; =\; u\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; s\}\}\; (u\; \{\backslash \; boldsymbol\; \{e\}\}\; \_\; \{s\})\; (\{\; \backslash \; boldsymbol\; \{u\}\}\; =\; u\; \{\backslash boldsymbol\; \{e\}\}\; \_\; \{s\},\; ~\; \{\backslash \; partial\; /\; \backslash \; partial\; s\}\; \backslash \; Equiv\; \{\backslash \; boldsymbol\; \{e\}\}\; \_\; \{s\}\; \backslash \; cdot\; \backslash \; nabla)\; \backslash \backslash \; =\; u\; \{\backslash \; frac\; \{\backslash \; partial\; u\}\; \{\backslash \; partial\; s\}\}\; \{\backslash \; boldsymbol\; \{e\}\}\; \_\; \{s\}\; +\; \{\backslash \; frac\; \{u\; ^\; \{2\}\}\; \{R\}\}\; \{\backslash \; boldsymbol\; \{e\}\}\; \_\; \{n\}\; (\backslash \; потому\; что\; ~\; \{\backslash \; frac\; \{\backslash \; partial\; \{\backslash \; boldsymbol\; \{e\}\}\; \_\; \{s\}\}\; \{\backslash \; partial\; s\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; \{\backslash \; boldsymbol\; \{e\}\; \}\; \_\; \{n\}),\; \backslash \; end\; \{align\}\}\}$

где $R\; \{\backslash \; displaystyle\; R\}$- радиус кривизны обтекания.

Следовательно, импульсная часть уравненийЭйлера для установившегося потока имеет простой вид:

$\{u\; \partial \; u\; \partial \; s\; =\; -\; 1\; \rho \; \partial \; p\; \partial \; s,\; u\; 2\; R\; =\; -\; 1\; \rho \; \partial \; p\; \partial \; n\; (\partial \; /\; \partial \; n\; \equiv \; en\; \cdot \; \nabla ),\; 0\; =\; -\; 1\; \rho \; \partial \; p\; \partial \; b\; (\partial \; /\; \partial \; b\; \equiv \; eb\; \cdot ).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{cases\}\; \backslash \; displaystyle\; u\; \{\backslash \; frac\; \{\backslash \; partial\; u\}\; \{\backslash \; partial\; s\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; s\}\},\; \backslash \backslash \backslash \; displaystyle\; \{u\; ^\; \{2\}\; \backslash \; over\; R\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; n\}\}\; (\{\backslash \; partial\; /\; \backslash \; partial\; n\}\; \backslash \; Equiv\; \{\backslash \; boldsymbol\; \{e\}\}\; \_\; \{n\}\; \backslash \; cdot\; \backslash \; nabla),\; \backslash \backslash \backslash \; displ\; aystyle\; 0\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; rho\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; b\}\}\; (\{\backslash \; partial\; /\; \backslash \; partial\; b\}\; \backslash \; Equiv\; \{\backslash \; boldsymbol\; \{e\}\}\; \_\; \{b\}\; \backslash \; cdot\; \backslash \; nabla).\; \backslash \; end\; \{cases\}\}\}$

Для баротропных расход $(\rho \; =\; \rho \; (p))\; \{\backslash \; displaystyle\; (\backslash \; rho\; =\; \backslash \; rho\; (p))\}$, Уравнение Бернулли выводится из первого уравнения:

$\partial \; \partial \; s\; (U\; 2\; 2\; +\; \int \; dp\; \rho )\; знак\; равно\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; s\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{u\; ^\; \{2\}\}\; \{2\}\}\; +\; \backslash \; int\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; p\}\; \{\backslash \; rho\}\}\; \backslash \; right)\; =\; 0.\; \}$

Второе уравнение выражает, что в случае искривления линии тока должен существовать градиент давления перпендикулярно линии тока, потому что центростремительное ускорение частицы жидкости создается только нормальным предварительным уверенным градиент.

Третье уравнение выражает, что давление постоянно вдоль оси бинормалей.

Теорема обтекаемой кривизны

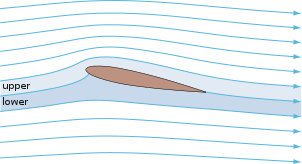
«Теорема обтекаемой кривизны» утверждает, что давление на верхней поверхностиаэродинамического профиля ниже, чем давление вдали, и что давление на нижней поверхности выше, чем давление вдали прочь; Следовательно, давлений между верхней и нижней поверхностями аэродинамического профиля разница подъемную силу.

Пусть $r\; \{\backslash \; displaystyle\; r\}$будет расстоянием от центра кривизны линии тока, тогда второе уравнение записывается следующим образом:

$\partial \; p\; \partial \; r\; =\; \rho \; u\; 2\; r\; (>0),\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; p\}\; \{\backslash \; partial\; r\}\}\; =\; \backslash \; rho\; \{\backslash \; frac\; \{u\; ^\; \{2\}\}\; \{r\}\}\; ~\; (>0),\}$

где / ∂ r = - ∂ / ∂ n. {\ Displaystyle {\ partial / \ partial r} = - / \ partial n}.}

Это уравнение утверждает:

В установившемся потоке невязкой жидкости без внешних сил центр кривизны линии тока лежит в уменьшении радиального давления.

Хотя эта взаимосвязь междуполем давления и кривизной потока очень полезна, она не имеет названия в русскоязычных ученых c Японские специалисты по гидродинамике называют эту взаимосвязь «теоремой о кривизне линии тока».

Э та «теорема» ясно объясняет, почему в центре вихрей, которые состоят из концентрических окружностей обтекает. Это также способ интуитивно объяснить, почему крыловые профили подъемную.

Все решения потенциального потока также являютсярешениями Эйлера, и в частности несжимаемой Уравнения Эйлера при гармоническом гармоническом решении. потенциале.

Двумерный параллельный сдвиговый поток.

Решениями уравнений Эйлера с завихренностью являются:

• параллельные сдвиговые потоки - где поток является однонаправленным, а скорость потока изменяется только в направлении поперечного потока, например в декартовой системы координат $(x,\; y,\; z)\; \{\backslash \; displaystyle\; (x,\; y,\; z)\}$потокнаходится, например, в $x\; \{\backslash \; displaystyle\; x\}$-направление - с единственным ненулевым компонентом скорости $ux\; (y,\; z)\; \{\backslash \; displaystyle\; u\_\; \{x\}\; (y,\; z)\}$зависит только от $y\; \{\backslash \; displaystyle\; y\; \}$и $z\; \{\backslash \; displaystyle\; z\}$, а не от $x.\; \{\backslash \; displaystyle\; x.\}$
• Поток Арнольда - Бельтрами - Чайлдресса - точное решение уравнения Эйлера для несжимаемой жидкости.
• Два решения трехмерных уравнений Эйлера с цилиндрической симметрией были представлены Гиббоном, Муром и Стюартом в 2003 году. Эти два решения имеют бесконечную энергию; они взрываются повсюду в визу за конечное время.

• теорему Бернулли
• теорему Кельвина о циркуляции
• уравнения Коши
• уравнения Маделунга
• число Фруда
• уравнения Навье - Стокса
• Уравнение Бюргерса

Примечания

Цитаты

Источники

Дополнительная литература