Потенциальный поток

редактировать

Потенциальный поток линии тока вокруг профиля NACA 0012 под углом 11 ° угол атаки, с указанием верхней и нижней трубок.

В гидродинамике, потенциальный поток описывает поле скорости как градиент скалярной функции: потенциал скорости. В результате потенциальный поток характеризуется полем безвихревой скорости , которое является допустимым приближением для нескольких приложений. Невращение потенциального потока обусловлено тем, что rot градиента скаляра всегда равен нулю.

В случае несжимаемого потока потенциал скорости удовлетворяет уравнению Лапласа, и теория потенциала применима. Однако потенциальные потоки также использовались для описания сжимаемых потоков. Подход потенциального потока применяется при моделировании как стационарных, так и нестационарных потоков. Примеры применения потенциального потока: внешнее поле потока для аэрокрыльей, водных волн, электроосмотического потока и потока грунтовых вод. Для потоков (или их частей) с сильными эффектами завихренности приближение потенциального потока не применимо.

Содержание

1 Характеристики и применение
- 1.1 Описание и характеристики
- 1.2 Несжимаемый поток
- 1.3 Сжимаемый поток
  - 1.3.1 Устойчивый поток
  - 1.3.2 Нестабильный поток
  - 1.3.3 Звуковые волны
- 1.4 Применимость и ограничения
2 Анализ двумерного потока
3 Примеры двумерных потоков
- 3.1 Законы мощности
  - 3.1.1 Законы мощности с n = 1: равномерный поток
  - 3.1.2 степенные законы с n = 2
  - 3.1.3 степенные законы с n = 3
  - 3.1.4 степенные законы с n = -1: дублет
  - 3.1.5 степенные законы с n = −2: квадруполь
- 3.2 Линейный источник и сток
- 3.3 Линейный вихрь
4 Анализ трехмерного потока
- 4.1 Точечный источник и сток
5 См. также
6 Примечания
7 Ссылки
8 Дополнительная литература
9 Внешние ссылки

Характеристики и приложения

Потенциальный поток создается путем добавления простых элементарных потоков и наблюдения за результатом.

Streamlines для несжимаемой жидкости потенциальное обтекание кругового цилиндра в однородном потоке w.

Описание и характеристики

В гидродинамике потенциальный поток описывается с помощью потенциала скорости φ, который является функцией пространства и времени. скорость vпотока является векторным полем , равным градиенту ∇ потенциала скорости φ:

v = ∇ φ. {\ displaystyle \ mathbf {v} = \ nabla \ varphi.}

{\mathbf {v}}=\nabla \varphi.

Иногда также используется определение v = −∇φ со знаком минус. Но здесь мы будем использовать определение, приведенное выше, без знака минус. Из векторного исчисления известно, что curl градиента равен нулю:

∇ × ∇ φ = 0, {\ displaystyle \ nabla \ times \ nabla \ varphi = \ mathbf {0} \,,}

{\ displaystyle \ nabla \ times \ nabla \ varphi = \ mathbf {0} \,,}

и, следовательно, завихренность, curl поля скорости v, равна нулю:

∇ × v = 0. {\ displaystyle \ nabla \ times \ mathbf {v} = \ mathbf {0} \,.}

{\ displaystyle \ nabla \ times \ mathbf {v} = \ mathbf {0} \,.}

Это означает, что потенциальный поток является безвихревым потоком. Это имеет прямые последствия для применимости потенциального потока. В областях потока, где известно, что завихренность важна, таких как следы и пограничные слои, теория потенциального потока не может обеспечить разумные предсказания потока. К счастью, часто существуют большие области потока, в которых допущение о безвихревости справедливо, поэтому потенциальный поток используется для различных приложений. Например, в: обтекание самолета, потока грунтовых вод, акустики, водных волн и электроосмотического потока.

Несжимаемый расход

В случае несжимаемого потока - например, жидкости, или газа при малых числах Маха ; но не для звуковых волн - скорость v имеет нулевую дивергенцию :

∇ ⋅ v = 0, {\ displaystyle \ nabla \ cdot \ mathbf {v} = 0 \,,}

{\ displaystyle \ nabla \ cdot \ mathbf { v} = 0 \,,}

с точкой, обозначающей внутренний продукт. В результате потенциал скорости φ должен удовлетворять уравнению Лапласа

∇ 2 φ = 0, {\ displaystyle \ nabla ^ {2} \ varphi = 0 \,,}

{\ displaystyle \ nabla ^ {2} \ varphi = 0 \,,}

где ∇ = ∇ ⋅ ∇ - это оператор Лапласа (иногда также пишется Δ). В этом случае поток может быть полностью определен из его кинематики : допущения о безвихревости и нулевой дивергенции потока. Динамика должна применяться только после того, как кто-то заинтересован в вычислении давлений: например, для обтекания аэродинамических поверхностей с помощью принципа Бернулли.

В двух измерениях потенциальный поток уменьшается до очень простая система, которая анализируется с помощью комплексного анализа (см. ниже).

Сжимаемый поток

Устойчивый поток

Теория потенциального потока также может использоваться для моделирования безвихревого сжимаемого потока. Уравнение полного потенциала, описывающее установившийся поток, задается следующим образом:

(1 - M x 2) ∂ 2 Φ ∂ x 2 + (1 - M y 2) ∂ 2 Φ ∂ y 2 + (1 - M z 2) ∂ 2 Φ ∂ z 2 - 2 M x M y ∂ 2 Φ ∂ x ∂ y - 2 M y M z ∂ 2 Φ ∂ y ∂ z - 2 M z M Икс ∂ 2 Φ ∂ Z ∂ Икс знак равно 0, {\ Displaystyle \ left (1-M_ {x} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial x ^ { 2}}} + \ left (1-M_ {y} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial y ^ {2}}} + \ left (1- M_ {z} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial z ^ {2}}} - 2M_ {x} M_ {y} {\ frac {\ partial ^ {2} \ Phi} {\ partial x \, \ partial y}} - 2M_ {y} M_ {z} {\ frac {\ partial ^ {2} \ Phi} {\ partial y \, \ partial z}} -2M_ {z} M_ {x} {\ frac {\ partial ^ {2} \ Phi} {\ partial z \, \ partial x}} = 0 \,,}

{\ displaystyle \ left (1-M_ {x} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial x ^ {2}}} + \ left (1-M_ {y} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial y ^ {2}}} + \ left ( 1-M_ {z} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial z ^ {2}}} - 2M_ {x} M_ {y} {\ frac {\ partial ^ {2} \ Phi} {\ partial x \, \ partial y}} - 2M_ {y} M_ {z} {\ frac {\ partial ^ {2} \ Phi} {\ partial y \, \ partial z }} - 2M_ {z} M_ {x} {\ frac {\ partial ^ {2} \ Phi} {\ partial z \, \ частичный x}} = 0 \,,}

с числом Маха компоненты

M x = 1 a ∂ Φ ∂ x, M y = 1 a ∂ Φ ∂ y и M z = 1 a ∂ Φ ∂ z, {\ displaystyle M_ {x} = {\ frac {1} {a}} {\ frac {\ partial \ Phi} {\ partial x}} \,, \ qquad M_ {y} = {\ frac {1} {a}} {\ frac {\ partial \ Phi} {\ частичный y}} \,, \ qquad {\ text {and}} \ qquad M_ {z} = {\ frac {1} {a}} {\ frac {\ partial \ Phi} {\ par tial z}} \,,}

M_{x}={\frac {1}{a}}{\frac {\partial \Phi }{\partial x}}\,,\qquad M_{y}={\frac {1}{a}}{\frac {\partial \Phi }{\partial y}}\,,\qquad {\text{and}}\qquad M_{z}={\frac {1}{a}}{\frac {\partial \Phi }{\partial z}}\,,

где a - местная скорость звука. Скорость потока v снова равна ∇Φ, а Φ - потенциал скорости. Полное уравнение потенциала действительно для суб-, транс- и сверхзвукового потока при произвольном угле атаки, если допущение

В случае дозвукового или сверхзвукового (но не трансзвукового или гиперзвукового ) потока, при малых углах атаки и тонких телах может быть сделано дополнительное предположение: Потенциал скорости разделяется на скорость невозмущенного потока V ∞ в x-направлении и небольшую скорость возмущения ∇φ. Итак:

∇ Φ = V ∞ x + ∇ φ. {\ displaystyle \ nabla \ Phi = V _ {\ infty} x + \ nabla \ varphi \,.}

{\ displaystyle \ nabla \ Phi = V _ {\ infty} x + \ nabla \ varphi \,.}

В этом случае можно использовать линеаризованное уравнение потенциала малых возмущений - приближение к уравнению полного потенциала -:

(1 - M ∞ 2) ∂ 2 φ ∂ Икс 2 + ∂ 2 φ ∂ Y 2 + ∂ 2 φ ∂ Z 2 = 0, {\ displaystyle \ left (1-M _ {\ infty} ^ {2} \ справа) {\ frac {\ partial ^ {2} \ varphi} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial y ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial z ^ {2}}} = 0,}

\left(1-M_{\infty }^{2}\right){\frac {\partial ^{2}\varphi }{\partial x^{2}}}+{\frac {\partial ^{2}\varphi }{\partial y^{2}}}+{\frac {\partial ^{2}\varphi }{\partial z^{2}}}=0,

с M ∞ = V ∞/a∞число Маха входящего свободном потоке. Это линейное уравнение намного проще решить, чем полное уравнение потенциала: его можно преобразовать в уравнение Лапласа путем простого растяжения координат в направлении оси x.

Вывод полного уравнения потенциала
Для устойчивого невязкого потока уравнения Эйлера - для плотности массы и количества движения - в нижнем индексе и в не- форме сохранения : $∂ ∂ xi (ρ vi) знак равно 0, ρ vj ∂ vi ∂ xj = - ∂ p ∂ xi, {\ displaystyle {\ begin {align} {\ frac {\ partial} {\ partial x_ {i}}} \ left (\ rho \, v_ {i} \ right) = 0 \,, \\\ rho \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j} }} = - {\ frac {\ partial p} {\ partial x_ {i}}} \,, \ end {выравнивается}}}$ ${\ displaystyle {\ begin {align} {\ frac {\ partial} {\ partial x_ {i}}} \ left (\ rho \, v_ {i} \ right) = 0 \,, \\\ rho \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = - {\ frac {\ partial p} {\ partial x_ {i} }} \,, \ end {align}}}$ при использовании соглашения о суммировании : поскольку встречается j более одного раза в члене в левой части уравнения импульса j суммируется по всем его компонентам (от 1 до 2 в двумерном потоке и от 1 до 3 в трех измерениях). Далее: ρ - плотность жидкости , p - давление , (x1, x 2, x 3) = (x, y, z) - координаты, а (v1, v 2, v 3) - соответствующие компоненты вектора скорости v. . Квадрат скорости звука a равен производная давления p по плотности ρ при постоянной энтропии S: $a 2 = [∂ p ∂ ρ] S. {\ displaystyle a ^ {2} = \ left [{\ frac {\ partial p} {\ partial \ rho}} \ right] _ {S}.}$ $a ^ {2} = \ left [{\ frac {\ partial p} {\ partial \ rho}} \ right] _ {S}.$ В результате уравнения потока можно записать в виде : $vi ∂ ρ ∂ xi + ρ ∂ vi ∂ xi = 0 и ρ vj ∂ vi ∂ xj = - a 2 ∂ ρ ∂ xi. {\ displaystyle v_ {i} \, {\ frac {\ partial \ rho} {\ partial x_ {i}}} + \ rho \, {\ frac {\ partial v_ {i}} {\ partial x_ {i} }} = 0 \ qquad {\ text {and}} \ qquad \ rho \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = - a ^ { 2} \, {\ frac {\ partial \ rho} {\ partial x_ {i}}} \,.}$ $v_{i}\,{\frac {\partial \rho }{\partial x_{i}}}+\rho \,{\frac {\partial v_{i}}{\partial x_{i}}}=0\qquad {\text{and}}\qquad \rho \,v_{j}\,{\frac {\partial v_{i}}{\partial x_{j}}}=-a^{2}\,{\frac {\partial \rho }{\partial x_{i}}}\,.$ Умножение (и суммирование) уравнения импульса на v i и использование Уравнение массы для устранения градиента плотности дает: $ρ vivj ∂ vi ∂ xj = ρ a 2 ∂ vi ∂ xi. {\ Displaystyle \ rho \, v_ {i} \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = \ rho \, a ^ {2} \, {\ frac {\ partial v_ {i}} {\ partial x_ {i}}} \,.}$ $\rho \,v_{i}\,v_{j}\,{\frac {\partial v_{i}}{\partial x_{j}}}=\rho \,a^{2}\,{\frac {\partial v_{i}}{\partial x_{i}}}\,.$ При делении на ρ и со всеми членами на одной стороне уравнения уравнение сжимаемого потока имеет следующий вид: $∂ vi ∂ xi - vivja 2 ∂ vi ∂ xj = 0. {\ displaystyle {\ frac {\ partial v_ {i}} {\ partial x_ {i}}} - {\ frac {v_ {i} \, v_ {j}} {a ^ {2}}} {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = 0 \,.}$ ${\ displaystyle {\ frac {\ partial v_ {i}} {\ partial x_ {i}}} - {\ frac {v_ {i} \, v_ {j}} {a ^ {2}}} {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = 0 \,.}$ Обратите внимание, что до этого этапа никаких предположений относительно потока не делалось (кроме того, что это устойчивый поток ). Теперь для безвихревого потока скорость v является градиентом потенциала скорости Φ, а компоненты местного числа Маха M i определены как: $vi = ∂ Φ ∂ xi и M i = via = 1 a ∂ Φ ∂ xi. {\ displaystyle v_ {i} = {\ frac {\ partial \ Phi} {\ partial x_ {i}}} \ qquad {\ text {and}} \ qquad M_ {i} = {\ frac {v_ {i} } {a}} = {\ frac {1} {a}} {\ frac {\ partial \ Phi} {\ partial x_ {i}}} \,.}$ $v_{i}={\frac {\partial \Phi }{\partial x_{i}}}\qquad {\text{and}}\qquad M_{i}={\frac {v_{i}}{a}}={\frac {1}{a}}{\frac {\partial \Phi }{\partial x_{i}}}\,.$ При использовании в уравнении потока полный Результаты потенциального уравнения: $∂ 2 Φ ∂ xi ∂ xi - M i M j ∂ 2 Φ ∂ xi ∂ xj = 0. {\ displaystyle {\ frac {\ partial ^ {2} \ Phi} {\ partial x_ {i} \, \ partial x_ {i}}} - M_ {i} \, M_ {j} \, {\ frac { \ partial ^ {2} \ Phi} {\ partial x_ {i} \, \ partial x_ {j}}} = 0 \,.}$ ${\frac {\partial ^{2}\Phi }{\partial x_{i}\,\partial x_{i}}}-M_{i}\,M_{j}\,{\frac {\partial ^{2}\Phi }{\partial x_{i}\,\partial x_{j}}}=0\,.$ Записано в компонентах, форма, приведенная в начале этого раздела, является получено. Когда предоставлено конкретное уравнение состояния, связывающее давление p и плотность ρ, можно определить скорость звука. Впоследствии, вместе с соответствующими граничными условиями, может быть решено полное уравнение потенциала (чаще всего с использованием кода вычислительной гидродинамики ).

Вывод полного уравнения потенциала

Для устойчивого невязкого потока уравнения Эйлера - для плотности массы и количества движения - в нижнем индексе и в не- форме сохранения :

∂ ∂ xi (ρ vi) знак равно 0, ρ vj ∂ vi ∂ xj = - ∂ p ∂ xi, {\ displaystyle {\ begin {align} {\ frac {\ partial} {\ partial x_ {i}}} \ left (\ rho \, v_ {i} \ right) = 0 \,, \\\ rho \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j} }} = - {\ frac {\ partial p} {\ partial x_ {i}}} \,, \ end {выравнивается}}}

{\ displaystyle {\ begin {align} {\ frac {\ partial} {\ partial x_ {i}}} \ left (\ rho \, v_ {i} \ right) = 0 \,, \\\ rho \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = - {\ frac {\ partial p} {\ partial x_ {i} }} \,, \ end {align}}}

при использовании соглашения о суммировании : поскольку встречается j более одного раза в члене в левой части уравнения импульса j суммируется по всем его компонентам (от 1 до 2 в двумерном потоке и от 1 до 3 в трех измерениях). Далее:

ρ - плотность жидкости ,
p - давление ,
(x1, x 2, x 3) = (x, y, z) - координаты, а
(v1, v 2, v 3) - соответствующие компоненты вектора скорости v.

. Квадрат скорости звука a равен производная давления p по плотности ρ при постоянной энтропии S:

a 2 = [∂ p ∂ ρ] S. {\ displaystyle a ^ {2} = \ left [{\ frac {\ partial p} {\ partial \ rho}} \ right] _ {S}.}

a ^ {2} = \ left [{\ frac {\ partial p} {\ partial \ rho}} \ right] _ {S}.

В результате уравнения потока можно записать в виде :

vi ∂ ρ ∂ xi + ρ ∂ vi ∂ xi = 0 и ρ vj ∂ vi ∂ xj = - a 2 ∂ ρ ∂ xi. {\ displaystyle v_ {i} \, {\ frac {\ partial \ rho} {\ partial x_ {i}}} + \ rho \, {\ frac {\ partial v_ {i}} {\ partial x_ {i} }} = 0 \ qquad {\ text {and}} \ qquad \ rho \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = - a ^ { 2} \, {\ frac {\ partial \ rho} {\ partial x_ {i}}} \,.}

v_{i}\,{\frac {\partial \rho }{\partial x_{i}}}+\rho \,{\frac {\partial v_{i}}{\partial x_{i}}}=0\qquad {\text{and}}\qquad \rho \,v_{j}\,{\frac {\partial v_{i}}{\partial x_{j}}}=-a^{2}\,{\frac {\partial \rho }{\partial x_{i}}}\,.

Умножение (и суммирование) уравнения импульса на v i и использование Уравнение массы для устранения градиента плотности дает:

ρ vivj ∂ vi ∂ xj = ρ a 2 ∂ vi ∂ xi. {\ Displaystyle \ rho \, v_ {i} \, v_ {j} \, {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = \ rho \, a ^ {2} \, {\ frac {\ partial v_ {i}} {\ partial x_ {i}}} \,.}

\rho \,v_{i}\,v_{j}\,{\frac {\partial v_{i}}{\partial x_{j}}}=\rho \,a^{2}\,{\frac {\partial v_{i}}{\partial x_{i}}}\,.

При делении на ρ и со всеми членами на одной стороне уравнения уравнение сжимаемого потока имеет следующий вид:

∂ vi ∂ xi - vivja 2 ∂ vi ∂ xj = 0. {\ displaystyle {\ frac {\ partial v_ {i}} {\ partial x_ {i}}} - {\ frac {v_ {i} \, v_ {j}} {a ^ {2}}} {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = 0 \,.}

{\ displaystyle {\ frac {\ partial v_ {i}} {\ partial x_ {i}}} - {\ frac {v_ {i} \, v_ {j}} {a ^ {2}}} {\ frac {\ partial v_ {i}} {\ partial x_ {j}}} = 0 \,.}

Обратите внимание, что до этого этапа никаких предположений относительно потока не делалось (кроме того, что это устойчивый поток ).

Теперь для безвихревого потока скорость v является градиентом потенциала скорости Φ, а компоненты местного числа Маха M i определены как:

vi = ∂ Φ ∂ xi и M i = via = 1 a ∂ Φ ∂ xi. {\ displaystyle v_ {i} = {\ frac {\ partial \ Phi} {\ partial x_ {i}}} \ qquad {\ text {and}} \ qquad M_ {i} = {\ frac {v_ {i} } {a}} = {\ frac {1} {a}} {\ frac {\ partial \ Phi} {\ partial x_ {i}}} \,.}

v_{i}={\frac {\partial \Phi }{\partial x_{i}}}\qquad {\text{and}}\qquad M_{i}={\frac {v_{i}}{a}}={\frac {1}{a}}{\frac {\partial \Phi }{\partial x_{i}}}\,.

При использовании в уравнении потока полный Результаты потенциального уравнения:

∂ 2 Φ ∂ xi ∂ xi - M i M j ∂ 2 Φ ∂ xi ∂ xj = 0. {\ displaystyle {\ frac {\ partial ^ {2} \ Phi} {\ partial x_ {i} \, \ partial x_ {i}}} - M_ {i} \, M_ {j} \, {\ frac { \ partial ^ {2} \ Phi} {\ partial x_ {i} \, \ partial x_ {j}}} = 0 \,.}

{\frac {\partial ^{2}\Phi }{\partial x_{i}\,\partial x_{i}}}-M_{i}\,M_{j}\,{\frac {\partial ^{2}\Phi }{\partial x_{i}\,\partial x_{j}}}=0\,.

Записано в компонентах, форма, приведенная в начале этого раздела, является получено. Когда предоставлено конкретное уравнение состояния, связывающее давление p и плотность ρ, можно определить скорость звука. Впоследствии, вместе с соответствующими граничными условиями, может быть решено полное уравнение потенциала (чаще всего с использованием кода вычислительной гидродинамики ).

Нестабильный поток

Теория потенциального потока также может использоваться для моделирования безвихревого сжимаемого потока. Уравнение полного потенциала, описывающее нестационарный поток, задается следующим образом:

- 1 a 2 [∂ ∂ t (∇ Φ ⋅ ∇ Φ) + ∂ 2 Φ ∂ t 2] + (1 - M x 2) ∂ 2 Φ ∂ x 2 + (1 - M y 2) ∂ 2 Φ ∂ y 2 + (1 - M z 2) ∂ 2 Φ ∂ z 2 - 2 M x M y ∂ 2 Φ ∂ x ∂ y - 2 M y M z ∂ 2 Φ ∂ y ∂ Z - 2 M z M x ∂ 2 Φ ∂ z ∂ x = 0 {\ displaystyle {\ begin {align} - {\ frac {1} {a ^ { 2}}} \ left [{\ frac {\ partial} {\ partial t}} (\ nabla \ Phi \ cdot \ nabla \ Phi) + {\ frac {\ partial ^ {2} \ Phi} {\ partial t ^ {2}}} \ right] \\ + \ left (1-M_ {x} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial x ^ {2} }} + \ left (1-M_ {y} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial y ^ {2}}} + \ left (1-M_ { z} ^ {2} \ right) {\ frac {\ partial ^ {2} \ Phi} {\ partial z ^ {2}}} - 2M_ {x} M_ {y} {\ frac {\ partial ^ {2 } \ Phi} {\ partial x \, \ partial y}} - 2M_ {y} M_ {z} {\ frac {\ partial ^ {2} \ Phi} {\ partial y \, \ partial z}} - 2M_ {z} M_ {x} {\ frac {\ partial ^ {2} \ Phi} {\ partial z \, \ partial x}} = 0 \ end {align}}}

{\begin{aligned}-{\frac {1}{a^{2}}}\left[{\frac {\partial }{\partial t}}(\nabla \Phi \cdot \nabla \Phi)+{\frac {\partial ^{2}\Phi }{\partial t^{2}}}\right]\\+\left(1-M_{x}^{2}\right){\frac {\partial ^{2}\Phi }{\partial x^{2}}}+\left(1-M_{y}^{2}\right){\frac {\partial ^{2}\Phi }{\partial y^{2}}}+\left(1-M_{z}^{2}\right){\frac {\partial ^{2}\Phi }{\partial z^{2}}}-2M_{x}M_{y}{\frac {\partial ^{2}\Phi }{\partial x\,\partial y}}-2M_{y}M_{z}{\frac {\partial ^{2}\Phi }{\partial y\,\partial z}}-2M_{z}M_{x}{\frac {\partial ^{2}\Phi }{\partial z\,\partial x}}=0\end{aligned}}

с числом Маха компоненты

M x = 1 a ∂ Φ ∂ x, M y = 1 a ∂ Φ ∂ y и M z = 1 a ∂ Φ ∂ z, {\ displaystyle M_ {x} = {\ frac {1} {a}} {\ frac {\ partial \ Phi} {\ partial x}} \,, \ qquad M_ {y} = {\ frac {1} {a} } {\ frac {\ partial \ Phi} {\ partial y}} \,, \ qquad {\ text {and}} \ qquad M_ {z} = {\ frac {1} {a}} {\ frac {\ partial \ Phi} {\ partial z}} \,,}

M_{x}={\frac {1}{a}}{\frac {\partial \Phi }{\partial x}}\,,\qquad M_{y}={\frac {1}{a}}{\frac {\partial \Phi }{\partial y}}\,,\qquad {\text{and}}\qquad M_{z}={\frac {1}{a}}{\frac {\partial \Phi }{\partial z}}\,,

, где a - местная скорость звука. Скорость потока v снова равна ∇Φ, а Φ - потенциал скорости. Полное уравнение потенциала действительно для суб-, транс- и сверхзвукового потока при произвольном угле атаки, если допущение

∇ Φ = V ∞ x + ∇ φ. {\ displaystyle \ nabla \ Phi = V _ {\ infty} x + \ nabla \ varphi \,.}

{\ displaystyle \ nabla \ Phi = V _ {\ infty} x + \ nabla \ varphi \,.}

- 1 a 2 [2 V ∞ ∂ 2 φ ∂ x ∂ t + ∂ 2 φ ∂ t 2] + (1 - M ∞ 2) ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 + ∂ 2 φ ∂ Z 2 знак равно 0, {\ Displaystyle - {\ frac {1} {a ^ {2}}} \ left [2V _ {\ infty} {\ frac {\ partial ^ {2} \ varphi} {\ partial x \ partial t}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial t ^ {2}}} \ right] + \ left (1-M _ {\ infty} ^ {2} \ right) { \ frac {\ partial ^ {2} \ varphi} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial y ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial z ^ {2}}} = 0,}

{\ displaystyle - {\ frac {1} {a ^ {2}}} \ left [2V _ {\ infty} {\ frac {\ partial ^ {2} \ varphi} {\ partial x \ partial t}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial t ^ {2}}} \ right] + \ left (1-M_ {\ infty} ^ {2} \ right) {\ frac {\ partial ^ {2} \ v arphi} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial y ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial z ^ {2}}} = 0,}

с M ∞ = V ∞/a∞числом Маха входящего свободного потока.

Вывод полного уравнения потенциала

Начнем с уравнения сохранения массы. $1 ρ ∂ ρ ∂ t + v → ⋅ ∇ ρ ρ + ∇ ⋅ v → = 0 {\ displaystyle {\ frac {1} {\ rho}} {\ frac {\ partial \ rho} {\ partial t}} + {\ frac {{\ vec {v}} \ cdot \ nabla \ rho} {\ rho}} + \ nabla \ cdot {\ vec {v}} = 0}$ ${\frac {1}{\rho }}{\frac {\partial \rho }{\partial t}}+{\frac {{\vec {v}}\cdot \nabla \rho }{\rho }}+\nabla \cdot {\vec {v}}=0$

Рассмотрим первый член. Используя принцип Бернулли, запишем

$1 ρ ∂ ρ ∂ t = 1 a 2 ρ ∂ p ∂ t = 1 a 2 ∂ ∂ t ∫ p 1 pdp ~ d ρ (p ~) = - 1 a 2 ∂ ∂ T [∂ Φ ∂ T + ∇ Φ ⋅ ∇ Φ 2] {\ displaystyle {\ frac {1} {\ rho}} {\ frac {\ partial \ rho} {\ partial t}} = { \ frac {1} {a ^ {2} \ rho}} {\ frac {\ partial p} {\ partial t}} = {\ frac {1} {a ^ {2}}} {\ frac {\ partial } {\ partial t}} \ int _ {p_ {1}} ^ {p} {\ frac {d {\ tilde {p}}} {d \ rho ({\ tilde {p}})}} = - {\ frac {1} {a ^ {2}}} {\ frac {\ partial} {\ partial t}} \ left [{\ frac {\ partial \ Phi} {\ partial t}} + {\ frac { \ nabla \ Phi \ cdot \ nabla \ Phi} {2}} \ right]}$ ${\ displaystyle {\ frac {1} {\ rho}} {\ frac {\ partial \ rho} {\ partial t}} = {\ frac {1} {a ^ {2} \ rho}} {\ frac {\ partial p} {\ partial t}} = {\ frac {1} {a ^ {2}}} {\ frac {\ partial} {\ partial t}} \ int _ {p_ {1}} ^ {p} {\ frac {d {\ tilde {p}}} {d \ rho ({\ tilde {p}})}} = - {\ frac {1} {a ^ {2}}} {\ frac {\ partial} {\ partial t}} \ left [{\ frac {\ partial \ Phi} {\ partial t}} + {\ frac {\ nabla \ Phi \ cdot \ nabla \ Phi} {2}} \ right]}$

Аналогичным образом второй член может быть записан

$v → ⋅ ∇ ρ ρ = v → ⋅ ∇ pa 2 ρ = - 1 a 2 v → ⋅ ∇ [∂ Φ ∂ t + ∇ Φ ⋅ ∇ Φ 2] = - 1 a 2 ∇ Φ ⋅ ∇ [∂ Φ ∂ t + ∇ Φ ⋅ ∇ Φ 2] {\ displaystyle {\ frac { {\ vec {v}} \ cdot \ nabla \ rho} {\ rho}} = {\ frac {{\ vec {v}} \ cdot \ nabla p} {a ^ {2} \ rho}} = - { \ frac {1} {a ^ {2}}} {\ vec {v}} \ cdot \ nabla \ left [{\ frac {\ partial \ Phi} {\ partial t}} + {\ frac {\ nabla \ Phi \ cdot \ nabla \ Phi} {2}} \ right] = - {\ frac {1} {a ^ {2}}} \ nabla \ P привет \ cdot \ nabla \ left [{\ frac {\ partial \ Phi} {\ partial t}} + {\ frac {\ nabla \ Phi \ cdot \ nabla \ Phi} {2}} \ right]}$ ${\frac {{\vec {v}}\cdot \nabla \rho }{\rho }}={\frac {{\vec {v}}\cdot \nabla p}{a^{2}\rho }}=-{\frac {1}{a^{2}}}{\vec {v}}\cdot \nabla \left[{\frac {\partial \Phi }{\partial t}}+{\frac {\nabla \Phi \cdot \nabla \Phi }{2}}\right]=-{\frac {1}{a^{2}}}\nabla \Phi \cdot \nabla \left[{\frac {\partial \Phi }{\partial t}}+{\frac {\nabla \Phi \cdot \nabla \Phi }{2}}\right]$

Собирая члены и переставляя, уравнение сохранения массы принимает вид

$∇ 2 Φ - 1 a 2 ∂ ∂ t [∂ Φ ∂ t + ∇ Φ ⋅ ∇ Φ 2] - 1 a 2 ∇ Φ ⋅ ∇ [∂ Φ ∂ t + ∇ Φ ⋅ ∇ Φ 2] знак равно 0 {\ Displaystyle \ nabla ^ {2} \ Phi - {\ frac {1} {a ^ {2}}} {\ frac {\ partial} {\ partial t}} \ left [{\ frac {\ partial \ Phi} {\ partial t}} + {\ frac {\ nabla \ Phi \ cdot \ nabla \ Phi} {2}} \ right] - {\ frac {1} {a ^ {2}}} \ nabla \ Phi \ cdot \ nabla \ left [{\ frac {\ partial \ Phi} {\ partial t}} + {\ frac {\ nabla \ Phi \ cdot \ nabla \ Phi} {2} } \ right] = 0}$ $\nabla ^{2}\Phi -{\frac {1}{a^{2}}}{\frac {\partial }{\partial t}}\left[{\frac {\partial \Phi }{\partial t}}+{\frac {\nabla \Phi \cdot \nabla \Phi }{2}}\right]-{\frac {1}{a^{2}}}\nabla \Phi \cdot \nabla \left[{\frac {\partial \Phi }{\partial t}}+{\frac {\nabla \Phi \cdot \nabla \Phi }{2}}\right]=0$

$∇ 2 Φ - 1 a 2 [∂ 2 Φ ∂ t 2 + ∂ ∂ t (∇ Φ ⋅ ∇ Φ) + ∇ Φ ⋅ ∇ (∇ Φ ⋅ ∇ Φ 2)] = 0 {\ displaystyle \ nabla ^ {2} \ Phi - {\ frac {1} {a ^ {2}}} \ left [{\ frac {\ partial ^ {2} \ Phi} {\ partial t ^ {2 }}} + {\ frac {\ partial} {\ partial t}} (\ nabla \ Phi \ cdot \ nabla \ Phi) + \ nabla \ Phi \ cdot \ nabla \ left ({\ frac {\ nabla \ Phi \ cdot \ nabla \ Phi} {2}} \ right) \ right] = 0}$ $\nabla ^{2}\Phi -{\frac {1}{a^{2}}}\left[{\frac {\partial ^{2}\Phi }{\partial t^{2}}}+{\frac {\partial }{\partial t}}(\nabla \Phi \cdot \nabla \Phi)+\nabla \Phi \cdot \nabla \left({\frac {\nabla \Phi \cdot \nabla \Phi }{2}}\right)\right]=0$

Звуковые волны

Звуковые волны малой амплитуды можно аппроксимировать с помощью следующей модели потенциального потока:

∂ 2 φ ∂ t 2 = a ¯ 2 Δ φ, {\ displaystyle {\ frac {\ partial ^ {2} \ varphi} {\ partial t ^ {2 }}} = {\ overline {a}} ^ {2} \ Delta \ varphi,}

\ frac {\ partial ^ 2 \ varphi} {\ partial t ^ 2} = \ overline {a} ^ 2 \ Delta \ varphi,

, которое является линейным волновым уравнением для потенциала скорости φ. Опять же, колебательная часть вектора скорости v связана с потенциалом скорости соотношением v = ∇φ, в то время как, как и раньше, Δ является оператором Лапласа, а ā - средняя скорость звука в однородной среде. Отметим, что также колебательные части давления p и плотности ρ каждая индивидуально удовлетворяет волновому уравнению в этом приближении.

Применимость и ограничения

Потенциальный поток не включает все характеристики потоков, которые встречаются в реальном мире. Теория потенциального течения не может применяться для вязких внутренних течений, за исключением течений между близко расположенными пластинами. Ричард Фейнман считал потенциальный поток настолько нефизическим, что единственной жидкостью, которая подчинялась предположениям, была «сухая вода» (цитируя Джона фон Неймана). Несжимаемый потенциальный поток также делает ряд неверных предсказаний, таких как парадокс Даламбера, в котором говорится, что сопротивление любого объекта, движущегося через бесконечную жидкость, в противном случае в состоянии покоя равно нулю. Точнее, потенциальный поток не может учитывать поведение потоков, которые включают в себя пограничный слой. Тем не менее понимание потенциального потока важно во многих разделах механики жидкости. В частности, простые потенциальные потоки (называемые элементарными потоками ), такие как свободный вихрь и точечный источник, имеют готовые аналитические решения. Эти решения могут быть наложены для создания более сложных потоков, удовлетворяющих различным граничным условиям. Эти потоки близко соответствуют реальным потокам во всей механике жидкости; кроме того, многие ценные выводы возникают при рассмотрении отклонения (часто небольшого) между наблюдаемым потоком и соответствующим потенциальным потоком. Потенциальный поток находит множество применений в таких областях, как проектирование самолетов. Например, в вычислительной гидродинамике один метод состоит в том, чтобы связать решение потенциального потока за пределами пограничного слоя с решением уравнений пограничного слоя внутри границы слой. Отсутствие эффектов пограничного слоя означает, что любую линию тока можно заменить твердой границей без изменения поля потока, метод, используемый во многих подходах к аэродинамическому проектированию. Другим методом может быть использование твердых тел Рябушинского.

Анализ двумерного потока

Потенциальный поток в двух измерениях просто проанализировать с помощью конформного отображения, используя преобразования комплексной плоскости . Однако использование комплексных чисел не требуется, как, например, в классическом анализе потока жидкости через цилиндр. Невозможно решить потенциальный поток с помощью комплексных чисел в трех измерениях.

Основная идея состоит в использовании голоморфного (также называемого аналитическим ) или мероморфная функция f, которая отображает физическую область (x, y) в преобразованную область (φ, ψ). Хотя все x, y, φ и ψ являются вещественными, удобно определить комплексные величины

z = x + i y и w = φ + i ψ. {\ displaystyle z = x + iy \ qquad {\ text {and}} \ qquad w = \ varphi + i \ psi \,.}

z=x+iy\qquad {\text{and}}\qquad w=\varphi +i\psi \,.

Теперь, если мы запишем отображение f как

f (x + iy) = φ + i ψ или f (z) = w. {\ displaystyle f (x + iy) = \ varphi + i \ psi \ qquad {\ text {or}} \ qquad f (z) = w \,.}

{\ displaystyle f (x + iy) = \ varphi + i \ psi \ qquad {\ текст {или}} \ qquad f (z) = w \,.}

Тогда, поскольку f - голоморфная или мероморфная функция, он должен удовлетворять уравнениям Коши – Римана

∂ φ ∂ x = ∂ ψ ∂ y, ∂ φ ∂ y = - ∂ ψ ∂ x. {\ displaystyle {\ frac {\ partial \ varphi} {\ partial x}} = {\ frac {\ partial \ psi} {\ partial y}} \,, \ qquad {\ frac {\ partial \ varphi} {\ partial y}} = - {\ frac {\ partial \ psi} {\ partial x}} \,.}

{\ displaystyle {\ frac {\ partial \ varphi} {\ partial x}} = {\ frac {\ partial \ psi} {\ partial y}} \,, \ qquad {\ fr ac {\ partial \ varphi} {\ partial y}} = - {\ frac {\ partial \ psi} {\ partial x}} \,.}

Можно получить компоненты скорости (u, v) в направлениях (x, y) соответственно непосредственно из f дифференцированием по z. То есть

dfdz = u - iv {\ displaystyle {\ frac {df} {dz}} = u-iv}

{\ frac {df} {dz}} = u-iv

Итак, поле скорости v = (u, v) указано по

u = ∂ φ ∂ x = ∂ ψ ∂ y, v = ∂ φ ∂ y = - ∂ ψ ∂ x. {\ displaystyle u = {\ frac {\ partial \ varphi} {\ partial x}} = {\ frac {\ partial \ psi} {\ partial y}}, \ qquad v = {\ frac {\ partial \ varphi} {\ partial y}} = - {\ frac {\ partial \ psi} {\ partial x}} \,.}

u={\frac {\partial \varphi }{\partial x}}={\frac {\partial \psi }{\partial y}},\qquad v={\frac {\partial \varphi }{\partial y}}=-{\frac {\partial \psi }{\partial x}}\,.

И φ, и ψ тогда удовлетворяют уравнению Лапласа :

Δ φ = ∂ 2 φ ∂ x 2 + ∂ 2 φ ∂ y 2 = 0 и Δ ψ = ∂ 2 ψ ∂ x 2 + ∂ 2 ψ ∂ y 2 = 0. {\ displaystyle \ Delta \ varphi = {\ frac {\ partial ^ {2} \ varphi} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial y ^ {2}}} = 0 \ qquad {\ text {and}} \ qquad \ Delta \ psi = {\ frac {\ partial ^ {2} \ psi} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} \ psi} {\ partial y ^ {2}}} = 0 \,.}

{\ displaystyle \ Delta \ varphi = {\ frac {\ partial ^ {2} \ varphi} {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} \ varphi} {\ partial y ^ {2}}} = 0 \ qquad {\ text {and}} \ qquad \ Delta \ psi = {\ frac {\ partial ^ {2} \ psi } {\ partial x ^ {2}}} + {\ frac {\ partial ^ {2} \ psi} {\ partial y ^ {2}}} = 0 \,.}

Таким образом, φ можно определить как потенциал скорости, а ψ называется функцией тока . Линии постоянного ψ известны как линии тока, а линии постоянного φ - как эквипотенциальные линии (см. эквипотенциальная поверхность ).

Линии тока и эквипотенциальные линии ортогональны друг другу, поскольку

∇ φ ⋅ ∇ ψ = ∂ φ ∂ x ∂ ψ ∂ x + ∂ φ ∂ y ∂ ψ ∂ y = ∂ ψ ∂ y ∂ ψ ∂ х - ∂ ψ ∂ x ∂ ψ ∂ у знак равно 0. {\ displaystyle \ nabla \ varphi \ cdot \ nabla \ psi = {\ frac {\ partial \ varphi} {\ partial x}} {\ frac {\ partial \ psi} {\ partial x}} + {\ frac {\ partial \ varphi} {\ partial y}} {\ frac {\ partial \ psi} {\ partial y}} = {\ frac {\ partial \ psi} {\ partial y}} {\ frac {\ partial \ psi} {\ partial x}} - {\ frac {\ partial \ psi} {\ partial x}} {\ frac {\ partial \ psi} {\ partial y}} = 0 \,.}

\nabla \varphi \cdot \nabla \psi ={\frac {\partial \varphi }{\partial x}}{\frac {\partial \psi }{\partial x}}+{\frac {\partial \varphi }{\partial y}}{\frac {\partial \psi }{\partial y}}={\frac {\partial \psi }{\partial y}}{\frac {\partial \psi }{\partial x}}-{\frac {\partial \psi }{\partial x}}{\frac {\partial \psi }{\partial y}}=0\,.

Таким образом, поток возникает вдоль линий постоянной ψ и под прямым углом к линиям постоянной φ.

Δψ = 0 также выполняется, что эквивалентно ∇ × v= 0. Итак, поток является безвихревым. Тогда автоматическое условие ∂Ψ / ∂x ∂y = ∂Ψ / ∂y ∂x дает ограничение несжимаемости ∇ · v = 0.

Примеры двумерных течений

Для f может использоваться любая дифференцируемая функция. В следующих примерах используются различные элементарные функции ; специальные функции также могут использоваться. Обратите внимание, что многозначные функции, такие как натуральный логарифм, могут использоваться, но внимание должно быть ограничено одной римановой поверхностью.

степенными законами

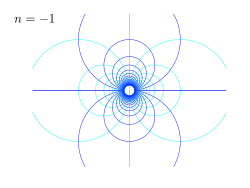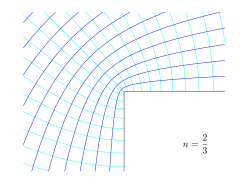
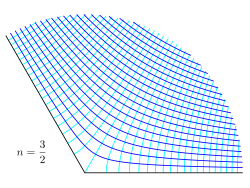
Примеры конформные карты для степенного закона w = Az, для различных значений мощности n. Показана плоскость z, показывающая линии постоянного потенциала φ и функции тока ψ, в то время как w = φ + iψ.

В случае применения следующей степенной -законной конформной карты от z = x + iy до w = φ + iψ:

w = A zn, {\ displaystyle w = Az ^ ​​{ n} \,,}

{\ displaystyle w = Az ^ ​​{n} \,,}

тогда, записав z в полярных координатах как z = x + iy = re, мы имеем

φ = A rn cos ⁡ n θ и ψ = A rn sin ⁡ n θ. {\ displaystyle \ varphi = Ar ^ {n} \ cos n \ theta \ qquad {\ text {and}} \ qquad \ psi = Ar ^ {n} \ sin n \ theta \,.}

\varphi =Ar^{n}\cos n\theta \qquad {\text{and}}\qquad \psi =Ar^{n}\sin n\theta \,.

На рисунках справа примеры приведены для нескольких значений n. Черная линия - это граница потока, более темные синие линии - это линии тока, а более светлые синие линии - это эквипотенциальные линии. Вот некоторые интересные степени n:

n = 1/2: это соответствует обтеканию полубесконечной пластины,
n = 2/3: обтеканию правого угла,
n = 1: тривиальный случай равномерного потока,
n = 2: поток через угол или около точки застоя, и
n = −1: поток из-за дублета источника

Константа A является параметром масштабирования: ее абсолютное значение | A | определяет масштаб, а его аргумент arg (A) вводит поворот (если не равен нулю).

Степенные законы с n = 1: равномерный поток

Если w = Az, то есть степенной закон с n = 1, линии тока (т. Е. Линии постоянной ψ) представляют собой систему прямые, параллельные оси x. Это легче всего увидеть, записав в терминах действительных и мнимых компонентов:

f (x + iy) = A (x + iy) = A x + i A y {\ displaystyle f (x + iy) = A \, (x + iy) = Ax + iAy}

f(x+iy)=A\,(x+iy)=Ax+iAy

, что дает φ = Ax и ψ = Ay. Этот поток можно интерпретировать как равномерный поток, параллельный оси x.

Законы мощности с n = 2

Если n = 2, то w = Az и линия тока, соответствующая конкретному значению ψ, - это те точки, которые удовлетворяют

ψ = A r 2 sin ⁡ 2 θ, {\ displaystyle \ psi = Ar ^ {2} \ sin 2 \ theta \,,}

{\ displaystyle \ psi = Ar ^ {2} \ sin 2 \ theta \,,}

, которая представляет собой систему прямоугольных гипербол. В этом можно убедиться, снова переписав реальную и мнимую составляющие. Отметив, что sin 2θ = 2 sin θ cos θ и переписав sin θ = y / r и cos θ = x / r, можно увидеть (при упрощении), что линии тока задаются как

ψ = 2 А ху. {\ displaystyle \ psi = 2Axy \,.}

{\ displaystyle \ psi = 2Axy \,.}

Поле скорости задается как ∇φ, или

(uv) = (∂ φ ∂ x ∂ φ ∂ y) = (+ ∂ ψ ∂ y - ∂ ψ ∂ x) = (+ 2 A x - 2 A y). {\ displaystyle {\ begin {pmatrix} u \\ v \ end {pmatrix}} = {\ begin {pmatrix} {\ frac {\ partial \ varphi} {\ partial x}} \\ [2px] {\ frac { \ partial \ varphi} {\ partial y}} \ end {pmatrix}} = {\ begin {pmatrix} + {\ partial \ psi \ over \ partial y} \\ [2px] - {\ partial \ psi \ over \ частичный x} \ end {pmatrix}} = {\ begin {pmatrix} + 2Ax \\ [2px] -2Ay \ end {pmatrix}} \,.}

{\ displaystyle {\ begin {pmatrix} u \\ v \ end {pmatrix}} = {\ begin {pmatrix} {\ frac {\ partial \ varphi} {\ partial x}} \\ [2px] {\ frac {\ partial \ varphi} {\ partial y}} \ end {pmatrix}} = {\ begin {pmatrix} + {\ partial \ psi \ over \ partial y} \ \ [2px] - {\ partial \ psi \ over \ partial x} \ end {pmatrix}} = {\ begin {pmatrix} + 2Ax \\ [2px] -2Ay \ end {pmatrix}} \,.}

В гидродинамике поле потока около начала координат соответствует точка застоя. Обратите внимание, что жидкость в начале координат покоится (это следует из дифференцирования f (z) = z при z = 0). Линия тока ψ = 0 особенно интересна: у нее есть две (или четыре) ветви, следующие за осями координат, т. Е. X = 0 и y = 0. Поскольку жидкость не течет поперек оси x, она (ось x) может рассматривать как твердую границу. Таким образом, можно игнорировать поток в нижней полуплоскости, где y < 0 and to focus on the flow in the upper halfplane. With this interpretation, the flow is that of a vertically directed jet impinging on a horizontal flat plate. The flow may also be interpreted as flow into a 90 degree corner if the regions specified by (say) x, y < 0 are ignored.

степенные законы с n = 3

Если n = 3, результирующий поток представляет собой своего рода гексагональную версию n = 2 рассмотренный выше случай. Линии тока задаются выражением ψ = 3xy - y, и поток в этом случае можно интерпретировать как поток в угол 60 °.

Законы мощности с n = −1: дублет

Если n = −1, линии тока задаются как

ψ = - A r sin ⁡ θ. {\ displaystyle \ psi = - {\ frac {A} {r}} \ sin \ theta.}

\psi =-{\frac {A}{r}}\sin \theta.

Это легче интерпретировать с точки зрения действительных и мнимых компонентов:

ψ = - A yr 2 = - A yx 2 + y 2, {\ displaystyle \ psi = {\ frac {-Ay} {r ^ {2}}} = {\ frac {-Ay} {x ^ {2} + y ^ {2}}} \,,}

{\ displaystyle \ psi = {\ frac {-Ay} {r ^ {2}} } = {\ frac {-Ay} {х ^ {2} + y ^ {2}}} \,,}

Икс 2 + Y 2 + A y ψ = 0, {\ displaystyle x ^ {2} + y ^ {2} + {\ frac {Ay} {\ psi}} = 0 \,, }

{\ displaystyle x ^ {2} + y ^ {2} + {\ frac {Ay} {\ psi}} = 0 \,,}

x 2 + (y + A 2 ψ) 2 = (A 2 ψ) 2. {\ displaystyle x ^ {2} + \ left (y + {\ frac {A} {2 \ psi}} \ right) ^ {2} = \ left ({\ frac {A} {2 \ psi}} \ right) ^ {2} \,.}

x^{2}+\left(y+{\frac {A}{2\psi }}\right)^{2}=\left({\frac {A}{2\psi }}\right)^{2}\,.

Таким образом, линии тока представляют собой окружности, которые касаются оси x в начале координат. Таким образом, круги в верхней полуплоскости текут по часовой стрелке, а круги в нижней - против часовой стрелки. Обратите внимание, что компоненты скорости пропорциональны r; и их значения в начале координат бесконечны. Эта структура потока обычно упоминается как дублет или диполь, и может быть интерпретирована как комбинация пары источник-сток бесконечной силы, сохраняемой на бесконечно малом расстоянии друг от друга. Поле скоростей задается формулой

(u, v) = (∂ ψ ∂ y, - ∂ ψ ∂ x) = (A y 2 - x 2 (x 2 + y 2) 2, - A 2 xy (x 2 + у 2) 2). {\ displaystyle (u, v) = \ left ({\ frac {\ partial \ psi} {\ partial y}}, - {\ frac {\ partial \ psi} {\ partial x}} \ right) = \ left (A {\ frac {y ^ {2} -x ^ {2}} {\ left (x ^ {2} + y ^ {2} \ right) ^ {2}}}, - A {\ frac {2xy } {\ left (x ^ {2} + y ^ {2} \ right) ^ {2}}} \ right) \,.}

(u,v)=\left({\frac {\partial \psi }{\partial y}},-{\frac {\partial \psi }{\partial x}}\right)=\left(A{\frac {y^{2}-x^{2}}{\left(x^{2}+y^{2}\right)^{2}}},-A{\frac {2xy}{\left(x^{2}+y^{2}\right)^{2}}}\right)\,.

или в полярных координатах:

(ur, u θ) = (1 r ∂ ψ ∂ θ, - ∂ ψ ∂ r) = (- A r 2 cos ⁡ θ, - A r 2 sin ⁡ θ). {\ displaystyle (u_ {r}, u _ {\ theta}) = \ left ({\ frac {1} {r}} {\ frac {\ partial \ psi} {\ partial \ theta}}, - {\ frac {\ partial \ psi} {\ partial r}} \ right) = \ left (- {\ frac {A} {r ^ {2}}} \ cos \ theta, - {\ frac {A} {r ^ { 2}}} \ sin \ theta \ right) \,.}

(u_{r},u_{\theta })=\left({\frac {1}{r}}{\frac {\partial \psi }{\partial \theta }},-{\frac {\partial \psi }{\partial r}}\right)=\left(-{\frac {A}{r^{2}}}\cos \theta,-{\frac {A}{r^{2}}}\sin \theta \right)\,.

Степенные законы с n = −2: квадруполь

Если n = −2, линии тока задаются как

ψ = - A r 2 sin ⁡ 2 θ. {\ displaystyle \ psi = - {\ frac {A} {r ^ {2}}} \ sin 2 \ theta \,.}

\psi =-{\frac {A}{r^{2}}}\sin 2\theta \,.

Это поле потока, связанное с квадруполем.

линейным источником и тонет

линейный источник или приемник силы $Q {\ displaystyle Q}$ $Q$ ( $Q>0 {\ displaystyle Q>0}$ $Q>0$ для источника и $Q < 0 {\displaystyle Q<0}$ ${\ displaystyle Q <0}$ для приемника) задается потенциалом

вес = Q 2 π ln ⁡ z {\ displaystyle w = {\ frac {Q} {2 \ pi}} \ ln z}

w={\frac {Q}{2\pi }}\ln z

где $Q {\ displaystyle Q}$ $Q$ фактически представляет собой объемный поток на единицу длины на поверхности, окружающей источник или сток. Поле скорости в полярных координатах:

ur = Q 2 π r, u θ = 0 {\ displaystyle u_ {r} = {\ frac {Q} {2 \ pi r}}, \ quad u _ {\ theta} = 0}

{ \ displaystyle u_ {r} = {\ frac {Q} {2 \ pi r}}, \ quad u _ {\ theta} = 0}

т.е. чисто радиальный поток.

Линейный вихрь

Линейный вихрь силы $Γ {\ displaystyle \ Gamma}$ $\ Gamma$ дается выражением

w = Γ 2 π i ln ⁡ z {\ displaystyle w = {\ frac {\ Gamma} {2 \ pi i} } \ ln z}

w={\frac {\Gamma }{2\pi i}}\ln z

где $Γ {\ displaystyle \ Gamma}$ $\ Gamma$ - это циркуляция вокруг любого простого замкнутого контура, охватывающего вихрь. Поле скорости в полярных координатах:

ur = 0, u θ = Γ 2 π r {\ displaystyle u_ {r} = 0, \ quad u _ {\ theta} = {\ frac {\ Gamma} {2 \ pi r}}}

{\ displaystyle u_ {r} = 0, \ quad u _ {\ theta} = {\ frac {\ Gamma} {2 \ pi r}}}

т.е. чисто азимутальный поток.

Анализ для трехмерного потока

Для трехмерных потоков невозможно получить комплексный потенциал.

Точечный источник и сток

Потенциал скорости точечного источника или стока силы $Q {\ displaystyle Q}$ $Q$ ( $Q>0 {\ displaystyle Q>0}$ $Q>0$ для источника и $Q < 0 {\displaystyle Q<0}$ ${\ displaystyle Q <0}$ для стока) в сферических полярных координатах определяется как

ϕ = - Q 4 π r {\ displaystyle \ phi = - {\ frac {Q} {4 \ pi r}}}

{\ displaystyle \ phi = - {\ frac {Q} {4 \ pi r}}}

где $Q {\ displaystyle Q}$ $Q$ на самом деле представляет собой объемный поток через замкнутую поверхность, окружающую источник или сток.

См. Также

Примечания

Ссылки

Бэтчелор, GK (1973), Введение в гидродинамику, Cambridge University Press, ISBN 0-521-09817-3
Chanson, H. (2009), Ап слоистая гидродинамика: введение в идеальные и реальные потоки жидкости, CRC Press, Taylor Francis Group, Лейден, Нидерланды, 478 страниц, ISBN 978-0-415-49271-3
Лэмб, Х. (1994) [1932], Гидродинамика (6-е изд.), Cambridge University Press, ISBN 978-0-521-45868-9
Милн-Томсон, Л. М. (1996) [1968], Теоретическая гидродинамика (5-е изд.), Довер, ISBN 0-486-68970-0

Дополнительная литература

Шансон, Х. (2007), «Le Potentiel de vitesse pour les écoulements de fluides réels: вклад Жозефа-Луи Лагранжа [Потенциал скорости в реальных потоках жидкости: вклад Жозефа-Луи Лагранжа]», La Houille Blanche (на французском языке) (5): 127–131, doi : 10.1051 / lhb: 2007072
Wehausen, JV ; Лайтоне, Э. (1960), «Поверхностные волны», в Flügge, S. ; Трусделл, К. (ред.), Encyclopedia of Physics, IX, Springer Verlag, стр. 446–778, архивировано с оригинала 05.01.2009, получено 29 марта 2009 г.

Внешние ссылки

На Викискладе есть материалы, связанные с Потенциальным потоком.

«Безвихревой поток невязкой жидкости». Генуэзский университет, инженерный факультет. Проверено 29 марта 2009 г.
"Галерея конформных карт". 3D-XplorMath. Проверено 29 марта 2009 г. - Java-апплеты для изучения конформных карт
Визуализации потенциальных потоков - Интерактивные веб-приложения