Метод конечных разностей

В численном анализе, методах конечных разностей (FDM ) представляет собой класс численных методов для решения дифференциальных уравнений путем аппроксимации производных с помощью конечных разностей. Как пространственная область, так и временной интервал (если применимо) дискретизируются или разбиваются на конечное число шагов, и значение решения в этих дискретных точках аппроксимируется путем решения алгебраических уравнений, содержащих конечные разности и значения. из близлежащих точек.

Методы конечных разностей преобразуют обыкновенные дифференциальные уравнения (ODE) или уравнения в частных производных (PDE), которые могут быть нелинейными, в система линейных уравнений, которая может быть решена методами матричной алгебры. Современные компьютеры могут эффективно выполнять эти вычисления линейной алгебры, что, наряду с их относительной простотой реализации, привело к широкому использованию FDM в современном численном анализе. Сегодня FDM являются одним из наиболее распространенных подходов к численному решению PDE, наряду с методами конечных элементов.

• 1 Вывод из полинома Тейлора
• 2 Точность и порядок
• 3 Пример: обыкновенное дифференциальное уравнение
• 4 Пример: уравнение теплопроводности
  • 4.1 Явный метод
  • 4.2 Неявный метод
  • 4.3 Метод Кривошипа – Николсона
  • 4.4 Сравнение
• 5 Пример: оператор Лапласа
  • 5.1 Согласованность
  • 5.2 Свойства
    • 5.2.1 Субгармоника
    • 5.2.2 Среднее значение
    • 5.2.3 Принцип максимума
• 6 Метод SBP-SAT
• 7 См. Также
• 8 Ссылки
• 9 Дополнительная литература
  • 9.1 Различные лекции и конспекты лекций

Во-первых, предположим, что функция, производные которой должны быть аппроксимированы, правильно ведет себя по теореме Тейлора, мы можем создать ряд Тейлора разложение

$f\; (x\; 0\; +\; h)\; =\; f\; (x\; 0)\; +\; f\; \prime \; (x\; 0)\; 1!\; ч\; +\; е\; (2)\; (х\; 0)\; 2!\; ч\; 2\; +\; \cdots \; +\; е\; (п)\; (х\; 0)\; п!\; час\; +\; р\; N\; (x),\; \{\backslash \; displaystyle\; f\; (x\_\; \{0\}\; +\; h)\; =\; f\; (x\_\; \{0\})\; +\; \{\backslash \; frac\; \{f\; \text{'}(x\_\; \{0\})\}\; \{1!\}\}\; h\; +\; \{\backslash \; гидроразрыв\; \{f\; ^\; \{(2)\}\; (x\_\; \{0\})\}\; \{2!\}\}\; h\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; \{\backslash \; frac\; \{f\; ^\; \{(n)\}\; (x\_\; \{0\})\}\; \{n\; !\}\}\; h\; ^\; \{n\}\; +\; R\_\; \{n\}\; (x),\}$

где n! обозначает факториал числа n, а R n (x) - это остаточный член, обозначающий разницу между многочленом Тейлора степени n и исходной функцией. Мы получим приближение для первой производной функции «f», сначала усекая многочлен Тейлора:

$f\; (x\; 0\; +\; h)\; =\; f\; (x\; 0)\; +\; f\; \prime \; (x\; 0)\; h\; +\; R\; 1\; (\; x),\; \{\backslash \; displaystyle\; f\; (x\_\; \{0\}\; +\; h)\; =\; f\; (x\_\; \{0\})\; +\; f\; \text{'}(x\_\; \{0\})\; h\; +\; R\_\; \{1\}\; (x),\}$

Настройка, x 0 = a имеем,

$f\; (a\; +\; h)\; =\; f\; (a)\; +\; f\; \prime \; (a)\; h\; +\; R\; 1\; (x),\; \{\backslash \; displaystyle\; f\; (a\; +\; h)\; =\; f\; (a)\; +\; f\; \text{'}(a)\; h\; +\; R\_\; \{1\}\; (x),\}$

Деление поперек на h дает:

$f\; (a\; +\; h)\; h\; =\; f\; (a)\; h\; +\; f\; \prime \; (a)\; +\; R\; 1\; (x)\; час\; \{\backslash \; displaystyle\; \{f\; (a\; +\; h)\; \backslash \; over\; h\}\; =\; \{f\; (a)\; \backslash \; over\; h\}\; +\; f\; \text{'}(a)\; +\; \{R\_\; \{1\}\; (x)\; \backslash \; over\; h\; \}\}$

Решение относительно f '(a):

$f\; \prime \; (a)\; =\; f\; (a\; +\; h)\; -\; f\; (a)\; h\; -\; R\; 1\; (x)\; h\; \{\backslash \; displaystyle\; f\text{'}\; (a)\; =\; \{f\; (a\; +\; h)\; -f\; (a)\; \backslash \; over\; h\}\; -\; \{R\_\; \{1\}\; (x)\; \backslash \; over\; h\}\}$

Предполагая, что $R\; 1\; (x)\; \{\backslash \; displaystyle\; R\_\; \{1\}\; (x)\}$достаточно мало, аппроксимация первой производной от «f» равна:

$f\; \prime \; (a)\; \approx \; f\; (a\; +\; h)\; -\; f\; (a)\; h.\; \{\backslash \; displaystyle\; f\; \text{'}(a)\; \backslash \; приблизительно\; \{f\; (a\; +\; h)\; -f\; (a)\; \backslash \; over\; h\}.\}$

Это, не случайно, похоже на определение производной, которое дается как:

$f\; \prime \; (a)\; =\; lim\; h\; \to \; 0\; f\; (a\; +\; h)\; -\; f\; (a)\; h.\; \{\backslash \; displaystyle\; f\; \text{'}(a)\; =\; \backslash \; lim\; \_\; \{h\; \backslash \; to\; 0\}\; \{\backslash \; frac\; \{f\; (a\; +\; h)\; -f\; (a)\}\; \{h\}\}.\}$

кроме предела к нулю ( метод назван в честь этого).

Погрешность решения метода определяется как разница между приближением и точным аналитическим решением. Двумя источниками ошибок в методах конечных разностей являются ошибка округления, потеря точности из-за компьютерного округления десятичных величин и ошибка усечения или ошибка дискретизации <269.>, разница между точным решением исходного дифференциального уравнения и точной величиной, предполагающей совершенную арифметику (то есть без округления).

Метод конечных разностей основан на дискретизации функции на сетке.

Чтобы использовать метод конечных разностей для аппроксимации решения проблемы, нужно сначала дискретизировать область задачи. Обычно это делается путем разделения домена на однородную сетку (см. Изображение справа). Это означает, что конечно-разностные методы производят наборы дискретных численных приближений производной, часто «ступенчато по времени».

Выражением общего интереса является ошибка локального усечения метода. Обычно выражается с использованием нотации Big-O, локальная ошибка усечения относится к ошибке из-за одного применения метода. То есть это величина $f\; \prime \; (xi)\; -\; fi\; \prime \; \{\backslash \; displaystyle\; f\; \text{'}(x\_\; \{i\})\; -\; f\text{'}\; \_\; \{i\}\}$, если $f\; \prime \; (\; xi)\; \{\backslash \; displaystyle\; f\; \text{'}(x\_\; \{i\})\}$относится к точному значению, а $fi\; \prime \; \{\backslash \; displaystyle\; f\text{'}\; \_\; \{i\}\}$к числовому приближение. Остаточный член полинома Тейлора удобен для анализа локальной ошибки усечения. Используя форму Лагранжа остатка от полинома Тейлора для $f\; (x\; 0\; +\; h)\; \{\backslash \; displaystyle\; f\; (x\_\; \{0\}\; +\; h)\}$, что равно

$R\; n\; (\; х\; 0\; +\; ч)\; знак\; равно\; е\; (п\; +\; 1)\; (\xi )\; (п\; +\; 1)!\; (час)\; n\; +\; 1\; \{\backslash \; displaystyle\; R\_\; \{n\}\; (x\_\; \{0\}\; +\; h)\; =\; \{\backslash \; frac\; \{f\; ^\; \{(n\; +\; 1)\}\; (\backslash \; xi)\}\; \{(n\; +\; 1)!\}\}\; (\; h)\; ^\; \{n\; +\; 1\}\}$, где ,

может быть обнаружен доминирующий член локальной ошибки усечения. Например, снова используя формулу прямой разности для первой производной, зная, что $f\; (xi)\; =\; f\; (x\; 0\; +\; ih)\; \{\backslash \; displaystyle\; f\; (x\_\; \{i\})\; =\; f\; (x\_\; \{0\}\; +\; ih)\}$,

$f\; (x\; 0\; +\; ih)\; =\; f\; (x\; 0)\; +\; f\; \prime \; (x\; 0)\; ih\; +\; f\; ″\; (\xi )\; 2!\; (ih)\; 2,\; \{\backslash \; displaystyle\; f\; (x\_\; \{0\}\; +\; ih)\; =\; f\; (x\_\; \{0\})\; +\; f\; \text{'}(x\_\; \{0\})\; ih\; +\; \{\backslash \; frac\; \{f\text{'}\; \text{'}(\backslash \; xi)\}\; \{2!\; \}\}\; (ih)\; ^\; \{2\},\}$

и с некоторыми алгебраическими манипуляциями это приводит к

$f\; (x\; 0\; +\; ih)\; -\; f\; (x\; 0)\; ih\; =\; f\; \prime \; (x\; 0)\; +\; f\; ″\; (\xi )\; 2!\; ih,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{f\; (x\_\; \{0\}\; +\; ih)\; -f\; (x\_\; \{0\})\}\; \{ih\}\}\; =\; f\; \text{'}(x\_\; \{0\})\; +\; \{\backslash \; frac\; \{f\text{'}\; \text{'}(\backslash \; xi)\}\; \{2!\}\}\; ih,\}$

и далее отмечая, что величина слева является приближением метода конечных разностей и что величина справа является точной величиной, представляющей интерес плюс остаток, ясно, что остаток - это локальная ошибка усечения. Окончательное выражение этого примера и его порядок:

$f\; (x\; 0\; +\; i\; h)\; -\; f\; (x\; 0)\; i\; h\; =\; f\; \text{'}(x\; 0)\; +\; O\; (h).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{f\; (x\_\; \{0\}\; +\; ih)\; -f\; (x\_\; \{0\})\}\; \{ih\}\}\; =\; f\; \text{'}(x\_\; \{0\})\; +\; O\; (h).\}$

Это означает что в этом случае локальная ошибка усечения пропорциональна размерам шага. Качество и продолжительность моделируемого решения FDM зависит от выбора уравнения дискретизации и размеров шага (временные и пространственные шаги). Качество данных и продолжительность моделирования значительно увеличиваются при меньшем размере шага. Следовательно, для практического использования необходим разумный баланс между качеством данных и продолжительностью моделирования. Большие временные шаги полезны для увеличения скорости моделирования на практике. Однако слишком большие временные шаги могут создать нестабильность и повлиять на качество данных.

Критерии фон Неймана и Куранта-Фридрихса-Леви часто используются для определения устойчивость численной модели.

Например, рассмотрим обыкновенное дифференциальное уравнение

$u\; \prime \; (x)\; =\; 3\; u\; (x)\; +\; 2.\; \{\backslash \; displaystyle\; u\; \text{'}(x)\; =\; 3u\; (x)\; +2.\; \backslash ,\}$

В методе Эйлера для решения этого уравнения используется коэффициент конечных разностей

$u\; (x\; +\; h)\; -\; u\; (x)\; h\; \approx \; u\; \prime \; (x)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{u\; (x\; +\; h)\; -u\; (x)\}\; \{h\}\}\; \backslash \; приблизительно\; u\; \text{'}(x)\}$

, чтобы аппроксимировать дифференциальное уравнение, сначала подставив это для u '(x), затем применяя небольшую алгебру (умножая обе стороны на h, а затем добавляя u (x) к обеим сторонам), чтобы получить

$u\; (x\; +\; h)\; =\; u\; (x)\; +\; h\; (3\; и\; (х)\; +\; 2).\; \{\backslash \; displaystyle\; u\; (x\; +\; h)\; =\; u\; (x)\; +\; h\; (3u\; (x)\; +2).\; \backslash ,\}$

Последнее уравнение является конечно-разностным уравнением, и решение этого уравнения дает приближенное решение дифференциальное уравнение.

Рассмотрим нормализованное уравнение теплопроводности в одном измерении с однородными граничными условиями Дирихле

$U\; t\; =\; U\; xx\; \{\backslash \; displaystyle\; U\_\; \{t\}\; =\; U\_\; \{xx\}\; \backslash ,\}$

$U\; (0,\; t)\; =\; U\; (1,\; t)\; =\; 0\; \{\backslash \; displaystyle\; U\; (0,\; t)\; =\; U\; (1,\; t)\; =\; 0\; \backslash ,\}$(граничное условие)

$U\; (x,\; 0)\; =\; U\; 0\; (x)\; \{\backslash \; displaystyle\; U\; (x,\; 0)\; =\; U\_\; \{0\}\; (x)\; \backslash ,\}$(начальное условие)

Один из способов численного решения этого уравнения - аппроксимировать все производные конечными разностями. Разделим область в пространстве с помощью сетки $x\; 0,...,\; x\; J\; \{\backslash \; displaystyle\; x\_\; \{0\},...,\; x\_\; \{J\}\}$и во времени с использованием сетки $t\; 0,....,\; т\; N\; \{\backslash \; displaystyle\; t\_\; \{0\},....,\; t\_\; \{N\}\}$. Мы предполагаем однородное разделение как в пространстве, так и во времени, поэтому разница между двумя последовательными точками пространства будет h, а между двумя последовательными моментами времени будет k. Точки

$u\; (xj,\; tn)\; =\; ujn\; \{\backslash \; displaystyle\; u\; (x\_\; \{j\},\; t\_\; \{n\})\; =\; u\_\; \{j\}\; ^\; \{n\}\}$

будут представлять численное приближение $u\; (xj,\; tn).\; \{\backslash \; displaystyle\; u\; (x\_\; \{j\},\; t\_\; \{n\}).\}$

Явный метод

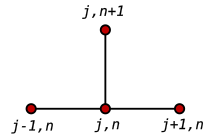
Шаблон для наиболее распространенного явного метода для уравнения теплопроводности.

Использование прямая разница в момент времени $tn\; \{\backslash \; displaystyle\; t\_\; \{n\}\}$и центральная разница второго порядка для пространственной производной в позиции $xj\; \{\backslash \; displaystyle\; x\_\; \{j\}\}$(FTCS ) получаем рекуррентное уравнение:

$ujn\; +\; 1\; -\; ujnk\; =\; uj\; +\; 1\; n\; -\; 2\; ujn\; +\; uj\; -\; 1\; nh\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; -u\_\; \{j\}\; ^\; \{n\}\}\; \{k\}\}\; =\; \{\backslash \; frac\; \{u\_\; \{j\; +\; 1\}\; ^\; \{n\}\; -2u\_\; \{j\; \}\; ^\; \{n\}\; +\; u\_\; \{j-1\}\; ^\; \{n\}\}\; \{h\; ^\; \{2\}\}\}.\; \backslash ,\}$

Это явный метод для решения одномерного уравнение теплопроводности.

Мы можем получить $ujn\; +\; 1\; \{\backslash \; displaystyle\; u\_\; \{j\}\; ^\; \{n\; +\; 1\}\}$из других значений следующим образом:

$ujn\; +\; 1\; =\; (1-2\; r)\; ujn\; +\; ruj\; -\; 1\; n\; +\; ruj\; +\; 1\; n\; \{\backslash \; displaystyle\; u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; =\; (1-2r)\; u\_\; \{j\}\; ^\; \{n\}\; +\; ru\_\; \{j-1\; \}\; ^\; \{n\}\; +\; ru\_\; \{j\; +\; 1\}\; ^\; \{n\}\}$

где $r\; =\; k\; /\; h\; 2.\; \{\backslash \; displaystyle\; r\; =\; k\; /\; h\; ^\; \{2\}.\}$

Итак, с этим рекуррентным соотношением и зная значения в момент времени n, можно получить соответствующие значения в момент времени n + 1. $u\; 0\; n\; \{\backslash \; displaystyle\; u\_\; \{0\}\; ^\; \{n\}\}$и $u\; J\; n\; \{\backslash \; displaystyle\; u\_\; \{J\}\; ^\; \{n\}\}$должен должны быть заменены граничными условиями, в этом примере они оба равны 0.

Этот явный метод известен как численно устойчивый и сходящийся всякий раз, когда $r\; \le \; 1/2\; \{\backslash \; displaystyle\; r\; \backslash \; leq\; 1/2\}$. Численные ошибки пропорциональны шагу по времени и квадрату шага по пространству:

$\Delta \; u\; =\; O\; (k)\; +\; O\; (h\; 2)\; \{\backslash \; displaystyle\; \backslash \; Delta\; u\; =\; O\; (k)\; +\; O\; (h\; ^\; \{\; 2\})\; \backslash ,\}$

Неявный метод

Шаблон неявного метода.

Если мы используем обратную разницу во время $tn\; +\; 1\; \{\backslash \; displaystyle\; t\_\; \{\; n\; +\; 1\}\}$и центральная разность второго порядка для пространственной производной в позиции $xj\; \{\backslash \; displaystyle\; x\_\; \{j\}\}$(время назад, метод центрированного пространства "BTCS") получаем рекуррентное уравнение:

$ujn\; +\; 1\; -\; ujnk\; =\; uj\; +\; 1\; n\; +\; 1-2\; ujn\; +\; 1\; +\; uj\; -\; 1\; n\; +\; 1\; h\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; -u\_\; \{j\}\; ^\; \{n\}\}\; \{k\}\}\; =\; \{\backslash \; frac\; \{u\_\; \{j\; +\; 1\}\; ^\; \{n\; +\; 1\}\; -2u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; +\; u\_\; \{j-1\}\; ^\; \{n\; +\; 1\}\}\; \{h\; ^\; \{2\}\}\}.\; \backslash ,\}$

Это неявный метод для решение одномерного уравнения теплопроводности.

Мы можем получить $ujn\; +\; 1\; \{\backslash \; displaystyle\; u\_\; \{j\}\; ^\; \{n\; +\; 1\}\}$из решения системы линейных уравнений:

$(1\; +\; 2\; r)\; ujn\; +\; 1\; -\; ruj\; -\; 1\; n\; +\; 1\; -\; ruj\; +\; 1\; n\; +\; 1\; =\; ujn\; \{\backslash \; displaystyle\; (1\; +\; 2r)\; u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; -ru\_\; \{j\; -1\}\; ^\; \{n\; +\; 1\}\; -ru\_\; \{j\; +\; 1\}\; ^\; \{n\; +\; 1\}\; =\; u\_\; \{j\}\; ^\; \{n\}\}$

Схема всегда численно устойчива и сходится, но обычно более трудоемкий в числовом отношении, чем явный метод, поскольку он требует решения системы численных уравнений на каждом временном шаге. Ошибки линейны по временному шагу и квадратичны по пространственному шагу:

$\Delta \; u\; =\; O\; (k)\; +\; O\; (h\; 2).\; \{\backslash \; displaystyle\; \backslash \; Delta\; u\; =\; O\; (k)\; +\; O\; (h\; ^\; \{2\}).\; \backslash ,\}$

Метод Кривошипа – Николсона

Наконец, если мы используем центральную разность в момент времени $tn\; +\; 1/2\; \{\backslash \; displaystyle\; t\_\; \{n\; +\; 1/2\}\}$и центральная разность второго порядка для пространственной производной в позиции $xj\; \{\backslash \; displaystyle\; x\_\; \{j\}\}$(«CTCS») получаем рекуррентное уравнение:

$ujn\; +\; 1\; -\; ujnk\; =\; 1\; 2\; (uj\; +\; 1\; n\; +\; 1-2\; ujn\; +\; 1\; +\; uj\; -\; 1\; n\; +\; 1\; h\; 2\; +\; uj\; +\; 1\; n\; -\; 2\; ujn\; +\; uj\; -\; 1\; nh\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; -u\_\; \{j\}\; ^\; \{n\}\}\; \{k\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{u\_\; \{j\; +\; 1\}\; ^\; \{n\; +\; 1\}\; -2u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; +\; u\_\; \{j-1\}\; ^\; \{n\; +\; 1\}\}\; \{h\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{u\_\; \{j\; +\; 1\}\; ^\; \{n\}\; -2u\_\; \{j\}\; ^\; \{n\}\; +\; u\_\; \{j-1\}\; ^\; \{n\}\}\; \{h\; ^\; \{2\}\}\}\; \backslash \; right).\; \backslash ,\}$

Эта формула известен как метод Crank – Nicolson.

Шаблон Crank – Nicolson.

Мы можем получить $ujn\; +\; 1\; \{\backslash \; displaystyle\; u\_\; \{j\}\; ^\; \{n\; +\; 1\}\}$от решения системы линейных уравнений:

$(2\; +\; 2\; r)\; ujn\; +\; 1\; -\; ruj\; -\; 1\; n\; +\; 1\; -\; ruj\; +\; 1\; n\; +\; 1\; =\; (2\; -\; 2\; r)\; ujn\; +\; ruj\; -\; 1\; n\; +\; ruj\; +\; 1\; n\; \{\backslash \; displaystyle\; (2\; +\; 2r)\; u\_\; \{j\}\; ^\; \{n\; +\; 1\}\; -ru\_\; \{j-1\}\; ^\; \{n\; +\; 1\}\; -ru\_\; \{j\; +\; 1\}\; ^\; \{n\; +\; 1\}\; =\; (\; 2-2r)\; u\_\; \{j\}\; ^\; \{n\}\; +\; ru\_\; \{j-1\}\; ^\; \{n\}\; +\; ru\_\; \{j\; +\; 1\}\; ^\; \{n\}\}$

Схема всегда численно устойчива и сходящийся, но обычно более интенсивный в числовом отношении, поскольку требует решения системы числовых уравнений на каждом временном шаге. Ошибки квадратичны как по временному шагу, так и по пространственному шагу:

$\Delta \; u\; =\; O\; (k\; 2)\; +\; O\; (h\; 2).\; \{\backslash \; displaystyle\; \backslash \; Delta\; u\; =\; O\; (k\; ^\; \{2\})\; +\; O\; (h\; ^\; \{2\}).\; \backslash ,\}$

Сравнение

Подводя итог, обычно схема Кранка – Николсона является наиболее подходящей. четкая схема для малых временных шагов Для больших временных шагов неявная схема работает лучше, так как она менее требовательна к вычислениям. Явная схема является наименее точной и может быть нестабильной, но также является наиболее простой в реализации и наименее трудоемкой.

Вот пример. На рисунках ниже представлены решения, полученные с помощью вышеуказанных методов для аппроксимации уравнения теплопроводности

$U\; t\; =\; \alpha \; U\; xx,\; \alpha \; =\; 1\; \pi \; 2,\; \{\backslash \; displaystyle\; U\_\; \{t\}\; =\; \backslash \; alpha\; U\_\; \{xx\},\; \backslash \; quad\; \backslash \; альфа\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; ^\; \{2\}\}\},\}$

с граничным условием

$U\; (0,\; t)\; =\; U\; (1,\; t)\; =\; 0.\; \{\backslash \; displaystyle\; U\; (\; 0,\; t)\; =\; U\; (1,\; t)\; =\; 0.\}$

Точное решение:

$U\; (x,\; t)\; =\; 1\; \pi \; 2\; e\; -\; t\; sin\; \; (\pi \; x).\; \{\backslash \; displaystyle\; U\; (x,\; t)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; ^\; \{2\}\}\}\; e\; ^\; \{-\; t\}\; \backslash \; sin\; (\backslash \; pi\; x).\}$

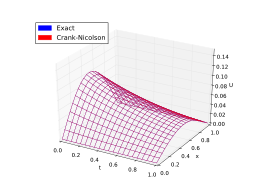
Сравнение методов конечных разностей Явный метод (нестабильный) Неявный метод (стабильный) Метод Кранка-Николсона (стабильный)

(непрерывный) оператор Лапласа в $n\; \{\backslash \; displaystyle\; n\}$-размеры задаются как $\Delta \; u\; (x)\; =\; \sum \; i\; =\; 1\; n\; \partial \; i\; 2\; u\; (x)\; \{\backslash \; displaystyle\; \backslash \; Delta\; u\; (\; x)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash \; partial\; \_\; \{i\}\; ^\; \{2\}\; u\; (x)\}$. Дискретный оператор Лапласа $\Delta \; hu\; \{\backslash \; displaystyle\; \backslash \; Delta\; \_\; \{h\}\; u\}$зависит от размерности $n\; \{\backslash \; displaystyle\; n\}$.

В 1D оператор Лапласа аппроксимируется как

$\Delta \; u\; (x)\; =\; u\; ″\; (x)\; \approx \; u\; (x\; -\; h)\; -\; 2\; u\; (x)\; +\; u\; (x\; +\; h)\; h\; 2\; =:\; \Delta \; hu\; (x).\; \{\backslash \; Displaystyle\; \backslash \; Delta\; u\; (x)\; =\; u\; \text{'}\text{'}\; (x)\; \backslash \; приблизительно\; \{\backslash \; frac\; \{u\; (xh)\; -2u\; (x)\; +\; u\; (x\; +\; h)\}\; \{h\; ^\; \{2\}\}\}\; =:\; \backslash \; Delta\; \_\; \{h\}\; u\; (x)\; \backslash ,.\}$

Это приближение обычно выражается с помощью следующего шаблона

$1\; h\; 2\; [1-2\; 1]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\; h\; ^\; \{2\}\}\}\; \{\backslash \; begin\; \{bmatrix\}\; 1\; -2\; 1\; \backslash \; end\; \{bmatrix\}\}\}$

и представляет собой симметричную трехдиагональную матрицу. Для равноудаленной сетки получается матрица Теплица.

. 2D-случай показывает все характеристики более общего nD-случая. Каждую вторую частную производную необходимо аппроксимировать аналогично одномерному случаю

$\Delta \; u\; (x,\; y)\; =\; uxx\; (x,\; y)\; +\; uyy\; (x,\; y)\; \approx \; u\; (x\; -\; h,\; y)\; -\; 2\; u\; (\; x,\; y)\; +\; u\; (x\; +\; h,\; y)\; h\; 2\; +\; u\; (x,\; y\; -\; h)\; -\; 2\; u\; (x,\; y)\; +\; u\; (x,\; y\; +\; h)\; h\; 2\; =\; u\; (x\; -\; h,\; y)\; +\; u\; (x\; +\; h,\; y)\; -\; 4\; u\; (x,\; y)\; +\; u\; (x,\; y\; -\; h)\; +\; u\; (x,\; y\; +\; h)\; h\; 2\; =:\; \Delta \; hu\; (x,\; y),\; \{\; \backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Delta\; u\; (x,\; y)\; =\; u\_\; \{xx\}\; (x,\; y)\; +\; u\_\; \{yy\}\; (x,\; y)\; \backslash \backslash \; \backslash \; приблизительно\; \{\backslash \; frac\; \{u\; (xh,\; y)\; -2u\; (x,\; y)\; +\; u\; (x\; +\; h,\; y)\}\; \{h\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{u\; (x,\; yh)\; -2u\; (x,\; y)\; +\; u\; (x,\; y\; +\; h)\}\; \{h\; ^\; \{2\}\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{u\; (xh,\; y)\; +\; u\; (x\; +\; h,\; y)\; -4u\; (x,\; y)\; +\; u\; (x,\; yh)\; +\; u\; (x,\; y\; +\; h)\}\; \{h\; ^\; \{2\}\}\}\; \backslash \backslash \; =:\; \backslash \; Delta\; \_\; \{h\}\; u\; (x,\; y)\; \backslash ,,\; \backslash \; end\; \{align\}\}\}$

, что является обычно задается следующим шаблоном

$1\; h\; 2\; [1\; 1\; -\; 4\; 1\; 1].\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{h\; ^\; \{2\}\}\}\; \{\backslash \; begin\; \{bmatrix\}\; 1\; \backslash \backslash \; 1\; -4\; 1\; \backslash \backslash \; 1\; \backslash \; end\; \{bmatrix\}\}\; \backslash ,.\}$

Согласованность

Согласованность вышеупомянутого приближения может быть продемонстрирована для очень регулярных функций, таких как $u\; \in \; C\; 4\; (\Omega )\; \{\backslash \; displaystyle\; u\; \backslash \; in\; C\; ^\; \{4\}\; (\backslash \; Omega)\}$. Утверждение:

$\Delta \; u\; -\; \Delta \; h\; u\; =\; O\; (h\; 2).\; \{\backslash \; displaystyle\; \backslash \; Delta\; u-\; \backslash \; Delta\; \_\; \{h\}\; u\; =\; \{\backslash \; mathcal\; \{O\}\}\; (h\; ^\; \{2\})\; \backslash ,.\}$

Чтобы доказать это, нужно заменить ряд Тейлора разложения до 3-го порядка в дискретный оператор Лапласа.

Свойства

Субгармоника

Подобно непрерывным субгармоническим функциям, можно определить субгармонические функции для конечно-разностных приближений $э-э\; \{\backslash \; displaystyle\; u\_\; \{\; h\}\}$

$-\; \Delta \; huh\; \le \; 0.\; \{\backslash \; displaystyle\; -\; \backslash \; Delta\; \_\; \{h\}\; u\_\; \{h\}\; \backslash \; leq\; 0\; \backslash ,.\}$

Среднее значение

Можно определить общий шаблон положительного типа через

$[\alpha \; N\; \alpha \; W\; -\; \alpha \; C\; \alpha \; E\; \alpha \; S],\; \alpha \; i>0,\; \alpha \; C\; =\; \sum \; i\; \in \; \{N,\; E,\; S,\; W\}\; \alpha \; i.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; alpha\; \_\; \{N\}\; \backslash \backslash \backslash \; alpha\; \_\; \{W\}\; -\; \backslash \; alpha\; \_\; \{C\}\; \backslash \; alpha\; \_\; \{E\}\; \backslash \backslash \; \backslash \; alpha\; \_\; \{S\}\; \backslash \; end\; \{bmatrix\}\}\; \backslash ,,\; \backslash \; quad\; \backslash \; alpha\; \_\; \{i\}>0\; \backslash ,,\; \backslash \; quad\; \backslash \; alpha\; \_\; \{C\}\; =\; \backslash \; sum\; \_\; \{i\; \backslash \; in\; \backslash \; \{N,\; E,\; S,\; W\; \backslash \}\}\; \backslash \; alpha\; \_\; \{i\}\; \backslash ,.\}$<45 Если $uh\; \{\backslash \; displaystyle\; u\_\; \{h\}\}$является (дискретной) субгармонической, то выполняется следующее свойство среднего значения

$uh\; (x\; C)\; \le \; \sum \; i\; \in \; \{N,\; E,\; S,\; W\}\; \alpha \; iuh\; (xi)\; \sum \; я\; \in \; \{N,\; E,\; S,\; W\}\; \alpha \; i,\; \{\backslash \; displaystyle\; u\_\; \{h\}\; (x\_\; \{C\})\; \backslash \; leq\; \{\backslash \; frac\; \{\backslash \; sum\; \_\; \{i\; \backslash \; in\; \backslash \; \{\; N,\; E,\; S,\; W\; \backslash \}\}\; \backslash \; alpha\; \_\; \{i\}\; u\_\; \{h\}\; (x\_\; \{i\})\}\; \{\backslash \; sum\; \_\; \{i\; \backslash \; in\; \backslash \; \{N,\; E,\; S,\; W\; \backslash \}\}\; \backslash \; alpha\; \_\; \{i\}\}\}\; \backslash ,,\}$

где аппроксимация оценивается в точках сетки, и предполагается, что шаблон имеет положительный тип.

Аналогичное свойство среднего значения также выполняется для непрерывного случая.

Принцип максимума

Для (дискретного т. е. функция субгармоники $э\; \{\backslash \; displaystyle\; u\_\; \{h\}\}$следующие утверждения:

$max\; \Omega \; да\; \le \; max\; \partial \; \Omega \; да,\; \{\backslash \; displaystyle\; \backslash \; max\; \_\; \{\backslash \; Omega\; \_\; \{h\}\; \}\; u\_\; \{h\}\; \backslash \; leq\; \backslash \; max\; \_\; \{\backslash \; partial\; \backslash \; Omega\; \_\; \{h\}\}\; u\_\; \{h\}\; \backslash ,,\}$

где $\Omega \; h,\; \partial \; \Omega \; h\; \{\backslash \; displaystyle\; \backslash \; Omega\; \_\; \{h\},\; \backslash \; partial\; \backslash \; Omega\; \_\; \{h\}\}$- дискретизации непрерывной области $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$, соответственно граница $\partial \; \Omega \; \{\backslash \; displaystyle\; \backslash \; partial\; \backslash \; Omega\}$.

Аналогичный принцип максимума также выполняется для непрерывного случая.

Метод SBP-SAT

Метод SBP-SAT - это стабильный и точный метод дискретизации и наложения граничных условий корректного уравнения в частных производных с использованием конечных разностей высокого порядка. Метод основан на конечных разностях, где операторы дифференцирования проявляют свойства суммирования по частям. Обычно эти операторы состоят из матриц дифференцирования с центральными разностными шаблонами внутри с тщательно подобранными односторонними граничными шаблонами, предназначенными для имитации интеграции по частям в дискретной настройке. Используя метод SAT, граничные условия PDE накладываются слабо, когда граничные значения «подтягиваются» к желаемым условиям, а не точно выполняются. Если параметры настройки (присущие методике SAT) выбраны правильно, результирующая система ODE будет демонстрировать такое же энергетическое поведение, что и непрерывное PDE, то есть система не имеет роста нефизической энергии. Это гарантирует стабильность, если используется схема интегрирования с областью устойчивости, которая включает части мнимой оси, например метод Рунге-Кутта четвертого порядка. Это делает метод SAT привлекательным методом наложения граничных условий для методов конечных разностей более высокого порядка, в отличие, например, от метода впрыска, который обычно не будет устойчивым при использовании операторов дифференцирования высокого порядка.

См. Также

• Метод конечных элементов
• Конечная разность
• Временная область конечных разностей
• Метод бесконечных разностей
• Шаблон (численный анализ)
• Коэффициенты конечных разностей
• Пять -точечный шаблон
• Теорема Лакса – Рихтмайера
• Конечно-разностные методы для оценки опционов
• Противоточная разностная схема для конвекции
• Центральная разностная схема
• Дискретное уравнение Пуассона
• Дискретный оператор Лапласа

Ссылки

Дополнительная литература

• кВт Мортон и Д.Ф. Майерс, Численное решение уравнений с частными производными, Введение. Cambridge University Press, 2005.
• Аутар Кау и Э. Эрик Калу, Численные методы с приложениями, (2008) [1]. Содержит краткое инженерное введение в FDM (для ODE) в главе 08.07.
• Джон Стрикверда (2004). Конечно-разностные схемы и уравнения с частными производными (2-е изд.). СИАМ. ISBN 978-0-89871-639-9.
• Смит, Г.Д. (1985), Численное решение уравнений с частными производными: методы конечных разностей, 3-е изд., Oxford University Press
• Питер Олвер (2013). Введение в уравнения с частными производными. Springer. Глава 5: Конечные различия. ISBN 978-3-319-02099-0..
• Рэндалл Дж. Левек, Конечно-разностные методы для обыкновенных и дифференциальных уравнений с частными производными, SIAM, 2007.

Различные лекции и конспекты лекций

• Конечно-разностный метод в электромагнетизме (см. И прослушайте лекцию 9)
• Лекционные заметки Ши-Хун Чен, Национальный центральный университет
• Численные методы для зависящие от времени дифференциальные уравнения в частных производных