Метод конечных элементов

Численный метод решения физических или инженерных проблем

Метод конечных элементов (МКЭ ) - наиболее широко используемый метод для решения задач инженерных и математических моделей. Типичные проблемные области, представляющие интерес, включают традиционные области структурного анализа, теплопередачи, потока жидкости, массопереноса и электромагнитного потенциала. FEM - это особый численный метод для решения уравнений в частных производных в двух или трех пространственных переменных (то есть некоторых краевых задач ). Для решения проблемы FEM разделяет большую систему на более мелкие и простые части, которые называются конечными элементами . Это достигается за счет особой пространственной дискретизации в измерениях пространства, которая реализуется путем построения сетки объекта: числовой области для решения, имеющей конечное число очков. Постановка краевой задачи методом конечных элементов в конечном итоге приводит к системе алгебраических уравнений. Метод аппроксимирует неизвестную функцию по области. Простые уравнения, моделирующие эти конечные элементы, затем собираются в более крупную систему уравнений, которая моделирует всю проблему. Затем FEM использует вариационные методы из вариационного исчисления для аппроксимации решения путем минимизации связанной функции ошибок.

Изучение или анализ явления с помощью FEM часто называют анализом конечных элементов (FEA ).

Содержание

• 1 Основные понятия
• 2 История
• 3 Техническое обсуждение
  • 3.1 Структура методов конечных элементов
  • 3.2 Иллюстративные проблемы P1 и P2
  • 3.3 Слабая формулировка
    • 3.3.1 Слабая форма P1
    • 3.3.2 Слабая форма P2
    • 3.3.3 Схема доказательства существования и единственности решения
• 4 Дискретность
  • 4.1 Для задачи P1
  • 4.2 Для задачи P2
  • 4.3 Выбор базиса
  • 4.4 Малая опора базиса
  • 4.5 Матричная форма задачи
  • 4.6 Общая форма метода конечных элементов
• 5 Различные типы методов конечных элементов
  • 5.1 AEM
  • 5.2 Обобщенный метод конечных элементов
  • 5.3 Смешанный метод конечных элементов
  • 5.4 Переменная - полиномиальная
  • 5.5 hpk-FEM
  • 5.6 XFEM
  • 5.7 Метод граничных масштабированных конечных элементов (SBFEM)
  • 5.8 S-FEM
  • 5.9 Метод спектральных элементов
  • 5.10 Методы без сетки
  • 5.11 Разрывные методы Галеркина
  • 5.12 Анализ предельных значений конечных элементов
  • 5.13 Метод растянутой сетки
  • 5.14 Итерация по Лабиньяку
• 6 лин. k с методом градиентной дискретизации
• 7 Сравнение с методом конечных разностей
• 8 Приложение
• 9 См. также
• 10 Ссылки
• 11 Дополнительная литература
• 12 Внешние ссылки

Основные концепции

Разделение всей области на более простые части имеет ряд преимуществ:

• Точное представление сложной геометрии
• Включение разнородных свойств материала
• Простое представление всего решения
• Улавливание локальных эффектов.

Типичная работа метода включает (1) разделение области проблемы на набор подобластей, при этом каждая подобласть представлена ​​набором уравнений элементов исходной задачи, с последующим (2) систематическим объединением всех наборов уравнений элементов в глобальную систему уравнений для окончательного расчета. Глобальная система уравнений имеет известные методы решения и может быть вычислена из начальных значений исходной задачи для получения числового ответа.

На первом шаге, описанном выше, уравнения элементов представляют собой простые уравнения, которые локально аппроксимируют исходные комплексные уравнения, подлежащие изучению, где исходные уравнения часто являются уравнениями в частных производных (PDE). Чтобы объяснить приближение в этом процессе, метод конечных элементов обычно вводится как частный случай метода Галеркина. На математическом языке процесс состоит в построении интеграла внутреннего произведения остатка и весовых функций и установке интеграла на ноль. Проще говоря, это процедура, которая сводит к минимуму ошибку аппроксимации путем подбора пробных функций в УЧП. Невязка - это ошибка, вызванная пробными функциями, а весовые функции - это полиномиальные аппроксимирующие функции, которые проецируют остаток. Процесс исключает все пространственные производные из PDE, таким образом аппроксимируя PDE локально с помощью

• набора алгебраических уравнений для задач устойчивого состояния,
• набора из обыкновенных дифференциальных уравнений для переходных задач.

Эти наборы уравнений являются уравнениями элементов. Они являются линейными, если лежащее в основе PDE является линейным, и наоборот. Наборы алгебраических уравнений, которые возникают в стационарных задачах, решаются с использованием методов численной линейной алгебры, в то время как наборы обыкновенных дифференциальных уравнений, возникающие в переходных задачах, решаются путем численного интегрирования с использованием стандартных методов. например метод Эйлера или метод Рунге-Кутты.

На шаге (2) выше глобальная система уравнений генерируется из уравнений элементов посредством преобразования координат из локальных узлов подобластей в глобальные узлы домена. Это пространственное преобразование включает в себя соответствующую ориентации корректировки, которые применяются в отношении к опорному системы координат. Процесс часто выполняется программным обеспечением FEM с использованием данных координат, сгенерированных из подобластей.

FEM лучше всего понять из его практического применения, известного как анализ конечных элементов (FEA) . FEA, применяемый в инжиниринге, представляет собой вычислительный инструмент для выполнения инженерного анализа. Он включает использование методов генерации сетки для разделения сложной задачи на мелкие элементы, а также использование программного обеспечения, закодированного с помощью алгоритма FEM. При применении FEA сложная проблема обычно представляет собой физическую систему с лежащей в основе физикой, такой как уравнение Эйлера-Бернулли, уравнение теплопроводности или Уравнения Навье-Стокса, выраженные либо в PDE, либо в интегральных уравнениях, в то время как разделенные небольшие элементы сложной задачи представляют различные области в физической системе.

FEA - хороший выбор для анализа проблем в сложных областях (таких как автомобили и нефтепроводы), когда область изменяется (как во время твердотельной реакции с движущейся границей), когда желаемая точность изменяется в пределах всю область, или когда решение не является гладким. Моделирование методом FEA является ценным ресурсом, поскольку оно устраняет многочисленные экземпляры создания и тестирования твердых прототипов для различных ситуаций с высокой точностью. Например, при моделировании лобового столкновения можно повысить точность прогнозирования в «важных» областях, таких как передняя часть автомобиля, и уменьшить ее в задней части (таким образом, снижая стоимость моделирования). Другой пример - численное прогнозирование погоды, где более важно иметь точные прогнозы развития сильно нелинейных явлений (таких как тропические циклоны в атмосфере или водовороты в океане), а не в относительно спокойных районах.

FEM сетка, созданная аналитиком перед поиском решения проблемы магнитного с помощью программного обеспечения FEM. Цвета указывают на то, что аналитик установил свойства материала для каждой зоны, в данном случае проводящая катушка оранжевого цвета; ферромагнитный компонент (возможно, железо ) голубого цвета; и воздух серым. Хотя геометрия может показаться простой, было бы очень сложно рассчитать магнитное поле для этой установки без программного обеспечения FEM, используя только уравнения . Решение задачи FEM слева, включающее цилиндрическое формованный магнитный экран. Цилиндрическая часть ферромагнетика экранирует область внутри цилиндра, отклоняя магнитное поле , создаваемое катушкой (прямоугольная область справа). Цвет представляет собой амплитуду из плотности магнитного потока, как показано шкалой во вставке легенды, красный цвет означает высокую амплитуду. Область внутри цилиндра имеет низкую амплитуду (темно-синий, с широко разнесенными линиями магнитного потока), что свидетельствует о том, что экран работает так, как он был разработан.

История

Хотя это сложно укажите дату изобретения метода конечных элементов, этот метод возник из-за необходимости решать сложные упругие и задачи структурного анализа в гражданском и авиационная техника. Его развитие восходит к работе А. Хренников и Р. Курант в начале 1940-х гг. Еще одним пионером был Иоаннис Аргирис. В СССР внедрение метода в практику обычно связывают с именем. В Китае в конце 1950-х - начале 1960-х годов, исходя из расчетов строительства плотин, К. Фэн предложил систематический численный метод решения уравнений в частных производных. Этот метод был назван методом конечных разностей, основанным на вариационном принципе, который был еще одним самостоятельным изобретением метода конечных элементов. Хотя подходы, используемые этими первопроходцами, различны, у них есть одна существенная характеристика: сетка дискретизация непрерывной области на набор дискретных подобластей, обычно называемых элементами.

Работа Хренникоффа дискретизирует область с помощью аналогии с решеткой , в то время как подход Куранта делит область на конечные треугольные подобласти для решения второго порядка эллиптического уравнения в частных производных (PDE), возникающие из задачи кручения цилиндра . Вклад Куранта был эволюционным, он опирался на большое количество более ранних результатов для PDE, разработанных Рэлеем, Ритцем и Галеркиным.

Метод конечных элементов получил свой настоящий импульс в 1960-е и 1970-е годы разработками Дж. Х. Аргирис с сотрудниками из Штутгартского университета, Р. У. Клаф с коллегами в Калифорнийском университете в Беркли, О. К. Зенкевич с сотрудниками Эрнест Хинтон, Брюс Айронс и другие в Университете Суонси, Филипп Дж. Сиарле в Университет Париж 6 и Ричард Галлахер с коллегами из Корнельского университета. Дальнейший импульс был придан в эти годы доступным программам конечных элементов с открытым исходным кодом. НАСА спонсировало оригинальную версию NASTRAN, а Калифорнийский университет в Беркли сделал программу конечных элементов SAP IV широко доступной. В Норвегии классификационное общество судов Det Norske Veritas (ныне DNV GL ) разработало Sesam в 1969 году для использования в анализе судов. Строгая математическая основа метода конечных элементов была предоставлена ​​в 1973 г. публикациями Strang и Fix. С тех пор этот метод был обобщен для численного моделирования физических систем в широком спектре инженерных дисциплин, например, электромагнетизм, теплопередача и гидродинамика.

Техническое обсуждение

Структура методов конечных элементов

Метод конечных элементов характеризуется вариационной формулировкой, дискретизацией стратегия, один или несколько алгоритмов решения и процедуры постобработки.

Примерами вариационной формулировки являются метод Галеркина, прерывистый метод Галеркина, смешанные методы и т. Д.

Под стратегией дискретизации понимается четко определенный набор процедуры, которые охватывают (а) создание сеток из конечных элементов, (b) определение базовой функции на опорных элементах (также называемых функциями формы) и (c) отображение опорных элементов на элементы сетки. Примеры стратегий дискретизации: h-версия, p-версия, hp-version, x-FEM, изогеометрический анализ и т. Д. Каждая стратегия дискретизации имеет определенные преимущества и недостатки. Разумным критерием при выборе стратегии дискретизации является достижение почти оптимальной производительности для самого широкого набора математических моделей в конкретном классе моделей.

Различные алгоритмы численного решения можно разделить на две большие категории; прямые и итерационные решатели. Эти алгоритмы предназначены для использования разреженности матриц, зависящих от выбора вариационной формулировки и стратегии дискретизации.

Процедуры постобработки предназначены для извлечения интересующих данных из решения методом конечных элементов. Чтобы соответствовать требованиям проверки решения, постпроцессоры должны обеспечивать апостериорную оценку ошибок с точки зрения представляющих интерес величин. Когда ошибки аппроксимации больше, чем считается приемлемым, дискретизация должна быть изменена либо автоматизированным адаптивным процессом, либо действием аналитика. Есть несколько очень эффективных постпроцессоров, которые обеспечивают реализацию сверхсходимости.

Иллюстративные задачи P1 и P2

Мы продемонстрируем метод конечных элементов на двух примерах задач, из которых можно экстраполировать общий метод. Предполагается, что читатель знаком с исчислением и линейной алгеброй.

P1 является одномерной задачей

$P1:\; \{u\; ″\; (x)\; =\; е\; (Икс)\; в\; (0,\; 1),\; u\; (0)\; =\; u\; (1)\; =\; 0,\; \{\backslash \; displaystyle\; \{\backslash \; t\_dv\; \{P1\}\}:\; \{\backslash \; begin\; \{cases\}\; u\; \text{'}\text{'}\; (x)\; =\; f\; (x)\; \{\backslash \; t\_dv\; \{in\}\}\; (0,1),\; \backslash \backslash \; u\; (0)\; =\; u\; (1)\; =\; 0,\; \backslash \; end\; \{cases\}\}\}$

где $f\; \{\backslash \; displaystyle\; f\}$задано, $u\; \{\backslash \; displaystyle\; u\}$- неизвестная функция от $x\; \{\backslash \; displaystyle\; x\}$и $u\; ″\; \{\; \backslash \; displaystyle\; u\; \text{'}\text{'}\}$- вторая производная от $u\; \{\backslash \; displaystyle\; u\}$по $x\; \{\backslash \; displaystyle\; x\}$.

P2 - это двумерная задача (задача Дирихле )

$P2:\; \{uxx\; (x,\; y)\; +\; uyy\; (x,\; y)\; =\; f\; (x,\; y)\; в\; \Omega ,\; u\; =\; 0\; на\; \partial \; \Omega ,\; \{\backslash \; Displaystyle\; \{\backslash \; t\_dv\; \{P2\}\}:\; \{\backslash \; begin\; \{cases\}\; u\_\; \{xx\}\; (x,\; y)\; +\; u\_\; \{yy\}\; (x,\; y)\; =\; f\; (x,\; y)\; \{\backslash \; t\_dv\; \{\; in\}\}\; \backslash \; Omega,\; \backslash \backslash \; u\; =\; 0\; \{\backslash \; t\_dv\; \{on\}\}\; \backslash \; partial\; \backslash \; Omega,\; \backslash \; end\; \{cases\}\}\}$

где $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$- связная открытая область в $(x,\; y)\; \{\backslash \; displaystyle\; (x,\; y)\}$плоскость, граница которой $\partial \; \Omega \; \{\backslash \; displaystyle\; \backslash \; partial\; \backslash \; Omega\}$хороша (например, гладкое многообразие или многоугольник ) и $uxx\; \{\backslash \; displaystyle\; u\_\; \{xx\}\}$и $uyy\; \{\backslash \; displaystyle\; u\_\; \{yy\}\}$обозначают вторые производные по отношению к $x\; \{\backslash \; displaystyle\; x\}$и $y\; \{\backslash \; displaystyle\; y\}$соответственно.

Проблема P1 может быть решена непосредственно путем вычисления первообразных. Однако этот метод решения краевой задачи (BVP) работает только тогда, когда существует одно пространственное измерение, и не обобщается на проблемы более высокой размерности или такие проблемы, как $u\; +\; u\; ″\; =\; f\; \{\backslash \; стиль\; отображения\; u\; +\; u\; \text{'}\text{'}\; =\; f\}$. По этой причине мы разработаем метод конечных элементов для P1 и опишем его обобщение для P2.

Наше объяснение состоит из двух шагов, которые отражают два важных шага, которые необходимо предпринять для решения краевой задачи (BVP) с использованием FEM.

• На первом этапе мы перефразируем исходный BVP в его слабой форме. Для этого шага обычно не требуется никаких вычислений. Преобразование выполняется вручную на бумаге.
• Второй шаг - это дискретизация, когда слабая форма дискретизируется в конечномерном пространстве.

После этого второго шага у нас есть конкретные формулы для большого но конечномерная линейная задача, решение которой приближенно решит исходную БВП. Затем эта конечномерная задача реализуется на компьютере.

Слабая формулировка

Первый шаг - преобразовать P1 и P2 в их эквивалент слабые формулировки.

Слабая форма P1

Если $u\; \{\backslash \; displaystyle\; u\}$решает P1, то для любой гладкой функции $v\; \{\backslash \; displaystyle\; v\}$, удовлетворяющей границе смещения условия, то есть $v\; =\; 0\; \{\backslash \; displaystyle\; v\; =\; 0\}$при $x\; =\; 0\; \{\backslash \; displaystyle\; x\; =\; 0\}$и $x\; =\; 1\; \{\; \backslash \; displaystyle\; x\; =\; 1\}$, имеем

(1) $\int \; 0\; 1\; f\; (x)\; v\; (x)\; dx\; =\; \int \; 0\; 1\; u\; ″\; (x)\; v\; (\; х)\; dx.\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; f\; (x)\; v\; (x)\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; u\; \text{'}\text{'}\; (x)\; v\; (x)\; \backslash ,\; dx.\}$

И наоборот, если $u\; \{\backslash \; displaystyle\; u\}$с $u\; (0)\; =\; u\; (1)\; =\; 0\; \{\backslash \; displaystyle\; u\; (0)\; =\; u\; (1)\; =\; 0\; \}$удовлетворяет (1) для каждой гладкой функции $v\; (x)\; \{\backslash \; displaystyle\; v\; (x)\}$, тогда можно показать, что это $u\; \{\backslash \; displaystyle\; u\; \}$решит P1. Доказательство проще для дважды непрерывно дифференцируемой $u\; \{\backslash \; displaystyle\; u\}$(теоремы о среднем значении ), но также может быть доказано в распределительном смысле.

Мы определяем новый оператор или карту $\varphi \; (u,\; v)\; \{\backslash \; displaystyle\; \backslash \; phi\; (u,\; v)\}$, используя интегрирование по частям в правой части (1):

(2) $\int \; 0\; 1\; f\; (x)\; v\; (x)\; dx\; =\; \int \; 0\; 1\; u\; ″\; (x)\; v\; (x)\; dx\; =\; u\; \prime \; (x)\; v\; (x)\; |\; 0\; 1\; -\; \int \; 0\; 1\; u\; \prime \; (x)\; v\; \prime \; (x)\; dx\; =\; -\; \int \; 0\; 1\; u\; \prime \; (x)\; v\; \prime \; (x)\; dx\; \equiv \; -\; \varphi \; (u,\; v),\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\; \}\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; f\; (x)\; v\; (x)\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; u\; \text{'}\text{'}\; (x)\; v\; (x)\; \backslash ,\; dx\; \backslash \backslash \; =\; u\; \text{'}(x)\; v\; (x)\; |\; \_\; \{0\}\; ^\; \{1\}\; -\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; u\text{'}\; (x)\; v\; \text{'}(x)\; \backslash ,\; dx\; \backslash \backslash \; =\; -\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; u\; \text{'}(x)\; v\text{'}\; (x)\; \backslash ,\; dx\; \backslash \; Equiv\; -\; \backslash \; phi\; (u,\; v),\; \backslash \; end\; \{align\}\}\}$

где мы использовали предположение, что $v\; (0)\; =\; v\; (1)\; =\; 0\; \{\backslash \; displaystyle\; v\; (0)\; =\; v\; (1)\; =\; 0\}$.

Слабая форма P2

Если мы интегрируем по частям, используя форму личности Грина, мы видим, что если $u\; \{\backslash \; displaystyle\; u\}$решает P2, то мы можем определить $\varphi \; (u,\; v)\; \{\backslash \; displaystyle\; \backslash \; phi\; (\; u,\; v)\}$для любого $v\; \{\backslash \; displaystyle\; v\}$по

$\int \; \Omega \; fvds\; =\; -\; \int \; \Omega \; \nabla \; u\; \cdot \; \nabla \; vds\; \equiv \; -\; \varphi \; (u,\; v),\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; fv\; \backslash ,\; ds\; =\; -\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; nabla\; u\; \backslash \; cdot\; \backslash \; nabla\; v\; \backslash ,\; ds\; \backslash \; Equiv\; -\; \backslash \; phi\; (u,\; v),\}$

где $\nabla \; \{\backslash \; displaystyle\; \backslash \; nabla\}$обозначает градиент, а $\cdot \; \{\backslash \; displaystyle\; \backslash \; cdot\}$обозначает скалярное произведение в tw o-мерная плоскость. Еще раз $\varphi \; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; \backslash \; Phi\}$можно превратить во внутренний продукт на подходящем пространстве $H\; 0\; 1\; (\Omega )\; \{\backslash \; displaystyle\; H\_\; \{0\}\; ^\; \{1\}\; (\backslash \; Omega)\}$из некогда дифференцируемых функций из $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$, которые равны нулю на $\partial \; \Omega \; \{\backslash \; displaystyle\; \backslash \; partial\; \backslash \; Омега\}$. Мы также предположили, что $v\; \in \; H\; 0\; 1\; (\Omega )\; \{\backslash \; displaystyle\; v\; \backslash \; in\; H\_\; \{0\}\; ^\; \{1\}\; (\backslash \; Omega)\}$(см. пространства Соболева ). Также можно показать существование и уникальность решения.

Доказательство существования и уникальности решения

Мы можем в общих чертах представить себе $H\; 0\; 1\; (0,\; 1)\; \{\backslash \; displaystyle\; H\_\; \{0\}\; ^\; \{1\}\; (\; 0,1)\}$быть абсолютно непрерывными функциями $(0,\; 1)\; \{\backslash \; displaystyle\; (0,1)\}$, которые $0\; \{\backslash \; displaystyle\; 0\}$при $x\; =\; 0\; \{\backslash \; displaystyle\; x\; =\; 0\}$и $x\; =\; 1\; \{\backslash \; displaystyle\; x\; =\; 1\}$(см. Пространства Соболева ). Такие функции (слабо) однократно дифференцируемы, и оказывается, что симметричное билинейное отображение $\varphi \; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; \backslash \; Phi\}$затем определяет внутренний product, который превращает $H\; 0\; 1\; (0,\; 1)\; \{\backslash \; displaystyle\; H\_\; \{0\}\; ^\; \{1\}\; (0,1)\}$в гильбертово пространство (подробное доказательство нетривиально). С другой стороны, левая часть $\int \; 0\; 1\; f\; (x)\; v\; (x)\; dx\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; f\; (x)\; v\; (x)\; dx\}$также является внутренним продуктом, на этот раз в пространстве Lp $L\; 2\; (0,\; 1)\; \{\backslash \; displaystyle\; L\; ^\; \{2\}\; (0,1)\}$. Применение теоремы о представлении Рисса для гильбертовых пространств показывает, что существует единственное $u\; \{\backslash \; displaystyle\; u\}$решение (2) и, следовательно, P1. Это решение априори является только членом $H\; 0\; 1\; (0,\; 1)\; \{\backslash \; displaystyle\; H\_\; \{0\}\; ^\; \{1\}\; (0,1)\}$, но с использованием эллиптическая регулярность, будет гладкой, если $f\; \{\backslash \; displaystyle\; f\}$.

Дискретизация

Функция в $H\; 0\; 1,\; \{\backslash \; displaystyle\; H\_\; \{0\}\; ^\; \{1\},\}$с нулевыми значениями в конечных точках (синий цвет) и кусочно-линейная аппроксимация (красный)

P1 и P2 готовы к дискретизации, что приводит к общей подзадаче (3). Основная идея состоит в том, чтобы заменить бесконечномерную линейную задачу:

Найти $u\; \in \; H\; 0\; 1\; \{\backslash \; displaystyle\; u\; \backslash \; in\; H\_\; \{0\}\; ^\; \{1\}\}$такое, что

$\forall \; v\; \in \; H\; 0\; 1,\; -\; \varphi \; (u,\; v)\; =\; \int \; fv\; \{\backslash \; displaystyle\; \backslash \; forall\; v\; \backslash \; in\; H\_\; \{0\}\; ^\; \{1\},\; \backslash ;\; -\; \backslash \; phi\; (u,\; v)\; =\; \backslash \; int\; fv\}$

с конечномерной версией:

(3) Найдите $u\; \in \; V\; \{\backslash \; displaystyle\; u\; \backslash \; in\; V\}$такое, что

$\forall \; v\; \in \; V,\; -\; \varphi \; (\; и,\; v)\; знак\; равно\; \int \; fv\; \{\backslash \; displaystyle\; \backslash \; forall\; v\; \backslash \; in\; V,\; \backslash ;\; -\; \backslash \; phi\; (u,\; v)\; =\; \backslash \; int\; fv\}$

где $V\; \{\backslash \; displaystyle\; V\}$- конечномерное подпространство в $H\; 0\; 1\; \{\backslash \; displaystyle\; H\_\; \{0\}\; ^\; \{1\}\}$. Есть много возможных вариантов для $V\; \{\backslash \; displaystyle\; V\}$(одна возможность приводит к спектральному методу ). Однако для метода конечных элементов мы берем $V\; \{\backslash \; displaystyle\; V\}$как пространство кусочно-полиномиальных функций.

Для задачи P1

Берем интервал $(0,\; 1)\; \{\backslash \; displaystyle\; (0,1)\}$, выбираем $n\; \{\backslash \; displaystyle\; n\}$значения $x\; \{\backslash \; displaystyle\; x\}$с , и мы определяем $V\; \{\backslash \; displaystyle\; V\}$по:

$V\; =\; \{v:\; [0,\; 1]\; \to \; R:\; v\; непрерывно,\; v\; |\; [xk,\; xk\; +\; 1]\; линейно\; для\; k\; =\; 0,\dots ,\; n,\; и\; v\; (0)\; =\; v\; (1)\; =\; 0\}\; \{\backslash \; displaystyle\; V\; =\; \backslash \; \{v:\; [0,1]\; \backslash \; rightarrow\; \backslash \; mathbb\; \{\; R\}\; \backslash \; ;:\; v\; \{\backslash \; t\_dv\; \{непрерывно,\}\}\; v\; |\; \_\; \{[x\_\; \{k\},\; x\_\; \{k\; +\; 1\}]\}\; \{\backslash \; t\_dv\; \{линейно\; для\}\}\; k\; =\; 0,\; \backslash \; dots,\; n\; \{\backslash \; t\_dv\; \{и\}\}\; v\; (0)\; =\; v\; (1)\; =\; 0\; \backslash \}\}$

где мы определяем $x\; 0\; =\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\; =\; 0\}$и $xn\; +\; 1\; =\; 1\; \{\backslash \; displaystyle\; x\_\; \{n\; +\; 1\}\; =\; 1\}$. Обратите внимание, что функции в $V\; \{\backslash \; displaystyle\; V\}$не дифференцируемы согласно элементарному определению исчисления. Действительно, если $v\; \in \; V\; \{\backslash \; displaystyle\; v\; \backslash \; in\; V\}$, тогда производная обычно не определяется ни при каком $x\; =\; xk\; \{\backslash \; displaystyle\; x\; =\; x\_\; \{k\}\}$, $k\; =\; 1,\dots ,\; n\; \{\backslash \; displaystyle\; k\; =\; 1,\; \backslash \; ldots,\; n\}$. Однако производная существует при любом другом значении $x\; \{\backslash \; displaystyle\; x\}$, и эту производную можно использовать для интегрирования по частям.

Кусочно-линейная функция в двух размеры

Для задачи P2

Нам необходимо, чтобы $V\; \{\backslash \; displaystyle\; V\}$представлял собой набор функций $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$. На рисунке справа мы проиллюстрировали триангуляцию 15-сторонней многоугольной области $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$в плоскости ( ниже), и кусочно-линейная функция (вверху, в цвете) этого многоугольника, линейная на каждом треугольнике триангуляции; пространство $V\; \{\backslash \; displaystyle\; V\}$будет состоять из функций, линейных для каждого треугольника выбранной триангуляции.

Можно надеяться, что по мере того, как нижележащая треугольная сетка становится все более и более тонкой, решение дискретной задачи (3) в некотором смысле сходится к решению исходной краевой задачи P2. Чтобы измерить тонкость этой сетки, триангуляция индексируется параметром с действительным знаком $h>0\; \{\backslash \; displaystyle\; h>0\}$которое считается очень маленьким. Этот параметр будет связан с размером самого большого или среднего треугольника. в триангуляции. По мере того как мы уточняем триангуляцию, пространство кусочно-линейных функций $V\; \{\backslash \; displaystyle\; V\}$также должно изменяться на $h\; \{\backslash \; displaystyle\; h\}$. По этой причине в литературе часто читается $V\; h\; \{\backslash \; displaystyle\; V\_\; \{h\}\}$вместо $V\; \{\backslash \; displaystyle\; V\}$. Поскольку мы не проводите такой анализ, мы не будем использовать это обозначение.

Выбор базиса

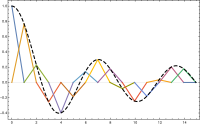Интерполяция функции Бесселя 16 масштабированных и сдвинутых треугольных базисных функций (цветов), используемых для восстановления функция Бесселя нулевого порядка J 0 (черный). 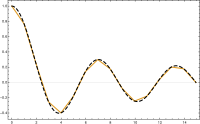линейная комбинация базисных функций (желтый) воспроизводит J 0 (синий) с любой желаемой точностью.

Чтобы завершить дискретизацию, мы должны выбрать базис из $V\; \{\; \backslash \; Displaystyle\; V\}$. В одномерном случае для каждой контрольной точки $xk\; \{\backslash \; displaystyle\; x\_\; \{k\}\}$мы выберем кусочно-линейную функцию $vk\; \{\backslash \; displaystyle\; v\_\; \{k\}\}$в $V\; \{\backslash \; displaystyle\; V\}$, значение которого равно $1\; \{\backslash \; displaystyle\; 1\}$в $xk\; \{\backslash \; displaystyle\; x\_\; \{k\}\; \}$и ноль на каждом $xj,\; j\; \ne \; k\; \{\backslash \; displaystyle\; x\_\; \{j\},\; \backslash ;\; j\; \backslash \; neq\; k\}$, т.е.

$vk\; (x)\; =\; \{x\; -\; xk\; -\; 1\; xk\; -\; xk\; -\; 1,\; если\; x\; \in \; [xk\; -\; 1,\; xk],\; xk\; +\; 1\; -\; xxk\; +\; 1\; -\; xk,\; если\; x\; \in \; [xk,\; xk\; +\; 1],\; 0\; в\; противном\; случае,\; \{\backslash \; displaystyle\; v\_\; \{k\}\; (x)\; =\; \{\backslash \; begin\; \{cases\}\; \{x-x\_\; \{k-1\}\; \backslash \; over\; x\_\; \{k\}\; \backslash ,\; -\; x\_\; \{k-1\}\}\; \{\backslash \; t\_dv\; \{if\}\}\; x\; \backslash \; in\; [\; x\_\; \{k-1\},\; x\_\; \{k\}],\; \backslash \backslash \; \{x\_\; \{k\; +\; 1\}\; \backslash ,\; -\; x\; \backslash \; over\; x\_\; \{k\; +\; 1\}\; \backslash ,\; -\; x\_\; \{k\}\}\; \{\backslash \; t\_dv\; \{if\}\}\; x\; \backslash \; in\; [x\_\; \{k\},\; x\_\; \{k\; +\; 1\}],\; \backslash \backslash \; 0\; \{\backslash \; t\_dv\; \{else\}\},\; \backslash \; end\; \{cases\}\}\}$

для $k\; =\; 1,\dots ,\; n\; \{\; \backslash \; Displaystyle\; к\; =\; 1,\; \backslash \; точки,\; п\}$; эта основа - сдвинутая и масштабированная функция тента. Для двумерного случая мы снова выбираем одну базисную функцию $vk\; \{\backslash \; displaystyle\; v\_\; \{k\}\}$на вершину $xk\; \{\backslash \; displaystyle\; x\_\; \{k\}\}$триангуляции плоской области $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$. Функция $vk\; \{\backslash \; displaystyle\; v\_\; \{k\}\}$является уникальной функцией для $V\; \{\backslash \; displaystyle\; V\}$, значение которой равно $1\; \{\backslash \; displaystyle\; 1\}$в $xk\; \{\backslash \; displaystyle\; x\_\; \{k\}\}$и ноль в каждом $xj,\; j\; \ne \; k\; \{\backslash \; displaystyle\; x\_\; \{j\},\; \backslash ;\; j\; \backslash \; neq\; k\}$.

В зависимости от автора слово «элемент» в «методе конечных элементов» относится либо к треугольникам в области, либо к кусочно-линейной базисной функции, либо к обоим. Так, например, автор, интересующийся изогнутыми доменами, может заменить треугольники изогнутыми примитивами и, таким образом, описать элементы как криволинейные. С другой стороны, некоторые авторы заменяют «кусочно линейный» на «кусочно-квадратичный» или даже «кусочно-полиномиальный». Тогда автор мог бы сказать «элемент более высокого порядка» вместо «полином более высокой степени». Метод конечных элементов не ограничивается треугольниками (или тетраэдрами в трехмерном пространстве, или симплексами более высокого порядка в многомерных пространствах), но может быть определен в четырехугольных подобластях (шестигранники, призмы или пирамиды в трехмерном пространстве и т. Д.). Формы более высокого порядка (криволинейные элементы) могут быть определены с помощью полиномиальных и даже неполиномиальных форм (например, эллипса или круга).

Примерами методов, использующих базисные функции кусочно-полиномиальных более высоких степеней, являются hp-FEM и спектральный FEM.

Более продвинутые реализации (адаптивные методы конечных элементов) используют метод для оценить качество результатов (на основе теории оценки ошибок) и изменить сетку во время решения, стремясь достичь приближенного решения в некоторых пределах от точного решения задачи континуума. Адаптивность сетки может использовать различные методы, наиболее популярными из которых являются:

• перемещение узлов (r-адаптивность)
• уточнение (и необработанные) элементы (h-адаптивность)
• изменение порядка базовых функций (p-адаптивность)
• комбинации вышеперечисленных (hp-адаптивность ).

Малая поддержка основы

Решение двумерной задачи $uxx\; +\; uyy\; =\; -\; 4\; \{\backslash \; displaystyle\; u\_\; \{xx\}\; +\; u\_\; \{yy\}\; =\; -\; 4\}$в круге с центром в начале координат и радиусом 1, с нулевыми граничными условиями.. (a) Триангуляция. (b) разреженная матрица L дискретизированной линейной системы (c) Вычисленное решение, $u\; (x,\; y)\; =\; 1\; -\; x\; 2\; -\; y\; 2.\; \{\backslash \; Displaystyle\; u\; (x,\; y)\; =\; 1-x\; ^\; \{2\}\; -y\; ^\; \{2\}.\}$

Основным преимуществом такого выбора базиса является то, что скалярные произведения

$⟨vj,\; vk⟩\; =\; \int \; 0\; 1\; vjvkdx\; \{\backslash \; displaystyle\; \backslash \; langle\; v\_\; \{j\},\; v\_\; \{k\}\; \backslash \; rangle\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; v\_\; \{j\}\; v\_\; \{k\}\; \backslash ,\; dx\}$

и

$\varphi \; (vj,\; vk)\; Знак\; равно\; \int \; 0\; 1\; vj\; \prime \; vk\; \prime \; dx\; \{\backslash \; displaystyle\; \backslash \; phi\; (v\_\; \{j\},\; v\_\; \{k\})\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; v\_\; \{j\}\; \text{'}v\_\; \{k\}\text{'}\; \backslash ,\; dx\; \}$

будет равно нулю почти для всех $j,\; k\; \{\backslash \; displaystyle\; j,\; k\}$. (Матрица, содержащая $⟨vj,\; vk⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; v\_\; \{j\},\; v\_\; \{k\}\; \backslash \; rangle\}$в $(j,\; k)\; \{\backslash \; displaystyle\; (j,\; k)\}$местоположение известно как матрица Грамиана.) В одномерном случае поддерживает из $vk\; \{\backslash \; displaystyle\; v\_\; \{k\; \}\}$- интервал $[xk\; -\; 1,\; xk\; +\; 1]\; \{\backslash \; displaystyle\; [x\_\; \{k-1\},\; x\_\; \{k\; +\; 1\}]\}$. Следовательно, подынтегральные выражения $⟨vj,\; vk⟩\; \{\backslash \; displaystyle\; \backslash \; langle\; v\_\; \{j\},\; v\_\; \{k\}\; \backslash \; rangle\}$и $\varphi \; (vj,\; vk)\; \{\backslash \; displaystyle\; \backslash \; phi\; (v\_\; \{j\},\; v\_\; \{k\})\}$идентичны нулю всякий раз, когда $|\; j\; -\; k\; |>1\; \{\backslash \; displaystyle\; |\; jk\; |>1\}$.

Аналогично, в плоском случае, если $xj\; \{\backslash \; displaystyle\; x\_\; \{j\}\}$и $xk\; \{\backslash \; displaystyle\; x\_\; \{k\}\}$не имеют общего ребра триангуляции, тогда интегралы

$\int \; \Omega \; vjvkds\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; v\_\; \{j\}\; v\_\; \{k\}\; \backslash ,\; ds\; \}$

и

$\int \; \Omega \; \nabla \; vj\; \cdot \; \nabla \; vkds\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\backslash \; Omega\}\; \backslash \; nabla\; v\_\; \{j\}\; \backslash \; cdot\; \backslash \; nabla\; v\_\; \{k\}\; \backslash ,\; ds\}$

оба равны нулю.

Матричная форма задачи

Если мы запишем $u\; (x)\; =\; \sum \; k\; =\; 1\; nukvk\; (x)\; \{\backslash \; displaystyle\; u\; (x)\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; u\_\; \{k\}\; v\_\; \{k\}\; (x)\}$и $f\; (x)\; =\; \sum \; k\; =\; 1\; nfkvk\; (x)\; \{\backslash \; displaystyle\; f\; (x)\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; f\_\; \{k\}\; v\_\; \{k\}\; (x)\}$затем задача (3), принимая $v\; (x)\; =\; vj\; (x)\; \{\backslash \; displaystyle\; v\; (x)\; =\; v\_\; \{j\}\; (x)\}$для $j\; =\; 1,\dots ,\; n\; \{\backslash \; displaystyle\; j\; =\; 1,\; \backslash \; dots,\; n\}$, становится

$-\; \sum \; k\; Знак\; равно\; 1\; нук\; \varphi \; (vk,\; vj)\; =\; \sum \; К\; =\; 1\; nfk\; \int \; vkvjdx\; \{\backslash \; displaystyle\; -\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; u\_\; \{k\}\; \backslash \; phi\; (v\_\; \{k\},\; v\_\; \{j\})\; =\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; f\_\; \{k\}\; \backslash \; int\; v\_\; \{k\}\; v\_\; \{j\}\; dx\}$для $j\; =\; 1,\dots ,\; n.\; \{\backslash \; displaystyle\; j\; =\; 1,\; \backslash \; dots,\; n.\}$(4)

Если мы обозначим $u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\}$и $f\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{f\}\}$векторы-столбцы $(u\; 1,\dots ,\; un)\; t\; \{\backslash \; displaystyle\; (u\_\; \{1\},\; \backslash \; dots,\; u\_\; \{n\})\; ^\; \{t\}\}$и $(f\; 1,\dots ,\; fn)\; t\; \{\backslash \; displaystyle\; (f\_\; \{1\},\; \backslash \; dots,\; f\_\; \{n\})\; ^\; \{t\}\}$, and if we let

$L\; =\; (\; L\; ij)\; \{\backslash displaystyle\; L=(L\_\{ij\})\}$

and

$M\; =\; (\; M\; ij)\; \{\backslash displaystyle\; M=(M\_\{ij\; \})\}$

be matrices whose entries are

$L\; ij\; =\; \varphi \; (\; vi,\; vj)\; \{\backslash displaystyle\; L\_\{ij\}=\backslash phi\; (v\_\{i\},v\_\{j\})\}$

and

$M\; ij\; =\; \int \; vivjdx\; \{\backslash displaystyle\; M\_\{ij\}=\backslash int\; v\_\{i\}v\_\{j\}dx\}$

then we may rephrase (4) as

$-\; L\; u\; =\; M\; f.\; \{\backslash displaystyle\; -L\backslash mathbf\; \{u\}\; =M\backslash mathbf\; \{f\}.\}$(5)

It is not necessary to assume $f\; (\; x)\; =\; \sum \; k\; =\; 1\; n\; f\; k\; v\; k\; (\; x)\; \{\backslash displaystyle\; f(x)=\backslash sum\; \_\{k=1\}^\{n\}f\_\{k\}v\_\{k\}(x)\}$. For a general function $f\; (\; x)\; \{\backslash displaystyle\; f(x)\}$, problem (3) with $v\; (\; x)\; =\; v\; j\; (\; x)\; \{\backslash displaystyle\; v(x)=v\_\{j\}(x)\}$for $j\; =\; 1,\; \dots ,\; n\; \{\backslash displaystyle\; j=1,\backslash dots,n\}$becomes actually simpler, since no matrix $M\; \{\backslash displaystyle\; M\}$is used,

$-\; L\; u\; =\; b\; \{\backslash displaystyle\; -L\backslash mathbf\; \{u\}\; =\backslash mathbf\; \{b\}\; \}$, (6)

where $b\; =\; (\; b\; 1,\; \dots ,\; b\; n)\; t\; \{\backslash displaystyle\; \backslash mathbf\; \{b\}\; =(b\_\{1\},\backslash dots,b\_\{n\})^\{t\}\}$and $b\; j\; =\; \int \; f\; v\; j\; d\; x\; \{\backslash displaystyle\; b\_\{j\}=\backslash int\; fv\_\{j\}dx\}$for $j\; =\; 1,\; \dots ,\; n\; \{\backslash displaystyle\; j=1,\backslash dots,n\}$.

As we have discussed before, most of the entries of $L\; \{\backslash displaystyle\; L\}$and $M\; \{\backslash displaystyle\; M\}$are zero because the basis functions $v\; k\; \{\backslash displaystyle\; v\_\{k\}\}$have small support. So we now have to solve a linear system in the unknown $u\; \{\backslash displaystyle\; \backslash mathbf\; \{u\}\; \}$where most of the entries of the matrix $L\; \{\backslash displaystyle\; L\}$, which we need to invert, are zero.

Such matrices are known as sparse matrices, and there are efficient solvers for such problems (much more efficient than actually inverting the matrix.) In addition, $L\; \{\backslash displaystyle\; L\}$is symmetric and positive definite, so a technique such as the conjugate gradient method is favored. For problems that are not too large, sparse LU decompositions and Cholesky decompositions still work well. For instance, MATLAB 's backslash operator (which uses sparse LU, sparse Cholesky, and other factorization methods) can be sufficient for meshes with a hundred thousand vertices.

The matrix $L\; \{\backslash displaystyle\; L\}$is usually referred to as the stiffness matrix, while the matrix $M\; \{\backslash displaystyle\; M\}$is dubbed the mass matrix.

General form of the finite element method

In general, the finite element method is characterized by the following process.

• One chooses a grid for $\Omega \; \{\backslash displaystyle\; \backslash Omega\; \}$. In the preceding treatment, the grid consisted of triangles, but one can also use squares or curvilinear polygons.
• Then, one chooses basis functions. In our discussion, we used piecewise linear basis functions, but it is also common to use piecewise polynomial basis functions.

Separate consideration is the smoothness of the basis functions. For second-order elliptic boundary value problems, piecewise polynomial basis function that is merely continuous suffice (i.e., the derivatives are discontinuous.) For higher-order partial differential equations, one must use smoother basis functions. For instance, for a fourth-order problem such as $u\; x\; x\; x\; x\; +\; u\; y\; y\; y\; y\; =\; f\; \{\backslash displaystyle\; u\_\{xxxx\}+u\_\{yyyy\}=f\}$, one may use piecewise quadratic basis functions that are $C\; 1\; \{\backslash displaystyle\; C^\{1\}\}$.

Another consideration is the relation of the finite-dimensional space $V\; \{\backslash displaystyle\; V\}$to its infinite-dimensional counterpart, in the examples above $H\; 0\; 1\; \{\backslash displaystyle\; H\_\{0\}^\{1\}\}$. A is one in which space $V\; \{\backslash displaystyle\; V\}$is a subspace of the element space for the continuous problem. The example above is such a method. If this condition is not satisfied, we obtain a, an example of which is the space of piecewise linear functions over the mesh which are continuous at each edge midpoint. Since these functions are in general discontinuous along the edges, this finite-dimensional space is not a subspace of the original $H\; 0\; 1\; \{\backslash displaystyle\; H\_\{0\}^\{1\}\}$.

Typically, one has an algorithm for taking a given mesh and subdividing it. If the main method for increasing precision состоит в том, чтобы разделить сетку, есть h-метод (h обычно - диаметр самого большого элемента в сетке). Таким образом, если кто-то показывает, что ошибка с сеткой $h\; \{\backslash \; displaystyle\; h\}$ограничен сверху $C\; hp\; \{\backslash \; displaystyle\; Ch\; ^\; \{p\}\}$, для некоторых и $p>0\; \{\backslash \; displaystyle\; p>0\}$, затем один имеет метод порядка p. При определенных гипотезах (например, если область является выпуклой), метод кусочного полинома порядка $d\; \{\backslash \; displaystyle\; d\}$будет иметь ошибку порядка $p\; =\; d\; +\; 1\; \{\backslash \; displaystyle\; p\; =\; d\; +\; 1\}$.

Если вместо уменьшения h увеличить степень полиномов, используемых в базовой функции, получится p-метод. Если объединить эти два уточнения типов, получается hp-метод (hp-FEM ). В hp-FEM степени полинома могут варьироваться от элемента к элементу nt. Методы высокого порядка с большим однородным p называются спектральными методами конечных элементов (SFEM ). Их не следует путать с спектральными методами.

. Для векторных уравнений в частных производных базисные функции могут принимать значения в $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\}$.

Различные типы методов конечных элементов

AEM

Метод прикладных элементов или AEM сочетает в себе функции как FEM, так и метода дискретных элементов или (DEM).

Обобщенный метод конечных элементов

Обобщенный метод конечных элементов (GFEM) использует локальные пространства, состоящие из функций, не обязательно полиномов, которые отражают доступную информацию о неизвестном решении и, таким образом, обеспечивают хорошее локальное приближение. Затем разбиение единицы используется для «скрепления» этих пространств вместе для формирования аппроксимирующего подпространства. Эффективность GFEM была продемонстрирована в применении к задачам с областями со сложными границами, задачам с микромасштабами и задачам с пограничными слоями.

Смешанный метод конечных элементов

Смешанный метод конечных элементов представляет собой тип метода конечных элементов, в котором дополнительные независимые переменные вводятся как узловые переменные во время дискретизации задачи уравнения в частных производных.

Переменная - полиномиальная

hp-FEM адаптивно комбинирует элементы с переменным размером h и полиномиальной степенью p для достижения исключительно быстрой экспоненциальной скорости сходимости.

hpk-FEM

Объединяет адаптивно элементы с переменным размером h, полиномиальной степенью локальных приближений p и глобальной дифференцируемостью локальных приближений (k-1) для достижения наилучших скоростей сходимости.

XFEM

Расширенный метод конечных элементов (XFEM) - это численный метод, основанный на обобщенном методе конечных элементов (GFEM) и методе разделения единицы (PUM). Он расширяет классический метод конечных элементов, обогащая пространство решений для решений дифференциальных уравнений с разрывными функциями. Расширенные методы конечных элементов обогащают пространство аппроксимации, так что оно может естественным образом воспроизводить сложные особенности, связанные с интересующей проблемой: разрыв, сингулярность, пограничный слой и т. Д. Было показано, что для некоторых задач такое вложение признака задачи в пространство аппроксимации может значительно улучшить скорость сходимости и точность. Кроме того, обработка проблем с неоднородностями с помощью XFEM устраняет необходимость в сетке и повторной сетке поверхностей неоднородностей, тем самым уменьшая вычислительные затраты и ошибки проекции, связанные с традиционными методами конечных элементов, за счет ограничения несплошностей краями сетки.

Несколько исследовательских кодов реализуют эту технику в различной степени: 1. GetFEM ++ 2. xfem ++ 3. openxfem ++

XFEM также был реализован в таких кодах, как Altair Radios, ASTER, Morfeo и Abaqus. Он все чаще внедряется в другое коммерческое программное обеспечение для конечных элементов с несколькими доступными плагинами и фактическими реализациями ядра (ANSYS, SAMCEF, OOFELIE и т.

Метод конечных элементов с масштабированной границей (SBFEM)

Введение метода конечных элементов с масштабированной границей (SBFEM) было предложено Сонг и Вольфом (1997). SBFEM стал одним из самых прибыльных достижений в области численного анализа проблем механики разрушения. Это полуаналитический метод без фундаментальных решений, который сочетает в себе преимущества формулировок и процедур конечных элементов, а также дискретизации граничных элементов. Однако, в отличие от метода граничных элементов, не требуется фундаментального дифференциального решения.

S-FEM

S-FEM, сглаженные методы конечных элементов, представляют собой особый класс алгоритмов численного моделирования для моделирования физических явлений. Он был разработан путем объединения бессеточных методов с методом конечных элементов.

Метод спектральных элементов

Методы спектральных элементов сочетают геометрическую гибкость конечных элементов и высокую точность спектральных методов. Спектральные методы представляют собой приближенное решение уравнений в частных слабых формах, которые основаны на лагранжевых интерполянтах высокого порядка и используются только с определенными квадратурными правилами.

Бессеточные методы

разрывные методы Галеркина

Анализ предела конечных элементов

Метод растянутой сетки

Итерация Лубиньяка

Итерация Лубиньяка - это итерационный метод в методах конечных элементов.

Связь с методом градиентной дискретизации

Некоторые типы методов конечных элементов (согласующиеся, несоответствующие, смешанные методы конечных элементов) являются частными случаями метода градиентной дискретизации (GDM). Следовательно, свойства сходимости GDM, которые установлены для ряда задач (линейные и нелинейные эллиптические задачи, линейные, нелинейные и вырожденные параболические задачи), также сохраняются для этих конкретных методов конечных элементов.

Сравнение с методом конечных разностей

Метод конечных разностей (FDM) является альтернативным способом аппроксимации решений УЧП. Различия между FEM и FDM заключаются в следующем:

• Наиболее привлекательной особенностью FEM является его способность относительно легко обрабатывать сложные геометрические формы (и границы). В то время как FDM в своей базовой форме ограничивается обработкой прямоугольных форм и их простых изменений, обработка геометрических фигур в FEM теоретически проста.
• FDM обычно не используется для нестандартных геометрических фигур САПР, но чаще прямоугольные или блочные модели.
• Самая привлекательная особенность конечных разностей состоит в том, что их очень легко реализовать.
• Есть несколько способов рассматривать FDM как частный случай подхода FEM. Например, FEM первого порядка идентичен FDM для уравнения Пуассона, если задача дискретизируется с помощью регулярной прямоугольной сетки, где каждый прямоугольник разделен на два треугольника.
• Есть причины считать математическую основу аппроксимации методом конечных элементов более надежной, например, потому что качество аппроксимации между точками сетки в FDM плохое.
• Качество аппроксимации FEM часто выше, чем в соответствующий подход FDM, но он в значительной степени зависит от проблемы, и можно привести несколько примеров обратного.

Как правило, FEM является методом выбора во всех типах анализа в строительной механике (т.е. решение для деформации и напряжений в твердом теле тел или динамики конструкций), в то время как вычислительная гидродинамика (CFD), как правило, использует FDM или другие методы, такие как метод конечных объемов (FVM). Задачи CFD обычно требуют дискретизации задачи на большое количество ячеек / точек сетки (миллионы и более), поэтому стоимость решения способствует более простой аппроксимации более низкого порядка в каждой ячейке. Это особенно верно для проблем с «внешним потоком», таких как воздушный поток вокруг автомобиля или самолета или моделирование погоды.

Приложение

Визуализация того, как автомобиль деформируется при асимметричном столкновении, с использованием анализа методом конечных элементов. [1]

Разнообразные специализации в рамках дисциплины машиностроения (например, авиационная, биомеханическая и автомобильная промышленность) обычно используют интегрированные МКЭ при проектировании и разработке своих продуктов. Несколько современных пакетов FEM включают специальные компоненты, такие как тепловые, электромагнитные, жидкостные и структурные рабочие среды. В структурном моделировании FEM очень помогает в визуализации жесткости и прочности, а также в минимизации веса, материалов и затрат.

FEM позволяет детально визуализировать изгиб или скручивание конструкций, а также показывает распределение напряжений и смещений. Программное обеспечение FEM предоставляет широкий спектр возможностей моделирования для управления сложностью моделирования и анализа системы. Точно так же можно одновременно управлять желаемым уровнем требуемой точности и соответствующими требованиями к вычислительному времени для решения большинства инженерных приложений. FEM позволяет конструировать, дорабатывать и оптимизировать целые конструкции еще до ее изготовления. Сетка является неотъемлемой частью модели, и для получения наилучших результатов за ней необходимо тщательно контролировать. Как правило, чем больше количество элементов в сетке, тем точнее решение дискретизированной задачи. Однако существует значение, при котором результаты сходятся, и дальнейшее уточнение сетки не увеличивает точность.

Конечно-элементная модель человеческого коленного сустава.

Этот мощный инструмент проектирования значительно улучшил стандарты инженерного проектирования и методология процесса проектирования во многих промышленных приложениях. Внедрение FEM существенно сократило время, необходимое для вывода продуктов от концепции до производственной линии. Тестирование и разработка были ускорены в первую очередь за счет улучшенных первоначальных прототипов с использованием МКЭ. Таким образом, преимущества FEM включают повышенную точность, улучшенный дизайн и лучшее понимание критических параметров конструкции, виртуальное прототипирование, меньшее количество аппаратных прототипов, более быстрый и менее затратный цикл проектирования, повышенную производительность и увеличение доходов.

3D модель переноса загрязняющих веществ - поле концентрации на уровне земли 3D модель переноса загрязнений - поле концентрации на перпендикулярной поверхности

В 1990-х годах FEA было предложено использовать в стохастическом моделировании для численного решения вероятностных моделей, а затем для оценки надежности.

.

.

См. также

• Метод прикладных элементов
• Метод граничных элементов
• Лемма Сеа
• Компьютерный эксперимент
• Метод прямой жесткости
• Оптимизация расположения разрывов
• Метод дискретных элементов
• Метод конечных разностей
• Машина конечных элементов
• Метод конечных элементов в строительной механике
• Метод конечных объемов
• Метод конечных объемов для нестационарного потока
• Метод бесконечных элементов
• Интервальный конечный элемент
• Isog Эометрический анализ
• Решеточные методы Больцмана
• Список пакетов программного обеспечения конечных элементов
• Meshfree методы
• Подвижный клеточный автомат
• Оптимизация многопрофильного проектирования
• Мультифизика
• Патч-тест
• Метод Рэлея – Ритца
• Отображение пространства
• Тесселяция (компьютерная графика)
• Ослабленная слабая форма

Ссылки

Дополнительная литература

• G. Аллер и А. Крейг: Численный анализ и оптимизация: введение в математическое моделирование и численное моделирование.
• К. J. Bathe: Численные методы в анализе конечных элементов, Prentice-Hall (1976).
• Thomas JR Hughes: The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Prentice-Hall (1987).
• Дж. Часкалович: Методы конечных элементов для технических наук, Springer Verlag, (2008).
• Endre Süli : Методы конечных элементов для уравнений с частными производными.
• O. К. Зенкевич, Р.Л. Тейлор, Дж. З. Чжу: Метод конечных элементов: его основы и основы, Баттерворт-Хайнеманн (2005).

Внешние ссылки

На Викискладе есть материалы по теме Моделирование методом конечных элементов.

• IFER - Интернет-ресурсы по конечным элементам - описывает и обеспечивает доступ к программному обеспечению для анализа методом конечных элементов через Интернет
• NAFEMS - Международная ассоциация инженерного моделирования
• Математика метода конечных элементов