Уравнение импульса Коши

редактировать

Уравнение импульса Коши представляет собой векторное уравнение в частных производных, представленное Коши, описывающий нерелятивистский перенос импульса в любом континууме.

Содержание

1 Основное уравнение
2 Дифференциальный вывод
- 2.1 Правая часть
- 2.2 Левая часть
- 2.3 Сравнение левой и правой сторон
3 Интегральная деривация
4 Форма сохранения
5 Конвективное ускорение
- 5.1 Оператор адвекции и тензорная производная
- 5.2 Форма Лэмба
- 5.3 Безвихревые потоки
6 Напряжения
7 Внешние силы
8 Обезразмерение
9 Явные трехмерные конвективные формы
- 9.1 Декартовы трехмерные координаты
- 9.2 Цилиндрические трехмерные координаты
10 См. Также
11 Примечания
12 Ссылки

Основное уравнение

В конвективной (или лагранжевой) форме уравнение импульса Коши записывается как:

D u D t = 1 ρ ∇ ⋅ σ + f {\ displaystyle {\ frac {D \ mathbf {u}} {Dt}} = {\ frac {1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} + \ mathbf {f}}

{\frac {D\mathbf {u} }{Dt}}={\frac {1}{\rho }}\nabla \cdot {\boldsymbol {\sigma }}+\mathbf {f}

где

$и [м / с] {\ displaystyle \ mathbf {u} \ [\ mathrm {m / s}] }$ $\mathbf {u} \ [\mathrm {m/s} ]$ - это векторное поле скорости потока, которое зависит от времени и пространства,
$t [s] {\ displaystyle t \ [\ mathrm {s}]}$ $t\ [\mathrm {s} ]$ равно время,
$D u D t [м / с 2] {\ displaystyle {\ frac {D \ mathbf {u}} {Dt}} \ [\ mathrm {m / s ^ {2} }]}$ ${\frac {D\mathbf {u} }{Dt}}\ [\mathrm {m/s^{2}} ]$ - производная материала, равная $∂ tu + u ⋅ ∇ u {\ displaystyle \ partial _ {t} \ mathbf {u} + \ mathbf {u} \ cdot \ nabla \ mathbf {u}}$ $\partial _{t}\mathbf {u} +\mathbf {u} \cdot \nabla \mathbf {u}$ ,
$ρ [кг / м 3] {\ displaystyle \ rho \ [\ mathrm {кг / м ^ {3}}]}$ $\rho \ [\mathrm {kg/m^{3}} ]$ равно плотность в данной точке континуума (для которой выполняется уравнение неразрывности ),
$σ [P a = N / m 2 = кг / м ⋅ s 2] {\ displaystyle { \ boldsymbol {\ sigma}} \ [\ mathrm {Па = Н / м ^ {2} = кг / м \ cdot s ^ {2}}]}$ ${\boldsymbol {\sigma }}\ [\mathrm {Pa=N/m^{2}=kg/m\cdot s^{2}} ]$ - тензор напряжений,
$е = [fxfyfz] [м / с 2] {\ displaystyle \ mathbf {f} = {\ begin {bmatrix} f_ {x} \\ f_ {y} \\ f_ {z} \ end {bmatrix}} \ [ \ mathrm {м / с ^ {2}}]}$ $\mathbf {f} ={\begin{bmatrix}f_{x}\\f_{y}\\f_{z}\end{bmatrix}}\ [\mathrm {m/s^{2}} ]$ - вектор, содержащий все ускорения, вызванные телесными силами (иногда просто ускорение свободного падения ),
$∇ ⋅ σ = [∂ σ xx ∂ x + ∂ σ yx ∂ y + ∂ σ zx ∂ z ∂ σ xy ∂ x + ∂ σ yy ∂ y + ∂ σ zy ∂ z ∂ σ xz ∂ x + ∂ σ yz ∂ y + ∂ σ zz ∂ z] [P a / m = кг / м 2 ⋅ s 2] {\ displaystyle \ nabla \ cdot {\ boldsymbol {\ sigma}} = {\ begin {bmatrix} {\ dfrac {\ partial \ sigma _ {xx}} {\ partial x}} + {\ dfrac {\ partial \ sigma _ {yx}} {\ partial y}} + {\ dfrac {\ partial \ sigma _ {zx}} {\ partial z}} \\ {\ dfrac {\ partial \ sigma _ {xy}} {\ partial x}} + {\ dfrac {\ partial \ sigma _ {yy}} {\ partial y}} + {\ dfrac {\ partial \ sigma _ {zy}} {\ partial z}} \\ {\ dfrac { \ partial \ sigma _ {xz}} {\ partial x}} + {\ dfrac {\ partial \ sigma _ {yz}} {\ partial y}} + {\ dfrac {\ partial \ sigma _ {zz}} { \ partial z}} \\\ end {bmatrix}} [\ mathrm {Па / м = кг / м ^ {2} \ cdot s ^ {2}}]}$ $\nabla \cdot {\boldsymbol {\sigma }}={\begin{bmatrix}{\dfrac {\partial \sigma _{xx}}{\partial x}}+{\dfrac {\partial \sigma _{yx}}{\partial y}}+{\dfrac {\partial \sigma _{zx}}{\partial z}}\\{\dfrac {\partial \sigma _{xy}}{\partial x}}+{\dfrac {\partial \sigma _{yy}}{\partial y}}+{\dfrac {\partial \sigma _{zy}}{\partial z}}\\{\dfrac {\partial \sigma _{xz}}{\partial x}}+{\dfrac {\partial \sigma _{yz}}{\partial y}}+{\dfrac {\partial \sigma _{zz}}{\partial z}}\\\end{bmatrix}}[\mathrm {Pa/m=kg/m^{2}\cdot s^{2}} ]$ это расхождение тензора напряжений.

Обратите внимание, что для ясности мы используем только векторы-столбцы (в декартовой системе координат), но уравнение написано нами физические компоненты (которые не являются ни ковариантами («столбец»), ни контравариантами («строка»)). Однако, если мы выбрали неортогональную криволинейную систему координат, тогда мы должны вычислять и записывать уравнения в ковариантной («векторы-строки») или контравариантной («векторы-столбцы») форме.

После соответствующей замены переменных его также можно записать в форме сохранения :

∂ j ∂ t + ∇ ⋅ F = s {\ displaystyle {\ frac {\ partial \ mathbf {j }} {\ partial t}} + \ nabla \ cdot \ mathbf {F} = \ mathbf {s}}

{\frac {\partial \mathbf {j} }{\partial t}}+\nabla \cdot \mathbf {F} =\mathbf {s}

где j - плотность импульса в данном пространстве. -времени, F - поток, связанный с плотностью импульса, а s содержит все объемные силы на единицу объема.

Дифференциальное вычисление

Давайте начнем с обобщенного принципа сохранения импульса, который можно записать следующим образом: «Изменение количества движения системы пропорционально результирующей силе, действующей на эта система ». Это выражается формулой:

p → (t + Δ t) - p → (t) = Δ t F ¯ → {\ displaystyle {\ vec {p}} (t + \ Delta t) - {\ vec {p}} (t) = \ Delta t {\ vec {\ bar {F}}}}

{\vec {p}}(t+\Delta t)-{\vec {p}}(t)=\Delta t{\vec {\bar {F}}}

где $p → (t) {\ displaystyle {\ vec {p}} (t)}$ ${\vec {p}}(t)$ - импульс во времени t, $F ¯ → {\ displaystyle {\ vec {\ bar {F}}}}$ ${\vec {\bar {F}}}$ - сила, усредненная по $Δ t {\ displaystyle \ Delta t}$ $\Delta t$ . После деления на $Δ t {\ displaystyle \ Delta t}$ $\Delta t$ и перехода к пределу $Δ t → 0 {\ displaystyle \ Delta t \ rightarrow 0}$ $\Delta t\rightarrow 0$ мы получить (производная ):

dp → dt = F → {\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = {\ vec {F}}}

{\frac {d{\vec {p}}}{dt}}={\vec {F}}

Давайте проанализируем каждую сторону приведенного выше уравнения.

Правая сторона

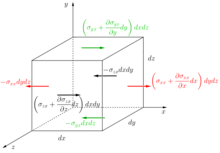
Компонент X сил, действующих на стенки кубического жидкого элемента (зеленый для верхних и нижних стенок; красный для левой и правой стороны; черный для передней и задней части).

In на верхнем графике мы видим аппроксимацию функции

f (x) {\ displaystyle f (x)}

f(x)

(синяя линия) с использованием конечной разности (желтая линия). На нижнем графике мы видим «бесконечно увеличенную окрестность точки

x 1 {\ displaystyle x_ {1}}

x_{1}

» (фиолетовый квадрат с верхнего графика). На нижнем графике желтая линия полностью закрыта синей и поэтому не видна. На нижнем рисунке использованы две эквивалентные производные формы:

f ′ (x 1) = df (x 1) dx 1 {\ displaystyle f '(x_ {1}) = {\ frac {df (x_ { 1})} {dx_ {1}}}}

f'(x_{1})={\frac {df(x_{1})}{dx_{1}}}

], и обозначение

Δ f = f (x 1 + Δ x) - f (x 1) {\ displaystyle \ Delta f = Было использовано f (x_ {1} + \ Delta x) -f (x_ {1})}

\Delta f=f(x_{1}+\Delta x)-f(x_{1})

Мы разделили силы на объемные силы $F → m {\ displaystyle {\ vec {F}} _ {m}}$ ${\vec {F}}_{m}$ и поверхностные силы $F → p {\ displaystyle {\ vec {F}} _ {p }}$ ${\vec {F}}_{p}$

F → = F → p + F → m {\ displaystyle {\ vec {F}} = {\ vec {F}} _ {p} + {\ vec {F}} _ {m}}

{\vec {F}}={\vec {F}}_{p}+{\vec {F}}_{m}

Поверхностные силы действуют на стенки кубического жидкого элемента. Для каждой стены компонент X этих сил был отмечен на рисунке кубическим элементом (в виде произведения напряжения и площади поверхности, например, $- σ xxdydz [P a ⋅ m ⋅ m = N m 2 ⋅ м ⋅ м = N] {\ displaystyle - \ sigma _ {xx} dydz \ [Pa \ cdot m \ cdot m = {\ frac {N} {m ^ {2}}} \ cdot m \ cdot m = N] }$ $-\sigma _{xx}dydz\ [Pa\cdot m\cdot m={\frac {N}{m^{2}}}\cdot m\cdot m=N]$ ).

Объяснение значения сил (приближения и минус), действующих на стенки куба.
Требуется пояснение, почему напряжение, приложенное к стенам, покрывающим оси координат, принимает знак минус (например, для левой стены мы имеем $- σ xx {\ displaystyle - \ sigma _ {xx}}$ $-\sigma _{xx}$ ). Для простоты давайте сосредоточимся на левой стене с натяжением $- σ x x {\ displaystyle - \ sigma _ {xx}}$ $-\sigma _{xx}$ . Знак минус связан с тем, что вектор, нормальный к этой стене $n → = [- 1, 0, 0] = - e → x {\ displaystyle {\ vec {n}} = [- 1,0, 0] = - {\ vec {e}} _ {x}}$ ${\vec {n}}=[-1,0,0]=-{\vec {e}}_{x}$ - отрицательный единичный вектор. Затем мы вычислили вектор напряжений по определению $s → = n → ⋅ σ = [- σ xx, - σ xy, - σ xz] {\ displaystyle {\ vec {s}} = {\ vec {n}} \ cdot {\ boldsymbol {\ sigma}} = [- \ sigma _ {xx}, - \ sigma _ {xy}, - \ sigma _ {xz}]}$ ${\vec {s}}={\vec {n}}\cdot {\boldsymbol {\sigma }}=[-\sigma _{xx},-\sigma _{xy},-\sigma _{xz}]$ , таким образом, компонент X этого вектора равен $sx = - σ xx {\ displaystyle s_ {x} = - \ sigma _ {xx}}$ $s_{x}=-\sigma _{xx}$ (мы используем аналогичные рассуждения для напряжений, действующих на нижнюю часть и задние стенки, например: $- σ yx, - σ zx {\ displaystyle - \ sigma _ {yx}, - \ sigma _ {zx}}$ $-\sigma _{yx},-\sigma _{zx}$ ). Второй элемент, требующий пояснения, - это аппроксимация значений напряжений, действующих на стены напротив стен, охватывающих оси. Давайте сосредоточимся на правой стене, где напряжение является приближением напряжения $σ xx {\ displaystyle \ sigma _ {xx}}$ $\sigma_{xx}$ от левой стены в точках с координатами $x + dx {\ displaystyle x + dx}$ $x+dx$ и это равно $σ xx + ∂ σ xx ∂ xdx {\ displaystyle \ sigma _ {xx} + {\ frac {\ partial \ sigma _ {xx }} {\ partial x}} dx}$ $\sigma _{xx}+{\frac {\partial \sigma _{xx}}{\partial x}}dx$ . Это приближение является результатом применения формулы Тейлора для аппроксимации функции, то есть $σ xx (x + dx) = σ xx (x) + dx ∂ σ xx (x) ∂ x + dx 2 2 ∂ 2 σ xx (x) ∂ x 2 +... {\ displaystyle \ sigma _ {xx} (x + dx) = \ sigma _ {xx} (x) + dx {\ frac {\ partial \ sigma _ {xx} (x)} {\ partial x}} + { \ frac {dx ^ {2}} {2}} {\ frac {\ partial ^ {2} \ sigma _ {xx} (x)} {\ partial x ^ {2}}} +...}$ $\sigma _{xx}(x+dx)=\sigm a _{xx}(x)+dx{\frac {\partial \sigma _{xx}(x)}{\partial x}}+{\frac {dx^{2}}{2}}{\frac {\partial ^{2}\sigma _{xx}(x)}{\partial x^{2}}}+...$ Поскольку значение $dx 2 {\ displaystyle dx ^ {2}}$ $dx^{2}$ бесконечно меньше значения $dx {\ displaystyle dx}$ $dx$ , поэтому все компоненты с $dx {\ displaystyle dx}$ $dx$ в степенях больше единицы может быть пропущено как незначимое. Таким образом, мы получили искомую аппроксимацию натяжения на противоположной стене. Более интуитивное представление значения аппроксимации $σ xx {\ displaystyle \ sigma _ {xx}}$ $\sigma_{xx}$ в точке $x + dx {\ displaystyle x + dx}$ $x+dx$ показан на рисунке под кубом. Мы продолжаем аналогичные рассуждения для аппроксимации напряжений $σ yx, σ zx {\ displaystyle \ sigma _ {yx}, \ sigma _ {zx}}$ $\sigma _{yx},\sigma _{zx}$ .

Объяснение значения сил (приближения и минус), действующих на стенки куба.

Требуется пояснение, почему напряжение, приложенное к стенам, покрывающим оси координат, принимает знак минус (например, для левой стены мы имеем $- σ xx {\ displaystyle - \ sigma _ {xx}}$ $-\sigma _{xx}$ ). Для простоты давайте сосредоточимся на левой стене с натяжением $- σ x x {\ displaystyle - \ sigma _ {xx}}$ $-\sigma _{xx}$ . Знак минус связан с тем, что вектор, нормальный к этой стене $n → = [- 1, 0, 0] = - e → x {\ displaystyle {\ vec {n}} = [- 1,0, 0] = - {\ vec {e}} _ {x}}$ ${\vec {n}}=[-1,0,0]=-{\vec {e}}_{x}$ - отрицательный единичный вектор. Затем мы вычислили вектор напряжений по определению $s → = n → ⋅ σ = [- σ xx, - σ xy, - σ xz] {\ displaystyle {\ vec {s}} = {\ vec {n}} \ cdot {\ boldsymbol {\ sigma}} = [- \ sigma _ {xx}, - \ sigma _ {xy}, - \ sigma _ {xz}]}$ ${\vec {s}}={\vec {n}}\cdot {\boldsymbol {\sigma }}=[-\sigma _{xx},-\sigma _{xy},-\sigma _{xz}]$ , таким образом, компонент X этого вектора равен $sx = - σ xx {\ displaystyle s_ {x} = - \ sigma _ {xx}}$ $s_{x}=-\sigma _{xx}$ (мы используем аналогичные рассуждения для напряжений, действующих на нижнюю часть и задние стенки, например: $- σ yx, - σ zx {\ displaystyle - \ sigma _ {yx}, - \ sigma _ {zx}}$ $-\sigma _{yx},-\sigma _{zx}$ ).

Второй элемент, требующий пояснения, - это аппроксимация значений напряжений, действующих на стены напротив стен, охватывающих оси. Давайте сосредоточимся на правой стене, где напряжение является приближением напряжения $σ xx {\ displaystyle \ sigma _ {xx}}$ $\sigma_{xx}$ от левой стены в точках с координатами $x + dx {\ displaystyle x + dx}$ $x+dx$ и это равно $σ xx + ∂ σ xx ∂ xdx {\ displaystyle \ sigma _ {xx} + {\ frac {\ partial \ sigma _ {xx }} {\ partial x}} dx}$ $\sigma _{xx}+{\frac {\partial \sigma _{xx}}{\partial x}}dx$ . Это приближение является результатом применения формулы Тейлора для аппроксимации функции, то есть

σ xx (x + dx) = σ xx (x) + dx ∂ σ xx (x) ∂ x + dx 2 2 ∂ 2 σ xx (x) ∂ x 2 +... {\ displaystyle \ sigma _ {xx} (x + dx) = \ sigma _ {xx} (x) + dx {\ frac {\ partial \ sigma _ {xx} (x)} {\ partial x}} + { \ frac {dx ^ {2}} {2}} {\ frac {\ partial ^ {2} \ sigma _ {xx} (x)} {\ partial x ^ {2}}} +...}

\sigma _{xx}(x+dx)=\sigm a _{xx}(x)+dx{\frac {\partial \sigma _{xx}(x)}{\partial x}}+{\frac {dx^{2}}{2}}{\frac {\partial ^{2}\sigma _{xx}(x)}{\partial x^{2}}}+...

Поскольку значение $dx 2 {\ displaystyle dx ^ {2}}$ $dx^{2}$ бесконечно меньше значения $dx {\ displaystyle dx}$ $dx$ , поэтому все компоненты с $dx {\ displaystyle dx}$ $dx$ в степенях больше единицы может быть пропущено как незначимое. Таким образом, мы получили искомую аппроксимацию натяжения на противоположной стене. Более интуитивное представление значения аппроксимации $σ xx {\ displaystyle \ sigma _ {xx}}$ $\sigma_{xx}$ в точке $x + dx {\ displaystyle x + dx}$ $x+dx$ показан на рисунке под кубом. Мы продолжаем аналогичные рассуждения для аппроксимации напряжений $σ yx, σ zx {\ displaystyle \ sigma _ {yx}, \ sigma _ {zx}}$ $\sigma _{yx},\sigma _{zx}$ .

Суммируя силы (их компоненты X), действующие на каждую из стенок куба, получаем:

F px = (σ xx + ∂ σ xx ∂ xdx) dydz - σ xxdydz + (σ yx + ∂ σ yx ∂ ydy) dxdz - σ yxdxdz + (σ zx + ∂ σ zx ∂ zdz) dxdy - σ zxdxdy {\ displaystyle F_ {p} ^ {x} = (\ sigma _ {xx} + {\ frac {\ partial \ sigma _ {xx}} {\ partial x}} dx) dydz- \ sigma _ {xx} dydz + (\ sigma _ {yx} + {\ frac {\ partial \ sigma _ {yx}} {\ partial y}} dy) dxdz- \ sigma _ {yx} dxdz + (\ sigma _ {zx} + {\ frac {\ partial \ sigma _ {zx}} {\ partial z}} dz) dxdy- \ sigma _ {zx} dxdy}

F_{p}^{x}=(\sigma _{xx}+{\frac {\partial \sigma _{xx}}{\partial x}}dx)dydz-\sigma _{xx}dydz+(\sigma _{yx}+{\frac {\partial \sigma _{yx}}{\partial y}}dy)dxdz-\sigma _{yx}dxdz+(\sigma _{zx}+{\frac {\partial \sigma _{zx}}{\partial z}}dz)dxdy-\sigma _{zx}dxdy

После заказа $F px {\ displaystyle F_ {p} ^ { x}}$ $F_{p}^{x}$ и аналогичные рассуждения для компонентов $F py, F pz {\ displaystyle F_ {p} ^ {y}, F_ {p} ^ {z}}$ $F_{p}^{y},F_{p}^{z}$ (они не показаны на рисунке, но это были бы векторы, параллельные осям Y и Z соответственно), получаем:

F px = ∂ σ xx ∂ xdxdydz + ∂ σ yx ∂ yd ydxdz + ∂ σ zx ∂ zdzdxdy {\ displaystyle F_ {p} ^ {x} = {\ frac {\ partial \ sigma _ {xx}} {\ partial x}} dxdydz + {\ frac {\ partial \ sigma _ {yx }} {\ partial y}} dydxdz + {\ frac {\ partial \ sigma _ {zx}} {\ partial z}} dzdxdy}

F_{p}^{x}={\frac {\partial \sigma _{xx}}{\partial x}}dxdydz+{\frac {\partial \sigma _{yx}}{\partial y}}dydxdz+{\frac {\partial \sigma _{zx}}{\partial z}}dzdxdy

F py = ∂ σ xy ∂ xdxdydz + ∂ σ yy ∂ ydydxdz + ∂ σ zy ∂ zdzdxdy {\ displaystyle F_ {p} ^ {y} = {\ frac {\ partial \ sigma _ {xy}} {\ partial x}} dxdydz + {\ frac {\ partial \ sigma _ {yy}} {\ partial y}} dydxdz + {\ frac {\ partial \ sigma _ {zy}} {\ partial z}} dzdxdy}

F_{p}^{y}={\frac {\partial \sigma _{xy}}{\partial x}}dxdydz+{\frac {\partial \sigma _{yy}}{\partial y}}dydxdz+{\frac {\partial \sigma _{zy}}{\partial z}}dzdxdy

F pz = ∂ σ xz ∂ xdxdydz + ∂ σ yz ∂ ydydxdz + ∂ σ zz ∂ zdzdxdy { \ Displaystyle F_ {p} ^ {z} = {\ frac {\ partial \ sigma _ {xz}} {\ partial x}} dxdydz + {\ frac {\ partial \ sigma _ {yz}} {\ partial y}} dydxdz + {\ frac {\ partial \ sigma _ {zz}} {\ partial z}} dzdxdy}

F_{p}^{z}={\frac {\partial \sigma _{xz}}{\partial x}}dxdydz+{\frac {\partial \sigma _{yz}}{\partial y}}dydxdz+{\frac {\partial \sigma _{zz}}{\partial z}}dzdxdy

Затем мы можем записать его в символической операционной форме:

F → p = (∇ ⋅ σ) dxdydz { \ displaystyle {\ vec {F}} _ {p} = (\ nabla \ cdot {\ boldsymbol {\ sigma}}) dxdydz}

{\vec {F}}_{p}=(\nabla \cdot {\boldsymbol {\sigma }})dxdydz

Внутри контрольного объема действуют массовые силы. Мы можем записать их, используя поле ускорения $f {\ displaystyle \ mathbf {f}}$ $\mathbf {f}$ (например, ускорение свободного падения):

F → m = f ρ dxdydz {\ displaystyle {\ vec { F}} _ {m} = \ mathbf {f} \ rho dxdydz}

{\vec {F}}_{m}=\mathbf {f} \rho dxdydz

Левая сторона

Вычислим импульс куба:

p → = um = u ρ dxdydz {\ displaystyle {\ vec {p}} = \ mathbf {u} m = \ mathbf {u} \ rho dxdydz}

{\vec {p}}=\mathbf {u} m=\mathbf {u} \rho dxdydz

Потому что мы предполагаем, что протестированная масса (куб) $m = ρ dxdydz {\ displaystyle m = \ rho dxdydz}$ $m=\rho dxdydz$ постоянно во времени, поэтому

dp → dt = dudt ρ dxdydz {\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = {\ frac {d \ mathbf {u}} {dt}} \ rho dxdydz}

{\frac {d{\vec {p}}}{dt}}={\frac {d\mathbf {u} }{dt}}\rho dxdydz

Сравнение левой и правой сторон

У нас есть

dp → dt = F → {\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = {\ vec {F}}}

{\frac {d{\vec {p}}}{dt}}={\vec {F}}

, затем

dp → dt = F → p + F → m {\ displaystyle {\ frac {d {\ vec {p}) }} {dt}} = {\ vec {F}} _ {p} + {\ vec {F}} _ {m}}

{\frac {d{\vec {p}}}{dt}}={\vec {F}}_{p}+{\vec {F}}_{m}

, затем

dudt ρ dxdydz = (∇ ⋅ σ) dxdydz + f ρ dxdydz {\ displaystyle {\ frac {d \ mathbf {u}} {dt}} \ rho dxdyd z = (\ nabla \ cdot {\ boldsymbol {\ sigma}}) dxdydz + \ mathbf {f} \ rho dxdydz}

{\frac {d\mathbf {u} }{dt}}\rho dxdydz=(\nabla \cdot {\boldsymbol {\sigma }})dxdydz+\mathbf {f} \rho dxdydz

Разделите обе стороны на $ρ dxdydz {\ displaystyle \ rho dxdydz}$ $\rho dxdydz$ , и потому что $dudt = D u D t {\ displaystyle {\ frac {d \ mathbf {u}} {dt}} = {\ frac {D \ mathbf {u}} {Dt}}}$ ${\frac {d\mathbf {u} }{dt}}={\frac {D\mathbf {u} }{Dt}}$ получаем:

D u D t = 1 ρ ∇ ⋅ σ + f {\ displaystyle {\ frac {D \ mathbf {u}} {Dt}} = {\ frac {1} {\ rho }} \ nabla \ cdot {\ boldsymbol {\ sigma}} + \ mathbf {f}}

{\frac {D\mathbf {u} }{Dt}}={\frac {1}{\rho }}\nabla \cdot {\boldsymbol {\sigma }}+\mathbf {f}

, что завершает вывод.

Интегральный вывод

Применение второго закона Ньютона (i-й компонент) к контрольному объему в моделируемом континууме дает:

mai = F i {\ displaystyle ma_ {i} = F_ {i}}

ma_{i}=F_{i}

Тогда, основываясь на теореме переноса Рейнольдса и используя обозначение материальной производной, можно написать

∫ Ω ρ D ui D td V = ∫ Ω ∇ j σ ijd V + ∫ Ω ρ fid V ∫ Ω (ρ D ui D t - ∇ j σ ij - ρ fi) d V = 0 ρ D ui D t - ∇ j σ ij - ρ fi знак равно 0 D ui D T - ∇ J σ ij ρ - fi = 0 {\ displaystyle {\ begin {align} \ int _ {\ Omega} \ rho {\ frac {Du_ {i}} { Dt}} \, dV = \ int _ {\ Omega} \ nabla _ {j} \ sigma _ {i} ^ {j} \, dV + \ int _ {\ Omega} \ rho f_ {i} \, dV \ \\ int _ {\ Omega} \ left (\ rho {\ frac {Du_ {i}} {Dt}} - \ nabla _ {j} \ sigma _ {i} ^ {j} - \ rho f_ {i} \ right) \, dV = 0 \\\ rho {\ frac {Du_ {i}} {Dt}} - \ nabla _ {j} \ sigma _ {i} ^ {j} - \ rho f_ {i} = 0 \\ {\ frac {Du_ {i}} {Dt}} - {\ frac {\ nabla _ {j} \ sigma _ {i} ^ {j}} {\ rho}} - f_ {i} = 0 \ end {align}}}

{\begin{aligned}\int _{\Omega }\rho {\frac {Du_{i}}{Dt}}\,dV=\int _{\Omega }\nabla _{j}\sigma _{i}^{j}\,dV+\int _{\Omega }\rho f_{i}\,dV\\\int _{\Omega }\left(\rho {\frac {Du_{i}}{Dt}}-\nabla _{j}\sigma _{i}^{j}-\rho f_{i}\right)\,dV=0\\\rho {\frac {Du_{i}}{Dt}}-\nabla _{j}\sigma _{i}^{j}-\rho f_{i}=0\\{\frac {Du_{i}}{Dt}}-{\frac {\nabla _{j}\sigma _{i}^{j}}{\rho }}-f_{i}=0\end{aligned}}

где Ω представляет собой контрольный объем. Поскольку это уравнение должно выполняться для любого контрольного объема, должно быть верно, что подынтегральное выражение равно нулю, из этого следует уравнение импульса Коши. Главный шаг (не сделанный выше) при выводе этого уравнения - установить, что производная тензора напряжений является одной из сил, составляющих F i.

Форма сохранения

Уравнение импульса Коши также может быть записано в следующей форме:

уравнение импульса Коши (форма сохранения)

$∂ j ∂ t + ∇ ⋅ F = s {\ displaystyle {\ frac {\ partial \ mathbf { j}} {\ partial t}} + \ nabla \ cdot \ mathbf {F} = \ mathbf {s}}$ ${\frac {\partial \mathbf {j} }{\partial t}}+\nabla \cdot \mathbf {F} =\mathbf {s}$

просто путем определения:

j = ρ u F = ρ u ⊗ u - σ s = ρ е {\ Displaystyle {\ begin {выровнено} {\ mathbf {j}} = \ rho \ mathbf {u} \\ {\ mathbf {F}} = \ rho \ mathbf {u} \ otimes \ mathbf { u} - {\ boldsymbol {\ sigma}} \\ {\ mathbf {s}} = \ rho \ mathbf {f} \ end {align}}}

{\begin{aligned}{\mathbf {j} }=\rho \mathbf {u} \\{\mathbf {F} }=\rho \mathbf {u} \otimes \mathbf {u} -{\boldsymbol {\sigma }}\\{\mathbf {s} }=\rho \mathbf {f} \end{aligned}}

где j - это плотность импульса в точке, рассматриваемой в континууме (для которой выполняется уравнение неразрывности ), F - поток, связанный с плотностью импульса, а s содержит все объемные силы на единицу объема. u⊗ u- это диада скорости.

Здесь j и s имеют то же количество измерений N, что и скорость потока и ускорение тела, а F, будучи тензор, имеет N.

В эйлеровых формах очевидно, что предположение об отсутствии девиаторного напряжения приводит уравнения Коши к уравнениям Эйлера.

Конвективное ускорение

Пример конвективное ускорение. Поток постоянный (не зависящий от времени), но жидкость замедляется по мере движения вниз по расширяющемуся каналу (в предположении несжимаемого или дозвукового сжимаемого потока).

Важной особенностью уравнений Навье – Стокса является наличие конвективного ускорения: эффект не зависящего от времени ускорения потока относительно пространства. Хотя отдельные частицы континуума действительно испытывают зависящее от времени ускорение, конвективное ускорение поля потока является пространственным эффектом, одним из примеров которого является ускорение жидкости в сопле.

Независимо от типа континуума, конвективное ускорение является нелинейным эффектом. Конвективное ускорение присутствует в большинстве потоков (исключения включают одномерный поток несжимаемой жидкости), но его динамический эффект не учитывается в ползущем потоке (также называемом потоком Стокса). Конвективное ускорение представлено нелинейной величиной u · ∇ u, которую можно интерпретировать как (u · ∇) u или как u · (∇ u ), где ∇ u тензорная производная вектора скорости и . Обе интерпретации дают одинаковый результат.

Оператор адвекции против производной тензора

Член конвекции $D u / D t {\ displaystyle D \ mathbf {u} / Dt}$ $D\mathbf {u} /Dt$ можно записать как (u · ∇) u, где u · - это оператор переноса. Это представление можно противопоставить представлению в терминах тензорной производной. Тензорная производная ∇ u - это покомпонентная производная вектора скорости, определяемая как [∇ u]mi= ∂ mvi, так что

[u ⋅ (∇ u)] i = ∑ mvm ∂ mvi = [(u ⋅ ∇) u] i. {\ displaystyle \ left [\ mathbf {u} \ cdot \ left (\ nabla \ mathbf {u} \ right) \ right] _ {i} = \ sum _ {m} v_ {m} \ partial _ {m} v_ {i} = \ left [(\ mathbf {u} \ cdot \ nabla) \ mathbf {u} \ right] _ {i} \,.}

\left[\mathbf {u} \cdot \left(\nabla \mathbf {u} \right)\right]_{i}=\sum _{m}v_{m}\partial _{m}v_{i}=\left[(\mathbf {u} \cdot \nabla)\mathbf {u} \right]_{i}\,.

Форма ягненка

тождество векторного исчисления перекрестного произведения локона выполняется:

v × (∇ × a) = ∇ a (v ⋅ a) - v ⋅ ∇ a {\ displaystyle \ mathbf { v} \ times \ left (\ nabla \ times \ mathbf {a} \ right) = \ nabla _ {a} \ left (\ mathbf {v} \ cdot \ mathbf {a} \ right) - \ mathbf {v} \ cdot \ nabla \ mathbf {a} \,}

\mathbf {v} \times \left(\nabla \times \mathbf {a} \right)=\nabla _{a}\left(\mathbf {v} \cdot \mathbf {a} \right)-\mathbf {v} \cdot \nabla \mathbf {a} \,

где используется нотация индекса Фейнмана ∇ a, что означает, что градиент с индексом действует только на множитель a.

Лэмб в своей знаменитой классической книге «Гидродинамика» (1895), которая все еще находится в печати, использовал это тождество для изменения конвективного члена скорости потока во вращательной форме, то есть без тензорной производной:

u ⋅ ∇ u Знак равно ∇ (‖ U ‖ 2 2) + (∇ × U) × U {\ Displaystyle \ mathbf {u} \ cdot \ nabla \ mathbf {u} = \ nabla \ left ({\ frac {\ | \ mathbf {u) } \ | ^ {2}} {2}} \ right) + \ left (\ nabla \ times \ mathbf {u} \ right) \ times \ mathbf {u}}

\mathbf {u} \cdot \nabla \mathbf {u} =\nabla \left({\frac {\|\mathbf {u} \|^{2}}{2}}\right)+\left(\nabla \times \mathbf {u} \right)\times \mathbf {u}

, где вектор $l = (∇ × u) × u {\ displaystyle \ mathbf {l} = \ left (\ nabla \ times \ mathbf {u} \ right) \ times \ mathbf {u}}$ $\mathbf {l} =\left(\nabla \times \mathbf {u} \right)\times \mathbf {u}$ называется Вектор ягненка. Уравнение импульса Коши принимает следующий вид:

∂ u ∂ t + 1 2 ∇ (u 2) + (∇ × u) × u ​​= 1 ρ ∇ ⋅ σ + f {\ displaystyle {\ frac {\ partial \ mathbf {u) }} {\ partial t}} + {\ frac {1} {2}} \ nabla \ left (u ^ {2} \ right) + (\ nabla \ times \ mathbf {u}) \ times \ mathbf {u } = {\ frac {1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} + \ mathbf {f}}

{\frac {\partial \mathbf {u} }{\partial t}}+{\frac {1}{2}}\nabla \left(u^{2}\right)+(\nabla \times \mathbf {u})\times \mathbf {u} ={\frac {1}{\rho }}\nabla \cdot {\boldsymbol {\sigma }}+\mathbf {f}

Использование тождества:

∇ ⋅ (σ ρ) = 1 ρ ∇ ⋅ σ - 1 ρ 2 σ ⋅ ∇ ρ {\ displaystyle \ nabla \ cdot \ left ({\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) = {\ frac {1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} - {\ frac {1} {\ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho}

\nabla \cdot \left({\frac {\boldsymbol {\sigma }}{\rho }}\right)={\frac {1}{\rho }}\nabla \cdot {\boldsymbol {\sigma }}-{\frac {1}{\rho ^{2}}}{\boldsymbol {\sigma }}\cdot \nabla \rho

Уравнение Коши принимает следующий вид:

∇ ⋅ (1 2 u 2 - σ ρ) - f = 1 ρ 2 σ ⋅ ∇ ρ + u × (∇ × u) - ∂ u ∂ t {\ displaystyle \ nabla \ cdot \ left ({\ frac {1} {2}} u ^ {2} - {\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) - \ mathbf {f} = {\ frac {1} { \ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho + \ mathbf {u} \ times (\ nabla \ times \ mathbf {u}) - {\ frac {\ partial \ mathbf {u}} {\ partial t}}}

\nabla \cdot \left({\frac {1}{2}}u^{2}-{\frac {\boldsymbol {\sigma }}{\rho }}\right)-\mathbf {f} ={\frac {1}{\rho ^{2}}}{\boldsymbol {\sigma }}\cdot \nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u})-{\frac {\partial \mathbf {u} }{\partial t}}

Фактически, в случае внешнего консервативное поле, определяя его потенциал φ:

∇ ⋅ (1 2 u 2 + ϕ - σ ρ) = 1 ρ 2 σ ⋅ ∇ ρ + u × (∇ × u) - ∂ u ∂ t {\ displaystyle \ nabla \ cdot \ left ({\ frac {1} {2}} u ^ {2} + \ phi - {\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) = {\ frac {1} {\ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho + \ mathbf {u} \ times (\ nabla \ times \ mathbf {u}) - { \ frac {\ partial \ mathbf {u}} {\ partial t}}}

\nabla \cdot \left({\frac {1}{2}}u^{2}+\phi -{\frac {\boldsymbol {\sigma }}{\rho }}\right)={\frac {1}{\rho ^{2}}}{\boldsymbol {\sigma }}\cdot \nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u})-{\frac {\partial \mathbf {u} }{\partial t}}

В случае установившегося потока производная скорости потока по времени исчезает, поэтому уравнение количества движения принимает вид:

∇ ⋅ (1 2 u 2 + ϕ - σ ρ) знак равно 1 ρ 2 σ ⋅ ∇ ρ + u × (∇ × u) {\ displaystyle \ nabla \ cdot \ left ({\ frac {1} {2}} u ^ {2} + \ phi - {\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) = {\ frac {1} {\ rho ^ {2}}} {\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho + \ mathbf {u} \ times (\ nabla \ times \ mathbf {u})}

\nabla \cdot \left({\frac {1}{2}}u^{2}+\phi -{\frac {\boldsymbol {\sigma }}{\rho }}\right)={\frac {1}{\rho ^{2}}}{\boldsymbol {\sigma }}\cdot \nabla \rho +\mathbf {u} \times (\nabla \times \mathbf {u})

И, проецируя уравнение импульса на направление потока, то есть вдоль линии тока , получается векторное произведение исчезает из-за тождества векторного исчисления тройного скалярного произведения :

u ⋅ ∇ ⋅ (1 2 U 2 + ϕ - σ ρ) знак равно 1 ρ 2 U ⋅ (σ ⋅ ∇ ρ) {\ displaystyle \ mathbf {u} \ cdot \ nabla \ cdot \ left ({\ frac {1} {2 }} u ^ {2} + \ phi - {\ frac {\ boldsymbol {\ sigma}} {\ rho}} \ right) = {\ frac {1} {\ rho ^ {2}}} \ mathbf {u } \ cdot ({\ boldsymbol {\ sigma}} \ cdot \ nabla \ rho)}

\mathbf {u} \cdot \nabla \cdot \left({\frac {1}{2}}u^{2}+\phi -{\frac {\boldsymbol {\sigma }}{\rho }}\right)={\frac {1}{\rho ^{2}}}\mathbf {u} \cdot ({\boldsymbol {\sigma }}\cdot \nabla \rho)

Если тензор напряжений изотропен, то входит только давление: $σ = - p I {\ displaystyle {\ boldsymbol {\ sigma}} = - p \ mathbf {I}}$ ${\boldsymbol {\sigma }}=-p\mathbf {I}$ (где I - тождественный тензор), и уравнение импульса Эйлера в случае установившейся несжимаемой жидкости принимает следующий вид:

U ⋅ ∇ (1 2 U 2 + ϕ + p ρ) + p ρ 2 U ⋅ ∇ ρ {\ displaystyle \ mathbf {u} \ cdot \ nabla \ left ({\ frac {1} {2}} u ^ { 2} + \ phi + {\ frac {p} {\ rho}} \ right) + {\ frac {p} {\ rho ^ {2}}} \ mathbf {u} \ cdot \ nabla \ rho}

\mathbf {u} \cdot \nabla \left({\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\right)+{\frac {p}{\rho ^{2}}}\mathbf {u} \cdot \nabla \rho

= 0

В случае установившейся несжимаемой жидкости уравнение массы просто:

u ⋅ ∇ ρ = 0, {\ displaystyle \ mathbf {u} \ cdot \ nabla \ rho = 0 \,,}

\mathbf {u} \cdot \nabla \rho =0\,,

то есть закон сохранения массы для установившегося потока несжимаемой жидкости утверждает, что плотность вдоль линии тока равна cons тант. Это приводит к значительному упрощению уравнения импульса Эйлера:

u ⋅ ∇ (1 2 u 2 + ϕ + p ρ) = 0 {\ displaystyle \ mathbf {u} \ cdot \ nabla \ left ({\ frac { 1} {2}} u ^ {2} + \ phi + {\ frac {p} {\ rho}} \ right) = 0}

\mathbf {u} \cdot \nabla \left({\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\right)=0

Удобство определения общего напора для поток невязкой жидкости теперь очевиден:

bl ≡ 1 2 u 2 + ϕ + p ρ, {\ displaystyle b_ {l} \ Equiv {\ frac {1} {2}} u ^ {2} + \ phi + {\ frac {p} {\ rho}} \,,}

b_{l}\equiv {\frac {1}{2}}u^{2}+\phi +{\frac {p}{\rho }}\,,

фактически, приведенное выше уравнение можно просто записать как:

u ⋅ ∇ bl = 0 {\ displaystyle \ mathbf {u} \ cdot \ nabla b_ {l} = 0}

\mathbf {u} \cdot \nabla b_{l}=0

То есть, баланс количества движения для устойчивого невязкого и несжимаемого потока во внешнем консервативном поле утверждает, что полный напор вдоль линии тока постоянен.

Безвихревые потоки

Форма Лэмба также полезна в безвихревом потоке, где curl скорости (называемой завихренностью ) ω = ∇ × u равно нулю. В этом случае член конвекции $D u / D t {\ displaystyle D \ mathbf {u} / Dt}$ $D\mathbf {u} /Dt$ сокращается до

u ⋅ ∇ u = ∇ (‖ u ‖ 2 2). {\ displaystyle \ mathbf {u} \ cdot \ nabla \ mathbf {u} = \ nabla \ left ({\ frac {\ | \ mathbf {u} \ | ^ {2}} {2}} \ right).}

{\mathbf {u}}\cdot \nabla {\mathbf {u}}=\nabla \left({\frac {\|{\mathbf {u}}\|^{2}}{2}}\right).

Напряжения

Влияние напряжения в непрерывном потоке представлено членами ∇p и ∇ · τ ; это градиенты поверхностных сил, аналогичные напряжениям в твердом теле. Здесь ∇p - это градиент давления, который возникает из-за изотропной части тензора напряжений Коши . Эта часть задается нормальными напряжениями, которые возникают почти во всех ситуациях. Анизотропная часть тензора напряжений дает ∇ · τ, которое обычно описывает вязкие силы; для несжимаемого потока это только эффект сдвига. Таким образом, τ - это тензор девиаторных напряжений, а тензор напряжений равен:

σ = - p I + τ {\ displaystyle {\ boldsymbol {\ sigma}} = -p \ mathbf {I} + {\ boldsymbol {\ tau}}}

{\boldsymbol {\sigma }}=-p\mathbf {I} +{\boldsymbol {\tau }}

где I - это единичная матрица в рассматриваемом пространстве, а τ тензор сдвига.

Все нерелятивистские уравнения сохранения импульса, такие как уравнение Навье – Стокса, можно получить, начав с уравнения импульса Коши и задав тензор напряжений через определяющее соотношение . Выражая тензор сдвига через вязкость и скорость жидкости и предполагая постоянные плотность и вязкость, уравнение импульса Коши приведет к уравнениям Навье – Стокса. Предполагая невязкий поток, уравнения Навье – Стокса можно упростить до уравнений Эйлера.

. Дивергенция тензора напряжений может быть записана как

∇ ⋅ σ = - ∇ p + ∇ ⋅ τ. {\ displaystyle \ nabla \ cdot {\ boldsymbol {\ sigma}} = - \ nabla p + \ nabla \ cdot {\ boldsymbol {\ tau}}.}

\nabla \cdot {\boldsymbol {\sigma }}=-\nabla p+\nabla \cdot {\boldsymbol {\tau }}.

Влияние градиента давления на поток заключается в ускорении поток в направлении от высокого давления к низкому давлению.

Как написано в уравнении импульса Коши, члены напряжения p и τ еще неизвестны, поэтому одно это уравнение нельзя использовать для решения задач. Помимо уравнений движения - второго закона Ньютона - необходима силовая модель, связывающая напряжения с движением потока. По этой причине предположения, основанные на естественных наблюдениях, часто применяются для определения напряжений в терминах других переменных потока, таких как скорость и плотность.

Внешние силы

Векторное поле f представляет объемные силы на единицу массы. Обычно они состоят только из ускорения силы тяжести, но могут включать и другие, например электромагнитные силы. В неинерциальных системах координат могут возникать другие «инерционные ускорения», связанные с координатами вращения.

Часто эти силы могут быть представлены как градиент некоторой скалярной величины χ, с f = ∇χ, и в этом случае они называются консервативными силами. Например, гравитация в направлении z - это градиент −ρgz. Поскольку давление от такой гравитации возникает только как градиент, мы можем включить его в член давления как объемную силу h = p - χ. Члены давления и силы в правой части уравнения Навье – Стокса становятся

- ∇ p + f = - ∇ p + ∇ χ = - ∇ (p - χ) = - ∇ h. {\ displaystyle - \ nabla p + \ mathbf {f} = - \ nabla p + \ nabla \ chi = - \ nabla \ left (p- \ chi \ right) = - \ nabla h.}

-\nabla p+{\mathbf {f}}=-\nabla p+\nabla \chi =-\nabla \left(p-\chi \right)=-\nabla h.

Также возможно включать внешние воздействия в термин «напряжение» $σ {\ displaystyle {\ boldsymbol {\ sigma}}}$ ${\boldsymbol {\sigma }}$ , а не в термин «сила тела». Это может даже включать антисимметричные напряжения (входные данные углового момента), в отличие от обычно симметричных внутренних вкладов в тензор напряжений.

Обезразмерение

Чтобы сделать уравнения безразмерными, характерная длина r 0 и характеристическая скорость u 0 должны быть определены. Их следует выбирать так, чтобы все безразмерные переменные были первого порядка. Таким образом, получены следующие безразмерные переменные:

ρ ∗ ≡ ρ ρ 0 u ∗ ≡ uu 0 r ∗ ≡ rr 0 t ∗ ≡ u 0 r 0 t ∇ ∗ ≡ r 0 ∇ f ∗ ≡ ff 0 p ∗ ≡ pp 0 τ ∗ ≡ τ τ 0 {\ Displaystyle {\ begin {align} \ rho ^ {*} \ Equiv {\ frac {\ rho} {\ rho _ {0}}} u ^ {*} \ Equiv { \ frac {u} {u_ {0}}} r ^ {*} \ Equiv {\ frac {r} {r_ {0}}} t ^ {*} \ Equiv {\ frac {u_ {0}} {r_ {0}}} t \\ [6pt] \ nabla ^ {*} \ Equiv r_ {0} \ nabla \ mathbf {f} ^ {*} \ Equiv {\ frac {\ mathbf {f} } {f_ {0}}} p ^ {*} \ Equiv {\ frac {p} {p_ {0}}} {\ boldsymbol {\ tau}} ^ {*} \ Equiv {\ frac {\ boldsymbol {\ tau}} {\ tau _ {0}}} \ end {align}}}

{\begin{aligned}\rho ^{*}\equiv {\frac {\rho }{\rho _{0}}}u^{*}\equiv {\frac {u}{u_{0}}}r^{*}\equiv {\frac {r}{r_{0}}}t^{*}\equiv {\frac {u_{0}}{r_{0}}}t\\[6pt]\nabla ^{*}\equiv r_{0}\nabla \mathbf {f} ^{*}\equiv {\frac {\mathbf {f} }{f_{0}}}p^{*}\equiv {\frac {p}{p_{0}}}{\boldsymbol {\tau }}^{*}\equiv {\frac {\boldsymbol {\tau }}{\tau _{0}}}\end{aligned}}

Подстановка этих перевернутых соотношений в уравнения импульса Эйлера дает:

ρ 0 u 0 2 r 0 ∂ ρ ∗ u ∗ ∂ t ∗ + ∇ ∗ r 0 ⋅ (ρ 0 u 0 2 ρ ∗ u ∗ ⊗ u ∗ + p 0 p ∗) = - τ 0 r 0 ∇ ∗ ⋅ τ ∗ + f 0 f ∗ {\ displaystyle { \ frac {\ rho _ {0} u_ {0} ^ {2}} {r_ {0}}} {\ frac {\ partial \ rho ^ {*} \ mathbf {u} ^ {*}} {\ partial t ^ {*}}} + {\ frac {\ nabla ^ {*}} {r_ {0}}} \ cdot \ left (\ rho _ {0} u_ {0} ^ {2} \ rho ^ {* } \ mathbf {u} ^ {*} \ otimes \ mathbf {u} ^ {*} + p_ {0} p ^ {*} \ right) = - {\ frac { \ tau _ {0}} {r_ {0}}} \ nabla ^ {*} \ cdot {\ boldsymbol {\ tau}} ^ {*} + f_ {0} \ mathbf {f} ^ {*}}

{\frac {\rho _{0}u_{0}^{2}}{r_{0}}}{\frac {\partial \rho ^{*}\mathbf {u} ^{*}}{\partial t^{*}}}+{\frac {\nabla ^{*}}{r_{0}}}\cdot \left(\rho _{0}u_{0}^{2}\rho ^{*}\mathbf {u} ^{*}\otimes \mathbf {u} ^{*}+p_{0}p^{*}\right)=-{\frac {\tau _{0}}{r_{0}}}\nabla ^{*}\cdot {\boldsymbol {\tau }}^{*}+f_{0}\mathbf {f} ^{*}

и делением на первый коэффициент:

∂ ρ ∗ u ∗ ∂ t ∗ + ∇ ∗ ⋅ (ρ ∗ u ∗ ⊗ u ∗ + p 0 ρ 0 u 0 2 p ∗) = - τ 0 ρ 0 u 0 2 ∇ ∗ ⋅ τ ∗ + е 0 р 0 U 0 2 f ∗ {\ displaystyle {\ frac {\ partial \ mathbf {\ rho} ^ {*} u ^ {*}} {\ partial t ^ {* }}} + \ nabla ^ {*} \ cdot \ left (\ rho ^ {*} \ mathbf {u} ^ {*} \ otimes \ mathbf {u} ^ {*} + {\ frac {p_ {0} } {\ rho _ {0} u_ {0} ^ {2}}} p ^ {*} \ right) = - {\ frac {\ tau _ {0}} {\ rho _ {0} u_ {0} ^ {2}}} \ nabla ^ {*} \ cdot {\ boldsymbol {\ tau}} ^ {*} + {\ frac {f_ {0} r_ {0}} {u_ {0} ^ {2}} } \ mathbf {f} ^ {*}}

{\frac {\partial \mathbf {\rho } ^{*}u^{*}}{\partial t^{*}}}+\nabla ^{*}\cdot \left(\rho ^{*}\mathbf {u} ^{*}\otimes \mathbf {u} ^{*}+{\frac {p_{0}}{\rho _{0}u_{0}^{2}}}p^{*}\right)=-{\frac {\tau _{0}}{\rho _{0}u_{0}^{2}}}\nabla ^{*}\cdot {\boldsymbol {\tau }}^{*}+{\frac {f_{0}r_{0}}{u_{0}^{2}}}\mathbf {f} ^{*}

Теперь определяем число Фруда :

F r = u 0 2 f 0 r 0, {\ displaystyle \ mathrm {Fr} = {\ frac {u_ {0} ^ {2}} {f_ {0} r_ {0}}},}

\mathrm {Fr} ={\frac {u_{0}^{2}}{f_{0}r_{0}}},

число Эйлера :

E u = p 0 ρ 0 u 0 2, {\ displaystyle \ mathrm { Eu} = {\ frac {p_ {0}} {\ rho _ {0} u_ {0} ^ {2}}},}

{\mathrm {Eu}}={\frac {p_{0}}{\rho _{0}u_{0}^{2}}},

и коэффициент поверхностного трения или один в области аэродинамики обычно называют коэффициентом сопротивления:

C f = 2 τ 0 ρ 0 u 0 2, {\ displaystyl e C _ {\ mathrm {f}} = {\ frac {2 \ tau _ {0}} {\ rho _ {0} u_ {0} ^ {2}}},}

C_{\mathrm {f} }={\frac {2\tau _{0}}{\rho _{0}u_{0}^{2}}},

, передавая соответственно объекту, т.е. плотность импульса и плотность силы :

j = ρ ug = ρ f {\ displaystyle {\ begin {align} \ mathbf {j} = \ rho \ mathbf {u} \\\ mathbf {g} = \ rho \ mathbf {f} \ end {align}}}

{\begin{aligned}\mathbf {j} =\rho \mathbf {u} \\\mathbf {g} =\rho \mathbf {f} \end{aligned}}

окончательно выражены уравнения (теперь без индексов):

уравнение импульса Коши (безразмерное консервативное форма)

∂ j ∂ T + ∇ ⋅ (1 ρ j ⊗ j + E вверх) = - C f 2 ∇ ⋅ τ + 1 F rg {\ displaystyle {\ frac {\ partial \ mathbf {j}} { \ partial t}} + \ nabla \ cdot \ left ({\ frac {1} {\ rho}} \ mathbf {j} \ otimes \ mathbf {j} + \ mathrm {Eu} \, p \ right) = - {\ frac {C _ {\ mathrm {f}}} {2}} \ nabla \ cdot {\ boldsymbol {\ tau}} + {\ frac {1} {\ mathrm {Fr}}} \ mathbf {g}}

{\frac {\partial \mathbf {j} }{\partial t}}+\nabla \cdot \left({\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +\mathrm {Eu} \,p\right)=-{\frac {C_{\mathrm {f} }}{2}}\nabla \cdot {\boldsymbol {\tau }}+{\frac {1}{\mathrm {Fr} }}\mathbf {g}

Уравнения Коши в пределе Фруда Fr → ∞ (соответствующие незначительному внешнему полю) называются свободными уравнениями Коши:

Уравнение свободного движения Коши (безразмерная консервативная форма)

∂ j ∂ t + ∇ ⋅ (1 ρ j ⊗ j + E вверх) = - С е 2 ∇ ⋅ τ {\ Displaystyle {\ frac {\ partial \ mathbf {j}} {\ partial t}} + \ nabla \ cdot \ left ({\ frac {1} {\ rho}} \ mathbf { j} \ otimes \ mathbf {j} + \ mathrm {Eu} \, p \ right) = - {\ frac {C _ {\ mathrm {f}}} {2}} \ nabla \ cdot {\ boldsymbol {\ tau }}}

{\frac {\partial \mathbf {j} }{\partial t}}+\nabla \cdot \left({\frac {1}{\rho }}\mathbf {j} \otimes \mathbf {j} +\mathrm {Eu} \,p\right)=-{\frac {C_{\mathrm {f} }}{2}}\nabla \cdot {\boldsymbol {\tau }}

и в конечном итоге могут быть уравнениями сохранения. Таким образом, предел больших чисел Фруда (низкое внешнее поле) является важным для таких уравнений и изучается с помощью теории возмущений.

Наконец, в конвективной форме уравнения следующие:

Уравнение импульса Коши (безразмерная конвективная форма)

D U D T + E U 1 ρ ∇ ⋅ σ = 1 F rf {\ displaystyle {\ frac {D \ mathbf {u}} {Dt}} + \ mathrm {Eu} \, {\ frac { 1} {\ rho}} \ nabla \ cdot {\ boldsymbol {\ sigma}} = {\ frac {1} {\ mathrm {Fr}}} \ mathbf {f}}

{\frac {D\mathbf {u} }{Dt}}+\mathrm {Eu} \,{\frac {1}{\rho }}\nabla \cdot {\boldsymbol {\sigma }}={\frac {1}{\mathrm {Fr} }}\mathbf {f}

явные трехмерные конвективные формы

Декартовы трехмерные координаты

Для асимметричных тензоров напряжений уравнения в целом принимают следующий вид:

x: ∂ ux ∂ t + ux ∂ ux ∂ x + uy ∂ ux ∂ y + uz ∂ ux ∂ z = 1 ρ (∂ σ xx ∂ x + ∂ σ yx ∂ y + ∂ σ zx ∂ z) + fxy: ∂ uy ∂ t + ux ∂ uy ∂ x + uy ∂ uy ∂ y + uz ∂ uy ∂ z = 1 ρ (∂ σ xy ∂ x + ∂ σ yy ∂ y + ∂ σ zy ∂ z) + fyz: ∂ uz ∂ t + ux ∂ uz ∂ x + uy ∂ uz ∂ y + uz ∂ uz ∂ z = 1 ρ ( ∂ σ xz ∂ x + ∂ σ yz ∂ y + ∂ σ zz ∂ z) + fz {\ displaystyle {\ begin {align} x : {\ frac { \ partial u_ {x}} {\ partial t}} + u_ {x} {\ frac {\ partial u_ {x}} {\ partial x}} + u_ {y} {\ frac {\ partial u_ {x} } {\ partial y}} + u_ {z} {\ frac {\ partial u_ {x}} {\ partial z}} = {\ frac {1} {\ rho}} \ left ({\ frac {\ partial \ sigma _ {xx}} {\ partial x}} + {\ frac {\ partial \ sigma _ {yx}} {\ partial y}} + {\ frac {\ partial \ sigma _ {zx}} {\ partial z}}\right)+f_{x}\\[8pt]y:{\frac {\partial u_{y}}{\partial t}}+u_{x}{\frac {\partial u_{ y}}{\partial x}}+u_{y}{\frac {\partial u_{y}}{\partial y}}+u_{z}{\frac {\partial u_{y}}{\partial z}}={\frac {1}{\rho }}\left({\frac {\partial \sigma _{xy}}{\partial x}}+{\frac {\partial \sigma _{yy }}{\partial y}}+{\frac {\partial \sigma _{zy}}{\partial z}}\right)+f_{y}\\[8pt]z:{\frac {\partial u_{z}}{\partial t}}+u_{x}{\frac {\partial u_{z}}{\partial x}}+u_{y}{\frac {\partial u_{z}}{ \partial y}}+u_{z}{\frac {\partial u_{z}}{\partial z}}={\frac {1}{\rho }}\left({\frac {\partial \ sigma _{xz}}{\partial x}}+{\frac {\partial \sigma _{yz}}{\partial y}}+{\frac {\partial \sigma _{zz}}{\partial z }}\ri ght)+f_{z}\end{aligned}}}

{\begin{aligned}x:{\frac {\partial u_{x}}{\partial t}}+u_{x}{\frac {\partial u_{x}}{\partial x}}+u_{y}{\frac {\partial u_{x}}{\partial y}}+u_{z}{\frac {\partial u_{x}}{\partial z}}={\frac {1}{\rho }}\left({\frac {\partial \sigma _{xx}}{\partial x}}+{\frac {\partial \sigma _{yx}}{\partial y}}+{\frac {\partial \sigma _{zx}}{\partial z}}\right)+f_{x}\\[8pt]y:{\frac {\partial u_{y}}{\partial t}}+u_{x}{\frac {\partial u_{y}}{\partial x}}+u_{y}{\frac {\p artial u_{y}}{\partial y}}+u_{z}{\frac {\partial u_{y}}{\partial z}}={\frac {1}{\rho }}\left({\frac {\partial \sigma _{xy}}{\partial x}}+{\frac {\partial \sigma _{yy}}{\partial y}}+{\frac {\partial \sigma _{zy}}{\partial z}}\right)+f_{y}\\[8pt]z:{\frac {\partial u_{z}}{\partial t}}+u_{x}{\frac {\partial u_{z}}{\partial x}}+u_{y}{\frac {\partial u_{z}}{\partial y}}+u_{z}{\frac {\partial u_{z}}{\partial z}}={\frac {1}{\rho }}\left({\frac {\partial \sigma _{xz}}{\partial x}}+{\frac {\partial \sigma _{yz}}{\partial y}}+{\frac {\partial \sigma _{zz}}{\partial z}}\right)+f_{z}\end{aligned}}

Cylindrical 3D coordinates

Below, we write the main equation in pressure-tau form assuming that the stress tensor is symmetrical ( $σ i j = σ j i ⟹ τ i j = τ j i {\displaystyle \sigma _{ij}=\sigma _{ji}\quad \Longrightarrow \quad \tau _{ij}=\tau _{ji}}$ $\sigma _{ij}=\sigma _{ji}\quad \Longrightarrow \quad \tau _{ij}=\tau _{ji}$ ):

r : ∂ u r ∂ t + u r ∂ u r ∂ r + u ϕ r ∂ u r ∂ ϕ + u z ∂ u r ∂ z − u ϕ 2 r = − 1 ρ ∂ P ∂ r + 1 r ρ ∂ ( r τ r r) ∂ r + 1 r ρ ∂ τ ϕ r ∂ ϕ + 1 ρ ∂ τ z r ∂ z − τ ϕ ϕ r ρ + f r ϕ : ∂ u ϕ ∂ t + u r ∂ u ϕ ∂ r + u ϕ r ∂ u ϕ ∂ ϕ + u z ∂ u ϕ ∂ z + u r u ϕ r = − 1 r ρ ∂ P ∂ ϕ + 1 r ρ ∂ τ ϕ ϕ ∂ ϕ + 1 r 2 ρ ∂ ( r 2 τ r ϕ) ∂ r + 1 ρ ∂ τ z ϕ ∂ z + f ϕ z : ∂ u z ∂ t + u r ∂ u z ∂ r + u ϕ r ∂ u z ∂ ϕ + u z ∂ u z ∂ z = − 1 ρ ∂ P ∂ z + 1 ρ ∂ τ z z ∂ z + 1 r ρ ∂ τ ϕ z ∂ ϕ + 1 r ρ ∂ ( r τ r z) ∂ r + f z {\displaystyle {\begin{aligned}r:{\frac {\partial u_{r}}{\partial t}}+u_{r}{\frac {\partial u_{r}}{\partial r}}+{\frac {u_{\phi }}{r}}{\frac {\partial u_{r}}{\partial \phi }}+u_{z}{\frac {\part ial u_{r}}{\partial z}}-{\frac {u_{\phi }^{2}}{r}}=-{\frac {1}{\rho }}{\frac {\partial P}{\partial r}}+{\frac {1}{r\rho }}{\frac {\partial \left(r\tau _{rr}\right)}{\partial r}}+{\frac {1}{r\rho }}{\frac {\partial \tau _{\phi r}}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial \tau _{zr}}{\partial z}}-{\frac {\tau _{\phi \phi }}{r\rho }}+f_{r}\\[8pt]\phi :{\frac {\partial u_{\phi }}{\partial t}}+u_{r}{\frac {\partial u_{\phi }}{\partial r}}+{\frac {u_{\phi }}{r}}{\frac {\partial u_{\phi }}{\partial \phi }}+u_{z}{\frac {\partial u_{\phi }}{\partial z}}+{\frac {u_{r}u_{\phi }}{r}}=-{\frac {1}{r\rho }}{\frac {\partial P}{\partial \phi }}+{\frac {1}{r\rho }}{\frac {\partial \tau _{\phi \phi }}{\partial \phi }}+{\frac {1}{r^{2}\rho }}{\frac {\partial \left(r^{2}\tau _{r\phi }\right)}{\partial r}}+{\frac {1}{\rho }}{\frac {\partial \tau _{z\phi }}{\partial z}}+f_{\phi }\\[8pt]z:{\frac {\partial u_{z}}{\partial t}}+u_{r}{\frac {\partial u_{z}}{\partial r}}+{\frac {u_{\phi }}{r}}{\fr ac {\partial u_{z}}{\partial \phi }}+u_{z}{\frac {\partial u_{z}}{\partial z}}=-{\frac {1}{\rho }}{\frac {\partial P}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial \tau _{zz}}{\partial z}}+{\frac {1}{r\rho }}{\frac {\partial \tau _{\phi z}}{\partial \phi }}+{\frac {1}{r\rho }}{\frac {\partial \left(r\tau _{rz}\right)}{\partial r}}+f_{z}\end{aligned}}}

{\begin{aligned}r:{\frac {\partial u_{r}}{\partial t}}+u_{r}{\frac {\partial u_{r}}{\partial r}}+{\frac {u_{\phi }}{r}}{\frac {\partial u_{r}}{\partial \phi }}+u_{z}{\frac {\partial u_{r}}{\partial z}}-{\frac {u_{\phi }^{2}}{r}}=-{\frac {1}{\rho }}{\frac {\partial P}{\partial r}}+{\frac {1}{r\rho }}{\frac {\partial \left(r\tau _{rr}\right)}{\partial r}}+{\frac {1}{r\rho }}{\frac {\partial \tau _{\phi r}}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial \tau _{zr}}{\partial z}}-{\frac {\tau _{\phi \phi }}{r\rho }}+f_{r}\\[8pt]\phi :{\frac {\partial u_{\phi }}{\partial t}}+u_{r}{\frac {\partial u_{\phi }}{\partial r}}+{\frac {u_{\phi }}{r}}{\frac {\partial u_{\phi }}{\partial \phi }}+u_{z}{\frac {\partial u_{\phi }}{\partial z}}+{\frac {u_{r}u_{\phi }}{r}}=-{\frac {1}{r\rho }}{\frac {\partial P}{\partial \phi }}+{\frac {1}{r\rho }}{\frac {\partial \tau _{\phi \phi }}{\partial \phi }}+{\frac {1}{r^{2}\rho }}{\frac {\partial \left(r^{2}\tau _{r\phi }\right)}{\partial r}}+{\frac {1}{\rho }}{\frac {\partial \tau _{z\phi }}{\partial z}}+f_{\phi }\\[8pt]z:{\frac {\partial u_{z}}{\partial t}}+u_{r}{\frac {\partial u_{z}}{\partial r}}+{\frac {u_{\phi }}{r}}{\frac {\partial u_{z}}{\partial \phi }}+u_{z}{\frac {\partial u_{z}}{\partial z}}=-{\frac {1}{\rho }}{\frac {\partial P}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial \tau _{zz}}{\partial z}}+{\frac {1}{r\rho }}{\frac {\partial \tau _{\phi z}}{\partial \phi }}+{\frac {1}{r\rho }}{\frac {\partial \left(r\tau _{rz}\right)}{\partial r}}+f_{z}\end{aligned}}