Эта статья о геометрической кривой. О термине, используемом в риторике, см.
Гипербола.

Гипербола - это открытая кривая с двумя ветвями, пересечение
плоскости с обеими половинами
двойного конуса. Плоскость не обязательно должна быть параллельна оси конуса; гипербола в любом случае будет симметричной.

Гипербола (красная): особенности
В математике, A гипербола ( слушать ) (прилагательное формы гиперболического, слушать ) (множественное число гиперболы, или гиперболы ( слушать )) является типом гладкого кривым, лежащим в плоскости, определяемой его геометрические свойствами или с помощью уравнений, для которых она является решением установленный. Гипербола состоит из двух частей, называемых связными компонентами или ветвями, которые являются зеркальным отображением друг друга и напоминают два бесконечных лука. Гипербола - это один из трех видов конического сечения, образованного пересечением плоскости. 

 и двойной конус. (Другие конические сечения - это парабола и эллипс. Окружность - это частный случай эллипса.) Если плоскость пересекает обе половины двойного конуса, но не проходит через вершины конусов, то коника является гиперболой..
и двойной конус. (Другие конические сечения - это парабола и эллипс. Окружность - это частный случай эллипса.) Если плоскость пересекает обе половины двойного конуса, но не проходит через вершины конусов, то коника является гиперболой..
Гиперболы возникают по-разному:
- как кривая, представляющая функцию в декартовой плоскости,

- как путь, по которому следует тень кончика солнечных часов,
- как форма открытой орбиты (в отличие от замкнутой эллиптической орбиты), такой как орбита космического корабля во время движения планеты с помощью гравитации или, в более общем смысле, любого космического корабля, превышающего скорость убегания ближайшей планеты,
- как путь кометы -призрака (которая движется слишком быстро, чтобы вернуться в Солнечную систему),
- как траектории рассеяния в виде субатомных частиц (действовал отталкивания вместо сил притяжения, но принцип тот же),
- в радионавигации, когда можно определить разницу между расстояниями до двух точек, но не сами расстояния,
и так далее.
Каждая ветвь гиперболы имеет два плеча, которые становятся более прямыми (более низкая кривизна) дальше от центра гиперболы. Противоположные по диагонали ответвления, по одному от каждой ветви, стремятся в пределе к общей линии, называемой асимптотой этих двух плеч. Итак, есть две асимптоты, пересечение которых находится в центре симметрии гиперболы, которую можно рассматривать как точку зеркала, относительно которой каждая ветвь отражается, образуя другую ветвь. В случае кривой асимптоты - это две оси координат. 
Гиперболы обладают многими аналитическими свойствами эллипсов, такими как эксцентриситет, фокус и направляющая. Обычно переписка может быть произведена только путем смены знака в каком-то термине. Многие другие математические объекты берут свое начало в гиперболе, например, гиперболические параболоиды (седловые поверхности), гиперболоиды («корзины для мусора»), гиперболическая геометрия ( знаменитая неевклидова геометрия Лобачевского ), гиперболические функции (sinh, cosh, tanh и т. Д..) и гировекторные пространства (геометрия, предложенная для использования как в теории относительности, так и в квантовой механике, которая не является евклидовой ).
СОДЕРЖАНИЕ
- 1 Этимология и история
- 2 Определения
- 2.1 Как место точек
- 2.2 Гипербола с уравнением y = A / x
- 2.3 По свойству директрисы
- 2.4 Плоское сечение конуса
- 2.5 Конструкция штифта и струны
- 2.6 Штейнеровское поколение гиперболы
- 2.7 Вписанные углы для гипербол y = a / ( x - b) + c и трехточечной формы
- 2.8 Как аффинный образ единичной гиперболы x ² - y ² = 1
- 2.9 Как аффинный образ гиперболы y = 1 / x
- 2.9.1 Касательная конструкция
- 2.9.2 Построение точки
- 2.9.3 Касательный-асимптот-треугольник
- 2.10 Возврат круга
- 2.11 Квадратное уравнение
- 3 В декартовых координатах
- 3.1 Уравнение
- 3.2 Асимптоты
- 3.3 Прямая полушария прямой кишки
- 3.4 Касательная
- 3.5 Прямоугольная гипербола
- 3.6 Параметрическое представление с гиперболическим синусом / косинусом
- 3.7 Сопряженная гипербола
- 4 В полярных координатах
- 5 Параметрические уравнения
- 6 гиперболических функций
- 7 Недвижимость
- 7.1 Касательная делит пополам угол между линиями к фокусам.
- 7.2 Середины параллельных хорд
- 7.3 Ортогональные касательные - ортоптические
- 7.4.Полярно -полярное соотношение для гиперболы
- 7.5 Другие свойства
- 8 Длина дуги
- 9 Производные кривые
- 10 Эллиптические координаты
- 11 Анализ конического сечения гиперболического вида окружностей
- 12 приложений
- 12.1 Солнечные часы
- 12.2 Мультилатерация
- 12.3 Путь, по которому следует частица
- 12.4 Уравнение Кортевега – де Фриза
- 12.5 Трисекция угла
- 12.6 Граница эффективного портфеля
- 12.7 Биохимия
- 13 Гиперболы как плоские сечения квадрик
- 14 См. Также
- 14.1 Другие конические сечения
- 14.2 Другие связанные темы
- 15 заметок
- 16 Ссылки
- 17 Внешние ссылки
Этимология и история
Слово «гипербола» происходит от греческого ὑπερβολή, что означает «переброшенный» или «чрезмерный», от которого также происходит английский термин « гипербола». Гиперболы были открыты Менахмом в его исследованиях проблемы удвоения куба, но затем были названы участками тупых конусов. Термин «гипербола», как полагают, был введен Аполлонием Пергским (ок. 262–190 до н. Э.) В его окончательной работе о конических сечениях « Коники». Названия двух других общих конических сечений, эллипса и параболы, происходят от соответствующих греческих слов, обозначающих «несовершенный» и «применяемый»; все три названия заимствованы из более ранней пифагорейской терминологии, которая относилась к сравнению стороны прямоугольников фиксированной площади с заданным отрезком линии. Прямоугольник может быть «применен» к сегменту (то есть иметь равную длину), быть короче сегмента или превышать сегмент.
Определения
Как место точек

Гипербола: определение расстоянием между точками до двух фиксированных точек (фокусов)

Гипербола: определение с круговой директрисой
Гипербола может быть определена геометрически как набор точек ( геометрическое место точек ) на евклидовой плоскости:
- Гипербола представляет собой набор точек, таким образом, что для любой точки множества, абсолютная разность расстояний до двух фиксированных точек (The фокусов) постоянна, обычно обозначается





Середина отрезка прямой, соединяющего фокусы, называется центром гиперболы. Линия, проходящая через фокусы, называется большой осью. Он содержит вершины, удаленные от центра. Расстояние фокусов до центра называется фокусным расстоянием или линейным эксцентриситетом. Частное - это эксцентриситет. 





Уравнение можно рассматривать по-другому (см. Диаграмму): если это круг со средней точкой и радиусом, то расстояние от точки правой ветви до круга равно расстоянию до фокуса: 







 называется круговой направляющей (связанной с фокусом) гиперболы. Чтобы получить левую ветвь гиперболы, нужно использовать круговую директрису, связанную с. Это свойство не следует путать с определением гиперболы с помощью директрисы (линии) ниже.
называется круговой направляющей (связанной с фокусом) гиперболы. Чтобы получить левую ветвь гиперболы, нужно использовать круговую директрису, связанную с. Это свойство не следует путать с определением гиперболы с помощью директрисы (линии) ниже. 

Гипербола с уравнением y = A / x

Вращение системы координат для описания прямоугольной гиперболы как графика функции

Три прямоугольные гиперболы с осями координат в виде красных асимптот: A = 1; пурпурный: A = 4; синий: A = 9

Если система координат xy повернута вокруг начала координат на угол и присвоены новые координаты, то. Прямоугольная гипербола (полуоси которой равны) имеет новое уравнение. Решение для урожайности






Таким образом, в системе координат xy график функции с уравнением 
-
 представляет собой прямоугольную гиперболу целиком в первом и третьем квадрантах с
представляет собой прямоугольную гиперболу целиком в первом и третьем квадрантах с
- оси координат как асимптоты,
- линия как большая ось,

- центр и полуось


- то вершины

- пол-Латус прямой кишка и радиус кривизны в вершинах

- линейный эксцентриситет и эксцентриситет


- касательной в точке


Вращение исходной гиперболы на приводит к прямоугольной гиперболе полностью во втором и четвертом квадрантах с такими же асимптотами, центром, полу-широтой прямой кишки, радиусом кривизны в вершинах, линейным эксцентриситетом и эксцентриситетом, как и в случае вращения., с уравнением 


- на полуоси

- линия как большая ось,

- то вершины

Сдвиг гиперболы с уравнением так, чтобы новый центр находился в положении, дает новое уравнение 


а новые асимптоты - и. Параметры формы остаются неизменными. 


По свойству директрисы

Гипербола: свойство директрисы

Гипербола: определение со свойством директрисы
Две прямые, удаленные от центра и параллельные малой оси, называются директрисами гиперболы (см. Диаграмму). 
Для произвольной точки гиперболы отношение расстояния до одного фокуса и соответствующей директрисы (см. Диаграмму) равно эксцентриситету: 

Доказательство для пары следует из того, что и удовлетворяют уравнению 



Второй случай доказывается аналогично.

Карандаш из конусов с общей вершиной и общей полуширокой прямой кишкой
Обратное утверждение также верно и может быть использовано для определения гиперболы (аналогично определению параболы):
Для любой точки (фокуса), любой прямой (директрисы), не проходящей через, и любого действительного числа с множеством точек (геометрическое место точек), для которых отношение расстояний до точки и до прямой равно






- это гипербола.
(Выбор дает параболу, а если и эллипс. ) 

- Доказательство
Позвольте и предположить является точкой на кривой. Директриса имеет уравнение. При соотношение дает уравнения 





-
 а также
а также 
Замена дает 

Это уравнение эллипса (), параболы () или гиперболы (). Все эти невырожденные коники имеют общее начало координат как вершину (см. Диаграмму). 


Если ввести новые параметры так, что, а затем приведенное выше уравнение станет 



которая представляет собой уравнение гиперболы с центром, осью x в качестве большой оси и большой / малой полуосью. 

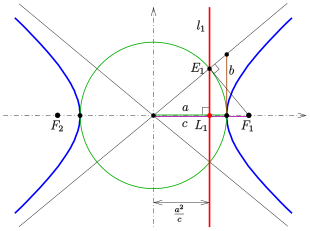
Гипербола: построение директрисы
- Построение директрисы
Поскольку точка директрисы (см. Диаграмму) и фокус инвертированы по отношению к инверсии окружности в окружности (на диаграмме зеленый). Следовательно, точка может быть построена с использованием теоремы Фалеса (не показана на диаграмме). Направляющая - это перпендикуляр к прямой, проходящей через точку. Альтернативное построение: Расчет показывает, что эта точка является пересечением асимптоты с ее перпендикуляром (см. Диаграмму). 











Как плоское сечение конуса

Гипербола (красная): два вида конуса и двух сфер Данделена d 1, d 2
Пересечение прямого двойного конуса плоскостью, не проходящей через вершину, с наклоном больше, чем наклон прямых на конусе, является гиперболой (см. Диаграмму: красная кривая). Чтобы доказать определяющее свойство гиперболы (см. Выше), используются две сферы Данделина, которые являются сферами, которые касаются конуса по окружностям, и пересекающейся плоскости (гиперболы) в точках и. Оказывается: являются фокусами гиперболы. 





- Позвольте быть произвольной точкой кривой пересечения.

- Образующая конуса, содержащего пересекает круг в точке и окружности в точке.





- Отрезки и касаются сферы и, следовательно, имеют одинаковую длину.



- Отрезки и касаются сферы и, следовательно, имеют одинаковую длину.



- Результат: не зависит от точки гиперболы, потому что независимо от того, где точки есть, должно быть на кругах, и отрезок должен пересечь вершину. Следовательно, когда точка перемещается по красной кривой (гиперболе), сегмент линии просто вращается вокруг вершины, не меняя своей длины.









Конструкция штифта и струны

Гипербола: конструкция штифта и струны
Определение гиперболы по ее фокусам и круговым направляющим (см. Выше) может быть использовано для рисования ее дуги с помощью булавок, веревки и линейки:
(0) Выберите фокусы, вершины и одну из круговых направляющих, например (круг с радиусом) (1) Линейка закреплена в точке, свободной для вращения. Точка отмечена на расстоянии. (2) Подготавливается веревка с длиной. (3) Один конец веревки прикрепляется к точке на линейке, другой конец - к точке. (4) Возьмите ручку и крепко прижмите шнур к краю линейки. (5) Вращение линейки побуждает перо нарисовать дугу правой ветви гиперболы из-за (см. Определение гиперболы с помощью круговых направляющих). 












Штейнеровское поколение гиперболы

Гипербола: поколение Штейнера

Гипербола y = 1 / x: поколение Штейнера
Следующий метод построения отдельных точек гиперболы основан на генерации Штейнера невырожденного конического сечения :
- Принимая во внимание два карандашей линий в двух точках (все строки, содержащие и, соответственно) и проективное, но не перспективное отображение из на, то точки пересечения соответствующих линий образуют невырожденную проективное коническое сечение.







Для создания точек гиперболы используются карандаши в вершинах. Позвольте быть точкой гиперболы и. Линейный сегмент делится на n равноотстоящих сегментов, и это деление проецируется параллельно диагонали в качестве направления на линейный сегмент (см. Диаграмму). Параллельная проекция является частью проективного отображения между пучками в и необходимо. Точки пересечения любых двух связанных прямых и являются точками однозначно определенной гиперболы. 










Замечание: Подразделение может быть расширено за пределы точек и для получения большего количества точек, но определение точек пересечения станет более неточным. Лучше всего расширить уже построенные точки с помощью симметрии (см. Анимацию). 

Замечание:
- Поколение Штейнера существует также для эллипсов и парабол.
- Генерацию Штейнера иногда называют методом параллелограмма, потому что можно использовать другие точки, а не вершины, которые начинаются с параллелограмма вместо прямоугольника.
Вписанные углы для гипербол y = a / ( x - b) + c и 3-точечной формы

Гипербола: теорема о вписанном угле
Гипербола с уравнением однозначно определяется тремя точками с разными координатами x и y. Простой способ определить параметры формы использует теорему о вписанном угле для гипербол: 


- Чтобы измерить угол между двумя линиями с помощью уравнений в этом контексте, используется частное


Аналогично теореме о вписанном угле для окружностей получаем
Теорема о вписанном угле для гипербол:,:
- Для четырех точек (см. Диаграмму) верно следующее утверждение:

- Четыре точки находятся на гиперболе с уравнением тогда и только тогда, когда углы равны и равны в смысле измерения выше. Это означает, что если




(Доказательство: прямое вычисление. Если точки находятся на гиперболе, можно предположить, что уравнение гиперболы есть.) 
Следствием теоремы о вписанном угле для гипербол является
Трехточечная форма уравнения гиперболы:
- Уравнение гиперболы, определяемой 3 точками, является решением уравнения


- для.

Как аффинный образ единичной гиперболы x ² - y ² = 1

Гипербола как аффинный образ единичной гиперболы
Другое определение гиперболы использует аффинные преобразования :
- Любая гипербола - это аффинный образ единичной гиперболы с уравнением.

- параметрическое представление
Аффинное преобразование евклидовой плоскости имеет вид, где - регулярная матрица (ее определитель не равен 0) и - произвольный вектор. Если - векторы-столбцы матрицы, единичная гипербола отображается на гиперболу 






 - центр, точка гиперболы и касательный вектор в этой точке.
- центр, точка гиперболы и касательный вектор в этой точке. 

- вершины
Обычно векторы не перпендикулярны. Это означает, что в общем случае это не вершины гиперболы. Но укажите направление асимптот. Касательный вектор в точке равен 




Поскольку в вершине касательная перпендикулярна большой оси гиперболы, параметр вершины получается из уравнения 

и, следовательно, из

который дает

( Были использованы формулы.) 
Две вершины гиперболы - это 
- неявное представление
Решая параметрическое представление по правилу Крамера и используя, получаем неявное представление 

-
 .
.
- гипербола в космосе
Определение гиперболы в этом разделе дает параметрическое представление произвольной гиперболы, даже в пространстве, если можно быть векторами в пространстве. 
Как аффинный образ гиперболы y = 1 / x

Гипербола как аффинный образ y = 1 / x
Поскольку единичная гипербола аффинно эквивалентна гиперболе, произвольную гиперболу можно рассматривать как аффинный образ (см. Предыдущий раздел) гиперболы.



 - центр гиперболы, векторы имеют направления асимптот и являются точкой гиперболы. Касательный вектор
- центр гиперболы, векторы имеют направления асимптот и являются точкой гиперболы. Касательный вектор 


В вершине касательная перпендикулярна большой оси. Следовательно

а параметр вершины равен
![{\ displaystyle t_ {0} = \ pm {\ sqrt [{4}] {\ tfrac {{\ vec {f}} _ {2} ^ {2}} {{\ vec {f}} _ {1} ^ {2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/889e751d77a1dfdfeccce6f0b5da5b35970c86aa)
 эквивалентно и являются вершинами гиперболы.
эквивалентно и являются вершинами гиперболы. 

Следующие свойства гиперболы легко доказываются с использованием представления гиперболы, введенного в этом разделе.
Касательная конструкция

Построение касательной: асимптоты и P даны → касательная
Касательный вектор можно переписать путем факторизации:

Это означает, что
- диагональ параллелограмма параллельна касательной в точке гиперболы (см. диаграмму).



Это свойство позволяет построить касательную в точке гиперболы.
Это свойство гиперболы является аффинной версией 3-точечного вырождения теоремы Паскаля.
- Площадь серого параллелограмма
Площадь серого параллелограмма на приведенной выше диаграмме равна 

и, следовательно, не зависит от точки. Последнее уравнение следует из расчета для случая, когда - вершина, а гипербола в ее каноническом виде


Конструкция точки

Построение точки: заданы асимптоты и P 1 → P 2
Для гиперболы с параметрическим представлением (для простоты центр - начало координат) верно следующее: 
- Для любых двух точек точки


- коллинеарны центру гиперболы (см. диаграмму).
Простое доказательство является следствием уравнения. 
Это свойство дает возможность строить точки гиперболы, если заданы асимптоты и одна точка.
Это свойство гиперболы является аффинной версией 4-точечного вырождения теоремы Паскаля.
Касательный-асимптот-треугольник

Гипербола: касательная-асимптоты-треугольник
Для простоты центр гиперболы может быть началом координат, а векторы имеют одинаковую длину. Если последнее предположение не выполняется, можно сначала применить преобразование параметров (см. Выше), чтобы сделать предположение верным. Отсюда вершины, охватывающие малую ось, и получается и. 




Для точек пересечения касательной в точке с асимптотами получаются точки 

Площадь треугольника может быть вычислена с помощью 2 × 2 детерминанта: 

(см. правила для определителей ). площадь ромба, образованного. Площадь ромба равна половине произведения его диагоналей. Диагонали - это полуоси гиперболы. Следовательно: 


- Площадь треугольника не зависит от точки гиперболы:


Возврат круга
Возвратно - поступательное движение из круга B в круге C всегда дает коническое сечение, таких как гиперболы. Процесс «возвратно-поступательного движения по кругу C » состоит в замене каждой линии и точки геометрической фигуры их соответствующими полюсами и полюсами соответственно. Полюс линии является инверсией ее ближайшей точки к окружности С, в то время как полярные точек есть обратная, а именно, линия, ближайшая точка С является инверсией точки.
Эксцентриситет конического сечения, полученного возвратно - поступательное движение представляет собой отношение расстояния между центрами два окружностей с радиусом R от взаимности окружности С. Если B и C представляют собой точки в центрах соответствующих окружностей, то

Так как эксцентриситет гиперболы всегда больше, чем один, центр В должен лежать за пределами возвратно - поступательным движением окружности С.
Это определение подразумевает, что гипербола является как локусом полюсов касательных к окружности B, а также конверт полярных линий точек на B. И наоборот, окружность B - это оболочка полярных точек на гиперболе и геометрическое место полюсов касательных прямых к гиперболе. Две касательные к B не имеют (конечных) полюсов, потому что они проходят через центр C возвратно-поступательной окружности C ; поляры соответствующих точек касания на B являются асимптотами гиперболы. Две ветви гиперболы соответствуют двум частям окружности B, разделенным этими точками касания.
Квадратное уровненеие
Гиперболу также можно определить как уравнение второй степени в декартовых координатах ( x, y) на плоскости,

при условии, что константы A xx, A xy, A yy, B x, B y и C удовлетворяют определяющему условию

Этот определитель условно называют дискриминантом конического сечения.
Частный случай гиперболы - вырожденной гиперболы, состоящей из двух пересекающихся прямых, - возникает, когда другой определитель равен нулю:

Этот определитель Δ иногда называют дискриминантом конического сечения.
Учитывая приведенную выше общую параметризацию гиперболы в декартовых координатах, эксцентриситет может быть найден с помощью формулы в разделе Коники # Эксцентриситет в терминах коэффициентов.
Центр ( x c, y c) гиперболы можно определить по формулам


В терминах новых координат, ξ = x - x c и η = y - y c, определяющее уравнение гиперболы может быть записано

Главные оси гиперболы составляют угол φ с положительной осью x, которая задается формулой

Поворот осей координат так, чтобы ось x была выровнена с поперечной осью, приводит уравнение к его канонической форме

Большая и малая полуоси a и b определяются уравнениями


где λ 1 и λ 2 являются корни этого квадратного уравнения

Для сравнения соответствующее уравнение для вырожденной гиперболы (состоящей из двух пересекающихся прямых) имеет вид

Касательная к данной точке ( x 0, y 0) на гиперболе определяется уравнением

где E, F и G определены как



Нормаль к гиперболе в той же точке задается уравнением

Нормальная линия перпендикулярна касательной, и обе проходят через одну и ту же точку ( x 0, y 0).
Из уравнения

левый фокус и правый фокус где e - эксцентриситет. Обозначим расстояния от точки ( x, y) до левого и правого фокусов как и Для точки на правой ветви, 




а для точки на левой ветви

Это можно доказать следующим образом:
Если ( x, y) - точка на гиперболе, расстояние до левой фокальной точки равно

Расстояние до правой фокальной точки составляет

Если ( x, y) - точка на правой ветви гиперболы, то и 


Вычитая эти уравнения, получаем

Если ( x, y) - точка на левой ветви гиперболы, то и 


Вычитая эти уравнения, получаем

В декартовых координатах
Уравнение
Если декартовы координаты вводятся так, что начало координат является центром гиперболы, а ось x является большой осью, то гипербола называется открывающейся с востока на запад и
- то фокусы являются точками,

- что вершины являются.

Для произвольной точки расстояния до фокуса является и вторым фокусом. Следовательно, точка находится на гиперболе, если выполняется следующее условие 





Удалите квадратные корни подходящими квадратами и используйте соотношение, чтобы получить уравнение гиперболы: 

Это уравнение называется канонической формой гиперболы, потому что любая гипербола, независимо от ее ориентации относительно декартовых осей и независимо от положения ее центра, может быть преобразована в эту форму заменой переменных, давая гиперболу, которая является соответствует оригиналу (см. ниже).
Оси симметрии или главные оси - это поперечная ось (содержащая отрезок длины 2 a с концами в вершинах) и сопряженная ось (содержащая отрезок длины 2 b, перпендикулярный поперечной оси и со средней точкой в центре гиперболы).. В отличие от эллипса, гиперболы имеет только две вершины:. Две точки на сопряженных осях не лежат на гиперболе. 

Из уравнения следует, что гипербола симметрична относительно обеих координатных осей и, следовательно, симметрична относительно начала координат.
Эксцентриситет
Для гиперболы в приведенной выше канонической форме эксцентриситет определяется выражением

Две гиперболы геометрически подобны друг другу - это означает, что они имеют одинаковую форму, так что одна может быть преобразована в другую жесткими движениями влево и вправо, вращением, зеркальным отображением и масштабированием (увеличением) - тогда и только тогда, когда у них такая же неординарность.
Асимптоты

Гипербола: полуоси a, b, линейный эксцентриситет c, полу-широчайшая прямая кишка p

Гипербола: 3 объекта
Решение уравнения (выше) гиперболы для доходностей 

Из этого следует, что гипербола приближается к двум прямым

для больших значений. Эти две прямые пересекаются в центре (начале координат) и называются асимптотами гиперболы.

По второму рисунку видно, что
-
 Перпендикулярное расстояние от фокуса до асимптоты либо является (пол-малой ось).
Перпендикулярное расстояние от фокуса до асимптоты либо является (пол-малой ось).
Из нормальной формы асимптот Гессе и уравнения гиперболы получаем: 
-
 Произведение расстояний от точки на гиперболу к оба асимптоте является константой, которая также может быть записана в терминах эксцентриситета е как
Произведение расстояний от точки на гиперболу к оба асимптоте является константой, которая также может быть записана в терминах эксцентриситета е как

Из уравнения гиперболы (см. Выше) можно вывести: 
-
 Продукт склонов линий от точки Р до двух вершин является постоянным
Продукт склонов линий от точки Р до двух вершин является постоянным
Кроме того, из (2) выше можно показать, что
-
 Произведение расстояний от точки на гиперболе до асимптот вдоль линий, параллельных асимптотам, есть константа
Произведение расстояний от точки на гиперболе до асимптот вдоль линий, параллельных асимптотам, есть константа
Полу-латусная прямая кишка
Длина хорды через один из фокусов, перпендикулярная большой оси гиперболы, называется прямой кишкой. Одна его половина - это прямая полу-латусная мышца. Расчет показывает 

Прямая кишка полу-латуса также может рассматриваться как радиус кривизны в вершинах. 
Касательная
Самый простой способ определить уравнение касательной в точке - неявно дифференцировать уравнение гиперболы. Обозначая dy / dx как y ′, это дает 


Относительно, уравнение касательной в точке имеет вид 


Определенная касательная линия отличает гиперболу от других конических секций. Пусть f - расстояние от вершины V (как на гиперболе, так и на ее оси, проходящей через два фокуса) до ближайшего фокуса. Тогда расстояние по линии, перпендикулярной этой оси, от этого фокуса до точки P на гиперболе будет больше 2 f. Касательная к гиперболе в точке P пересекает эту ось в точке Q под углом ∠PQV более 45 °.
Прямоугольная гипербола
В этом случае гипербола называется прямоугольной (или равносторонней), потому что ее асимптоты пересекаются под прямым углом. В этом случае линейный эксцентриситет равен эксцентриситету и полу-латусной прямой кишке. График уравнения представляет собой прямоугольную гиперболу. 




Параметрическое представление с гиперболическим синусом / косинусом
Используя функции гиперболического синуса и косинуса, можно получить параметрическое представление гиперболы, которое аналогично параметрическому представлению эллипса: 


которое удовлетворяет декартову уравнению, поскольку 
Дальнейшие параметрические представления приведены в разделе « Параметрические уравнения» ниже.

Здесь a = b = 1, что дает
единичную гиперболу синим цветом и сопряженную ей гиперболу зеленым цветом, разделяя одни и те же красные асимптоты.
Сопряженная гипербола
Обменяем и получаем уравнение сопряженной гиперболы (см. Диаграмму): 

-
 также написано как
также написано как 
В полярных координатах

Гипербола: полярные координаты с полюсом = фокус

Гипербола: полярные координаты с полюсом = центром
Для полюса = фокус:
Полярные координаты, используемые чаще всего для гиперболы, определяются относительно декартовой системы координат, которая имеет начало в фокусе, а ось x указывает на начало «канонической системы координат», как показано на первой диаграмме. В этом случае угол называется истинной аномалией. 
Относительно этой системы координат имеем

а также

для полюса = центр:
С полярными координатами относительно «канонической системы координат» (см. Вторую диаграмму) мы имеем

Для правой ветви гиперболы диапазон равен 

Параметрические уравнения
Гипербола с уравнением может быть описана несколькими параметрическими уравнениями: 

-
 ( рациональное представление).
( рациональное представление). 
- Наклон касательной как параметр:
- Параметрическое представление, использующее наклон касательной в точке гиперболы, может быть получено аналогично случаю эллипса: заменить в случае эллипса на и использовать формулы для гиперболических функций. Один получает




-
 это верхняя и нижняя половина гиперболы. Точки с вертикальными касательными (вершины) не покрываются представлением.
это верхняя и нижняя половина гиперболы. Точки с вертикальными касательными (вершины) не покрываются представлением.

- Уравнение касательной в точке:


- Это описание касательных гиперболы является важным инструментом для определения ортоптики гиперболы.
Гиперболические функции
Основная статья:
гиперболические функции 
Луч, проходящий через
единичную гиперболу в точке, где вдвое больше площади между лучом, гиперболой и осью. Для точек на гиперболе ниже оси - площадь считается отрицательной.





Подобно тому, как тригонометрические функции определены в терминах единичной окружности, гиперболические функции определены в терминах единичной гиперболы, как показано на этой диаграмме. В единичном круге угол (в радианах) равен удвоенной площади кругового сектора, который образует этот угол. Аналогичный гиперболический угол определяется как удвоенная площадь гиперболического сектора.
Пусть будет вдвое больше площади между осью и лучом, проходящим через начало координат, пересекающим единичную гиперболу, и определим как координаты точки пересечения. Тогда площадь гиперболического сектора равна площади треугольника за вычетом изогнутой области за вершиной в: 




который упрощается до гиперболического косинуса площади

Решение для дает экспоненциальную форму гиперболического косинуса: 

От одного получает 

и обратная ему площадь гиперболического синуса :

Другие гиперболические функции определяются в соответствии с гиперболическим косинусом и гиперболическим синусом, например,

Характеристики
Касательная делит пополам угол между линиями к фокусам

Гипербола: касательная делит пополам линии, проходящие через фокусы
Касательная в точке делит угол между линиями пополам. 

- Доказательство
Позвольте быть точкой на линии с расстоянием до фокуса (см. Диаграмму, это большая полуось гиперболы). Линия - это биссектриса угла между линиями. Чтобы доказать, что это касательная линия в точке, проверяется, что любая точка на прямой, отличная от, не может находиться на гиперболе. Следовательно, имеет только общую точку с гиперболой и, следовательно, является касательной в точке. Из диаграммы и неравенства треугольника один признает, что имеет место, что означает:. Но если это точка гиперболы, разница должна быть. 


















Середины параллельных хорд

Гипербола: середины параллельных хорд лежат на одной прямой.

Гипербола: середина хорды - это середина соответствующей хорды асимптот.
Середины параллельных хорд гиперболы лежат на прямой, проходящей через центр (см. Диаграмму).
Точки любой хорды могут лежать на разных ветвях гиперболы.
Доказательство свойства на мидпойнтах лучше всего проводить для гиперболы. Поскольку любая гипербола является аффинным изображением гиперболы (см. Раздел ниже), а аффинное преобразование сохраняет параллелизм и середины отрезков прямых, это свойство верно для всех гипербол: для двух точек гиперболы



- середина аккорда

- наклон хорды

Для параллельных хорд наклон постоянный, а середины параллельных хорд лежат на прямой 
Следствие: для любой пары точек хорды существует косое отражение с осью (набором неподвижных точек), проходящей через центр гиперболы, которая меняет местами точки и оставляет гиперболу (в целом) неподвижной. Косое отражение - это обобщение обычного отражения поперек линии, где все пары точка-изображение находятся на линии, перпендикулярной к. 



Поскольку косое отражение оставляет гиперболу неподвижной, пара асимптот также остается фиксированной. Следовательно, середина хорды также делит пополам соответствующий отрезок прямой между асимптотами. Это значит что. Это свойство можно использовать для построения дальнейших точек гиперболы, если заданы точка и асимптоты. 





Если хорда вырождается в касательную, то точка касания делит отрезок прямой между асимптотами на две половины.
Ортогональные касательные - ортоптические

Гипербола с ее ортопедическим (пурпурным) Основная статья:
Ортоптика (геометрия) Для гиперболы точки пересечения ортогональных касательных лежат на окружности. Этот круг называется ортоптиком данной гиперболы. 

Касательные могут принадлежать точкам на разных ветвях гиперболы.
В случае отсутствия пар ортогональных касательных. 
Полярно-полярное соотношение для гиперболы

Гипербола: полярно-полярное отношение
Любую гиперболу можно описать в подходящей системе координат уравнением. Уравнение касательной в точке гиперболы: Если разрешить точку быть произвольной точкой, отличной от начала координат, то 



- точка отображается на линию, а не через центр гиперболы.


Это отношение между точками и линиями является взаимно однозначным.
В обратной функции карты
- линия на точку и


- линия на точку


Такое отношение между точками и линиями, порожденными коникой, называется полярно-полярным отношением или просто полярностью. Полюс - это точка, полярная линия. См. Полярный и полярный.
Расчетным путем проверяются следующие свойства полярно-полярной связи гиперболы:
- Для точки (полюса) на гиперболе поляра является касательной в этой точке (см. Диаграмму:).

- Для полюса вне гиперболы точки пересечения его поляры с гиперболой являются точками касания двух проходящих касательных (см. Диаграмму:).



- Для точки внутри гиперболы полярная точка не имеет общей точки с гиперболой. (см. диаграмму:).

Примечания:
- Точка пересечения двух полярных полюсов ( например:) - это полюс прямой, проходящей через их полюса (здесь:).


- Фокусы и соответственно и направляющие и соответственно принадлежат парам полюса и полюса.




Отношения между полюсами и полюсами существуют также для эллипсов и парабол.
Прочие свойства
- Следующие элементы являются параллельными : (1) окружность, проходящая через фокусы гиперболы с центром в центре гиперболы; (2) любая из прямых, касающихся гиперболы в вершинах; и (3) любая из асимптот гиперболы.
- Следующие элементы также совпадают: (1) круг с центром в центре гиперболы и проходящий через вершины гиперболы; (2) либо директриса; и (3) любая из асимптот.
Длина дуги
Длина дуги гиперболы не имеет выражения в замкнутой форме. Верхняя половина гиперболы может быть параметризована как

Тогда интеграл, дающий длину дуги от до, может быть вычислен численно : 



После использования подстановки это также можно представить с помощью эллиптического интеграла второго рода с параметром: 

![{\ displaystyle s = -ib {\ Biggr [} E \ left (iz \, {\ Biggr |} \, 1 + {\ frac {a ^ {2}} {b ^ {2}}} \ right) { \ Biggr]} _ {\ operatorname {arcosh} {\ frac {x_ {1}} {a}}} ^ {\ operatorname {arcosh} {\ frac {x_ {2}} {a}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9da98f39af4a19ebaadb989066b99d613939b09c)
Производные кривые
 Синусоидальные спирали
Синусоидальные спирали : равносторонняя
гипербола ( n = −2), прямая ( n = −1),
парабола ( n = - 1/2),
кардиоидный ( n =1/2),
круг ( n = 1) и
лемниската Бернулли ( n = 2), где r
n = −1
n cos nθ в
полярных координатах и их эквиваленты в
прямоугольных координатах.
Некоторые другие кривые могут быть получены из гиперболы путем инверсии, так называемые обратные кривые гиперболы. Если центр инверсии выбран как собственный центр гиперболы, обратная кривая будет лемнискатой Бернулли ; лемниската - это также оболочка из кругов с центром на прямоугольной гиперболе, проходящая через начало координат. Если центр инверсии выбран в фокусе или вершине гиперболы, получающиеся обратные кривые будут лимитом или строфоидом соответственно.
Эллиптические координаты
Семейство софокусных гипербол является основой системы эллиптических координат в двух измерениях. Эти гиперболы описываются уравнением

где фокусы расположены на расстоянии c от начала координат по оси x, и где θ - угол асимптоты с осью x. Каждая гипербола в этом семействе ортогональна любому эллипсу с одним и тем же фокусом. Эта ортогональность может быть продемонстрирована конформным отображением декартовой системы координат w = z + 1 / z, где z = x + iy - исходные декартовы координаты, а w = u + iv - координаты после преобразования.
Другие ортогональные двумерные системы координат, включающие гиперболы, могут быть получены с помощью других конформных отображений. Например, отображение w = z 2 преобразует декартову систему координат в два семейства ортогональных гипербол.
Анализ конического сечения гиперболического вида окружностей
 Центральная проекция
Центральная проекция кругов на сферу: центр проекции O находится внутри сферы, плоскость изображения красная. В качестве изображений кругов получается круг (пурпурный), эллипсы, гиперболы и линии. Частный случай параболы в этом примере не фигурирует. (Если бы центр O находился на сфере, все изображения кругов были бы кругами или линиями; см.
Стереографическую проекцию ).
Помимо обеспечения единообразного описания кругов, эллипсов, парабол и гипербол, конические сечения также можно понимать как естественную модель геометрии перспективы в случае, когда просматриваемая сцена состоит из кругов или, в более общем смысле, эллипса. Наблюдателем обычно является камера или человеческий глаз, а изображение сцены представляет собой центральную проекцию на плоскость изображения, то есть все проекционные лучи проходят через фиксированную точку O, центр. Плоскость линзы является плоскость, параллельная плоскости изображения на линзах O.
Образ круга c есть
- а) круг, если круг c находится в особом положении, например, параллельно плоскости изображения и др. (см. стереографическую проекцию),
- б) эллипс, если c не имеет общей точки с плоскостью линзы,
- c) парабола, если c имеет одну общую точку с плоскостью линзы и
- г) гипербола, если c имеет две общие точки с плоскостью линзы.
(Особые положения, в которых плоскость окружности содержит точку O, опускаются.)
Эти результаты можно понять, если осознавать, что процесс проецирования можно увидеть в два этапа: 1) круг c и точка O создают конус, который 2) разрезается плоскостью изображения, чтобы создать изображение.
Человек видит гиперболу всякий раз, когда видит часть круга, пересеченного плоскостью линзы. Неспособность видеть большую часть ветвей видимой ветви в сочетании с полным отсутствием второй ветви делает практически невозможным для зрительной системы человека распознать связь с гиперболами.
Приложения

Гиперболы как линии склонения на солнечных часах

Зона контакта
ударной волны горизонтального сверхзвукового самолета на плоской земле (желтый) является частью гиперболы, поскольку земля пересекает конус параллельно его оси.
Солнечные часы
Гиперболы можно увидеть на многих солнечных часах. В любой день солнце вращается по кругу на небесной сфере, и его лучи, падая на точку на солнечных часах, образуют конус света. Пересечение этого конуса с горизонтальной плоскостью земли образует коническое сечение. На большинстве населенных широт и в большую часть времени года это коническое сечение представляет собой гиперболу. На практике тень от наконечника шеста очерчивает гиперболу на земле в течение дня (этот путь называется линией склонения). Форма этой гиперболы меняется в зависимости от географической широты и времени года, поскольку эти факторы влияют на конус солнечных лучей относительно горизонта. Собрание таких гипербол за целый год в данном месте греки называли пелекиноном, так как он напоминает двуручный топор.
Мультилатерация
Гипербола является основой для решения задач мультилатерации, задачи определения местоположения точки по разнице ее расстояний до заданных точек - или, что то же самое, по разнице во времени прихода синхронизированных сигналов между точкой и заданными точками. Такие проблемы важны в судоходстве, особенно на воде; Судно может определить свое местоположение по разнице во времени прибытия сигналов от передатчиков LORAN или GPS. И наоборот, самонаводящийся радиомаяк или любой передатчик можно определить путем сравнения времени прихода его сигналов на двух отдельных приемных станциях; такие методы могут использоваться для отслеживания объектов и людей. В частности, множество возможных положений точки, которая имеет разность расстояний 2 a от двух заданных точек, является гиперболой разделения вершин 2 a, фокусами которой являются две заданные точки.
Путь, по которому идет частица
Путь, по которому проходит любая частица в классической задаче Кеплера, представляет собой коническое сечение. В частности, если полная энергия E частицы больше нуля (то есть, если частица не связана), путь такой частицы представляет собой гиперболу. Это свойство полезно при изучении атомных и субатомных сил путем рассеяния частиц высокой энергии; например, эксперимент Резерфорд показал существование атомного ядра, исследуя рассеяние альфа - частицы из золота атомов. Если пренебречь короткодействующими ядерными взаимодействиями, атомное ядро и альфа-частица взаимодействуют только посредством кулоновской силы отталкивания, которая удовлетворяет требованию закона обратных квадратов для задачи Кеплера.
Уравнение Кортевега – де Фриза
Гиперболическая триггерная функция появляется как одно из решений уравнения Кортевега – де Фриза, которое описывает движение солитонной волны в канале. 
Трисекция угла

Трисекция угла (AOB) с использованием гиперболы с эксцентриситетом 2 (желтая кривая)
Как впервые показал Аполлоний Пергский, гиперболу можно использовать, чтобы разрезать пополам любой угол - хорошо изученная проблема геометрии. Принимая во внимание угол, сначала нарисовать окружность с центром в его вершине O, который пересекает стороны угла в точках A и B. Затем нарисуйте отрезок прямой с конечными точками A и B и его серединный перпендикуляр. Построить гиперболу эксцентриситета е = 2 с, как директрисы и B в качестве фокуса. Пусть P - пересечение (верхнее) гиперболы с окружностью. Угол POB делит угол AOB пополам. 

Чтобы доказать это, отражают отрезок линии OP относительно линии получения точки P» как образ P. Сегмент AP ' имеет ту же длину, что и сегмент BP из-за отражения, в то время как сегмент PP' имеет ту же длину, что и сегмент BP из-за эксцентриситета гиперболы. Поскольку OA, OP ', OP и OB являются радиусами одного и того же круга (и, следовательно, имеют одинаковую длину), треугольники OAP', OPP ' и OPB все совпадают. Следовательно, угол был разделен на три части, поскольку 3 × POB = AOB. 
Граница эффективного портфеля
В теории портфелей локус эффективных портфелей со средним отклонением (так называемая эффективная граница) - это верхняя половина открывающейся на восток ветви гиперболы, построенной с горизонтальным графиком стандартного отклонения доходности портфеля и вертикальным графиком его ожидаемого значения; согласно этой теории, все рациональные инвесторы выбрали бы портфель, характеризуемый некоторой точкой в этом локусе.
Биохимия
В биохимии и фармакологии, то уравнение Хилла и уравнения Хилла-Ленгмюра соответственно описывают биологические реакции и образование белковых комплексов лиганд- как функции концентрации лиганда. Оба они представляют собой прямоугольные гиперболы.
Гиперболы как плоские сечения квадрик
Гиперболы выглядят как плоские секции следующих квадрик :
Смотрите также
Прочие конические сечения
Другие связанные темы
Примечания
использованная литература
- Казаринов, Николас Д. (2003), Правитель и Круг, Минеола, Нью-Йорк: Довер, ISBN 0-486-42515-0
- Окли, Колорадо, доктор философии (1944), Схема исчисления, Нью-Йорк: Barnes amp; Noble
- Protter, Murray H.; Морри, Чарльз Б., младший (1970), Вычисление колледжа с аналитической геометрией (2-е изд.), Чтение: Addison-Wesley, LCCN 76087042
внешние ссылки
 Гипербола - это открытая кривая с двумя ветвями, пересечение плоскости с обеими половинами двойного конуса. Плоскость не обязательно должна быть параллельна оси конуса; гипербола в любом случае будет симметричной.
Гипербола - это открытая кривая с двумя ветвями, пересечение плоскости с обеими половинами двойного конуса. Плоскость не обязательно должна быть параллельна оси конуса; гипербола в любом случае будет симметричной.  Гипербола (красная): особенности
Гипербола (красная): особенности ![]()
![]()
![]() и двойной конус. (Другие конические сечения - это парабола и эллипс. Окружность - это частный случай эллипса.) Если плоскость пересекает обе половины двойного конуса, но не проходит через вершины конусов, то коника является гиперболой..
и двойной конус. (Другие конические сечения - это парабола и эллипс. Окружность - это частный случай эллипса.) Если плоскость пересекает обе половины двойного конуса, но не проходит через вершины конусов, то коника является гиперболой.. Гипербола: определение расстоянием между точками до двух фиксированных точек (фокусов)
Гипербола: определение расстоянием между точками до двух фиксированных точек (фокусов)  Гипербола: определение с круговой директрисой
Гипербола: определение с круговой директрисой  Вращение системы координат для описания прямоугольной гиперболы как графика функции
Вращение системы координат для описания прямоугольной гиперболы как графика функции  Три прямоугольные гиперболы с осями координат в виде красных асимптот: A = 1; пурпурный: A = 4; синий: A = 9
Три прямоугольные гиперболы с осями координат в виде красных асимптот: A = 1; пурпурный: A = 4; синий: A = 9  Гипербола: свойство директрисы
Гипербола: свойство директрисы  Гипербола: определение со свойством директрисы
Гипербола: определение со свойством директрисы  Карандаш из конусов с общей вершиной и общей полуширокой прямой кишкой
Карандаш из конусов с общей вершиной и общей полуширокой прямой кишкой  Гипербола: построение директрисы
Гипербола: построение директрисы  Гипербола (красная): два вида конуса и двух сфер Данделена d 1, d 2
Гипербола (красная): два вида конуса и двух сфер Данделена d 1, d 2  Гипербола: конструкция штифта и струны
Гипербола: конструкция штифта и струны  Гипербола: поколение Штейнера
Гипербола: поколение Штейнера  Гипербола y = 1 / x: поколение Штейнера
Гипербола y = 1 / x: поколение Штейнера  Гипербола: теорема о вписанном угле
Гипербола: теорема о вписанном угле  Гипербола как аффинный образ единичной гиперболы
Гипербола как аффинный образ единичной гиперболы  Гипербола как аффинный образ y = 1 / x
Гипербола как аффинный образ y = 1 / x  Построение касательной: асимптоты и P даны → касательная
Построение касательной: асимптоты и P даны → касательная  Построение точки: заданы асимптоты и P 1 → P 2
Построение точки: заданы асимптоты и P 1 → P 2  Гипербола: касательная-асимптоты-треугольник
Гипербола: касательная-асимптоты-треугольник  Гипербола: полуоси a, b, линейный эксцентриситет c, полу-широчайшая прямая кишка p
Гипербола: полуоси a, b, линейный эксцентриситет c, полу-широчайшая прямая кишка p  Гипербола: 3 объекта
Гипербола: 3 объекта  Здесь a = b = 1, что дает единичную гиперболу синим цветом и сопряженную ей гиперболу зеленым цветом, разделяя одни и те же красные асимптоты.
Здесь a = b = 1, что дает единичную гиперболу синим цветом и сопряженную ей гиперболу зеленым цветом, разделяя одни и те же красные асимптоты.  Гипербола: полярные координаты с полюсом = фокус
Гипербола: полярные координаты с полюсом = фокус  Гипербола: полярные координаты с полюсом = центром
Гипербола: полярные координаты с полюсом = центром  Луч, проходящий через единичную гиперболу в точке, где вдвое больше площади между лучом, гиперболой и осью. Для точек на гиперболе ниже оси - площадь считается отрицательной.
Луч, проходящий через единичную гиперболу в точке, где вдвое больше площади между лучом, гиперболой и осью. Для точек на гиперболе ниже оси - площадь считается отрицательной.  Гипербола: касательная делит пополам линии, проходящие через фокусы
Гипербола: касательная делит пополам линии, проходящие через фокусы  Гипербола: середины параллельных хорд лежат на одной прямой.
Гипербола: середины параллельных хорд лежат на одной прямой.  Гипербола: середина хорды - это середина соответствующей хорды асимптот.
Гипербола: середина хорды - это середина соответствующей хорды асимптот.  Гипербола с ее ортопедическим (пурпурным) Основная статья: Ортоптика (геометрия)
Гипербола с ее ортопедическим (пурпурным) Основная статья: Ортоптика (геометрия)  Гипербола: полярно-полярное отношение
Гипербола: полярно-полярное отношение  Синусоидальные спирали : равносторонняя гипербола ( n = −2), прямая ( n = −1), парабола ( n = - 1/2), кардиоидный ( n =1/2), круг ( n = 1) и лемниската Бернулли ( n = 2), где r n = −1 n cos nθ в полярных координатах и их эквиваленты в прямоугольных координатах.
Синусоидальные спирали : равносторонняя гипербола ( n = −2), прямая ( n = −1), парабола ( n = - 1/2), кардиоидный ( n =1/2), круг ( n = 1) и лемниската Бернулли ( n = 2), где r n = −1 n cos nθ в полярных координатах и их эквиваленты в прямоугольных координатах.  Центральная проекция кругов на сферу: центр проекции O находится внутри сферы, плоскость изображения красная. В качестве изображений кругов получается круг (пурпурный), эллипсы, гиперболы и линии. Частный случай параболы в этом примере не фигурирует. (Если бы центр O находился на сфере, все изображения кругов были бы кругами или линиями; см. Стереографическую проекцию ).
Центральная проекция кругов на сферу: центр проекции O находится внутри сферы, плоскость изображения красная. В качестве изображений кругов получается круг (пурпурный), эллипсы, гиперболы и линии. Частный случай параболы в этом примере не фигурирует. (Если бы центр O находился на сфере, все изображения кругов были бы кругами или линиями; см. Стереографическую проекцию ).  Гиперболы как линии склонения на солнечных часах
Гиперболы как линии склонения на солнечных часах  Зона контакта ударной волны горизонтального сверхзвукового самолета на плоской земле (желтый) является частью гиперболы, поскольку земля пересекает конус параллельно его оси.
Зона контакта ударной волны горизонтального сверхзвукового самолета на плоской земле (желтый) является частью гиперболы, поскольку земля пересекает конус параллельно его оси.  Трисекция угла (AOB) с использованием гиперболы с эксцентриситетом 2 (желтая кривая)
Трисекция угла (AOB) с использованием гиперболы с эксцентриситетом 2 (желтая кривая) 



