Разложение периодических функций на суммы более простых синусоидальных форм
В математике Фурье series () - это периодическая функция, составленная из гармонически связанных синусоид, объединенных посредством взвешенного суммирования. При соответствующих весах один цикл (или период) суммирования может быть выполнен для аппроксимации произвольной функции в этом интервале (или всей функции, если она также является периодической). Таким образом, суммирование представляет собой синтез другой функции. Преобразование Фурье с дискретным временем является примером ряда Фурье. Процесс определения весов, описывающих данную функцию, представляет собой форму анализа Фурье. Для функций на неограниченных интервалах аналогами анализа и синтеза являются преобразование Фурье и обратное преобразование.

Функция

(красным цветом) представляет собой сумму шести синусоидальных функций разных амплитуд и гармонически связанных частот. Их суммирование называется рядом Фурье. Преобразование Фурье,

(синим цветом), которое отображает зависимость амплитуды от частоты, показывает 6 частот (в нечетных гармониках) и их амплитуды (1 / нечетное число).
Содержание
- 1 История
- 2 Определение
- 2.1 Комплексные функции
- 2.2 Другие общепринятые обозначения
- 3 Сходимость
- 4 Примеры
- 4.1 Пример 1 : простой ряд Фурье
- 4.2 Пример 2: Мотивация Фурье
- 4.3 Другие приложения
- 5 Начало
- 5.1 Рождение гармонического анализа
- 6 Расширения
- 6.1 Ряд Фурье на квадрате
- 6.2 Ряд Фурье решеточно-периодической функции Браве
- 6.3 Интерпретация гильбертова пространства
- 7 Свойства
- 7.1 Таблица основных свойств
- 7.2 Свойства симметрии
- 7.3 Лемма Римана – Лебега
- 7.4 Производная свойство
- 7.5 Теорема Парсеваля
- 7.6 Теорема Планшереля
- 7.7 Теоремы о свертке
- 7.8 Компактные группы
- 7.9 Римановы многообразия
- 7.10 Локально компактные абелевы группы
- 8 Таблица общий ряд Фурье
- 9 Аппроксимация и сходимость ряда Фурье
- 9.1 Свойство наименьших квадратов
- 9.2 Сходимость
- 9.3 Дивергенция
- 10 См. также
- 11 Примечания
- 12 Ссылки
- 12.1 Дополнительная литература
- 13 Внешние ссылки
История
Ряд Фурье назван в честь Жана-Батиста Жозефа Фурье (1768–1830), внесшего важный вклад в исследование из тригонометрического ряда, после предварительных исследований Леонарда Эйлера, Жана ле Ронд д'Аламбера и Даниэля Бернулли. Фурье ввел ряд с целью решения уравнения теплопроводности в металлической пластине, опубликовав свои первые результаты в своей книге 1807 Mémoire sur la distribution de la chaleur dans les corps solides (Трактат о распространение тепла в твердых телах) и опубликовал его Théorie analytique de la chaleur (Аналитическая теория тепла) в 1822 году. Mémoire ввел анализ Фурье, в частности, ряды Фурье. Исследованиями Фурье был установлен факт, что произвольная (непрерывная) функция может быть представлена тригонометрическим рядом. Первое сообщение об этом великом открытии было сделано Фурье в 1807 году перед Французской академией. Ранние идеи разложения периодической функции на сумму простых осциллирующих функций восходят к 3 веку до нашей эры, когда древние астрономы предложили эмпирическую модель движения планет, основанную на деферентах и эпициклах.
уравнении теплопроводности - это уравнение в частных производных. До работы Фурье в общем случае не было известно решение уравнения теплопроводности, хотя частные решения были известны, если источник тепла вел себя простым образом, в частности, если источник тепла был синусом или косинус волна. Эти простые решения теперь иногда называют собственными решениями. Идея Фурье состояла в том, чтобы смоделировать сложный источник тепла как суперпозицию (или линейную комбинацию ) простых синусоидальных и косинусоидальных волн и записать решение как суперпозицию соответствующего собственные решения. Эта суперпозиция или линейная комбинация называется рядом Фурье.
С современной точки зрения результаты Фурье несколько неформальны из-за отсутствия точного понятия функции и интеграла в начале девятнадцатого века. Позже Петер Густав Лежен Дирихле и Бернхард Риман выразили результаты Фурье с большей точностью и формальностью.
Хотя первоначальной мотивацией было решение уравнения теплопроводности, позже стало очевидно, что те же методы можно применить к широкому кругу математических и физических задач, особенно к тем, которые связаны с линейными дифференциальными уравнениями с постоянными коэффициентами, для собственными решениями которых являются синусоиды. Серия Фурье имеет множество таких применений в электротехнике, анализе вибрации, акустике, оптике, обработке сигналов, обработка изображений, квантовая механика, эконометрика, теория тонкостенных оболочек и т. Д.
Определение
Рассмотрим функцию с действительным знаком,  , то есть интегрируемую на интервале длины
, то есть интегрируемую на интервале длины  , который будет периодом ряда Фурье. Типичные примеры интервалов анализа:
, который будет периодом ряда Фурье. Типичные примеры интервалов анализа:
![{\ displaystyle x \ in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c68354ed86bae40d711eba3ef26c4ec740fcc8fc) и
и 
![{\displaystyle x\in [-\pi,\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f68d2390bdd36e72e19b37682380f02214d52b2) и
и 
Процесс анализа определяет веса, индексированные целым числом  , которое также является числом циклов гармоники
, которое также является числом циклов гармоники  в интервале анализа. Следовательно, длина цикла в единицах
в интервале анализа. Следовательно, длина цикла в единицах  равна
равна  . И соответствующая частота гармоники равна
. И соответствующая частота гармоники равна  .
.  гармоники:
гармоники:  и
и  , а их амплитуды (веса) находятся путем интегрирования в интервале длины
, а их амплитуды (веса) находятся путем интегрирования в интервале длины  :
:
коэффициенты Фурье
 | | (Eq.1) |
- Если
 является
является  -периодическим, тогда достаточно любого интервала такой длины.
-периодическим, тогда достаточно любого интервала такой длины.  и
и  можно уменьшить до
можно уменьшить до  и
и  .
.- Многие тексты выбирают
 , чтобы упростить аргумент синусоидальных функций.
, чтобы упростить аргумент синусоидальных функций.
Процесс синтеза ( фактический ряд Фурье):
ряд Фурье, синус-косинусная форма
 | | (Eq.2) |
В общем, целое число  теоретически бесконечно. Даже в этом случае ряд может не сходиться или точно соответствовать
теоретически бесконечно. Даже в этом случае ряд может не сходиться или точно соответствовать  при всех значениях
при всех значениях  (например, одноточечный разрыв) в интервале анализа. Для «хороших» функций, типичных для физических процессов, обычно предполагается равенство.
(например, одноточечный разрыв) в интервале анализа. Для «хороших» функций, типичных для физических процессов, обычно предполагается равенство.
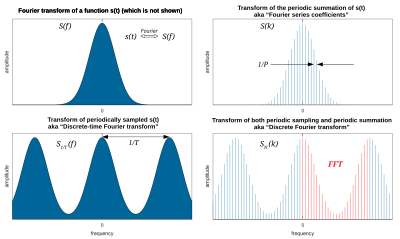
Если

- функция, содержащаяся в интервале длины

( и ноль в другом месте), верхний правый квадрант является примером того, как могут выглядеть его коэффициенты ряда Фурье (

), если их сопоставить с соответствующими частотами гармоник.. Левый верхний квадрант - это соответствующее преобразование Фурье

Суммирование ряда Фурье (не показано) синтезирует периодическое суммирование

, тогда как обратное преобразование Фурье (не показано) синтезирует только

Использование тригонометрического тождества:

и определения  и
и  , пары синус и косинус могут быть выражены как одна синусоида со смещением фазы, аналогично преобразованию между ортогональными (декартовыми) и полярными координатами:
, пары синус и косинус могут быть выражены как одна синусоида со смещением фазы, аналогично преобразованию между ортогональными (декартовыми) и полярными координатами:
Ряд Фурье, амплитуда-фаза
 | | (уравнение 3) |
Обычная форма для обобщения на комплексные значения  (следующий раздел) получается с использованием формулы Эйлера для разделения функции косинуса на комплексные экспоненты. Здесь комплексное сопряжение обозначено звездочкой:
(следующий раздел) получается с использованием формулы Эйлера для разделения функции косинуса на комплексные экспоненты. Здесь комплексное сопряжение обозначено звездочкой:

Следовательно, с определениями:

окончательный результат :
Ряд Фурье, экспоненциальная форма
 | | (Eq.4) |
Комплексные функции
Если  является комплексной функцией от вещественная переменная
является комплексной функцией от вещественная переменная  оба компонента (действительная и мнимая части) являются функциями с действительными значениями, которые могут быть представлены рядом Фурье. Два набора коэффициентов и частичная сумма определяются по формуле:
оба компонента (действительная и мнимая части) являются функциями с действительными значениями, которые могут быть представлены рядом Фурье. Два набора коэффициентов и частичная сумма определяются по формуле:
 и
и 

Определение  возвращает:
возвращает:
 | | (уравнение 5) |
Это идентично уравнению 4, за исключением  и
и  больше не являются комплексными конъюгатами. Формула для
больше не являются комплексными конъюгатами. Формула для  также не изменилась:
также не изменилась:
![{\displaystyle {\begin{aligned}c_{n}={\frac {1}{P}}\int _{P}\operatorname {Re} \{s(x)\}\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx+i\cdot {\frac {1}{P}}\int _{P}\operatorname {Im} \{s(x)\}\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx\\[4pt]={\frac {1}{P}}\int _{P}\left(\operatorname {Re} \{s(x)\}+i\cdot \operatorname {Im} \{s(x)\}\right)\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx\ =\ {\frac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32ab5a1982824b357f94d5fe7410bfb84fef8e6b)
Другие распространенные обозначения
Обозначение  неадекватно для обсуждения коэффициентов Фурье нескольких разные функции. Поэтому его обычно заменяют модифицированной формой функции (в данном случае
неадекватно для обсуждения коэффициентов Фурье нескольких разные функции. Поэтому его обычно заменяют модифицированной формой функции (в данном случае  ), например
), например  или
или ![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586) , а функциональная нотация часто заменяет индекс:
, а функциональная нотация часто заменяет индекс:
![{\displaystyle {\begin{aligned}s_{\infty }(x)=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{i\,2\pi nx/P}\\[6pt]=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{j\,2\pi nx/P}\scriptstyle {\mathsf {common\ engineering\ notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a0ce35db68aa1a4984b746f18928b5d8b6eebfc)
В инженерии, особенно когда переменная  представляет время, последовательность коэффициентов называется представление в частотной области. Квадратные скобки часто используются, чтобы подчеркнуть, что область действия этой функции представляет собой дискретный набор частот.
представляет время, последовательность коэффициентов называется представление в частотной области. Квадратные скобки часто используются, чтобы подчеркнуть, что область действия этой функции представляет собой дискретный набор частот.
Другое широко используемое представление в частотной области использует коэффициенты ряда Фурье для модуляции гребенки Дирака :
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)
где  представляет непрерывную частотную область. Когда переменная
представляет непрерывную частотную область. Когда переменная  имеет единицы измерения в секундах,
имеет единицы измерения в секундах,  имеет единицы измерения герц. «Зубцы» гребенки разнесены на интервалы, кратные гармоникам )
имеет единицы измерения герц. «Зубцы» гребенки разнесены на интервалы, кратные гармоникам )  , что называется основной частота.
, что называется основной частота.  можно восстановить из этого представления с помощью обратного преобразования Фурье :
можно восстановить из этого представления с помощью обратного преобразования Фурье :
![{\ displaystyle {\ begin {align} {\ mathcal {F}} ^ {-1} \ {S (f) \} = \ int _ {- \ infty} ^ {\ infty} \ left (\ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot \ delta \ left (f - {\ frac {n} {P}} \ right) \ right) e ^ {i2 \ pi fx} \, df, \\ [6pt] = \ sum _ {n = - \ infty} ^ {\ infty} S [n ] \ cdot \ int _ {- \ infty} ^ {\ infty} \ delta \ left (f - {\ frac {n} {P}} \ right) e ^ {i2 \ pi fx} \, df, \\ [6pt] = \ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot e ^ {i \, 2 \ pi nx / P} \ \ \ triangleq \ s _ {\ infty} ( x). \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)
Построенная функция  поэтому обычно называют преобразованием Фурье, хотя интеграл Фурье периодической функции не сходится на частотах гармоник.
поэтому обычно называют преобразованием Фурье, хотя интеграл Фурье периодической функции не сходится на частотах гармоник.
Сходимость
В инженерных приложениях обычно предполагается, что ряды Фурье сходятся почти везде (исключения находящиеся на дискретных разрывах), поскольку функции, встречающиеся в инженерии, ведут себя лучше чем функции, которые математики могут предоставить в качестве контрпримеров этому предположению. В частности, если  является непрерывным и производная от
является непрерывным и производная от  (что может не существуют везде) интегрируем в квадрате, то ряд Фурье
(что может не существуют везде) интегрируем в квадрате, то ряд Фурье  абсолютно и равномерно сходится к
абсолютно и равномерно сходится к  . Если функция интегрируема с квадратом на интервале
. Если функция интегрируема с квадратом на интервале ![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba) , то ряд Фурье сходится к функции почти в каждой точке. Сходимость рядов Фурье также зависит от конечного числа максимумов и минимумов функции, которая широко известна как одно из условий Дирихле для рядов Фурье. См. Сходимость рядов Фурье. Можно определить коэффициенты Фурье для более общих функций или распределений, в таких случаях обычно представляет интерес сходимость по норме или слабая сходимость.
, то ряд Фурье сходится к функции почти в каждой точке. Сходимость рядов Фурье также зависит от конечного числа максимумов и минимумов функции, которая широко известна как одно из условий Дирихле для рядов Фурье. См. Сходимость рядов Фурье. Можно определить коэффициенты Фурье для более общих функций или распределений, в таких случаях обычно представляет интерес сходимость по норме или слабая сходимость.
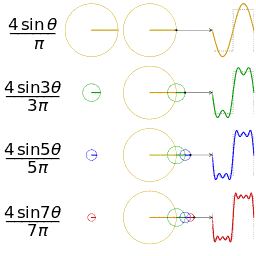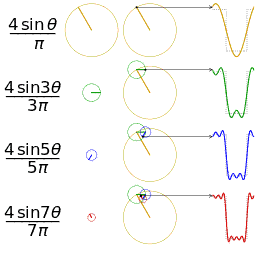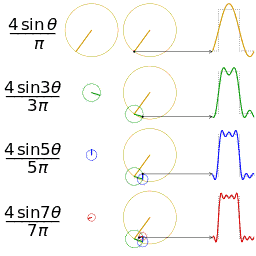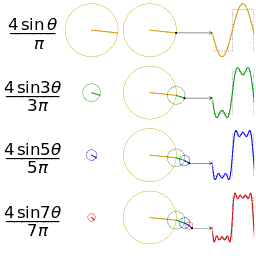
Четыре частичные суммы (ряд Фурье) длиной 1, 2, 3 и 4 члена, показывающие, как приближение к прямоугольной волне улучшается по мере увеличения количества членов (анимация)

Четыре частичные суммы ( Ряд Фурье) длиной 1, 2, 3 и 4 члена, показывающий, как приближение к пилообразной волне улучшается по мере увеличения числа членов (анимация)

Пример сходимости к несколько произвольной функции. Обратите внимание на развитие «звона» (феномен Гиббса) на переходах в / из вертикальных участков.
Здесь можно увидеть интерактивную анимацию .
Примеры
Пример 1: простой ряд Фурье

График
пилообразной волны, периодического продолжения линейная функция

на интервале
![(-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)

Анимированный график первых пяти последовательных частных рядов Фурье
Теперь мы используем приведенную выше формулу, чтобы дать разложение в ряд Фурье очень простой функции. Рассмотрим пилообразную волну
В этом случае коэффициенты Фурье определяются как
![{\displaystyle {\begin{aligned}a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0.\\[4pt]b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]=-{\frac {2}{\pi n}}\cos(n\pi)+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi)\\[4pt]={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd645b661c531998472837b4709b23bf2d2c939)
Можно доказать, что ряд Фурье сходится к  в каждой точке
в каждой точке  где
где  дифференцируемый, и, следовательно:
дифференцируемый, и, следовательно:
![{\displaystyle {\begin{aligned}s(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\[4pt]={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c051045100b8d31eada1c7fcfd414759404ed25b) | | (Eq.7) |
Когда  , ряд Фурье сходится к 0, который представляет собой полусумму левого и правого пределов s в
, ряд Фурье сходится к 0, который представляет собой полусумму левого и правого пределов s в  . Это частный пример теоремы Дирихле для рядов Фурье.
. Это частный пример теоремы Дирихле для рядов Фурье.

Распределение тепла в металлической пластине с использованием метода Фурье
Этот пример приводит нас к решению проблемы Базеля.
Пример 2: Мотивация Фурье
Разложение в ряд Фурье нашего функция в примере 1 выглядит более сложной, чем простая формула  , поэтому не сразу понятно, почему потребуется ряд Фурье. Хотя существует множество приложений, мотивация Фурье заключалась в решении уравнения теплопроводности. Например, рассмотрим металлическую пластину в форме квадрата со стороной
, поэтому не сразу понятно, почему потребуется ряд Фурье. Хотя существует множество приложений, мотивация Фурье заключалась в решении уравнения теплопроводности. Например, рассмотрим металлическую пластину в форме квадрата со стороной  метров с координатами
метров с координатами ![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610) . Если внутри пластины нет источника тепла и если температура на трех из четырех сторон составляет 0 градусов Цельсия, а четвертая сторона, заданная как
. Если внутри пластины нет источника тепла и если температура на трех из четырех сторон составляет 0 градусов Цельсия, а четвертая сторона, заданная как  поддерживается на уровне температурного градиента
поддерживается на уровне температурного градиента  градусов Цельсия для
градусов Цельсия для  в
в  , тогда можно показать, что стационарное распределение тепла (или распределение тепла после длительного время истекло) определяется как
, тогда можно показать, что стационарное распределение тепла (или распределение тепла после длительного время истекло) определяется как

Здесь sinh - это функция гиперболического синуса. Это решение уравнения теплопроводности получается путем умножения каждого члена Eq.7на  . Хотя в нашем примере функция
. Хотя в нашем примере функция  , кажется, имеет излишне сложный ряд Фурье, распределение тепла
, кажется, имеет излишне сложный ряд Фурье, распределение тепла  нетривиально. Функция
нетривиально. Функция  не может быть записана как выражение в закрытой форме. Этот метод решения тепловой проблемы стал возможным благодаря работе Фурье.
не может быть записана как выражение в закрытой форме. Этот метод решения тепловой проблемы стал возможным благодаря работе Фурье.
Другие приложения
Еще одно применение этого ряда Фурье - решение проблемы Базеля с использованием теоремы Парсеваля. Пример обобщает, и можно вычислить ζ (2n) для любого положительного целого числа n.
Начало
Жозеф Фурье писал:

Умножение обеих сторон на  , а затем интегрирование от
, а затем интегрирование от  до
до  дает:
дает:

— Жозеф Фурье,
Память о пропаганде шаллера в солидном корпусе. (1807)
Это немедленно дает любой коэффициент a k из тригонометрического ряда для φ (y) для любой функции, которая имеет такое расширение. Это работает, потому что если φ имеет такое разложение, то (при подходящих условиях сходимости) интеграл

можно проводить посменно. Но все члены, содержащие  для j ≠ k исчезают при интегрировании от -1 до 1, оставляя только k-й член.
для j ≠ k исчезают при интегрировании от -1 до 1, оставляя только k-й член.
В этих нескольких строках, которые близки к современному формализму, используемому в рядах Фурье, Фурье произвел революцию как в математике, так и в физике. Хотя аналогичные тригонометрические ряды ранее использовались Эйлером, Даламбером, Даниэлем Бернулли и Гауссом, Фурье полагал, что такие тригонометрические ряды могут представляют любую произвольную функцию. В каком смысле это действительно так, это довольно тонкий вопрос, и многолетние попытки прояснить эту идею привели к важным открытиям в теориях конвергенции, функциональных пространств и гармонический анализ.
Когда Фурье представил более позднее эссе о конкурсе в 1811 году, комитет (в который входили Лагранж, Лаплас, Малус и Лежандр и др.) Пришел к выводу:... способ, которым автор приходит к этим уравнениям, не лишен трудностей и... его анализ по их интеграции все еще оставляет желать лучшего в плане общности и даже строгость.
Рождение гармонического анализа
Со времен Фурье было открыто множество различных подходов к определению и пониманию концепции рядов Фурье, все из которых согласуются друг с другом, но каждый из них подчеркивает разные аспекты темы. Некоторые из наиболее мощных и элегантных подходов основаны на математических идеях и инструментах, которые не были доступны в то время, когда Фурье завершил свою первоначальную работу. Первоначально Фурье определил ряд Фурье для вещественнозначных функций вещественных аргументов и использовал функции синуса и косинуса в качестве базисного набора для разложения.
С тех пор было определено множество других преобразований Фурье, которые распространили первоначальную идею на другие приложения. Эта общая область исследований теперь иногда называется гармоническим анализом. Однако ряд Фурье можно использовать только для периодических функций или для функций на ограниченном (компактном) интервале.
Расширения
Ряд Фурье на квадрате
Мы также можем определить ряд Фурье для функций двух переменных  и
и  в квадрате
в квадрате ![{\displaystyle [-\pi,\pi ]\times [-\pi,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb) :
:
![{\displaystyle {\begin{aligned}f(x,y)=\sum _{j,k\,\in \,\mathbb {Z} {\text{ (integers)}}}c_{j,k}e^{ijx}e^{iky},\\[5pt]c_{j,k}={1 \over 4\pi ^{2}}\int _{-\pi }^{\pi }\int _{-\pi }^{\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71f5aaa23f00684f16ecbf31838ff5ac61f807db)
Помимо будучи полезным для решения уравнений в частных производных, таких как уравнение теплопроводности, одно из примечательных применений ряда Фурье на квадрате - это сжатие изображения. В частности, стандарт сжатия изображений jpeg использует двумерное дискретное косинусное преобразование , которое является преобразованием Фурье с использованием косинусных базисных функций.
Ряд Фурье периодической-решеточной-функции Браве
Трехмерная решетка Браве определяется как набор векторов вида:

где  - целые числа, а
- целые числа, а  - три линейно независимых вектора. Предположим, у нас есть некоторая функция,
- три линейно независимых вектора. Предположим, у нас есть некоторая функция,  , такая, что она подчиняется следующему условию для любого вектора решетки Браве
, такая, что она подчиняется следующему условию для любого вектора решетки Браве  , мы могли бы составить из него ряд Фурье. Такого рода функцией может быть, например, эффективный потенциал, который один электрон «ощущает» внутри периодического кристалла. Тогда полезно составить ряд Фурье потенциала, применяя теорему Блоха. Во-первых, мы можем записать любой произвольный вектор
, мы могли бы составить из него ряд Фурье. Такого рода функцией может быть, например, эффективный потенциал, который один электрон «ощущает» внутри периодического кристалла. Тогда полезно составить ряд Фурье потенциала, применяя теорему Блоха. Во-первых, мы можем записать любой произвольный вектор  в системе координат решетки:
в системе координат решетки:

где 
Таким образом, мы можем определить новую функцию

Эта новая функция,  , теперь является функцией трех переменных, каждая из которых имеет периодичность a 1, a 2, a 3 соответственно:
, теперь является функцией трех переменных, каждая из которых имеет периодичность a 1, a 2, a 3 соответственно:

Если мы напишем серию для g на интервале [0, a 1 ] для x 1, мы можем определить следующее:

И тогда мы можем написать:

Дальнейшее определение:
![{\ displaystyle {\ begin {align} h ^ {\ mathrm {two}} (m_ {1}, m_ {2}, x_ { 3}) \ треугольникq {\ frac {1} {a_ {2}}} \ int _ {0} ^ {a_ {2}} h ^ {\ mathrm {one}} (m_ {1}, x_ {2 }, x_ {3}) \ cdot e ^ {- i2 \ pi {\ frac {m_ {2}} {a_ {2}}} x_ {2}} \, dx_ {2} \\ [12pt] = {\ frac {1} {a_ {2}}} \ int _ {0} ^ {a_ {2}} dx_ {2} {\ frac {1} {a_ {1}}} \ int _ {0} ^ {a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_ {1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/342f2441863562e2188c632ea98d105ddb4ce5f1)
Мы можем написать  еще раз как:
еще раз как:

Finally applying the same for the third coordinate, we define:
![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})\triangleq {\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c3fac5e04d1272c87fd58d3217a691214d09b)
We write  as:
as:

Re-arranging:

Now, every reciprocal lattice vector can be written as  , where
, where  are integers and
are integers and  are the reciprocal lattice vectors, we can use the fact that
are the reciprocal lattice vectors, we can use the fact that  to calculate that for any arbitrary reciprocal lattice vector
to calculate that for any arbitrary reciprocal lattice vector  and arbitrary vector in space
and arbitrary vector in space  , their scalar product is:
, their scalar product is:

And so it is clear that in our expansion, the sum is actually over reciprocal lattice vectors:

где

Предполагая, что

мы можем решить эту систему трех линейных уравнений относительно  ,
,  и
и  в виде
в виде  ,
,  и
и  для вычисления элемента объема в исходной декартовой системе координат. Если у нас есть
для вычисления элемента объема в исходной декартовой системе координат. Если у нас есть  ,
,  и
и  в терминах
в терминах  ,
,  и
и  , мы можем вычислить определитель Якоби :
, мы можем вычислить определитель Якоби :
![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}{\dfrac {\partial x_{1}}{\partial y}}{\dfrac {\partial x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}{\dfrac {\partial x_{2}}{\partial y}}{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}{\dfrac {\partial x_{3}}{\partial y}}{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)
которое после некоторых вычислений и применения некоторого нетривиального перекрестного Идентификаторы продуктов могут быть показаны равными:

(может быть полезно для упрощения вычислений, чтобы работать в такой декартовой системе координат, в которой так уж получилось, что  параллельно оси x,
параллельно оси x,  лежит в плоскости xy, а
лежит в плоскости xy, а  имеет компоненты всех трех осей). Знаменатель - это в точности объем примитивной элементарной ячейки, которая окружена тремя примитивными векторами
имеет компоненты всех трех осей). Знаменатель - это в точности объем примитивной элементарной ячейки, которая окружена тремя примитивными векторами  ,
,  и
и  . В частности, теперь мы знаем, что
. В частности, теперь мы знаем, что

Теперь мы можем написать  как интеграл с традиционной системой координат по объему примитивной ячейки, вместо
как интеграл с традиционной системой координат по объему примитивной ячейки, вместо  ,
,  и
и  переменные:
переменные:

И  - примитивная элементарная ячейка, таким образом,
- примитивная элементарная ячейка, таким образом,  - объем примитивной элементарной ячейки.
- объем примитивной элементарной ячейки.
Интерпретация гильбертова пространства
На языке гильбертовых пространств набор функций  - это ортонормированный базис для пространства
- это ортонормированный базис для пространства ![{\displaystyle L^{2}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0) квадратично интегрируемых функций на
квадратично интегрируемых функций на ![[-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) . Это пространство на самом деле является гильбертовым пространством с внутренним продуктом, заданным для любых двух элементов
. Это пространство на самом деле является гильбертовым пространством с внутренним продуктом, заданным для любых двух элементов  и
и  по
по

Основной результат ряда Фурье для гильбертовых пространств может быть записан как


Синусы и косинусы образуют ортонормированный набор, как показано выше. Интеграл синуса, косинуса и их произведения равен нулю (зеленая и красная области равны и сокращаются), когда

,

или функции различны, а число "пи" - только в том случае, если

и

равны, а используемая функция одинакова.
Это точно соответствует комплексной экспоненциальной формулировке, приведенной выше. Версия с синусами и косинусами также оправдана интерпретацией гильбертова пространства. Действительно, синусы и косинусы образуют ортогональный набор :


(где δ mn - дельта Кронекера ) и

кроме того, синусы и косинусы ортогональны постоянной функции  . Ортонормированный базис для
. Ортонормированный базис для ![{\displaystyle L^{2}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0) , состоящий из действительных функций, образован функции
, состоящий из действительных функций, образован функции  и
и  ,
,  с n = 1, 2,... Плотность их диапазона является следствием теоремы Стоуна – Вейерштрасса, но также следует из свойств классических ядер, таких как ядро Фейера.
с n = 1, 2,... Плотность их диапазона является следствием теоремы Стоуна – Вейерштрасса, но также следует из свойств классических ядер, таких как ядро Фейера.
Свойства
Таблица основных свойств
В этой таблице показаны некоторые математические операции во временной области и соответствующий эффект в коэффициентах ряда Фурье. Обозначение:
 - комплексное сопряжение числа
- комплексное сопряжение числа  .
. обозначает
обозначает  -периодические функции, определенные на
-периодические функции, определенные на ![{\displaystyle F[n],G[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61e397cb4324837020cdcdf1d32bb9f00e3bacc3) обозначают коэффициенты ряда Фурье (экспоненциальная форма) для
обозначают коэффициенты ряда Фурье (экспоненциальная форма) для  и
и  , как определено в уравнении уравнение 5 .
, как определено в уравнении уравнение 5 .
| Свойство | Временная область | Частотная область ( экспоненциальная форма) | Примечания | Ссылка |
|---|
| Линейность |  | ![{\ displaystyle a \ cdot F [n] + b \ cdot G [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc955a6cf808d4921d875ff75eb9a0ef841fecc9) | комплексные числа  | |
| Поворот времени / Изменение частоты |  | ![{\displaystyle F[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b4a4823263d9c8be71e81b434efa1e0e7f7b78) | | |
| Временное сопряжение |  | ![{\ displaystyle F [-n] ^ {*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a0bb8e1ac85b41420733bbc3176752128cb2ad1) | | |
| Обращение времени и спряжение |  | ![{\displaystyle F[n]^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a49c30283e8c78c1a9bedb82bc10d910060b88d) | | |
| Реальная часть времени |  | ![{\displaystyle {\frac {1}{2}}(F[n]+F[-n]^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561b550cd40e3a9b9094047184114aa358f1a96b) | | |
| Мнимая часть времени |  | ![{\displaystyle {\frac {1}{2i}}(F[n]-F[-n]^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2317f4fc3c68ae6247b484faefb4afcfb05dfbb) | | |
| Действительная часть частоты |  | ![{\displaystyle \operatorname {Re} {(F[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46139e55f1d3fefaedc2c50c143c2070a71cdb80) | | |
| Мнимая часть по частоте |  | ![{\displaystyle \operatorname {Im} {(F[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b17cae376b2d16a948caa8532ba478bc7b78dbf) | | |
| Сдвиг во времени / Модуляция по частоте |  | ![{\displaystyle F[n]\cdot e^{-i{\frac {2\pi x_{0}}{T}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0867072969dbc9aa6f27cca71a9ffeb6a6853a75) | вещественное число  | |
| Сдвиг частоты / Модуляция во времени |  | ![{\displaystyle F[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ff33ce94b62cdac1424cda391a7a63d678bb78) | целое число  | |
Свойства симметрии
Когда действительная и мнимая части сложной функции разлагаются на их четную и нечетную части, есть четыре компонента, обозначенных ниже индексами RE, RO, IE, и IO. И существует взаимно-однозначное соответствие между четырьмя компонентами комплексной функции времени и четырьмя компонентами ее комплексного частотного преобразования:

Отсюда очевидны различные отношения, например:
- Преобразование функция с действительным знаком (f RE+ f RO) - это даже симметричная функция F RE+ i F IO. И наоборот, четно-симметричное преобразование подразумевает действительную временную область.
- Преобразование мнимозначной функции (если IE+, если IO) является нечетно-симметричным функция F RO+ i F IE, и верно обратное.
- Преобразование четно-симметричной функции (f RE+ if IO) является вещественнозначной функцией F RE+ F RO, и верно обратное.
- Преобразование нечетно-симметричной функции (f RO+ if IE) является мнимозначной функцией i F IE+ i F IO, и верно обратное.
Лемма Римана – Лебега
Если  интегрируемо,
интегрируемо,  ,
,  и
и  Этот результат известен как лемма Римана – Лебега.
Этот результат известен как лемма Римана – Лебега.
Свойство производной
Мы говорим, что  принадлежит
принадлежит  если
если  - 2π-периодическая функция на
- 2π-периодическая функция на  , которая
, которая  раз дифференцируема, а ее k-я производная непрерывна.
раз дифференцируема, а ее k-я производная непрерывна.
- Если
 , то коэффициенты Фурье
, то коэффициенты Фурье  производной
производной  может быть выражено через коэффициенты Фурье
может быть выражено через коэффициенты Фурье  функции
функции  , по формуле
, по формуле  .
. - Если
 , затем
, затем  . В частности, поскольку для фиксированного
. В частности, поскольку для фиксированного  мы имеем
мы имеем  как
как  , следует, что
, следует, что  стремится к нулю, что означает, что коэффициенты Фурье сходятся к нулю быстрее, чем k-я степень из n для любого
стремится к нулю, что означает, что коэффициенты Фурье сходятся к нулю быстрее, чем k-я степень из n для любого  .
.
Если  принадлежит
принадлежит ![{\displaystyle L^{2}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0) , затем
, затем  .
.
Если  - коэффициенты, а
- коэффициенты, а  тогда существует уникальная функция
тогда существует уникальная функция ![f\in L^2([-\pi,\pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5) так, что
так, что  для каждого
для каждого  .
.
Теоремы о свертке
- Первая теорема о свертке утверждает, что если
 и
и  находятся в
находятся в ![{\displaystyle L^{1}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b21b8374f535846a563ce5f7724edf4023c080b4) , коэффициенты ряда Фурье 2π-периодичности свертка из
, коэффициенты ряда Фурье 2π-периодичности свертка из  и
и  задаются следующим образом:
задаются следующим образом:
 = 2\pi\cdot \hat{f}(n)\cdot\hat{g}(n),](https://wikimedia.org/api/rest_v1/media/math/render/svg/956ea404aa998519c088c08c9a9e9f29c9bd38f0)
- где:
\ \triangleq \int _{-\pi }^{\pi }f(u)\cdot g[\operatorname {pv} (x-u)]\,du,{\big (}{\text{and }}\underbrace {\operatorname {pv} (x)\ \triangleq \operatorname {Arg} (e^{ix})} _{\text{principal value}}\,{\big)}\\=\int _{-\pi }^{\pi }f(u)\cdot g(x-u)\,du,{\text{when }}g(x){\text{ is }}2\pi {\text{-periodic.}}\\=\int _{2\pi }f(u)\cdot g(x-u)\,du,{\text{when both functions are }}2\pi {\text{-periodic, and the integral is over any }}2\pi {\text{ interval.}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d2105aae4f5eb50bf6d6541e8a28ef6d0a75db5)
- Вторая теорема о свертке утверждает, что коэффициенты ряда Фурье произведения
 и
и  задаются дискретной сверткой элементов
задаются дискретной сверткой элементов  и
и  последовательности:
последовательности:
 = [\hat{f}*\hat{g}](n).](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a01ca431cbe51c2353a325265bb70204e5a1ae1)
- A дважды бесконечная последовательность
 in
in  - последовательность коэффициентов Фурье функции из
- последовательность коэффициентов Фурье функции из ![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8) тогда и только тогда, когда это свертка двух последовательностей в
тогда и только тогда, когда это свертка двух последовательностей в  . См.
. См.
Компактные группы
Одно из интересных свойств преобразования Фурье, о котором мы упоминали, заключается в том, что оно переносит свертки в точечные произведения. Если это свойство, которое мы стремимся сохранить, можно построить ряд Фурье на любой компактной группе. Типичные примеры включают те классические группы, которые являются компактными. Это обобщает преобразование Фурье на все пространства вида L (G), где G - компактная группа, таким образом, что преобразование Фурье переводит свертки в точечные произведения. Ряд Фурье существует и сходится аналогично случаю [−π, π].
Альтернативным расширением компактных групп является теорема Питера – Вейля, которая доказывает результаты о представлениях компактных групп, аналогичные представлениям о конечных группах.
Римановы многообразия
 атомные орбитали
атомные орбитали в
химии частично описываются
сферическими гармониками, которые можно использовать для получения рядов Фурье по сфера .
Если домен не является группой, то внутренне определенной свертки нет. Однако, если  - компакт риманово многообразие, оно имеет оператор Лапласа – Бельтрами. Оператор Лапласа – Бельтрами - это дифференциальный оператор, который соответствует оператору Лапласа для риманова многообразия
- компакт риманово многообразие, оно имеет оператор Лапласа – Бельтрами. Оператор Лапласа – Бельтрами - это дифференциальный оператор, который соответствует оператору Лапласа для риманова многообразия  . Затем по аналогии можно рассмотреть уравнения теплопроводности на
. Затем по аналогии можно рассмотреть уравнения теплопроводности на  . Поскольку Фурье пришел к своей основе, пытаясь решить уравнение теплопроводности, естественным обобщением является использование в качестве основы собственных решений оператора Лапласа – Бельтрами. Это обобщает ряд Фурье на пространства типа
. Поскольку Фурье пришел к своей основе, пытаясь решить уравнение теплопроводности, естественным обобщением является использование в качестве основы собственных решений оператора Лапласа – Бельтрами. Это обобщает ряд Фурье на пространства типа  , где
, где  - риманово многообразие. Ряд Фурье сходится способами, аналогичными случаю
- риманово многообразие. Ряд Фурье сходится способами, аналогичными случаю ![[-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) . Типичный пример - взять
. Типичный пример - взять  как сферу с обычной метрикой, и в этом случае базис Фурье состоит из сферических гармоник.
как сферу с обычной метрикой, и в этом случае базис Фурье состоит из сферических гармоник.
Локально компактные абелевы группы
Обобщение на компактные группы, рассмотренное выше, не распространяется на некомпактные, неабелевы группы. Однако есть прямое обобщение на локально компактные абелевы (LCA) группы.
Это обобщает преобразование Фурье на  или
или  , где
, где  - группа LCA. Если
- группа LCA. Если  компактно, также получается ряд Фурье, сходящийся аналогично
компактно, также получается ряд Фурье, сходящийся аналогично ![[-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6) случай, но если
случай, но если  некомпактный, вместо него получается интеграл Фурье. Это обобщение приводит к обычному преобразованию Фурье, когда базовая локально компактная абелева группа имеет вид
некомпактный, вместо него получается интеграл Фурье. Это обобщение приводит к обычному преобразованию Фурье, когда базовая локально компактная абелева группа имеет вид  .
.
Таблица общих рядов Фурье
Некоторые общие пары периодических функций и их коэффициенты ряда Фурье показаны в таблице ниже. Применяются следующие обозначения:
 обозначает периодическую функцию, определенную на
обозначает периодическую функцию, определенную на  обозначают коэффициенты ряда Фурье (синус-косинусная форма) периодической функции
обозначают коэффициенты ряда Фурье (синус-косинусная форма) периодической функции  , как определено в Уравнение 4 .
, как определено в Уравнение 4 .
Временная область.  | График | Частотная область (синус-косинусная форма).  | Примечания | Ссылка |
|---|
|  |  | Двухполупериодный выпрямленный синус | |
| 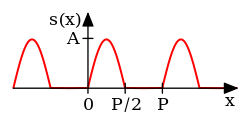 |  | Полуволновой выпрямленный синус | |
|  |  |  | |
| 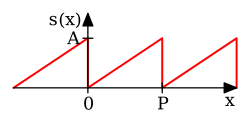 |  | | |
|  |  | | |
|  |  | | |
Аппроксимация и сходимость рядов Фурье
Важным вопросом как для теории, так и для приложений является сходимость. В частности, в приложениях часто бывает необходимо заменить бесконечный ряд  конечным,
конечным,

Это называется частичной суммой. Мы хотели бы знать, в каком смысле  сходится к
сходится к  as
as  .
.
Свойство наименьших квадратов
Мы говорим, что  - это тригонометрический полином степени
- это тригонометрический полином степени  , когда он имеет форму
, когда он имеет форму

Обратите внимание, что  - тригонометрический полином степени
- тригонометрический полином степени  . Теорема Парсеваля означает, что
. Теорема Парсеваля означает, что
теорема. Тригонометрический полином  - единственный лучший тригонометрический полином степени
- единственный лучший тригонометрический полином степени  , аппроксимирующий
, аппроксимирующий  в том смысле, что для любого тригонометрического полинома
в том смысле, что для любого тригонометрического полинома  степени
степени  , имеем
, имеем

где норма гильбертова пространства определяется как:

Сходимость
Благодаря свойству наименьших квадратов и полноте базиса Фурье мы получаем результат элементарной сходимости.
Теорема. Если  принадлежит
принадлежит ![{\displaystyle L^{2}(\left[-\pi,\pi \right])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9f22db3f847b6cab3b1fb2f43e32dd574acc1f) , тогда
, тогда  сходится к
сходится к  в
в ![{\displaystyle L^{2}(\left[-\pi,\pi \right])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9f22db3f847b6cab3b1fb2f43e32dd574acc1f) , то есть
, то есть  сходится к 0 при
сходится к 0 при  .
.
Мы уже упоминали, что если  непрерывно дифференцируемо, то
непрерывно дифференцируемо, то  - n-й коэффициент Фурье производной
- n-й коэффициент Фурье производной  . По сути, из неравенства Коши – Шварца следует, что
. По сути, из неравенства Коши – Шварца следует, что  абсолютно суммируем. Сумма этого ряда является непрерывной функцией, равной
абсолютно суммируем. Сумма этого ряда является непрерывной функцией, равной  , поскольку ряд Фурье сходится в среднем к
, поскольку ряд Фурье сходится в среднем к  :
:
Теорема. Если  , то
, то  сходится к
сходится к  равномерно (и, следовательно, также точечно.)
равномерно (и, следовательно, также точечно.)
Это результат может быть легко доказан, если  далее предполагается равным
далее предполагается равным  , поскольку в этом case
, поскольку в этом case  стремится к нулю при
стремится к нулю при  . В более общем смысле, ряд Фурье абсолютно суммируем, поэтому сходится равномерно к
. В более общем смысле, ряд Фурье абсолютно суммируем, поэтому сходится равномерно к  , при условии, что
, при условии, что  удовлетворяет условие Гельдера порядка
удовлетворяет условие Гельдера порядка  . В абсолютно суммируемом случае неравенство
. В абсолютно суммируемом случае неравенство  доказывает равномерную конвергенцию.
доказывает равномерную конвергенцию.
Известно много других результатов, касающихся сходимости рядов Фурье, начиная от умеренно простого результата, что ряд сходится при  если
если  дифференцируем в
дифференцируем в  , в гораздо более сложный результат Леннарта Карлесона что ряд Фурье функции
, в гораздо более сложный результат Леннарта Карлесона что ряд Фурье функции  на самом деле сходится почти везде.
на самом деле сходится почти везде.
Эти теоремы и их неофициальные варианты, которые не определяют условия сходимости, в общем, иногда называют «теоремой Фурье» или «теоремой Фурье».
Дивергенция
Поскольку ряды Фурье обладают такими хорошими свойствами сходимости, многие часто удивляются некоторым из отрицательные результаты. Например, ряд Фурье непрерывной T-периодической функции может не сходиться поточечно. Принцип равномерной ограниченности дает простое неконструктивное доказательство этого факта.
В 1922 году Андрей Колмогоров опубликовал статью «Une série de Fourier-Lebesgue divergente presque partout», в которой он привел пример интегрируемой по Лебегу функции, ряд Фурье которой расходится почти всюду. Позже он построил пример интегрируемой функции, ряд Фурье которой расходится всюду (Katznelson 1976).
См. Также
Примечания
Ссылки
Дополнительная литература
Внешние ссылки
. Эта статья включает материал из примера серии Фурье на PlanetMath, который находится под лицензией Creative Commons Attribution / Share-Alike License.
 Функция
Функция  (красным цветом) представляет собой сумму шести синусоидальных функций разных амплитуд и гармонически связанных частот. Их суммирование называется рядом Фурье. Преобразование Фурье,
(красным цветом) представляет собой сумму шести синусоидальных функций разных амплитуд и гармонически связанных частот. Их суммирование называется рядом Фурье. Преобразование Фурье,  (синим цветом), которое отображает зависимость амплитуды от частоты, показывает 6 частот (в нечетных гармониках) и их амплитуды (1 / нечетное число).
(синим цветом), которое отображает зависимость амплитуды от частоты, показывает 6 частот (в нечетных гармониках) и их амплитуды (1 / нечетное число). 

![{\ displaystyle x \ in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c68354ed86bae40d711eba3ef26c4ec740fcc8fc) и
и 
![{\displaystyle x\in [-\pi,\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f68d2390bdd36e72e19b37682380f02214d52b2) и
и 










 является
является  -периодическим, тогда достаточно любого интервала такой длины.
-периодическим, тогда достаточно любого интервала такой длины. и
и  можно уменьшить до
можно уменьшить до  и
и  .
. , чтобы упростить аргумент синусоидальных функций.
, чтобы упростить аргумент синусоидальных функций.



 Если
Если  - функция, содержащаяся в интервале длины
- функция, содержащаяся в интервале длины  ( и ноль в другом месте), верхний правый квадрант является примером того, как могут выглядеть его коэффициенты ряда Фурье (
( и ноль в другом месте), верхний правый квадрант является примером того, как могут выглядеть его коэффициенты ряда Фурье ( ), если их сопоставить с соответствующими частотами гармоник.. Левый верхний квадрант - это соответствующее преобразование Фурье
), если их сопоставить с соответствующими частотами гармоник.. Левый верхний квадрант - это соответствующее преобразование Фурье  Суммирование ряда Фурье (не показано) синтезирует периодическое суммирование
Суммирование ряда Фурье (не показано) синтезирует периодическое суммирование  , тогда как обратное преобразование Фурье (не показано) синтезирует только
, тогда как обратное преобразование Фурье (не показано) синтезирует только 










 и
и 






![{\displaystyle {\begin{aligned}c_{n}={\frac {1}{P}}\int _{P}\operatorname {Re} \{s(x)\}\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx+i\cdot {\frac {1}{P}}\int _{P}\operatorname {Im} \{s(x)\}\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx\\[4pt]={\frac {1}{P}}\int _{P}\left(\operatorname {Re} \{s(x)\}+i\cdot \operatorname {Im} \{s(x)\}\right)\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx\ =\ {\frac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi nx}{P}}}\ dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32ab5a1982824b357f94d5fe7410bfb84fef8e6b)



![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s_{\infty }(x)=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{i\,2\pi nx/P}\\[6pt]=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{j\,2\pi nx/P}\scriptstyle {\mathsf {common\ engineering\ notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a0ce35db68aa1a4984b746f18928b5d8b6eebfc)

![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)





![{\ displaystyle {\ begin {align} {\ mathcal {F}} ^ {-1} \ {S (f) \} = \ int _ {- \ infty} ^ {\ infty} \ left (\ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot \ delta \ left (f - {\ frac {n} {P}} \ right) \ right) e ^ {i2 \ pi fx} \, df, \\ [6pt] = \ sum _ {n = - \ infty} ^ {\ infty} S [n ] \ cdot \ int _ {- \ infty} ^ {\ infty} \ delta \ left (f - {\ frac {n} {P}} \ right) e ^ {i2 \ pi fx} \, df, \\ [6pt] = \ sum _ {n = - \ infty} ^ {\ infty} S [n] \ cdot e ^ {i \, 2 \ pi nx / P} \ \ \ triangleq \ s _ {\ infty} ( x). \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)






![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
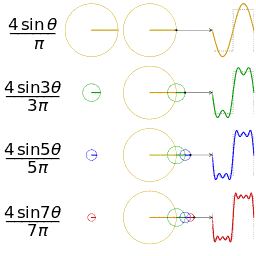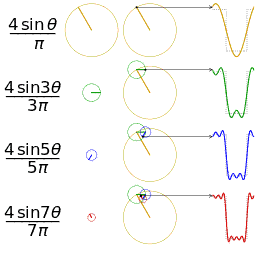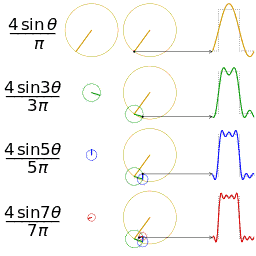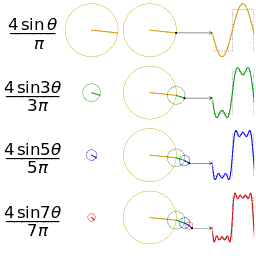


 График пилообразной волны, периодического продолжения линейная функция
График пилообразной волны, периодического продолжения линейная функция  на интервале
на интервале ![(-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)
 Анимированный график первых пяти последовательных частных рядов Фурье
Анимированный график первых пяти последовательных частных рядов Фурье ![{\displaystyle {\begin{aligned}a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\,dx=0,\quad n\geq 0.\\[4pt]b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\sin(nx)\,dx\\[4pt]=-{\frac {2}{\pi n}}\cos(n\pi)+{\frac {2}{\pi ^{2}n^{2}}}\sin(n\pi)\\[4pt]={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd645b661c531998472837b4709b23bf2d2c939)



![{\displaystyle {\begin{aligned}s(x)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\[4pt]={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c051045100b8d31eada1c7fcfd414759404ed25b)


 Распределение тепла в металлической пластине с использованием метода Фурье
Распределение тепла в металлической пластине с использованием метода Фурье 

![{\displaystyle (x,y)\in [0,\pi ]\times [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)
















![{\displaystyle [-\pi,\pi ]\times [-\pi,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\displaystyle {\begin{aligned}f(x,y)=\sum _{j,k\,\in \,\mathbb {Z} {\text{ (integers)}}}c_{j,k}e^{ijx}e^{iky},\\[5pt]c_{j,k}={1 \over 4\pi ^{2}}\int _{-\pi }^{\pi }\int _{-\pi }^{\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71f5aaa23f00684f16ecbf31838ff5ac61f807db)












![{\ displaystyle {\ begin {align} h ^ {\ mathrm {two}} (m_ {1}, m_ {2}, x_ { 3}) \ треугольникq {\ frac {1} {a_ {2}}} \ int _ {0} ^ {a_ {2}} h ^ {\ mathrm {one}} (m_ {1}, x_ {2 }, x_ {3}) \ cdot e ^ {- i2 \ pi {\ frac {m_ {2}} {a_ {2}}} x_ {2}} \, dx_ {2} \\ [12pt] = {\ frac {1} {a_ {2}}} \ int _ {0} ^ {a_ {2}} dx_ {2} {\ frac {1} {a_ {1}}} \ int _ {0} ^ {a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_ {1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/342f2441863562e2188c632ea98d105ddb4ce5f1)


![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})\triangleq {\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c3fac5e04d1272c87fd58d3217a691214d09b)

























![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}{\dfrac {\partial x_{1}}{\partial y}}{\dfrac {\partial x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}{\dfrac {\partial x_{2}}{\partial y}}{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}{\dfrac {\partial x_{3}}{\partial y}}{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)
















![{\displaystyle L^{2}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)
![[-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




 Синусы и косинусы образуют ортонормированный набор, как показано выше. Интеграл синуса, косинуса и их произведения равен нулю (зеленая и красная области равны и сокращаются), когда
Синусы и косинусы образуют ортонормированный набор, как показано выше. Интеграл синуса, косинуса и их произведения равен нулю (зеленая и красная области равны и сокращаются), когда  ,
,  или функции различны, а число "пи" - только в том случае, если
или функции различны, а число "пи" - только в том случае, если  и
и  равны, а используемая функция одинакова.
равны, а используемая функция одинакова. 



![{\displaystyle L^{2}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)



 - комплексное сопряжение числа
- комплексное сопряжение числа  .
. обозначает
обозначает  -периодические функции, определенные на
-периодические функции, определенные на ![{\displaystyle F[n],G[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61e397cb4324837020cdcdf1d32bb9f00e3bacc3) обозначают коэффициенты ряда Фурье (экспоненциальная форма) для
обозначают коэффициенты ряда Фурье (экспоненциальная форма) для  и
и  , как определено в уравнении уравнение 5 .
, как определено в уравнении уравнение 5 .
![{\ displaystyle a \ cdot F [n] + b \ cdot G [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc955a6cf808d4921d875ff75eb9a0ef841fecc9)


![{\displaystyle F[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b4a4823263d9c8be71e81b434efa1e0e7f7b78)

![{\ displaystyle F [-n] ^ {*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a0bb8e1ac85b41420733bbc3176752128cb2ad1)

![{\displaystyle F[n]^{*}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a49c30283e8c78c1a9bedb82bc10d910060b88d)

![{\displaystyle {\frac {1}{2}}(F[n]+F[-n]^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/561b550cd40e3a9b9094047184114aa358f1a96b)

![{\displaystyle {\frac {1}{2i}}(F[n]-F[-n]^{*})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2317f4fc3c68ae6247b484faefb4afcfb05dfbb)

![{\displaystyle \operatorname {Re} {(F[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46139e55f1d3fefaedc2c50c143c2070a71cdb80)

![{\displaystyle \operatorname {Im} {(F[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b17cae376b2d16a948caa8532ba478bc7b78dbf)

![{\displaystyle F[n]\cdot e^{-i{\frac {2\pi x_{0}}{T}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0867072969dbc9aa6f27cca71a9ffeb6a6853a75)


![{\displaystyle F[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ff33ce94b62cdac1424cda391a7a63d678bb78)











 , то коэффициенты Фурье
, то коэффициенты Фурье  производной
производной  может быть выражено через коэффициенты Фурье
может быть выражено через коэффициенты Фурье  функции
функции  , по формуле
, по формуле  .
. , затем
, затем  . В частности, поскольку для фиксированного
. В частности, поскольку для фиксированного  мы имеем
мы имеем  как
как  , следует, что
, следует, что  стремится к нулю, что означает, что коэффициенты Фурье сходятся к нулю быстрее, чем k-я степень из n для любого
стремится к нулю, что означает, что коэффициенты Фурье сходятся к нулю быстрее, чем k-я степень из n для любого  .
.
![{\displaystyle L^{2}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)



![f\in L^2([-\pi,\pi])](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)


 и
и  находятся в
находятся в ![{\displaystyle L^{1}([-\pi,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b21b8374f535846a563ce5f7724edf4023c080b4) , коэффициенты ряда Фурье 2π-периодичности свертка из
, коэффициенты ряда Фурье 2π-периодичности свертка из  и
и  задаются следующим образом:
задаются следующим образом: = 2\pi\cdot \hat{f}(n)\cdot\hat{g}(n),](https://wikimedia.org/api/rest_v1/media/math/render/svg/956ea404aa998519c088c08c9a9e9f29c9bd38f0)
\ \triangleq \int _{-\pi }^{\pi }f(u)\cdot g[\operatorname {pv} (x-u)]\,du,{\big (}{\text{and }}\underbrace {\operatorname {pv} (x)\ \triangleq \operatorname {Arg} (e^{ix})} _{\text{principal value}}\,{\big)}\\=\int _{-\pi }^{\pi }f(u)\cdot g(x-u)\,du,{\text{when }}g(x){\text{ is }}2\pi {\text{-periodic.}}\\=\int _{2\pi }f(u)\cdot g(x-u)\,du,{\text{when both functions are }}2\pi {\text{-periodic, and the integral is over any }}2\pi {\text{ interval.}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d2105aae4f5eb50bf6d6541e8a28ef6d0a75db5)
 и
и  задаются дискретной сверткой элементов
задаются дискретной сверткой элементов  и
и  последовательности:
последовательности: = [\hat{f}*\hat{g}](n).](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a01ca431cbe51c2353a325265bb70204e5a1ae1)
 in
in  - последовательность коэффициентов Фурье функции из
- последовательность коэффициентов Фурье функции из ![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8) тогда и только тогда, когда это свертка двух последовательностей в
тогда и только тогда, когда это свертка двух последовательностей в  . См.
. См. атомные орбитали в химии частично описываются сферическими гармониками, которые можно использовать для получения рядов Фурье по сфера .
атомные орбитали в химии частично описываются сферическими гармониками, которые можно использовать для получения рядов Фурье по сфера .




![[-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)





![[-\pi,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)


 обозначает периодическую функцию, определенную на
обозначает периодическую функцию, определенную на  обозначают коэффициенты ряда Фурье (синус-косинусная форма) периодической функции
обозначают коэффициенты ряда Фурье (синус-косинусная форма) периодической функции  , как определено в Уравнение 4 .
, как определено в Уравнение 4 .








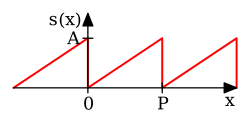























![{\displaystyle L^{2}(\left[-\pi,\pi \right])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9f22db3f847b6cab3b1fb2f43e32dd574acc1f)


![{\displaystyle L^{2}(\left[-\pi,\pi \right])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e9f22db3f847b6cab3b1fb2f43e32dd574acc1f)






















