 Формы первых пяти атомных орбиталей равны: 1s, 2s, 2p x, 2p y и 2p z. Два цвета показывают фазу или знак волновой функции в каждой области. Каждое изображение - это раскраска области функции ψ (x, y, z), которая зависит от координаты одного электрона. Чтобы увидеть удлиненную форму функций ψ (x, y, z), которые более точно показывают плотность вероятности, см. Изображения d-орбиталей ниже.
Формы первых пяти атомных орбиталей равны: 1s, 2s, 2p x, 2p y и 2p z. Два цвета показывают фазу или знак волновой функции в каждой области. Каждое изображение - это раскраска области функции ψ (x, y, z), которая зависит от координаты одного электрона. Чтобы увидеть удлиненную форму функций ψ (x, y, z), которые более точно показывают плотность вероятности, см. Изображения d-орбиталей ниже. В атомной теории и квантовая механика, атомная орбиталь - это математическая функция, описывающая местоположение и волнообразное поведение электрона в атоме. Функция Эта может быть программа для ядер вероятности нахождения любого электрона атома в любой области вокруг ядра атома. Термин атомная орбиталь может также относиться к физической области или пространству, где электрон может быть вычислен как присутствующий, как предсказано математической формы орбитали.
Каждая орбиталь в атоме характеризуется уникальным набором характеристик квантовых чисел n, ℓ и m, которые соответственно соответствуют энергии, угловому моменту электрона и угловому моменту компонент вектора (магнитное квантовое число ). Каждая такая орбиталь может быть занята максимум двумя электронами, каждый со своим собственным квантовым числом спина s. Простые названия s орбитальная, p-орбитальная, d-орбитальная и f-орбитальная принадлежность к орбиталям с квантовым числом углового ℓ = 0., 1, 2 и 3 соответственно. Эти имена вместе со значением используются для описания электронных данных элементов. Они получены из описания ранними спектроскопистами настоящего спектроскопических линий щелочных металлов как s арфа, p rincipal, d если предохранитель, и f фундаментальный. Орбитали для ℓ>3 продолжаются в алфавитном порядке, опуская j (g, h, i, k,...), потому что на некоторых языках различаются буквы «i» и «j».
Атомные орбитали - это основные блоки модели атомной орбиты (также известная как модель электронного облака или волновой механики), современные основы для визуализации субмикроскопического поведения электронов в веществе. В этой модели электронное много облакаэлектронного атома можно рассматривать как построенное (в приближении) электронную конфигурацию, которая является продуктом более простых водородоподобных атомных орбиталей. Повторяющаяся периодичность блоков из 2, 6, 10 и 14 элементов в разделах периодической таблицы естественным образом возникает из общего количества электронов, которые занимают полный набор s, p, dи f атомные орбитали, соответственно, определенные подоболочек становятся очень похожими, и поэтому порядок, в котором они, как говорят, заселены электронами ( например, Cr = [Ar] 4s3d и Cr = [Ar] 3d), может быть объяснен лишь несколько произвольно.
 Атомные орбитали электрона в атоме водорода на разных уровнях энергии. Вероятность нахождения электрона обозначена цветом, как показано в ключе вверху справа.
Атомные орбитали электрона в атоме водорода на разных уровнях энергии. Вероятность нахождения электрона обозначена цветом, как показано в ключе вверху справа. С развитием квантовой механики и экспериментальных результатов (таких как дифракция электронов на двух щелях) стало возможным и что вращающиеся электроны вокруг ядра не могут быть полностью развиты как частицы, но должны быть объяснены дуализмом волна-частица. В этом смысле электроны обладают своими свойствами:
Волнообразные свойства:
Свойства, частиц частиц:
Таким образом, электроны нельзя описывать просто как твердые частицы. Можно вокруг провести аналогию с большой и часто странной формы «атмосферой» (электроном), распределенной относительно крошечной планеты (атомного ядра). Атомные орбитали точно описывают форму этой «атмосферы» только тогда, когда в атоме присутствует единственный электрон. Когда к одному атому добавляется больше электронов, дополнительные электроны имеют тенденцию вокруг более равномерно заполняющего объем пространства вокруг ядра, так что результирующая совокупность (иногда называемая "электронным облаком" атома) стремится к общей сферической вероятности, описывающей местоположение электрона из-за принципа неопределенности.
Атомные орбитали могут быть определены более точно на формальном квантовомеханическом языке. Они используют приближенным решением уравнения Шредингера для электронов, связанное с атомом электрическое полем ядра ядра. В частности, в квантовой механике состояние атома, т. Е. собственное состояние атомного гамильтониана, аппроксимируется расширением (см. конфигурационное взаимодействие разложение и базисный набор ) в линейные комбинации антисимметризованных продуктов (определители Слейтера ) одноэлектронных функций. Пространственные компоненты этих одноэлектронных функций называются атомными орбиталями. (Если рассматривать также их компонент спина, мы говорим об атомных спиновых орбиталях .) Состояние фактически является функцией координат всех электронов, так что их движение коррелировано, но это часто аппроксимируется моделью независимых частиц произведений волновых функций одного электрона. (Лондонская дисперсионная сила, например, зависит от корреляции движения электронов.)
В атомной физике атомные спектральные линии соответствуют переходам (квантовые скачки ) между квантовыми состояниями атома. Эти состояния помечены набором квантовых чисел, суммированных в символе и обычно связанных с конкретными электронными конфигурациями, т. Е. Схемами заполнения атомных орбиталей (например, 1s 2s 2p для основного состояния неонового -термного символа: S 0).
Это обозначение означает, что соответствующие детерминанты Слейтера имеют явно более высокий вес в раскрытии различных конфигураций. Таким образом концепция атомной орбиты является ключевой для визуализации процесса возбуждения, связанного с данным переходом . Например, для данного перехода можно сказать, что он соответствует возбужденному электрона с занятой орбитали на службу незанятую орбиталь. Тем не менее, нужно иметь в виду, что электроны - это фермионы, управляемые принципом исключения Паули, и их нельзя отличить друг от друга. Более того, иногда случается, что в разложении волновой функции очень медленно говорить, и о простой однодетерминантной волновой функции вообще нельзя говорить. Это тот случай, когда электронная корреляция велика.
По сути, атомная орбиталь - это одноэлектронная волновая функция, хотя большинство электронов не существует в одноэлектронных атомах, и поэтому одноэлектронное представление является приблизительным. Когда мы думаем об орбиталей, нам часто дают визуализацию орбиталей, которая сильно влияет на приближение Хартри - Фока, которое является одним из способов уменьшить сложность теории молекулярных орбиталей.
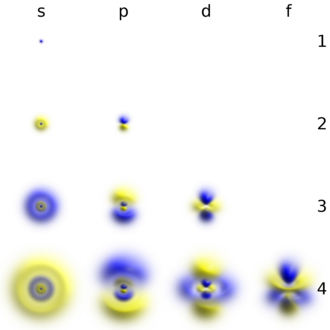 Трехмерные изображения некоторые водородоподобных атомных орбиталей, показательная плотность и фазу вероятности (g орбитали и выше не показаны)
Трехмерные изображения некоторые водородоподобных атомных орбиталей, показательная плотность и фазу вероятности (g орбитали и выше не показаны) Атомные орбитали могут быть водородоподобными «орбиталями», которые являются точными решениями уравнения Шредингера для водородоподобного «атома» (т. Е. Атома с одним электроном). В качестве альтернативы, атомные орбитали относительной функции, которые зависят от координат одного электрона (то есть есть орбитали), но используются в качестве отправных точек для прибли волновых функций, которые зависят от одинаковых координат всех электронов в атоме или молекуле. системы координат, выбранные для атомных орбиталей, обычно - это сферические координаты (r, θ, φ) в атомах и декартовы (x, y, z) в многоатомных молекулах.. Основная сферическая система координат (для атомов) состоит в том, что орбитальная волновая функция представляет собой произведение трех факторов, каждый из которых зависит от одной координаты: ψ (r, θ, φ) = R (r) Θ (θ) Φ (φ). Угловые факторы атомных орбиталей Θ (θ) Φ (φ) генерируют s, p, d и т. Д. Функции как действительные комбинации сферических гармоник Yℓm(θ, φ) (где ℓ и m - квантовые числа). Обычно существуют три математические формы для радиальных функций R (r), которые можно выбрать в качестве отправной точки для расчета характеристик атомов и молекул с большим количеством электронов:
 .
.Хотя водородобные орбитали все еще используются в качестве педагогических инструментов, появление компьютеров сделало STO предпочтительными атомами и двухатомных молекул, так как комбинации STO может узлы на водородоподобной атомной орбитали. Гауссианы обычно используются в молекулах с тремя или более атомами. Хотя сами по себе они не так точны, как STO, комбинации многих гауссианов могут достичь точности водородоподобных орбиталей.
Термин «орбитальный» был введен Робертом Малликеном в 1932 году как сокращение для одноэлектронной орбитальной волновой функции. Однако идея о том, что электроны могут вращаться вокруг компактного ядра с определенным угловым моментом, эффективно аргументирована, по крайней мере, 19 лет ранее Нильсом Бором, а японский физик Хантаро Нагаока опубликовал орбитальную основанная на гипотезе электронного поведения еще в 1904 году. Объяснение поведения этих электронных "орбитов" было одной из движущих сил развития квантовой механики.
с Дж.. Открытие Дж. Томсоном электрона в 1897 г. стало ясно, что атомы не являются мельчайшими строительными блоками, а представляют собой скорее составные частицы природы. Недавно открытая структура внутри элементов заставила многих представить, как составные части атома могут взаимодействовать друг с другом. Томсон предположил, что несколько электронов вращаются по орбитальным кольцам внутри положительно заряженного желеобразного вещества, и между открытием электрона и 1909 г. эта «модель сливового пудинга » была наиболее широко распространенным объяснением атомной структуры.
Вскоре после открытия Томсона Хантаро Нагаока предсказал другую модель электронной структуры. В от модели сливового пудинга, положительный заряд в «Модели Сатурна» Нагаоки сконцентрирован в центральном ядре, отличие вытягивая электроны по круговым орбитам, напоминающим кольца Сатурна. Этот классический объект не может поддерживать орбитальное движение, потому что он ускоряется и, следовательно, теряет энергию из-за электромагнитного излучения. Тем не менее, модель Сатурна оказалась более общей с современной теорией, чем любая из ее современников.
В 1909 году Эрнест Резерфорд обнаружил, что основная масса атомной массы плотно конденсирована в ядро, которое также оказалось положительно заряженным. Из его анализа в 1911 году стало ясно, что модель сливового пудинга не может объяснить атомную структуру. В 1913 году аспирант Резерфорда, Нильс Бор, использует новую модель атома, в которой электроны вращались вокруг ядра с классическими периодами, но им разрешалось иметь только дискретные значения углового момента, квантованные в единицах. ч / 2π. Это ограничение автоматически допускало только значения энергии электронов. Модель Бора атома решила проблему потери энергии из-за излучения из основного состояния (заявив, что состояния ниже этого не было), и, что более важно, объяснила происхождение спектральных линий.
 Модель Резерфорда-Бора атома водорода.
Модель Резерфорда-Бора атома водорода. После того, как Бор использовал объяснение Эйнштейном фотоэлектрического эффекта для связи уровней энергии в атомах с длиной волнылучаемого света, связь между структурой электронов в атомах и эмиссионными и спектрами поглощения элементов становится все более полезным инструментом в понимании электронов в атомах. Наиболее характерной особенностью спектров возбуждает (экспериментально с середины XIX века). Значение модели Бора состояло в том, что она связала линии в спектрах излучения и поглощения с разницей в энергии между орбитами, которые электроны перемещали вокруг атома. Однако через этот путь придания электронам каких-то волнообразных свойств, как идея о том, что электроны могут вести себя как материальные волны, возникла только одиннадцатью годами позже. Тем не менее, использование в моделях Бора квантованных угловых моментов и, следовательно, квантованных уровней энергии было значительным на пути к пониманию электронов в атомах, а также значительным шагом в развитии квантовой механики, предполагающей, что квантованные ограничения должны Приводят все прерывистые уровни энергии и спектры в атомах.
С предположением де Бройля о существовании волн электронной материи в 1924 году и за короткое время до полного рассмотрения уравнением Шредингера в 1926 году водородоподобный атом, «Длина волны» боровского электрона могла быть видна как функция его импульса, таким образом, было замечено, что орбитальный электрон вращается по кругу с кратностью его длины волны (это физически неверно Модель Бора до сих часто преподают начинающим студентам). В течение короткого времени модель Бора можно рассматривать как классическую модель с дополнительным ограничением, обусловленным аргументом «длиной волны». Однако этот период был немедленно заменен полной трехмерной волновой механикой 1926 года. В нашем нынешнем понимании физики модель Бора называется полуклассической моделью из-за ее квантования углового момента, а не в первую очередь из-за ее связи с длиной волныов, появившейся задним числом через десяток лет того, как была предложена модель Бора.
Модель Бора смогла объяснить спектры излучения и поглощения водорода. Энергии электронов в состояниях n = 1, 2, 3 и т. Д. В модели Бора объединяет с энергиями современной физики. Однако это не объясняет сходства между разными атомами, как выражено в периодической таблице, например, тот факт, что гелий (два электрона), неон (10 электронов) и аргон ( 18 электронов) проявляют аналогичную химическую инертность. Современная квантовая механика объясняет это в терминах электронных оболочек и подоболочек, каждая из которых может содержать некоторое количество электронов, определяемое принципом исключения Паули. Таким образом, состояние n = 1 может содержать один или два электрона, в то время как состояние n = 2 может содержать до восьми электронов в подоболочках 2s и 2p. В гелии все состояния n = 1 полностью заняты; то же самое верно для n = 1 и n = 2 в неоне. В аргоне подоболочки 3s и 3p аналогичным образом полностью заняты восемью электронами; квантовая механика также допускает трехмерную подоболочку, но она имеет более высокую энергию, чем 3s и 3p в аргоне (в отличие от ситуации с атомом водорода), и остается пустой.
Сразу после того, как Гейзенберг открыл свой принцип неопределенности, Бор отметил, что существование любого вида волнового пакета подразумевает неопределенность в частоте и длине волны, поскольку для создания самого пакета требуется разброс частот. В квантовой механике, где все импульсы частиц связаны с волнами, именно формирование такого волнового пакета локализует волну и, следовательно, частицу в пространстве. В состояниях, когда квантово-механическая частица связана, она должна быть локализована как волновой пакет, а существование пакета и его минимальный размер подразумевает разброс и минимальное значение длины волны частицы, а, следовательно, также импульса и энергии. В квантовой механике, когда частица локализуется в меньшей области пространства, соответствующий сжатый волновой пакет требует все большего и большего диапазона импульсов и, следовательно, большей кинетической энергии. Таким образом, энергия связи для удержания или захвата частицы в меньшей области пространства неограниченно возрастает по мере того, как область пространства становится меньше. Частицы не могут быть ограничены геометрической точкой в пространстве, так как для этого потребуется бесконечный импульс частицы.
В химии Шредингер, Полинг, Малликен и другие отметили, что следствием отношения Гейзенберга было то, что электрон как волновой пакет, нельзя было считать, что он имеет точное местоположение на своей орбите. Макс Борн предположил, что положение электрона должно быть описано распределением вероятностей, которое связано с обнаружением электрона в некоторой точке волновой функции, которая описывает связанный с ним волновой пакет. Новая квантовая механика не дала точных результатов, а только вероятности появления множества возможных таких результатов. Гейзенберг считал, что путь движущейся частицы не имеет значения, если мы не можемего наблюдать, как мы не можем наблюдать электроны в атоме.
В квантовой картине Гейзенберга, Шредингера и другие известные числа атома Бора для каждого орбитали стало как наиболее вероятная энергия вероятности волновой пакет электрона, окружающий атом.
Орбитальные имена, которые обычно даются в форме:

где X - уровень энергии, соответствующий главному квантовому существу n; тип представляет собой строчную букву, обозначающую форму или подоболочку орбитали, соответствующую угловому квантовому существу ℓ; а y - количество электронов на этой орбитали.
Например, орбитальная единица (произносится как отдельные цифры и буквы: «'one' 'ess' 'two'») имеет два электрона и является самым низким энергетическим уровнем (n = 1) и имеет угловое квантовое число = 0, обозначаемое s.
Существует также другая, менее распространенная система, все еще используемая в науке о рентгеновских лучах, известная как Обозначение рентгеновских лучей, которая является продолжением Обозначения, используемый, до орбитальной теории, были хорошо поняты. В этой системе главному квантовому агрегату присваивается связанная с ним буква. Для n = 1, 2, 3, 4, 5,…, буквы, связанные с этим числами, - это K, L, M, N, O,... соответственно.
Простейшие атомные орбитали - это те, которые рассчитываются для систем с одним электроном, таких как атом водорода. Атом любого другого элемента , ионизированный до одного электрона, очень похож на водород, и орбитали принимают такую же форму. В уравнении Шредингера для этой системы из одной отрицательной и одной положительной частицы атомные орбитали являются собственными состояниями оператора Гамильтона для энергии. Их можно получить аналитически, а это означает, что полученные орбитали произведений полиномиального ряда, экспоненциальных и тригонометрических функций. (см. атом водорода ).
Для элементов с двумя более электронами определяющими уравнениями могут быть решены только методы и методы аппроксимации. Орбитали многоэлектронных элементов качественно похожи на орбитали водорода, и в простейших моделях, что они имеют такую же форму. Для более строгого и точного анализа необходимо использовать численные приближения.
Данная (водородоподобная) атомная орбиталь идентифицируется уникальными значениями трех квантовых чисел: n, ℓ и mℓ. Правила, ограничивающие значения квантовых чисел и их энергии (см. Ниже), объясняют электронную конфигурацию элементов и периодическую таблицу.
Стационарные состояния (квантовые состояния ) водородоподобные атомы являются его атомными орбиталями. Однако в целом поведение электрона не полностью описывается одной орбиталью. Электронные состояния лучше всего представлены зависящими от времени «смесями» (линейными комбинациями ) множества орбиталей. См. Линейная комбинация атомных орбиталей, метод молекулярных орбиталей.
Квантовое число n впервые появилось в модели Бора, где оно определяет радиус каждой круговой электронной орбиты. Однако в современной квантовой механике определить среднее расстояние электрона от ядра; все электроны с одинаковым средним значением находятся на одинаковом расстоянии. По этой причине, что орбитали с одинаковым значением составляют «оболочку ». Орбитали с одинаковым значением n и одинаковым значением ℓ даже более связаны и, как говорят, «подоболочку ».
Из-за квантово-механической природы электронов вокруг ядра атомные орбитали могут быть однозначно определенным набором целых чисел, известных как квантовые числа. Эти квантовые числа встречаются только в определенных комбинациях значений, и их физическая интерпретация меняется в зависимости от того, используются ли реальные или сложные версии атомных орбиталей.
В физике наиболее распространенных описаний орбиталей на основе решений для атома водорода, где орбитали задаются радиальной функцией и чистой сферической гармоники. Квантовые числа вместе с правилами, определяющими их возможные значения, следующие:
главное квантовое число n энергии электрона и всегда является положительным целым числом. Фактически, это может быть любое положительное целое число, но по причинам, обсуждаемым ниже, большие числа встречаются редко. Каждый атом, как правило, имеет множество орбиталей, связанных с каждым n; эти орбитали вместе иногда называют электронными оболочками.
. азимутальное квантовое число ℓ неотрицательный угловой момент каждого электрона и является неотрицательным целым числом. В оболочке, где n - некоторое целое число n 0, ℓ охватывает все (целые) значения, удовлетворяющие продуцированию 



магнитное квантовое число, 




Приведенные выше результаты можно обобщить в следующей таблице. Каждая ячейка представляет собой подоболочку и перечисляет значения 
| ℓ = 0 | ℓ = 1 | ℓ = 2 | ℓ = 3 | ℓ = 4 | .. | |
|---|---|---|---|---|---|---|
| n = 1 |  | |||||
| n = 2 | 0 | −1, 0, 1 | ||||
| n = 3 | 0 | - 1, 0, 1 | −2, −1, 0, 1, 2 | |||
| n = 4 | 0 | −1, 0, 1 | −2, −1, 0, 1, 2 | −3, −2, −1, 0, 1, 2, 3 | ||
| n = 5 | 0 | −1, 0, 1 | −2, −1, 0, 1, 2 | −3, −2, −1, 0, 1, 2, 3 | −4, −3, −2, −1, 0, 1, 2, 3, 4 | |
| ... | ... | ... | ... | ... | ... | ... |
Подоболочки обычно идентифицируются по их 





Каждый электрон также имеет квантовое число спина , s, которое является каждым спинным электрона (спин вверх или вниз). Число s может быть +1/2 или -1/2.
Принцип исключения Паули гласит, что никакие два электрона в атоме не могут иметь одинаковые значения всех четырех квантовых чисел. Если на орбитали находятся два электрона с заданными значениями трех квантовых чисел (n, ℓ, m), эти два электрона должны различаться по их спину.
Вышеупомянутые подразумевают предпочтительную ось (например, направление z в декартовых координатах), а также подразумевают предпочтительное направление вдоль этой предпочтительной оси. В противном случае не было бы смысла отличать m = +1 от m = −1. Таким образом, модель наиболее полезна при применении к физическим системам, которые разделяют эти симметрии. Один из магнитных примеров - эксперимент Штерна-Герлаха, в котором атом подвергается воздействию воздействия поля.
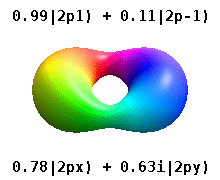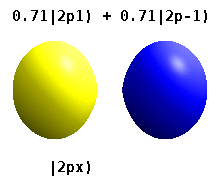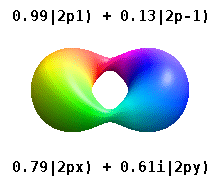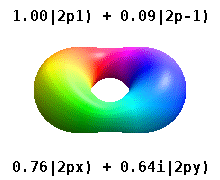 Анимация непрерывно меняющихся суперпозиций между
Анимация непрерывно меняющихся суперпозиций между  и
и  орбитали.
орбитали. Атом, заключенный в кристаллическое твердое тело, часто множественные предпочтительные оси, но нет предпочтительного направления. Вместо построения атомных орбиталей из произведений радиальных функций и единственной сферической гармоники обычно используются линейные комбинации сферических гармоник, разработанные таким образом, что мнимая часть сферических гармоник компенсируется. Эти реальные орбитали являются строительными блоками, наиболее часто показываемыми при визуализации орбиты.
В реальных водородоподобных орбиталях, например, n и ℓ ту же интерпретацию и значение, что и их сложные аналоги, но m больше не является хорошим квантовым значением (хотя его абсолютное есть). Орбиталям даны новые требования в зависимости от формы по отношению к стандартизированной декартовой основе. Реальные водородоподобные p-орбитали задаются следующим образом:



где p 0 = R n 1 Y 1 0, p 1 = R n 1 Y 1 1 и p −1 = R n 1 Y 1 −1, - комплексные орбитали, соответствующие ℓ = 1.
Уравнения для орбиталей p x и p y зависят от фазового соглашения, используемого для сферических гармоник. Приведенные выше уравнения предполагают, что сферические гармоники определяют следующим образом: 
 Вид прозрачного облака на вычисленной 6s (n = 6, ℓ = 0, m = 0) орбитали атома водорода. S-орбитали, хотя и сферически симметричны, имеют радиально расположенные волновые узлы для n>1. Только s-орбитали всегда имеют центральный антиузел; другие типы никогда не делают.
Вид прозрачного облака на вычисленной 6s (n = 6, ℓ = 0, m = 0) орбитали атома водорода. S-орбитали, хотя и сферически симметричны, имеют радиально расположенные волновые узлы для n>1. Только s-орбитали всегда имеют центральный антиузел; другие типы никогда не делают. Простые изображения, показывающие орбитальные формы, предназначены для описания угловых форм областей в космосе, где вероятно обнаружение электронов, занимающих орбиталь. Диаграммы не могут показать всю область, где можно найти электрон, поскольку согласно квантовой механике существует ненулевая вероятность найти электрон (почти) в любом месте пространства. Вместо этого диаграммы являются приблизительными изображениями границ или контурных поверхностей, где плотность вероятности | ψ (r, θ, φ) | имеет постоянное значение, выбранное так, чтобы была определенная вероятность (например, 90%) нахождения электрона внутри контура. Хотя | ψ | поскольку квадрат абсолютного значения везде неотрицателен, знак волновой функции ψ (r, θ, φ) часто указывается в каждой подобласти орбитального изображения.
Иногда график ψ-функции будет отображать ее фазы, а не | ψ (r, θ, φ) | который показывает плотность вероятности, но не имеет фаз (которые были потеряны в процессе получения абсолютного значения, поскольку ψ (r, θ, φ) - комплексное число). | ψ (r, θ, φ) | орбитальные графы, как правило, имеют менее сферические и более тонкие лепестки, чем графы ψ (r, θ, φ), но имеют одинаковое количество лепестков в одних и тех же местах, и в остальном они узнаваемы. В этой статье, чтобы показать фазы волновой функции, в основном показаны графики ψ (r, θ, φ).
Лепестки можно рассматривать как стоячую волну интерференцию между двумя встречно вращающимися кольцевыми резонансными бегущей волной «m» и «- m "мод, с проекцией орбитали на плоскость xy, имеющей резонансные длины волн" m "по окружности. Хотя решения с бегущей волной изображаются редко, их можно рассматривать как вращающиеся торы с полосами, где полосы представляют информацию о фазе. Для каждого m существует два решения со стоячей волной ⟨m⟩ + ⟨− m⟩ и ⟨m⟩ − ⟨− m⟩. Для случая, когда m = 0, орбиталь вертикальная, информация о встречном вращении неизвестна, а орбиталь симметрична по оси z. Для случая, когда ℓ = 0, режимы встречного вращения отсутствуют. Есть только радиальные моды, а форма сферически симметрична. Для любого заданного n чем меньше ℓ, тем больше радиальных узлов. Для любого заданного ℓ, чем меньше n, тем меньше радиальных узлов (ноль для любого n, которое первым имеет эту орбиталь). Грубо говоря, n - это энергия, - это аналог эксцентриситета, а m - ориентация. В классическом случае кольцевая резонансная бегущая волна, например, в кольцевой линии передачи, если ее активно не принудить, спонтанно распадется на кольцевую резонансную стоячую волну, потому что со временем будут нарастать отражения даже при малейшем дефекте или неоднородности.
Вообще говоря, число n определяет размер и энергию орбитали для данного ядра: с увеличением n размер орбитали увеличивается. При сравнении различных элементов, более высокий ядерный заряд Z более тяжелых элементов вызывает сужение их орбиталей по сравнению с более легкими, так что общий размер всего атома остается примерно постоянным, даже если количество электронов в более тяжелых элементах (более высокое Z) увеличивается.
 Экспериментальные изображения 1s и 2p орбиталей остовных электронов Sr, включая эффекты тепловых колебаний атомов и уширения возбуждения, полученные с помощью энергодисперсионной рентгеновской спектроскопии (EDX) в сканирующей просвечивающей электронной микроскопии (STEM).
Экспериментальные изображения 1s и 2p орбиталей остовных электронов Sr, включая эффекты тепловых колебаний атомов и уширения возбуждения, полученные с помощью энергодисперсионной рентгеновской спектроскопии (EDX) в сканирующей просвечивающей электронной микроскопии (STEM). Также в общих чертах, ℓ определять форму орбиты и m ℓ ее ориентацию. Однако, поскольку некоторые орбитали описываются уравнениями в комплексных чисел, форма иногда также зависит от m ℓ. Вместе весь набор орбиталей для заданных ℓ и n заполняет пространство настолько симметрично, насколько это возможно, хотя и со все более сложными наборами лепестков и узлов.
Одиночные s-орбитали (
Формы p, d и f-орбиталей развития здесь словесно и графически показаны в таблице орбиталей. Три p-орбитали для n = 2 имеют форму двух эллипсоидов с точкой касания в ядре (иногда используется двухлопастная форма "гантель " - две лепестки в противоположные стороны друг от друга). Три p-орбитали в каждой оболочке ориентированы под прямым углом друг к другу, что определяет их положение линейной комбинацией значений m ℓ. Общий результат - лепесток, указывающий вдоль каждого направления основных осей.
Четыре из пяти d-орбиталей для n = 3 выглядят одинаково, каждым с четырьмя грушевидными лепестками, каждое из которых касается двух других под прямым углом, а центры всех четырех лежат в одной плоскости. Три из этих плоскостей имеют плоскостность xy, xz и yz - лепестки находятся между парами основных осей, а четвертая проходит вдоль самих осей x и y. Пятая и последняя d-орбиталь состоит из трех областей с высокой плотностью вероятности: тора с двумя грушевидными областями, расположенными симметрично относительно оси z. Всего 18 лепестков указаний в каждом первичной и между каждой парой.
Есть семь f-орбиталей, каждая из которых имеет более сложную форму, чем d-орбитали.
Кроме того, как и в случае с-орбита отдельными, отдельными p, d, f и возможными g-орбитали со значениями n выше наименьшего значения, демонстрируют дополнительные поврежденные радиальные узлы, которые напоминают гармонические волны того же типа по сравнением с низшей (или основной) модой волны. Как и в s-орбиталей, это явление обеспечивает орбитали p, d, f и g при дополнительном более высоком возможном значении n (например, 3p орбитали по сравнению с использованием 2p), узел в каждом лепестке. Еще более высокие значения увеличивают количество радиальных узлов для каждого типа орбиты.
Формы атомных орбиталей в одноэлектронном атоме связаны с 3-мерными сферическими гармониками. Эти формы не уникальны, и любая линейная комбинация допустима, как преобразование в кубические гармоники, на самом деле можно генерировать наборы, в которых все d имеют одинаковую форму, точно так же, как p x, p y и p z имеют одинаковую форму.
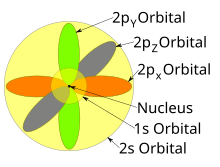 1с, 2с и 2п орбитали атома натрия.
1с, 2с и 2п орбитали атома натрия. Хотя отдельные орбитали чаще всего показывают независимые друг от друга друг от друга, орбитали сосуществуют вокруг ядра одновременно. Кроме того, в 1927 году Альбрехт Унсельд доказал, что если суммировать электронную плотность всех орбиталей определенного азимутального квантового числа ℓ одной и той же оболочки n (например, всех трех 2p-орбиталей или всех пяти трехмерных орбиталей), каждая орбиталь занята электроном или каждой электронной парой, тогда всякая угловая зависимость исчезает; то есть результирующая общая плотность всех атомных орбиталей в этой подоболочке (с одинаковым). Это известно как теорема Унсельда.
В этой таблице показаны все орбитальные конфигурации для реальных водородоподобных волновых функций до 7, и, следовательно, описывается простая электронная конфигурация для всех элементов в таблице Менделеева до радия. Графики «ψ» отображались с фазами - и +волновой функцией, данными показателями разными цветами (произвольно красным и синим). Орбиталь p z такая же, как орбиталь p 0, но p x и p y формируются путем взятия линейных комбинаций орбиталей p +1 и p −1 (поэтому они под меткой m = ± 1). Кроме того, p +1 и p −1 не такие же формы, как p 0, поскольку они являются чистыми сферическими гармониками.
| s (ℓ = 0) | p (ℓ = 1) | d (ℓ = 2) | f (ℓ = 3) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m = 0 | m = 0 | m = ± 1 | m = 0 | m = ± 1 | m = ± 2 | m = 0 | m = ± 1 | m = ± 2 | m = ± 3 | |||||||
| s | pz | px | py | dz | dxz | dyz | dxy | dx - y | fz | fxz | fyz | fxyz | fz (x - y) | fx (x - 3y) | fy (3x - y) | |
| n = 1 |  | |||||||||||||||
| n = 2 |  |  |  |  | ||||||||||||
| n = 3 |  |  |  |  |  |  |  |  |  | |||||||
| n = 4 |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |  |
| n = 5 |  |  |  |  |  |  |  |  |  | ... | ... | ... | ... | ... | ... | .. |
| n = 6 |  |  |  |  | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | .. |
| n = 7 |  | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
Формы атомных орбиталей можно качественно понять, рассматривая аналогичный случай стоячих волн на круглом барабане. Чтобы увидеть, как это происходит в этой точке, относительно этой точки от центра барабана. голова. Как показывают различные формы атомных орбиталей, многие моды колеблющегося диска образуют паттерны, которые отслеживают различные формы атомных орбиталей. Основная причина этого соответствия заключается в том, что распределение кинетической энергии и импульса в достаточном веществе предсказывает, где будет находиться частица, связанная с волной. То есть вероятность нахождения электрона в данном месте также функция среднего положения электрона в этой точке, высокий импульс электрона в данном положении имеет тенденцию "локализовать" электрон в этом положении через свойства электрона. волновые пакеты (подробнее о механизме см. принцип неопределенности Гейзенберга ).
Это соотношение означает, что некоторые ключевые особенности наблюдаются как в режимах мембраны барабана, так и в атомных орбиталях. Например, во всех режимах, аналогичных s орбиталям (верхний ряд на анимированной иллюстрации ниже), можно увидеть, что самый центр мембраны барабана вибрирует наиболее сильно, что соответствует пучности на всех s орбиталях в атоме. Эта пучность означает, что электрон, скорее всего, находится в физическом ядре, которое он проходит прямо через него, рассеивая и не ударяя его, поскольку он движется (в среднем) наиболее быстро в этой точке, придавая ему максимальный импульс.
Мысленная картина "планетной орбиты", наиболее близкая к поведению электронов на s орбиталях, все из не имеют углового момента, возможно, может быть картиной кеплеровской орбиты с эксцентриситетом орбиты, равным 1, но с конечной большой осью, что физически невозможно (что частицы должны быть столкнуться), но можно представить как предел орбиты с одинаковыми главными осями, но увеличивающимся эксцентриситетом.
Ниже показаны ряд мод колебаний мембраны и соответствующие волновые функции атома водорода. Можно рассмотреть соответствие, в котором волновые функции вибрирующей головки барабана соответствуют двухкоординатной системе ψ (r, θ), а волновые функции колеблющейся сферы - трехкоординатной ψ (r, θ, φ).

Режим ударных

Режим ударных

Режим барабана

Волновая функция орбитальной единицы (действительная часть, 2D-разрез, 

Волновая функция орбиты 2s (действительная часть, 2D-разрез, 

Волновая функция орбиты 3s (действительная часть, 2D- разрез, 
Ни один из других наборов механизмов в мембране барабана не имеет центральной пучности, и во всех них центр барабана не движется. Все эти орбитали имеют некоторый угловой момент, а в планетарной модели они соответствуют частицам на орбите с эксцентриситетом меньше 1.0, так что они не проходят прямо через центр основного тела, а держатся н а некотором расстоянии от него.
Кроме того, режимы барабана, аналогичные режимы p и d в атоме, демонстрируют пространственную неравномерность вдоль различных радиальных направлений от центра барабана, тогда как все режимы, аналогичные s Моды идеально симметричны в радиальном направлении. Свойства нерадиальной симметрии не- s орбиталей необходимы для локализации частиц с угловым моментом и волновой природой на орбитали, где она должна стремиться держаться дальше от центральной силы притяжения, поскольку любая часть локализована в точке центрального притяжения не может иметь количество движения. В этих режимах волны в головке барабана стремятся избегать центральной точки. Такие особенности еще раз подчеркивают, что формы атомных орбиталей являются прямым следствием волновой природы электронов.

Режим ударных

Режим ударных

Режим барабана

Волновая функция 2p орбитальной (действующая часть, 2D-разрез, 
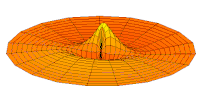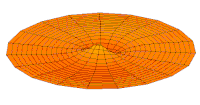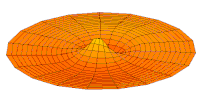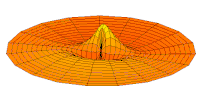
Волновая функция орбиты 3p (действительная часть, 2D-разрез, 

Волновая функция орбиты 4p (действительная часть, 2D- нарезка, 

Mode 

Режим 

Режим 
В атомах с одним электроном (водородоподобные атомы ) энергию орбитали (и, следовательно, любых электронов на орбите) опр еделяется главным образом 






В атомах с множеством электронов энергия электрона зависит не только от внутренних свойств его орбитали, но и от его взаимодействия с другими электронами. Эти взаимодействуют от деталей его пространственного распределения вероятностей, поэтому уровни энергии орбиталей зависят не только от 




Увеличение энергии подоболочек с увеличивающимся угловым моментом в более крупных атомах происходит из-за эффектов электрон-электронное взаимодействие и, в частности, связано со способностью электронов с низким угловым моментом, более эффективно проникать в ядро, где они менее защищены. заряда промежуточных электронов. Таким образом, в атомах с более высоким атомным номером 

Энергетическая последовательность первых 35 подоболочек (например, 1s, 2p, 3d и т. Д.) Приведена в следующей таблице. Каждая ячейка представляет собой подоболочку с 

| s | p | d | f | g | h | |
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 2 | 2 | 3 | ||||
| 3 | 4 | 5 | 7 | |||
| 4 | 6 | 8 | 10 | 13 | ||
| 5 | 9 | 11 | 14 | 17 | 21 | |
| 6 | 12 | 15 | 18 | 22 | 26 | 31 |
| 7 | 16 | 19 | 23 | 27 | 32 | 37 |
| 8 | 20 | 24 | 28 | 33 | 38 | 44 |
| 9 | 25 | 29 | 34 | 39 | 45 | 51 |
| 10 | 30 | 35 | 40 | 46 | 52 | 59 |
Примечание: пустые ячейки указывают на несуществующие подуровни, а числа, выделенные курсивом, указывают подуровни, которые могут (такие) Существовать, но не удерживают электроны ни в одном из известных в настоящее время элементов.
 Электрон атомная и молекулярная орбитали. Схема орбиталей (слева ) устроена путем увеличения энергии (см. правило Маделунга ). Обратите внимание, что атомные орбиты выполняют функции трех чисел (два угла и расстояние r от ядра). Эти изображения точно соответствуют угловой составляющей орбитали, но не полностью репрезентативны для орбитали в целом.
Электрон атомная и молекулярная орбитали. Схема орбиталей (слева ) устроена путем увеличения энергии (см. правило Маделунга ). Обратите внимание, что атомные орбиты выполняют функции трех чисел (два угла и расстояние r от ядра). Эти изображения точно соответствуют угловой составляющей орбитали, но не полностью репрезентативны для орбитали в целом.  Воспроизвести медиа Атомные орбитали и построение периодической таблицы
Воспроизвести медиа Атомные орбитали и построение периодической таблицы Несколько правил регулируют размещение электронов на орбиталях (электронная конфигурация ). Первый гласит, что никакие два электрона в атоме не имеют одинаковый набор значений квантовых чисел (это принцип исключения Паули ). Эти квантовые числа включают три, которые определяют орбитали, а также s или квантовое число спина. Таким образом, два электрона могут занимать одну орбиталь, если они имеют разные значения s. Однако только два электрона из-за их спина могут быть связаны с каждой орбиталью.
Кроме того, электрон всегда стремится перейти в состояние с наименьшей возможной энергией. Он может занимать любую орбиталь, если он не нарушает принцип исключения Паули, но если доступны орбитали с более низкой энергией, это состояние нестабильно. Электрон в конечном итоге потеряет энергию (высвободив фотон ) и упадет на нижнюю орбиталь. Таким образом, электроны заполняют орбитали в порядке, заданном приведенной выше энергетической последовательностью.
Это поведение за устойчивость периодической таблицы. Таблица может быть разделена на несколько строк (называемых «точками»), пронумерованных, начиная с 1 вверху. Известные в настоящее время элементы занимают семь периодов. Если некоторый период имеет номер i, он состоит из элементов, наиболее удаленные электроны, которые попадают в i-ю оболочку. Нильс Бор был первым, кто предположил (1923), что периодичность в свойствах элементов может быть объяснена периодическим заполнением энергетических уровней электронов, что приводит к электронной структуре атом.
Периодическая таблица также может быть разделена на несколько пронумерованных прямоугольных «блоков ». Элементы, относящиеся к данному блоку, имеют общую общую особенность: их электроны с наивысшей энергией все принадлежат одному и тому же состоянию-(но, связанное с этим-состоянием, зависит от этого периода). Например, два крайних левых столбца составляют «s-блок». Самые удаленные электроны Li и Be соответственно принадлежат к подоболочке 2s, а электроны Na и Mg - к подоболочке 3s.
Ниже приведен порядок заполнения орбиталей "подоболочки", который также дает порядок "блоков" в периодической таблице:
"периодический" характер заполнения орбиталей, а также появление s, p, dи f «блоки» более очевиден, если этот порядок заполнения задан в матричной форме с формы главных квантовых чисел, начиная с новых строк («периодов») в матрице. Затем каждая подоболочка (состоит из первых двух квантовых чисел) повторяется столько раз, сколько требуется для каждой пары электронов, которую она может содержать. В результате получается сжатая периодическая таблица, в которой каждая запись представляет собой два последовательных элемента:
| 1s | |||||||||||||||
| 2s | 2p | 2p | 2p | ||||||||||||
| 3s | 3p | 3p | 3p | ||||||||||||
| 4s | 3d | 3d | 3d | 3d | 3d | 4p | 4p | 4p | |||||||
| 5s | 4d | 4d | 4d | 4d | 4d | 5p | 5p | 5p | |||||||
| 6s | 4f | 4f | 4f | 4f | 4f | 4f | 4f | 5d | 5d | 5d | 5d | 5d | 6p | 6p | 6p |
| 7s | 5f | 5f | 5f | 5f | 5f | 5f | 5f | 6d | 6d | 6d | 6d | 6d | 7p | 7p | 7p |
Хотя это общий порядок орбитальное заполнение в соответствии с правилом Маделунга, есть исключения, и фактические электронные энергии каждого элемента также зависят от дополнительных деталей атомов (см. Электронная конфигурация # Атомы: принцип Ауфбау и правило Маделунга ).
Число электронов в электрически нейтральном атоме увеличивается с увеличением атомного номера . Электроны во внешней оболочке или валентные электроны, как правило, ответственны за химическое поведение элемента. Элементы, содержащие одинаковое количество валентных электронов, могут быть сгруппированы вместе и отображать аналогичные химические свойства.
Для элементов с большим атомным номером Z эффекты теории относительности становятся более выраженными, особенно для s-электронов, которые движутся с релятивистскими скоростями, проникая через экранирующие электроны вблизи ядро атомов с высоким Z. Это релятивистское увеличение импульса для высокоскоростных электронов вызывает соответствующее уменьшение длины волны и сокращение 6s-орбиталей относительно 5d-орбиталей (по сравнению с соответствующими s- и d-электронами в более легких элементах в том же столбце периодической таблицы); это приводит к понижению энергии 6s валентных электронов.
Примеры значительных физических результатов этого эффекта включают пониженную температуру плавления ртути (которая является результатом того, что 6s электронов недоступны для металлических связей) и золотистый цвет золота и цезий.
В модели Бора электрон с n = 1 имеет скорость, определяемую как 


В релятивистских орбитальных плотностях нет узлов, хотя отдельные компоненты волновой функции будут иметь узлы.
В конце периода - Предполагается, что 8 элементов гибрид 8p 3/2 и 9p 1/2, где «3/2» и «1/2» относятся к квантовое число полного углового момента. Этот гибрид «pp» может быть ответственным за p-блок периода из-за свойств, аналогичных p подоболочкам в обычных валентных оболочках. Уровни энергии 8p 3/2 и 9p 1/2 приближаются из-за релятивистских спин-орбитальных эффектов ; подоболочка 9s также должна участвовать, поскольку ожидается, что эти элементы будут аналогичны соответствующим элементам 5p индий - ксенон.
Связанные квантовые состояния имеют дискретную энергию уровни. Применительно к атомным орбиталям это означает, что разность энергий между состояниями также дискретна. Таким образом, переход между этими состояниями (т.е. электрон, поглощающий или излучающий фотон) может происходить только в том случае, если фотон имеет энергию, соответствующую точной разнице энергий между упомянутыми состояниями.
Рассмотрим два состояния атома водорода:
Состояние 1) n = 1, ℓ = 0, m ℓ = 0 и s = +1/2
Состояние 2) n = 2, ℓ = 0, m ℓ = 0 и s = +1/2
Согласно квантовой теории состояние 1 имеет фиксированную энергию E 1, а состояние 2 имеет фиксированную энергию E 2. Итак, что произойдет, если электрон из состояния 1 перейдет в состояние 2? Чтобы это произошло, электрон должен набрать энергию точно E 2 - E 1. Если электрон получает энергию, которая меньше или больше этого значения, он не может перейти из состояния 1 в состояние 2. Теперь предположим, что мы облучаем атом широким спектром света. Фотоны, достигающие атома с энергией E 2 - E 1, будут поглощены электроном в состоянии 1, и этот электрон перейдет в состояние 2. Однако фотоны которые имеют большую или меньшую энергию, не могут быть поглощены электроном, потому что электрон может перейти только на одну из орбиталей, он не может перейти в состояние между орбиталями. В результате атом поглощает только фотоны определенной частоты. Это создает линию в спектре, известную как линия поглощения, которая соответствует разности энергий между состояниями 1 и 2.
Таким образом, модель атомной орбиты предсказывает линейчатые спектры, которые наблюдаются экспериментально. Это одна из основных проверок модели атомной орбиты.
Модель атомной орбиты, тем не менее, является приближением полной квантовой теории, которая распознает только многие электронные состояния. Предсказания линейчатых спектров качественно полезны, но не точны количественно для атомов и ионов, кроме тех, которые содержат только один электрон.
| На Викискладе есть материалы, связанные с атомными орбиталями. |