| Гексагональная мозаика | |
|---|---|
 . . | |
| Тип | Обычная мозаика |
| Конфигурация вершин | 6.6.6 (или 6). |
| Конфигурация лица | V3.3.3.3.3.3 (или V3) |
| символ (символы) Шлефли | {6,3}. t {3,6} |
| символ Wythoff (s)) | 3 | 6 2. 2 6 | 3. 3 3 3 | |
| Диаграмма (-ы) Кокстера | |
| Симметрия | p6m, [6,3], (* 632) |
| Поворотная симметрия | p6, [6,3], (632) |
| Двойная | Треугольная мозаика |
| Свойства | Вершинно-транзитивная, реберная транзитивная, гранная транзитивная |
В геометрии шестиугольная мозаика или шестиугольная мозаика - это правильная мозаика евклидовой плоскости, в которой три шестиугольника пересекаются на каждая вершина. Он имеет символ Шлефли из {6,3} или t {3,6} (в виде усеченного треугольного разбиения).
Английский математик Джон Конвей назвал это шестигранником .
Внутренний угол шестиугольника составляет 120 градусов, поэтому три шестиугольника в одной точке составляют полные 360 градусов. Это одно из трех правильных мозаик плоскости. Два других - это треугольная мозаика и квадратная мозаика.
Гексагональная мозаика - самый плотный способ расположить круги в двух измерениях. Гипотеза о сотах утверждает, что шестиугольная мозаика - лучший способ разделить поверхность на области равной площади с наименьшим общим периметром. Оптимальная трехмерная структура для создания сот (или, скорее, мыльных пузырей) была исследована лордом Кельвином, который считал, что структура Кельвина (или объемно-центрированная кубическая решетка) является оптимальным. Однако менее регулярная структура Уира – Фелана немного лучше.
Эта структура существует в природе в форме графита, где каждый лист графена напоминает проволочную сетку с прочными ковалентными углеродными связями. Синтезированы трубчатые листы графена; они известны как углеродные нанотрубки. У них есть много потенциальных применений из-за их высокой прочности на разрыв и электрических свойств. Силицен аналогичен.
Куриная проволока состоит из гексагональной решетки (часто нерегулярной) проволоки.

Самая плотная круговая упаковка расположена как шестиугольники в этой мозаике

Куриная проволока ограждение


A углеродная нанотрубка можно рассматривать как мозаику шестиугольника на цилиндрическая поверхность
Гексагональная мозаика появляется во многих кристаллах. В трех измерениях гранецентрированная кубическая и гексагональная плотная упаковка являются обычными кристаллическими структурами. Это самые плотные из известных сфер в трех измерениях, которые считаются оптимальными. Конструктивно они представляют собой параллельные слои гексагональных плиток, аналогичные структуре графита. Они отличаются тем, как слои расположены в шахматном порядке, причем гранецентрированный кубик является более правильным из двух. Чистая медь среди других материалов образует гранецентрированную кубическую решетку.
Существует три различных однородной окраски гексагональной мозаики, все они получены из отражательной симметрии конструкций Wythoff. (H, k) представляют собой периодическое повторение одной цветной плитки, считая гексагональные расстояния как h первым, а k вторым. Такой же подсчет используется в многогранниках Голдберга с обозначениями {p +, 3} h, k и может применяться к гиперболическим мозаикам при p>6.
| k-uniform | 1-uniform | 2-uniform | 3-uniform | ||||
|---|---|---|---|---|---|---|---|
| Симметрия | p6m, (* 632) | p3m1, (* 333) | p6m, (* 632) | p6, (632) | |||
| Изображение |  |  |  |  |  |  |  |
| Цвета | 1 | 2 | 3 | 2 | 4 | 2 | 7 |
| (h, k) | (1,0) | (1,1) | (2,0) | (2,1) | |||
| Шлефли | {6, 3} | t {3,6} | t {3} | ||||
| Wythoff | 3 | 6 2 | 2 6 | 3 | 3 3 3 | | ||||
| Кокстер | |||||||
| Конвей | H | tΔ | cH = t6daH | wH = t6dsH | |||
Трехцветная мозаика - это мозаика, созданная с помощью пермутоэдров порядка 3 .
A с фаской шестиугольная мозаика, в которой края заменяются новыми шестиугольниками и трансформируется в другую шестиугольную мозаику. В пределе исходные грани исчезают, а новые шестиугольники вырождаются в ромбы, и получается ромбическая мозаика.
| Шестиугольники (H) | шестиугольники с фаской (cH) | Ромби (daH) | ||
|---|---|---|---|---|
 |  |  |  |  |
Шестиугольники можно разрезать на наборы из 6 треугольников. Этот процесс приводит к двум 2-однородным мозаикам и треугольным мозаикам :
| Правильным мозаикам | Разрезание | 2-однородным мозаикам | Правильным мозаикам | |
|---|---|---|---|---|
 . Исходный . Исходный |  . .  |  . 1/3 рассеченный . 1/3 рассеченный |  . 2/3 рассеченный . 2/3 рассеченный |  . полностью рассеченный . полностью рассеченный |
| Обычная мозаика | Врезка | 2-однородные двойные элементы | Обычная мозаика | |
 . Исходный . Исходный |  |  . 1/3 вставка . 1/3 вставка |  . 2/3 вставка . 2/3 вставка |  . полностью вставка . полностью вставка |
Гексагональную плитку можно рассматривать как удлиненную ромбическую плитку, где каждая вершина ромбической плитки растягивается на новое ребро. Это похоже на соотношение мозаик ромбического додекаэдра и ромбо-гексагонального додекаэдра в 3-х измерениях.
 . Ромбическая мозаика . Ромбическая мозаика |  . Гексагональная мозаика . Гексагональная мозаика |  . Ограждение использует это отношение . Ограждение использует это отношение |
Также возможно разделить прототипы некоторых шестиугольных мозаик на два, три, четыре или девять равных пятиугольников:
 . Пятиугольная мозаика тип 1 с наложением правильных шестиугольников (каждый из которых состоит из двух пятиугольников). . Пятиугольная мозаика тип 1 с наложением правильных шестиугольников (каждый из которых состоит из двух пятиугольников). |  . пятиугольная мозаика типа 3 с наложением правильных шестиугольников (каждый из которых состоит из трех пятиугольников). . пятиугольная мозаика типа 3 с наложением правильных шестиугольников (каждый из которых состоит из трех пятиугольников). |  . Пятиугольная мозаика типа 4 с перекрытиями полуправильных шестиугольников (каждый из которых состоит из четырех пятиугольников). . Пятиугольная мозаика типа 4 с перекрытиями полуправильных шестиугольников (каждый из которых состоит из четырех пятиугольников). |  . Пятиугольная мозаика типа 3 с перекрытиями двух размеров правильных шестиугольников (состоящих из 3 и 9 пятиугольников соответственно). . Пятиугольная мозаика типа 3 с перекрытиями двух размеров правильных шестиугольников (состоящих из 3 и 9 пятиугольников соответственно). |
Эта мозаика топологически связана как часть последовательности правильных мозаик с шестиугольными гранями, начиная с шестиугольной мозаики, с символом Шлефли { 6, n} и диаграмма Кокстера ![]()
![]()
![]()
![]()
![]() , стремящаяся к бесконечности.
, стремящаяся к бесконечности.
* n62 мутация симметрии правильных мозаик: {6, n} [
| ||||||||
|---|---|---|---|---|---|---|---|---|
| Сферические | Евклидовы | Гиперболические мозаики | ||||||
 . {6,2} . {6,2} |  . {6,3 } . {6,3 } |  . {6,4} . {6,4} |  . {6,5} . {6,5} |  . {6,6} . {6,6} |  . . |  . {6,8} . {6,8} | ... |  . {6, ∞} . {6, ∞} |
Эта мозаика топологически связана с правильными многогранниками с фигурой вершины n, как часть последовательности, которая продолжается в гиперболическую плоскость.
* n32, изменение симметрии правильных мозаик: {n, 3} [
| |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Компактная гиперб. | Парако. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞, 3} | {12i, 3} | {9i, 3} | {6i, 3} | {3i, 3} |
Он аналогичным образом связан с однородным усеченным многогранником с фигурой вершины n.6.6.
* n32 мутация симметрии усеченных плиток: n.6.6 [
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим.. * n42. [n, 3] | Сферический | Евклид. | Компактный | Parac. | Некомпактный гиперболический | |||||||
| * 232. [2,3] | * 332. [3,3] | * 432. [4, 3] | * 532. [5,3] | * 632. [6,3] | * 732. [7,3 ] | * 832. [8,3]... | * ∞32. [∞, 3] | [12i, 3] | [9i, 3] | [6i, 3] | ||
| Усеченные. цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфигурация | 2.6.6 | 3.6.6 | 4.6. 6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis. цифры |  |  |  |  |  |  |  | |||||
| Конфиг. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Эта мозаика также является частью последовательности усеченных ромбических многогранников и мозаик с симметрией [n, 3] группы Кокстера. Куб можно рассматривать как ромбический шестигранник, в котором ромбы представляют собой квадраты. У усеченных форм есть правильные n-угольники в усеченных вершинах и нерегулярные шестиугольные грани.
| Мутации симметрии двойных квазирегулярных мозаик: V (3.n) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| * n32 | Сферический | Евклидов | Гиперболический | ||||||||
| * 332 | * 432 | * 532 | * 632 | * 732 | * 832... | * ∞32 | |||||
| Мозаика |  |  |  |  |  |  |  | ||||
| Конф. | В (3,3) | В (3,4) | В (3,5) | В (3,6) | В (3,7) | В (3,8) | В (3.∞) | ||||
Подобно однородным многогранникам существует восемь однородных мозаик, которые могут быть основаны на правильном шестиугольном мозаичном покрытии ( или двойная треугольная мозаика ).
Рисование плиток красного цвета на исходных гранях, желтого цвета в исходных вершинах и синего цвета вдоль исходных краев, есть 8 форм, 7 из которых топологически различны. (Усеченная треугольная мозаика топологически идентична шестиугольной мозаике.)
| Однородные шестиугольные / треугольные мозаики | ||||||||
|---|---|---|---|---|---|---|---|---|
| Фундаментальные. области | Симметрия : [6,3], (* 632) | [6,3], (632) | ||||||
| {6,3} | t {6,3} | r {6,3} | t {3,6} | {3,6} | rr {6,3} | tr {6,3} | sr {6,3} | |
 |  |  |  |  |  |  |  |  |
| Конфиг. | 6 | 3.12.12 | (6.3) | 6.6.6 | 3 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 |
Существует 3 типа моноэдральных выпуклых шестиугольных мозаик. Все они равногранны. У каждого есть параметрические вариации в пределах фиксированной симметрии. Тип 2 содержит отражения скольжения и является 2-изоэдральным, сохраняя хиральные пары различными.
| 1 | 2 | 3 | |
|---|---|---|---|
| p2, 2222 | pgg, 22 × | p2, 2222 | p3, 333 |
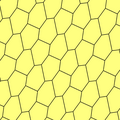 |  |  |  |
 . b = e. B + C + D = 360 ° . b = e. B + C + D = 360 ° |  . b = e, d = f. B + C + E = 360 ° . b = e, d = f. B + C + E = 360 ° |  . a = f, b = c, d = e. B = D = F = 120 ° . a = f, b = c, d = e. B = D = F = 120 ° | |
 . Решетка из 2 плиток . Решетка из 2 плиток |  . Решетка из 4 плиток . Решетка из 4 плиток |  . Решетка из 3 плиток . Решетка из 3 плиток | |
Шестиугольные мозаики могут быть выполнены с одинаковыми {6, 3} топология как правильная мозаика (3 шестиугольника вокруг каждой вершины). Существует 13 вариантов с изоэдральными гранями. Приведенная симметрия предполагает, что все грани одного цвета. Цвета здесь обозначают позиции решетки. Одноцветные (1-тайловые) решетки представляют собой параллелогон шестиугольники.
| pg (××) | p2 (2222) | p3 (333) | pmg (22 *) | |||
|---|---|---|---|---|---|---|
 |  |  |  |  |  | |
| pgg (22 ×) | p31m (3 * 3) | p2 (2222) | cmm (2 * 22) | p6m (* 632) | ||
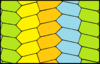 |  |  |  |  |  |  |
Другие изоэдрально-мозаичные топологические шестиугольные мозаики рассматриваются как четырехугольники и пятиугольники, которые не стыкуются между собой, а интерпретируются как коллинеарные смежные ребра:
| pmg (22 *) | pgg (22 ×) | cmm (2 * 22) | p2 (2222) | |||
|---|---|---|---|---|---|---|
 . Параллелограмм . Параллелограмм |  . Трапеция . Трапеция |  . Параллелограмм . Параллелограмм |  . Прямоугольник . Прямоугольник |  . Параллелограмм . Параллелограмм |  . Прямоугольник . Прямоугольник |  . Прямоугольник . Прямоугольник |
| p2 (2222) | pgg (22 ×) | p3 (333) |
|---|---|---|
 |  |  |
2-форма и 3-однородные мозаики имеют степень свободы вращения, которая искажает 2/3 шестиугольников, в том числе коллинеарный случай, который также можно рассматривать как мозаику шестиугольников и больших треугольников без края до края.
Его также можно деформировать в хиральную четырехцветную трехстороннюю плетеную фигуру. attern, искажая некоторые шестиугольники в параллелограммы. Плетеный узор с двумя цветными гранями имеет вращательную симметрию 632 (p6). Узор шеврон имеет симметрию pmg (22 *), которая понижается до p1 (°) с 3 или 4 цветными плитками.
| Обычный | Гирированный | Обычный | Плетеный | Шеврон |
|---|---|---|---|---|
| p6m, (* 632) | p6, ( 632) | p6m (* 632) | p6 (632) | p1 (°) |
 |  |  |  |  |
| p3m1, (* 333) | p3, (333) | p6m (* 632) | p2 (2222) | p1 (°) |
 |  |  |  |  |
Шестиугольная мозаика может быть используется как упаковка кругов, помещая круги одинакового диаметра в центре каждой точки. Каждый круг находится в контакте с 3 другими кругами в упаковке (число поцелуев ). Зазор внутри каждого шестиугольника позволяет разместить один круг, создавая наиболее плотную упаковку из треугольной мозаики , при этом каждый круг контактирует максимум с 6 кругами.

Есть 2 правильных комплексных апейрогона, имеющих общие вершины шестиугольной мозаики. Регулярные сложные апейрогоны имеют вершины и ребра, причем ребра могут содержать 2 и более вершины. Регулярные апейрогоны p {q} r ограничены: 1 / p + 2 / q + 1 / r = 1. Ребра имеют p вершин, а фигуры вершин r-угольные.
Первая состоит из 2 -ребра, по три вокруг каждой вершины, вторая имеет шестиугольные ребра, по три вокруг каждой вершины. Третий комплексный апейрогон, имеющий одни и те же вершины, является квазирегулярным, в котором чередуются 2-ребра и 6-ребра.
 |  |  |
| 2 {12} 3 или | 6 {4} 3 или |
|---|
| На Викискладе есть материалы, связанные с Гексагональной плиткой порядка 3. |
| ||||||
|---|---|---|---|---|---|---|
 |  |  |  |  / /  / /  | ||
| {3} | δ3 | hδ3 | qδ3 | Гексагональный | ||
| {3} | δ4 | hδ4 | qδ4 | |||
| {3} | δ5 | hδ5 | qδ5 | 24-элементный сотовый | ||
| {3} | δ6 | hδ6 | qδ6 | |||
| {3} | δ7 | hδ7 | qδ7 | 222 | ||
| {3} | δ8 | hδ8 | qδ8 | 133 • 331 | ||
| {3} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 | ||
| {3} | δ10 | hδ10 | qδ10 | |||
| {3} | δn | hδ n | qδ n | 1 k2 • 2 k1 • k21 | ||