| Ромбический додекаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Каталонский твердый |
| Диаграмма Кокстера | |
| Обозначение Конвея | jC |
| Тип лица | V3.4.3.4 |
| Лица | 12 |
| Края | 24 |
| Вершины | 14 |
| Вершины по типу | 8 {3} +6 {4} |
| Группа симметрии | O h, B 3, [4,3], (* 432) |
| Группа вращения | О, [4,3] +, (432) |
| Двугранный угол | 120 ° |
| Характеристики | выпуклый, гранно-транзитивный равногранный, изотоксальный, параллелоэдр |
 Кубооктаэдр ( двойственный многогранник ) Кубооктаэдр ( двойственный многогранник ) |  Сеть Сеть |
 3d модель ромбического додекаэдра
3d модель ромбического додекаэдра В геометрии, то ромбический додекаэдр является выпуклым многогранник с 12 конгруэнтных ромбическими лиц. У него 24 ребра и 14 вершин 2-х типов. Это Каталонский твердое и двойственный многогранник из кубооктаэдр.
Ромбический додекаэдр - это зоноэдр. Его многогранный двойник - кубооктаэдр. Длина длинной диагонали лица ровно √ 2 раза больше длины диагонали короткой стороны; таким образом, острые углы на каждой грани измеряют arccos (1/3), или примерно 70,53 °.
Будучи двойственным к архимедову многограннику, ромбический додекаэдр является гранно-транзитивным, что означает, что группа симметрии твердого тела транзитивно действует на его множестве граней. В элементарных терминах это означает, что для любых двух граней A и B существует вращение или отражение твердого тела, в результате чего оно занимает одну и ту же область пространства при перемещении грани A к грани B.
Ромбический додекаэдр можно рассматривать как выпуклую оболочку объединения вершин куба и октаэдра. 6 вершин, где встречаются 4 ромба, соответствуют вершинам октаэдра, а 8 вершин, в которых встречаются 3 ромба, соответствуют вершинам куба.
Ромбический додекаэдр - один из девяти реберно-транзитивных выпуклых многогранников, остальные - пять Платоновых тел, кубооктаэдр, икосододекаэдр и ромбический триаконтаэдр.
Ромбический додекаэдр можно использовать для мозаики трехмерного пространства: его можно сложить, чтобы заполнить пространство, так же, как шестиугольники заполняют плоскость.
Этот многогранник в пространстве заполнения тесселяции можно рассматривать как Вороную тесселяцию в гранецентрированной кубической решетке. Это зона Бриллюэна объемно-центрированных кубических (ОЦК) кристаллов. Некоторые минералы, такие как гранат, образуют ромбический додекаэдрический кристалл. Как отметил Иоганн Кеплер в своей книге о снежинках 1611 года ( Strena seu de Nive Sexangula), медоносные пчелы используют геометрию ромбических додекаэдров для формирования сот из мозаики ячеек, каждая из которых представляет собой шестиугольную призму, покрытую половиной ромбического додекаэдра. Ромбический додекаэдр также встречается в элементарных ячейках алмаза и алмазоидов. В этих случаях четыре вершины (чередующиеся тройные) отсутствуют, но химические связи лежат на остальных ребрах.
График ромбического додекаэдра негамильтонов.
Ромбический додекаэдр можно разрезать на четыре тупых треугольных трапеции вокруг его центра. Эти ромбоэдры являются ячейками треугольных трапециевидных сот. Аналогия: правильный шестиугольник можно разрезать на 3 ромба вокруг его центра. Эти ромбы представляют собой плитки ромбика.
В коллекциях Лувра есть матрица в форме ромбического додекадрона, датируемая Птолемеевым Египтом. Грани начертаны греческими буквами, представляющими числа от 1 до 12: Α Β Γ Δ Ε Ζ Ϛ Η Θ Ι ΙΑ ΙΒ. Функция матрицы неизвестна.

Ромбический додекаэдр

Ромбически рассеченный шестиугольник

Гранатовый кристалл

На этой анимации показано построение ромбического додекаэдра из куба путем инвертирования пирамид куба с центральными гранями.
Обозначив a длину ребра ромбического додекаэдра,
Площадь поверхности A и объем V ромбического додекаэдра с длиной ребра a равны:
Ромбического додекаэдра имеет четыре специальные ортогональные проекции вдоль его оси симметрии, сосредоточенных на лице, кромки, и два типа вершин, в три раза и в четыре раза. Последние два соответствуют плоскостям Кокстера B 2 и A 2.
| Проективная симметрия | [4] | [6] | [2] | [2] |
|---|---|---|---|---|
| Ромбический додекаэдр |  |  |  |  |
| Кубооктаэдр (двойственный) |  |  |  |  |
 Вариации пиритоэдра между кубом и ромбическим додекаэдром Вариации пиритоэдра между кубом и ромбическим додекаэдром |  Расширение ромбического додекаэдра Расширение ромбического додекаэдра |
Восемь вершин, где три грани встречаются под тупыми углами, имеют декартовы координаты :
Координаты шести вершин, где четыре грани пересекаются под острыми углами:
Ромбический додекаэдр можно рассматривать как вырожденный предельный случай пиритоэдра с перестановкой координат (± 1, ± 1, ± 1) и (0, 1 + h, 1 - h 2) с параметром h = 1.
Ромбического додекаэдра является параллелоэдр, А пространство заполнения полиэдр, dodecahedrille, будучи двойственной к tetroctahedrille или половину кубического соты, и описываются двумя схемами Кокстера :![]()
![]()
![]()
![]()
![]() а также
а также ![]()
![]()
![]()
![]()
![]() . При симметрии D 3d его можно рассматривать как удлиненный тригональный трапецоэдр.
. При симметрии D 3d его можно рассматривать как удлиненный тригональный трапецоэдр.
 Ромбический додекаэдр может замощить пространство посредством трансляционных копий самого себя, как и звездчатый ромбический додекаэдр. Ромбический додекаэдр может замощить пространство посредством трансляционных копий самого себя, как и звездчатый ромбический додекаэдр. | 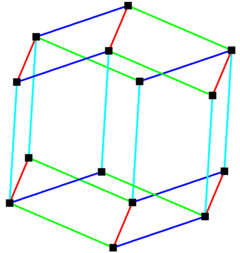 Ромбический додекаэдр может быть построен с 4 наборами 6 параллельных ребер. Ромбический додекаэдр может быть построен с 4 наборами 6 параллельных ребер. |
Другие конструкции симметрии ромбического додекаэдра также заполняют пространство, и как параллелоэдры они похожи на вариации заполняющих пространство усеченных октаэдров.
Например, с 4 квадратными гранями и ромбическими гранями под углом 60 градусов и двугранной симметрией D 4h, порядок 16. Его можно рассматривать как кубооктаэдр с квадратными пирамидами, увеличенными сверху и снизу.
 |  Сеть Сеть | Координаты
|
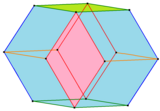 Додекаэдр Билинского с краями и передними гранями, окрашенными в соответствии с их положением симметрии. Додекаэдр Билинского с краями и передними гранями, окрашенными в соответствии с их положением симметрии. |  Додекаэдр Билинского, раскрашенный параллельными гранями Додекаэдр Билинского, раскрашенный параллельными гранями |
В 1960 году Станко Билински открыл второй ромбический додекаэдр с 12 совпадающими гранями ромба, додекаэдр Билински. Он имеет ту же топологию, но другую геометрию. Ромбические грани в этой форме имеют золотое сечение.
| Первая форма | Вторая форма |
|---|---|
 | 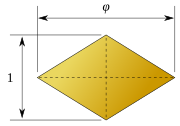 |
| √ 2: 1 | √ 5 + 1/2: 1 |

 Чертеж и кристаллическая модель дельтовидного додекаэдра
Чертеж и кристаллическая модель дельтовидного додекаэдра Другой топологически эквивалентный вариант, иногда называемый дельтовидным додекаэдром или трапециевидным додекаэдром, является изоэдрическим с тетраэдрическим порядком симметрии 24, искажая ромбические грани в воздушных змеев (дельтоидов). Он имеет 8 вершин, изменяемых внутрь или наружу в альтернативных наборах по 4, с предельным случаем тетраэдрической огибающей. Вариации можно параметризовать с помощью ( a, b), где b и a зависят друг от друга, так что тетраэдр, определяемый четырьмя вершинами грани, имеет нулевой объем, то есть является плоской гранью. (1,1) - ромбическое решение. По мере приближения ( а)1/2, ( б) стремится к бесконечности. Всегда держит1/а + 1/б = 2, причем a, bgt; 1/2.
| (1,1) | (7/8,7/6) | (3/4,3/2) | (2/3, 2) | (5/8,5/2) | (9/16,9/2) |
|---|---|---|---|---|---|
 |  |  |  |  |  |
 Сферический ромбический додекаэдр
Сферический ромбический додекаэдр | Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия : [4,3], (* 432) | [4,3] + (432) | [1 +, 4,3] = [3,3] (* 332) | [3 +, 4] (3 * 2) | |||||||
| {4,3} | т {4,3} | г {4,3} г {3 1,1 } | т {3,4} т {3 1,1 } | {3,4} {3 1,1 } | rr {4,3} s 2 {3,4} | tr {4,3} | sr {4,3} | ч {4,3} {3,3} | ч 2 {4,3} т {3,3} | с {3,4} с {3 1,1 } |
| | | | | | | | | | ||
| | | | | | | | ||||
| | | | | | | | | | | |
| Двойники к однородным многогранникам | ||||||||||
| V4 3 | V3.8 2 | В (3,4) 2 | V4.6 2 | V3 4 | V3.4 3 | V4.6.8 | V3 4.4 | V3 3 | V3.6 2 | V3 5 |
| | | | | | | | | | | |
| | | | | | | | ||||
| | | | | | | | | | | |
При проецировании на сферу (см. Справа) можно увидеть, что ребра образуют ребра двух тетраэдров, расположенных в их двойных положениях (стелла octangula). Эта тенденция продолжается с дельтоидальным икоситетраэдром и дельтоидальным гексеконтаэдром для двойных пар других правильных многогранников (наряду с треугольной бипирамидой, если следует учитывать неправильные мозаики), давая этой форме альтернативное систематическое название дельтоидного додекаэдра.
| Симметрия * n 32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| * 232 [2,3] | * 332 [3,3] | * 432 [4,3] | * 532 [5,3] | * 632 [6,3] | * 732 [7,3] | * 832 [8,3]... | * ∞32 [∞, 3] | |
| Рисунок Config. |  V3.4.2.4 V3.4.2.4 |  V3.4.3.4 V3.4.3.4 |  V3.4.4.4 V3.4.4.4 |  V3.4.5.4 V3.4.5.4 |  V3.4.6.4 V3.4.6.4 |  V3.4.7.4 V3.4.7.4 |  V3.4.8.4 V3.4.8.4 |  V3.4.∞.4 V3.4.∞.4 |
Этот многогранник является частью последовательности ромбических многогранников и мозаик с симметрией [ n, 3] группы Кокстера. Куб можно рассматривать как ромбический шестигранник, в котором ромбы представляют собой квадраты.
| Изменения симметрии двойственных квазирегулярных мозаик: V (3.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| * n32 | Сферический | Евклидово | Гиперболический | ||||||||
| * 332 | * 432 | * 532 | * 632 | * 732 | * 832... | * ∞32 | |||||
| Черепица |  |  |  |  |  |  |  | ||||
| Конф. | В (3,3) 2 | В (3,4) 2 | В (3,5) 2 | В (3,6) 2 | В (3,7) 2 | V (3.8) 2 | V (3.∞) 2 | ||||
| * n 42 изменения симметрии квазирегулярных двойственных мозаик: V (4.n) 2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия * 4n2 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | ||||||
| * 342 [3,4] | * 442 [4,4] | * 542 [5,4] | * 642 [6,4] | * 742 [7,4] | * 842 [8,4]... | * ∞42 [∞, 4] | [iπ / λ, 4] | ||||
| Кафельная конф. |  V4.3.4.3 V4.3.4.3 |  V4.4.4.4 V4.4.4.4 |  V4.5.4.5 V4.5.4.5 |  V4.6.4.6 V4.6.4.6 |  V4.7.4.7 V4.7.4.7 |  V4.8.4.8 V4.8.4.8 |  V4.∞.4.∞ V4.∞.4.∞ | V4.∞.4.∞ | |||
Точно так же это относится к бесконечной серии мозаик с конфигурациями граней V3.2 n.3.2 n, первая в евклидовой плоскости, а остальные в гиперболической плоскости.
 V3.4.3.4 (нарисовано сеткой ) V3.4.3.4 (нарисовано сеткой ) |  V3.6.3.6 Мозаика на евклидовой плоскости Ромбилловая мозаика V3.6.3.6 Мозаика на евклидовой плоскости Ромбилловая мозаика | 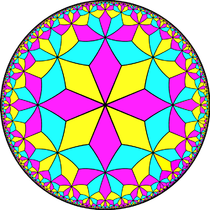 V3.8.3.8 Гиперболическая мозаика на плоскости (нарисованная в модели диска Пуанкаре ) V3.8.3.8 Гиперболическая мозаика на плоскости (нарисованная в модели диска Пуанкаре ) |
Как и многие выпуклые многогранники, ромбический додекаэдр можно сделать звездчатым, если удлинить грани или ребра до тех пор, пока они не встретятся, чтобы сформировать новый многогранник. Несколько таких звездочек были описаны Дорманом Люком.
 На этой анимации показано построение звездчатого ромбического додекаэдра путем инвертирования пирамид с центральной гранью ромбического додекаэдра.
На этой анимации показано построение звездчатого ромбического додекаэдра путем инвертирования пирамид с центральной гранью ромбического додекаэдра. Первая звездчатая форма, которую часто называют звездчатым ромбическим додекаэдром, хорошо известна. Его можно рассматривать как ромбический додекаэдр с каждой гранью, увеличенной путем присоединения к нему пирамиды с ромбической основой, с такой высотой пирамиды, что стороны лежат в плоскостях граней соседних граней:

Первая звездчатая форма ромбического додекаэдра

3D модель разложения на 12 пирамид и 4 полукуба
Лука описывает еще четыре звёздчатых звезды: вторую и третью звёздчатые (расширяющиеся наружу), одна образована удалением второй из третьей, а другая - добавлением исходного ромбического додекаэдра к предыдущему.
| Второй | В третьих |
|---|---|
 Звездчатый ромбический додекаэдр Звездчатый ромбический додекаэдр |  Большой звездчатый ромбический додекаэдр Большой звездчатый ромбический додекаэдр |
 В идеальной проекции с ориентацией на вершину две вершины тессеракта (отмечены бледно-зеленым цветом) проецируются точно в центр ромбического додекаэдра.
В идеальной проекции с ориентацией на вершину две вершины тессеракта (отмечены бледно-зеленым цветом) проецируются точно в центр ромбического додекаэдра. Ромбический додекаэдр образует оболочку трехмерной проекции тессеракта с первой вершиной. Есть ровно два способа разложения ромбического додекаэдра на четыре конгруэнтных ромбоэдра, давая восемь возможных ромбоэдров в качестве проекций тессерактов из 8 кубических ячеек. Один набор проективных векторов: u = (1,1, -1, -1), v = (- 1,1, -1,1), w = (1, -1, -1,1).
Ромбический додекаэдр формирует максимальное поперечное сечение 24-ячейки, а также образует оболочку его параллельной проекции, обращенной к вершине, в трех измерениях. Ромбический додекаэдр можно разложить на шесть конгруэнтных (но нерегулярных) квадратных дипирамид, встречающихся в одной вершине в центре; они образуют изображения шести пар октаэдрических ячеек с 24 ячейками. Остальные 12 октаэдрических ячеек выступают на грани ромбического додекаэдра. Неравномерность этих изображений связана с проективным искажением; грани 24-ячейки являются правильными октаэдрами в 4-м пространстве.
Это разложение дает интересный метод построения ромбического додекаэдра: разрезать куб на шесть равных квадратных пирамид и прикрепить их к граням второго куба. Треугольные грани каждой пары соседних пирамид лежат в одной плоскости и поэтому сливаются в ромбы. 24-элементная ячейка также может быть построена аналогичным образом с использованием двух тессерактов.
В компоновке реактивного колеса космического корабля обычно используется четырехгранная конфигурация четырех колес. Для колес, которые работают одинаково (с точки зрения максимального крутящего момента и максимального углового момента) в обоих направлениях вращения и по всем четырем колесам, максимальный крутящий момент и максимальный крутящий момент для 3-осевой системы управления ориентацией (с учетом идеализированных приводов) задаются путем проецирования. тессеракт, представляющий пределы крутящего момента или импульс каждого колеса в 3D пространства через матрицу колесных осей 3 × 4; полученный трехмерный многогранник представляет собой ромбический додекаэдр. Такое расположение реактивных колес - не единственная возможная конфигурация (более простое расположение состоит из трех колес, установленных для вращения вокруг ортогональных осей), но оно дает преимущество в обеспечении избыточности для смягчения отказа одного из четырех колес (с ухудшенными общими характеристиками. доступный с оставшихся трех активных колес) и в обеспечении более выпуклой оболочки, чем куб, что приводит к меньшей зависимости маневренности от направления оси (с точки зрения привода / установки). Массовые характеристики космического корабля влияют на общий импульс и маневренность системы, поэтому уменьшение отклонения границы оболочки не обязательно приводит к увеличению однородности предпочтительных смещений осей (то есть, даже с идеально распределенным пределом характеристик внутри подсистемы исполнительного механизма, предпочтительные оси вращения не обязательно произвольны. на системном уровне).