 . Инволюционная симметрия. Cs, (*). [] = . Инволюционная симметрия. Cs, (*). [] = |  . Циклическая симметрия. Cnv, (* nn). [n] = . Циклическая симметрия. Cnv, (* nn). [n] = |  . Двугранная симметрия. Dnh, (* n22). [n, 2] = . Двугранная симметрия. Dnh, (* n22). [n, 2] = | |
| Группа полиэдров, [n, 3], (* n32) | |||
|---|---|---|---|
 . Тетраэдрическая симметрия. Td, (* 332). [3,3] = . Тетраэдрическая симметрия. Td, (* 332). [3,3] = |  . Октаэдрическая симметрия. Oh, (* 432). [4,3] = . Октаэдрическая симметрия. Oh, (* 432). [4,3] = |  . Икосаэдрическая симметрия. Ih, (* 532). [5,3] = . Икосаэдрическая симметрия. Ih, (* 532). [5,3] = | |
В геометрии, двугранная симметрия в Трехмерная - одна из трех бесконечных последовательностей точечных групп в трех измерениях, которые имеют группу симметрии, которая в качестве абстрактной группы является группой диэдра Dih n (n ≥ 2).
Всего 3 типа диэдральной симметрии в трех измерениях, каждое из которых показано ниже в трех обозначениях: обозначение Шенфлиса, обозначение Кокстера и обозначение орбифолда.
Для данного n все три имеют n-кратную симметрию вращения относительно одной оси (поворот на угол 360 ° / n не изменяет объект), и 2 -сгиб вокруг перпендикулярной оси, следовательно, около n из них. Для n = ∞ они соответствуют трем фризовым группам. Обозначение Шёнфлиса, с нотацией Кокстера в скобках и орбифолдной нотацией в скобках. Термин горизонтальный (h) используется по отношению к вертикальной оси вращения.
В 2D группа симметрии D n включает отражения в линиях. Когда 2D-плоскость встроена горизонтально в 3D-пространство, такое отражение можно рассматривать либо как ограничение этой плоскости отражения в вертикальной плоскости, либо как ограничение плоскости поворота вокруг линии отражения на 180 °. В 3D различают две операции: группа D n содержит только вращения, но не отражения. Другая группа - это пирамидальная симметрия Cnvтого же порядка.
При симметрии отражения относительно плоскости, перпендикулярной n-кратной оси вращения, мы имеем D nh [n], (* 22n).
Dnd(или D nv), [2n, 2], (2 * n) имеет вертикальные зеркальные плоскости между горизонтальными осями вращения, а не через них. В результате вертикальная ось представляет собой ось 2n-кратного вращения.
Dnh- это группа симметрии для правильной n-сторонней призмы, а также для правильной n-сторонней бипирамиды. D nd - группа симметрии для правильной n-сторонней антипризмы, а также для правильного n-стороннего трапецоэдра. D n - группа симметрии частично повернутой призмы.
n = 1 не включается, потому что три симметрии равны другим:
Для n = 2 нет одной главной оси и двух дополнительных осей, но есть три эквивалентных.
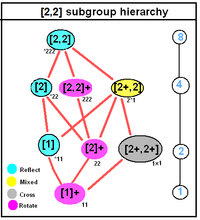 . D2h, [2,2], (* 222) . D2h, [2,2], (* 222) | 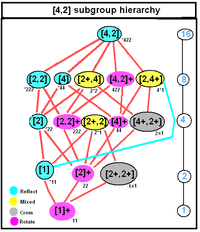 . D4h, [4,2], (* 224) . D4h, [4,2], (* 224) |
Для D nh, [n, 2], (* 22n), порядок 4n
Для D nd, [2n, 2], (2 * n), порядок 4n
Dndтакже является подгруппой D 2nh.
| D2h, [2,2], (* 222). Порядок 8 | D2d, [4,2], (2 * 2). Порядок 8 | D3h, [3,2], (* 223). Заказ 12 |
|---|---|---|
 . баскетбол пути шва . баскетбол пути шва |  . бейсбол пути шва. (без учета направления шва) . бейсбол пути шва. (без учета направления шва) |  . Пляжный мяч. (без учета цветов) . Пляжный мяч. (без учета цветов) |
Dnh, [n], (* 22n):
 . призмы . призмы |
D5h, [5], (* 225):
 . Пентаграммическая призма . Пентаграммическая призма |  . Пентаграммическая антипризма . Пентаграммическая антипризма |
D4d, [8,2], (2 * 4):
 . Курносая квадратная антипризма . Курносая квадратная антипризма |
D5d, [10,2], (2 * 5):
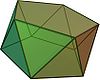 . Пятиугольная антипризма . Пятиугольная антипризма |  . Пентаграмма скрещенная антипризма . Пентаграмма скрещенная антипризма | 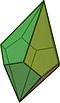 . пятиугольный трапецоэдр . пятиугольный трапецоэдр |
D17d, [ 34,2], (2 * 17):
 . Гептадекагональная антипризма . Гептадекагональная антипризма |