Войти
В математике используется бивектор или 2-вектор . величина в внешней алгебре или геометрической алгебре, которая расширяет идею скаляров и векторов. Если скаляр считается величиной нулевого порядка, вектор - величиной первого порядка, то бивектор можно рассматривать как второго порядка. Бивекторы находят применение во многих областях математики и физики. Они связаны с комплексными числами в двух измерениях и с псевдовекторами и кватернионами в трех измерениях. Их можно использовать для создания поворотов в любом количестве измерений. Они также используются в физике, связывая вместе ряд не связанных друг с другом величин.
Бивекторы генерируются с помощью вектора внешнего продукта на векторх: с учетом двухов a и b их внешний продукт a∧ bявляется бивектором, как и сумма любых бивекторов. Не все бивекторы могут быть созданы как единый внешний продукт. Точнее, бивектор, который может быть выражен как внешний продукт, называется основным; в трех измеренийх все бивекторы просты, но в более высоких измеренийх дело обстоит иначе. Внешнее произведение двух векторов является антикоммутативным и чередующимся, поэтому b∧ aявляется отрицанием бивектора a∧ b, производя противоположную ориентацию, а a∧ a- нулевой бивектор.
Сегменты параллельной плоскости с одинаковой плоскостью ориентации, формы одному и тому же бивектору a∧ b.Геометрический простой бивектор можно интерпретировать как ориентированный сегмент плоскости , так же как другого могут рассматриваться как направлено отрезки линии. Бивектор a∧ bимеет , равную площадь параллелограмма с ребрами a и b, имеет положение плоскости, охватываемой a и направлением b, и имеет ориентацию, являющуюся выровняемым вращением, которое выровняло бы a с b.
. В терминах любой поверхности является одним и тем же бивектором, если она имеет одинаковую площадь, одинаковую ориентацию и параллельна одной плоскости (см. Рисунок).
Бивектор был впервые определен в 1844 году немецким математиком Германом Грассманном во внешней алгебре как результат двух внешних произведений векторов. Буквально в прошлом году в Ирландии Уильям Роуэн Гамильтон открыл кватернионы. Только когда английский математик Уильям Кингдон Клиффорд в 1888 году добавил геометрическое произведение к алгебре Грассмана, идеи Гамильтона и Грассмана, и основал алгебру Клиффорда, что бивектор как он есть сегодня известно было полностью понято.
Примерно в это время Джозия Уиллард Гиббс и Оливер Хевисайд разработали векторное исчисление, котороеало отдельные кросс-продукт и скалярные произведения, полученные в результате умножения кватернионов. Успех удовлетворит исчисления и книги Гиббса Векторный анализ и Уилсона привел к тому, что идеи Гамильтона и Клиффорда долгое время игнорировались, начиная с 20-го века. математика и физика века были сформулированы в векторных терминах. Гиббс используется, чтобы заполнить роль бивекторов в трех измерениях, и использовать «бивектор» для описания несвязанной величины, использование, иногда копировалось. Сегодня бивектор в основном изучается как тема в геометрической алгебре, алгебре Клиффорда над действительным или комплексным векторным пространством с невырожденная квадратичная форма. Возрождение его возглавил Дэвид Хестенес, который вместе с другими применил геометрическую алгебру к ряду новых приложений в физике.
В этой статье бивектором будет рассматриваться только в реальных геометрических алгебрах. На практике это не является большим ограничением, поскольку все полезные приложения основаны на таких алгебрах. Кроме того, если не указано, все примеры имеют евклидову метрику и, следовательно, Положительно-определенную , имеют квадратичную форму.
бивектор из определения геометрического произведения над векторным пространством. Для векторов a, bи c геометрическое произведение векторов определяется следующим образом:
Где Q - квадратичная форма, | a | - величина для a, а ϵ a- сигнатура метрики. Для пространства с евклидовой метрикой ϵ aравно 1, поэтому его можно опустить, и условие сжатия станет: 
Из ассоциативности a(ab) = ab, скаляр, умноженный на b . Когда b не параллелен и, следовательно, не является скалярным кратным a, ab, не может быть скаляром. Но
- это сумма скаляров и, следовательно, скаляр. Согласно закону косинусов на треугольнике, образованном воздушном пространстве, его значение равно | a||b| cosθ, где θ - угол между векторами. Следовательно, он идентичен внутреннему произведению между двумя явлениями и записывается таким же образом:
Он симметричен со скалярным знаком, И может быть, установление угла между двумя векторами: в частности, если a и b ортогональны, произведение равно нулю.
Так же, как интерьерный продукт может быть сформулирован как симметричная часть геометрического продукта другого количества, внешний продукт (иногда известный как «клин» или «прогрессивный» продукт) можно определить как его антисимметричная часть :
Он антисимметричен в a и b
и путем добавления:
То есть геометрическое произведение представляет собой симметричный внутренний продукт и антисимметричный внешний продукт.
Чтобы изучить природу a∧ b, рассмотрим формулу
который с использованием тригонометрического тождества Пифагора дает значение (a∧ b)
С отрицательным вектором квадратом он может быть скалярной или величиной, поэтому это объект нового типа, бивектор . | b | | sinθ |, где θ - угол между вектором ми, и поэтому равенство нулю для параллельных векторов.
Чтобы отличить их от дизайна, bi здесь написаны жирным шрифтом, например:
, хотя используются и другие соглашения, в частности, как и бивекторы, элементы геометрической алгебры.
Алгебра, сгенерированная геометрическим продуктом, - это геометрическая алгебра над векторным пространством. Для евклидова пространство записывается 
Подалгебра, порожденная бивекторами, является четной подалгеброй геометрической алгебры, записываемой Cℓ +. сущ. Эта алгебра является результатом рассмотрения всех произведений скаляров и бивекторов, порожденных геометрическим произведением. Он имеет размерность 2 и содержит как линейное подпространство с размерностью 1 / 2n (n - 1) (треугольное число ). В двух и трех измерениях четная подалгебра содержит только скаляры и бив, и каждый из них представляет особый интерес. В двух измеренийх четная подалгебра изоморфна комплексным числам, ℂ, тогда как в трех измерениях она изоморфна кватернионам, ℍ. В более общем смысле, четная подалгебра может быть сестра для создания поворотов в любом измерении и может быть сгенерирована бивекторами в алгебре.
Как отмечено в предыдущем разделе, простым простым бивектора, произведено производство двух векторов a <169 и b, это | a||b| sin θ, где θ - угол между векторами. Записано | B |, где B - бивектор.
Для обычных бивекторов величина может быть вычислена, взяв норму бивектора, рассматриваемого как вектор в простран ∧ℝ. Если величина равна нулю, то все компоненты бивектора равны нулю, а бивектор - это нулевой бивектор, который как элемент геометрической алгебры равен скалярному нулю.
Единичный бивектор - это единичный бивектор. Он может быть получен из любого ненулевого бивектора бивектора на его часть, то есть
Особый интерес представляют единичные бивекторы, образованные из произведений стандартного базиса . Если eiи ejявляются базисными векторами, то произведение ei∧ ejявляется бивектором. Технически ми ортогональны, это просто eiej, записанное как eij, с единичной величиной, существующим единичными днями. Множество всех таких бивекторов составляет основу ∧ℝ. Например, в четырех измерениях основанием для ∧ℝ является (e1e2, e1e3, e1e4, e2e3, e2e4, e3e4) или (e12, e13, e14, e23, e24, e34).
Внешнее произведение двухов является бивектором, но не все бивекторы являются внешними произведениями двух векторов. бивектор
не может быть Бивектор, который можно записать как внешнее произведение двух векторов, прост. Бивектор имеет реальный квадрат тогда и только тогда, когда он простой, и только простые биве кторы могут быть геометрически представлены ориентированной плоской областью.
Геометрическое произведение двух бивекторов, A и B,
Величина A· B- это продукт интерьера со скалярными значениями, а A∧ B- это внешний продукт 4 степени, который возникает в четырех или более измерениях. Величина A× B- это бивекторное произведение коммутатора, заданное формулой
Пространство бивекторов ∧ℝ является алгеброй Ли над, с коммутаторное произведение в виде скобки Ли. Полное геометрическое произведение бивекторов порождает четную подалгебру.
Особый интерес представляет продукт бивектора с самим собой. Коммутаторное произведение антисимметрично, упрощается до
Если бивектор простой, последний член равен нулю, которое представляет собой скалярное значение A· A, которое можно использовать для проверки простоты. В частности, внешний продукт бивекторов существует только в четырех или более измерениях, поэтому все бивекторы в двух и трех измерениях просты.
При работе с координатами геометрической алгебре обычно для записи базисных векторов как (e1, e2,...), соглашение, которое будет работать здесь.
A вектор в реальном двумерном пространстве ℝ можно записать a = a 1e1+ a 2e2, где a 1 и a 2 - действительные числа, e1и e2- ортонормированные базисные свойства. Геометрическое произведение двух таких векторов равно
Его можно разделить на симметричное скалярное внутреннее произведение и антисимметричное бивекторное внешнее произведение:
Все бивекторы в двух измерениях имеют эту форму, которая кратна бивектору e1e2, написано e12, чтобы подчеркнуть, что это бивектор, а не вектор. Величина e12равна 1, причем
, поэтому он называется единичный бивектор . Термин «единичный бивектор» местный язык в других измерениях, но он определен однозначно (с точностью до знака) только в двух измерениях, и все бивекторы кратны e12. В качестве элемента наивысшего уровня алгебры e12является также псевдоскаляр , используемый символ i.
Благодаря свойствам отрицательного квадрата и единичной величины единичный бивектор может быть идентифицирован с мнимой единицей из комплексных чисел. Бивекторы и скаляры вместе образуют четную подалгебру геометрической алгебры, которая изоморфна комплексным числам ℂ. Четная подалгебра имеет базис (1, e12), вся алгебра имеет базис (1, e1, e2, e12).
Комплексные числа обычно идентифицируются с помощью координатных осей и двумерных векторов, что означает связывание их с векторными элементами геометрической алгебры. В этом нет противоречия, для перехода от устройства к комплексному ось должна быть идентифицирована как действительная ось, скажем e1. Он умножается на все для создания элементов четной подалгебры.
Все свойства комплексных чисел могут быть получены из бивекторов, но два из них имеют особый интерес. Во-первых, как и в случае с комплексными числами, произведения бивекторов и четной подалгебры коммутативны. Это только для двух измерений, поэтому свойства бивектора в двух измерениях, которые зависят от коммутативности, обычно не распространяются на более высокие измерения.
Во-вторых, общий бивектор можно записать
где θ - это настоящий номер. Помещение этого в ряд Тейлора для экспоненциальной карты и использование e12= −1 приводит к бивекторной версии формулы Эйлера,
который при умножении на любой вектор поворачивает его на угол θ относительно начала координат:
Произведение вектора с бивектором в двух измерениях является антикоммутативным, поэтому все следующие произведения генерируют одинаковое вращение
Из них последний продукт - тот, который обобщает на более высокие измерения. Необходимое количество называется ротор и обозначается символом R, поэтому в двух измерениях ротор, который вращается на угол θ, может быть записан как
и вращение, которое он генерирует, равно
В трех измеренийх геометрическое произведение два вектора:
можно разделить на симметричное скалярнозначное внутреннее произведение и антисимметричное бивекторнозначное внешнее произведение:
В трех измерениях все бивекторы просты и, следовательно, результатом внешнего продукта. Единичные бивекторы e23, e31и e12образуют основу пространства бивекторов ∧ℝ, само является трехмерным линейным пространством. Итак, если общий бивектор равен:
их можно складывать как поверхность
, а при умножении они дают следующее
который можно разделить на симметричную скалярную и антисимметр ичная бивекторные части следующим образом:
Внешний продукт двух бивекторов в измерении трехх равенстве нулю.
Бивектор B может быть записан как произведение его величины и единичного бивектора, поэтому записываем β вместо | B | и используя Тейлора для экспоненциального ряда изображений, можно показать, что
Это еще одна версия формулы Эйлера, но с общим бивектором в трех измеренийх. В отличие от двухмерных бивекторов не коммутативны, поэтому, зависящие от коммутативности, не применяются в трех измерениях. Например, в целом e ≠ ee в трех (или более) измерениях.
Полная геометрическая алгебра в трех измерениях, Cℓ 3 (ℝ), имеет базис (1, e1, e2, e3, e23, e31, e12, e123). Элемент e123 является тривектором, а псевдоскаляр для геометрии. Бивекторы в трех измерениях иногда отождествляются с псевдовекторами, они связаны, как обсуждается ниже.
Бивекторы не закрываются геометрическим произведением, но четная подалгебра. В трех измерений он состоит из всех скалярных и бивекторных элементов геометрической алгебры, поэтому общий элемент может быть записан, например, a + A, где a - скалярная часть, а A - бивекторная часть. Он написан Cℓ +. 3 и имеет основу (1, e23, e31, e12). Произведение двух общих элементов четной подалгебры:
Четная подалгебра, то есть алгебра, состоящая из скаляров и бивекторов, изоморфна кватернионам, ℍ. Это можно увидеть, сравнивая основу с кватернионной продуктам или из указанного продукта, который идентичен кватернионному продукту, за исключением знака, которое относится к отрицательным продуктам в бивекторном внутреннем продукте A· B. Другие свойства кватернионов похожи на другие, связанные с геометрической алгеброй или получены из нее.
Это говорит о том, что обычное разделение кватерниона на скалярную и векторную части было бы лучше представить как разделение на скалярную и бивекторную части; если это сделано, произведение кватерниона будет просто геометрическим произведением. Он также связывает кватернионы в трех измерениях с комплексными числами в двух, поскольку каждый изоморфен четной подалгебре для измерения, полученный на более высоких измерениях.
Вектор вращения представления вращений ось-угол представляет собой компактный способ представления вращений в трех измерениях. В своей наиболее компактной форме он представляет собой единое средство движения ω, которое представляет собой ось вращения , на (подписанный) угол поворот θ, так что величина полного вектора поворота θω равна (беззнаковому) угла поворота.
Кватернион, связанный с вращением:
В геометрической алгебре вращение представленного бивектором. Это можно увидеть в его отношении к кватернионам. Пусть Ω - единичный бивектор в плоскости вращения, а θ - угол поворота . Тогда бивектор вращения - это Ωθ. Кватернион близко соответствует экспоненте половины бивектора Ωθ. То есть компоненты кватерниона соответствуют скалярной и бивекторной частей следующего выражения:
Экспоненту можно определить в ее степенном ряду и легко вычислить, используя тот факт, что квадрат Ω равен -1.
Итак, вращения можно представить бивекторами. Подобно тому, как кватернионы имеют геометрической алгебры, они связаны экспоненциальным изменением в этой алгебре.
Бивектор Ω θ генерирует вращение через экспоненциальную карту. Сгенерированные четные элементы вращают общий вектор в трех измерениях, как кватернионы:
Что касается двух измерений, величина e называется ротор и обозначается R. Величина e тогда равна R, и они генерируют вращение следующим образом: 622>v ′ = R v R - 1. {\ displaystyle \ mathbf {v} '= R \ mathbf {v} R ^ {- 1}. \,}
Это идентично двум измерениям, за исключением того, что здесь роторы выделяют собой четырехмерные объекты, изоморфные кватернионам. Это можно обобщить на все измерения, с роторами, элементами четной подалгебры с единичной величиной, генерируемым экспоненциальным отображением из бивекторов. Они образуют двойную крышку над группой, поэтому роторы R и -R представляют собой одно и то же вращение.
Бивекторы изоморфны кососимметричным матрицам ; общий бивектор B 23e23+ B 31e31+ B 12e12отображается в матрицу
Это умножение на с разных сторон дает тот же вектор, что и произведение искусства и бивектора за вычетом внешнего произведения; Примером является тензор угловой скорости.
Кососимметричные матрицы генерируют ортогональные матрицы с детерминантом 1 через экспоненциальную карту. В частности, показатель степени бивектора, связанного с поворотом, представляет собой матрицу вращения , то есть матрица вращения M R, заданная вышеуказанная кососимметричной матрицей, равна
Вращение, описываемое M R, такое же, как и вращение ротора R, заданное как
и матрица M R также могут быть рассчитаны непосредственно из ротора R:
Бивекторы связаны с собственные значения матрицы вращения. Для данной матрицы собственных значений могут быть вычислены другие решения классического уравнения для этой матрицы 0 = det (M - λI). Согласно основной теореме алгебры у этого есть три корня, но только один действительный корень, поскольку существует только один собственный вектор, ось вращения. Остальные корни должны быть комплексно сопряженной парой. У них есть единица величины, то есть чисто мнимые логарифмы, равные величины бивектора, связанного с вращением, который также является углом вращения. Собственные правила, связанные с комплексными собственными значениями, находятся в плоскости бивектора, поэтому внешнее произведение двух непараллельных векторов дает бивектор или, по крайней мере, кратное ему.
Трехмерный угловой момент как бивектор (плоский элемент) и осевой вектор частицы массы m с мгновенным 3-позиционным положением x и 3-импульс p.Вектор вращения является примером аксиального вектора . Осевые векторы или псевдовекторы - это векторы со специальной особенностью, заключающейся в том, что их координаты претерпевают изменение знака относительно обычных векторов (также называемых "полярными векторами") при инверсии через начало координат, отражении в плоскости или другом линейном преобразовании с изменением ориентации.. Примеры включают такие величины, как крутящий момент, угловой момент и векторные магнитные поля. Величины, которые будут использовать аксиальные векторы в векторной алгебре, правильно представлены бивекторами в геометрической алгебре. Точнее, если выбрана основная ориентация, аксиальные векторы естественным образом идентифицируются с обычными векторами; дуальный элемент Ходжа затем дает изоморфизм между аксиальными векторами и бивекторами, поэтому каждый аксиальный вектор связан с бивектором и наоборот; то есть
где ∗ обозначает двойственный по Ходжу. Обратите внимание, что если базовая ориентация меняется на противоположную путем инверсии через начало координат, как идентификация аксиальных векторов с обычными векторами, так и двойной знак Ходжа меняются, но бивекторы не сдвигаются. В качестве альтернативы, использование псевдоскалярного элемента в Cℓ 3 (ℝ), i = e1e2e3дает
Это проще в использовании, так как продукт просто геометрический товар. Но он антисимметричен, потому что (как и в двух измерениях) единичный псевдоскаляр i возводится в квадрат с -1, поэтому в одном из произведений требуется отрицательный результат.
Это отношение распространяется на такие операции, как векторное значение кросс-произведение и бивекторное внешнее произведение, поскольку при записи в виде детерминанты они вычисляются таким же образом:
поэтому связаны двойственным по Ходжу:
Бивекторы имеют ряд преимуществ перед аксиальными движениями. Они лучше устраняют неоднозначность аксиальных и полярных векторов, то есть представляемые ими величин, поэтому становится более ясным, какие операции разрешены и каковы их результаты. Например, внутреннее произведение полярного вектора и осевого вектора, полученного в результате перекрестного произведения в тройном произведении, должно привести к псевдоскалярному, результат, более очевиден, если вычисление представляет собой внешнее произведение искусства и бивектора. Они распространяются на другие измерения; в частности, бивекторы нагрудные для описания таких величин, как крутящий момент и угловой момент, в двух, а также в трех измерениях. Кроме того, они во многом соответствуют геометрической интуиции.
Сегменты параллельной плоскости с одинаковой ориентацией и пространством, одним и тем же бивектору a∧ b.Предлагается одна из привлекательных сторонних организаций в том, что они они создают. имеют естественную геометрическую интерпретацию. Это можно описать в любом измерении, но лучше всего сделать это в трех измерениях, где можно провести параллели с более знакомыми объектами, прежде чем применять к более высоким измерениям. В двух измерениях геометрическая интерпретация тривиальна, поэтому имеет одну плоскость, и все бивекторы связаны с ней, отличаясь только масштабным коэффициентом.
Все бивекторы можно интерпретировать как плоскости, а точнее как сегменты плоскости. В трех измерениях есть три свойства бивектора, которые можно интерпретировать геометрически:
).
Перекрестное произведение a× bравно ортогонально бивектору a∧ b.В трех измеренийх все бивекторы могут быть сгенерированы произведением двухов. Если бивектор B= a∧ b, то величина B равна
где θ - угол между векторами. Это площадь параллелограммы с ребрами a и b, как показано на диаграмме. Одна интерпретация состоит в том, что область выметается b, когда она движется вдоль a . Внешний антисимметричен, поэтому изменение порядка a и b, чтобы заставить a двигаться вд оль b приводит к бивектору с противоположным направлением, которое является отрицательным из первого направлением. Плоскость бивектора a∧ bсодержит оба элемента a и b, поэтому они оба параллельны плоскости.
Бивекторы и аксиальные связанные связаны посредством двойного Ходжа. В векторном представлении используется двойное изображение со своим ортогональным дополнением, поэтому, если бивектор представлен плоскостью, используется вектор с ним аксиальный, просто нормалью поверхности плоскости. Плоскость имеет две нормали, по одной с каждой стороны, что дает две возможные ориентации для плоскости и бивектора.
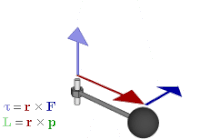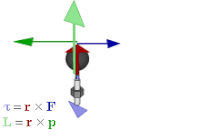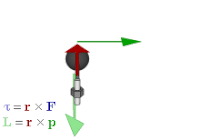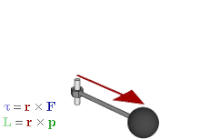Взаимосвязь между силой F, крутящим моментом τ, моментом pи угловым моментом L.. Это связывает векторное произведение с внешним произведением. Его также можно использовать для представления физических величин, таких как крутящий момент и угловой момент. В векторной алгебре они обычно представляют собой изображения, перпендикулярные плоскости силы, импульса или с ущербом, из которых они вычисляются. Но если вместо этого используется плоскость бивектора, то это более естественный способ и то, как они являются плоскостью. Это также в отличие от представленного на другое измерение.
Произведение двух бивекторов имеет геометрическую интерпретацию. Для ненулевых бивекторов A и B произведение может быть разделено на симметричную и антисимметричную часть следующим образом:
Подобно векторам, они имеют присвоение | A· B| = | A||B| cos θ и | A× B| = | A||B| sin θ, где θ - угол между плоскостями. В трех измерениях это то же самое, что угол между вектором изображенияли, двойными плоскостями, и в некоторой степени он обобщается в более высоких измерениях.
Два бивектора, две из непараллельных сторон призмы, добавляются, чтобы получить третий бивектор. Бивекторы можно складывать вместе как области. Учитывая два ненулевых бивектора B и C в трех измерениях, всегда можно найти вектор, который содержится в обоих, скажем a, поэтому бивекторы могут быть записано как внешние продукты, включающие a:
Это можно интерпретировать геометрически, как показано на диаграмме: две области суммируются, чтобы дать третью, с три области, образующие грани призмы с краями a, b, cи b+ c. Это двум способам вычисления площади с использованием распределения внешнего продукта:
Это работает только в трех измерениях, поскольку это единственное измерение, в котором вектор параллелен обоим бивекторы должны существовать. В более высоких измерениях бивекторы обычно не связаны с одной плоскостью, если они (простые бивекторы), два бивектора не имеют общего движения, и, таким образом, суммируются в непростой бивектор.
В четырех измерениях базисными элементами для пространства бивекторов являются (e12, e13, e14, e23, e24, e34), поэтому общий бивектор имеет форму
В четырех измерениях двойственный по Ходжу бивектору является бивектором, а пространство ∧ℝ двойственно самому себе. Нормальные не уникальны, вместо этого каждая плоскость ортогональна всем плоскость в ее двойном пространстве Ходжа. Это можно использовать для разделения бивекторов на «половину» следующим образом. У нас есть три пары ортогональных бивекторов: (e12, e34), (e13, e24) и (e14, e23). Есть четыре различных способа выбрать один бивектор из каждой из двух первых двух пар, и их сумма дает третий бивектор из другой пары. Например, (e12, e13, e14) и (e23, e24, e34).
В четырех измерениях бивекторы генерируются произведением векторов в ℝ, но с одним важным отличием от ℝ и ℝ. В четырех измерениях не все бивекторы просты. Существуют бивекторы, такие как e12+ e34, которые не могут быть сгенерированы произведением двух векторов. Это также означает, что у них нет реального, то есть скалярного, квадрата. В этом случае
Элемент e1234 - это псевдоскаляр в Cℓ 4, отличный от скаляра, поэтому квадрат не скалярный.
Все бивекторы в четырех измерениях могут быть созданы с использованием не более двух внешних продуктов и четырех векторов. Вышеупомянутый бивектор можно записать как
Точно так же каждый бивектор можно записать как сумму двух простых бивекторов. Для этого полезно выбрать два ортогональных бивектора, и это всегда возможно. Более того, для типичного бивектора выбор простых бивекторов уникален, т. Е. Существует только один способ разложения на ортогональные бивекторы; единственное исключение - когда два ортогональных бивектора имеют равные величины (как в приведенном выше примере): в этом случае разложение не уникально. В случае простых бивекторов разложение всегда уникально, с дополнительным бонусом, заключающимся в том, что одна из ортогональных частей равна нулю.
Как и в трех измерениях, бивекторы в четырех измерениях генерируют вращения посредством экспоненциальной карты, и все вращения могут быть сгенерированы таким образом. Как и в трех измерениях, если B является бивектором, то ротор R равен e, и вращения генерируются таким же образом:
3D-проекция тессеракта, выполняющая изоклиническое вращение.Однако генерируемые вращения более сложны. Их можно разделить на следующие категории:
Они генерируются бивекторами простым способом. Простые вращения простыми бивекторами, при этом неподвижная плоскость двойственна или ортогональна плоскости бивектора. Можно сказать, что вращение происходит вокруг этой плоскости, в плоскости бивектора. Все бивекторы производят двойное вращение, причем два угла поворота равны величине двух простых бивекторов, из которых состоит непростой бивектор. Изоклинические вращения возникают, когда эти величины равны, и в этом случае разложение на два простых бивектора не единственно.
Бивекторы в общем случае не коммутируют, но одним исключением являются ортогональные бивекторы и их показатели. Таким образом, если бивектор B= B1+ B2, где B1и B2- ортогональные простые бивекторы, используются для генерации вращения, он распадается на два простых поворота, которые коммутируют следующим образом:
Это всегда возможно, поскольку все бивекторы могут быть выраженными в виде суммы ортогональных бивекторов.
Пространство-время - математическая модель Вселенной, используемая в специальной теории относительности. Он состоит из трех измерений пространства и одного измерения времени, объединенных в одно четырехмерное пространство. Его естественным образом описывают с помощью геометрической алгебры и бивекторов, причем евклидова метрика заменяется метрикой Минковского. Эта алгебра идентична алгебре евклидова пространства, за исключением того, что подпись изменена, поэтому
(Обратите внимание внимание на порядок и индексы выше не универсальны - здесь e4- временное измерение). Геометрическая алгебра - это Cℓ 3,1 (ℝ), а подпространство бивекторов - это.
Простые бивекторы бывают двух типов. Простые бивекторы e23, e31и e12имеют отрицательные квадраты и охватывают бивекторы трехмерного подпространства, соответствующие евклидову пространству, ℝ. Эти бивекторы производят обычные вращения в.
Простые бивекторы e14, e24и e34имеют положительные квадраты и как плоскость, охватывают пространственное измерение и временное измерение. Они также генерируют вращение посредством экспоненциального отображения, но вместо тригонометрических функций необходимы гиперболические функции, которые генерируют ротор следующим образом:
где Ω - бивектор (e14и т. Д.), Идентифицированный через метрику с антисимметричным линейным преобразованием из ℝ. Это повышения Лоренца, указанные особенно компактно, с использованием той же алгебры, что и в выражении в и ℝ.
В общем, все вращения пространства-времени генерируются из бивекторов через экспоненциальную карту, то есть общий ротор, генерируемый бивектором A, имеет форму
Множество всех вращений в пространстве времени образуют группу Лоренца, а из них большую часть можно вывести специальную теорию относительности. В более общем плане это показывает, как все преобразования в евклидовом пространстве и пространстве-времени могут быть использованы с использованием одной и той же алгебры.
(Примечание: в этом разделе традиционных 3-стандартных линий обозначений над символами, вектором пространства-времени и бивекторами - жирными символами, с деревьями J и A исключительно в верхнем углу)
Уравнения Максвелла используются в физике для описания взаимосвязи между электрическими и магнитным полями. Обычно они имеют вид четырех различных формул, они имеют особенно компактную форму, когда поля выражаются как бивектор пространства-времени из. Если электрическое и магнитное поля в равны E и B, то электромагнитный бивектор равенство
где e4снова является базисным вектором для временного измерения, а c - скорость света. Произведение B e123 дает бивектор, который по Ходжу двойственен B в трех измерениях, как, описанный выше, тогда как E e4как произведение ортогональных векторов также имеет бивекторное значение. В целом это электромагнитный тензор , более компактно выраженный как бивектор, и используется следующим образом. Во-первых, это связано с 4-безым J, векторной величиной, задаваемой
, где j - плотность тока, а ρ - плотность заряда. Они связаны дифференциальным оператором ∂, который равен
Оператор ∇ дифференциальный оператор в геометрической алгебре, действующий формулой пространства и задаваемый M = ∇ · M + ∇∧ M . При использовании к векторам ∇ · M - это дивергенция, а ∇∧ M - curl, но с бивекторным, а не векторным результатом, это двойное в трех измерениях к локону. Для общего количества M они представляют собой как низкие и повышающие дифференциальные операторы. В частности, если M является скаляром, то этот оператор представляет собой просто градиент, и его можно рассматривать как геометрический алгебраический оператор del.
Вместе они могут использоваться для использования особенно компактной формы формул Максвелла в вакууме:
Это при разложении по геометрической алгебре с использованием геометрических произведений, которые имеют эффекты повышения и понижения оценки, эквивалентно четырем параметрам Максвелла. Это форма в вакууме, но общая форма лишь немного сложнее. Это также связано с электромагнитным четырехпотенциалом, вектором A, заданным как
где A - векторный магнитный потенциал, а V - электрический потенциал. Он связан с электромагнитным бивектором следующим образом:
с использованием того же дифференциального оператора ∂.
Как предлагалось в предыдущих разделах, большая часть геометрической алгебры хорошо обобщается на более высоких измерениях. Геометрическая алгебра вещественного пространства - это Cℓ n (ℝ), а подпространство бивекторов -.
Количество простых бивекторов, необходимых для формирования общего бивектора, увеличенного размера, поэтому для нечетного n оно равно (n - 1) / 2, для четного n - n / 2. Итак, для четырех и пять измерений необходимы только два простых бивектора, но три требуются для шести и семи измерений. Например, в замере со стандартным основанием (e1, e2, e3, e4, e5, e6) бивектор
- это сумма трех простых бивекторов, но не меньше. Так как в четырех измерениях для этой суммы всегда можно найти ортогональные простые бивекторы.
Как в трех, так и в четырех измерениях роторы генерируются экспоненциальной картой, поэтому
- это ротор, созданный бивектором B . Простые вращения, которые происходят в плоскости вращения вокруг фиксированной лопасти размера (n - 2), генерируются простыми бивекторами, в то время как другие бивекторы генерируют более сложные вращения, которые могут быть описываются в терминах простых бивекторов, которые они представляют собой суммы, каждый из которых связан с плоскостью вращения. Все бивекторы могут быть выражены как сумма ортогональных и коммутативных простых бивекторов, поэтому вращения всегда можно разложить на набор коммутативных поворотов вокруг плоскостей, связанных с этими бивекторами. Группа роторов в n измерениях - это спиновая группа, Spin (n).
Одна примечательная особенность, связанная с количеством простых бивекторов и, следовательно, плоскостей вращения, состоит в том, что в нечетных размерах каждое вращение имеет фиксированную ось - ошибочно называть ее осью вращения, поскольку в более высоких измерениях происходит в нескольких ортогональных ему плоскостях. Это связано с бивекторами, так как бивекторы в нечетных размерах распадаются на то же количество бивекторов, что и четное измерение ниже, поэтому имеют такое же количество плоскостей, но одно дополнительное измерение. Поскольку каждая плоскость генерирует вращения в двух измерениях в нечетных измерениях, должно быть одно измерение, то есть ось, которая не вращается.
Бивекторы также связаны с матрицей вращения в n измерениях. Как и в трех измерениях, характеристическое уравнение матрицы может быть решено, чтобы найти собственные значения. В нечетных измерениях у этого есть один действительный корень, с собственным вектором - фиксированной осью, а в четных измерениях он не имеет реальных корней, поэтому либо все, либо все корни, кроме одного, являются комплексно сопряженными парами. Каждая пара связана с простым компонентом бивектора, связанным с вращением. В частности, логарифм каждой пары равен ± величине, в то время как собственные векторы, генерируемые из корней, параллельны бивектору и поэтому могут использоваться для создания бивектора. В общем, собственные значения и бивекторы уникальны, а набор собственных значений дает полное разложение на простые бивекторы; если корни повторяются, то разложение бивектора на простые бивекторы не единственно.
Геометрическая алгебра может быть применена к проективной геометрии простым способом. Используемая геометрическая алгебра - Cℓ n (ℝ), n ≥ 3, алгебра действительного векторного пространства ℝ. Используется для описания объектов в реальном проективном пространстве ℝℙ. Ненулевые векторы в Cℓ n (ℝ) или ℝ связаны с точками в проективном пространстве, поэтому векторы, которые отличаются только масштабным коэффициентом, поэтому их внешний продукт равен нулю, отображаются в одну и ту же точку. Ненулевые простые бивекторы в ∧ℝ представляют собой линии в, причем бивекторы, отличающиеся только (положительным или отрицательным) масштабным коэффициентом, представляют ту же линию.
Описание проективной геометрии может быть построено в геометрической алгебре с использованием основных операций. Например, учитывая две различные точки в ℝℙ, представленные векторами a и b, линия между ними задается как a∧ b(или b∧ a). Две прямые пересекаются в точке, если A∧ B= 0 для их бивекторов A и B . Эта точка задается вектором
Операция " ⋁ "- это совпадение, которое может быть определено, как указано выше, в терминах соединения, J = A∧ Bдля ненулевого A∧ B. Используя эти операции, проективную геометрию можно сформулировать в терминах геометрической алгебры. Например, для третьего (ненулевого) бивектора C точка p лежит на линии, заданной C тогда и только тогда, когда
Таким образом, условие коллинеарности строк, заданных в A, Bи C, -
который в Cℓ 3 (ℝ) и ℝℙ упрощается до
, где угловые скобки обозначают скалярную часть геометрического произведения. Таким же образом все операции в проективном пространстве могут быть записаны в терминах геометрической алгебры с бивекторами, представляющими общие прямые в проективном пространстве, поэтому вся геометрия может быть развита с помощью геометрической алгебры.
Как отмечалось выше, бивектор может быть записан как кососимметричная матрица, которая посредством экспоненциальной карты генерирует матрицу вращения, описывающую то же вращение, что и ротор, также сгенерированная экспоненциальной картой, но примененная к вектор. Но он также используется с другими бивекторами, такими как тензор угловой скорости и электромагнитный тензор, соответственно, кососимметричная матрица или тензор 3 × 3 и 4 × 4.
Вещественные бивекторы в изоморфны кососимметричным матрицам n × n или, альтернативно, антисимметричным тензорам порядка 2 на. Хотя бивекторы изоморфны векторам (через двойственное) в трех измерениях, они могут быть представлены кососимметричными матрицами в любом измерении. Это полезно для соотнесения бивекторов с проблемами, описываемыми матрицами, чтобы их можно было преобразовать в термины бивекторов с учетом геометрической интерпретации, а затем часто легче решать или геометрически связывать с другими проблемами бивекторов.
В более общем плане каждая вещественная геометрическая алгебра изоморфна матричной алгебре. Они содержат бивекторы в качестве подпространства, хотя часто это не особенно полезно. Эти матрицы в основном представляют интерес как способ классификации алгебр Клиффорда.
 | Найдите бивектор в Викисловаре, бесплатном словаре. |
