| Snub cube | |
|---|---|
 . (Щелкните здесь, чтобы вращаться модель) . (Щелкните здесь, чтобы вращаться модель) | |
| Type | Archimedean solid. Uniform polyhedron |
| Элементы | F = 38, E = 60, V = 24 (χ = 2) |
| Лица по сторонам | (8 + 24) {3} +6 {4} |
| Обозначение Конвея | sC |
| символы Шлефли | sr {4,3} или  |
| ht0,1,2 {4,3} | |
| Символ Wythoff | | 2 3 4 |
| Диаграмма Кокстера | |
| Группа симметрии | O, 1 / 2B 3, [4,3], (432), порядок 24 |
| Группа вращения | O, [ 4,3], (432), порядок 24 |
| Двугранный угол | 3-3: 153 ° 14′04 ″ (153,23 °). 3-4: 142 ° 59′00 ″ (142,98 °) |
| Ссылки | U 12, C 24, W 17 |
| Свойства | Полурегулярные выпуклые хиральные |
 . Цветные грани . Цветные грани |  . 3.3.3.3.4. (Вершинная фигура ) . 3.3.3.3.4. (Вершинная фигура ) |
 . Пятиугольный икоситетраэдр. (двойной многогранник ) . Пятиугольный икоситетраэдр. (двойной многогранник ) | 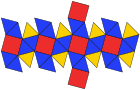 . Сетка . Сетка |
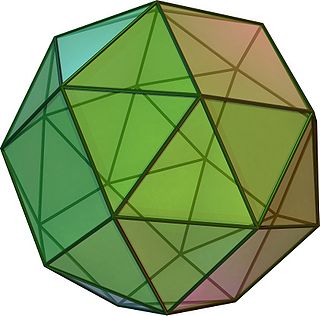
 3D модель курносого куба
3D модель курносого куба В геометрии курносый куб или курносый кубооктаэдр, является архимедовым телом с 38 гранями: 6 квадратами и 32 равносторонними треугольниками. Оно имеет 60 ребер и 24 вершины.
Это киральный многогранник; то есть он имеет две различные формы, которые являются зеркальными отображениями (или «энантиоморфами ») каждого другое. Объединение обеих форм представляет собой соединение двух плоских кубов, а выпуклая оболочка обоих наборов вершин представляет собой усеченный кубооктаэдр.
Ke Плер впервые назвал его в латинском как cubus simus в 1619 году в его Harmonices Mundi. Х. С.М. Коксетер, отметив, что он может быть получен в равной степени из октаэдра и куба, назвал его курносым кубооктаэдром с вертикально вытянутым символом Шлефли 

Для плоского куба с длиной ребра 1 его площадь поверхности и объем равны:

где t - константа трибоначчи
![{\ displaystyle t = { \ frac {1 + {\ sqrt [{3}] {19-3 {\ sqrt {33}}}} + {\ sqrt [{3}] {19 + 3 {\ sqrt {33}}}}} { 3}} \ приблизительно 1,839 \, 286 \, 755 \, 21.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00b5dd3c4eadfd955c9c41e5b960d0f19ac5ca7e)
Если исходный курносый куб имеет длину ребра 1, его двойной пятиугольный икоситетраэдр имеет длину стороны
 .
.В общем, объем курносого куба с длиной стороны 

Декартовы координаты для верт льды курносого куба - это все четные перестановки из
с четным числом знаков плюс, вместе со всеми нечетные перестановки с нечетным количеством знаков плюс, где t ≈ 1,83929 - константа трибоначчи. Взяв четные перестановки с нечетным числом знаков плюс и нечетные перестановки с четным числом знаков плюс, мы получим другой пренебрежительный куб, зеркальное отображение. Взяв их все вместе, мы получим соединение из двух плоских кубиков.
У этого плоскостного куба есть ребра длиной 

и может быть записано как
![{\ displaystyle {\ begin {align} \ alpha = {\ sqrt {{ \ frac {4} {3}} - {\ frac {16} {3 \ beta}} + {\ frac {2 \ beta} {3}}}} \ приблизительно 1.609 \, 72 \\\ beta = { \ sqrt [{3}] {26 + 6 {\ sqrt {33}}}} \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a8d7d106963ee92fcc2a3159bcccb8de89d6bfb)
Чтобы получить курносый куб с единичной длиной ребра, разделите все координаты выше на значение α, указанное выше.
 Курносый куб не имеет точечной симметрии, поэтому вершина спереди не соответствует противоположной вершине сзади.
Курносый куб не имеет точечной симметрии, поэтому вершина спереди не соответствует противоположной вершине сзади. Курносый куб имеет две специальные ортогональные проекции по центру на двух типах граней: треугольники и квадраты соответствуют плоскостям Кокстера A 2 и B 2.
| по центру на | Грань. Треугольник | Грань. Квадрат | Край |
|---|---|---|---|
| Сплошной |  |  |  |
| Каркас |  |  |  |
| Проективная. симметрия | [3] | [4pting | [2] |
| Двойной |  |  |  |
Курносый куб также может быть представлен как сферическое мозаичное изображение и проецирование на плоскость через стереографическую проекцию . Эта проекция конформна, сохраняя углы, но не площади или длины. Дуги большого круга (геодезические) на сфере проецируются как дуги окружности на плоскость.
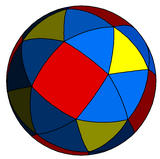 |  . квадрат с центром . квадрат с центром |
| Ортогональная проекция | Стереографическая проекция |
|---|


 Куб, ромбокубооктаэдр и плоскостопийный куб (анимированные расширение и скручивание )
Куб, ромбокубооктаэдр и плоскостопийный куб (анимированные расширение и скручивание )Курносый куб можно создать, взяв шесть граней куба, потянув их наружу, чтобы они больше не соприкасались, а затем слегка повернув их центры (все по часовой стрелке или все против- по часовой стрелке) до тех пор, пока промежутки между ними не будут заполнены равносторонними треугольниками.


 Равномерное чередование усеченного кубооктаэдра
Равномерное чередование усеченного кубооктаэдра Курносый куб также может быть получен из усеченного кубооктаэдра с помощью процесса чередование. 24 вершины усеченного кубооктаэдра образуют многогранник, топологически эквивалентный курносому кубу; остальные 24 образуют его зеркальное отображение. Полученный многогранник вершинно-транзитивный, но не однородный.
"Улучшенный" курносый куб с квадратной гранью чуть меньшего размера и треугольными гранями большего размера. к однородному курносому кубу Архимеда, полезен в качестве сферической конструкции.
Курносый куб - один из семейства однородных многогранников, связанных с кубом и правильным октаэдром.
| Однородные октаэдрические многогранники | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия : [4,3], (* 432) | [4,3]. (432) | [1, 4,3] = [3,3]. (* 332) | [3,4]. (3 * 2) | |||||||
| {4,3} | t {4,3} | r {4,3}. r {3} | t{3,4}. t {3} | {3, 4}. {3} | rr {4,3}. s2{3,4} | tr {4,3} | sr {4,3} | h {4,3}. {3,3} | div class="ht"{4,3}. t {3,3} | s {3,4}. s {3} |
| Дублирует к однородным многогранникам | ||||||||||
| V4 | V3.8 | V (3.4) | V4.6 | V3 | V3.4 | V4. 6.8 | V3.4 | V3 | V3.6 | V3 |
Этот полуправильный многогранник является членом последовательности плоскостных многогранников и мозаик с фигурами вершин (3.3.3.3.n) и Диаграмма Кокстера – Дынкина ![]()
![]()
![]()
![]()
![]() . Эти фигуры и их двойники имеют (n32) вращательную симметрию, находясь в евклидовой плоскости для n = 6 и гиперболической плоскости для любых более высоких n. Можно считать, что серия начинается с n = 2, с одним набором граней, выродившихся в дигоны.
. Эти фигуры и их двойники имеют (n32) вращательную симметрию, находясь в евклидовой плоскости для n = 6 и гиперболической плоскости для любых более высоких n. Можно считать, что серия начинается с n = 2, с одним набором граней, выродившихся в дигоны.
n32 мутации симметрии курносых мозаик: 3.3.3.3.n
| ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия. n32 | Сферическое | Евклидово | Компактное гиперболическое | Паракомп. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Snub. цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Гироскоп. цифры |  |  |  |  |  |  |  |  |
| Конфиг. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3. 3.3.3.8 | V3.3.3.3.∞ |
Курносый куб является вторым в серии курносых многогранников и мозаик с вершинной фигурой 3.3.4.3.n.
Мутации 4n2 симметрии курносых элементов: 3.3.4.3.n [
| ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия. 4n2 | Сферическая | Евклидова | Компактная гиперболическая | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Snub. цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Гироскоп. цифры |  |  |  |  | ||||
| Конфиг. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
| Плоский кубический граф | |
|---|---|
 4-кратная симметрия 4-кратная симметрия | |
| Вершины | 24 |
| Ребра | 60 |
| Автоморфизмы | 24 |
| Свойства | Гамильтониан, обычный |
| Таблица графиков и параметров | |
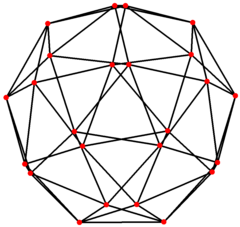
В математическом поле теории графов, курносый кубический граф - это граф вершин и ребер курносого куба, одного из архимедовых тел. Он имеет 24 вершины и 60 ребер и является архимедовым графом.
 |