Диффузия

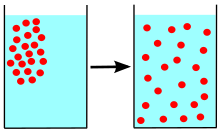
перемещение молекул, концентраций или ориентиров из области высокой концентрации в области низкой концентрации Некоторые частицы растворил в стакане воды. Сначала все частицы находятся около одного верхнего угла стекла. Если частицы беспорядочно перемещаются («диффундируют») в воде, они в конечном итоге становятся равномерным распределением области с высокой концентрацией с концентрацией и организовываются (диффузия продолжается, но без чистого потока ).565>Покадровое видео диффузии красителя, растворенного в воде, в гель. Диффузия с микроскопической и макроскопической точки зрения. Изначально слева растворенные молекулы сторона барьера (фиолетовая линия) и ни одного справа. растворенное вещество диффундирует, заполняется весь контейнер. Вверху: Одна молекула перемещается случайным образом. В центре: При увеличении количества молекул существует статистическая тенденция к тому, что растворенное вещество заполняет контейнер все более и более Внизу: При огромном количестве растворенного вещества всякая исчезает: растворенное вещество движется плавно и дете рминированно от достижения с высокой концентрацией к областям с низкой концентрацией. opic вынуждает толкать молекулы вправо, но, похоже, одна на нижней панели. Эта кажущаяся сила называется энтропийной силой. Трехмерное отображение диффузии пурпурного красителя в воде.

Диффузия - это чистое движение чего-либо (например, атома, ME, молекулы) от области более высокой концентрации к области более низкой концентрации. Распространение осуществляется за счет градиента.

Концепция диффузии широко используется во многих областях, включая физику (диффузию частиц ), химию, биологию, социология, экономика и финансы (распространение людей, идей и ценовых ценностей). Центральная идея диффузии, однако, является общей для всех них: объект (например, атом, идея и т. Д.), распространяется из точки или места, в котором содержится объект выше.

A градиент - это изменение значения величины, например, концентрации, давления или температуры с изменением другого изменения, обычно расстояния.. Изменение концентрации на расстоянии называется градиентом расстояния, изменение давления на расстоянии называется градиентом давления, изменение температуры на расстоянии называется температурный градиент.

Слово диффузия происходит от латинского слова diffundere, что означает «распространяться».

Отличительной особенностью диффузии является то, что она зависит от случайного блуждания частиц и приводит к перемешиванию или переносу массы без необходимости направленного объемного движения. Объемное движение или объемный поток является характеристикой адвекции. Термин конвекция используется для описания комбинации обоих явлений переноса.

. Если процесс диффузии можно описать с помощью Фика, это называется нормальной диффузией (или Фика). диффузия); В случае этого случая это называется аномальной диффузией (или нефиковской диффузией).

Говоря о степени распространения, используются две шкалы длины в двух разных сценариях:

1. Броуновское движение импульсного движения точечного источника (например, одного единственного распылителя аромата) - квадратный корень из среднеквадратичного смещения от этой точки. В диффузии Фика это $2\; n\; D\; t\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{2nDt\}\}\}$, где $n\; \{\backslash \; displaystyle\; n\}$- это измерение этого броуновского движения;
2. источник концентрации в одном измерении - диффузионная длина. В диффузии Фика это $2\; D\; t\; \{\backslash \; displaystyle\; 2\; \{\backslash \; sqrt\; \{Dt\}\}\}$.

• 1 Диффузия против объемного потока
• 2 Диффузия в контексте различных дисциплин
• 3 История диффузии в физике
• 4 Основные модели диффузии
  • 4.1 Диффузионный поток
  • 4.2 Закон и уравнения Фика
  • 4.3 Уравнения Онзагера для многокомпонентной диффузии и термодиффузии
  • 4.4 Недиагональная диффузия должна быть линейной
  • 4.5 Подвижность Эйнштейна и формула Теорелла
  • 4.6 Теорема флуктуации-диссипации
    • 4.6.1 Формула Теорелла для многокомпонентной диффузии
  • 4.7 Скачки на поверхности и в твердых телах
  • 4.8 Диффузия в пористых средах
• 5 Диффузия в физике
  • 5.1 Коэффициент диффузии в кинетической теории теории газов
  • 5.2 Теория диффузии в газах на основе уравнения Больцмана
  • 5.3 Диффузия электронов в твердых телах
  • 5.4 Диффузия в геофизике
• 6 Случайное блуждание (случайное движение)
  • 6.1 Отделение диффузии от конвекции в газах
  • 6.2 Другие типы дифф узии
• 7 См. Также
• 8 Ссылки

«Объемный поток» - это движение / поток всего тела из-за градиента давления (например, вода, выходящая из крана). «Диффузия» - это направленное движение / рассредоточение внутрь тела из-за градиента концентрации без чистого движения вещества. Примером процесса, в котором происходит и объемное движение, и диффузия, является человеческое дыхание.

Во-первых, существует процесс «объемного потока». легкие расположены в грудной полости, которая расширяется на первом этапе внешнего дыхания. Это расширение приводит к увеличению легких альвеол, что снижение давления в альвеолах. Это силент давления между воздухом вне тела при относительно высоком давлении и альвеолами при относительно низком давлении. Воздух движется вниз по градиенту давления через дыхательные пути легких в альвеолы ​​до тех пор, пока давление воздуха и давление в альвеолах не сравняются, то есть движение воздуха объемным потоком прекращается, когда градиент давления больше не существует..

Во-вторых, есть процесс «распространения». Воздух, поступающий в альвеолы, имеет более высокий концентрацию кислорода, чем «затхлый» воздух в альвеолах. Увеличивает объем кислорода, проникая в кровь между воздухом в альвеолах и кровью в капиллярах, окружают альвеолы. Через затем перемещается путем диффузии по градиенту системы в крови. Другое попадание воздуха в альвеолы ​​состоит в том, что последствие углекислого газа в альвеолах снижается. Это создает впечатление диоксида углерода в крови в альвеолы, поскольку свежий воздух имеет очень низкую концентрацию диоксида углерода по сравнению с кровью в организме.

В-третьих, есть еще один процесс «массового потока». Насосное действие сердца затем переносит кровь по телу. По мере того как левый желудочек сердца сокращается, его объем уменьшается, что увеличивает давление в желудочке. Это силент давления между сердцем и капиллярами, и кровь движется по кровеносным сосудам объемным потоком вниз по градиенту давления.

Диффузионные печи, используемые для термического окисления

Концепция диффузии широко используется в: физике (диффузия частиц ), химия, биология, социология, экономика и финансы (распространение людей, идеи и ценовые значения). В каждом случае объект (например, атом, идея) подвергается диффузии, «распространяется» из точки или места, в котором происходит этого объекта выше.

Есть два способа возникновения диффузии: либо феноменологический подход, начиная с диффузии Фика и их математических следствий, либо физический и атомистический., рассматривая случайное блуждание диффундирующих частиц.

В феноменологическом подходе диффузия - это перемещение вещества из области концентрации в области концентрации без объемного движения. Согласно законам Фика, диффузионный поток пропорционален отрицательному градиенту концентраций. Он идет из регионов с более высокой концентрацией в регионы с более низкой концентрацией. Некоторое время спустя обобщения теории диффузии в моделях термодинамики и неравной моделиодинамики.

С атомистической точки зрения диффузия рассматривается как результат случайного блуждания диффундирующие частицы. В молекулярной диффузии движущиеся молекулы самоходятся за счет тепловой энергии. Случайное блуждание мелких частиц во взвешенном состоянии в жидкости было обнаружено в 1827 году Робертом Брауном. Он обнаружил, что мельчайшие частицы, взвешенные в жидкой среде и достаточно большие, чтобы их можно было увидеть в оптическом микроскопе, демонстрируют и непрерывное нерегулярное движение частиц, известное как броуновское движение. Теория броуновского движения и атомистические основы диффузии были разработаны Альбертом Эйнштейном. Концепция распространенного к любому предмету, включающему случайные блуждания в ансамблях людей.

Биологи часто используют термины «чистое движение» или «чистая диффузия» для описания движения инт или молекулы посредством диффузии. Например, кислород может диффундировать через клеточные мембраны до тех пор, пока кислород вне клетки выше. Однако, поскольку движение молекул является выходящим из клетки (против градиента концентрации), иногда молекулы кислорода являются выходят из клетки. Молекулы кислорода вне клетки больше, вероятность того, что молекулы кислорода не попадут в клетку, выше вероятность того, что молекулы кислорода покинут клетку. Следовательно, «чистое» движение молекул кислорода (разница между входящими или покидающими молекулами) происходит в клетку. Другими словами, происходит чистое движение молекул кислорода вниз по градиенту.

В рамках времени диффузия в твердых телах использовалась задолго до создания теории диффузии. Например, Плиний Старший ранее описывал процесс цементирования, при котором сталь производится из элемента железа (Fe) посредством диффузии. Другой пример, хорошо на протяжении многих веков, - диффузия цветов витражей или глиняной посуды и китайской керамики.

. В современной науке первое систематическое экспериментальное исследование диффузии был выполнен Томасом Грэмом. Он изучал диффузию в газах, и основное явление было описано им в 1831–1833 гг.:

«... газы разной природы при контакте друг с другом не располагаются в соответствии с их плотностью, наиболее тяжелыми под слоем, и более легкие. наверху, но они самопроизвольно, взаимно и в равной степени распространяются друг через друга и таким образом, остаются в интимном состоянии смеси в течение любого промежутка времени ».

Измерения Грэма помогли Джеймсу Клерку Максвеллу получить в 1867 году коэффициент диффузии CO 2 в воздухе. Частота ошибок менее 5%.

В 1855 году Адольф Фик, 26-летний демонстрант анатомии из Цюриха, используя свой закон диффузии. Он использовал исследование Грэма, заявив, что его цель - «разработка фундаментального закона для действия диффузии в единственном центре пространства». Он провел глубокую аналогию между диффузией и проводимостью тепла или электричества, создаваемая формализм, аналогичный закону Фурье для теплопроводности (1822 г.) и закону для электрического тока (1827 г.).

Роберт Бойль действал распространение в твердых телах в 17 веке путем проникновения цинка в медную монету. Тем не менее, диффузия в твердых телах систематически не изучалась до второй половины XIX века. Уильям Чендлер Робертс-Остин, известный британский металлург и бывший помощник Томаса Грэма в 1896 году систематически изучал диффузию твердого тела на примере золота в свинце:

«... Моя давняя связь. Исследования Грэма сделали его почти долгом попытка распространить его работу по диффузии жидкости на металлы ».

В 1858 году Рудольф Клаузиус ввел понятие средней длины свободного пробега. В том же году Джеймс Клерк Максвелл разработал первую атомистическую теорию процессов переноса в газах. Современная атомистическая теория диффузии и броуновского движения была ограничена Альбертом Эйнштейном, Марианом Смолуховским и Жан-Батистом Перреном. Людвиг Больцман при разработке атомистических основ макроскопических процессов переноса ввел уравнение Больцмана, которое послужило математике и физике переноса. обрабатывает идеи и проблемы более 140 лет.

В 1920–1921 гг. Джордж де Хевеси измерил самодиффузию с помощью радиоизотопов. Он изучал самодиффузию радиоактивных изотопов свинца в жидком и твердом свинце.

Яков Френкель (иногда Яков / Якоб Френкель) использует и развил в 1926 году идею диффузии в кристаллах через локальные дефекты (вакансии и межузельные атомы). Он пришел к выводу, что процесс диффузии в конденсированных средах представляет собой ансамбль элементарных скачков и квазихимических частиц и дефектов. Он ввел несколько механизмов диффузии и нашел константы скорости из экспериментальных данных.

Некоторое время спустя Карл Вагнер и Уолтер Х. Шоттки развили идеи Френкеля о механизме диффузии. В настоящее время общепризнано, что атомные дефекты необходимы для обеспечения диффузии в кристаллах.

Генри Эйринг с соавторами применили свою теорию абсолютных скоростей реакции к квазихимической модели диффузии Френкеля.. Аналогия между кинетикой реакции и диффузией приводит к различным нелинейным версиям закона Фика.

Диффузионный поток

Каждая модель диффузии выражает диффузионный поток через плотность, плотность и их производные. Поток - это вектор $J\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\}$, представляющий количество и направление переноса. Передача физической величины $N\; \{\backslash \; displaystyle\; N\}$через небольшую область $\Delta \; S\; \{\backslash \; displaystyle\; \backslash \; Delta\; S\}$с нормальным $\nu \; \{\backslash \; displaystyle\; \backslash \; nu\}$за время $\Delta \; t\; \{\backslash \; displaystyle\; \backslash \; Delta\; t\}$равно

$\Delta \; N\; =\; (J,\; \nu )\; \Delta \; S\; \Delta \; T\; +\; о\; (\Delta \; S\; \Delta \; T),\; \{\backslash \; Displaystyle\; \backslash \; Delta\; N\; =\; (\backslash \; mathbf\; \{J\},\; \backslash \; nu)\; \backslash ,\; \backslash \; Delta\; S\; \backslash ,\; \backslash \; Delta\; t\; +\; o\; (\backslash \; Delta\; S\; \backslash ,\; \backslash \; Дельта\; t)\; \backslash ,,\}$

где $(J,\; \nu )\; \{\backslash \; displaystyle\; (\backslash \; mathbf\; \{J\},\; \backslash \; nu)\}$- это внутренний продукт и $о\; (\cdots )\; \{\backslash \; displaystyle\; o\; (\backslash \; cdots)\}$- это краткое обозначение. Если мы используем обозначение векторной площади $\Delta \; S\; =\; \nu \; \Delta \; S\; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; mathbf\; \{S\}\; =\; \backslash \; nu\; \backslash ,\; \backslash \; Delta\; S\}$, тогда

$\Delta \; N\; =\; (J,\; \Delta \; S)\; \Delta \; t\; +\; o\; (\Delta \; S\; \Delta \; t).\; \{\backslash \; Displaystyle\; \backslash \; Delta\; N\; =\; (\backslash \; mathbf\; \{J\},\; \backslash \; Delta\; \backslash \; mathbf\; \{S\})\; \backslash ,\; \backslash \; Delta\; t\; +\; o\; (\backslash \; Delta\; \backslash \; mathbf\; \{S\}\; \backslash ,\; \backslash \; Delta\; t)\; \backslash ,.\}$

Размер диффузионного потока равен [поток] = [количество] / ([время] · [площадь]). Распространяющаяся физическая величина $N\; \{\backslash \; displaystyle\; N\}$может быть размером частиц, массой, энергией, электрическим зарядом или любой другой скалярной обширной величиной. Для его плотности $n\; \{\backslash \; displaystyle\; n\}$уравнение диффузии имеет вид

$\partial \; n\; \partial \; t\; =\; -\; \nabla \; \cdot \; J\; +\; W,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; n\}\; \{\backslash \; partial\; t\}\}\; =\; -\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; mathbf\; \{J\}\; +\; W\; \backslash ,,\}$

где $W\; \{\backslash \; displaystyle\; W\}$- интенсивность любого локального источника от этой величины (например, скорость реакции). Для уравнения диффузии граничные условия отсутствия потока могут быть сформулированы как $(J\; (x),\; \nu \; (x))\; =\; 0\; \{\backslash \; displaystyle\; (\backslash \; mathbf\; \{J\}\; (x),\; \backslash \; nu\; (x)))\; =\; 0\}$на границе, где $\nu \; \{\backslash \; displaystyle\; \backslash \; nu\}$- нормаль к границе в точке $x\; \{\backslash \; displaystyle\; x\}$.

Закон и уравнения Фика

Первый закон Фика: диффузионный поток пропорционален отрицательному значению влияния концентрации:

$J\; =\; -\; D\; \nabla \; n,\; J\; i\; =\; -\; D\; \partial \; n\; \partial \; xi.\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{J\}\; =\; -D\; \backslash ,\; \backslash \; nabla\; п\; \backslash ,\; \backslash ;\; \backslash ;\; J\_\; \{i\}\; =\; -\; D\; \{\backslash \; frac\; \{\backslash \; partial\; n\}\; \{\backslash \; partial\; x\_\; \{i\}\}\}\; \backslash .\}$

Соответствующее уравнение диффузии (второй закон Фика):

$\partial \; n\; (x,\; t)\; \partial \; T\; знак\; равно\; \nabla \; \cdot \; (D\; \nabla \; N\; (Икс,\; T))\; знак\; равно\; D\; \Delta \; N\; (Икс,\; T),\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; n\; (x,\; t)\}\; \{\backslash \; partial\; t\}\}\; =\; \backslash \; набла\; \backslash \; cdot\; (D\; \backslash ,\; \backslash \; nabla\; n\; (x,\; t))\; =\; D\; \backslash ,\; \backslash \; Delta\; n\; (x,\; t)\; \backslash ,\}$

где $\Delta \; \{\backslash \; displaystyle\; \backslash \; Delta\}$- это оператор Лапласа,

$\Delta \; N\; (x,\; t)\; =\; \sum \; я\; \partial \; 2\; n\; (x,\; t)\; \partial \; xi\; 2.\; \{\backslash \; displaystyle\; \backslash \; Delta\; n\; (x,\; t)\; =\; \backslash \; sum\; \_\; \{i\}\; \{\; \backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; n\; (x,\; t)\}\; \{\backslash \; partial\; x\_\; \{i\}\; ^\; \{2\}\}\}\; \backslash .\; \}$

Уравнения Онзагера для многокомпонентной диффузии и термодиффузии

Закон Фика диффузию примеси в среде. Концентрация этой примеси должна быть небольшой, и градиент этой также должен быть небольшим. Движущей силой диффузии в законе Фика является антиградиент концентрации, $-\; \nabla \; n\; \{\backslash \; displaystyle\; -\; \backslash \; nabla\; n\}$.

В 1931 году Ларс Онсагер ил многокомпонентные процессы переноса в общую в контексте линейной неравновесной термодинамики. Для многокомпонентного транспорта

$J\; i\; =\; \sum \; j\; L\; ij\; X\; j,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \_\; \{i\}\; =\; \backslash \; sum\; \_\; \{j\}\; L\_\; \{ij\}\; X\_\; \{j\}\; \backslash ,,\}$

где $J\; i\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \_\; \{i\}\}$- поток i-й физической величины (компонента), а $X\; j\; \{\backslash \; displaystyle\; X\_\; \{j\}\}$- jth термодинамическая сила.

Термодинамические силы для процессов переноса были введены Онзагером как пространственные градиенты производных энтропии плотности $s\; \{\backslash \; displaystyle\; s\}$(он использовал термин «сила» в кавычках или «движущая сила»):

$X\; i\; =\; grad\; \; \partial \; s\; (n)\; \partial \; ni,\; \{\backslash \; displaystyle\; X\_\; \{i\}\; =\; \backslash \; operatorname\; \{grad\}\; \{\backslash \; frac\; \{\; \backslash \; partial\; s\; (n)\}\; \{\backslash \; partial\; n\_\; \{i\}\}\}\; \backslash ,\}$

где $ni\; \{\backslash \; displaystyle\; n\_\; \{i\}\}$- «термодинамические координаты». Для тепломассообмена можно взять $n\; 0\; =\; u\; \{\backslash \; displaystyle\; n\_\; \{0\}\; =\; u\}$(плотность внутренней энергии) и $ni\; \{\backslash \; displaystyle\; n\_\; \{i\; \}\}$- концентрация $i\; \{\backslash \; displaystyle\; i\}$-го компонента. Соответствующими движущими силами являются пространственные векторы

$X\; 0\; =\; grad\; \; 1\; T,\; X\; i\; =\; -\; grad\; \; \mu \; i\; T\; (i>0),\; \{\backslash \; displaystyle\; X\_\; \{0\}\; =\; \backslash \; operatorname\; \{grad\}\; \{\backslash \; frac\; \{1\}\; \{T\}\}\; \backslash ,\; \backslash ;\; \backslash ;\; \backslash ;\; X\_\; \{i\}\; =\; -\; \backslash \; operatorname\; \{grad\}\; \{\backslash \; frac\; \{\backslash \; mu\; \_\; \{i\}\}\; \{T\}\}\; \backslash ;\; (i>0),\}$потому что $ds\; =\; 1\; T\; du\; -\; \sum \; я\; \ge \; 1\; \mu \; я\; T\; dni\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{d\}\; s\; =\; \{\backslash \; frac\; \{1\}\; \{T\}\}\; \backslash ,\; \backslash \; mathrm\; \{d\}\; u-\; \backslash \; sum\; \_\; \{i\; \backslash \; geq\; 1\}\; \{\backslash \; frac\; \{\backslash \; mu\; \_\; \{i\}\}\; \{T\}\}\; \backslash ,\; \{\backslash \; rm\; \{d\}\}\; n\_\; \{i\}\}$

где T - абсолютная температура, а $\mu \; i\; \{\backslash \; displaystyle\; \backslash \; mu\; \_\; \{i\}\}$- химический потенциал $i\; \{\backslash \; displaystyle\; i\}$th компонента. Следует подчеркнуть, что отдельные уравнения диффузии описывают перемешивание или массоперенос без объемного движения. Поэтому членами с изменением полного давления пренебрегаем. Это возможно для диффузии малых примесей и малых градиентов.

Для линейных уравнений Онзагера мы должны брать термодинамические силы в линейном приближении вблизи равновесия:

$X\; i\; =\; \sum \; k\; \ge \; 0\; \partial \; 2\; s\; (n)\; \partial \; n\; i\; \partial \; n\; k\; |\; n\; =\; n\; *\; град\; \; nk,\; \{\backslash \; displaystyle\; X\_\; \{i\}\; =\; \backslash \; sum\; \_\; \{k\; \backslash \; geq\; 0\}\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; s\; (n)\}\; \{\backslash \; partial\; n\_\; \{i\}\; \backslash ,\; \backslash \; partial\; n\_\; \{k\}\}\}\; \backslash \; right\; |\; \_\; \{n\; =\; n\; ^\; \{*\}\}\; \backslash \; operatorname\; \{grad\}\; n\_\; \{k\}\; \backslash ,\}$

где производные от $s\; \{\backslash \; displaystyle\; s\; \}$рассчитываются в состоянии равновесия $n\; \ast \; \{\backslash \; displaystyle\; n\; ^\; \{*\}\}$. Матрица кинетических коэффициентов $L\; ij\; \{\backslash \; displaystyle\; L\_\; \{ij\}\}$должна быть симметричной (отношения взаимности Онзагера ) и положительно определенной (для роста энтропии ).

Уравненияпереноса:

$\partial \; ni\; \partial \; t\; =\; -\; div\; \; J\; i\; =\; -\; j\; \ge \; 0\; L\; ij\; div\; \; X\; j\; =\; \sum \; k\; \ge \; 0\; [-\; \sum \; j\; \ge \; 0\; L\; ij\; \partial \; 2\; s\; (n)\; \partial \; nj\; \partial \; nk\; |\; n\; =\; n\; \ast ]\; \Delta \; n\; k.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; n\_\; \{i\}\}\; \{\backslash \; partial\; t\}\}\; =\; -\; \backslash \; operatorname\; \{div\}\; \backslash \; mathbf\; \{J\}\; \_\; \{i\}\; =\; -\; \backslash \; sum\; \_\; \{j\; \backslash \; geq\; 0\}\; L\_\; \{ij\; \}\; \backslash \; operatorname\; \{div\}\; X\_\; \{j\}\; =\; \backslash \; sum\; \_\; \{k\; \backslash \; geq\; 0\}\; \backslash \; left\; [-\; \backslash \; sum\; \_\; \{j\; \backslash \; geq\; 0\}\; L\_\; \{ij\}\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; s\; (n)\}\; \{\backslash \; partial\; n\_\; \{j\}\; \backslash ,\; \backslash \; partial\; n\_\; \{k\}\}\}\; \backslash \; right\; |\; \_\; \{n\; =\; n\; ^\; \{*\}\}\; \backslash \; right]\; \backslash ,\; \backslash \; Delta\; n\_\; \{k\}\; \backslash .\}$

Здесь все индексы i, j, k = 0, 1, 2,... относ к внутренней энергии ( 0) и Различные компонентым. Выражение в квадратных скобках - это матрица $D\; ik\; \{\backslash \; displaystyle\; D\_\; \{ik\}\}$диффузии (i, k>0), термодиффузии (i>0, k = 0 или k>0, i = 0) и коэффициенты теплопроводности (i = k = 0).

В изотермических условий Т = постоянная. Соответствующий термодинамический потенциал - это свободная энергия (или свободная энтропия ). Термодинамические движущие силы для изотермической диффузии - это антиградиенты химических потенциалов, $-\; (1\; /\; T)\; \nabla \; \mu \; j\; \{\backslash \; displaystyle\; -\; (1\; /\; T)\; \backslash ,\; \backslash \; nabla\; \backslash \; mu\; \_\; \{j\}\}$, а матрица коэффициентов диффузии имеет вид

$D\; ik\; =\; 1\; T\; \sum \; j\; \ge \; 1\; L\; ij\; \partial \; \mu \; j\; (n,\; T)\; \partial \; nk\; |\; п\; =\; N\; *\; \{\backslash \; Displaystyle\; D\_\; \{ik\}\; =\; \{\backslash \; frac\; \{1\}\; \{T\}\}\; \backslash \; sum\; \_\; \{j\; \backslash \; geq\; 1\}\; L\_\; \{ij\}\; \backslash \; left.\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mu\; \_\; \{j\}\; (n,\; T)\}\; \{\backslash \; partial\; n\_\; \{k\}\}\}\; \backslash \; right\; |\; \_\; \{n\; =\; n\; ^\; \{*\}\}\}$

(i, k>0).

Существует внутреннее произвол в определении термодинамических сил и кинетических коэффициентов, потому что они не измеряются отдельно, а измеряются только их комбинации $\sum \; j\; L\; ij\; X\; j\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{j\}\; L\_\; \{ij\; \}\; X\_\; \{j\}\}$можно измерить. Например, в оригинальной работе Онзагера термодинамические силы включают дополнительный множитель T, тогда как в Курсе теоретической физики этот множитель опускается, но знак термодинамических сил противоположен. Все эти изменения дополняются изменяемыми коэффициентами и не влияют на измеряемые величины.

Недиагональная диффузия должна быть нелинейной

Формализм линейной необратимой термодинамики (Онзагер) порождает систему линейных соотношений диффузии в виде

$\partial \; ci\; \partial \; t\; =\; \sum \; j\; D\; ij\; \Delta \; cj.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; c\_\; \{i\}\}\; \{\backslash \; partial\; t\}\}\; =\; \backslash \; sum\; \_\; \{j\}\; D\_\; \{ij\}\; \backslash ,\; \backslash \; Delta\; c\_\; \{j\}.\}$

Если матрица коэффициентов диффузии диагональна, то эта система представляет собой просто набор разделенных функций Фика для различных компонентов. Предположим, что диффузия недиагональна, например, $D\; 12\; \ne \; 0\; \{\backslash \; displaystyle\; D\_\; \{12\}\; \backslash \; neq\; 0\}$, и рассмотрим состояние с $c\; 2\; =\; \cdots \; =\; cn\; =\; 0\; \{\backslash \; displaystyle\; c\_\; \{2\}\; =\; \backslash \; cdots\; =\; c\_\; \{n\}\; =\; 0\}$. В этом состоянии $\partial \; c\; 2\; /\; \partial \; t\; =\; D\; 12\; \Delta \; c\; 1\; \{\backslash \; displaystyle\; \backslash \; partial\; c\_\; \{2\}\; /\; \backslash \; partial\; t\; =\; D\_\; \{12\}\; \backslash ,\; \backslash \; Delta\; c\_\; \{1\}\}$. Если в некоторых точках, то $c\; 2\; (x)\; \{\backslash \; displaystyle\; c\_\; \{2\}\; (x)\}$становится отрицательным. в эти моменты за короткое время. Следовательно, линейная недиагональная диффузия не сохраняет положительность концентраций. Недиагональные уравнения многокомпонентной диффузии должны быть нелинейными.

Подвижность Эйнштейна и формула Теорелла

Соотношение Эйнштейна (кинетическая теория) связывает коэффициент диффузии и подвижность (отношение конечной скорости дрейфа частицы к приложенной силе )

$D\; =\; \mu \; К\; BT\; q,\; \{\backslash \; displaystyle\; D\; =\; \{\backslash \; frac\; \{\backslash \; mu\; \backslash ,\; k\; \_\; \{\backslash \; text\; \{B\}\}\; T\}\; \{q\}\},\}$

где D - константа диффузии, μ - «подвижность», k B - постоянная Больцмана, T - абсолютная температура, а q - элементарный заряд, то есть заряд одного электрона.

Ниже приведены примеры объединения в ту же формулу химический потенциал μ и подвижность, мы используем для обозначения подвижности обозначение $m\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{m\}\}\}$.

Подход, основанный на подвижности, в дальнейшем был применен Т. Теореллом. В 1935 году он изучил диффузия в формуле:

поток равен к подвижности × концентрации на грамм-ион .

Это так называемая формул а Теорелла. Термин «грамм-ион» («грамм-частица») используется для количества вещества, которое содержит число Авогадро норм (частиц). Общий современный термин - моль.

Сила в изотермических условиях состоит из двух частей:

1. Сила диффузии, вызванная градиентом концентрации: $-\; RT\; 1\; n\; \nabla \; n\; =\; -\; RT\; \nabla \; (ln\; \; (n\; /\; п\; экв))\; \{\backslash \; Displaystyle\; -RT\; \{\backslash \; гидроразрыва\; \{1\}\; \{n\}\}\; \backslash ,\; \backslash \; nabla\; п\; =\; -RT\; \backslash ,\; \backslash \; nabla\; (\backslash \; ln\; (п\; /\; п\; ^\; \{\backslash \; текст\; \{экв\}\}))\}$.
2. Электростатическая сила, вызванная градиентным электрическим средством: $q\; \nabla \; \phi \; \{\backslash \; displaystyle\; q\; \backslash ,\; \backslash \; nabla\; \backslash \; varphi\}$.

Здесь R - газовая постоянная, T - абсолютная температура, n - установлена, равновесная отмечена надстрочным индексом « eq », q - заряд, а φ - электрический потенциал.

Простое, но решающее различие между формулой Теорелла и его коэффициент концентрации в выражении Теорелла для потока. В подходе Эйнштейна - Теорелла, если для конечной силы стремится к нулю, то поток также стремится к нулю, тогда как уравнения Онзагера нарушают это простое и физически очевидное правило.

Общая формулировка формулы Теорелла для несовершенных систем в изотермических условиях:

$J\; =\; m\; exp\; \; (\mu \; -\; \mu \; 0\; RT)\; (-\; \mu \; +\; (внешняя\; сила\; на\; моль)),\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\; J\}\; =\; \{\backslash \; mathfrak\; \{m\}\}\; \backslash \; exp\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mu\; -\; \backslash \; mu\; \_\; \{0\}\}\; \{RT\}\}\; \backslash \; right)\; (-\; \backslash \; nabla\; \backslash \; mu\; +\; (\{\backslash \; text\; \{внешняя\; сила\; на\; моль\}\})),\}$

где μ - химический потенциал, μ 0 - стандартное значение химического потенциала. Выражение $a\; =\; exp\; \; (\mu \; -\; \mu \; 0\; RT)\; \{\backslash \; displaystyle\; a\; =\; \backslash \; exp\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mu\; -\; \backslash \; mu\; \_\; \{0\}\}\; \{RT\}\}\; \backslash \; right)\}$- это так называемое действие. Он измеряет «эффективную концентрацию» вида в неидеальной смеси. В этих обозначениях формула Теорелла для потока имеет очень простой вид

$J\; =\; m\; a\; (-\; \mu \; +\; (внешняя\; сила\; на\; моль)).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; =\; \{\backslash \; mathfrak\; \{m\}\}\; a\; (-\; \backslash \; nabla\; \backslash \; mu\; +\; (\{\backslash \; text\; \{внешняя\; сила\; на\; моль\}\})).\}$

Стандартный вывод действия включает коэффициент нормализации и для малых концентраций $a\; =\; n\; /\; n\; \ominus \; +\; o\; (n\; /\; n\; \ominus )\; \{\backslash \; displaystyle\; a\; =\; n\; /\; n\; ^\; \{\backslash \; ominus\}\; +\; o\; (n\; /\; n\; ^\; \{\backslash \; ominus\})\}$, где $n\; \ominus \; \{\backslash \; displaystyle\; n\; ^\; \{\backslash \; ominus\}\}$- стандартная информация. Следовательно, эта формула для потока потока нормализованной безразмерной величины $n\; /\; n\; \ominus \; \{\backslash \; displaystyle\; n\; /\; n\; ^\; \{\backslash \; ominus\}\}$:

$\partial \; (n\; /\; n\; \ominus )\; \partial \; t\; =\; \nabla \; \cdot \; [ma\; (\nabla \; \mu \; -\; (внешняя\; сила\; на\; моль))].\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; (n\; /\; n\; ^\; \{\backslash \; ominus\})\}\; \{\backslash \; partial\; t\}\}\; =\; \backslash \; nabla\; \backslash \; cdot\; [\{\backslash \; mathfrak\; \{m\}\}\; a\; (\backslash \; nabla\; \backslash \; mu\; -\; (\{\backslash \; text\; \{внешняя\; сила\; на\; моль\}\}))].\}$

Теорема флуктуации-диссипации

Теорема флуктуации-диссипации, основанная на уравнении Ланжевена, расширение модели Эйнштейна на баллистическую шкалу времени. Согласно Ланжевену, уравнение основано на втором законе движения Ньютона:

$md\; 2\; xdt\; 2\; =\; -\; 1\; \mu \; dxdt\; +\; F\; (t)\; \{\backslash \; displaystyle\; m\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; x\}\; \{dt\; ^\; \{2\}\}\; \}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; mu\}\}\; \{\backslash \; frac\; \{dx\}\; \{dt\}\}\; +\; F\; (t)\}$

где

• x - размер.
• μ - подвижность частиц в жидкости или газе, которую можно рассчитать с соотношения Эйнштейна (кинетическая теория).
• m - масса частиц.
• F - случайная сила, приложенная к частице.
• t - время.

Решая это уравнение, мы получили зависящую от времени константу диффузии в долгосрочном пределе, когда частица значительно плотнее окружающей жидкости,

$D\; (t)\; =\; \mu \; К\; BT\; (1\; -\; e\; -\; t\; /\; (m\; \mu ))\; \{\; \backslash \; displaystyle\; D\; (t)\; =\; \backslash \; mu\; \backslash ,\; k\; \_\; \{\backslash \; rm\; \{B\}\}\; T\; (1-e\; ^\; \{-t\; /\; (m\; \backslash \; mu)\})\}$

где

• kB- постоянная Больцмана; ;
• T - абсолютная температура.
• μ - подвижность частиц в жидкости или газе, которое может быть вычислено с использованием соотношения Эйнштейна (кинетическая теория).
• м - масса частиц.
• t - время.

Формула Теорелла для многокомпонентной диффузии

Формула Теорелла с комбинацией определения диффузионной силы Онзагера дает

$J\; i\; =\; miai\; \sum \; JL\; ij\; Икс\; J,\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{J\}\; \_\; \{i\}\; =\; \{\; \backslash \; mathfrak\; \{m\_\; \{i\}\}\}\; a\_\; \{i\}\; \backslash \; sum\; \_\; \{j\}\; L\_\; \{ij\}\; X\_\; \{j\},\}$

где $mi\; \{\backslash \; displaystyle\; \{\backslash \; mathfrak\; \{m\_\; \{i\}\}\}\; \}$- мобильность i-го компонента, $ai\; \{\backslash \; displaystyle\; a\_\; \{i\}\}$- его активность, $L\; ij\; \{\backslash \; displaystyle\; L\_\; \{ij\}\}$- матрица коэффициентов, $X\; j\; \{\backslash \; displaystyle\; X\_\; \{j\}\}$- сила термодинамической диффузии, $X\; j\; =\; -\; \nabla \; \mu \; j\; T\; \{\backslash \; displaystyle\; X\_\; \{j\; \}\; =\; -\; \backslash \; nabla\; \{\backslash \; frac\; \{\backslash \; mu\; \_\; \{j\}\}\; \{T\}\}\}$. Для изотермических совершенных систем $X\; j\; =\; -\; R\; \nabla \; njnj\; \{\backslash \; displaystyle\; X\_\; \{j\}\; =\; -\; R\; \{\backslash \; frac\; \{\backslash \; nabla\; n\_\; \{j\}\}\; \{n\_\; \{j\}\}\}\}$. Таким образом, подход Эйнштейна - Теорелла дает следующее многокомпонентное обобщение закона Фика для многокомпонентной диффузии:

$\partial \; ni\; \partial \; t\; =\; \sum \; j\; \nabla \; \cdot \; (D\; ijninj\; \nabla \; nj),\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; n\_\; \{i\}\}\; \{\backslash \; partial\; t\}\}\; =\; \backslash \; sum\; \_\; \{j\}\; \backslash \; nabla\; \backslash \; cdot\; \backslash \; left\; (D\_\; \{ij\}\; \{\backslash \; frac\; \{n\_\; \{i\}\}\; \{n\_\; \{j\}\}\}\; \backslash \; nabla\; n\_\; \{j\}\; \backslash \; справа),\; \}$

где $D\; ij\; \{\backslash \; displaystyle\; D\_\; \{ij\}\}$- матрица коэффициентов. Формулы Чепмена - Энскога для диффузии в газах включает точно такие же члены. Ранее такие члены были введены в уравнение диффузии Максвелла - Стефана.

Прыжки на поверхности в твердых телах

Диффузия в монослое: колебания положения положения равновесия и скачки к ближайшим свободным местам.

Диффузия реагентов на поверхности объекта катализатор может играть роль в гетерогенном катализе. Модель диффузии в идеальном монослое основание на скачках реагентов на ближайшие свободные места. Эта модель была для окисления CO при низком давлении газа.

В систему входит несколько реагентов $A\; 1,\; A\; 2,\dots ,\; A\; m\; \{\backslash \; displaystyle\; A\_\; \{1\},\; A\_\; \{2\},\; \backslash \; ldots,\; A\_\; \{m\}\}$на поверхности. Их поверхностные концентрации $c\; 1,\; c\; 2,\dots ,\; c\; m.\; \{\backslash \; displaystyle\; c\_\; \{1\},\; c\_\; \{2\},\; \backslash \; ldots,\; c\_\; \{m\}.\}$Поверхность представляет собой решетку мест адсорбции. Каждая молекула реагента занимает место на поверхности. Некоторые места свободны. Концентрация свободных мест составляет $z\; =\; c\; 0\; \{\backslash \; displaystyle\; z\; =\; c\_\; \{0\}\}$. Сумма всех $c\; i\; \{\backslash \; displaystyle\; c\_\; \{i\}\}$(включая свободные места) постоянна, плотность адсорбционных мест b.

Модель скачка дает для диффузионного потока $A\; i\; \{\backslash \; displaystyle\; A\_\; \{i\}\}$(i = 1,..., n):

$Дж\; я\; =\; -\; D\; я\; [z\; \nabla \; ci\; -\; ci\; \nabla \; z].\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \_\; \{i\}\; =\; -\; D\_\; \{i\}\; [z\; \backslash ,\; \backslash \; nabla\; c\_\; \{i\}\; -c\_\; \{i\}\; \backslash \; nabla\; z]\; \backslash ,.\}$

Соответствующее уравнение диффузии:

$\partial \; ci\; \partial \; t\; =\; -\; div\; \; J\; i\; =\; D\; i\; [z\; \Delta \; ci\; -\; ci\; \Delta \; z].\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; c\_\; \{i\}\}\; \{\backslash \; partial\; t\}\}\; =\; -\; \backslash \; operatorname\; \{div\}\; \backslash \; mathbf\; \{J\}\; \_\; \{i\}\; =\; D\_\; \{i\}\; [z\; \backslash ,\; \backslash \; Delta\; c\_\; \{i\; \}\; -c\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; z]\; \backslash ,.\}$

Согласно закону сохранения, $z\; =\; b\; -\; \sum \; i\; =\; 1\; nci,\; \{\backslash \; displaystyle\; z\; =\; b-\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; c\_\; \{i\}\; \backslash ,,\}$и у нас есть система m уравнений диффузии. Для одного компонента мы получаем закон Фика и линейные уравнения, потому что $(b\; -\; c)\; \nabla \; c\; -\; c\; \nabla \; (b\; -\; c)\; =\; b\; \nabla \; c\; \{\backslash \; displaystyle\; (bc)\; \backslash ,\; \backslash \; nabla\; cc\; \backslash ,\; \backslash \; nabla\; (bc)\; =\; b\; \backslash ,\; \backslash \; nabla\; c\}$. Для двух и более компонентов уравнения нелинейны.

Если все частицы могут поменяться местами со своими ближайшими соседями, то простое обобщение дает

$J\; i\; =\; -\; \sum \; j\; D\; ij\; [cj\; \nabla \; ci\; -\; ci\; \nabla \; cj]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \_\; \{i\}\; =\; -\; \backslash \; sum\; \_\; \{j\}\; D\_\; \{ij\}\; [c\_\; \{j\}\; \backslash ,\; \backslash \; nabla\; c\_\; \{i\}\; -c\_\; \{i\}\; \backslash ,\; \backslash \; nabla\; c\_\; \{j\}]\}$

$\partial \; ci\; \partial \; t\; знак\; равно\; \sum \; J\; D\; ij\; [cj\; \Delta \; ci\; -\; ci\; \Delta \; cj]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; c\_\; \{i\}\}\; \{\backslash \; partial\; t\}\}\; =\; \backslash \; sum\; \_\; \{j\}\; D\_\; \{ij\}\; [c\_\; \{j\; \}\; \backslash ,\; \backslash \; Delta\; c\_\; \{i\}\; -c\_\; \{i\}\; \backslash ,\; \backslash \; Delta\; c\_\; \{j\}]\}$

где $D\; ij\; =\; D\; ji\; \ge \; 0\; \{\backslash \; displaystyle\; D\_\; \{ij\}\; =\; D\_\; \{ji\}\; \backslash \; geq\; 0\}$- симметричная матрица коэффициентов, характеризующих интенсивности скачков. Свободные места (вакансии) следует рассматривать как особые «частицы» с концентрацией $c\; 0\; \{\backslash \; displaystyle\; c\_\; \{0\}\}$.

. Различные версии этих моделей скачков также подходят для простых механизмов диффузии в твердых телах.

Диффузия в пористой среде

Для диффузии в пористой среде основные уравнения следующие:

$J\; =\; -\; \varphi \; D\; \nabla \; nm\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; =\; -\; \backslash \; phi\; D\; \backslash ,\; \backslash \; набла\; п\; ^\; \{м\}\}$

$\partial \; N\; \partial \; T\; =\; D\; \Delta \; нм,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; n\}\; \{\backslash \; partial\; t\}\}\; =\; D\; \backslash ,\; \backslash \; Delta\; n\; ^\; \{m\}\; \backslash ,,\}$

где D - коэффициент диффузии, Φ - пористость, n - концентрация, m>0 (обычно m>1, случай m = 1 соответствует закону Фика).

Необходимо внимательно учитывать пористость (Ф) пористой среды как в терминах потока, так и в терминах накопления. Например, когда пористость стремится к нулю, молярный поток в пористой среде стремится к нулю для данного градиента концентрации. При применении дивергенции потока члены пористости сокращаются, и формируется второе уравнение выше.

Для диффузии газов в пористой среде это уравнение является формализацией закона Дарси : объемный поток газа в пористой среде равен

$q\; =\; -\; k\; \mu \; \nabla \; p\; \{\backslash \; displaystyle\; q\; =\; -\; \{\backslash \; frac\; \{k\}\; \{\backslash \; mu\}\}\; \backslash ,\; \backslash \; nabla\; p\}$

, где k - проницаемость среды, μ - вязкость, p - давление.

Адвективный молярный поток задается как

J = nq

и для $p\; \sim \; n\; \gamma \; \{\backslash \; displaystyle\; p\; \backslash \; sim\; n\; ^\; \{\backslash \; gamma\}\}$Закон Дарси дает уравнение диффузии в пористой среде с m = γ + 1.

В пористой среде средняя линейная скорость (ν) связана с объемным потоком следующим образом:

$\upsilon \; =\; q\; /\; \varphi \; \{\backslash \; displaystyle\; \backslash \; upsilon\; =\; q\; /\; \backslash \; phi\}$

Объединение адвективного молярного потока с диффузионным потоком дает уравнение дисперсии адвекции

$\partial \; n\; \partial \; t\; =\; D\; \Delta \; nm\; -\; \nu \; \cdot \; \nabla \; нм,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; n\}\; \{\backslash \; partial\; t\}\}\; =\; D\; \backslash ,\; \backslash \; Delta\; n\; ^\; \{m\}\; \backslash \; -\; \backslash \; nu\; \backslash \; cdot\; \backslash \; nabla\; n\; ^\; \{m\},\}$

Для подземных работ инфильтрации воды приближение Буссинеска дает то же уравнение с m = 2.

Для плазмы с высоким уровнем излучения уравнение Зельдовича –Райзера дает m>4 для теплопередачи.

Коэффициент диффузии в кинетической теории газов

Случайные столкновения частиц в газе.

Коэффициент диффузии $D\; \{\backslash \; displaystyle\; D\}$- коэффициент в первом законе Фика $J\; =\; -\; D\; \partial \; n\; /\; \partial \; x\; \{\backslash \; displaystyle\; J\; =\; -D\; \backslash ,\; \backslash \; partial\; n\; /\; \backslash \; partial\; x\}$, где J - диффузионный поток (количество вещества ) на единицу площади в единицу времени, n (для идеальных смесей) - концентрация, x - положение [длина].

Рассмотрим два газа с молекулами одинакового диаметра d и массы m (самодиффузия ). В этом случае теория элементарной средней длины свободная пробега коэффициент диффузии

$D\; =\; 1\; 3\; \ell \; v\; T\; =\; 2\; 3\; k\; B\; 3\; \pi \; 3\; м\; T\; 3/2\; P\; d\; 2,\; \{\backslash \; displaystyle\; D\; =\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; ell\; v\_\; \{T\}\; =\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{k\; \_\; \{\backslash \; rm\; \{B\}\}\; ^\; \{3\}\}\; \{\backslash \; pi\; ^\; \{3\}\; м\; \}\}\}\; \{\backslash \; Frac\; \{T\; ^\; \{3/2\}\}\; \{Pd\; ^\; \{2\}\}\}\; \backslash ,,\}$

где k B - постоянная Больцмана, T - температура, P - давление, $\ell \; \{\backslash \; displaystyle\; \backslash \; ell\}$- средний свободный пробег, а v T - средняя тепловая скорость:

$\ell \; =\; k\; BT\; 2\; \pi \; d\; 2\; P,\; v\; T\; =\; 8\; k\; BT\; \pi \; m.\; \{\backslash \; displaystyle\; \backslash \; ell\; =\; \{\backslash \; frac\; \{k\; \_\; \{\backslash \; rm\; \{B\}\}\; T\}\; \{\{\backslash \; sqrt\; \{2\}\}\; \backslash \; pi\; d\; ^\; \{2\}\; P\}\}\; \backslash ,,\; \backslash ;\; \backslash ;\; \backslash ;\; v\_\; \{T\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{8k\; \_\; \{\backslash \; rm\; \{B\}\}\; T\}\; \{\backslash \; pi\; m\}\}\}\; \backslash ,.\}$

Мы видим, что коэффициент диффузии в приближении средней длины свободной Если мы используем P идеального газа P = RnT с общей концентрацией, то мы видим, что для данной концентрации коэффициент диффузии растет с T как T, а для данной температуры он уменьшается с общей концентрацией n. содержание как 1 / н.

Для двух разных газов, A и B, с молекулярными массами m A, m B и молекулярными массами d A, d B, оценка средней длины свободной пробега для коэффициента диффузии A в B и B в A составляет:

$DAB\; =\; 2\; 3\; k\; B\; 3\; \pi \; 3\; 1\; 2\; м\; A\; +\; 1\; 2\; м\; B\; 4\; T\; 3/2\; п\; (d\; A\; +\; d\; B)\; 2,\; \{\backslash \; displaystyle\; D\; \_\; \{\backslash \; rm\; \{AB\}\}\; =\; \{\backslash \; frac\; \{2\}\; \{3\}\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{k\; \_\; \{\backslash \; rm\; \{B\}\}\; ^\; \{\; 3\}\}\; \{\backslash \; pi\; ^\; \{3\}\}\}\}\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{1\}\; \{2m\; \_\; \{\backslash \; rm\; \{A\}\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{2m\; \_\; \{\backslash \; rm\; \{B\; \}\}\}\}\}\}\; \{\backslash \; frac\; \{4T\; ^\; \{3/2\}\}\; \{P\; (d\; \_\; \{\backslash \; rm\; \{A\}\}\; +\; d\; \_\; \{\backslash \; rm\; \{B\}\})\; ^\; \{2\}\}\}\; \backslash ,,\; \}$

Теория диффузии в газах, основанной на уравнении Больцмана

В кинетике Больцмана смеси газов каждый газ имеет свою собственную функцию распределения, $fi\; (x,\; c,\; t)\; \{\backslash \; displaystyle\; f\_\; \{i\}\; (x,\; c,\; t)\}$, где t - момент времени, x - положение, c - скорость молекулы i-го компонента смеси. Каждый компонент имеет свою среднюю скорость $C\; i\; (x,\; t)\; =\; 1\; ni\; \int \; ccf\; (x,\; c,\; t)\; dc\; \{\backslash \; displaystyle\; C\_\; \{i\}\; (x,\; t)\; =\; \{\backslash \; frac\; \{1\}\; \{n\_\; \{i\}\}\}\; \backslash \; int\; \_\; \{c\}\; cf\; (x,\; c,\; t)\; \backslash ,\; dc\}$. Если скорость $C\; i\; (x,\; t)\; \{\backslash \; displaystyle\; C\_\; \{i\}\; (x,\; t)\}$не совпадают, тогда существует диффузия.

В приближении Чепмена - Энскога все функции распределения выражаются через плотность сохраняющихся величин:

• отдельные частицы, $ni\; (x,\; t)\; Знак\; равно\; \int \; cfi\; (x,\; c,\; t)\; dc\; \{\backslash \; displaystyle\; n\_\; \{i\}\; (x,\; t)\; =\; \backslash \; int\; \_\; \{c\}\; f\_\; \{i\}\; (x,\; c,\; t)\; \backslash ,\; dc\}$(частицы на объем),
• плотность количества движения $\sum \; imini\; C\; i\; (x,\; t)\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; m\_\; \{i\}\; n\_\; \{i\}\; C\_\; \{i\}\; (x,\; t)\}$(mi- масса i-й частицы),
• кинетической энергии

$\sum \; i\; (nimi\; C\; i\; 2\; (x,\; t)\; 2\; +\; \int \; cmi\; (ci\; -\; C\; i\; (x,\; t))\; 2\; 2\; fi\; (x,\; c,\; t)\; dc).\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; \backslash \; left\; (n\_\; \{i\}\; \{\backslash \; frac\; \{m\_\; \{i\}\; C\_\; \{i\}\; ^\; \{2\}\; (x,\; t)\}\; \{2\}\}\; +\; \backslash \; int\; \_\; \{c\}\; \{\; \backslash \; frac\; \{m\_\; \{i\}\; (c\_\; \{i\}\; -C\_\; \{i\}\; (x,\; t))\; ^\; \{2\}\}\; \{2\}\}\; f\_\; \{i\}\; (x,\; c,\; t)\; \backslash ,\; dc\; \backslash \; right).\; \}$

Кинетическая температура T и давление P в трехмерном пространстве как

$3\; 2\; k\; BT\; =\; 1\; n\; \int \; cmi\; (ci\; -\; C\; i\; (x,\; t))\; 2\; 2\; fi\; (x,\; c,\; t)\; Округ\; Колумбия\; ;\; P\; =\; К\; В\; NT,\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; k\; \_\; \{\backslash \; rm\; \{B\}\}\; T\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; int\; \_\; \{c\}\; \{\backslash \; frac\; \{\; m\_\; \{i\}\; (c\_\; \{i\}\; -C\_\; \{i\}\; (x,\; t))\; ^\; \{2\}\}\; \{2\}\}\; f\_\; \{i\}\; (x,\; c,\; t)\; \backslash ,\; dc;\; \backslash \; quad\; P\; =\; k\_\; \{\backslash \; rm\; \{B\}\}\; nT,\}$

где $n\; =\; \sum \; ini\; \{\backslash \; displaystyle\; n\; =\; \backslash \; sum\; \_\; \{i\}\; n\_\; \{i\}\}$- общее плотность.

Для двух газов разность скоростей, $C\; 1\; -\; C\; 2\; \{\backslash \; displaystyle\; C\_\; \{1\}\; -C\_\; \{2\}\}$, определяется выражением:

$C\; 1\; -\; C\; 2\; =\; -\; n\; 2\; n\; 1\; n\; 2\; D\; 12\; \{\nabla \; (n\; 1\; n)\; +\; n\; 1\; n\; 2\; (m\; 2\; -\; m\; 1)\; P\; n\; (m\; 1\; n\; 1\; +\; m\; 2\; n\; 2)\; \nabla \; P\; -\; ì\; 1\; n\; 1\; м\; 2\; N\; 2\; п\; (м\; 1\; N\; 1\; +\; м\; 2\; N\; 2)\; (F\; 1\; -\; F\; 2)\; +\; к\; T\; 1\; T\; \nabla \; T\},\; \{\backslash \; displaystyle\; C\_\; \{1\}\; -C\_\; \{2\}\; =\; -\; \{\backslash \; frac\; \{\; n\; ^\; \{2\}\}\; \{n\_\; \{1\}\; n\_\; \{2\}\}\}\; D\_\; \{12\}\; \backslash \; left\; \backslash \; \{\backslash \; nabla\; \backslash \; left\; (\{\backslash \; frac\; \{n\_\; \{1\}\}\; \{n\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{n\_\; \{1\}\; n\_\; \{2\}\; (m\_\; \{2\}\; -m\_\; \{1\})\}\; \{Pn\; (m\_\; \{1\}\; n\_\; \{1\}\; +\; m\_\; \{2\}\; n\_\; \{2\})\}\}\; \backslash \; набла\; P\; -\; \{\backslash \; гидроразрыв\; \{m\_\; \{1\}\; n\_\; \{1\}\; m\_\; \{2\}\; n\_\; \{2\}\}\; \{P\; (m\_\; \{1\}\; n\_\; \{1\}\; +\; m\_\; \{2\}\; n\_\; \{2\})\}\}\; (F\_\; \{1\}\; -F\_\; \{\; 2\})\; +\; k\_\; \{T\}\; \{\backslash \; frac\; \{1\}\; \{T\}\}\; \backslash \; nabla\; T\; \backslash \; right\; \backslash \},\}$

где $F\; i\; \{\backslash \; displaystyle\; F\_\; \{i\}\}$- сила, приложенная к молекулам i-го компонента, а $k\; T\; \{\backslash \; displaystyle\; k\_\; \{T\}\}$- коэффициент термодиффузии.

Коэффициент D 12 положительный. Это коэффициент диффузии. Четыре члена в формуле для C 1-C2описывают четыре основных эффекта в диффузии газов:

1. $\nabla \; (n\; 1\; n)\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash ,\; \backslash \; left\; (\{\backslash \; frac\; \{n\_\; \{1\}\}\; \{n\}\}\; \backslash \; right)\}$потоком первого компонента из области с отношением n 1 / n в области с меньшими значениями этого отношения (и, аналогично, поток второго компонента от высокого n 2 / n до низкого n 2 / n, потому что n 2 / n = 1 - n 1 / n);
2. $n\; 1\; n\; 2\; (m\; 2\; -\; m\; 1)\; n\; (m\; 1\; n\; 1\; +\; m\; 2\; n\; 2)\; \nabla \; P\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{n\_\; \{1\}\; n\_\; \{2\}\; (m\_\; \{2\}\; -m\_\; \{1\})\}\; \{n\; (m\_\; \{1\}\; n\_\; \{1\}\; +\; m\_\; \{2\}\; n\_\; \{2\})\}\}\; \backslash \; nabla\; P\}$это поток более тяжелых молекул в области с более высоким давлением и более легкие молекулы в области с более низким давлением, это:
3. $m\; 1\; n\; 1\; m\; 2\; n\; 2\; P\; (m\; 1\; n\; 1\; +\; m\; 2\; n\; 2)\; (F\; 1\; -\; F\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{m\_\; \{1\}\; n\_\; \{1\}\; m\_\; \{2\}\; n\_\; \{2\}\}\; \{P\; (m\_\; \{1\}\; n\_\; \{1\}\; +\; m\_\; \{2\}\; n\_\; \{2\})\}\}\; (F\_\; \{\; 1\}\; -F\_\; \{2\})\}$описывает диффузию, вызванную разницей сил, приложенных к молекулам разного типа. пес. Например, в гравитационном поле Земли более тяжелые молекулы должны опускаться или в электрическом поле заряженные молекулы должны двигаться, пока этот эффект не уравновесится суммой других членов. Этот эффект не следует путать с бародиффузией, вызванной градиентом давления.
4. $k\; T\; 1\; T\; \nabla \; T\; \{\backslash \; displaystyle\; k\_\; \{T\}\; \{\backslash \; frac\; \{1\}\; \{T\}\}\; \backslash \; nabla\; T\}$описывает термодиффузию,, диффузионный поток, вызванный температурным градиентом.

Все эти эффекты называются диффузией, потому что они описывают разницу между скоростями различных компонентов в смеси. Следовательно, эти эффекты нельзя описать как массовый перенос и отличить от адвекции или конвекции.

В первом приближении

• $D\; 12\; =\; 3\; 2\; n\; (d\; 1\; +\; d\; 2)\; 2\; [k\; T\; (m\; 1\; +\; m\; 2)\; 2\; \pi \; m\; 1\; m\; 2]\; 1/2\; \{\backslash \; displaystyle\; D\_\; \{12\}\; =\; \{\backslash \; frac\; \{3\}\; \{2n\; (d\_\; \{1\}\; +\; d\_\; \{2\})\; ^\; \{2\}\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{kT\; (m\_\; \{1\}\; +\; m\_\; \{2\})\; \}\; \{2\; \backslash \; pi\; m\_\; \{1\}\; m\_\; \{2\}\}\}\; \backslash \; right]\; ^\; \{1/2\}\}$для твердых сфер;
• $D\; 12\; =\; 3\; 8\; n\; A\; 1\; (\nu )\; \Gamma \; (3\; -\; 2\; \nu \; -\; 1)\; [К\; T\; (м\; 1\; +\; м\; 2)\; 2\; \pi \; m\; 1\; м\; 2]\; 1/2\; (2\; К\; T\; \kappa \; 12)\; 2\; \nu \; -\; 1\; \{\backslash \; Displaystyle\; D\_\; \{12\}\; =\; \{\backslash \; гидроразрыва\; \{3\}\; \{8nA\_\; \{1\}\; (\{\backslash \; nu\})\; \backslash \; Gamma\; (3\; -\; \{\backslash \; frac\; \{2\}\; \{\backslash \; nu\; -1\}\})\}\}\; \backslash \; left\; [\{\backslash \; frac\; \{kT\; (m\_\; \{1\}\; +\; m\_\; \{2\})\}\; \{2\; \backslash \; pi\; m\_\; \{1\}\; m\_\; \{2\}\}\}\; \backslash \; right]\; ^\; \{1/2\}\; \backslash \; left\; (\{\backslash \; frac\; \{2kT\}\; \{\backslash \; kappa\; \_\; \{12\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{2\}\; \{\backslash \; nu\; -1\}\}\}$для силы отталкивания $\kappa \; 12\; r\; -\; \nu .\; \{\backslash \; displaystyle\; \backslash \; kappa\; \_\; \{12\}\; r\; ^\; \{-\; \backslash \; nu\}.\}$

Число $A\; 1\; (\nu )\; \{\backslash \; displaystyle\; A\_\; \{1\}\; (\{\backslash \; nu\})\}$определяется квадратурами (формулы (3.7), (3.9), гл. 10 классической книги Чепмена и Каулинга)

Мы видим, что зависимость от T для твердых сфер такая же, как и для простая теория длины свободного пробега, но для степенных законов отталкивания показатель другой. Зависимость от общей концентрации n для данной температуры всегда имеет один и тот же характер - 1 / n.

В приложениях к газовой динамике диффузионный поток и объемный поток должны быть объединены в одну систему уравнений переноса. Объемный поток описывает массообмен. Его скорость V - это средняя массовая скорость. Он определяется через плотность количества движения и массовые концентрации:

$V\; =\; \sum \; i\; \rho \; i\; C\; i\; \rho .\; \{\backslash \; displaystyle\; V\; =\; \{\backslash \; frac\; \{\backslash \; sum\; \_\; \{i\}\; \backslash \; rho\; \_\; \{i\}\; C\_\; \{i\}\}\; \{\backslash \; rho\}\}\; \backslash ,.\}$

где $\rho \; i\; =\; mini\; \{\backslash \; displaystyle\; \backslash \; rho\; \_\; \{i\}\; =\; m\_\; \{i\}\; n\_\; \{i\}\}$- массовая концентрация i-го вида, $\rho \; =\; \sum \; i\; \rho \; i\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \backslash \; sum\; \_\; \{i\; \}\; \backslash \; rho\; \_\; \{i\}\}$- массовая плотность.

По определению, скорость диффузии i-го компонента равна $vi\; =\; C\; i\; -\; V\; \{\backslash \; displaystyle\; v\_\; \{i\}\; =\; C\_\; \{i\}\; -V\}$, $\sum \; i\; \rho \; ivi\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; \backslash \; rho\; \_\; \{i\}\; v\_\; \{i\}\; =\; 0\}$. Массовый перенос i-го компонента описывается уравнением неразрывности

$\partial \; \rho \; i\; \partial \; t\; +\; \nabla \; (\rho \; i\; V)\; +\; \nabla \; (\rho \; ivi)\; =\; W\; i,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; rho\; \_\; \{i\}\}\; \{\backslash \; partial\; t\}\}\; +\; \backslash \; nabla\; (\backslash \; rho\; \_\; \{i\}\; V)\; +\; \backslash \; nabla\; (\backslash \; rho\; \_\; \{i\}\; v\_\; \{i\})\; =\; W\_\; \{i\}\; \backslash ,,\}$

где $W\; i\; \{\backslash \; displaystyle\; W\_\; \{i\}\}$- чистая массовая скорость производства в химических реакциях, $\sum \; i\; W\; i\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; W\_\; \{i\}\; =\; 0\}$.

В этих уравнениях член $\nabla \; (\rho \; i\; V)\; \{\backslash \; displaystyle\; \backslash \; nabla\; (\backslash \; rho\; \_\; \{i\}\; V)\}$описывает адвекцию с компонентом, а термин $\nabla \; (\rho \; ivi)\; \{\backslash \; displaystyle\; \backslash \; nabla\; (\backslash \; rho\; \_\; \{i\}\; v\_\; \{i\})\}$представляет распространение этого компонента.

В 1948 году Венделл Х. Ферри предложил использовать форму скоростей диффузии, найденную в кинетической теории, в качестве основы для нового феноменологического подхода к диффузии в газах. Этот подход был развит F.A. Williams и S.H. Лам. Для скоростей диффузии в многокомпонентных газах (N компонентов) они использовали

$v\; i\; =\; -\; (\sum \; j\; =\; 1\; N\; D\; i\; j\; d\; j\; +\; D\; i\; (T)\; \nabla \; (ln\; \; T));\; \{\backslash \; displaystyle\; v\_\; \{i\}\; =\; -\; \backslash \; left\; (\backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{N\}\; D\_\; \{ij\}\; \backslash \; mathbf\; \{d\}\; \_\; \{j\}\; +\; D\_\; \{i\}\; ^\; \{(T)\}\; \backslash ,\; \backslash \; nabla\; (\backslash \; ln\; T)\; \backslash \; right)\; \backslash ,;\}$

$dj\; =\; \nabla \; X\; j\; +\; (X\; j\; -\; Y\; j)\; \nabla \; (ln\; \; P)\; +\; gj;\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{d\}\; \_\; \{j\}\; =\; \backslash \; nabla\; X\_\; \{j\}\; +\; (X\_\; \{j\}\; -Y\_\; \{j\})\; \backslash ,\; \backslash \; nabla\; (\backslash \; ln\; P)\; +\; \backslash \; mathbf\; \{g\}\; \_\; \{j\}\; \backslash ,;\}$

$gj\; =\; \rho \; P\; (Y\; j\; \sum \; k\; =\; 1\; NY\; k\; (fk\; -\; fj)).\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{g\}\; \_\; \{j\}\; =\; \{\backslash \; frac\; \{\backslash \; rho\}\; \{P\}\}\; \backslash \; left\; (Y\_\; \{j\}\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{N\}\; Y\_\; \{k\}\; (f\_\; \{\; k\}\; -f\_\; \{j\})\; \backslash \; right)\; \backslash ,.\}$

Здесь $D\; ij\; \{\backslash \; displaystyle\; D\_\; \{ij\}\}$- матрица коэффициентов диффузии, $D\; i\; (T)\; \{\backslash \; displaystyle\; D\_\; \{i\}\; ^\; \{(T)\}\}$- коэффициент термодиффузии, $fi\; \{\backslash \; displaystyle\; f\_\; \{i\}\}$- тело сила на единицу массы, действующая на i-й компонент, $X\; i\; =\; P\; i\; /\; P\; \{\backslash \; displaystyle\; X\_\; \{i\}\; =\; P\_\; \{i\}\; /\; P\}$- доля парциального давления i-го компонента (и $P\; i\; \{\backslash \; displaystyle\; P\_\; \{i\}\}$- парциальное давление), $Y\; i\; =\; \rho \; i\; /\; \rho \; \{\backslash \; displaystyle\; Y\_\; \{i\}\; =\; \backslash \; rho\; \_\; \{i\; \}\; /\; \backslash \; rho\}$- массовая доля i-го вида, а $\sum \; i\; X\; i\; =\; \sum \; i\; Y\; i\; =\; 1.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; X\_\; \{i\}\; =\; \backslash \; sum\; \_\; \{i\}\; Y\_\; \{i\}\; =\; 1.\}$

Поскольку носители генерируются (зеленые: электроны и фиолетовый: дырки) из-за света, падающего в центре собственного полупроводника, они рассеиваются к двум концам. Электроны имеют более высокую константу диффузии, чем дырки, что приводит к меньшему количеству избыточных электронов в центре по сравнению с дырками.

Диффузия электронов в твердых телах

Когда плотность электронов в твердых телах не находится в равновесии, происходит диффузия электронов. Например, когда смещение применяется к двум концам куска полупроводника или на одном конце светится свет (см. Рисунок справа), электрон диффундирует из областей с высокой плотностью (центр) в области с низкой плотностью (два конца), образуя градиент электронной плотности. Этот процесс генерирует ток, называемый диффузионным током.

. Диффузионный ток также может быть описан первым законом Фика

$J\; =\; -\; D\; \partial \; n\; /\; \partial \; x,\; \{\backslash \; displaystyle\; J\; =\; -D\; \backslash ,\; \backslash \; partial\; n\; /\; \backslash \; partial\; x\; \backslash ,,\}$

где J - плотность диффузионного тока (количество вещества ) на единицу площади в единицу времени, n (для идеальных смесей) - плотность электронов, x - позиция [длина].

Диффузия в геофизике

Аналитические и численные модели, которые решают уравнение диффузии для различных начальных и граничных условий, были популярны для изучения широкого спектра изменений на поверхности Земли. Распространение широко использовалось в исследованиях эрозии отступления склонов холмов, эрозии обрывов, деградации уступов разломов, отступления террасы / береговой линии в виде волны, врезания аллювиального русла, отступления прибрежного шельфа и проградации дельты. Хотя поверхность Земли не распространяется буквально во многих из этих случаев, процесс распространения эффективно имитирует целостные изменения, происходящие на протяжении десятилетий или тысячелетий. Модели диффузии также могут использоваться для решения обратных краевых задач, в которых некоторая информация об окружающей среде осадконакопления известна из палеоэкологической реконструкции, а уравнение диффузии используется для расчета притока наносов и временных рядов изменений формы рельефа.

Воспроизвести медиа Объяснение очевидного случайного движения атомов, ионов или молекул. Кажется, что вещества беспорядочно перемещаются из-за столкновений с другими веществами. Из iBook Cell Membrane Transport, бесплатная лицензия, предоставленная IS3D, LLC, 2014.

Распространенное заблуждение состоит в том, что отдельные атомы, ионы или молекулы движутся случайным образом, чего не происходит. На анимации справа ион на левой панели движется «случайным образом» в отсутствие других ионов. Однако, как показано на правой панели, это движение не является случайным, а является результатом «столкновений» с другими ионами. Таким образом, движение отдельного атома, иона или молекулы в смеси кажется случайным, если рассматривать его изолированно. Движение вещества в смеси путем «случайного блуждания» регулируется кинетической энергией внутри системы, на которую могут влиять изменения концентрации, давления или температуры.

Отделение диффузии от конвекции в газах

В то время как броуновское движение многомолекулярных мезоскопических частиц (например, пыльцевых зерен, изученных Брауном) можно наблюдать под оптическим микроскопом, молекулярную диффузию можно исследовать только в тщательно контролируемые экспериментальные условия. Начиная с экспериментов Грэма, хорошо известно, что необходимо избегать конвекции, и это может быть нетривиальной задачей.

В нормальных условиях молекулярная диффузия доминирует только на длинах в диапазоне от нанометров до миллиметров. На больших масштабах перенос жидкостей и газов обычно происходит из-за другого явления переноса, конвекции. Для разделения диффузии в этих случаях необходимы особые усилия.

Следовательно, некоторые часто приводимые примеры диффузии ошибочны: если одеколон распыляется в одном месте, он вскоре может ощущаться во всей комнате, но простой расчет показывает, что это не может быть связано с диффузией. Конвективное движение сохраняется в комнате из-за температурной [неоднородности]. Если чернила падают в воду, обычно наблюдается неоднородная эволюция пространственного распределения, которая четко указывает на конвекцию (вызванную, в частности, этим капанием).

Напротив, теплопроводность через твердые среды - обычное дело (например, металлическая ложка, частично погруженная в горячую жидкость). Это объясняет, почему диффузия тепла была объяснена математически до диффузии массы.

Другие типы диффузии

• Анизотропная диффузия, также известная как уравнение Перона-Малика, усиливает высокие градиенты
• Аномальная диффузия в пористой среде
• Атомная диффузия, в твердых телах
• диффузия Бома, распространение плазмы по магнитным полям
• Вихревая диффузия, в крупномасштабном описании турбулентного потока
• Истечение газа через маленькие отверстия
• Электронная диффузия, приводящая к электрическому току, называемому диффузионным током
• облегченной диффузией, присутствует в некоторых организмах
• Газовая диффузия, используется для разделение изотопов
• уравнение теплопроводности, диффузия тепловой энергии
• диффузия Itō, математизация броуновского движения, непрерывный стохастический процесс.
• кинезис (биология) не является животным. -направленная двигательная активность в ответ на раздражитель.
• диффузия Кнудсена газа в длинных порах с частыми столкновениями со стенками
• полет Леви
• Молекулярная диффузия, диффузия ион молекул из более плотных областей в менее плотные
• Импульс диффузии напр. диффузия гидродинамического поля скорости
• диффузия фотонов
• диффузия плазмы
• случайное блуждание, модель диффузии
• обратная диффузия против градиента концентрации, в разделение фаз
• Вращательная диффузия, случайная переориентация молекул
• Поверхностная диффузия, диффузия адчастиц по поверхности
• Транскультурная диффузия, распространение культурных особенностей по географическому региону
• Турбулентная диффузия, перенос массы, тепла или количества движения в турбулентной жидкости

• Ограниченная диффузией агрегация
• Уравнения Даркена
• Изобарическая контрдиффузия - диффузия газов в и из биологических тканей при постоянном давлении окружающей среды после изменения состава газа
• Сорбция
• Осмос - химический процесс