Законы диффузии Фика

О методе измерения сердечного выброса см. Принцип Фика.

Молекулярная диффузия с микроскопической и макроскопической точки зрения. Изначально молекулы растворенных веществ находятся на левой стороне барьера (фиолетовая линия), а на правой - нет. Барьер удаляется, и растворенное вещество диффундирует, заполняя весь контейнер. Вверху: одна молекула движется случайным образом. В центре: при увеличении количества молекул наблюдается четкая тенденция к тому, что растворенное вещество заполняет контейнер все более и более равномерно. Внизу: с огромным количеством молекул растворенного вещества случайность становится необнаружимой: растворенное вещество, кажется, плавно и систематически перемещается из областей с высокой концентрацией в области с низкой концентрацией. Этот плавный поток описывается законами Фика.

Законы диффузии Фика описывает диффузию и были получены путем Адольфа Фика в 1855. Они могут быть использованы для решения для коэффициента диффузии, D. Первый закон Фика можно использовать для вывода его второго закона, который, в свою очередь, идентичен уравнению диффузии.

Процесс диффузии, подчиняющийся законам Фика, называется нормальной диффузией или диффузией Фика; в противном случае это называется аномальной диффузией или нефиковской диффузией.

• 1 История
• 2 первый закон Фика
  • 2.1 Альтернативные формулировки первого закона
  • 2.2 Вывод первого закона Фика для газов
• 3 второй закон Фика
  • 3.1 Вывод второго закона Фика
• 4 Примеры решений и обобщение
  • 4.1 Пример раствора 1: источник постоянной концентрации и длина диффузии
  • 4.2 Пример решения 2: броуновская частица и среднеквадратичное смещение
  • 4.3 Обобщения
• 5 приложений
  • 5.1 Течение Фика в жидкостях
  • 5.2 Скорость сорбции и частота столкновений разбавленных растворенных веществ
  • 5.3 Биологическая перспектива
  • 5.4 Применение в производстве полупроводников
• 6 См. Также
• 7 Примечания
• 8 ссылки
• 9 Внешние ссылки

В 1855 году физиолог Адольф Фик впервые сообщил о своих теперь хорошо известных законах, управляющих переносом массы посредством диффузии. Работа Фика была вдохновлена ​​более ранними экспериментами Томаса Грэхема, в которых не были предложены фундаментальные законы, благодаря которым Фик стал известен. Закон Фика аналогичен отношениям, обнаруженным в ту же эпоху другими выдающимися учеными: закону Дарси (гидравлический поток), закону Ома (перенос заряда) и закону Фурье (перенос тепла).

Эксперименты Фика (по образцу Грэма) касались измерения концентраций и потоков соли, диффундирующей между двумя резервуарами через водяные трубки. Примечательно, что работа Фика в первую очередь касалась диффузии в жидкостях, потому что в то время диффузия в твердых телах не считалась вообще возможной. Сегодня законы Фика составляют основу нашего понимания диффузии в твердых телах, жидкостях и газах (при отсутствии движения объемной жидкости в последних двух случаях). Когда процесс диффузии не следует законам Фика (что происходит, среди прочего, в случаях диффузии через пористые среды и диффузии набухающих пенетрантов), это называется нефики.

Первый закон Фика связывает диффузный поток с градиентом концентрации. Он постулирует, что поток идет из областей с высокой концентрацией в области с низкой концентрацией, с величиной, которая пропорциональна градиенту концентрации (пространственная производная), или, упрощенно говоря, концепция, что растворенное вещество будет перемещаться из области высокой концентрации в область низкой концентрации через градиент концентрации. В одном (пространственном) измерении закон может быть записан в различных формах, где наиболее распространенная форма (см.) Находится в молярной основе:

${\ displaystyle J = -D {\ frac {d \ varphi} {dx}}}$

куда

• J - диффузионный поток, размерность которого - количество вещества на единицу площади в единицу времени. J измеряет количество вещества, которое будет протекать через единицу площади за единичный интервал времени.
• D - коэффициент диффузии или коэффициент диффузии. Его размерность - это площадь в единицу времени.
• φ (для идеальных смесей) - это концентрация, размерность которой - количество вещества в единице объема.
• x - позиция, размерность которой равна длине.

D пропорционален квадрату скорости диффундирующих частиц, который зависит от температуры, вязкости жидкости и размера частиц согласно соотношению Стокса – Эйнштейна. В разбавленных водных растворах коэффициенты диффузии большинства ионов близки и имеют значения, которые при комнатной температуре находятся в диапазоне(0.6-2) × 10 ^-9  м ² / с. Для биологических молекул коэффициенты диффузии обычно находятся в диапазоне от 10 ^-11 до 10 ^-10  м ² / с.

В двух или более измерениях мы должны использовать ∇, оператор del или градиента, который обобщает первую производную, получая

${\ displaystyle \ mathbf {J} = -D \ nabla \ varphi}$

где J обозначает вектор диффузионного потока.

Движущей силой одномерной диффузии является величина - ∂ φ/∂ x, который для идеальных смесей является градиентом концентрации.

Альтернативные формулировки первого закона

Другая форма первого закона - записать его с первичной переменной как массовая доля ( y i, например, в кг / кг), тогда уравнение изменится на:

${\ displaystyle \ mathbf {J_ {i}} = - {\ frac {\ rho D} {M_ {i}}} \ nabla y_ {i}}$

куда

• индекс i обозначает i- й вид,
• J i - вектор диффузионного потока i- гокомпонента(например, в моль / м ² -с),
• М я это молярная масса из я - го вида, и
• ρ - плотность смеси (например, в кг / м ³).

Обратите внимание, что это находится за пределами оператора градиента. Это потому что: ${\ displaystyle \ rho}$

${\ Displaystyle y_ {я} = {\ гидроразрыва {\ rho _ {si}} {\ rho}}}$

где ρ si - парциальная плотность i- го вида.

Помимо этого, в химических системах, отличных от идеальных растворов или смесей, движущей силой диффузии каждого вида является градиент химического потенциала этого вещества. Тогда первый закон Фика (одномерный случай) можно записать

${\ displaystyle J_ {i} = - {\ frac {Dc_ {i}} {RT}} {\ frac {\ partial \ mu _ {i}} {\ partial x}}}$

куда

• индекс i обозначает i- й вид.
• c - концентрация (моль / м ³).
• R - универсальная газовая постоянная (Дж / К / моль).
• Т - абсолютная температура (К).
• μ - химический потенциал (Дж / моль).

Движущая сила закона Фика может быть выражена как разница в летучести:

${\ displaystyle J_ {i} = - {\ frac {D} {RT}} {\ frac {\ partial f_ {i}} {\ partial x}}}$

Fugacity имеет единицы Па. - парциальное давление компонента i в паровой или жидкой фазе. При парожидкостном равновесии поток испарения равен нулю, потому что. ${\ displaystyle f_ {i}}$${\ displaystyle f_ {i}}$${\ displaystyle f_ {i} ^ {G}}$${\ displaystyle f_ {i} ^ {L}}$${\ displaystyle f_ {i} ^ {G} = f_ {i} ^ {L}}$

Вывод первого закона Фика для газов.

Ниже приведены четыре варианта закона Фика для бинарных газовых смесей. Они предполагают: термодиффузия незначительна; сила тела на единицу массы одинакова для обоих видов; и либо давление постоянно, либо оба вещества имеют одинаковую молярную массу. В этих условиях Ref. подробно показано, как уравнение диффузии из кинетической теории газов сводится к этой версии закона Фика:

$${\ displaystyle \ mathbf {V_ {i}} = -D \ nabla \ ln y_ {i},}$$

где V i - скорость диффузии компонента i. С точки зрения видового потока это

$${\ displaystyle \ mathbf {J_ {i}} = - {\ frac {\ rho D} {M_ {i}}} \ nabla y_ {i}.}$$

Если, кроме того, это сводится к наиболее распространенной форме закона Фика, ${\ displaystyle \ nabla \ rho = 0}$

$${\ displaystyle \ mathbf {J_ {i}} = -D \ nabla \ varphi.}$$

Если (вместо или в дополнение к) оба вида имеют одинаковую молярную массу, закон Фика принимает следующий вид: ${\ displaystyle \ nabla \ rho = 0}$

$${\ displaystyle \ mathbf {J_ {i}} = - {\ frac {\ rho D} {M_ {i}}} \ nabla x_ {i},}$$

где - мольная доля вида i. ${\ displaystyle x_ {i}}$

Второй закон Фика предсказывает, как диффузия вызывает изменение концентрации во времени. Это уравнение в частных производных, которое в одном измерении гласит:

${\ displaystyle {\ frac {\ partial \ varphi} {\ partial t}} = D \, {\ frac {\ partial ^ {2} \ varphi} {\ partial x ^ {2}}}}$

куда

• φ - концентрация в размерах [(количество вещества) длина ^-3 ], например моль / м ³ ; φ = φ ( x, t) - функция, которая зависит от местоположения x и времени t
• t время, пример s
• D - коэффициент диффузии в размере [длина ² раз ^-1 ], например, м ² / с.
• x - позиция [длина], пример m

В двух или более измерениях мы должны использовать лапласиан Δ = ², который обобщает вторую производную, получая уравнение

${\ displaystyle {\ frac {\ partial \ varphi} {\ partial t}} = D \ Delta \ varphi}$

Второй закон Фика имеет ту же математическую форму, что и уравнение тепла, и его фундаментальное решение такое же, как и ядро тепла, за исключением переключения теплопроводности с коэффициентом диффузии: ${\ displaystyle k}$${\ displaystyle D}$

$${\ displaystyle \ varphi (x, t) = {\ frac {1} {\ sqrt {4 \ pi Dt}}} \ exp \ left (- {\ frac {x ^ {2}} {4Dt}} \ right).}$$

Вывод второго закона Фика

Второй закон Фика может быть выведен из первого закона Фика и сохранения массы в отсутствие каких-либо химических реакций:

${\ displaystyle {\ frac {\ partial \ varphi} {\ partial t}} + {\ frac {\ partial} {\ partial x}} J = 0 \ Rightarrow {\ frac {\ partial \ varphi} {\ partial t }} - {\ frac {\ partial} {\ partial x}} \ left (D {\ frac {\ partial} {\ partial x}} \ varphi \ right) \, = 0}$

Считая коэффициент диффузии D постоянным, можно поменять порядок дифференцирования и умножить на константу:

${\ displaystyle {\ frac {\ partial} {\ partial x}} \ left (D {\ frac {\ partial} {\ partial x}} \ varphi \ right) = D {\ frac {\ partial} {\ partial x}} {\ frac {\ partial} {\ partial x}} \ varphi = D {\ frac {\ partial ^ {2} \ varphi} {\ partial x ^ {2}}}}$

и, таким образом, получают форму уравнений Фика, как было указано выше.

Для случая диффузии в двух или более измерениях второй закон Фика принимает вид

${\ displaystyle {\ frac {\ partial \ varphi} {\ partial t}} = D \ nabla ^ {2} \ varphi,}$

которое аналогично уравнению теплопроводности.

Если коэффициент диффузии не является постоянным, а зависит от координаты или концентрации, второй закон Фика дает

${\ displaystyle {\ frac {\ partial \ varphi} {\ partial t}} = \ nabla \ cdot (D \ nabla \ varphi).}$

Важным примером является случай, когда φ находится в установившемся состоянии, то есть концентрация не изменяется со временем, так что левая часть приведенного выше уравнения тождественно равна нулю. В одном измерении с постоянным D решением для концентрации будет линейное изменение концентраций вдоль x. В двух или более измерениях мы получаем

${\ Displaystyle \ набла ^ {2} \ varphi = 0}$

которое является уравнением Лапласа, решения которого математики называют гармоническими функциями.

Второй закон Фика - это частный случай уравнения конвекции-диффузии, в котором нет адвективного потока и нет чистого объемного источника. Его можно вывести из уравнения неразрывности :

${\ displaystyle {\ frac {\ partial \ varphi} {\ partial t}} + \ набла \ cdot \ mathbf {j} = R,}$

где j - полный поток, а R - чистый объемный источник для φ. Предполагается, что единственным источником потока в этой ситуации является диффузионный поток:

${\ displaystyle \ mathbf {j} _ {\ text {diffusion}} = - D \ nabla \ varphi}$

Подставляя определение диффузионного потока к уравнению неразрывности и предполагая, что источника нет ( R = 0), мы приходим ко второму закону Фика:

${\ displaystyle {\ frac {\ partial \ varphi} {\ partial t}} = D {\ frac {\ partial ^ {2} \ varphi} {\ partial x ^ {2}}}}$

Если бы поток был результатом как диффузионного, так и адвективного потоков, то результатом было бы уравнение конвекции-диффузии.

Пример решения 1: источник постоянной концентрации и длина диффузии

Простым случаем диффузии со временем t в одном измерении (взятом как ось x) от границы, расположенной в позиции x = 0, где концентрация поддерживается на значении n 0, является

${\ displaystyle n \ left (x, t \ right) = n_ {0} \ operatorname {erfc} \ left ({\ frac {x} {2 {\ sqrt {Dt}}}} \ right).}$

где erfc - дополнительная функция ошибок. Это тот случай, когда коррозионные газы диффундируют через окислительный слой к поверхности металла (если предположить, что концентрация газов в окружающей среде постоянна, а диффузионное пространство, то есть слой продуктов коррозии, является полубесконечным, начиная с 0 на поверхности и бесконечно глубоко растекаясь в материале). Если, в свою очередь, диффузионное пространство бесконечно (продолжающееся как через слой с n ( x, 0) = 0, x gt; 0, так и через слой с n ( x, 0) = n 0, x ≤ 0), то решение вносится только с коэффициентом1/2перед n 0 (поскольку теперь диффузия происходит в обоих направлениях). Этот случай справедлив, когда некоторый раствор с концентрацией n 0 контактирует со слоем чистого растворителя. (Bokstein, 2005) Длина 2 √ Dt называется диффузионной длиной и дает меру того, насколько далеко концентрация распространилась в x- направлении за счет диффузии во времени t (Bird, 1976).

В качестве быстрого приближения функции ошибок можно использовать первые 2 члена ряда Тейлора:

${\ displaystyle n \ left (x, t \ right) = n_ {0} \ left [1-2 \ left ({\ frac {x} {2 {\ sqrt {Dt \ pi}}}} \ right) \ Правильно]}$

Если D зависит от времени, длина диффузии становится

${\ displaystyle 2 {\ sqrt {\ int _ {0} ^ {t} D \ tau \, d \ tau}}.}$

Эта идея полезна для оценки длины диффузии в цикле нагрева и охлаждения, где D изменяется в зависимости от температуры.

Пример решения 2: броуновская частица и среднеквадратичное смещение

Другой простой случай диффузии - это броуновское движение одной частицы. Среднеквадратичное смещение частицы от ее исходного положения составляет:

$${\ Displaystyle {\ текст {MSD}} \ Equiv \ langle (\ mathbf {x} - \ mathbf {x_ {0}}) ^ {2} \ rangle = 2nDt}$$

где - размерность броуновского движения частицы. Например, диффузия молекулы через клеточную мембрану толщиной 8 нм представляет собой одномерную диффузию из-за сферической симметрии; Однако диффузия молекулы от мембраны к центру эукариотической клетки представляет собой трехмерную диффузию. Для цилиндрического кактуса диффузия от фотосинтетических клеток на его поверхности к его центру (оси его цилиндрической симметрии) является двумерной диффузией. ${\ displaystyle n}$

Квадратный корень из MSD,, часто используется как характеристика того, как далеко переместилась частица по истечении времени. МСД симметрично распределен в одномерном, двухмерном и трехмерном пространстве. Таким образом, распределение вероятностей величины MSD в 1D является гауссовым, а в 3D - распределением Максвелла-Больцмана. ${\ displaystyle {\ sqrt {2nDt}}}$${\ displaystyle t}$

Обобщения

• В неоднородных средах коэффициент диффузии изменяется в пространстве D = D ( x). Эта зависимость не влияет на первый закон Фика, но меняется второй закон: $${\ displaystyle {\ frac {\ partial \ varphi (x, t)} {\ partial t}} = \ nabla \ cdot {\ bigl (} D (x) \ nabla \ varphi (x, t) {\ bigr) } = D (x) \ Delta \ varphi (x, t) + \ sum _ {i = 1} ^ {3} {\ frac {\ partial D (x)} {\ partial x_ {i}}} {\ гидроразрыв {\ partial \ varphi (x, t)} {\ partial x_ {i}}}}$$
• В анизотропных средах коэффициент диффузии зависит от направления. Это симметричный тензор D = D ij. Первый закон Фика меняется на $${\ Displaystyle J = -D \ набла \ varphi,}$$ это произведение тензора и вектора: $${\ displaystyle J_ {i} = - \ sum _ {j = 1} ^ {3} D_ {ij} {\ frac {\ partial \ varphi} {\ partial x_ {j}}}.}$$ Для уравнения диффузии эта формула дает $${\ displaystyle {\ frac {\ partial \ varphi (x, t)} {\ partial t}} = \ nabla \ cdot {\ bigl (} D \ nabla \ varphi (x, t) {\ bigr)} = \ sum _ {i = 1} ^ {3} \ sum _ {j = 1} ^ {3} D_ {ij} {\ frac {\ partial ^ {2} \ varphi (x, t)} {\ partial x_ { i} \ partial x_ {j}}}.}$$ Симметричная матрица коэффициентов диффузии D ij должна быть положительно определенной. Это нужно, чтобы правая часть оператора была эллиптической.
• Для неоднородных анизотропных сред эти две формы уравнения диффузии следует объединить в $${\ displaystyle {\ frac {\ partial \ varphi (x, t)} {\ partial t}} = \ nabla \ cdot {\ bigl (} D (x) \ nabla \ varphi (x, t) {\ bigr) } = \ sum _ {i, j = 1} ^ {3} \ left (D_ {ij} (x) {\ frac {\ partial ^ {2} \ varphi (x, t)} {\ partial x_ {i } \ partial x_ {j}}} + {\ frac {\ partial D_ {ij} (x)} {\ partial x_ {i}}} {\ frac {\ partial \ varphi (x, t)} {\ partial x_ {i}}} \ right).}$$
• Подход, основанный на подвижности Эйнштейна и формуле Теорелла, дает следующее обобщение уравнения Фика для многокомпонентной диффузии совершенных компонентов: $${\ displaystyle {\ frac {\ partial \ varphi _ {i}} {\ partial t}} = \ sum _ {j} \ nabla \ cdot \ left (D_ {ij} {\ frac {\ varphi _ {i}) } {\ varphi _ {j}}} \ nabla \, \ varphi _ {j} \ right).}$$ где φ i - концентрации компонентов, а D ij - матрица коэффициентов. Здесь индексы i и j относятся к различным компонентам, а не к пространственным координатам.

В формулах Чепмена-Энскога для диффузии в газах включают в себя одни и те же сроки. Эти физические модели диффузии отличаются от тестовых моделей ∂ t φ i = Σ j D ij Δ φ j, которые действительны для очень малых отклонений от равномерного равновесия. Ранее такие члены были введены в уравнение диффузии Максвелла – Стефана.

Для анизотропных многокомпонентных коэффициентов диффузии необходим тензор четвертого ранга, например D ij, αβ, где i, j относятся к компонентам, а α, β = 1, 2, 3 соответствуют пространственным координатам.

Уравнения, основанные на законе Фика, обычно используются для моделирования процессов переноса в пищевых продуктах, нейронах, биополимерах, фармацевтических препаратах, пористых почвах, динамике популяций, ядерных материалах, физике плазмы и процессах легирования полупроводников. Теория вольтамперометрических методов основана на решениях уравнения Фика. С другой стороны, в некоторых случаях «фикианское» описание неадекватно. Например, в науке о полимерах и пищевых продуктах требуется более общий подход для описания переноса компонентов в материалах, претерпевающих стеклование. Еще одна общая структура - это диффузионные уравнения Максвелла-Стефана для многокомпонентного массопереноса, из которых можно получить закон Фика как предельный случай, когда смесь чрезвычайно разбавлена ​​и каждый химический компонент взаимодействует только с объемной смесью, а не с ней. другие виды. Чтобы учесть присутствие нескольких видов в неразбавленной смеси, используются несколько вариаций уравнений Максвелла – Стефана. См. Также недиагональные связанные транспортные процессы ( отношение Онзагера ).

Течение Фика в жидкостях

Когда две смешивающиеся жидкости контактируют и происходит диффузия, макроскопическая (или средняя) концентрация изменяется в соответствии с законом Фика. В мезоскопическом масштабе, то есть между макроскопическим масштабом, описываемым законом Фика, и молекулярным масштабом, где происходят случайные молекулярные блуждания, нельзя пренебрегать флуктуациями. Такие ситуации можно успешно моделировать с помощью флуктуирующей гидродинамики Ландау-Лифшица. В этой теоретической схеме диффузия обусловлена ​​флуктуациями, размеры которых варьируются от молекулярного до макроскопического масштаба.

В частности, флуктуирующие уравнения гидродинамики включают член Фика с заданным коэффициентом диффузии, а также уравнения гидродинамики и стохастические члены, описывающие флуктуации. При вычислении флуктуаций пертурбативным подходом приближение нулевого порядка является законом Фика. Первый порядок дает флуктуации, и получается, что флуктуации вносят вклад в диффузию. Это представляет собой своего рода тавтологию, поскольку явления, описываемые приближением более низкого порядка, являются результатом приближения более высокого порядка: эта проблема решается только путем перенормировки флуктуирующих уравнений гидродинамики.

Скорость сорбции и частота столкновений разбавленных растворенных веществ

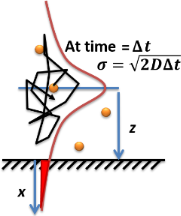Схема молекулярной диффузии в растворе. Оранжевые точки - это молекулы растворенного вещества, молекулы растворителя не нарисованы, черная стрелка - это пример траектории случайного блуждания, а красная кривая - функция вероятности диффузионного гауссова уширения из закона диффузии Фика. ^{:Инжир. 9}

Скорость адсорбции или абсорбции разбавленного растворенного вещества на поверхности или границе раздела в растворе (газе или жидкости) может быть рассчитана с использованием законов диффузии Фика. Накопленное количество молекул, адсорбированных на поверхности, выражается уравнением Ленгмюра-Шефера на кратковременном пределе путем интегрирования уравнения диффузии по времени:

${\ displaystyle \ Gamma = 2AC {\ sqrt {\ frac {Dt} {\ pi}}}}$

где - площадь поверхности, - числовая концентрация молекулы в объеме раствора. ${\ displaystyle A}$${\ displaystyle C}$

Уравнение Ленгмюра-Шефера может быть расширено до уравнения Уорда-Торда, чтобы учесть «обратную диффузию» отклоненных молекул с поверхности:

${\ displaystyle \ Gamma = 2AC {\ sqrt {\ frac {Dt} {\ pi}}} - A {\ sqrt {\ frac {D} {\ pi}}} \ int _ {0} ^ {\ sqrt { t}} {\ frac {Cb (\ tau)} {\ sqrt {t- \ tau}}} d \ tau}$

где - объемная концентрация, - подповерхностная концентрация (которая является функцией времени в зависимости от модели реакции адсорбции) и является фиктивной переменной. ${\ displaystyle C}$${\ displaystyle Cb}$${\ Displaystyle \ тау}$

В пределе ультракороткого времени, в порядке времени диффузии a ² / D, где a - радиус частицы, диффузия описывается уравнением Ланжевена. Со временем уравнение Ланжевена сливается с уравнением Стокса – Эйнштейна. Последнее подходит для состояния разбавленного раствора, в котором рассматривается дальняя диффузия. В соответствии с теоремой флуктуации-диссипации, основанной на уравнении Ланжевена в долгосрочном пределе, и когда частица значительно плотнее окружающей жидкости, зависящая от времени константа диффузии равна:

${\ displaystyle D (t) = \ mu \, k _ {\ rm {B}} T \ left (1-e ^ {- t / (m \ mu)} \ right)}$

куда

• k B - постоянная Больцмана.
• Т - абсолютная температура.
• μ - подвижность частицы в жидкости или газе, которую можно рассчитать с помощью соотношения Эйнштейна (кинетическая теория).
• m - масса частицы.
• т время.

Для отдельной молекулы, такой как органические молекулы или биомолекулы (например, белки) в воде, экспоненциальный член пренебрежимо мал из-за небольшого произведения mμ в пикосекундной области.

Когда интересующей областью является размер молекулы (в частности, длинной цилиндрической молекулы, такой как ДНК), уравнение скорости адсорбции представляет собой частоту столкновения двух молекул в разбавленном растворе, при этом одна молекула имеет определенную сторону, а другая - не стерическую. зависимость, т. е. молекула (случайная ориентация) ударилась с одной стороны о другую. Константу диффузии необходимо обновить до относительной постоянной диффузии между двумя диффундирующими молекулами. Эта оценка особенно полезна при изучении взаимодействия между небольшой молекулой и более крупной молекулой, такой как белок. В эффективной константе диффузии преобладает меньшая, вместо нее можно использовать константу диффузии.

Вышеупомянутое уравнение скорости столкновения также полезно для предсказания кинетики самосборки молекул на поверхности. В объемном растворе молекулы ориентированы случайным образом. Предполагая, что 1/6 молекул имеет правильную ориентацию относительно участков связывания на поверхности, то есть 1/2 направления z в трех измерениях x, y, z, таким образом, интересующая концентрация составляет всего 1/6 от объемной концентрации. Поместив это значение в уравнение, вы сможете рассчитать теоретическую кинетическую кривую адсорбции с использованием модели адсорбции Ленгмюра. В более жесткой картине 1/6 можно заменить стерическим фактором геометрии привязки.

Биологическая перспектива

Первый закон приводит к следующей формуле:

${\ displaystyle {\ text {flux}} = {- P \ left (c_ {2} -c_ {1} \ right)}}$

в котором,

• P - проницаемость, экспериментально определенная « проводимость » мембраны для данного газа при данной температуре.
• c 2 - c 1 - разница в концентрации газа через мембрану для направления потока (от c 1 до c 2).

Первый закон Фика также важен для уравнений переноса излучения. Однако в этом контексте он становится неточным, когда постоянная диффузии мала и излучение ограничивается скоростью света, а не сопротивлением материала, через который проходит излучение. В этой ситуации можно использовать ограничитель потока.

Скорость обмена газа через жидкую мембрану можно определить, используя этот закон вместе с законом Грэма.

В условиях разбавленного раствора, когда диффузия берет на себя управление, проницаемость мембраны, упомянутая в предыдущем разделе, может быть теоретически рассчитана для растворенного вещества с использованием уравнения, упомянутого в последнем разделе (используйте с особой осторожностью, потому что уравнение выводится для плотных растворенных веществ, в то время как биологические молекулы не плотнее воды):

${\ Displaystyle P = 2A_ {p} \ eta _ {tm} {\ sqrt {D / (\ pi t)}}}$

куда

• ${\ displaystyle A_ {P}}$- общая площадь пор на мембране (единица м ²).
• ${\ displaystyle \ eta _ {tm}}$трансмембранная эффективность (безразмерная), которую можно рассчитать по стохастической теории хроматографии.
• D - постоянная диффузии растворенного вещества м ² с ^-1.
• t - единица времени с.
• Концентрация c 2, c 1 должна быть выражена в единицах моль м ⁻³, поэтому единицей измерения потока становится моль с ⁻¹.

Приложения для производства полупроводников

Технологии изготовления интегральных схем, модельные процессы, такие как химическое осаждение из паровой фазы, термическое окисление, влажное окисление, легирование и т. Д., Используют уравнения диффузии, полученные из закона Фика.

В некоторых случаях решения получают для граничных условий, таких как диффузия с постоянной концентрацией источника, ограниченная концентрация источника или диффузия по движущейся границе (когда глубина перехода продолжает перемещаться в подложку).

• Диффузия
• Осмос
• Поток массы
• Диффузия Максвелла – Стефана
• Уравнение Черчилля – Бернштейна
• Уравнение Нернста – Планка
• Газообмен
• Ложная диффузия
• Адвекция

• Смит, У.Ф. (2004). Основы материаловедения и инженерии (3-е изд.). Макгроу-Хилл.
• Берг, ХК (1977). Случайные блуждания в биологии. Принстон.
• Птица, РБ; Стюарт, МЫ; Лайтфут, EN (1976). Явления переноса. Джон Вили и сыновья.
• Крэнк, Дж. (1980). Математика диффузии. Издательство Оксфордского университета.
• Бокштейн Б.С.; Менделев М.И.; Сроловиц, диджей, ред. (2005). Термодинамика и кинетика в материаловедении: краткий курс. Оксфорд: Издательство Оксфордского университета. стр.  167 -171.
• Фик, А. (1855). «О жидкостной диффузии». Annalen der Physik und Chemie. 94: 59.- перепечатано в Fick, Adolph (1995). «О жидкостной диффузии». Журнал мембрановедения. 100: 33–38. DOI : 10.1016 / 0376-7388 (94) 00230-V.

• Уравнения Фика, преобразование Больцмана и т. Д. (С фигурами и анимацией)
• Второй закон Фика об OpenStax