Определение уравнения (физика)

В физике, определяющие уравнения - это уравнения которые определяют новые количества в терминах базовых количеств. В этой статье используется текущая система СИ из единиц, а не натуральных или характеристических единиц.

• 1 Описание единиц и физических величин
  • 1.1 Аналогия смешения цветов
• 2 Мотивация
• 3 Построение определяющих уравнений
  • 3.1 Объем определений
  • 3.2 Определения с множественным выбором
• 4 Ограничения определений
• 5 Одноразовые определения
• 6 См. Также
• 7 Сноски
• 8 Источники
• 9 Дополнительная литература

Физические величины и единицы следуют той же иерархии; выбранные базовые величины имеют определенные базовые единицы, из которых могут быть выведены любые другие величины и соответствующие производные единицы.

Аналогия смешения цветов

Определение количеств аналогично смешиванию цветов и может быть классифицировано аналогичным образом, хотя это не является стандартом. Основные цвета соответствуют базовым количествам; вторичные (или третичные) цвета относятся к производным величинам. Смешивание цветов аналогично объединению величин с помощью математических операций. Но цвета могут быть для света или краски, и аналогично система единиц может быть одной из многих форм: например, СИ (сейчас наиболее распространена), CGS, гауссовский, старые имперские единицы, особая форма натуральных единиц или даже произвольно определенные единицы, характерные для рассматриваемой физической системы (характерные единицы ).

Выбор базовой системы величин и единиц произвольный; но однажды выбранный, он должен соблюдаться на протяжении всего последующего анализа для согласованности. Нет смысла путать разные системы единиц. Выбор системы единиц, одной системы из СИ, СГС и т. Д., Подобен выбору использования краски или светлых тонов.

В свете этой аналогии первичные определения - это базовые величины без определяющего уравнения, но с определенным стандартизированным условием, «вторичные» определения - это количества, определенные исключительно в терминах базовых величин, «третичные» для количеств в терминах обоих базовые и «вторичные» количества, «четвертичные» для количеств в терминах основных, «вторичных» и «третичных» величин и так далее.

Большая часть физики требует, чтобы уравнения имели смысл.

Теоретические выводы: Определения важны, поскольку они могут привести к новому пониманию области физики. Два таких примера встречаются в классической физике. Когда была определена энтропия S - диапазон термодинамики был значительно расширен за счет связывания хаоса и беспорядка с числовой величиной, которая может относиться к энергии и температуре, что привело к понимание второй термодинамического закона и статистической механики.

Также action функционал (также пишется S) ( вместе с обобщенными координатами и импульсами и функцией Лагранжа ), первоначально альтернативная формулировка классической механики законам Ньютона, теперь расширяет диапазон современной физики в целом - в частности, квантовой механики, физики элементарных частиц и общей теории относительности.

Аналитическое удобство: Они позволяют другим уравнения должны быть записаны более компактно, что упрощает математические операции; включив параметр в определение, вхождения параметра можно включить в подставляемую величину и удалить из уравнения.

Пример

В качестве примера рассмотрим закон Ампера (с поправкой Максвелла) в интегральной форме для произвольного токонесущего проводника в вакууме (т.е. нулевая намагниченность из-за среды, т.е. M= 0):

$\oint \; SB\; \cdot \; dl\; =\; \mu \; 0\; \oint \; S\; (J\; +\; ϵ\; 0\; \partial \; E\; \partial \; T)\; \cdot \; d\; A\; \{\backslash \; displaystyle\; \backslash \; oint\; \_\; \{S\}\; \backslash \; mathbf\; \{B\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{l\}\; =\; \backslash \; mu\; \_\; \{0\}\; \backslash \; oint\; \_\; \{S\}\; \backslash \; left\; (\backslash \; mathbf\; \{J\}\; +\; \backslash \; epsilon\; \_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{E\}\}\; \{\backslash \; partial\; t\}\}\; \backslash \; right)\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\; \backslash ,\; \backslash !\}$

с использованием основного определения

$B\; =\; \mu \; 0\; H,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; =\; \backslash \; mu\; \_\; \{0\}\; \backslash \; mathbf\; \{H\},\; \backslash ,\; \backslash !\; \}$

и определение плотности тока

$I\; =\; \oint \; SJ\; \cdot \; d\; A,\; \{\backslash \; displaystyle\; I\; =\; \backslash \; oint\; \_\; \{S\}\; \backslash \; mathbf\; \{J\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\},\; \backslash ,\; \backslash !\}$

аналогично для тока смещения плотности

$J\; d\; =\; ϵ\; 0\; \partial \; E\; \partial \; t\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \_\; \{\backslash \; rm\; \{d\}\}\; =\; \backslash \; epsilon\; \_\; \{0\}\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; mathbf\; \{E\}\}\; \{\backslash \; partial\; t\}\}\; \backslash ,\; \backslash !\}$приводящий к току смещения $I\; d\; Знак\; равно\; \oint \; SJ\; d\; \cdot \; d\; A,\; \{\backslash \; displaystyle\; I\_\; \{d\}\; =\; \backslash \; oint\; \_\; \{S\}\; \backslash \; mathbf\; \{J\}\; \_\; \{\backslash \; rm\; \{d\}\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\},\; \backslash ,\; \backslash !\}$

у нас есть

$\oint \; SB\; \cdot \; dl\; =\; \mu \; 0\; \oint \; SJ\; \cdot \; d\; A\; +\; \mu \; 0\; \oint \; SJ\; d\; \cdot \; d\; A,\; \{\backslash \; displaystyle\; \backslash \; oint\; \_\; \{S\}\; \backslash \; mathbf\; \{B\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{l\}\; =\; \backslash \; mu\; \_\; \{0\}\; \backslash \; oint\; \_\; \{S\}\; \backslash \; mathbf\; \{J\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\}\; +\; \backslash \; mu\; \_\; \{\; 0\}\; \backslash \; oint\; \_\; \{S\}\; \backslash \; mathbf\; \{J\}\; \_\; \{\backslash \; rm\; \{d\}\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{A\},\; \backslash ,\; \backslash !\}$

$\oint \; SH\; \cdot \; dl\; =\; I\; +\; I\; d,\; \{\backslash \; displaystyle\; \backslash \; oint\; \_\; \{S\}\; \backslash \; mathbf\; \{H\}\; \backslash \; cdot\; \{\backslash \; rm\; \{d\}\}\; \backslash \; mathbf\; \{l\}\; =\; I\; +\; I\_\; \{d\},\; \backslash ,\; \backslash !\}$

что является проще писать, даже если уравнение такое же.

Простота сравнения: Они позволяют сравнивать измерения, когда они могут показаться неоднозначными и неясными в противном случае.

Пример

Базовый пример - массовая плотность. Непонятно, как сравнивать, сколько материи состоит из множества веществ, учитывая только их массы или только их объемы. Учитывая и то, и другое для каждого вещества, масса m на единицу объема V или массовая плотность ρ обеспечивает значимое сравнение между веществами, поскольку для каждого из них фиксированный объем будет соответствовать количеству массы в зависимости от вещества. Чтобы проиллюстрировать это; если два вещества A и B имеют массы m A и m B соответственно, занимая объемы V A и V B соответственно, используя определение массовой плотности дает:

ρA= m A / V A, ρ B = m B / V B

после этого можно увидеть, что:

• если m A>mBили m A< mBи V A = V B, то ρ A>ρBили ρ A< ρB,
• , если m A = m B и V A>VBили V A< VB, тогда ρ A< ρBили ρ A>ρB,
• , если ρ A = ρ B, затем m A / V A = m B / V B, поэтому m A / m B = V A / V B, демонстрируя, что если m A>mBили m A< mB, то V A>VBили V A< VB.

Проведение таких сравнений без такого логического использования математики было бы не столь систематическим.

Объем определений

Определяющие уравнения обычно формулируются в терминах элементарной алгебры и исчисления, векторная алгебра и исчисление, или для самых общих приложений тензорная алгебра и исчисление, в зависимости от уровня изучения и изложения, сложности темы и области применения. Функции могут быть включены в определение, в случае исчисления это необходимо. Величины также могут быть комплексными -значными для теоретического преимущества, но для физического измерения важна действительная часть, а мнимая часть может быть отброшена. Для более продвинутых методов лечения уравнение может быть записано в эквивалентной, но альтернативной форме с использованием других определяющих уравнений, чтобы определение было полезным. Часто определения могут начинаться с элементарной алгебры, затем преобразовываться в векторы, а затем в предельных случаях может использоваться исчисление. Как правило, используются различные уровни математики.

Обычно определения являются явными, то есть определяющая величина является предметом уравнения, но иногда уравнение не записывается явно - хотя определяющая величина может быть решена для того, чтобы сделать уравнение явным. Для векторных уравнений иногда определяющая величина находится в виде перекрестного или скалярного произведения и не может быть решена явно как вектор, но компоненты могут.

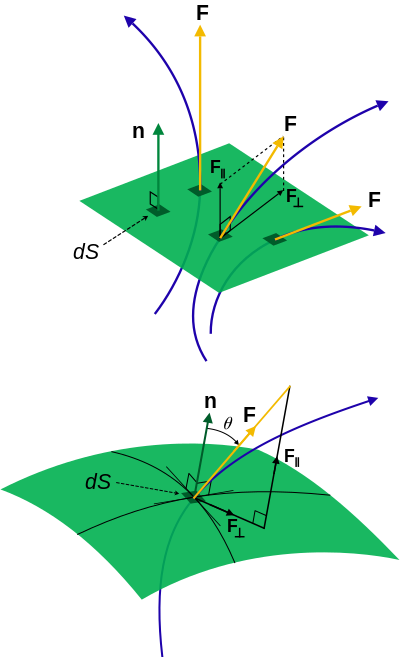Поток Fчерез поверхность , d S - это элемент дифференциальной векторной области, n - единица нормаль к поверхности. Для физических примеров здесь плотность тока Jили магнитное поле Bна диаграмме будет F . Угловой момент; скалярные и векторные компоненты.

Примеры

Плотность электрического тока - пример, охватывающий все эти методы, Угловой момент - пример, который не требует исчисления. См. Раздел классической механики ниже для номенклатуры и диаграмм справа.

Элементарная алгебра

Операции - это просто умножение и деление. Уравнения могут быть записаны в форме произведения или частного, оба, конечно же, эквивалентны.

	Угловой момент	Плотность электрического тока
Форма коэффициента	$p\; =\; L\; r\; \{\backslash \; displaystyle\; p\; =\; \{\backslash \; frac\; \{L\}\; \{r\}\}\; \backslash ,\; \backslash !\}$	$Дж\; =\; IA\; \{\backslash \; displaystyle\; J\; =\; \{\backslash \; frac\; \{I\}\; \{A\}\}\; \backslash ,\; \backslash !\}$
Форма продукта	$L\; =\; pr\; \{\backslash \; displaystyle\; L\; =\; pr\; \backslash ,\; \backslash !\}$	$I\; =\; JA\; \{\backslash \; displaystyle\; I\; =\; JA\; \backslash ,\; \backslash !\}$

Векторная алгебра

Невозможно разделить вектор на вектор, поэтому нет форм произведения или частного.

	Угловой момент	Плотность электрического тока
Форма коэффициента	Н / Д	$J\; \cdot \; n\; ^\; =\; IA\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\; \backslash \; hat\; \{n\}\}\; =\; \{\backslash \; frac\; \{I\}\; \{A\}\}\; \backslash ,\; \backslash !\}$
Форма продукта	Начиная с $L\; =\; pr,\; \{\backslash \; displaystyle\; L\; =\; pr,\; \backslash ,\; \backslash !\}$ с L= 0, когда p и r являются параллельным или антипараллельным, и является максимум в перпендикулярном направлении, так что единственный компонент p, который вносит вклад в L, - это тангенциальный | p | sin θ, величину углового момента L нужно переписать как $L\; =\; p\; r\; sin\; \; \theta .\; \{\backslash \; displaystyle\; L\; =\; pr\; \backslash \; sin\; \backslash \; theta.\; \backslash ,\; \backslash !\}$ Поскольку r, pи L образуют правую триаду, это приводит к векторной форме $L\; =\; r\; \times \; п.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{L\}\; =\; \backslash \; mathbf\; \{r\}\; \backslash \; times\; \backslash \; mathbf\; \{p\}.\; \backslash ,\; \backslash !\}$	$J\; \cdot \; n\; ^\; A\; =\; I,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; A\; =\; I,\; \backslash ,\; \backslash !\}$ $J\; \cdot \; A\; =\; I,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \backslash \; cdot\; \backslash \; mathbf\; \{A\}\; =\; I,\; \backslash ,\; \backslash !\}$

Элементарное исчисление

Арифметические операции модифицированы для предельных случаев дифференцирования и интегрирования. Уравнения могут быть выражены этими эквивалентными и альтернативными способами.

	Плотность тока
Дифференциальная форма	$J\; =\; lim\; A\; \to \; 0\; IA\; =\; d\; I\; d\; A\; \{\backslash \; displaystyle\; J\; =\; \backslash \; lim\; \_\; \{A\; \backslash \; rightarrow\; 0\}\; \{\backslash \; frac\; \{I\}\; \{A\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; I\}\; \{\backslash \; mathrm\; \{d\}\; A\}\}\; \backslash ,\; \backslash !\}$
Интегральная форма	$I\; =\; lim\; A\; i\; \to \; 0\; \sum \; я\; JA\; я\; знак\; равно\; \int \; SJ\; d\; A\; \{\backslash \; displaystyle\; I\; =\; \backslash \; lim\; \_\; \{A\_\; \{i\}\; \backslash \; rightarrow\; 0\}\; \backslash \; sum\; \_\; \{i\}\; JA\_\; \{i\}\; =\; \backslash \; int\; \_\; \{S\}\; J\; \{\backslash \; mathrm\; \{d\; \}\; A\}\; \backslash ,\; \backslash !\}$ где dA означает дифференциальный элемент площади (см. Также интеграл поверхности ). В качестве альтернативы для интегральной формы $d\; I\; =\; J\; d\; A,\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{d\}\; I\; =\; J\; \{\backslash \; mathrm\; \{d\}\; A\},\; \backslash ,\; \backslash !\}$ $I\; =\; \int \; SJ\; d\; A.\; \{\backslash \; displaystyle\; I\; =\; \backslash \; int\; \_\; \{S\}\; J\; \{\backslash \; mathrm\; \{d\}\; A\}.\; \backslash ,\; \backslash !\}$

Векторное исчисление

	Плотность тока
Дифференциальная форма	$J\; \cdot \; n\; ^\; =\; d\; Я\; d\; A\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{J\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; I\}\; \{\backslash \; mathrm\; \{d\}\; A\}\}\; \backslash ,\; \backslash !\}$
Интегральная форма	$I\; =\; \int \; SJ\; \cdot \; d\; A\; \{\backslash \; displaystyle\; I\; =\; \backslash \; int\; \_\; \{S\}\; \backslash \; mathbf\; \{J\}\; \backslash \; cdot\; \backslash \; mathrm\; \{d\}\; \backslash \; mathbf\; \{A\}\; \backslash ,\; \backslash !\}$ где d A= ndA - это дифференциальная векторная площадь.

Тензорный анализ

Векторы являются тензорами ранга 1. Приведенные ниже формулы - это не более чем векторные уравнения на языке тензоров.

	Угловой момент	Плотность электрического тока
Дифференциальная форма	Н / Д	$Дж\; ini\; =\; d\; I\; d\; A\; \{\backslash \; displaystyle\; J\_\; \{i\}\; n\_\; \{i\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; I\}\; \{\backslash \; mathrm\; \{d\}\; A\}\}\; \backslash ,\; \backslash !\}$
Произведение / интегральная форма	Начиная с $L\; =\; r\; \times \; p\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{L\}\; =\; \backslash \; mathbf\; \{r\}\; \backslash \; times\; \backslash \; mathbf\; \{p\}\; \backslash ,\; \backslash !\}$ компоненты: L i, r j, p i, где i, j, k - каждый фиктивный индекс, каждый из которого принимает значения 1, 2, 3, с использованием тождества из тензорного анализа $a\; =\; b\; \times \; c,\; ai\; =\; ϵ\; ijkbjck,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{a\}\; =\; \backslash \; mathbf\; \{b\}\; \backslash \; times\; \backslash \; mathbf\; \{c\},\; \backslash \; quad\; a\_\; \{i\}\; =\; \backslash \; epsilon\; \_\; \{ijk\}\; b\_\; \{j\}\; c\_\; \{k\},\; \backslash ,\; \backslash !\; \}$ , где ε ijk - это перестановка / тензор Леви-Сита, приводит к $L\; i\; =\; ϵ\; ijkrjpk.\; \{\backslash \; displaystyle\; L\_\; \{i\}\; =\; \backslash \; epsilon\; \_\; \{ijk\}\; r\_\; \{j\}\; p\_\; \{k\}.\; \backslash ,\; \backslash !\}$	Использование соглашения о суммировании Эйнштейна, $J\; inid\; A\; =\; d\; I\; \{\backslash \; displaystyle\; J\_\; \{i\}\; n\_\; \{i\}\; \backslash \; mathrm\; \{d\}\; A\; =\; \backslash \; mathrm\; \{d\}\; I\; \backslash ,\; \backslash !\}$ $\int \; SJ\; id\; A\; i\; =\; I\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{S\}\; J\_\; \{i\}\; \backslash \; mathrm\; \{d\}\; A\_\; \{i\}\; =\; I\; \backslash ,\; \backslash !\}$

Определения с множественным выбором

Иногда в рамках выбранной системы единиц все еще есть свобода определять одну или несколько величин более чем одним способом. Ситуация делится на два случая:

Взаимоисключающие определения: Существует ряд возможных вариантов определения количества в терминах других, но можно использовать только один, а другие нельзя. Выбор более одного из исключительных уравнений для определения приводит к противоречию - одно уравнение может требовать, чтобы величина X была определена одним способом с использованием другой величины Y, в то время как другое уравнение требует обратного, Y должно быть определено с помощью X, но затем другое уравнение может исказить использование как X, так и Y и так далее. Из-за взаимного несогласия невозможно сказать, какое уравнение какое количество определяет.

Эквивалентные определения: Определение уравнений, которые эквивалентны и самосогласованы с другими уравнениями и законами в рамках физической теории, просто написанные по-разному.

В каждом случае есть две возможности:

Одно определяющее уравнение - одна определенная величина: Определяющее уравнение используется для определения одной величины через ряд других.

Одно определяющее уравнение - количество определенных величин: Определяющее уравнение используется для определения количества величин в терминах ряда других. Одно определяющее уравнение не должно содержать одну величину, определяющую все остальные величины в том же уравнении, иначе снова возникнут противоречия. Отдельного определения определенных величин не существует, поскольку они определяются одной величиной в одном уравнении. Кроме того, определенные количества могут быть уже определены ранее, поэтому, если другая величина определяет их в том же уравнении, между определениями возникает конфликт.

Можно избежать противоречий, определяя количества последовательно; порядок, в котором определены количества, должен быть учтен. Примеры, охватывающие эти случаи, встречаются в электромагнетизме и приведены ниже.

Дифференциальная магнитная сила dFиз-за небольшого элемента заряда dq, составляющего электрический ток I (используется обычный ток ). Сила должна быть интегрирована по линии вдоль пути прохождения тока относительно вектора линейного элемента dr.

Примеры

Взаимоисключающие определения:

Магнитная индукция поле Bможет быть определено в терминах электрического заряда q или тока I, и силы Лоренца (магнитный член) F испытываемые носителями заряда из-за поля,

$F\; =\; q\; (v\; \times \; B)\; =\; (\int \; I\; dt)\; (drdt\; \times \; B)\; =\; (\int \; I\; dtdrdt)\; \times \; B\; =\; I\; (\int \; dr)\; \times \; B\; =\; I\; (L\; \times \; B),\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{F\}\; =\; q\; \backslash \; left\; (\backslash \; mathbf\; \{v\}\; \backslash \; times\; \backslash \; mathbf\; \{B\}\; \backslash \; right)\; \backslash \backslash \; =\; \backslash \; left\; (\backslash \; int\; I\; \backslash \; mathrm\; \{d\}\; t\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; mathbf\; \{r\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; times\; \backslash \; mathbf\; \{B\}\; \backslash \; right)\; \backslash \backslash \; =\; \backslash \; left\; (\backslash \; int\; I\; \backslash \; mathrm\; \{d\}\; t\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; mathbf\; \{r\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash \; right)\; \backslash \; times\; \backslash \; mathbf\; \{B\}\; \backslash \backslash \; =\; I\; \backslash \; left\; (\backslash \; int\; \backslash \; mathrm\; \{d\}\; \backslash \; mathbf\; \{r\}\; \backslash \; right)\; \backslash \; times\; \backslash \; mathbf\; \{B\}\; \backslash \backslash \; =\; I\; \backslash \; left\; (\backslash \; mathbf\; \{l\}\; \backslash \; times\; \backslash \; mathbf\; \{B\}\; \backslash \; right),\; \backslash \; end\; \{align\}\}\; \backslash ,\; \backslash !\}$

где $l\; =\; \int \; dr\; \{\backslash \; displaystyle\; \backslash \; math\; bf\; \{l\}\; =\; \backslash \; int\; \backslash \; mathrm\; \{d\}\; \backslash \; mathbf\; \{r\}\; \backslash ,\; \backslash !\}$- это изменение положения, которое проходят носители заряда (при условии, что ток не зависит от положения, если это не так, линейный интеграл должен производиться вдоль пути тока) или в терминах магнитного потока Φ B через поверхность S, где площадь используется как скаляр A и вектор: $A\; =\; A\; n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{A\}\; =\; A\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; \backslash ,\; \backslash !\}$и $n\; ^\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; \backslash ,\; \backslash !\}$- единица, нормальная к A, либо в дифференциальной форме

$B\; \cdot \; n\; ^\; =\; d\; \Phi \; B\; d\; A,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; Phi\; \_\; \{B\}\}\; \{\backslash \; mathrm\; \{d\}\; A\}\},\; \backslash ,\; \backslash !\}$

или целая форма,

$B\; \cdot \; n\; ^\; d\; A\; =\; d\; \Phi \; B,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{B\}\; \backslash \; cdot\; \backslash \; mathbf\; \{\backslash \; hat\; \{n\}\}\; \backslash \; mathrm\; \{d\}\; A\; =\; \backslash \; mathrm\; \{d\}\; \backslash \; Phi\; \_\; \{B\},\; \backslash ,\; \backslash !\}$

$\Phi \; B\; =\; \int \; SB\; \cdot \; d\; A.\; \{\backslash \; displaystyle\; \backslash \; Phi\; \_\; \{B\}\; =\; \backslash \; int\; \_\; \{S\}\; \backslash \; mathbf\; \{B\}\; \backslash \; cdot\; \backslash \; mathrm\; \{d\}\; \backslash \; mathbf\; \{A\}.\; \backslash ,\; \backslash !\}$

Однако только одно из приведенных выше уравнений может использоваться для определения B по следующей причине, учитывая, что A, r, vи F были определены в другом месте однозначно (скорее всего, механика и евклидова геометрия ).

Если уравнение силы определяет B, где q или I были ранее определены, тогда уравнение магнитного потока определяет Φ B, поскольку B был определен ранее однозначно. Если уравнение магнитного потока определяет B, где Φ B, уравнение силы может быть определяющим уравнением для I или q. Обратите внимание на противоречие, когда B оба уравнения определяют B одновременно и когда B не является базовой величиной; уравнение силы требует, чтобы q или I были определены в другом месте, в то время как уравнение потока требует, чтобы q или I определялись уравнением силы, аналогично уравнение силы требует, чтобы Φ B определялось потоком уравнение, в то же время уравнение потока требует, чтобы Φ B было определено в другом месте. Чтобы оба уравнения одновременно использовались в качестве определений, B должно быть базовой величиной, чтобы можно было определить F и Φ B как производные от B однозначно.

Эквивалентные определения:

Другой пример - индуктивность L, для которого используются два эквивалентных уравнения.

В терминах I и Φ B, индуктивность определяется выражением

$L\; =\; N\; d\; \Phi \; B\; d\; I,\; \{\backslash \; displaystyle\; L\; =\; N\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; Phi\; \_\; \{B\}\}\; \{\backslash \; mathrm\; \{d\; \}\; I\}\},\; \backslash ,\; \backslash !\}$

через I и наведенную ЭДС V

$V\; =\; -\; L\; d\; I\; dt.\; \{\backslash \; displaystyle\; V\; =\; -L\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; I\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}.\; \backslash ,\; \backslash !\}$

Эти два эквивалента согласно закону индукции Фарадея :

$V\; =\; -\; N\; d\; \Phi \; B\; dt,\; \{\backslash \; displaystyle\; V\; =\; -N\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; Phi\; \_\; \{B\}\}\; \{\backslash \; mathrm\; \{d\}\; t\}\},\; \backslash ,\; \backslash !\}$

$V\; dt\; =\; -\; N\; d\; \Phi \; B,\; \{\backslash \; displaystyle\; V\; \{\backslash \; mathrm\; \{d\}\; t\}\; =\; -\; N\; \backslash \; mathrm\; \{d\}\; \backslash \; Phi\; \_\; \{B\},\; \backslash ,\; \backslash !\}$

подстановка в первое определение для L

$L\; =\; -\; V\; dtd\; I\; \{\backslash \; displaystyle\; L\; =\; -V\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; t\}\; \{\backslash \; mathrm\; \{d\}\; I\}\}\; \backslash ,\; \backslash !\}$

$V\; =\; -\; L\; d\; I\; dt\; \{\backslash \; displaystyle\; V\; =\; -L\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; I\}\; \{\backslash \; mathrm\; \{d\}\; t\}\}\; \backslash ,\; \backslash !\}$

и поэтому они не исключают друг друга.

Одно определяющее уравнение - количество определенных величин

Обратите внимание, что L не может одновременно определять I и Φ B - это не имеет смысла. I, Φ B и V, скорее всего, все ранее были определены как (Φ B, приведенное выше в уравнении потока);

$V\; =\; d\; W\; dq,\; I\; =\; dqdt,\; \{\backslash \; displaystyle\; V\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{d\}\; W\}\; \{\backslash \; mathrm\; \{d\}\; q\}\},\; \backslash \; quad\; I\; =\; \{\backslash \; frac\; \{\backslash \; mathrm\; \{\; d\}\; q\}\; \{\backslash \; mathrm\; \{d\}\; t\}\},\; \backslash ,\; \backslash !\}$

где W = работа, выполненная на заряде q. Кроме того, не существует определения ни I, ни Φ B по отдельности - потому что L определяет их в одном уравнении.

Однако, используя силу Лоренца для электромагнитного поля :

$F\; =\; q\; [E\; +\; (v\; \times \; B)],\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; q\; \backslash \; left\; [\backslash \; mathbf\; \{E\}\; +\; \backslash \; left\; (\backslash \; mathbf\; \{v\}\; \backslash \; times\; \backslash \; mathbf\; \{B\}\; \backslash \; right)\; \backslash \; right],\; \backslash ,\; \backslash !\}$

в качестве одного определяющего уравнения для электрическое поле Eи магнитное поле B разрешены, поскольку E и B определяются не только одной переменной, но и тремя; сила F, скорость v и заряд q. Это согласуется с отдельными определениями E и B, поскольку E определяется с помощью F и q:

$E\; =\; F\; /\; q.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{E\}\; =\; \backslash \; mathbf\; \{F\}\; /\; q.\; \backslash ,\; \backslash !\}$

и B, определенные как F, v, и q, как указано выше.

Определения и функции: Определение количества может варьироваться в зависимости от параметров, отличных от тех, что указаны в определении. Определяющее уравнение только определяет, как вычислить определенное количество, оно не может описать, как количество изменяется в зависимости от других параметров, поскольку функция будет варьироваться от одного приложения к другому. То, как определяемая величина изменяется в зависимости от других параметров, описывается определяющим уравнением или уравнениями, поскольку оно изменяется от одного приложения к другому и от одного приближения (или упрощения) к другому.

Примеры

Массовая плотность ρ определяется с использованием массы m и объема V, но может изменяться в зависимости от температуры T и давления p, ρ = ρ (p, T)

угловая частота ω распространения волны определяется с использованием частоты (или, эквивалентно, периода времени T) колебания как функции от волнового числа k, ω = ω (k). Это дисперсионное соотношение для распространения волн.

Коэффициент восстановления для столкновения объекта определяется с использованием скоростей разделения и приближения по отношению к точке столкновения, но зависит от природы рассматриваемых поверхностей.

Определения и теоремы : существует очень важное различие между определением уравнений и общими или производными результатами, теоремами или законами. Определяющие уравнения не обнаруживают какую-либо информацию о физической системе, они просто повторно формулируют одно измерение в терминах других. Результаты, теоремы и законы, с другой стороны, действительно предоставляют значимую информацию, хотя бы небольшую, поскольку они представляют собой расчет величины с учетом других свойств системы и описывают, как система ведет себя при изменении переменных.

Примеры

Выше был приведен пример закона Ампера. Другой - сохранение импульса для N 1 исходных частиц, имеющих начальные импульсы pi, где i = 1, 2... N 1 и N 2 конечные частицы, имеющие конечный импульс pi(некоторые частицы могут взорваться или прилипнуть), где j = 1, 2... N 2, уравнение сохранения гласит:

$\sum \; i\; N\; 1\; pi\; =\; \sum \; j\; N\; 2\; pj\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; ^\; \{N\_\; \{1\}\}\; \backslash \; mathbf\; \{p\}\; \_\; \{\backslash \; rm\; \{i\}\}\; =\; \backslash \; sum\; \_\; \{j\}\; ^\; \{N\_\; \{2\}\}\; \backslash \; mathbf\; \{\; p\}\; \_\; \{\backslash \; rm\; \{j\}\}\; \backslash ,\; \backslash !\}$

Использование определения количества движения в терминах скорости:

$p\; =\; mv\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; =\; m\; \backslash \; mathbf\; \{v\}\; \backslash ,\; \backslash !\}$

так, чтобы для каждой частицы:

$pi\; =\; mivi\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; \_\; \{\backslash \; rm\; \{i\}\}\; =\; m\_\; \{i\}\; \backslash \; mathbf\; \{v\}\; \_\; \{\backslash \; rm\; \{\; i\}\}\; \backslash ,\; \backslash !\}$и $pj\; =\; mjvj\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; \_\; \{\backslash \; rm\; \{j\}\}\; =\; m\_\; \{j\}\; \backslash \; mathbf\; \{v\}\; \_\; \{\backslash \; rm\; \{j\}\}\; \backslash ,\; \backslash !\}$

уравнение сохранения можно записать как

$\sum \; i\; N\; 1\; mivi\; =\; \sum \; j\; N\; 2\; mivi.\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\}\; ^\; \{N\_\; \{1\}\}\; m\_\; \{i\}\; \backslash \; mathbf\; \{v\}\; \_\; \{\backslash \; rm\; \{i\}\}\; =\; \backslash \; sum\; \_\; \{j\}\; ^\; \{N\_\; \{2\}\}\; m\_\; \{i\; \}\; \backslash \; mathbf\; \{v\}\; \_\; \{\backslash \; rm\; \{i\}\}.\; \backslash ,\; \backslash !\}$

Он идентичен предыдущей версии. Никакая информация не теряется или не приобретается при изменении количества при замене определений, но само уравнение дает информацию о системе.

Некоторые уравнения, обычно получаемые в результате вывода, включают полезные величины, которые служат одноразовым определением в пределах их области применения.

Примеры

В специальной теории относительности, релятивистская масса находит поддержку и осуждение со стороны физиков. Он определяется как:

$m\; =\; \gamma \; m\; 0\; \{\backslash \; displaystyle\; m\; =\; \backslash \; gamma\; m\_\; \{0\}\; \backslash ,\; \backslash !\}$

, где m 0 - масса покоя объекта, а γ - фактор Лоренца. Это позволяет легко получить некоторые величины, такие как импульс p и энергия E движущегося массивного объекта из других уравнений, просто используя релятивистскую массу:

$p\; =\; mv\; \to \; p\; =\; \gamma \; m\; 0\; v\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{p\}\; =\; m\; \backslash \; mathbf\; \{v\}\; \backslash \; rightarrow\; \backslash \; mathbf\; \{p\}\; =\; \backslash \; gamma\; m\_\; \{0\}\; \backslash \; mathbf\; \{v\}\}$

$E\; =\; mc\; 2\; \to \; E\; =\; \gamma \; m\; 0\; c\; 2\; \{\backslash \; displaystyle\; E\; =\; mc\; ^\; \{2\}\; \backslash \; rightarrow\; E\; =\; \backslash \; gamma\; m\_\; \{0\}\; c\; ^\; \{2\}\}$

Однако это не всегда применимо, например, кинетическая энергия T и сила Fтого же объекта не определяется выражением:

$T\; =\; m\; 2\; v\; \cdot \; v\; \nrightarrow \; T\; =\; \gamma \; m\; 0\; 2\; v\; \cdot \; v\; \{\backslash \; displaystyle\; T\; =\; \{\backslash \; frac\; \{m\}\; \{2\}\}\; \backslash \; mathbf\; \{v\}\; \backslash \; cdot\; \backslash \; mathbf\; \{v\}\; \backslash \; nrightarrow\; T\; =\; \{\backslash \; frac\; \{\backslash \; gamma\; m\_\; \{0\}\}\; \{2\}\}\; \backslash \; mathbf\; \{v\}\; \backslash \; cdot\; \backslash \; mathbf\; \{v\}\}$

$F\; =\; ma\; \nrightarrow \; F\; =\; \gamma \; m\; 0\; a\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; m\; \backslash \; mathbf\; \{a\}\; \backslash \; nrightarrow\; \backslash \; mathbf\; \{F\}\; =\; \backslash \; gamma\; m\_\; \{0\}\; \backslash \; mathbf\; \{a\}\}$

Фактор Лоренца имеет более глубокое значение значение и происхождение, и используется в терминах собственного времени и координатного времени с четырьмя векторами. Приведенные выше правильные уравнения являются следствием применения определений в правильном порядке.

Магнитное поле, отклоняющее заряженную частицу, псевдоопределяющее магнитную жесткость для частицы.

В электромагнетизме, заряженная частица (с массой m и зарядом q) в однородное магнитное поле B отклоняется полем по круговой винтовой дуге со скоростью v и радиусом кривизны r, при этом спиральная траектория наклонена под углом θ к В . магнитная сила - это центростремительная сила, поэтому сила F, действующая на частицу, равна;

$F\; =\; -\; m\; (v\; \cdot \; v)\; r\; ^\; |\; г\; |\; знак\; равно\; Q\; (v\; \times \; B),\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{F\}\; =\; -\; \{\backslash \; frac\; \{m\; \backslash \; left\; (\backslash \; mathbf\; \{v\}\; \backslash \; cdot\; \{\backslash \; mathbf\; \{v\}\}\; \backslash \; right)\; \backslash \; mathbf\; \{\backslash \; hat\; \{r\; \}\}\}\; \{\backslash \; left\; |\; \backslash \; mathbf\; \{r\}\; \backslash \; right\; |\}\}\; =\; q\; \backslash \; left\; (\backslash \; mathbf\; \{v\}\; \backslash \; times\; \backslash \; mathbf\; \{B\}\; \backslash \; right),\; \backslash ,\; \backslash !\}$

приведение к скалярной форме и решение для | B||r|;

$м\; |\; v\; |\; 2\; |\; г\; |\; =\; q\; |\; v\; |\; |\; B\; |\; грех\; \; \theta ,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{m\; \backslash \; left\; |\; \backslash \; mathbf\; \{v\}\; \backslash \; right\; |\; ^\; \{2\}\}\; \{\backslash \; left\; |\; \backslash \; mathbf\; \{r\}\; \backslash \; right\; |\}\}\; =\; q\; \backslash \; left\; |\; \backslash \; mathbf\; \{\; v\}\; \backslash \; right\; |\; \backslash \; left\; |\; \backslash \; mathbf\; \{B\}\; \backslash \; right\; |\; \backslash \; sin\; \backslash \; theta,\; \backslash ,\; \backslash !\}$

$m\; |\; v\; |\; |\; г\; |\; =\; q\; |\; B\; |\; грех\; \; \theta ,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{m\; \backslash \; left\; |\; \backslash \; mathbf\; \{v\}\; \backslash \; right\; |\}\; \{\backslash \; left\; |\; \backslash \; mathbf\; \{r\}\; \backslash \; right\; |\}\}\; =\; q\; \backslash \; left\; |\; \backslash \; mathbf\; \{B\}\; \backslash \; right\; |\; \backslash \; sin\; \backslash \; theta,\; \backslash ,\; \backslash !\}$

$|\; B\; |\; |\; г\; |\; =\; m\; |\; v\; |\; д\; грех\; \; \theta ,\; \{\backslash \; displaystyle\; \backslash \; left\; |\; \backslash \; mathbf\; \{B\}\; \backslash \; right\; |\; \backslash \; left\; |\; \backslash \; mathbf\; \{r\}\; \backslash \; right\; |\; =\; \{\backslash \; frac\; \{m\; \backslash \; left\; |\; \backslash \; mathbf\; \{v\}\; \backslash \; right\; |\}\; \{q\; \backslash \; sin\; \backslash \; theta\}\},\; \backslash ,\; \backslash !\}$

служит определением для магнитной жесткости частицы. Поскольку это зависит от массы и заряда частицы, это полезно для определения степени отклонения частицы в поле B, что происходит экспериментально в масс-спектрометрии и частица. детекторы.

• Основное уравнение
• Определяющее уравнение (физическая химия)
• Список уравнений электромагнетизма
• Список уравнений классической механики
• Список уравнений механики жидкости
• Список уравнения гравитации
• Список уравнений ядерной физики и физики элементарных частиц
• Список уравнений квантовой механики
• Список уравнений фотоники
• Список релятивистских уравнений
• Таблица уравнений термодинамики

• PM Уилан; М.Дж. Ходжесон (1978). Основные принципы физики (2-е изд.). Джон Мюррей. ISBN 0-7195-3382-1.
• G. Вон (2010). Кембриджский справочник по физическим формулам. Издательство Кембриджского университета. ISBN 978-0-521-57507-2.
• А. Хальперн (1988). 3000 Решенных задач по физике, Серия Шаум. Мак Гроу Хилл. ISBN 978-0-07-025734-4.
• R.G. Лернер; Г.Л. Тригг (2005). Энциклопедия физики (2-е изд.). Издательство VHC, Ханс Варлимонт, Springer. С. 12–13. ISBN 978-0-07-025734-4.
• C.B. Паркер (1994). Энциклопедия физики Макгроу Хилла (2-е изд.). Макгроу Хилл. ISBN 0-07-051400-3.
• П.А. Типлер; Г. Моска (2008). Физика для ученых и инженеров: с современной физикой (6-е изд.). W.H. Freeman and Co. ISBN 978-1-4292-0265-7.
• L.N. Рука; Дж. Д. Финч (2008). Аналитическая механика. Издательство Кембриджского университета. ISBN 978-0-521-57572-0.
• T.B. Аркилл; Си Джей Миллар (1974). Механика, колебания и волны. Джон Мюррей. ISBN 0-7195-2882-8.
• Х.Дж. Боль (1983). Физика колебаний и волн (3-е изд.). Джон Вили и сыновья. ISBN 0-471-90182-2.
• Дж. Р. Форшоу; А.Г. Смит (2009). Динамика и относительность. Вайли. ISBN 978-0-470-01460-8.
• G.A.G. Беннет (1974). Электричество и современная физика (2-е изд.). Эдвард Арнольд (Великобритания). ISBN 0-7131-2459-8.
• I.S. Грант; W.R. Phillips; Манчестерская физика (2008). Электромагнетизм (2-е изд.). Джон Вили и сыновья. ISBN 978-0-471-92712-9.
• Д.Дж. Гриффитс (2007). Введение в электродинамику (3-е изд.). Pearson Education, Дорлинг Киндерсли. ISBN 81-7758-293-3.

• L.H. Гринберг (1978). Физика в современных приложениях. Holt-Saunders International W.B. Saunders and Co. ISBN 0-7216-4247-0.
• J.B. Марион; W.F. Горняк (1984). Принципы физики. Международный колледж Сондерса Холт-Сондерс. ISBN 4-8337-0195-2.
• А. Байзер (1987). Концепции современной физики (4-е изд.). Макгроу-Хилл (международный). ISBN 0-07-100144-1.
• H.D. Молодые; Р.А. Фридман (2008). Университетская физика - с современной физикой (12-е изд.). Эддисон-Уэсли (Pearson International). ISBN 0-321-50130-6.