Войти
A Многогранник - это фигура, состоящая из нескольких многогранников с общим центром . Они являются трехмерными аналогами многоугольных соединений, таких как гексаграмма.
. Внешние вершины соединения могут быть соединены, образуя выпуклый многогранник, называемый его выпуклая оболочка. Соединение - это грань его выпуклой оболочки.
Другой выпуклый многогранник образован небольшим центральным пространством, общим для всех элементов соединения. Этот многогранник может использоваться как ядро для набора звёздчатых звёзд.
Правильное полиэдрическое соединение может быть определено как соединение, которое, как и правильный многогранник, вершинно-транзитивно, реберно-транзитивно и гранно-транзитивный. Существует пять правильных соединений многогранников:
| Правильное соединение. (символ Кокстера) | Изображение | Сферическое | Выпуклая оболочка | Общее ядро | Группа симметрии | Подгруппа., ограничивающая. одним. составляющим | Двойное регулярное соединение |
|---|---|---|---|---|---|---|---|
| Два тетраэдра. {4,3} [2 {3, 3}] {3,4} |  |  | Куб | Октаэдр | * 432. [4,3]. Oh | * 332. [3,3]. Td | Два тетраэдра |
| Пять тетраэдров. {5,3} [5 {3,3}] {3,5} |  |  | Додекаэдр | Икосаэдр | 532. [5,3]. I | 332. [3,3 ]. T | Хирал двойник. (Энантиоморф) |
| Десять тетраэдров. 2 {5,3} [10 {3,3}] 2 {3,5} |  |  | Додекаэдр | Икосаэдр | * 532. [5,3]. Ih | 332. [3,3]. T | Десять тетраэдров |
| Пять кубов. 2 {5,3} [5 {4,3}] |  |  | Додекаэдр | Ромбический триаконтаэдр | * 532. [5,3]. Ih | 3 * 2. [3,3]. Th | Пять октаэдров |
| Пять октаэдров. [5 {3,4}] 2 {3,5} |  |  | Икосододекаэдр | Икосаэдр | * 532. [5,3]. Ih | 3 * 2. [3,3]. Th | Пять кубиков |
Будь Известно, что это правильное соединение двух тетраэдров, часто называемое stella octangula, имя, данное ему Кеплером. Вершины двух тетраэдров определяют куб , а их пересечение определяет правильный октаэдр , который имеет те же плоскости граней, что и соединение. Таким образом, соединение двух тетраэдров является звёздчатой звёздчатой октаэдром и фактически его единственной конечной звёздчатой формой.
Обычное соединение пяти тетраэдров существует в двух энантиоморфных версиях, которые вместе составляют правильное соединение десяти тетраэдров. Правильное соединение десяти тетраэдров также может быть построено с пятью октангулами Stellae.
Каждое из правильных тетраэдрических соединений самодвойственно или двойственно своему хиральному двойнику; правильное соединение пяти кубов и правильное соединение пяти октаэдров двойственно друг другу.
Следовательно, правильные полиэдрические соединения могут также рассматриваться как двойные регулярные соединения. .
Обозначения Кокстера для регулярных соединений приведены в таблице выше, включая символы Шлефли. Материал в квадратных скобках [d {p, q}] обозначает компоненты соединения: d отдельные {p, q} 's. Материал перед квадратными скобками обозначает расположение вершин соединения: c {m, n} [d {p, q}] - это соединение d {p, q}, разделяющих вершины {m, n}, подсчитанные c раз. Материал после квадратных скобок обозначает расположение граней соединения: [d {p, q}] e {s, t} - это соединение d {p, q}, имеющих общие грани {s, t}, подсчитано е раз. Их можно комбинировать: таким образом, c {m, n} [d {p, q}] e {s, t} - это соединение d {p, q}, разделяющих вершины {m, n}, подсчитанных c раз и лица {s, t} сосчитали e раз. Это обозначение может быть обобщено для соединений любого количества измерений.
Усеченный тетраэдр (светлый) и триакис-тетраэдр (темный) 
Плоский куб (светлый) и пятиугольный икоситетраэдр (темный) 
Икосододекаэдр (светлый) и ромбический триаконтаэдр (темный) Двойные соединения архимеда и Каталонское твердое тело A двойное соединение состоит из многогранника и его двойного, расположенного взаимно вокруг общей межсферы или средней сферы, так что край одного многогранника пересекает двойную кромку двойного многогранника. Есть пять двойственных соединений правильных многогранников.
Ядром является ректификация обоих твердых веществ. Оболочка является двойственной этому выпрямлению, а ее ромбические грани имеют пересекающиеся ребра двух тел в качестве диагоналей (и имеют четыре альтернативные вершины). Для выпуклых тел это выпуклая оболочка.
| Двойное соединение | Изображение | Корпус | Сердечник | Группа симметрии |
|---|---|---|---|---|
| Два тетраэдры. (Соединение двух тетраэдров, звездчатый октаэдр ) |  | Куб | Октаэдр | * 432. [4,3]. Oh |
| Куб - октаэдр. (Соединение куба и октаэдра ) |  | Ромбический додекаэдр | Кубооктаэдр | * 432. [4,3]. Oh |
| Додекаэдр - икосаэдр. (Соединение додекаэдра и икосаэдр ) |  | Ромбический триаконтаэдр | Икосододекаэдр | * 532. [5,3]. Ih |
| Малый звездчатый додекаэдр - большой додекаэдр. (Соединение sD и gD ) |  | Медиальный ромбический триаконтаэдр. (Выпуклый: Икосаэдр ) | Додекадодекаэдр. (Выпуклый: Додекаэдр ) | * 532. [5,3]. Ih |
| Большой икосаэдр - большой звездчатый додекаэдр. (Соединение gI и gsD ) |  | Большой ромбический триаконтаэдр. (Выпуклый: Додекаэдр ) | Большой икосододекаэдр. (Выпуклый: Икосаэдр ) | * 532. [ 5,3]. Ih |
Тетраэдр самодвойственный, поэтому двойное соединение тетраэдра с его двойником - это правильный звездчатый октаэдр.
Октаэдрические и икосаэдрические двойные соединения являются первыми звездчатыми образованиями кубооктаэдр и икосододекаэдр соответственно.
В 1976 году Джон Скиллинг опубликовал Uniform Compounds of Uniform Polyhedra, в котором перечислено 75 соединений (включая 6 как бесконечные призматические наборы соединений, # 20- # 25) сделаны из однородных многогранников с вращательной симметрией. (Каждая вершина является вершинно-транзитивной, и каждая вершина транзитивна со всеми остальными вершинами.) Этот список включает пять регулярных соединений, указанных выше. [1]
75 однородных соединений перечислены в таблице ниже. Большинство из них окрашены в индивидуальный цвет каждым элементом многогранника. Некоторые киральные пары групп граней окрашены симметрией граней внутри каждого многогранника.
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |  |  |
 |  |  |  |
 |  |  |  |  |  |
 |  |
 |  |
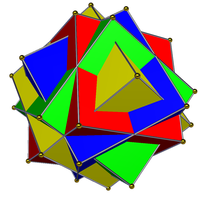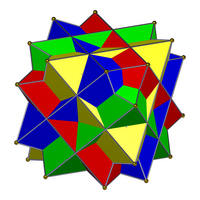| Соединение из четырех кубиков (слева) не является ни обычным соединением, ни двойным соединением, ни однородным соединением. Его двойник, соединение четырех октаэдров (справа), представляет собой однородное соединение. | |
Два многогранника, которые являются составными, но имеют свои элементы, жестко закрепленные на месте, - это небольшой сложный икосододекаэдр (соединение икосаэдр и большой додекаэдр ) и большой сложный икосододекаэдр (соединение малого звездчатого додекаэдра и большого икосаэдра ). Если определение однородного многогранника обобщено, они будут однородными.
Раздел для пар энантиоморфов в списке Скиллинга не содержит соединения двух больших курносых додецикозододекаэдров, поскольку лица пентаграммы совпадают. Удаление совпадающих граней приводит к соединению двадцати октаэдров.
 |  |
| 75 {4,3,3} | 75 {3, 3,4} |
|---|
В четырехмерном пространстве существует большое количество правильных соединений правильных многогранников. Коксетер перечисляет некоторые из них в своей книге Регулярные многогранники. Макмаллен добавил шесть в своей статье «Новые регулярные соединения 4-многогранников».
Самодвойственные:
| Состав | Составляющая | Симметрия |
|---|---|---|
| 120 5-ячеечная | 5-ячеечная | [5,3,3 ], порядок 14400 |
| 120 5 ячеек | 5 ячеек | порядок 1200 |
| 720 5 ячеек | 5 ячеек | [5,3,3 ], заказ 14400 |
| 5 24 элемента | 24 элемента | [5,3,3], заказ 14400 |
Двойные пары:
| Соединение 1 | Соединение 2 | Симметрия |
|---|---|---|
| 3 16-ячеек | 3 тессеракты | [3,4,3], порядок 1152 |
| 15 16-ячеек | 15 тессеракты | [ 5,3,3], заказ 14400 |
| 75 16 ячеек | 75 тессеракты | [5,3,3], заказ 14400 |
| 75 16 ячеек | 75 тессеракты | порядок 600 |
| 300 16 ячеек | 300 тессеракты | [5,3,3], порядок 7200 |
| 600 16 ячеек | 600 тессерактов | [5,3,3], порядок 14400 |
| 25 24 ячеек | 25 24 ячеек | [5, 3,3], порядок 14400 |
Однородные соединения и двойники с выпуклыми 4-многогранниками:
| Соединение 1. Вершинно-транзитивное | Соединение 2. Ячеисто-транзитивное | Симметрия |
|---|---|---|
| 2 16 ячеек | 2 тессеракты | [4, 3,3], порядок 384 |
| 100 24 ячейки | 100 24 ячейки | [5,3,3], порядок 7200 |
| 200 24 ячейки | 200 24 ячейки | [5,3,3], порядок 14400 |
| 5 600 ячеек | 5 120 ячеек | [5,3,3], порядок 7200 |
| 10 600 ячеек | 10 120 ячеек | [5,3,3], порядок 14400 |
| 25 24 ячеек | 25 24- ячейки | порядок 600 |
Верхний индекс (var) в приведенных выше таблицах указывает, что меченые соединения отличаются от других соединений с таким же количеством компонентов.
Самодвойные звездные соединения:
| Соединение | Симметрия |
|---|---|
| 5 {5,5 / 2,5} | [5, 3,3], заказ 7200 |
| 10 {5,5 / 2,5} | [5,3,3], заказ 14400 |
| 5 {5 / 2,5,5 / 2 } | [5,3,3], заказ 7200 |
| 10 {5 / 2,5,5 / 2} | [5,3,3], заказ 14400 |
Двойные пары составных звезд:
| Соединение 1 | Соединение 2 | Симметрия |
|---|---|---|
| 5 {3,5,5 / 2} | 5 {5 / 2,5, 3} | [5,3,3], заказ 7200 |
| 10 {3,5,5 / 2} | 10 {5 / 2,5,3} | [5,3,3], заказ 14400 |
| 5 {5,5 / 2,3} | 5 {3,5 / 2,5} | [ 5,3,3], заказ 7200 |
| 10 {5,5 / 2,3} | 10 {3,5 / 2,5} | [5,3,3 ], заказ 14400 |
| 5 {5 / 2,3,5} | 5 {5,3,5 / 2} | [5,3,3], заказ 7200 |
| 10 {5 / 2,3,5} | 10 {5,3,5 / 2} | [5,3,3], порядок 14400 |
Однородные составные звезды и двойные :
| Соединение 1. Вершинно-транзитивный | Соединение 2. Ячейко-транзитивный | Симметрия |
|---|---|---|
| 5 {3,3,5 / 2} | 5 { 5 / 2,3,3} | [5,3,3], заказ 7200 |
| 10 {3,3,5 / 2} | 10 {5 / 2,3,3} | [5,3,3], заказ 14400 |
Двойные позиции:
| Соединение | Составляющий | Симметрия |
|---|---|---|
| 2 5 ячеек | 5 ячеек | [[3,3,3]], порядок 240 |
| 24 ячейки | [[3,4, 3]], заказ 2304 | |
| 1 тессеракт, 1 16 ячеек | тессеракт, 16 ячеек | |
| 120 ячеек, 600 ячеек | ||
| отлично 120-элементный | ||
| большой звездчатый 120-элементный | ||
| икосаэдрический 120-элементный, малый звездчатый 120-элементный | ||
| большой 120-элементный, большой звездчатый 120-элементный | ||
| большой 120-элементный, большой икосаэдрический 120-элементный | ||
| великий грандиозный 120-элементный звездчатый, большой 600-элементный |
С точки зрения теории групп , если G является группой симметрии полиэдрального соединения, а группа действует транзитивно на многогранники (так что каждый многогранник может быть отправлен любому из других, как в однородных соединениях), то если H является стабилизатором одного выбранного многогранника, многогранники могут быть идентифицированы с пространством орбит G / H - смежный класс gH соответствует тому, в какой многогранник g переводится выбранный многогранник.
Существует восемнадцать двухпараметрических семейств регулярных составных мозаик евклидовой плоскости. В гиперболической плоскости известно пять однопараметрических семейств и семнадцать единичных случаев, но полнота этого списка не была перечислена.
Евклидовы и гиперболические составные семейства 2 {p, p} (4 ≤ p ≤ ∞, p - целое число) аналогичны сферической stella octangula, 2 {3,3}.
| Самодвойственные | Двойные | Самодвойственные | |
|---|---|---|---|
| 2 {4,4} | 2 {6,3} | 2 {3,6} | 2 {∞, ∞} |
 |  |  |  |
| 3 {6,3} | 3 {3,6} | 3 {∞, ∞} | |
 |  |  | |
Известный Семейство регулярных евклидовых составных сот в пяти или более измерениях представляет собой бесконечное семейство составных частей гиперкубических сот, все вершины и грани которых совпадают с другими гиперкубическими сотами. Это соединение может иметь любое количество гиперкубических сот.
Есть также двойные регулярные мозаичные составы. Простым примером является соединение E гексагональной мозаики и ее двойной треугольной мозаики, которая имеет общие ребра с дельтоидальной трехгексагональной мозаикой. Евклидовы соединения двух гиперкубических сот являются как правильными, так и двойными регулярными.
