| Алгебраическая структура → Теория групп Теория групп | ||||
|---|---|---|---|---|
 | ||||
Основные понятия
| ||||
Конечные группы
| ||||
Модульные группы
| ||||
Топологические группы и группы Ли
| ||||
| Алгебраические группы | ||||
|
В теории групп, разделе математики, для данной группы G при бинарной операции ∗ подмножество H в G называется подгруппой в G, если H также образует группу при операции ∗. Точнее, Н является подгруппой G, если ограничение на * до H × H является операцией группы на H. Обычно это обозначается H ≤ G, читается как « H - подгруппа G ».
Единичная подгруппа любой группы является подгруппой { х }, состоящей только из единичного элемента.
Собственная подгруппа группы G является подгруппой Н, которая является собственное подмножество из G (то есть, H ≠ G). Обычно это обозначается как H lt; G, читается как « H - собственная подгруппа G ». Некоторые авторы также исключают тривиальную группу из собственной (то есть H ≠ { e }).
Если Н является подгруппой группы G, то G иногда называют надгруппа из H.
Те же определения применяются в более общем случае, когда G - произвольная полугруппа, но эта статья будет иметь дело только с подгруппами групп. Группу G иногда обозначают упорядоченной парой ( G, ∗), обычно для того, чтобы подчеркнуть операцию ∗, когда G содержит множественные алгебраические или другие структуры.
 G - группа, целые числа по модулю 8 сложены. Подгруппа H содержит только 0 и 4 и изоморфна. У H есть четыре левых смежных класса: сам H, 1 + H, 2 + H и 3 + H (написано с использованием аддитивной записи, поскольку это аддитивная группа ). Вместе они разбивают всю группу G на неперекрывающиеся множества равного размера. Индекс [G: H] равен 4.
G - группа, целые числа по модулю 8 сложены. Подгруппа H содержит только 0 и 4 и изоморфна. У H есть четыре левых смежных класса: сам H, 1 + H, 2 + H и 3 + H (написано с использованием аддитивной записи, поскольку это аддитивная группа ). Вместе они разбивают всю группу G на неперекрывающиеся множества равного размера. Индекс [G: H] равен 4. Для подгруппы H и некоторого a в G определим левый смежный класс aH = { ah : h в H }. Поскольку a обратимо, отображение φ: H → aH, заданное формулой φ ( h) = ah, является биекцией. Более того, каждый элемент G содержится ровно в одном левом классе смежности H ; левые классы являются классами эквивалентности, соответствующие отношению эквивалентности 1 \ 2 тогда и только тогда, когда 1 -12 в H. Число левых смежных классов H называется индексом из H в G и обозначается [ G : H ].
Теорема Лагранжа утверждает, что для конечной группы G и подгруппы H,
где | G | и | H | обозначают порядки групп G и H соответственно. В частности, порядок каждой подгруппы группы G (и порядок каждого элемента группы G) должен быть делителем | G |,
Правые классы смежности определяются аналогично: Ha = { ha : h в H }. Они также являются классами эквивалентности для подходящего отношения эквивалентности, и их количество равно [ G : H ].
Если aH = Ha для любого a из G, то H называется нормальной подгруппой. Каждая подгруппа индекса 2 является нормальной: левые смежные классы, а также правые смежные классы - это просто подгруппа и ее дополнение. В более общем смысле, если p - младшее простое число, делящее порядок конечной группы G, то любая подгруппа индекса p (если таковая существует) является нормальной.
Пусть G - циклическая группа Z 8, элементы которой равны
и чья групповая операция - сложение по модулю восемь. Его Кэли таблица является
| + | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 4 | 2 | 6 | 1 | 5 | 3 | 7 |
| 4 | 4 | 0 | 6 | 2 | 5 | 1 | 7 | 3 |
| 2 | 2 | 6 | 4 | 0 | 3 | 7 | 5 | 1 |
| 6 | 6 | 2 | 0 | 4 | 7 | 3 | 1 | 5 |
| 1 | 1 | 5 | 3 | 7 | 2 | 6 | 4 | 0 |
| 5 | 5 | 1 | 7 | 3 | 6 | 2 | 0 | 4 |
| 3 | 3 | 7 | 5 | 1 | 4 | 0 | 6 | 2 |
| 7 | 7 | 3 | 1 | 5 | 0 | 4 | 2 | 6 |
Эта группа имеет два нетривиальных подгруппы: J = {0,4} и H = {0,4,2,6}, где J также подгруппа H. Таблица Кэли для H - это верхний левый квадрант таблицы Кэли для G ; Таблица Кэли для J находится в верхнем левом квадранте таблицы Кэли для H. Группа G является циклической, и поэтому ее подгруппы. В общем случае подгруппы циклических групп также являются циклическими.
В каждой группе столько же малых подгрупп, сколько нейтральных элементов на главной диагонали:
Единичная группа и два элемента группы Z 2. Эти небольшие подгруппы не включены в следующий список.
 Симметрическая группа S 4, показывающая все перестановки из 4 элементов Симметрическая группа S 4, показывающая все перестановки из 4 элементов |  Все 30 подгрупп Все 30 подгрупп  Упрощенный Хассе диаграммы по решетке подгрупп из S 4 Упрощенный Хассе диаграммы по решетке подгрупп из S 4 |
 Знакопеременная группа 4 показана только четные подстановки Подгруппа:
Знакопеременная группа 4 показана только четные подстановки Подгруппа: 




 Группа диэдра порядка 8 Подгруппы: Группа диэдра порядка 8 Подгруппы:   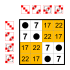 |  Группа диэдра порядка 8 Подгруппы: Группа диэдра порядка 8 Подгруппы: 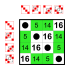  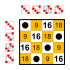 |  Группа диэдра порядка 8 Подгруппы: Группа диэдра порядка 8 Подгруппы: 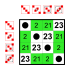  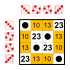 |
 Симметричная группа S 3 Подгруппа: Симметричная группа S 3 Подгруппа:  |  Симметричная группа S 3 Подгруппа: Симметричная группа S 3 Подгруппа:  |  Симметричная группа S 3 Подгруппа: Симметричная группа S 3 Подгруппа:  |  Симметричная группа S 3 Подгруппа: Симметричная группа S 3 Подгруппа:  |
 Кляйн четыре группы Кляйн четыре группы |  Кляйн четыре группы Кляйн четыре группы |  Кляйн четыре группы Кляйн четыре группы |  Кляйн четыре группы Кляйн четыре группы |
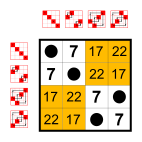 Циклическая группа Z 4 Циклическая группа Z 4 |  Циклическая группа Z 4 Циклическая группа Z 4 |  Циклическая группа Z 4 Циклическая группа Z 4 |
 Циклическая группа Z 3 Циклическая группа Z 3 | 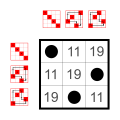 Циклическая группа Z 3 Циклическая группа Z 3 | 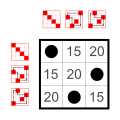 Циклическая группа Z 3 Циклическая группа Z 3 |  Циклическая группа Z 3 Циклическая группа Z 3 |