Метрика Керра

Метрика Керра или геометрия Керра эта геометрия пустого пространства-времени вокруг вращающейся незаряженной аксиально-симметричной черной дыры с квазисферическим горизонтом событий. Метрика Керра является точным решением уравнения поля Эйнштейна из общей теории относительности ; эти уравнения очень нелинейны, что затрудняет поиск точных решений.

• 1 Обзор
• 2 Метрика
  • 2.1 Координаты Бойера - Линдквиста
  • 2.2 Координаты Керра - Шильда
  • 2.3 Координаты солитона
• 3 Масса вращательной энергии
• 4 Волновой оператор
• 5 Перетаскивание кадра
• 6 Важные поверхности
• 7 Эргосфера и процесс Пенроуза
• 8 Особенности геометрии Керра
  • 8.1 Уравнения траектории
• 9 Симметрии
• 10 Сверхэкстремальные решения Керра
• 11 Черные дыры Керра как кротовые норы
• 12 Связь с другими точными решениями
• 13 Мультипольные моменты
• 14 Открытые проблемы
• 15 См. Также
• 16 Сноски
• 17 Ссылки
  • 17.1 Дополнительная литература

Метрика Керра является обобщением вращающегося тела метрики Шварцшильда, открытый Карлом Шварцшильдом в 1915 году и описывающей геометрию пространство-время вокруг незаряженного, сферически-симметричного и невращающегося тела. Соответствующее решение для заряженного сферического невращающегося тела, метрика Рейсснера - Нордстрёма, было обнаружено вскоре после этого (1916–1918). Однако точное решение для незаряженной вращающейся черной дыры, метрика Керра, оставалось нерешенным до 1963 года, когда его открыл Рой Керр. Естественное продолжение заряженной вращающейся черной дыры, метрика Керра - Ньюмана, было обнаружено вскоре после этого в 1965 году. Эти четыре связанных решения можно резюмировать в следующей таблице:

	Невращающаяся (J = 0)	Вращающийся (J ≠ 0)
Незаряженный (Q = 0)	Шварцшильд	Керр
Заряженный (Q ≠ 0)	Рейсснер - Нордстрём	Керр - Ньюман

где Q представляет электрический заряд тела, а J представляет его спин угловой момент.

Согласно метрике Керра, вращающееся тело должно демонстрировать перетаскивание кадра. (также известный как прецессия Лензе - Тирринга ), характерное предсказание общей теории относительности. Первое измерение этого эффекта перетаскивания кадра выполнено в 2011 году в эксперименте Gravity Probe B. Грубо говоря, этот эффект предсказывает, что объекты, вращающиеся в вращающемся массе, участвуют в вращающемся вращении не из-за какого-либо приложения силы или вращающегося момента, которые можно почувствовать, а, скорее, из-за закрученной визуализации самого пространства. -времени, связанного с вращающимися телами.. В случае вращающейся черной дыры на достаточно близком расстоянии все объекты - даже свет - должны вращаться вместе с черной дырой; область, в которой это выполняется, называется эргосферой.

У вращающихся черных дыр есть поверхности, на метрика, кажется, имеет очевидные сингулярности ; размер и форма этих поверхностей зависят от массы черной дыры и углового момента. Внешняя поверхность окружает эргосферу и имеет форму, подобную сплющенной сфере. Внутренняя поверхность отмечает горизонт событий ; объекты, попадающие внутрь этого горизонта, никогда больше не общаться с миром за пределами этого горизонта. Однако ни одна из поверхностей не является истинной сингулярностью, поскольку их особенность может быть устранена в другой системе координат. Как отмечалось выше, объекты между этими двумя поверхностями вращаться вместе с вращающейся черной дырой; функция в этой книге инсталляция для извлечения энергии из вращающейся черной дыры до ее инвариантной массы энергии, Mc.

Эксперимент LIGO, впервые обнаруживший гравитационные волны, анонсированный в 2016 году, также обеспечил первое наблюдение пары черных дыр Керра.

Метрика Керра обычно выражается в одной из двух форм: форме Бойера - Линдквиста и форме Керра - Шильда. Его легко получить из метрики Шварцшильда, используя формализм Ньюмана - Пенроуза (также известный как формализм спиновых коэффициентов).

Координаты Бойера - Линдквиста

Метрика Керра указанной геометрии пространство-время в окрестностях массы $M\; \{\backslash \; displaystyle\; M\}$, вращающейся с угловым моментом $J\; \{\backslash \; стиль\; отображения\; J\}$. Метрика (или эквивалентно ее элемент строки для собственного времени ) в координатах Бойера - Линдквиста is

$g\; =\; -\; c\; 2\; d\; \tau \; 2\; =\; -\; (1\; -\; rsr\; \Sigma )\; c\; 2\; dt\; 2\; +\; \Sigma \; \Delta \; dr\; 2\; +\; \Sigma \; d\; \theta \; 2\; +\; (r\; 2\; +\; a\; 2\; +\; rsra\; 2\; \Sigma \; sin\; 2\; \; \theta )\; sin\; 2\; \; \theta \; d\; \varphi \; 2-2\; rsra\; sin\; 2\; \; \theta \; \Sigma \; cdtd\; \varphi \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; g\; =\; -\; c\; ^\; \{2\}\; d\; \backslash \; tau\; ^\; \{2\}\; \backslash \backslash \; =\; -\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\_\; \{s\}\; r\}\; \{\backslash \; Sigma\}\}\; \backslash \; right)\; c\; ^\; \{2\}\; dt\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{\backslash \; Sigma\}\; \{\backslash \; Delta\}\}\; dr\; ^\; \{2\}\; +\; \backslash \; Sigma\; d\; \backslash \; theta\; ^\; \{2\}\; +\; \backslash \; left\; (r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{r\_\; \{s\}\; ra\; ^\; \{2\}\}\; \{\backslash \; Sigma\}\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \backslash \; right)\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \backslash \; d\; \backslash \; phi\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{2r\_\; \{s\}\; ra\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\; \{\backslash \; Sigma\}\}\; cdt\; \backslash ,\; d\; \backslash \; phi\; \backslash \; end\; \{align\}\}\}$

(1)

где координаты $r,\; \theta ,\; \varphi \; \{\backslash \; displaystyle\; r,\; \backslash \; theta,\; \backslash \; phi\}$- стандартные сферические системы координат, которые эквивалентны декартовым координатам

$x\; =\; r\; 2\; +\; a\; 2\; грех\; \; \theta \; соз\; \; \varphi \; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; sqrt\; \{r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\}\}\; \backslash \; sin\; \backslash \; theta\; \backslash \; cos\; \backslash \; phi\}$

(2)

$y\; знак\; равно\; р\; 2\; +\; 2\; грех\; \; \theta \; грех\; \; \varphi \; \{\backslash \; displaystyle\; y\; =\; \{\backslash \; sqrt\; \{r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\}\}\; \backslash \; sin\; \backslash \; theta\; \backslash \; sin\; \backslash \; phi\}$

(3)

$z\; =\; r\; cos\; \; \theta ,\; \{\backslash \; displaystyle\; z\; =\; r\; \backslash \; cos\; \backslash \; theta,\}$

(4)

где $rs\; \{\backslash \; displaystyle\; r\_\; \{\; s\}\}$- радиус Шварцшильда

$rs\; =\; 2\; GM\; c\; 2,\; \{\backslash \; displaystyle\; r\_\; \{s\}\; =\; \{\backslash \; frac\; \{2GM\}\; \{c\; ^\; \{2\}\}\},\}$

(5)

и где для краткости длины $a,\; \Sigma \; \{\backslash \; displaystyle\; a,\; \backslash \; Sigma\}$и $\Delta \; \{\backslash \; displaystyle\; \backslash \; Delta\}$были введены как

$a\; =\; JM\; c,\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; frac\; \{J\}\; \{Mc\}\},\}$

(6)

$\Sigma \; =\; r\; 2\; +\; a\; 2\; cos\; 2\; \; \theta ,\; \{\backslash \; displaystyle\; \backslash \; Sigma\; =\; r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\; \backslash \; cos\; ^\; \{2\}\; \backslash \; theta,\}$

(7)

$\Delta \; =\; r\; 2\; -\; rsr\; +\; a\; 2.\; \{\backslash \; displaystyle\; \backslash \; Дельта\; =\; r\; ^\; \{2\}\; -r\_\; \{s\}\; r\; +\; a\; ^\; \{2\}.\}$

(8)

Ключевой особенностью, которую следует отметить в вышеуказанной метрике, термин является перекрестным произведением $dtd\; \varphi .\; \{\backslash \; displaystyle\; dt\; \backslash ,\; d\; \backslash \; phi.\}$Это означает, что существует связь между временем и движением в плоскости вращения, которая исчезает, когда угловой момент черной дыры стремится к нулю.

В нерелятивистском пределе, где $M\; \{\backslash \; displaystyle\; M\}$(или, эквивалентно, $rs\; \{\backslash \; displaystyle\; r\_\; \{s\}\}$) стремится к нулю, метрика Керра становится ортогональной метрикой для сжатых сфероидальных координат

$g\; ⟶\; M\; \to \; 0\; -\; c\; 2\; dt\; 2\; +\; \Sigma \; r\; 2\; +\; a\; 2\; dr\; 2\; +\; \Sigma \; d\; \theta \; 2\; +\; (р\; 2\; +\; a\; 2)\; 2\; \; \theta \; d\; грех\; \varphi \; 2\; \{\backslash \; displaystyle\; g\; \backslash \; mathop\; \{\backslash \; longrightarrow\}\; \_\; \{M\; \backslash \; to\; 0\}\; -c\; ^\; \{2\}\; dt\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{\backslash \; Sigma\}\; \{r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\}\}\; dr\; ^\; \{2\}\; +\; \backslash \; Sigma\; d\; \backslash \; theta\; ^\; \{2\}\; +\; \backslash \; left\; (r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\; \backslash \; right)\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; d\; \backslash \; phi\; ^\; \{2\}\}$

(9)

Координаты Керра - Шильда

Метрика Керра может быть выражена в форме «Керра - Шильда», используя конкретный набор декартовых координат следующим образом. Эти решения были предложены Керром и Шильдом в 1965 году.

$г\; \mu \; \nu \; знак\; равно\; \eta \; \mu \; \nu \; +\; fk\; \mu \; К\; \nu \; \{\backslash \; displaystyle\; g\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; =\; \backslash \; eta\; \_\; \{\backslash \; mu\; \backslash \; nu\}\; +\; fk\; \_\; \{\backslash \; mu\}\; k\; \_\; \{\backslash \; nu\}\; \backslash \; !\}$

(10)

$f\; =\; 2\; GM\; r\; 3\; r\; 4\; +\; a\; 2\; z\; 2\; \{\backslash \; displaystyle\; f\; =\; \{\backslash \; frac\; \{2GMr\; ^\; \{3\}\}\; \{r\; ^\; \{4\}\; +\; a\; ^\; \{2\; \}\; z\; ^\; \{2\}\}\}\}$

(11)

$k\; =\; (kx,\; ky,\; kz)\; =\; (rx\; +\; ayr\; 2\; +\; a\; 2,\; ry\; -\; axr\; 2\; +\; a\; 2,\; zr)\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{k\}\; =\; (k\_\; \{x\},\; k\_\; \{y\},\; k\_\; \{z\})\; =\; \backslash \; left\; (\{\backslash \; frac\; \{rx\; +\; ay\}\; \{r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\}\},\; \{\; \backslash \; frac\; \{ry-ax\}\; \{r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\}\},\; \{\backslash \; frac\; \{z\}\; \{r\}\}\; \backslash \; right)\}$

(12)

$k\; 0\; =\; 1.\; \{\backslash \; displaystyle\; k\_\; \{0\}\; =\; 1.\; \backslash !\}$

(13)

Обратите внимание, что k - это единичный вектор. Здесь M - постоянная масса вращающегося объекта, η - тензор Минковского, а a - постоянный вращающегося объекта. Понятно, что вектор $a\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{a\}\}\}$направлен вдоль положительной оси z. Величина r не является радиусом, а скорее неявно определяет как

$x\; 2\; +\; y\; 2\; r\; 2\; +\; a\; 2\; +\; z\; 2\; r\; 2\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{z\; ^\; \{2\}\}\; \{r\; ^\; \{2\}\}\}\; =\; 1\}$

(14)

Обратите внимание, что величина r становится обычным радиусом R

$r\; \to \; R\; =\; x\; 2\; +\; y\; 2\; +\; z\; 2\; \{\backslash \; displaystyle\; r\; \backslash \; to\; R\; =\; \{\backslash \; sqrt\; \{x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\}\; \}\}$

, когда вращения вращается приближается к нулю. В этой форме решения единицы выбраны так, чтобы скорость света была равна единице (c = 1). На больших расстояниях от источника (R>>a) эти уравнения сводятся к форме Эддингтона - Финкельштейна метрики Шварцшильда.

В форме Керра - Шильда метрики Керра детерминант метрического тензораду сравнительному, даже приближенному.

Координаты солитона

Временная метрика Керра (вместе с метрикой) является осесимметричной, ее можно преобразовать в форму, к которой можно применить преобразование Белинского - Захарова. Это означает, что черная дыра Керра имеет формулу гравитационного солитона.

Если полная энергия вращения $E\; rot\; =\; c\; 2\; (M\; -\; M\; irr)\; \{\backslash \; displaystyle\; E\; \_\; \{\; \backslash \; rm\; \{rot\}\}\; =\; c\; ^\; \{2\}\; \backslash \; left\; (MM\; \_\; \{\backslash \; rm\; \{irr\}\}\; \backslash \; right)\}$черная дыры извлекается, например, с помощью Процесс Пенроуза, оставшаяся масса не может уменьшиться ниже неснижаемой массы. Следовательно, если черная дыра вращается со спином $a\; =\; M\; \{\backslash \; displaystyle\; a\; =\; M\}$, ее общий эквивалент массы $M\; \{\backslash \; displaystyle\; M\}$выше в $2\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{2\}\}\}$по форме с черной дырой Шварцшильда, где $M\; \{\backslash \; displaystyle\; M\}$равно $M\; irr\; \{\backslash \; Displaystyle\; M\; \_\; \{\backslash \; rm\; \{irr\}\}\}$. Это в том числе, чтобы заставить статическое вращаться, необходимо приложить энергию к системе. Из-за эквивалент массы и энергии эта энергия также имеет массовый эквивалент, который прибавляется к общей массе-энергии системы, $M\; \{\backslash \; displaystyle\; M\}$.

Общий эквивалент массы $M\; \{\backslash \; displaystyle\; M\}$(включая его гравитирующая масса) тела (включая его гравитирующую массу ) и его несократимую массу $M\; irr\; \{\backslash \; displaystyle\; M\; \_\; \{\backslash \; rm\; \{irr\}\}\}$связаны взаимодействением

$M\; irr\; =\; M\; 4\; -\; J\; 2\; c\; 2\; G\; 2\; +\; M\; 2\; 2\; ⟶\; M\; =\; 2\; M\; irr\; 4\; 4\; M\; irr\; 2\; -\; a\; 2\; c\; 4\; G\; 2.\; \{\backslash \; displaystyle\; M\; \_\; \{\; \backslash \; rm\; \{irr\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\{\backslash \; sqrt\; \{M\; ^\; \{4\}\; -\; \{\backslash \; frac\; \{J\; ^\; \{2\}\; c\; ^\; \{2\}\}\; \{G\; ^\; \{2\})\}\}\}\}\; +\; M\; ^\; \{2\}\}\; \{2\}\}\}\; \backslash \; longrightarrow\; M\; =\; 2\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{M\; \_\; \{\backslash \; rm\; \{irr\}\}\; ^\; \{4\}\}\; \{4M\; \_\; \{\backslash \; rm\; \{irr\}\}\; ^\; \{\; 2\}\; -\; \{\backslash \; frac\; \{a\; ^\; \{2\}\; c\; ^\; \{4\}\}\; \{G\; ^\; \{2\}\}\}\}\}\}.\}$

Даже прямая проверка метрика Керра включает в себя громоздкие вычисления, контравариантные компоненты $gik\; \{\backslash \; displaystyle\; g\; ^\; \{ik\}\}$метрического тензора в координатах Бойера - Линдквиста продемонстрировал ниже в выражении для квадрата четырехградиента оператора :

$g\; \mu \; \nu \; \partial \; \partial \; x\; \mu \; \partial \; \partial \; x\; \nu \; =\; 1\; c\; 2\; \Delta \; (r\; 2\; +\; a\; 2\; +\; rsra\; 2\; \Sigma \; sin\; 2\; \; \theta )\; (\partial \; \partial \; t)\; 2\; +\; 2\; rsrac\; \Sigma \; \Delta \; \partial \; \partial \; \varphi \; \partial \; \partial \; t\; -\; 1\; \Delta \; sin\; 2\; \; \theta \; (1\; -\; rsr\; \Sigma )\; (\partial \; \partial \; \varphi )\; 2\; -\; \Delta \; \Sigma \; (\partial \; \partial \; г)\; 2-1\; \Sigma \; (\partial \; \partial \; \theta )\; 2\; \{\backslash \; displaystyle\; g\; ^\; \{\backslash \; mu\; \backslash \; nu\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; x\; ^\; \{\backslash \; mu\}\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; частичный\; x\; ^\; \{\backslash \; nu\; \}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{c\; ^\; \{2\}\; \backslash \; Delta\}\}\; \backslash \; left\; (r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{r\_\; \{s\}\; ra\; ^\; \{2\}\}\; \{\; \backslash \; Sigma\}\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; t\}\}\; \backslash \; right)\; ^\; \{2\}\; +\; \{\backslash \; frac\; \{2r\_\; \{s\}\; ra\}\; \{\; c\; \backslash \; Sigma\; \backslash \; Delta\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; phi\}\}\; \{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \{t\}\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Delta\; \backslash \; sin\; ^\; \{\; 2\}\; \backslash \; theta\}\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\_\; \{s\}\; r\}\; \{\backslash \; Sigma\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; phi\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{\backslash \; Delta\}\; \{\backslash \; Sigma\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; r\}\}\; \backslash \; right)\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; Sigma\}\; \}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; par\; tial\; \backslash \; theta\}\}\; \backslash \; right)\; ^\; \{2\}\}$

(15)

Мы можем переписать метрику Керра (1) в следующем виде:

$c\; 2\; d\; \tau \; 2\; знак\; равно\; (gtt\; -\; gt\; \varphi \; 2\; g\; \varphi \; \varphi )\; dt\; 2\; +\; grrdr\; 2\; +\; g\; \theta \; \theta \; d\; \theta \; 2\; +\; g\; \varphi \; \varphi \; (d\; \varphi \; +\; gt\; \varphi \; g\; \varphi \; \varphi \; dt)\; 2.\; \{\backslash \; displaystyle\; c\; ^\; \{2\}\; d\; \backslash \; tau\; ^\; \{2\}\; =\; \backslash \; left\; (g\_\; \{tt\}\; -\; \{\backslash \; frac\; \{g\_\; \{t\; \backslash \; phi\}\; ^\; \{2\}\}\; \{g\; \_\; \{\backslash \; phi\; \backslash \; phi\}\}\}\; \backslash \; справа)\; dt\; ^\; \{2\}\; +\; g\_\; \{rr\}\; dr\; ^\; \{2\}\; +\; g\; \_\; \{\backslash \; theta\; \backslash \; theta\}\; d\; \backslash \; theta\; ^\; \{2\}\; +\; g\; \_\; \{\backslash \; phi\; \backslash \; phi\}\; \backslash \; left\; (d\; \backslash \; phi\; +\; \{\backslash \; frac\; \{g\_\; \{t\; \backslash \; phi\})\; \}\; \{g\; \_\; \{\backslash \; phi\; \backslash \; phi\}\}\}\; dt\; \backslash \; right)\; ^\; \{2\}.\}$

(16)

Эта метрика соответствующей вращающейся системы записи, которая вращается с угловой скоростью Ω, которая зависит как от радиуса r, так и от широты θ, где Ω называется горизонтом смерти.

$\Omega \; =\; -\; gt\; \varphi \; g\; \varphi \; \varphi \; =\; rsrac\; \Sigma \; (r\; 2\; +\; а\; 2)\; +\; rsra\; 2\; sin\; 2\; \; \theta .\; \{\backslash \; displaystyle\; \backslash \; Omega\; =\; -\; \{\backslash \; frac\; \{g\_\; \{t\; \backslash \; phi\}\}\; \{g\; \_\; \{\backslash \; phi\; \backslash \; phi\}\}\}\; =\; \{\backslash \; frac\; \{r\_\; \{s\}\; rac\}\; \{\backslash \; Sigma\; \backslash \; left\; (r\; ^\; \{2\; \}\; +\; a\; ^\; \{2\}\; \backslash \; right)\; +\; r\_\; \{s\}\; ra\; ^\; \{2\}\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\}.\}$

(17)

Таким образом, инерциальная система отсчета увлекается вращающейся центральной масса для участия во вращении последней; это называется перетаскиванием кадра и было протестировано экспериментально. Качественно перетаскивание кадра можно рассматривать как гравитационный аналог электромагнитной индукции. «Фигуристка», движущаяся по орбите над экватором и вращающаяся в состоянии покоя относительно, протягивает руки. Рука, протянутая к черной дыре, будет закручена во вращение. Рука, протянутая от черной дыры, будет закручена против вращения. Следовательно, ее вращение будет ускоряться в противоположном направлении по отношению к черной дыре. Это противоположно тому, что происходит в повседневной жизни. Инерционные эффекты и эффекты перетаскивания кадра уравновешиваются, и ее вращение не изменяется. Из-за принципа эквивалентности гравитационные эффекты локально неотличимы от инерционных эффектов, поэтому эта скорость вращения, при которой она разгибает руки, ничего не происходит, ее локальным ориентиром для отсутствия вращения. Эта рамка вращается относительно неподвижных звезд и вращается в противоположных направлениях относительно черной дыры. Полезная метафора - это система планетарной передачи, где черная дыра является солнечной шестерней, фигурист - планетарной шестерней, а внешняя вселенная - кольцевой шестерней. Это также можно интерпретировать через принцип Маха.

Расположение горизонтов, эргосфер и кольцевой сингулярности пространства-времени Керра в декартовых координатах Керра-Шильда. 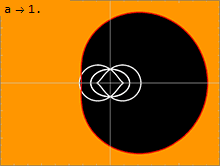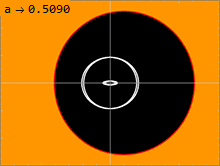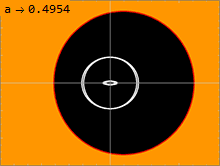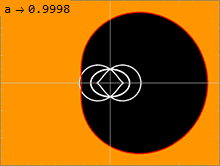Сравнение тени (черный) и важные поверхности (белые) черной дыры. Параметр вращения a изменяется от 0 до M, в то время как левая сторона черной дыры вращается в направлении наблюдателя.

Метрика Керра (1) имеет две физически значимые поверхности, на которых она кажется сингулярной. Внутренняя поверхность соответствует горизонту событий, подобному тому, который наблюдается в метрике Шварцшильда ; это происходит, когда чисто радиальная составляющая g rr метрики стремится к бесконечности. Решение квадратного уравнения ⁄ grr= 0 дает решение:

$r\; H\; \pm \; =\; rs\; \pm \; rs\; 2-4\; a\; 2\; 2\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; rm\; \{H\}\}\; ^\; \{\backslash \; pm\}\; =\; \{\backslash \; frac\; \{\; r\_\; \{s\}\; \backslash \; pm\; \{\backslash \; sqrt\; \{r\_\; \{s\}\; ^\; \{2\}\; -4a\; ^\; \{2\}\}\}\}\; \{2\}\}$

который в натуральных единицах (что дает G = M = c = 1) упрощается до:

$r\; H\; \pm \; =\; 1\; \pm \; 1\; -\; a\; 2\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; rm\; \{H\}\}\; ^\; \{\backslash \; pm\}\; =\; 1\; \backslash \; pm\; \{\backslash \; sqrt\; \{1-a\; ^\; \{2\}\}\}\; \}$

Другая очевидная особенность возникает, когда чисто временной компонент g tt метрики меняет знак с положительного отрицательного. Снова решение квадратного уравнения g tt = 0 дает решение:

$r\; E\; \pm \; =\; rs\; \pm \; rs\; 2-4\; a\; 2\; cos\; 2\; \; \theta \; 2\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; rm\; \{E\}\}\; ^\; \{\backslash \; pm\}\; =\; \{\backslash \; frac\; \{r\_\; \{s\}\; \backslash \; pm\; \{\backslash \; sqrt\; \{r\_\; \{s\}\; ^\; \{2\}\; -4a\; ^\; \{2\}\; \backslash \; cos\; ^\; \{2\}\; \backslash \; theta\}\}\}\; \{2\}\}\}$

или в натуральных единицах:

$r\; E\; \pm \; =\; 1\; \pm \; 1\; -\; a\; 2\; cos\; 2\; \; \theta \; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; rm\; \{E\}\}\; ^\; \{\backslash \; pm\}\; =\; 1\; \backslash \; pm\; \{\backslash \; sqrt\; \{1\; -a\; ^\; \{2\}\; \backslash \; cos\; ^\; \{2\}\; \backslash \; theta\}\}\}$

Из-за члена cosθ в квадратном корне эта внешняя поверхность напоминает сплющенную сферу, которая касается внутренней поверхности на полюсах оси вращения, где ширина θ равна 0 или π; пространство между этими поверхностями называется эргосферой. В этом чисто временная составляющая g tt является отрицательной, то есть действует как чисто внешняя метрическая составляющая. Следовательно, частицы внутри этой эргосферы должны вращаться вместе с внутренней массой, если они хотят сохранить свой временноподобный характер. Движущаяся частица испытывает положительное собственное время вдоль своей мировой линии, свой путь через пространство-время. Это невозможно в пределах эргосферы, где g tt отрицательно, если только частица не вращается вместе с внутренней массой M с угловой скоростью не менее Ω. Таким образом, никакая часть не может вращаться против центральной массы внутри эргосферы.

Как и в случае с горизонтом событий в метрике Шварцшильда, видимые сингулярности в r H и r E являются иллюзиями, созданными выбором координат ( т. е. это координатные особенности ). Фактически, пространство-время может быть плавно продолжено через них другим выбором координат.

Черная дыра в целом окружена поверхностью, называемой горизонтом событий, и содержащей на радиусе Шварцшильда для невращающейся черной дыры, где убегающая скорость равна скорости света. Внутри этой поверхности ни один наблюдатель / частица не может поддерживать постоянный радиус. Он вынужден падать внутрь, поэтому это иногда называют статическим пределом.

Вращающаяся черная дыра имеет такой же статический предел на горизонте событий, но есть дополнительная поверхность за пределами горизонта событий, названная «эргоповерхность», заданная как

$(r\; -\; M)\; 2\; =\; M\; 2\; -\; J\; 2\; соз\; 2\; \; \theta \; \{\backslash \; displaystyle\; (rM)\; ^\; \{2\}\; =\; M\; ^\; \{2\}\; -J\; ^\; \{2\}\; \backslash \; cos\; ^\; \{2\}\; \backslash \; theta\}$

в координатах Бойера - Линдквиста, которую можно интуитивно охарактеризовать как сферу, в которой «скорость вращения окружающего пространства» увлекается вместе со скоростью света. Внутри этой сферы притягивает скорость света.

Область за пределами горизонта событий, но внутри поверхности, где скорость вращения соответствует скорости света, называется эргосферой (от греческого ergon, означающего работу). Частицы, попадающие в эргосферу, вынуждены вращаться быстрее и тем самым приобретать энергию. Они все еще находятся за пределами горизонта событий. Чистый процесс состоит в том, что вращающаяся черная дыра испускает энергичные частицы за счет своей собственной энергии. Возможность извлечения энергии спина из вращающейся черной дыры была впервые предложена математиком Роджером Пенроузом в 1969 году и поэтому называется процесс Пенроуза. Вращающиеся черные дыры в астрофизике являются потенциальным источником большого количества энергии и используются для объяснения энергетических явлений, таких как гамма-всплески.

Геометрия Керра демонстрирует множество примечательные особенности: максимальное аналитическое расширение включает последовательность асимптотически плоских внешних областей, каждая из которых связана с эргосферой, стационарными предельными поверхностями, горизонтами событий, Горизонты Коши, замкнутые времяподобные кривые и кольцевая сингулярность кривизны. Уравнение геодезии может быть решено точно в замкнутой форме.Помимо двух векторных полей Киллинга (соответствующие сдвигу во времени и осесимметрии), геометрия Керра допускает замечательный тензор Киллинга. Существует пара основных нулевых конгруэнций (входящая и исходящая). Тензор Вейля является алгебраически специальным, фактически он имеет тип Петрова D. Глобальная структура известна. Топологически гомотопический тип пространства-времени Керра можно просто охарактеризовать как линию с кружками, прикрепленными к каждой целочисленной точке.

Обратите внимание на то, что внутренняя геометрия Керра нестабильна по отношению к возмущениям во внутренней области. Эта нестабильность означает, что, хотя метрика Керра осесимметрична, черная дыра, созданная в результате гравитационного коллапса, может быть не такой. Эта нестабильность также подразумевает, что многие особенности геометрии Керра, описанной выше, отсутствовать внутри такой черной дыры.

Поверхность, на которой свет может вращаться вокруг черной дыры, называется фотонной сферой. Решение Керра имеет бесконечно много фотонных сфер, лежащих между внутренней и внешней. В невращающемся решении Шварцшильда с a = 0 внутренняя и внешняя фотонные сферы вырождаются, так что существует только одна фотонная сфера с одним радиусом. Чем больше вращение черной дыры, тем дальше друг от друга движутся внутренняя и внешняя фотонные сферы. Луч света, движущийся направление в противоположном вращении черной дыры, будет вращаться вокруг дыры во внешней фотонной сфере. Луч света, движущийся в том же направлении, что и вращение черной дыры, будет вращаться по круговой орбите во внутренней фотонной сфере. Орбитальные геодезические с некоторыми угловым моментом, перпендикулярным вращением черной дыры, будут вращаться на фотонных сферах между этими двумя крайностями. Такие орбиты демонстрируют прецессию, поскольку происходит сдвиг в пространстве $\varphi \; \{\backslash \; displaystyle\; \backslash \; phi\; \backslash ,\}$после завершения одного периода в $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\; \backslash ,\; \}$переменная.

Траекторные уравнения

Анимация орбиты пробной частицы вокруг вращающейся черной дыры. Слева: вид сверху, справа: вид сбоку. Еще одна траектория пробной массы вокруг вращающейся черной дыры (Керра). В отличие от орбиты вокруг черной дыры Шварцшильда, орбита не ограничена одной плоскостью, а эргодически заполняет тороподобную область вокруг экватора.

Уравнения движение для пробных частиц в пространстве времени Керра регулируется четырьмя константами движения. Первый - это инвариантная масса $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$пробной частицы, определяемой использованием

$-\; \mu \; 2\; =\; p\; \alpha \; g\; \alpha \; \beta \; p\; \beta ,\; \{\backslash \; displaystyle\; -\; \backslash \; mu\; ^\; \{2\; \}\; =\; p\; ^\; \{\backslash \; alpha\}\; g\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; p\; ^\; \{\backslash \; beta\},\}$

где $p\; \alpha \; \{\backslash \; displaystyle\; p\; ^\; \{\backslash \; alpha\}\}$- это четырехимпульс частицы. Кроме того, существуют две константы движения, определяемые симметрично сдвига и вращения пространства-времени: энергия $E\; \{\backslash \; displaystyle\; E\}$и составляющая орбитального углового момента, параллельная спину черной дыры $L\; z\; \{\; \backslash \; displaystyle\; L\_\; \{z\}\}$.

$E\; =\; -\; pt\; \{\backslash \; displaystyle\; E\; =\; -p\_\; \{t\}\}$и

$L\; z\; =\; -\; p\; \varphi \; \{\backslash \; displaystyle\; L\_\; \{z\}\; =\; -\; p\; \_\; \{\backslash \; phi\}\}$

Используя теорию Гамильтона - Якоби, Брэндон Картер показал, что существует четвертая постоянная движения, $Q\; \{\backslash \; displaystyle\; Q\}$, теперь обозначается как константа Картера. Он связан с полным угловым моментом частицы и определяется выражением

$Q\; =\; p\; \theta \; 2\; +\; cos\; 2\; \; \theta \; (a\; 2\; (\mu \; 2\; -\; E\; 2)\; +\; (L\; z\; sin\; \; \theta )\; 2)\; \{\backslash \; displaystyle\; Q\; =\; п\; \_\; \{\backslash \; theta\}\; ^\; \{2\}\; +\; \backslash \; cos\; ^\; \{2\}\; \backslash \; theta\; \backslash \; left\; (a\; ^\; \{2\}\; \backslash \; left\; (\backslash \; mu\; ^\; \{2\}\; -E\; ^\; \{2\}\; \backslash \; right)\; +\; \backslash \; left\; (\{\backslash \; frac\; \{L\_\; \{z\}\}\; \{\backslash \; sin\; \backslash \; theta\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right)\}$.

Существуют четыре (независимых) константы движения для степеней свободы, уравнения движения для пробная частица в пространстве-времени Керра интегрируема.

Используя эти константы движения, можно записать уравнения траектории для пробной частицы (с использованием натуральных единиц G = M = c = 1),

$\Sigma \; drd\; \lambda \; =\; \pm \; R\; (r)\; \Sigma \; d\; \theta \; d\; \lambda \; =\; \pm \; \Theta \; (\theta )\; \Sigma \; d\; \varphi \; d\; \lambda \; =\; -\; (a\; E\; -\; L\; z\; sin\; 2\; \; \theta )\; +\; a\; ∆\; P\; (r)\; \Sigma \; dtd\; \lambda \; =\; -\; a\; (a\; E\; грех\; 2\; \; \theta \; -\; LZ)\; +\; р\; 2\; +\; a\; 2\; \Delta \; п\; (г)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; Sigma\; \{\backslash \; frac\; \{dr\}\; \{d\; \backslash \; lambda\}\}\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{R\; (r)\}\}\; \backslash \backslash \backslash \; Sigma\; \{\backslash \; frac\; \{d\; \backslash \; theta\}\; \{d\; \backslash \; lambda\}\}\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{\backslash \; Theta\; (\backslash \; theta)\}\}\; \backslash \backslash \backslash \; Sigma\; \{\backslash \; frac\; \{d\; \backslash \; phi\}\; \{d\; \backslash \; lamb\; da\}\}\; =\; -\; \backslash \; left\; (aE\; -\; \{\backslash \; frac\; \{L\_\; \{z\}\}\; \{\backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{a\}\; \{\backslash \; Delta\}\}\; P\; (r)\; \backslash \backslash \backslash \; Sigma\; \{\backslash \; frac\; \{dt\}\; \{d\; \backslash \; lambda\}\}\; =\; -\; a\; \backslash \; left\; (aE\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\; -L\_\; \{z\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\}\; \{\backslash \; Delta\}\}\; P\; (r)\; \backslash \; end\; \{align\}\}\}$

с

$\Theta \; (\theta )\; =\; Q\; -\; cos\; 2\; \; \theta \; (a\; 2\; (\mu \; 2\; -\; E\; 2)\; +\; L\; z\; 2\; грех\; 2\; \; \theta )\; \{\backslash \; displaystyle\; \backslash \; Theta\; (\backslash \; theta)\; =\; Q-\; \backslash \; cos\; ^\; \{2\}\; \backslash \; theta\; \backslash \; left\; (a\; ^\; \{2\}\; \backslash \; left\; (\backslash \; mu\; ^\; \{2\}\; -E\; ^\; \{2\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{L\_\; \{z\}\; ^\; \{2\}\}\; \{\backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\}\; \backslash \; right)\}$

$P\; (г)\; знак\; равно\; Е\; (р\; 2\; +\; a\; 2)\; -\; a\; L\; z\; \{\backslash \; displaystyle\; P\; (r)\; =\; E\; \backslash \; left\; (r\; ^\; \{2\}\; +\; a\; ^\; \{2\}\; \backslash \; right)\; -aL\_\; \{z\}\}$

$Р\; (г)\; знак\; равно\; п\; (г)\; 2\; -\; \Delta \; (\mu \; 2\; р\; 2\; +\; (LZ\; -\; а\; Е)\; 2\; +\; Q)\; \{\backslash \; Displaystyle\; R\; (г)\; =\; P\; (г)\; ^\; \{2\}\; -\; \backslash \; Delta\; \backslash \; left\; (\backslash \; mu\; ^\; \{2\}\; r\; ^\; \{2\}\; +\; (L\_\; \{z\}\; -aE)\; ^\; \{2\}\; +\; Q\; \backslash \; right)\}$

Где, $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$- это аффинный параметр такой, что $dx\; \alpha \; d\; \lambda \; =\; p\; \alpha \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dx\; ^\; \{\backslash \; alpha\}\}\; \{d\; \backslash \; lambda\}\}\; =\; p\; ^\; \{\backslash \; альфа\}\}$. В частности, когда $\mu >0\; \{\backslash \; displaystyle\; \backslash \; mu>0\}$аффинный параметр $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, связанный с данным временем $\backslash \; displaystyle\; tau\; 386>-$ \lambda \; =\; \tau \; /\; \mu \; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; \backslash \; tau\; /\; \backslash \; mu\}$$.

Из-за эффекта перетаскивания кадра нулевой Наблюдатель углового момента (ZAMO) вращается с угловой скоростью $\Omega \; \{\backslash \; Displaystyle\; \backslash \; Omega\}$, которая определяет относительно координатного времени бухгалтера $t\; \{\backslash \; displaystyle\; t\}$.альная скорость $v\; \{\backslash \; displaystyle\; v\}$тестовая частицы измеряется относительно зонда вращающегося с $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$. Гравитационное замедление времени между ZAMO при фиксированном $r\; \{\backslash \; displaystyle\; r\}$и неподвижным наблюдателем вдали от массы составляет

$T\; \tau \; знак\; равно\; (a\; 2\; +\; r\; 2)\; 2\; -\; a\; 2\; \Delta \; sin\; 2\; \; \theta \; \Delta \; \Sigma \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{t\}\; \{\backslash \; tau\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; left\; (a\; ^\; \{2\}\; +\; r\; ^\; \{2\}\; \backslash \; right)\; ^\; \{2\}\; -a\; ^\; \{2\}\; \backslash \; Delta\; \backslash \; sin\; ^\; \{2\}\; \backslash \; theta\}\; \{\backslash \; Delta\; \backslash \; \backslash \; Sigma\}\}\}\}$.

Группа изометрии метрики Керра - это подгруппа десятимерной группы Пуанкаре, которая переводит двумерное геометрическое место особенности в себя. Он сохраняет перевод времени (одно измерение) и вращения вокруг своей оси (одно измерение). Таким образом, он имеет два измерения. Как и группа Пуанкаре, она имеет четыре компонента связности: компонент тождества; компонент, меняющий местами время и долготу; компонент, отражающийся через экваториальную плоскость; и компонент, который делает и то, и другое.

В физике симметрии обычно связаны с сохраняющимися постоянными движениями в соответствии с теоремой Нётер. Как показано выше, уравнения геодезических четырех сохраняющихся величин: одна из которых формируются из симметрии сдвига во времени и вращения геометрии Керра. Четвертая сохраняющаяся величина не возникает из-за симметрии в стандартном смысле и обычно называется скрытой симметрией.

Местоположение горизонта событий определяется большим корнем из $\Delta \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; Delta\; =\; 0\}$. Когда (то есть ), для этого уравнения нет (действующих) решений и нет горизонта событий. Без горизонтов событий, которые могли бы скрыть ее от остальной Вселенной, черная дыра перестала быть черной дырой и вместо этого будет голой сингулярностью.

Хотя Керровский решение кажется сингулярным в корнях Δ = 0, это фактически координатные особенности, и при соответствующем выборе новых координатных решений Керра может быть плавно расширено до значений $r\; \{\backslash \; displaystyle\; r\}$, соответствующих этим корням. Более крупный из этих корней определить местоположение горизонта событий, а меньший - местоположение горизонта Коши. Кривая (направленная в будущее, похожая на время) может начинаться снаружи и проходить через горизонт событий. После прохождения горизонта событий координата $r\; \{\backslash \; displaystyle\; r\}$теперь ведет себя как координата времени, поэтому она должна уменьшаться, пока кривая не пройдет через горизонт Коши.

Область за горизонтом Коши имеет несколько удивительных возможностей. Координата $r\; \{\backslash \; displaystyle\; r\}$снова ведет себя как пространственная координата и может свободно меняться. Внутренняя область имеет симметрию отражения, так что кривая (направленная в будущее, похожая на время) может продолжаться по симметричному пути, который продолжается через второй горизонт Коши, через второй горизонт событий и выходит в новую внешнюю область, которая является изометрична внешней области решения Керра. Затем кривая может войти в будущий горизонт событий новой области и повторить процесс. Этот второй внешний вид иногда воспринимается как другая вселенная. С другой стороны, в решении Керра особенность - это кольцо , и кривая может проходить через центр этого кольца. Область за пределами допускает замкнутые временные кривые. Наблюдатели в этой области. Это внутреннее решение вряд ли будет физическим и будет рассматривать как чисто математический артефакт.

Хотя ожидается, что все вращающиеся черные дыры в конечном итоге подходят к метрике Керра. внутренняя область раствор кажется нестабильной, как карандаш, балансирующий на острие. Это связано с идеей космической цензуры.

Геометрия является частным примером стационарного вакуумного решения к уравнению поля Эйнштейна. Семейство всех стационарных осесимметричных вакуумных решений уравнения поля Эйнштейна - это.

Решение связано с различными невакуумными решениями, которые моделируют черные дыры. Например, электровакуум Керра - Ньюмана моделирует (вращается) черную дыру, наделенную электрический заряд, в то время как моделирует (вращающуюся) дыру с падающим электромагнитным излучением.

Особый случай $a\; =\; 0\; \{\backslash \; displaystyle\; a\; =\; 0\}$метрики Керра дает метрику Шварцшильда, которая моделирует невращающуюся черную дыру, которая является статическим и сферически симметричным в координатах Шварцшильда. (В этом случае каждый момент Героха, кроме массы, равенство нулю.)

Внутренняя часть геометрии Керра, или, скорее, ее часть, является примером модели. Это особенно интересно, потому что глобальная структура этого решения CPW сильно отличается от структуры геометрии Керра, и в принципе экспериментатор мог бы надеяться изучить геометрию (внешнюю часть) Керровской внутренней части путем организации столкновения двух подходящих гравитационных плоские волны.

Каждый асимптотически плоский вакуум Эрнста можно охарактеризовать, дав бесконечную последовательность релятивистских мультипольных моментов, первые два из которых могут быть интерпретируется как масса и угловой момент источника поля. Существуют альтернативные формулировки релятивистских мультипольных моментов Хансена, Торна и Героха, которые, как оказалось, согласуются друг с другом. Релятивистские мультипольные моменты геометрии Керра были вычислены Хансеном; они оказываются равными

$M\; n\; =\; M\; [ia]\; n\; \{\backslash \; displaystyle\; M\_\; \{n\}\; =\; M\; [ia]\; ^\; \{n\}\}$

Таким образом, частный случай вакуума Шварцшильда (a = 0) дает "монополь точечный источник " общей теории относительности.

Мультипольные моменты Вейля возникают из-за обработки определенной метрической функции (формально соответствующей ньютоновскому гравитационному потенциалу), которая выглядит как Диаграмма Вейля-Папапетру для семейства Эрнста всех стационарных осесимметричных вакуумных решений с использованием стандартного евклидова скаляра мультипольных моментов. Они отличаются от моментов, вычисленных Хансеном выше. В некотором смысле моменты Вейля лишь (косвенно) характеризуют «массовое распределение» изолированного источника и, как оказывается, зависят только от релятивистских моментов четного порядка. В случае решений, симметричных относительно экваториальной плоскости, моменты Вейля нечетного порядка обращаются в нуль. Для вакуумных решений Керра первые несколько моментов Вейля задаются как

$a\; 0\; =\; M,\; a\; 1\; =\; 0,\; a\; 2\; =\; M\; (M\; 2\; 3\; -\; a\; 2)\; \{\backslash \; displaystyle\; a\_\; \{0\}\; =\; M,\; \backslash \; qquad\; a\_\; \{1\}\; =\; 0,\; \backslash \; qquad\; a\_\; \{2\}\; =\; M\; \backslash \; left\; (\{\backslash \; frac\; \{M\; ^\; \{2\}\}\; \{3\}\}\; -\; a\; ^\; \{2\}\; \backslash \; right)\}$

В частности, мы Видно, что вакуум Шварцшильда имеет ненулевой момент Вейля второго порядка, соответствующий тому факту, что решением является «монополь Вейля», а не вакуумное решение Шварцшильда, которое возникает из ньютоновского потенциала определенного тонкого стержня с однородной плотностью конечной длины.

В общей теории относительности слабого поля удобно рассматривать изолированные источники с помощью другого типа мультиполей, которые обобщают моменты Вейля на массовые мультипольные моменты и импульсные мультипольные моменты, характеризующие, соответственно, распределение масса и импульса источника. Это многоиндексированные величины, чьи соответственно симметризованные и антисимметризованные части могут быть довольно сложным образом связаны с действительной и мнимой частями релятивистских моментов для полной нелинейной теории.

Перес и Морески дали альтернативное понятие «монопольных решений», расширив стандартную тетраду NP вакуума Эрнста по степеням r (радиальная координата в диаграмме Вейля-Папапетру). Согласно этой формулировке:

• изолированный массовый монопольный источник с нулевым угловым моментом представляет собой семейство вакуума Шварцшильда (один параметр),
• изолированный массовый монопольный источник с радиальным угловым моментом представляет собой семейство вакуума Тауба - NUT (два элемента; не совсем асимптотически плоский),
• изолированный монопольный источник с осевым угловым моментом является семейством вакуума Керра (два параметра).

В этом смысле вакуумы являются простейшими стационарными осесимметричными асимптотически плоскими вакуумными решениями в общей теории относительности.

Геометрия Керра используется как модель вращающейся черной дыры. Но если мы будем считать решение действительным только за некоторой некоторой компактной области (с некоторыми ограничениями), в принципе мы будем иметь возможность использовать его как модель гравитационного поля вокруг вращающегося массивного объекта, отличного от черной дыры, такого как нейтронная звезда или Земля. Это очень хорошо работает для невращающегося случая, когда мы согласовываем внешний вид вакуума Шварцшильда с интерьером и действительно с более общими статическими сферически симметричными идеальными жидкостными решениями. Проблема поиска вращающегося внутреннего пространства с идеальным внешним решением оказалась очень сложной. В частности, жидкость Уолквиста, когда-то считалась кандидатом на внешнему виду Керра, теперь, как известно, не допускает такого соответствия. Моделирующие медленно вращающиеся жидкие шары. (Медленно вращающиеся жидкие шары являются релятивистским аналогом сплюснутых сфероидальных шаров с ненулевой массой и угловым моментом, но исчезающими высшими мультипольными моментами.) Внешняя поверхность точного пылевого раствора, моделирующего вращающийся тонкий диск, приближается в предельном случае к $GM\; 2\; =\; c\; J\; \{\backslash \; displaystyle\; GM\; ^\; \{2\}\; =\; cJ\}$геометрии Керра. Известны решения в виде физических тонких дисков, полученные путем идентификации частей пространства-времени Керра.

• Метрика Шварцшильда
• Метрика Керра - Ньюмана
• Метрика Рейсснера - Нордстрема
• Вращение -flip
• Пространство-время Керра - Шильда
• Вращающаяся черная дыра

Дополнительная литература

• Wiltshire, David L.; Виссер, Мэтт; Скотт, Сьюзен М., ред. (2009). Пространство-время Керра: вращающиеся черные дыры в общей теории относительности. Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-88512-6.
• Стефани, Ханс; Крамер, Дитрих; Маккаллум, Малькольм; Хенселаерс, Корнелиус; Герлт, Эдуард (2003). Точные решения поля Эйнштейна. Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-46136-8.
• Майнель, Рейнхард ; Ансорг, Маркус; Кляйнвахтер, Андреас; Нойгебауэр, Гернот; Петров, Давид (2008). Релятивистские фигуры равновесия. Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-86383-4.
• О'Нил, Барретт (1995). Геометрия керровских черных дыр. Уэлсли, Массачусетс: А. К. Петерс. ISBN 978-1-56881-019-5.
• Д'Инверно, Рэй (1992). Введение в теорию относительности Эйнштейна. Оксфорд: Clarendon Press. ISBN 978-0-19-859686-8.См. Главу 19 для удобного использования на продвинутом уровне бакалавриата.
• Чандрасекхар, С. (1992). Математическая теория черных дыр. Оксфорд: Clarendon Press. ISBN 978-0-19-850370-5.См. Главы 6-10 для очень тщательного изучения на уровне продвинутых выпускников.
• Гриффитс, Дж. Б. (1991). Встречающиеся плоские волны в общей теории относительности. Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-853209-5.См. Главу 13 для модели Чандрасекара Феррари CPW.
• Адлер, Рональд; Базен, Морис; Шиффер, Менахем (1975). Введение в общую теорию относительности (Второе изд.). Нью-Йорк: Макгроу-Хилл. ISBN 978-0-07-000423-8.См. Главу 7.
• Пенроуз Р. (1968). под ред. К. де Витта и Дж. Уиллера (ред.). Battelle Rencontres. В. А. Бенджамин, Нью-Йорк. п. 222.
• Перес, Алехандро; Морески, Освальдо М. (2000). «Характеризация точных решений из асимптотических физических понятий». arXiv : gr-qc / 0012100v1.Характеристика трех стандартных семейств вакуумных растворов, как указано выше.
• Сотириу, Томас П.; Апостолатос, Теохарис А. (2004). "Поправки и комментарии к мультипольным момента осесимметричного электровакуумного пространства-времени". Класс. Квантовая гравитация. 21 (24): 5727–5733. arXiv : gr-qc / 0407064. Bibcode : 2004CQGra..21.5727S. doi : 10.1088 / 0264-9381 / 21/24/003.Дает релятивистские мультипольные моменты для вакуума Эрнста (плюс электромагнитные и гравитационные релятивистские мультипольные моменты для заряженного обобщения).
• Картер, Б. (1971). «Осесимметричная черная дыра имеет только две степени свободы». Письма с физическим обзором. 26 (6): 331–333. Bibcode : 1971PhRvL.. 26..331C. doi : 10.1103 / PhysRevLett.26.331.
• Уолд, Р. М. (1984). Общая теория относительности. Чикаго: Издательство Чикагского университета. С. 312–324. ISBN 978-0-226-87032-8.
• Керр, Р.П.; Шильд, А. (2009). «Републикация: новый класс вакуумных решений поля Эйнштейна». Общая теория относительности и гравитации. 41 (10): 2485–2499. Bibcode : 2009GReGr..41.2485K. doi : 10.1007 / s10714-009-0857-z.
• Красиньски, Анджей; Вердагер, Энрик; Керр, Рой Патрик (2009). "От редакции: Р. П. Керру и А. Шильду, Новый класс вакуумных решений поля Эйнштейна". Общая теория относительности и гравитации. 41 (10): 2469–2484. Bibcode : 2009GReGr..41.2469K. doi : 10.1007 / s10714-009-0856-0.«… Эта заметка предназначена для тех читателей, которые хотят проверить все детали [происхождения Керра решение]…»