инвариантная масса, масса покоя, собственная масса, собственная масса, или, в случае связанных систем, просто масса, - часть общей массы объекта . ect или system объектов, которые не зависят от общего движения системы. Точнее, это характеристика полной энергии и импульса системы, которая одинакова во всех системах отсчета, связанных с помощью преобразований Лоренца. Если для системы существует система отсчета центра импульсов, то инвариантная масса системы равна ее полной массе в этой «системе покоя». В других системах отсчета, где импульс системы отличен от нуля, полная масса (также известная как релятивистская масса ) системы больше, чем инвариантная масса, но инвариантная масса остается неизменной.
Из-за эквивалентности массы и энергии, энергия покоя системы - это просто инвариантная масса, умноженная на скорость света в квадрате. Точно так же полная энергия системы равна ее полной (релятивистской) массе, умноженной на квадрат скорости света.
Системы, у которых четырехимпульс является нулевым вектором (например, один фотон или несколько фотонов, движущихся в одном и том же направлении), имеют ноль инвариантной массы, и называются безмассовыми. Физический объект или частица, движущиеся быстрее скорости света, имели бы пространственно-подобные четыре импульса (такие как гипотетический тахион ), а они, похоже, не существуют. Любой подобный времени четырехимпульс обладает системой отсчета, в которой импульс (3-мерный) равен нулю, которая является центром системы отсчета количества движения. В этом случае инвариантная масса положительна и называется массой покоя.
Если объекты в системе находятся в относительном движении, то инвариантная масса всей системы будет отличаться от суммы масс покоя объектов. Это также равно полной энергии системы, деленной на c. См. эквивалентность массы и энергии для обсуждения определений массы. Поскольку масса систем должна быть измерена с помощью весов или весов в системе координат центра импульса, в которой вся система имеет нулевой импульс, такая шкала всегда измеряет инвариантную массу системы. Например, весы будут измерять кинетическую энергию молекул в баллоне с газом как часть инвариантной массы баллона и, следовательно, также его массу покоя. То же самое верно и для безмассовых частиц в такой системе, которые добавляют инвариантную массу, а также массу покоя системам в соответствии с их энергией.
Для изолированной массивной системы центр масс системы движется по прямой с постоянной субсветовой скоростью (со скоростью, зависящей от опорный кадр, используемый для его просмотра). Таким образом, всегда можно разместить наблюдателя, чтобы он двигался вместе с ним. В этой системе отсчета, которая является системой отсчета центра импульса, полный импульс равен нулю, и систему в целом можно рассматривать как «покоящуюся», если это связанная система (например, баллон с газом). В этой системе отсчета, которая существует при этих предположениях, инвариантная масса системы равна полной энергии системы (в системе отсчета без импульса), деленной на c. Эта полная энергия в центре системы отсчета импульса является минимальной энергией, которую система может иметь при наблюдении различными наблюдателями из различных инерциальных систем отсчета.
Обратите внимание, что по причинам, указанным выше, такая система покоя не существует для одиночных фотонов или лучей света, движущихся в одном направлении. Однако, когда два или более фотона движутся в разных направлениях, существует система центра масс (или «система покоя», если система связана). Таким образом, масса системы из нескольких фотонов, движущихся в разных направлениях, положительна, что означает, что для этой системы существует инвариантная масса, даже если она не существует для каждого фотона.
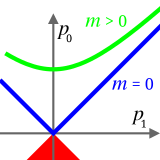 Возможные 4-импульсы частиц. Один имеет нулевую инвариантную массу, другой массивен
Возможные 4-импульсы частиц. Один имеет нулевую инвариантную массу, другой массивен Инвариантная масса системы включает в себя массу любой кинетической энергии составляющих системы, которая остается в системе отсчета центра импульса, поэтому инвариантная масса системы может быть больше, чем сумма инвариантных масс (масс покоя) ее отдельных составляющих.. Например, масса покоя и инвариантная масса равны нулю для отдельных фотонов, даже если они могут добавлять массу к инвариантной массе систем. По этой причине инвариантная масса, как правило, не является аддитивной величиной (хотя есть несколько редких ситуаций, когда это может быть, как в случае, когда массивные частицы в системе без потенциальной или кинетической энергии могут быть добавлены к общей массе).
Рассмотрим простой случай системы двух тел, когда объект A движется к другому объекту B, который изначально находится в состоянии покоя (в любой конкретной системе отсчета). Величина инвариантной массы этой системы двух тел (см. Определение ниже) отличается от суммы масс покоя (то есть их соответствующих масс в неподвижном состоянии). Даже если мы рассмотрим ту же систему в системе отсчета центра импульса, где чистый импульс равен нулю, величина инвариантной массы системы не равна сумме масс покоя частиц внутри нее.
Кинетическая энергия таких частиц и потенциальная энергия силовых полей увеличивают общую энергию сверх суммы масс покоя частиц, и оба члена вносят вклад в инвариантную массу системы. Сумма кинетических энергий частиц, вычисленная наблюдателем, является наименьшей в центре системы отсчета импульса (также называемой «системой покоя», если система связана).
Они также часто взаимодействуют посредством одной или нескольких фундаментальных сил, давая им потенциальную энергию взаимодействия, возможно отрицательную.
Для изолированной массивной системы центр массы движется по прямой линии с постоянной субсветовой скоростью. Таким образом, всегда можно разместить наблюдателя, чтобы он двигался вместе с ним. В этом кадре, который является центром импульса кадра, общий импульс равен нулю, и систему в целом можно рассматривать как "покоящуюся", если это связанная система (например, бутылка газа). В этой системе отсчета, которая существует всегда, инвариантная масса системы равна полной энергии системы (в системе отсчета без импульса), деленной на c.
В физике элементарных частиц, инвариантная масса m0равна массе в остальном кадра частицы, и может быть вычислено с помощью энергии E частицы и ее импульса p, измеренных в любой системе отсчета, с помощью соотношения энергия-импульс :

или в натуральных единицах, где c = 1,

Эта инвариантная масса одинакова во всех системы отсчета (см. также специальная теория относительности ). Это уравнение говорит, что инвариантная масса - это псевдоевклидова длина четырехвектора (E, p ), вычисленная с использованием релятивистской версии теоремы Пифагора который имеет другой знак для измерений пространства и времени. Эта длина сохраняется при любом увеличении Лоренца или вращении в четырех измерениях, точно так же, как обычная длина вектора сохраняется при вращениях. В квантовой теории инвариантная масса - это параметр в релятивистском уравнении Дирака для элементарной частицы. Квантовый оператор Дирака соответствует вектору четырех импульсов частицы.
Поскольку инвариантная масса определяется из величин, которые сохраняются во время распада, инвариантная масса, вычисляемая с использованием энергии и импульса продуктов распада отдельной частицы, равна массе распавшейся частицы. Массу системы частиц можно рассчитать по общей формуле:

где
 - инвариантная масса системы частиц, равная массе распадающейся частицы.
- инвариантная масса системы частиц, равная массе распадающейся частицы. - сумма энергий частиц
- сумма энергий частиц представляет собой векторную сумму импульса частиц (включает как величину, так и направление импульсов)
представляет собой векторную сумму импульса частиц (включает как величину, так и направление импульсов)Термин инвариантная масса также используется в экспериментах по неупругому рассеянию. Учитывая неупругую реакцию с полной поступающей энергией, превышающей полную зарегистрированную энергию (т. Е. Не все исходящие частицы обнаруживаются в эксперименте), инвариантная масса (также известная как «недостающая масса») W реакции определяется следующим образом (в натуральные единицы):

Если есть одна доминирующая частица, которая не была обнаружена во время В эксперименте график инвариантной массы покажет резкий пик массы пропущенной частицы.
В тех случаях, когда невозможно измерить импульс в одном направлении (например, в случае нейтрино, присутствие которого определяется только из недостающей энергии ) Поперечная масса используется.
При столкновении двух частиц (или распаде двух частиц) квадрат инвариантной массы (в натуральных единицах ) равен
 |  |
 |
Инвариантная масса системы, состоящей из двух безмассовых частиц, импульсы которых образуют угол 
 |  |
![= [(p_ {1}, 0,0, p_ {1}) + (p_ {2 }, 0, p_ {2} \ sin \ theta, p_ {2} \ cos \ theta)] ^ {2} = (p_ {1} + p_ {2}) ^ {2} -p_ {2} ^ { 2} \ sin ^ {2} \ theta - (p_ {1} + p_ {2} \ cos \ theta) ^ {2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa5d86c424abef404ae001bc7e053c9bc15e67f0) | |
 |
В экспериментах с коллайдером частиц часто определяют угловое положение частицы в терминах азимутальный угол 



 |  |
энергия покоя 
 ,
,где 
Концепция энергии покоя следует из специальной теории относительности, которая приводит к знаменитому выводу Эйнштейна об эквивалентности энергии и массы. См. фон для эквивалентности массы и энергии.
С другой стороны, концепция эквивалентной инвариантной массы покоя Дирака может быть определена в терминах собственной энергии, соответствующей произведению геометрического тока материи и обобщенного потенциала как части единое определение массы в геометрической единой теории.