| Правильный семиугольник | |
|---|---|
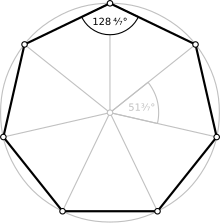 Правильный семиугольник Правильный семиугольник | |
| Тип | Правильный многоугольник |
| Края и вершины | 7 |
| символ Шлефли | {7} |
| диаграмма Кокстера | |
| группа симметрии | двугранный (D7), порядок 2 × 7 |
| внутренний угол (градусы ) | ≈128,571 ° |
| Двойной многоугольник | Собственный |
| Свойства | Выпуклый, циклический, равносторонний, изогональный, изотоксальный |
В геометрии семиугольник представляет собой семигранный многоугольник или 7-угольник.
Гептагон иногда называют септагоном, используя «септ-» (elision из septua-, латинское -производный числовой префикс, а не гепта-, числовой префикс , производный от греческого ; оба являются родственными) вместе с греческим суффиксом «-агон», что означает угол.
A правильный семиугольник, в котором все стороны и все углы равны, имеет внутренние углы 5π / 7 радиан (128 ⁄ 7градусов ). Его символ Шлефли - {7}.
Площадь (A) правильного семиугольника с длиной стороны a определяется как:

Это видно разделив семиугольник с единичными сторонами на семь треугольных «кусочков пирога» с вершинами в центре и в вершинах семиугольника, а затем разделив пополам каждый треугольник, используя апофему в качестве общей стороны. Апофема составляет половину котангенса 
Точное алгебраическое выражение, начиная с кубического многочлена 8x + 4x - 4x - 1 (один из корней равен 
![{\ displaystyle A = {\ frac {a ^ {2}} {4}} {\ sqrt {{\ frac {7} {3}} \ left (35 + 2 {\ sqrt [{ 3}] {196}} \ left ({\ sqrt [{3}] {13-3i {\ sqrt {3}}}} + {\ sqrt [{3}] {13 + 3i {\ sqrt {3}) }}} \ right) \ right)}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee4a0e485c1fd2ddbeb7141f8eef064a997f70e5)
в котором мнимые части смещают друг друга, оставляя выражение с действительным знаком. Это выражение нельзя алгебраически переписать без сложных компонентов, поскольку указанная кубическая функция есть casus unducibilis.
Площадь правильного семиугольника , вписанного в круг радиус R равен 

Поскольку 7 - это Pierpont простое число, но не простое число Ферма, правильный семиугольник не построим с циркулем и линейкой, но можно построить с помеченной линейкой и компас. Это самый маленький правильный многоугольник с этим свойством. Этот тип конструкции называется конструкцией neusis. Его также можно построить с помощью циркуля, линейки и трисектора угла. Невозможность построения линейки и циркуля следует из наблюдения, что 
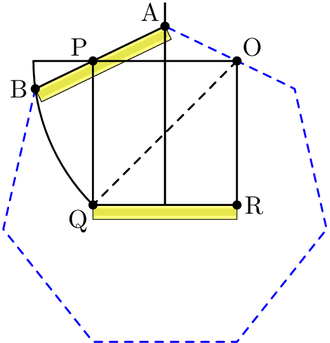 . Построение внутреннего угла в правильном семиугольнике неусисом. . Построение внутреннего угла в правильном семиугольнике неусисом. | 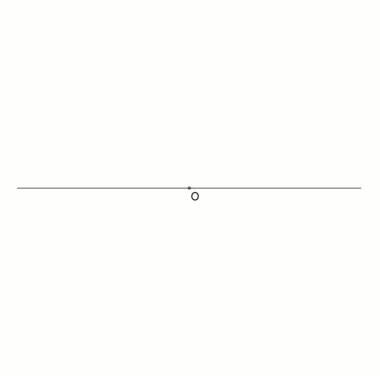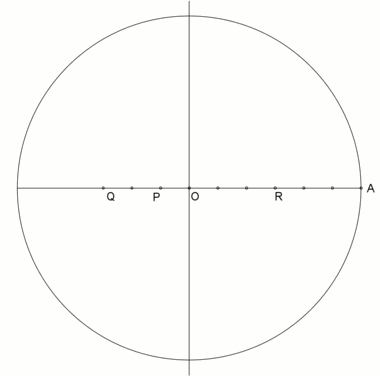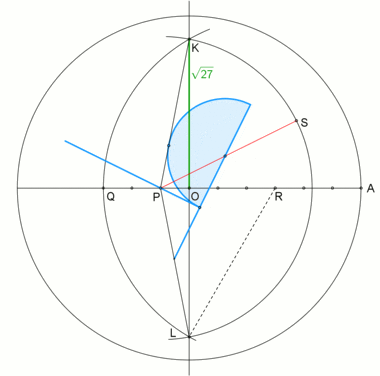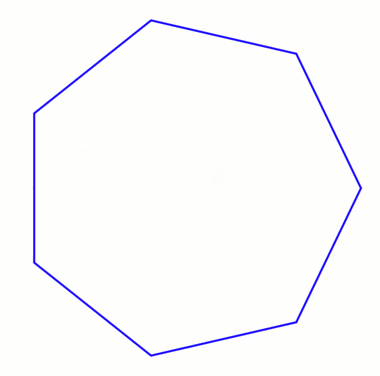 . Анимация из конструкции neusis с радиусом описанной окружности . Анимация из конструкции neusis с радиусом описанной окружности  , согласно Эндрю М. Глисон на основе трисекции угла с помощью Tomahawk. Эта конструкция основана на том факте, что , согласно Эндрю М. Глисон на основе трисекции угла с помощью Tomahawk. Эта конструкция основана на том факте, что |
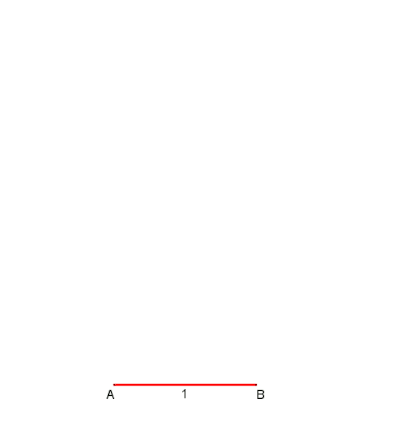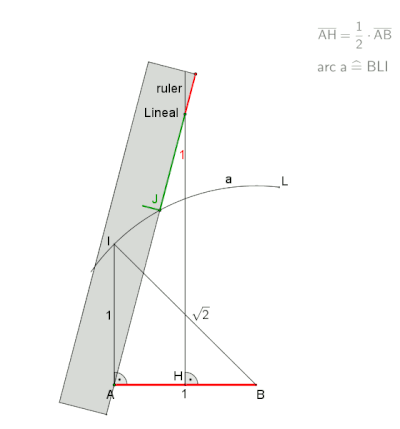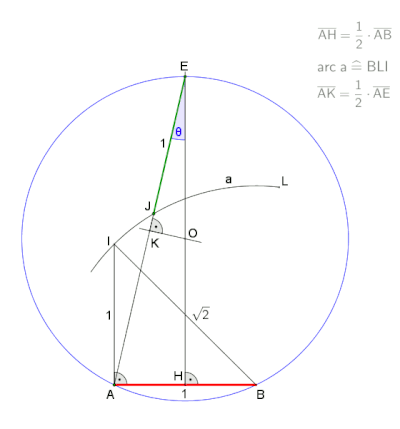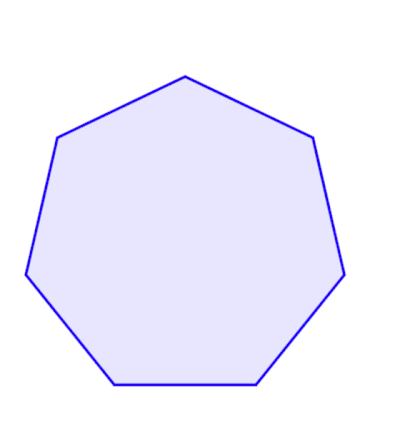 Гептагон с заданной длиной стороны:. Анимация из конструкции neusis с отмеченной линейкой, согласно Дэвиду Джонсону Лейску (Крокетт Джонсон ), пауза в конце 30 с.
Гептагон с заданной длиной стороны:. Анимация из конструкции neusis с отмеченной линейкой, согласно Дэвиду Джонсону Лейску (Крокетт Джонсон ), пауза в конце 30 с. .
Джерард 'т Хофт показывает правильный семиугольник, состоящий всего из 15 полосок Meccano с размером стержней 8 и 11.
 Meccano семиугольник 2
Meccano семиугольник 2 Конструкция включает два равнобедренных треугольника, которые удерживают остальные стержни неподвижно. Сторона правильного семиугольника a, сторона более короткого равнобедренного треугольника e и сторона более длинного равнобедренного треугольника d удовлетворяют условию


Формула получена из этой формулы шестиугольного треугольника :

Небольшие возможные конструкции семиугольника:
| Heptagon | a | d | e |
|---|---|---|---|
| 1 | 3 | 4 | 1 |
| 2 | 8 | 11 | 6 |
| 3 | 33 | 46 | 29 |
| 4 | 40 | 53 | 6 |
| 5 | 55 | 74 | 27 |
Наименьший семиугольник меккано 1: 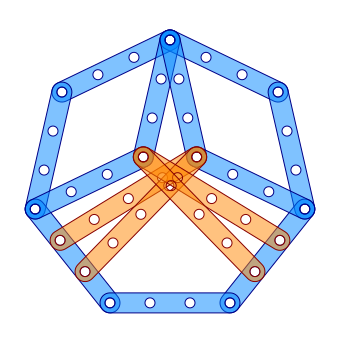
.
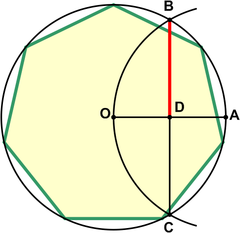
На чертеже показано приближение для практического использования с погрешностью около 0,2%. to Альбрехт Дюрер. Пусть A лежит на окружности описанной окружности. Нарисуйте дугу BOC. Тогда 
В этом приближении используется 

Пример для иллюстрации ошибки:. При радиусе описанной окружности r = 1 м абсолютная погрешность 1-й стороны будет приблизительно -1,7 мм
 семиугольник, аппроксимированный по методу Меккано. Размеры стержней - 20, 36 и 45.
семиугольник, аппроксимированный по методу Меккано. Размеры стержней - 20, 36 и 45. Конструкция аппроксимации механики может быть построена с одиннадцатью стержнями размером 20, 36 и 45. Эти значения оставляют ошибку около 0,1%..
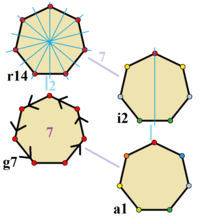 Симметрия правильного семиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. Порядок вращения дан в центре.
Симметрия правильного семиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. Порядок вращения дан в центре. Правильный семиугольник принадлежит D7h точечной группе (нотация Шенфлиса ), порядок 28. Элементами симметрии являются: 7-кратное собственное вращение ось C 7, 7-кратная ось неправильного вращения, S 7, 7 вертикальных зеркальных плоскостей, σ v, 7 2-кратных осей вращения, C 2, в плоскости семиугольника и горизонтальной зеркальной плоскости, σ h, также в плоскости семиугольника.
.
 a = красный, b = синий, c = зеленые линии
a = красный, b = синий, c = зеленые линии Сторона правильного семиугольника a, более короткая диагональ b и более длинная диагональ c, причем a и, следовательно, и Таким образом, –b / c, c / a и a / b все удовлетворяют кубическое уравнение Приблизительные длины диагоналей в терминах стороны правильного семиугольника равны У нас также есть и A семиугольный треугольник имеет вершин, совпадающих с первой, второй и четвертой вершинами правильного семиугольника (от произвольной начальной вершины), и углы Два типа звездных семиугольников (гептаграммы ) можно построить из правильных семиугольников, помеченных символами Шлефли {7/2} и {7/3}, причем делитель интервал подключения. В настоящее время (2020 г.) Соединенное Королевство имеет две семиугольные монеты , 50 пенсов и 20 пенсов. штук, и барбадосский доллар также семиугольные. В монете номиналом 20 евроцентов углубления размещены аналогично. Строго говоря, форма монет представляет собой семиугольник Рело, криволинейный семиугольник, чтобы сделать их кривыми постоянной ширины : стороны изогнуты наружу, так что монета будет плавно катиться при установке в торговый автомат . Пула Ботсваны монеты достоинством 2 Пула, 1 Пула, 50 Фив и 5 Фив также имеют форму семиугольника равносторонней кривой. Монеты в форме семиугольника Рило также находятся в обращении на Маврикии, ОАЭ, Танзании, Самоа, Папуа-Новой Гвинее, Сан-Томе и Принсипи, Гаити, Ямайке, Либерии, Гане, Гамбии, Иордании, Джерси, Гернси, острове Мэн, Гибралтар, Гайана, Соломоновы острова, Фолклендские острова и остров Святой Елены. Монета Замбии в 1000 квач представляет собой настоящий семиугольник. Монета Бразилия 25 центов имеет семиугольник, начертанный на диске монеты. В некоторых старых версиях герба Грузии, в том числе в советские времена, в качестве элемента использовалась гептаграмма {7/2}. В архитектуре семиугольные планы этажей встречаются очень редко. Замечательный пример - Мавзолей принца Эрнста в Штадтхагене, Германия. Многие полицейские значки в США имеют контур гептаграммы {7/2}. За исключением семиугольной призмы и семиугольной антипризмы, ни один выпуклый многогранник, полностью состоящий из правильных многоугольников, не содержит семиугольника в качестве грани. Обычные семиугольники могут перекрывать гиперболическую плоскость, как показано в этой проекции модели диска Пуанкаре : K 7полный граф часто рисуется как правильный семиугольник со всеми 21 ребром, соединенным. Этот граф также представляет собой ортогональную проекцию 7 вершин и 21 ребра 6-симплекса. правильный косой многоугольник по периметру называется многоугольник Петри.


 . Синие, {7/2} и зеленые {7/3} звездные семиугольники внутри красного семиугольника.
. Синие, {7/2} и зеленые {7/3} звездные семиугольники внутри красного семиугольника. Задача геометрии поверхности семиугольника, разделенного на треугольники, на глиняной табличке, принадлежащей школе писцов; Сузы, первая половина 2-го тысячелетия до нашей эры
Задача геометрии поверхности семиугольника, разделенного на треугольники, на глиняной табличке, принадлежащей школе писцов; Сузы, первая половина 2-го тысячелетия до нашей эры  . 6-симплекс (6D)
. 6-симплекс (6D)![]()
Найдите heptagon в Викисловаре, бесплатном словаре.