 (красные) боковые края тетрагонального дифеноида представляют собой правильный зигзагообразный перекос четырехугольника.
(красные) боковые края тетрагонального дифеноида представляют собой правильный зигзагообразный перекос четырехугольника. В геометрии наклонный многоугольник - это многоугольник, не все вершины которого копланарны. Наклонные многоугольники должны иметь не менее 4 вершин. Внутренняя поверхность (или площадь) такого многоугольника не определена однозначно.
Косые бесконечные многоугольники (апейрогоны) имеют вершины, которые не все коллинеарны.
A зигзагообразный косой многоугольник или антипризматический многоугольник имеет вершины, которые чередуются на двух параллельных плоскостях, и, следовательно, должны быть четными.
Правильные косые многоугольники в трех измерениях (и правильные косые апейрогоны в двух измерениях) всегда зигзагообразны.
 Равномерная n-угольная антипризма имеет двухсторонний правильный наклонный многоугольник, определенный вдоль его боковых сторон.
Равномерная n-угольная антипризма имеет двухсторонний правильный наклонный многоугольник, определенный вдоль его боковых сторон. A правильный наклонный многоугольник равен изогональный с равной длиной ребра. В 3-х измерениях правильный косой многоугольник - это зигзагообразный перекос (или антипризматический многоугольник ) с чередующимися вершинами между двумя параллельными плоскостями. Стороны n- антипризмы могут определять правильные скошенные 2n-угольники.
Правильному наклонному n-угольному элементу можно присвоить символ {p} # {} как смесь правильного многоугольника, {p} и ортогонального отрезка линии <148.>, {}. Операция симметрии между последовательными вершинами: скользящее отражение.
Примеры показаны на однородных квадратной и пятиугольной антипризмах. Звездные антипризмы также генерируют правильные косые многоугольники с разным порядком соединения верхнего и нижнего многоугольников. Закрашенные верхний и нижний многоугольники нарисованы для ясности структуры и не являются частью наклонных многоугольников.
| Наклонный квадрат | Наклонный шестиугольник | Наклонный восьмиугольник | Наклонный десятиугольник | Наклонный десятиугольник | ||
| {2} # {} | {3} # {} | {4} # {} | {5} # {} | {5/2} # {} | {5/3} # {} | {6 } # {} |
 | 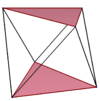 |  |  |  |  | 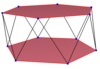 |
| s {2,4} | s {2,6} | s {2,8} | s {2,10} | sr {2,5 / 2 } | s {2,10 / 3} | s {2,12} |
Обычный составной скошенный 2n-угольник можно построить аналогичным образом, добавив второй скошенный многоугольник путем поворота. У них те же вершины, что и у призматического соединения антипризм.
| Косые квадраты | Наклонные шестиугольники | Наклонные десятиугольники | |
| Два { 2} # {} | Три {2} # {} | Два {3} # {} | Два {5/3} # {} |
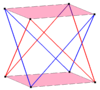 | 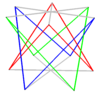 |  |  |
Петри полигоны - это правильные косые многоугольники, определенные внутри правильных многогранников и многогранников. Например, 5 Платоновых тел имеют 4-, 6- и 10-сторонние правильные косые многоугольники, как видно на этих ортогональных проекциях с красными краями вокруг проекционной оболочки .. Тетраэдр и октаэдр включают в себя все вершины зигзагообразного косого многоугольника и могут рассматриваться как двуугольные и треугольные антипризмы соответственно.

У правильного косого многогранника есть правильные грани и правильные косые многоугольники фигуры с вершинами. Три являются бесконечными , заполняющими пространство в 3-м пространстве, а другие существуют в 4-пространстве, некоторые в пределах равномерного 4-многогранника.
| {4,6 | 4} | {6,4 | 4} | {6,6 | 3} |
|---|---|---|
 . Правильный перекос шестиугольник. {3} # {} . Правильный перекос шестиугольник. {3} # {} |  . Правильный наклонный квадрат. {2} # {} . Правильный наклонный квадрат. {2} # {} | 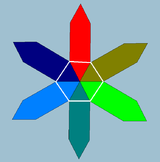 . Правильный наклонный шестиугольник. {3} # {} . Правильный наклонный шестиугольник. {3} # {} |
изогональный косой многоугольник - это косой многоугольник с одним типом вершины, соединенный двумя типами ребер. Изогональные косые многоугольники с равной длиной ребер также можно считать квазирегулярными. Он похож на зигзагообразный многоугольник с перекосом, существующий в двух плоскостях, за исключением того, что позволяет одному краю пересекать противоположную плоскость, а другому краю оставаться в той же плоскости.
Изогональные косые многоугольники могут быть определены на четных n-угольных призмах, попеременно следующих по краю одного бокового многоугольника и перемещаясь между многоугольниками. Например, по вершинам куба. Вершины чередуются между верхним и нижним квадратами с красными краями между сторонами и синими краями вдоль каждой стороны.
| Восьмиугольник | Додекагон | Икосикайтетрагон | ||||
|---|---|---|---|---|---|---|
 . Куб, квадратно-диагональный . Куб, квадратно-диагональный |  . Куб . Куб |  . Перекрещенный куб . Перекрещенный куб | 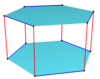 . Гексагональная призма . Гексагональная призма | 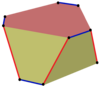 . Гексагональная призма . Гексагональная призма | 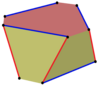 . Шестиугольная призма . Шестиугольная призма |  . Скрученная призма . Скрученная призма |
В 4-х измерениях правильный наклонный многоугольник может иметь вершины на торе Клиффорда и связаны между собой Смещение Клиффорда. В отличие от зигзагообразных косоугольных многоугольников, косые многоугольники при двойном повороте могут иметь нечетное количество сторон.
многоугольники Петри из правильного 4-многогранника определяют правильные наклонные многоугольники. Число Кокстера для каждой симметрии группы Кокстера выражает, сколько сторон имеет многоугольник Петри. Это 5 сторон для 5-ячеек, 8 сторон для тессеракта и 16-ячеечного, 12 сторон для 24-ячеечного и 30 сторон для 120-ячеек и 600-ячеек.
При ортогональной проекции на плоскость Кокстера эти правильные наклонные многоугольники выглядят как правильные многоугольные огибающие в самолет.
| A4, [3,3,3] | B4, [4,3,3] | F4, [3,4,3] | H4, [5,3,3] | ||
|---|---|---|---|---|---|
| Пентагон | Octagon | Dodecagon | Triacontagon | ||
 . 5-элементный. {3,3,3} . 5-элементный. {3,3,3} |  . tesseract. {4,3,3} . tesseract. {4,3,3} |  . 16 -ячейка. {3,3,4} . 16 -ячейка. {3,3,4} |  . 24-ячейка. {3,4,3} . 24-ячейка. {3,4,3} |  . 120-ячейка. {5,3, 3} . 120-ячейка. {5,3, 3} |  . 600-cell. {3,3,5} . 600-cell. {3,3,5} |
nn дуопризма и двойная дуопирамида также имеют 2n-угольные многоугольники Петри. (тессеракт - это дуопризма 4-4, а 16-ячеечная - дуопирамида 4-4.)
| Шестиугольник | Десятиугольник | Додекагон | |||
|---|---|---|---|---|---|
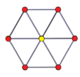 . Дуопризма 3-3 . Дуопризма 3-3 |  . Дуопирамида 3-3 . Дуопирамида 3-3 | 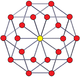 . 5-5 дуопризма . 5-5 дуопризма | 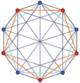 . Дуопирамида 5-5 . Дуопирамида 5-5 |  . Дуопирамида 6-6 . Дуопирамида 6-6 |  . 6-6 дуопирамида . 6-6 дуопирамида |