Бета-распределение

Распределение вероятностей

Бета

Функция плотности вероятности
Кумулятивная функция распределения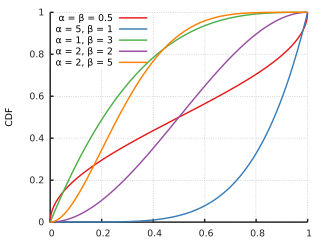
Обозначение	Бета (α, β)
Параметры	α>0 форма (действительная ). β>0 форма (реальный )
Поддержка	$x\; \in \; [0,\; 1]\; \{\backslash \; displaystyle\; x\; \backslash \; in\; [0,1]\; \backslash !\}$или $x\; \in \; (0,\; 1)\; \{\backslash \; Displaystyle\; х\; \backslash \; в\; (0,1)\; \backslash !\}$
PDF	$х\; \alpha \; -\; 1\; (1\; -\; x)\; \beta \; -\; 1\; B\; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{x\; ^\; \{\backslash \; альфа\; -1\}\; (1-x)\; ^\; \{\backslash \; beta\; -1\}\}\; \{\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; \backslash !\}$. где $B\; (\alpha ,\; \beta )\; =\; \Gamma \; (\alpha )\; \Gamma \; (\beta )\; \Gamma \; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; =\; \{\backslash \; frac\; \{\backslash \; Gamma\; (\backslash \; alpha)\; \backslash \; Gamma\; (\backslash \; beta)\}\; \{\backslash \; Gamma\; (\; \backslash \; альфа\; +\; \backslash \; бета)\}\}\}$и $\Gamma \; \{\backslash \; displaystyle\; \backslash \; Gamma\}$- это Гамма-функция.
CDF	$I\; x\; (\; \alpha ,\; \beta )\; \{\backslash \; displaystyle\; I\_\; \{x\}\; (\backslash \; alpha,\; \backslash \; beta)\; \backslash !\}$ (регуляризованная неполна я бета-функция )
Среднее	$E\; \; [X]\; =\; \alpha \; \alpha \; +\; \beta \; \{\backslash \; диспла\; ystyle\; \backslash \; operatorname\; \{E\}\; [X]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\; \backslash \; !\}$. $Е\; \; [пер\; \; Икс]\; =\; \psi \; (\alpha )\; -\; \psi \; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [\backslash \; пер\; X]\; =\; \backslash \; psi\; (\backslash \; alpha)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; бета)\; \backslash !\}$.. $Е\; \; [Икс\; пер\; \; Икс]\; =\; \alpha \; \alpha \; +\; \beta \; [\psi \; (\alpha \; +\; 1)\; -\; \psi \; (\alpha \; +\; \beta \; +\; 1)]\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [X\; \backslash ,\; \backslash \; ln\; X]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\; \backslash ,\; \backslash \; left\; [\backslash \; psi\; (\backslash \; alpha\; +1)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\; \backslash \; right]\; \backslash !\}$. (см. функция дигаммы и раздел: Геометрический средний)
Медиана	$I\; 1\; 2\; [-\; 1]\; (\alpha ,\; \beta )\; (в\; общем)\; \approx \; \alpha \; -\; 1\; 3\; \alpha \; +\; \beta \; -\; 2\; 3\; для\; \alpha ,\; \beta >1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{matrix\}\; I\; \_\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; ^\; \{[-\; 1]\}\; (\backslash \; alpha,\; \backslash \; beta)\; \{\backslash \; text\; \{(в\; общем)\}\; \}\; \backslash \backslash \; [0.5em]\; \backslash \; приблизительно\; \{\backslash \; frac\; \{\backslash \; alpha\; -\; \{\backslash \; tfrac\; \{1\}\; \{3\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -\; \{\backslash \; tfrac\; \{2\}\; \{3\}\}\}\}\; \{\backslash \; text\; \{\; for\}\}\; \backslash \; alpha,\; \backslash \; beta>1\; \backslash \; end\; \{matrix\}\}\}$
Режим	$\alpha \; -\; 1\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; \{\backslash \; fra\; c\; \{\backslash \; alpha\; -1\}\; \{\backslash \; альфа\; +\; \backslash \; бета\; -2\}\}\; \backslash !\}$для α, β>1 любое значение в $(0,\; 1)\; \{\backslash \; displaystyle\; (0,1)\}$для α, β = 1 {0, 1} (бимодальный) для α, β < 1 0 для α ≤ 1, β>1 1 для α>1, β ≤ 1
Дисперсия	$var\; \; [X]\; =\; \alpha \; \beta \; (\alpha \; +\; \beta )\; 2\; (\alpha \; +\; \beta \; +\; 1)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [X]\; =\; \{\backslash \; frac\; \{\; \backslash \; alpha\; \backslash \; beta\}\; \{(\backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{2\}\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\}\}\; \backslash !\}$. $var\; \; [ln\; \; X]\; знак\; равно\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; X]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; бета)\; \backslash !\}$. (см. тригамма-функция и раздел: Геометрическая дисперсия)
Асимметрия	$2\; (\beta \; -\; \alpha )\; \alpha \; +\; \beta \; +\; 1\; (\alpha \; +\; \beta \; +\; 2)\; \alpha \; \beta \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{2\; \backslash ,\; (\backslash \; beta\; -\; \backslash \; alpha)\; \{\backslash \; sqrt\; \{\backslash \; alpha\; +\; \backslash \; beta\; +1\}\}\}\; \{(\backslash \; alpha\; +\; \backslash \; beta\; +2)\; \{\backslash \; sqrt\; \{\backslash \; альфа\; \backslash \; бета\}\}\}\}\}$
Пример. эксцесс	$6\; [(\alpha \; -\; \beta )\; 2\; (\alpha \; +\; \beta \; +\; 1)\; -\; \alpha \; \beta \; (\alpha \; +\; \beta \; +\; 2)]\; \alpha \; \beta \; (\alpha \; +\; \beta \; +\; 2)\; (\alpha \; +\; \beta \; +\; 3)\; \{\backslash \; displaystyle\; \{\; \backslash \; frac\; \{6\; [(\backslash \; alpha\; -\; \backslash \; beta)\; ^\; \{2\}\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\; -\; \backslash \; alpha\; \backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; +2)]\}\; \{\backslash \; alpha\; \backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; +2)\; (\backslash \; alpha\; +\; \backslash \; beta\; +3)\}\}\}$
Энтропия	$ln\; \; B\; (\alpha ,\; \beta )\; -\; (\alpha \; -\; 1)\; \psi \; (\alpha )\; -\; (\beta \; -\; 1)\; \psi \; (\; \beta )\; +\; (\alpha \; +\; \beta \; -\; 2)\; \psi \; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{matrix\}\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; -\; (\backslash \; alpha\; -1)\; \backslash \; psi\; (\backslash \; альфа)\; -\; (\backslash \; beta\; -1)\; \backslash \; psi\; (\backslash \; beta)\; \backslash \backslash \; [0.5em]\; +\; (\backslash \; alpha\; +\; \backslash \; beta\; -2)\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\; \backslash \; end\; \{matrix\}\}\}$
MGF	$1\; +\; \sum \; k\; =\; 1\; \infty \; (\prod \; r\; =\; 0\; k\; -\; 1\; \alpha \; +\; r\; \alpha \; +\; \beta \; +\; r)\; tkk!\; \{\backslash \; displaystyle\; 1+\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (\backslash \; prod\; \_\; \{r\; =\; 0\}\; ^\; \{k-1\}\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; r\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; +\; r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{t\; ^\; \{k\}\}\; \{k!\}\}\}$
CF	$1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; it)\; \{\backslash \; displaystyle\; \{\}\; \_\; \{1\}\; F\_\; \{1\; \}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; i\; \backslash ,\; t)\; \backslash !\}$(см. конфлюэнтная гипергеометрическая функция )
информация Фишера	$[var\; \; [ln\; \; X]\; cov\; \; [пер\; X,\; пер\; \; (1\; -\; X)]\; cov\; \; [пер\; \; X,\; пер\; \; (1\; -\; X)]\; var\; \; [пер\; [пер\; (1\; -\; X)]]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\; \}\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; X]\; \backslash \; operatorname\; \{cov\}\; [\backslash \; ln\; X,\; \backslash \; ln\; (1-X)]\; \backslash \backslash \backslash \; operatorname\; \{cov\}\; [\backslash \; ln\; X,\; \backslash \; ln\; (1-X)]\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\; \backslash \; end\; \{bmatrix\}\}\}$. см. раздел: информационная матрица Фишера
Метод моментов	$\alpha \; =\; (E\; [X]\; (1\; -\; E\; [X])\; V\; [X]\; -\; 1)\; E\; [X]\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \backslash \; left\; (\{\backslash \; frac\; \{E\; [X]\; (1-E\; [X])\}\; \{V\; [X]]\; \})\}\; -1\; \backslash \; справа)\; E\; [X]\}$. $\beta \; =\; (E\; [X]\; (1\; -\; E\; [X])\; V\; [X]\; -\; 1)\; (1\; -\; E\; [X])\; \{\backslash \; displaystyle\; \backslash \; бета\; =\; \backslash \; left\; (\{\backslash \; frac\; \{E\; [X]\; (1-E\; [X])\}\; \{V\; [X]\}\}\; -\; 1\; \backslash \; справа)\; (1-E\; [X])\}$

В теории вероятностей и статистика, бета-распределение представляет собой семейство непрерывных распределений вероятностей, определенные на интервале [0, 1] , параметры двумя положительными определены, обозначаемые α и β, которые появляются как показатели случайной величины и управляют распределением. Обобщение на несколько величин называется распределением Дирихле.

Бета-распределение было применено для моделирования поведения случайных величин, ограниченных интервалами конечной длины в широком спектре дисциплин.

В байесовском выводе бета-распределение представляет собой сопряженное априорное распределение вероятностей для Бернулли, биномиального, отрицательное биномиальное <708ное>и геометрическое распределения. Бета-модель является подходящей моделью для случайного поведения и пропорций.

Обсуждаемая здесь формулировка бета-распределения также известна как бета-распределение первого типа, тогда как бета-распределение второго типа является альтернативным названием для бета-простого распределения.

Содержание

• 1 Определения
  • 1.1 Функция вероятности плотности
  • 1.2 Кумулятивная функция распределения
  • 1.3 Альтернативные параметры распределения
    • 1.3.1 Два параметра
      • 1.3.1.1 Среднее и размер выборки
      • 1.3.1.2 Режим и свойство
      • 1.3.1.3 Среднее значение (частота аллелей) и генетическое расстояние (Райта) между двумя популяциями
      • 1.3.1.4 Среднее значение и дисперсия
    • 1.3.2 Четыре параметра
• 2 Свойства
  • 2.1 Меры центральной тенденции
    • 2.1.1 Мода
    • 2.1.2 Медиана
    • 2.1.3 Среднее
    • 2.1.4 Среднее геометрическое
    • 2.1.5 Гармоническое среднее
  • 2.2 Меры статистическая дисперсия
    • 2.2.1 Дисперсия
    • 2.2.2 Геометрическая дисперсия и ковариация
    • 2.2.3 Средн ее абсолютное отклонение около среднего
    • 2.2.4 Средняя абсолютная разница
  • 2. 3 Асимметрия
  • 2.4 эксцесс
  • 2.5 Характеристическая функция
  • 2.6 Другие моменты
    • 2.6.1 Производящая функция момента
    • 2.6.2 Высшие моменты
    • 2.6.3 Моменты преобразованных случайных величин
      • 2.6.3.1 Моменты линейно преобразованных, произведенных и инвертированных случайных величин
      • 2.6.3.2 Моменты логарифмически преобразованных случайных величин
  • 2.7 Количество информации (энтропия)
  • 2.8 Взаимосвязи между статистическими показателями
    • 2.8.1 Среднее, мода и медианное соотношение
    • 2.8.2 Среднее, ограниченное среднее и гармоническое среднее соотношение
    • 2.8.3 эксцесс, ограниченный квадратом асимметрии
  • 2.9 Симметрия
  • 2.10 Геометрия функции плотности вероятности
    • 2.10.1 Точки перегиба
    • 2.10.2 Формы
      • 2.10.2.1 Симметричные (α = β)
      • 2.10.2.2 Перекос (α ≠ β)
• 3 Связанные распределения
  • 3.1 Преобразования
  • 3.2 Особые и предельные случаи
  • 3.3 Получено из других распределений
  • 3.4 Комбинация с другими дистрибутивами
  • 3.5 Составление с другими распределителями
  • 3.6 Обобщения
• 4 Статистический вывод
  • 4.1 Оценка параметров
    • 4.1.1 Метод моментов
      • 4.1.1.1 Два неизвестных других
      • 4.1.1.2 Четыре неизвестных параметра
    • 4.1.2 Максимальное правдоподобие
      • 4.1.2.1 Два неизвестных параметра
      • 4.1.2.2 Четыре неизвестных параметра
    • 4.1.3 Информационная матрица Fisher
      • 4.1.3.1 Два руководства
      • 4.1.3.2 Четыре параметра
  • 4.2 Байесовский вывод
    • 4.2.1 Правило следовать
    • 4.2.2 Байесовская априорная вероятность (бета (1,1))
    • 4.2.3 Априорная вероятность Холдейна ( бета (0,0))
    • 4.2.4 Априорная вероятность Джеффриса (бета (1 / 2,1 / 2) для распределения Бернулли или биномиального распределения)
    • 4.2.5 Влияние различных вариантов априорной вероятности на апостериорное бета-распределение
• 5 Возникновение и приложения
  • 5.1 Статистика заказов
  • 5.2 Субъективная логика
  • 5.3 Вейвлет-анализ
  • 5.4 Управление проектом: моделирование затрат и расписания
• 6 Вычислительные методы
  • 6.1 Генерация бета-распределения случайные переменные
• 7 История
• 8 Ссылки
• 9 Внешние ссылки

Определения

Функция плотности вероятности

Анимация бета-распределения для различных значений его параметров.

функция плотности вероятности (pdf) бета-распределения для 0 ≤ x ≤ 1 и параметров α, β>0 представляет собой степенную функцию переменной x и его отражение (1 - x) следующим образом:

$f\; (x;\; \alpha ,\; \beta )\; =\; константа\; \cdot \; x\; \alpha \; -\; 1\; (1\; -\; x)\; \beta \; -\; 1\; =\; x\; \alpha \; -\; 1\; (1\; -\; x)\; \beta \; -\; 1\; \int \; 0\; 1\; u\; \alpha \; -\; 1\; (1\; -\; u)\; \beta \; -\; 1\; du\; =\; \Gamma \; (\alpha \; +\; \beta )\; \Gamma \; (\alpha )\; \Gamma \; (\beta )\; x\; \alpha \; -\; 1\; (1\; -\; x)\; \beta \; -\; 1\; =\; 1\; B\; (\alpha ,\; \beta )\; x\; \alpha \; -\; 1\; (1\; -\; x)\; \beta \; -\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; =\; \backslash \; mathrm\; \{constant\}\; \backslash \; cdot\; x\; ^\; \{\backslash \; alpha\; -1\}\; (\; 1-х)\; ^\; \{\backslash \; бета\; -1\}\; \backslash \backslash \; [3pt]\; =\; \{\backslash \; гидроразрыва\; \{х\; ^\; \{\backslash \; альфа\; -1\}\; (1-х)\; ^\; \{\backslash \; бета\; -1\}\}\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{\; 0\}\; ^\; \{1\}\; u\; ^\; \{\backslash \; alpha\; -1\}\; (1-u)\; ^\; \{\backslash \; beta\; -1\}\; \backslash ,\; du\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; frac\; \{\backslash \; Gamma\; (\backslash \; alpha\; +\; \backslash \; beta)\}\; \{\backslash \; Gamma\; (\backslash \; alpha)\; \backslash \; Gamma\; (\backslash \; beta)\}\}\; \backslash ,\; x\; ^\; \{\backslash \; alpha\; -1\}\; (1-x)\; ^\; \{\backslash \; beta\; -1\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; frac\; \{\; 1\}\; \{\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; x\; ^\; \{\backslash \; alpha\; -1\}\; (1-x)\; ^\; \{\backslash \; beta\; -1\}\; \backslash \; end\; \{align\}\}\}$

где Γ ( z) - это гамма-функция. бета-функция, $B\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{B\}\}$, является константой нормализации, чтобы риск, что общая вероятность равна 1. В приведенное выше уравнение x является реализацией - фактически имевшим место текущим периодом - случайного процесса X.

Это определение включает оба конца x = 0 и x = 1, что согласуется с определениями для других непрерывных распределений, поддерживаемых в ограниченном интервале, которые являются частными случаями бета-распределения, например распределение арксинуса , и согласуется с местами авторами, такими как N. Л. Джонсон и С. Коц. Однако включение x = 0 и x = 1 не работает для α, β < 1; accordingly, several other authors, including W. Feller, следует исключить концы x = 0 и x = 1 (так, чтобы два конца не были частями определения функции плотности) и вместо этого рассмотрите 0 < x < 1.

Несколько авторов, включая Н. Л. Джонсон и С. Коц, используйте символы p и q (вместо α и β) для параметров формы бета-распределения, напоминающие символы, традиционно используемые для параметров распределения Бернулли, потому что бета-версия распределения приближается к распределению Бернулли в пределе, когда оба варианта формы α и β приближаются к значению нуля.

Далее случайная величина X с бета-распределением параметров α и β будет обозначаться следующим образом:

$X\; \sim \; Beta\; \; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Beta\}\; (\backslash \; alpha,\; \backslash \; beta)\}$

Другие обозначения для бета-распределенных случайных величин, используемые в статистической литературе: $X\; \sim \; B\; e\; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \{\backslash \; mathcal\; \{B\}\}\; е\; (\backslash \; альфа,\; \backslash \; бета)\}$и $X\; \sim \; \beta \; \alpha ,\; \beta \; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; beta\; \_\; \{\backslash \; alpha,\; \backslash \; beta\}\}$.

Кумулятивная функция распределения

CDF для симметричного бета-распределения в зависимости от x и α = β CDF для искаженного бета-распределения в зависимости от x и β = 5α

кумулятивная функция распределения равна

$F\; (x;\; \alpha ,\; \beta )\; знак\; равно\; В\; (Икс;\; \alpha ,\; \beta )\; В\; (\alpha ,\; \beta )\; =\; я\; Икс\; (\alpha ,\; \beta )\; \{\backslash \; Displaystyle\; F\; (х;\; \backslash \; альфа,\; \backslash \; бета)\; =\; \{\backslash \; гидроразрыва\; \{\backslash \; mathrm\; \{B\}\; \{\; \}\; (x;\; \backslash \; alpha,\; \backslash \; beta)\}\; \{\backslash \; mathrm\; \{B\}\; \{\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; =\; I\_\; \{x\}\; (\backslash \; alpha,\; \backslash \; beta)\}$

где $B\; (\; Икс;\; \alpha ,\; \beta )\; \{\backslash \; Displaystyle\; \backslash \; ма\; thrm\; \{B\}\; (х;\; \backslash \; альфа,\; \backslash \; бета)\}$- неполная бета-функция и $I\; x\; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; I\_\; \{x\}\; (\backslash \; alpha,\; \backslash \; beta)\}$- это регуляризованная неполная бета-функция.

.

Альтернативные параметры

Два параметра

Среднее и размер выборки

Бета-распределение также может быть повторно параметризовано в терминах его среднего μ (0 < μ < 1) and the addition of both shape parameters ν = α + β>0 (стр. 83). Обозначая αPosterior и βPosterior параметры апостериорного бета-распределения, полученного в результате применения теоремы Байеса к биномиальной функции правдоподобия и априорной вероятности, интерпретации обоих параметров формы как размер выборки = ν = α · Posterior + β · Апостериорная верна только для априорной вероятности Холдейна Бета (0,0). В частности, для байесовского (однородного) предшествующего бета (1,1) правильной интерпретацией будет размер выборки = α · задний + β задний - 2 или ν = (размер выборки) + 2. Конечно, для размера выборки намного больше чем 2, р азница между этими двумя априорными числами становится незначительной. (Подробнее см. Байесовский вывод.) В остальной части этой статьи ν = α + β будет называться «размером выборки», но следует помнить, строго говоря, «размер выборки» биномиальной функции правдоподобия только При использовании бета-версии Холдейна (0,0) до теоремы Байеса.

Эта параметризация может быть полезна при оценке байесовских параметров. Например, можно провести тест нескольким людям. ≤ 1), что является статистикой является среднее значение этого распределения. Параметры среднего и размера связаны с определенными параметрами α и β через

α = μν, β = (1 - μ) ν

Под этой параметризацией можно использовать неинформативная априорная вероятность по сравнению со средним и нечеткая априорная вероятность (например, экспоненциальное или гамма-распределение) по положительным действительным значениям для размера выборки, если они и априорные данные и / или убеждения подтверждают это.

Режим и свойство

Режим и «свойство» $\kappa \; =\; \alpha \; +\; \beta \; \{\backslash \; displaystyle\; \backslash \; kappa\; =\; \backslash \; alpha\; +\; \backslash \; beta\}$также могут быть используются для расчета параметров бета-распределения.

$\alpha \; знак\; равно\; \omega \; (\kappa \; -\; 2)\; +\; 1\; \beta \; =\; (1\; -\; \omega )\; (\kappa \; -\; 2)\; +\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; alpha\; =\; \backslash \; omega\; (\backslash \; kappa\; -2)\; +1\; \backslash \backslash \backslash \; beta\; =\; (1-\; \backslash \; omega)\; (\backslash \; kappa\; -2)\; +1\; \backslash \; end\; \{align\}\}\}$

Среднее (частота аллелей) и (Райта) генетические расстояния между двумя популяциями

Модель Болдинга - Николса - это двухпараметрическая параметризация бета-распределения, используемая в популяционной генетике. Это статистическое описание частоты аллелей в компонентах подразделяемой популяции:

$\alpha \; =\; \mu \; \nu ,\; \beta \; =\; (1\; -\; \mu )\; \nu ,\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; alpha\; =\; \backslash \; mu\; \backslash \; nu,\; \backslash \backslash \backslash \; бета\; =\; (1-\; \backslash \; mu)\; \backslash \; nu,\; \backslash \; end\; \{align\}\}\}$

где $\nu \; =\; \alpha \; +\; \beta \; =\; 1\; -\; FF\; \{\backslash \; displaystyle\; \backslash \; nu\; =\; \backslash \; alpha\; +\; \backslash \; beta\; =\; \{\backslash \; frac\; \{1-F\}\; \{F\}\}\}$и ; здесь F - генетическая дистанция (Райта) между двумя популяциями.

См. Статьи Модель Болдинга - Николса, F-статистика, индекс фиксации и коэффициент взаимосвязи, для дальнейшая информация.

Среднее значение и дисперсия

Решение системы (связанных) уравнений, приведенных в предыдущих разделах, в виде уравнений для среднего и дисперсии бета-распределения в конечных исходных α и β, параметрах α и β можно выразить через среднее (μ) и дисперсию (var):

Эта параметризация бета-распределения может к более интуитивному пониманию, чем то, которое основано на исходных параметрах α и β. Например, выражая моду, асимметрию, избыточный эксцесс и дифференциальную энтропию в виде среднего и дисперсии:

Четыре параметра

Бета-структура с двумя действующими элементами [0,1] или (0, 1). Можно изменить местоположение и распределение, введя два режима, представляющих минимальное, максимальное значение c (c>a), значения распределения, путем линейного преобразования, заменяющего безразмерную переменную переменную x в терминах новой переменной y (с поддержкой [a, c] или (a, c)) и параметры a и c:

$y\; =\; x\; (c\; -\; a)\; +\; a,\; поэтому\; x\; =\; y\; -\; ac\; -\; a.\; \{\backslash \; displaystyle\; y\; =\; x\; (ca)\; +\; a,\; \{\backslash \; text\; \{следовательно\}\}\; x\; =\; \{\backslash \; frac\; \{ya\}\; \{ca\}\}.\}$

функция плотности вероятности четырех размеров бета-распределения одинаково двухпараметрическому распределению, масштабированному диапазону (ca) (так, чтобы общая площадь под кривой плотности равнялась вероятности, равной единице), и с переменной «y», смещенной и масштабированной следующим образом:

$f\; (y;\; \alpha ,\; \beta ,\; a,\; c)\; =\; f\; (x;\; \alpha ,\; \beta )\; c\; -\; a\; =\; (y\; -\; ac\; -\; a)\; \alpha \; -\; 1\; (c\; -\; yc\; -\; a)\; \beta \; -\; 1\; (c\; -\; a)\; B\; (\alpha ,\; \beta )\; =\; (\; y\; -\; a)\; \alpha \; -\; 1\; (c\; -\; y)\; \beta \; -\; 1\; (c\; -\; a)\; \alpha \; +\; \beta \; -\; 1\; B\; (\alpha ,\; \beta ).\; \{\backslash \; displaystyle\; f\; (y;\; \backslash \; alpha,\; \backslash \; beta,\; a,\; c)\; =\; \{\backslash \; frac\; \{f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\}\; \{ca\}\}\; =\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{ya\; \}\; \{ca\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\; -1\}\; \backslash \; left\; (\{\backslash \; frac\; \{cy\}\; \{ca\}\}\; \backslash \; right)\; ^\; \{\backslash \; beta\; -1\}\}\; \{(ca)\; B\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; =\; \{\backslash \; frac\; \{(ya)\; ^\; \{\backslash \; alpha\; -1\}\; (cy)\; ^\; \{\backslash \; beta\; -1\}\}\; \{(ca)\; ^\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\; B\; (\backslash \; alpha,\; \backslash \; beta)\}\}.\}$

То, что случайная величина Y является бета-распределенной с включением элементов α, β, a и c, будет обозначаться как:

$Y\; \sim \; B\; eta\; (\alpha ,\; \beta ,\; a,\; c).\; \{\backslash \; displaystyle\; Y\; \backslash \; sim\; Beta\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c).\}$

Измерения центрального местоположения масштабируются (на (ca)) и сдвигаются (на a) следующим образом:

$μ Y = μ X (c - a) + a = (α α + β) (c - a) + a = α c + β a α + β режим (Y) = режим (X) (c - a) + a = (α - 1 α + β - 2) (c - a) + a = (α - 1) c + (β - 1) a α + β - 2, если α, β>1 медиана (Y) = медиана (X) ( c - a) + a = (I 1 2 [- 1] (α, β)) (c - a) + a Неправильно !!: GY = GX (c - a) + a = (e ψ (α) - ψ (α + β)) (c - a) + a Неправильно !!: HY = HX (c - a) + a = (α - 1 α + β - 1) (c - a) + a, если α, β>0 {\ displaystyle {\ begin {align} \ mu _ {Y} = \ mu _ {X} (ca) + a = \ left ({\ frac {\ alpha} {\ alpha + \ beta}} \ right) (ca) + a = {\ frac {\ alpha c + \ beta a} {\ alpha + \ beta}} \\ {\ text {mode}} (Y) = {\ text {режим}} (X) (ca) + a = \ left ({\ frac {\ alpha -1} {\ alpha + \ beta -2}} \ right) (ca) + a = {\ frac {(\ alpha -1) c + (\ beta -1) a} {\ alpha + \ beta -2}} \, \ qquad {\ text {if}} \ alpha, \ beta>1 \ \ {\ text {median}} (Y) = {\ text {median}} (X) (ca) + a = \ left (I _ {\ frac {1} {2}} ^ {[- 1] } (\ alpha, \ beta) \ right) (ca) + a \\ {\ text {Неправильно !!:}} G_ {Y} = G_ {X} (ca) + a = \ left (e ^ { \ psi (\ alpha) - \ psi (\ alpha + \ beta)} \ right) (ca) + a \\ {\ text {Неправильно !!:}} H_ {Y} = H_ {X} (ca) + a = \ left ({\ frac {\ alpha -1} {\ alpha + \ beta -1}} \ right) (ca) + a, \, \ qquad {\ text {if}} \ alpha, \ beta>0 \\\ конец {выровнено}}}$

. (среднее геометрическое и среднее гармоническое не могут быть преобразованы

Параметры формы Y могут быть записаны в его член среднего и дисперсии как

$\alpha \; =\; (a\; -\; \mu \; Y)\; (ac\; -\; a\; \mu \; Y\; -\; c\; \mu \; Y\; +\; \mu \; Y\; 2\; +\; \sigma \; Y\; 2)\; \sigma \; Y\; 2\; (с\; -\; а)\; \beta \; знак\; равно\; -\; (с\; -\; \mu \; Y)\; (ac\; -\; a\; \mu \; Y\; -\; с\; \mu \; Y\; +\; \mu \; Y\; 2\; +\; \sigma \; Y\; 2)\; \sigma \; Y\; 2\; (с\; -\; а)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{(a\; -\; \backslash \; mu\; \_\; \{Y\})\; (a\; \backslash ,\; ca\; \backslash ,\; \backslash \; mu\; \_\; \{Y\}\; -c\; \backslash ,\; \backslash \; mu\; \_\; \{Y\}\; +\; \backslash \; mu\; \_\; \{Y\}\; ^\; \{2\}\; +\; \backslash \; sigma\; \_\; \{Y\}\; ^\; \{2\})\}\; \{\backslash \; sigma\; \_\; \{Y\}\; ^\; \{2\}\; (ca)\}\}\; \backslash \backslash \backslash \; бета\; =\; -\; \{\backslash \; frac\; \{(c-\; \backslash \; mu\; \_\; \{Y\})\; (a\; \backslash ,\; ca\; \backslash ,\; \backslash \; mu\; \_\; \{Y\}\; -c\; \backslash ,\; \backslash \; mu\; \_\; \{Y\}\; +\; \backslash \; mu\; \_\; \{Y\}\; ^\; \{\; 2\}\; +\; \backslash \; sigma\; \_\; \{Y\}\; ^\; \{2\})\}\; \{\backslash \; sigma\; \_\; \{Y\}\; ^\; \{2\}\; (ca)\}\}\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

Меры статистической дисперсии масштабируются (их не нужно сдвигать, потому что они уже центрированы по среднему) по диапазону (ca), линейно для среднего о тклонение и нелинейно для дисперсии:

$(среднее\; отклонение\; от\; среднего)\; (Y)\; =\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{(среднее\; отклонение)\; от\; среднего)\}\}\; (Y)\; =\}$

$((среднее\; откл\; онение\; от\; среднего)\; (Икс))\; (с\; -\; а)\; знак\; равно\; 2\; \alpha \; \alpha \; \beta \; \beta \; В\; (\alpha ,\; \beta )\; (\alpha \; +\; \beta )\; \alpha \; +\; \beta \; +\; 1\; (с\; -\; а)\; \{\backslash \; displaystyle\; (\{\backslash \; text\; \{(\; среднее\; отклонение\; от\; среднего)\}\}\; (X))\; (ca)\; =\; \{\backslash \; frac\; \{2\; \backslash \; alpha\; ^\; \{\backslash \; alpha\}\; \backslash \; beta\; ^\; \{\backslash \; beta\}\}\; \{\backslash \; math\; rm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; (\; \backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{\backslash \; alpha\; +\; \backslash \; beta\; +1\}\}\}\; (ca)\}$

$var\; (Y)\; =\; var\; (X)\; (c\; -\; a)\; 2\; =\; \alpha \; \beta \; (c\; -\; a)\; 2\; (\; \alpha \; +\; \beta )\; 2\; (\alpha \; +\; \beta \; +\; 1).\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{var\}\}\; (Y)\; =\; \{\backslash \; text\; \{var\}\}\; (X)\; (ca)\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; \backslash \; beta\; (ca)\; ^\; \{2\}\}\; \{(\; \backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{2\}\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\}\}.\}$

Бук асимметрия и избыточный эксцесс являются безразмерными величинами (поскольку моменты в среднем и нормализованные на стандартное отклонение ), они не зависят от параметров a и c и, следовательно, равны выражениям, приведенным выше в терминах X (с support [0,1] или (0,1)):

$асимметрия\; (Y)\; =\; асимметрия\; (X)\; =\; 2\; (\beta \; -\; \alpha )\; \alpha \; +\; \beta \; +\; 1\; (\alpha \; +\; \beta \; +\; 2)\; \alpha \; \beta .\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{skewness\}\}\; (Y)\; =\; \{\backslash \; text\; \{skewness\}\}\; (X)\; =\; \{\backslash \; frac\; \{2\; (\backslash \; beta\; -\; \backslash \; alpha)\; \{\backslash \; sqrt\; \{\backslash \; alpha\; +\; \backslash \; beta\; +1\}\}\; \}\; \{(\backslash \; alpha\; +\; \backslash \; beta\; +2)\; \{\backslash \; sqrt\; \{\backslash \; alpha\; \backslash \; beta\}\}\}\}.\}$

$избытоктокцесса\; (Y)\; =\; избыток\; эксцесса\; (X)\; =\; 6\; [(\alpha \; -\; \beta )\; 2\; (\alpha \; +\; \beta \; +\; 1)\; -\; \alpha \; \beta \; (\alpha \; +\; \beta \; +\; 2)]\; \alpha \; \beta \; (\alpha \; +\; \beta \; +\; 2)\; (\alpha \; +\; \beta \; +\; 3)\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{избыток\; эксцесса\}\}\; (Y)\; =\; \{\backslash \; text\; \{избыток\; эксцесса\}\}\; (X)\; =\; \{\backslash \; frac\; \{6\; [(\backslash \; alpha\; -\; \backslash \; beta)\; ^\; \{2\}\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\; -\; \backslash \; alpha\; \backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; +2)]\; \}\; \{\backslash \; alpha\; \backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; +2)\; (\backslash \; alpha\; +\; \backslash \; beta\; +3)\}\}\}$

Свойства

Меры центральной тенденции

Режим

Режим бета-распределенной случайной величины X с α, β>1 - наиболее вероятное значение распределения (соответствующее пику в PDF), и дается следующим выражением:

$\alpha \; -\; 1\; \alpha \; +\; \beta \; -\; 2.\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}.\}$

Когда оба меньше единицы (α, β < 1), this is the anti-mode: the lowest point of the probability density curve.

Если α = β, выражение для режима упрощенной ается до 1/2, форма, что для α = β>1 режим (соотв. анти-режим, когда α, β < 1), is at the center of the distribution: it is symmetric in those cases. See Фигуры раздел в этой статье для полного списка случаев режима, для произвольных значений α и β. Для некоторых из этих самых больших значений плотности находится на одном или обоих концах. В некоторых случаях (максимальное) значение функции плотности, встречающееся в конце, является конечным. Например, в случае α = 2, β = 1 (или α = 1, β = 2) функция плотности становится распределением прямоугольного треугольника, которое является конечным на обоих концах. В некоторых других случаях существует особенность на одном конце, где значение функции плотности приближается к бесконечности. Например, в случае α = β = 1/2, бета-распределение упрощается и становится распределением арксинуса. Среди математиков ведутся споры о некоторых из этих случаев. определить, могут ли концы (x = 0 и x = 1) называться режимами или нет.

Режим для бета-распределения 1 ≤ α ≤ 5 и 1 ≤ β ≤ 5

• Являются ли концы частью области функции плотности
• Может ли особенность когда-либо называться режимом
• Следует ли называть случаи с двумя максимумами бимодальными

Медиана

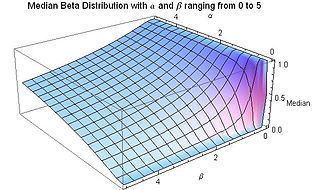
Медиана для бета-распределения для 0 ≤ α ≤ 5 и 0 ≤ β ≤ 5 (Среднее - Медиана) для бета-распределения по сравнению с альфа и бета от 0 до 2

Медиана бета-распределения - это уникальное действительное число $x\; =\; I\; 1\; 2\; [-\; 1]\; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; x\; =\; I\; \_\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; ^\; \{[-\; 1]\}\; (\backslash \; alpha,\; \backslash \; beta\; которых)\}$, для регуляризованная неполная бета-функция $Я\; Икс\; (\alpha ,\; \beta )\; знак\; равно\; 1\; 2\; \{\backslash \; Displaystyle\; I\_\; \{x\}\; (\backslash \; альфа,\; \backslash \; бета)\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\}$. Не существует общего выражения в закрытой форме для медианы бета-распределения для произвольных значений α и β. Выражения в закрытой форме для значений параметров α и β следующих:

• Для симметричных случаев α = β, медиана = 1/2.
• Для α = 1 и β>0, медиана $=\; 1-2-1\; \beta \; \{\backslash \; displaystyle\; =\; 1-2\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{\backslash \; beta\}\}\}\}$(в данном зеркальное отображение распределения степенной функции [0,1])
• Для α>0 и β = 1 медиана = $2-1\; \alpha \; \{\; \backslash \; displaystyle\; 2\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{\backslash \; alpha\}\}\}\}$(в данном случае - распределение степенной функции [0,1])
• Для α = 3 и β = 2 медиана = 0,6142724318676105..., реальное решение уравнения четвертой степени 1 - 8x + 6x = 0, которое находится в [0,1].
• Для α = 2 и β = 3 медиана = 0,38572756813238945... = 1-медиана (Beta (3, 2))

Ниже приведены пределы с одним конечным параметром (ненулевым) и другими, приближающимся к этим пределам:

$lim\; \beta \; \to \; 0\; медиана\; =\; lim\; \alpha \; \to \; \infty \; медиана\; =\; 1,\; lim\; \alpha \; \to \; 0\; медиана\; =\; lim\; \beta \; \to \; \infty \; медиана\; =\; 0.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; 0\}\; \{\backslash \; text\; \{median\}\}\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; text\; \{median\}\}\; =\; 1,\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; \{\backslash \; text\; \{\; median\}\}\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; text\; \{median\}\}\; =\; 0.\; \backslash \; end\; \{align\}\}\}$

Разумное приближение значений медианы бета-распределения для обоих α и β, больших или равных единице, дается формулой

$медиана\; \approx \; \alpha \; -\; 1\; 3\; \alpha \; +\; \beta \; -\; 2\; 3\; для\; \alpha ,\; \beta \; \ge \; 1.\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{median\}\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{\backslash \; alpha\; -\; \{\backslash \; tfrac\; \{\; 1\}\; \{3\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -\; \{\backslash \; tfrac\; \{2\}\; \{3\}\}\}\}\; \{\backslash \; text\; \{for\}\}\; \backslash \; alpha,\; \backslash \; beta\; \backslash \; geq\; 1.\}$

Когда α, β ≥ 1, относительная погрешность (абсолютная ошибка , деленная на медианное значен ие) в этом приближении составляет менее 4%, а для α ≥ 2 и β ≥ 2 она составляет менее 1%. абсолютная ошибка, деленная на разницу между средним и модой, также мала:

Среднее

Среднее для бета-распределения для 0 ≤ α ≤ 5 и 0 ≤ β ≤ 5

ожидаемое значение (среднее) (μ) бета-распределение случайная величина X с двумя функциями α и β является функцией только отношений β / α этих параметров:

$\mu \; =\; E\; \; [X]\; =\; \int \; 0\; 1\; xf\; (x;\; \alpha ,\; \beta )\; dx\; =\; \int \; 0\; 1\; xx\; \alpha \; -\; 1\; (1\; -\; x)\; \beta \; -\; 1\; B\; (\alpha ,\; \beta )\; dx\; =\; \alpha \; \alpha \; +\; \beta \; =\; 1\; 1\; +\; \beta \; \alpha \; \{\backslash \; Displaystyle\; \{\; \backslash \; begin\; \{align\}\; \backslash \; mu\; =\; \backslash \; operatorname\; \{E\}\; [X]\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; xf\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; \backslash ,\; dx\; \backslash \; \backslash \; =\; \backslash \; int\; \_\; \{0\; \}\; ^\; \{1\}\; x\; \backslash ,\; \{\backslash \; frac\; \{x\; ^\; \{\backslash \; alpha\; -1\}\; (1-x)\; ^\; \{\backslash \; beta\; -1\}\}\; \{\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; \backslash ,\; dx\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{1\; +\; \{\backslash \; frac\; \{\backslash \; beta\}\; \{\backslash \; alpha\}\}\}\}\; \backslash \; end\; \{\; align\}\}\}$

приведенном выше выражении, получаем μ = 1/2, что для α = β среднее значение находится в центре распределения: оно симметрично. Кроме того, из приведенного выше выражения можно получить следующие пределы:

$lim\; \beta \; \alpha \; \to \; 0\; \mu \; =\; 1\; lim\; \beta \; \alpha \; \to \; \infty \; \mu \; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; lim\; \_\; \{\{\backslash \; frac\; \{\backslash \; \backslash \; beta\}\; \{\backslash \; alpha\}\}\; \backslash \; to\; 0\}\; \backslash \; mu\; =\; 1\; \backslash \backslash \backslash \; lim\; \_\; \{\{\backslash \; frac\; \{\backslash \; beta\}\; \{\backslash \; alpha\}\}\; \backslash \; to\; \backslash \; infty\}\; \backslash \; mu\; =\; 0\; \backslash \; end\; \{выровнено\}\}\}$

Следовательно, для β / α → 0 или для α / β → ∞ среднее значение находится на правом правом, x = 1. Для этих предельных значений бета распределение становится одноточечным вырожденным распределением. с дельта-функция Дирака, пик на правом конце, x = 1, с вероятностью 1 и нулевой вероятностью везде. 100% вероятность (абсолютная уверенность) сосредоточена на правом конце, x = 1.

Аналогично, для β / α → ∞ или для α / β → 0 среднее значение находится на левом конце., x = 0. Бета-распределение становится одно-точечным вырожденным распределением с всплеском дельта-функции Дирака на левом конце, x = 0, с вероятностью 1 и нулевой вероятностью везде. еще. 100% вероятность (абсолютная уверенность) сосредоточена на левом конце, x = 0. Ниже приведены пределы с одним конечным параметром (ненулевым), и другой приближается к этому пределу:

$lim\; \beta \; \to \; 0\; \mu \; =\; lim\; \alpha \; \to \; \infty \; \mu \; знак\; 1\; lim\; \alpha \; \to \; 0\; \mu \; знак\; равно\; lim\; \beta \; \to \; \infty \; \mu \; знак\; равно\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; 0\}\; \backslash \; mu\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; \backslash \; mu\; =\; 1\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; \backslash \; mu\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; \backslash \; mu\; =\; 0\; \backslash \; end\; \{align\}\}\}$

В то время как для типичных унимодальных известно, что выборочное среднее (как оценка местоположения) не такой <1275 распределений (с центрально расположенными модами, точками перегиба по обеим сторонам от моды и более длинными хвостами) (с Beta (α, β) таким, что α, β>2)>устойчивый, как медиана выборки, наоборот, для равномерных или «U-образных» бимодальных распределений (с Beta (α, β), таким, что α, β ≤ 1), с модами, расположенными в конце раздачи. Как отмечают Мостеллер и Тьюки (стр. 207), «среднее двух крайних наблюдений использует всю выборочную информацию. Это показывает, как для распределений с коротким хвостом крайние наблюдения должны иметь больший вес ». Напротив, из этого следует, что медиана «U-образных» бимодальных распределений с модами на краю распределения (с Beta (α, β) такими, что α, β ≤ 1) не устойчивой, так как медиана выборки снижает крайние выборочные наблюдения из рассмотрение. Практическое применение этого имеет место, например, для случайных блужданий, поскольку вероятность для времени последнего посещения исходной точки в случайном блуждании распределяется как распределение арксинусов бета (1/2, 1/2): среднее из числа реализаций случайного блуждания является гораздо более надежной оценкой, чем медиана (которая в данном случае является неподходящей оценочной выборочной мерой).

Среднее геометрическое

(Среднее - GeometricMean) для бета-распределения по сравнению с α и β от 0 до 2, форма асимметрии между α и β для среднего геометрического Средние геометрические для бета-распределения Фиолетовый = G (x), желтый = G (1 - x), меньшие значения α и β спереди Средние геометрические для бета-распределения. фиолетовый = G (x), желтый = G (1 - x), большие значения α и β впереди

Логарифм среднего геометрического GXраспределения с случайной величиной X - среднее арифметическое ln ( X) или, что эквивалентно, его ожидаемое значение:

$ln\; \; GX\; =\; E\; \; [ln\; \; X]\; \{\backslash \; displaystyle\; \backslash \; ln\; G\_\; \{X\}\; =\; \backslash \; operatorname\; \{E\}\; [\backslash \; ln\; X]\}$

Для бета-распределения интеграл ожидаемого значения дает:

$E ⁡ [ln ⁡ X] = ∫ 0 1 ln ⁡ xf (x; α, β) dx = ∫ 0 1 ln ⁡ xx α - 1 (1 - x) β - 1 B (α, β) dx = 1 B (α, β) ∫ 0 1 ∂ x α - 1 (1 - x) β - 1 ∂ α dx = 1 B (α, β) ∂ ∂ α ∫ 0 1 x α - 1 (1 - x) β - 1 dx = 1 B (α, β) ∂ B (α, β) ∂ α = ∂ ln ⁡ B (α, β) ∂ α = ∂ ln ⁡ Γ (α) ∂ α - ∂ ln ⁡ Γ (α + β) ∂ α = ψ (α) - ψ (α + β) {\ displaystyle {\ begin {выровнено} \ operatorname {E} [\ ln X] = \ int _ { 0} ^ {1} \ ln x \, f (x; \ alpha, \ beta) \, dx \\ [4pt] = \ int _ {0} ^ {1} \ ln x \, {\ frac { x ^ {\ alpha -1} (1-x) ^ {\ beta -1}} {\ mathrm {B} (\ alpha, \ beta)}} \, dx \ \ [4pt] = {\ frac { 1} {\ mathrm {B} (\ alpha, \ beta)}} \, \ int _ {0} ^ {1} {\ frac {\ p artial x ^ {\ alpha -1} (1-x) ^ {\ beta -1}} {\ partial \ alpha}} \, dx \\ [4pt] = {\ frac {1} {\ mathrm {B } (\ alpha, \ beta)}} {\ frac {\ partial} {\ partial \ alpha}} \ int _ {0} ^ {1} x ^ {\ alpha -1} (1-x) ^ {\ бета -1} \, dx \\ [4pt] = {\ frac {1} {\ mathrm {B} (\ alpha, \ beta)}} {\ frac {\ partial \ mathrm {B} (\ alpha, \ beta)} {\ partial \ alpha}} \\ [4pt] = {\ frac {\ partial \ ln \ mathrm {B} (\ alpha, \ beta)} {\ partial \ alpha}} \\ [4pt ] = {\ frac {\ partial \ ln \ Gamma (\ alpha)} {\ partial \ alpha}} - {\ frac {\ partial \ ln \ Gamma (\ alpha + \ beta)} {\ partial \ alpha} } \\ [4pt] = \ psi (\ alpha) - \ psi (\ alpha + \ beta) \ end {align}}}$

где ψ - дигамма-функция.

Следовательно, геометрическая Среднее значение бета-распределения с параметрами формы α и β является экспонентой дигамма-функций α и β следующим образом:

$GX\; =\; e\; E\; \; [ln\; \; X]\; =\; e\; \psi \; (\alpha )\; -\; \psi \; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; G\_\; \{X\}\; =\; e\; ^\; \{\backslash \; operatorname\; \{E\}\; [\backslash \; ln\; X]\}\; =\; e\; ^\; \{\backslash \; psi\; (\backslash \; alpha)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\}\}$

Хотя для бета-распределение с одинаковыми параметрами формы α = β, оно Отсюда следует, что асимметрия = 0 и режим = среднее = медиана = 1/2, среднее геометрическое меньше 1/2: 0 < GX< 1/2. The reason for this is that the logarithmic transformation strongly weights the values of X close to zero, as ln(X) strongly tends towards negative infinity as X approaches zero, while ln(X) flattens towards zero as X → 1.

Вдоль линии α = β применяются следующие ограничения:

$lim\; \alpha \; =\; \beta \; \to \; 0\; GX\; знак\; равно\; 0\; lim\; \alpha \; =\; \beta \; \to \; \infty \; GX\; =\; 1\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; 0\}\; G\_\; \{X\}\; =\; 0\; \backslash \backslash \; \backslash \; lim\; \_\; \{\; \backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; G\_\; \{X\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; end\; \{align\}\}\}$

Ниже приведены ограничения с одним конечным параметром (ненулевым) и другие, приближающиеся к этим пределам:

$lim\; \beta \; \to \; 0\; GX\; =\; lim\; \alpha \; \to \; \infty \; GX\; =\; 1\; lim\; \alpha \; \to \; 0\; GX\; =\; lim\; \beta \; \to \; \infty \; GX\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; в\; 0\}\; G\_\; \{X\}\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; G\_\; \{X\}\; =\; 1\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; G\_\; \{X\}\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; G\_\; \{X\}\; =\; 0\; \backslash \; end\; \{align\}\}\}$

На прилагаемом графике показана разница между средним и средним геометрическим для параметров формы α и β от нуля до 2. Помимо того, что разница между они стремятся к нулю, когда α и β приближаются к бесконечности, и что разница становится большой при значениях α и β, приближающихся к нулю, на e можно наблюдать очевидную асимметрию среднего геометрического относительно параметров формы α и β. Разница между средним геометрическим и средним значением больше для малых значений α по отношению к β, чем при обмене величинами β и α.

Н. Л. Джонсон и С. Коц предлагает логарифмическое приближение к дигамма-функции ψ (α) ≈ ln (α - 1/2), которое приводит к следующему приближению к среднему геометрическому:

$GX\; \approx \; \alpha \; -\; 1\; 2\; \alpha \; +\; \beta \; -\; 1\; 2,\; если\; \alpha ,\; \beta >1.\; \{\backslash \; displaystyle\; G\_\; \{X\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{\backslash \; alpha\; \backslash ,\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\}\; \{\backslash \; текст\; \{if\}\}\; \backslash \; alpha,\; \backslash \; beta>1.\}$

Числовые значения для относительной ошибки в этом приближении следующие: [(α = β = 1): 9,39%]; [(α = β = 2): 1,29%]; [(α = 2, β = 3): 1,51%]; [(α = 3, β = 2): 0,44%]; [(α = β = 3): 0,51%]; [(α = β = 4): 0,26%]; [(α = 3, β = 4): 0,55%]; [(α = 4, β = 3): 0, 24%].

Аналогичным образом можно вычислить параметры формы, необходимые для того, чтобы среднее геометрическое было равно 1/2. Ответ заключается в том, что (при β>1) желаемое значение α стремится к β + 1/2 при β → ∞. Например, все эти пары имеют одно и то же среднее геометрическое 1/2: [ β = 1, α = 1,4427], [β = 2, α = 2,4695 8], [β = 3, α = 3,47943], [β = 4, α = 4,48449], [β = 5, α = 5,48756], [β = 10, α = 10,4938], [β = 100, α = 100,499].

Фундаментальное свойство среднего геометрического, которое может быть доказано как ложное для любого другого среднего, - это

$G\; (1\; -\; X)\; =\; e\; E\; \; [ln\; \; (1\; -\; X)]\; =\; e\; \psi \; (\beta )\; -\; \psi \; (\alpha \; +\; \beta )\; \{\backslash \; Displaystyle\; G\; \_\; \{(1-X)\}\; =\; e\; ^\; \{\backslash \; operatorname\; \{E\}\; [\backslash \; ln\; (1-X)]\}\; =\; e\; ^\; \{\backslash \; psi\; (\backslash \; beta)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta))\}\}$

Вдоль линии α = β применяются следующие ограничения:

$lim\; \alpha \; знак\; равно\; \beta \; \to \; 0\; G\; (1\; -\; Икс)\; =\; 0\; lim\; \alpha \; =\; \beta \; \to \; \infty \; G\; (1\; -\; X)\; =\; 1\; 2\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; 0\}\; G\; \_\; \{(1-X)\}\; =\; 0\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; G\; \_\; \{(1-X)\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; end\; \{выровнено\}\}\}$

Ниже приведены пределы с одним конечным параметром (), а другой приближается к этому пределу:

$lim\; \beta \; \to \; 0\; G\; (1\; -\; X)\; =\; lim\; \alpha \; \to \; \infty \; G\; (1\; -\; X)\; Знак\; равно\; 0\; lim\; \alpha \; \to \; 0\; G\; (1\; -\; Икс)\; =\; lim\; \beta \; \to \; \infty \; G\; (1\; -\; Икс)\; =\; 1\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; 0\}\; G\; \_\; \{(1-X)\}\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; G\; \_\; \{(1-\; X)\}\; =\; 0\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; G\; \_\; \{(1-X)\}\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; G\; \_\; \{(1-X)\}\; =\; 1\; \backslash \; end\; \{align\}\}\}$

Имеет следующее приблизительное значение:

$G\; (1\; -\; X)\; \approx \; \beta \; -\; 1\; 2\; \alpha \; +\; \beta \; -\; 1\; 2,\; если\; \alpha ,\; \beta >1.\; \{\backslash \; Displaystyle\; G\; \_\; \{(1-X)\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{\backslash \; beta\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha,\; \backslash \; beta>1.\}$

Хотя и G X, и G (1-X) асимметричны, в случае, если обе формы равны α = β, средние геометрические равны: G X = G (1 - X). Это равенство следует из следующей симметрии, подход для обоими средними геометрическими:

$GX\; (В\; (\alpha ,\; \beta ))\; =\; G\; (1\; -\; Икс)\; (B\; (\beta ,\; \alpha )).\; \{\backslash \; Displaystyle\; G\_\; \{X\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; альфа,\; \backslash \; бета))\; =\; G\_\; \{(1-X)\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha)).\}$

Гармоническое среднее

Гармоническое среднее для бета-распределения для 0 < α < 5 and 0 < β < 5 Гармоническое среднее для бета-распределения в зависимости от α и β от 0 до 2 Средние гармонические для бета-распределения Фиолетовый = H (X), желтый = H (1 - X), меньшие значения α и β спереди Средние гармонические для бета-распределения Pu rple = H (X), желтый = H (1 - X), большие значения α и β впере

Обратна я величина гармонического (HXсреднего распределения с случайной величиной значения X - это среднее арифметическое 1 / X или, что то же самое, его ожидаемое. Следовательно, среднее гармоническое (HX) бета-распределение с предусмотренной формой α и β составляет:

$HX\; =\; 1\; E\; \; [1\; X]\; =\; 1\; \int \; 0\; 1\; f\; (x;\; \alpha ,\; \beta )\; xdx\; Знак\; равно\; 1\; \int \; 0\; 1\; Икс\; \alpha \; -\; 1\; (1\; -\; Икс)\; \beta \; -\; 1\; Икс\; В\; (\alpha ,\; \beta )\; dx\; =\; \alpha \; -\; 1\; \alpha \; +\; \beta \; -\; 1,\; если\; \alpha >1\; и\; \beta >0\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\; \}\; H\_\; \{X\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{X\}\}\; \backslash \; right]\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \{\backslash \; frac\; \{f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\}\; \{x\}\}\; \backslash ,\; dx\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \{\backslash \; frac\; \{x\; ^\; \{\backslash \; alpha\; -1\}\; (1-x)\; ^\; \{\backslash \; beta\; -1\}\}\; \{x\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; \backslash ,\; dx\}\}\; \backslash \; \backslash \; =\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha>1\; \{\backslash \; text\; \{and\}\}\; \backslash \; beta>0\; \backslash \backslash \backslash \; конец\; \{выровнен\; \}\}\}$

среднее гармоническое (HX) бета-распределение с α < 1 is undefined, because its defining expression is not bounded in [0, 1] for shape parameter α less than unity.

Доп усти м, что α = β в приведенном выше выражении получается

$HX\; =\; \alpha \; -\; 1\; 2\; \alpha \; -\; 1,\; \{\backslash \; displaystyle\; H\_\; \{X\}\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\}\; \{2\; \backslash \; alpha\; -1\}\},\; \}$

показывает, что при α = β среднее гармоническое колеблется от 0 при α = β = 1 до 1/2 при α = β → ∞.

Ниже приведены пределы с одним конечным параметром (ненулевым) и другим, приближающимся к этому пределам:

$lim\; \alpha \; \to \; 0\; HX\; не\; определено\; lim\; \alpha \; \to \; 1\; HX\; =\; lim\; \beta \; \to \; \infty \; HX\; =\; 0\; lim\; \beta \; \to \; 0\; HX\; =\; lim\; \alpha \; \to \; \infty \; HX\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; H\_\; \{X\}\; \{\backslash \; text\; \{is\; undefined\}\}\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 1\}\; H\_\; \{X\}\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; H\_\; \{X\}\; =\; 0\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; 0\}\; H\_\; \{X\}\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; H\_\; \{X\}\; =\; 1\; \backslash \; end\; \{align\}\}\}$

Гармоническое среднее играет роль в максимальном правдоподобии для случая с четырьмя элементами в дополнение к среднему геометрическому геометрическому. Фактически, при выполнении оценки правдоподобия для случая с четырьмя функции, помимо гармонического среднего H X на основе случайной величины X, появляется еще одно гармоническое среднее: гармоническое среднее, основанное на линейном преобразовании (1 - X), зеркальное отображение X, обозначаемое H 1 - X :

$H\; 1\; -\; X\; =\; 1\; E\; \; [1\; 1\; -\; X]\; =\; \beta \; -\; 1\; \alpha \; +\; \beta \; -\; 1,\; если\; \beta >1,\; и\; \alpha >0.\; \{\backslash \; Displaystyle\; H\_\; \{1-X\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right]\}\}\; =\; \{\backslash \; frac\; \{\backslash \; beta\; -\; 1\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; beta>1,\; \{\backslash \; text\; \{and\}\}\; \backslash \; alpha>0.\}$

Гармоническое среднее (H (1 - X)) бета-распределения с β < 1 is undefined, because its defining expression is not bounded in [0, 1] for shape parameter β less than unity.

Допустим, что α = β в приведенном выше выражении, получаем

$ЧАС\; (1\; -\; Икс)\; знак\; равно\; \beta \; -\; 1\; 2\; \beta \; -\; 1,\; \{\backslash \; displaystyle\; H\; \_\; \{(1-X)\}\; =\; \{\backslash \; frac\; \{\backslash \; beta\; -1\}\; \{2\; \backslash \; beta\; -1\}\},\}$

среднее гармоническое колеблется от 0 при α = β = 1 до 1/2 при α = β → ∞.

Ниже приведены пределы с одним конечным параметром (ненулевым) и другой приближается к этому пределу :

$lim\; \beta \; \to \; 0\; H\; 1\; -\; X\; не\; определено\; lim\; \beta \; \to \; 1\; H\; 1\; -\; X\; =\; lim\; \alpha \; \to \; \infty \; H\; 1\; -\; X\; =\; 0\; lim\; \alpha \; \to \; 0\; H\; 1\; -\; X\; =\; lim\; \beta \; \to \; \infty \; ЧАС\; 1\; -\; Икс\; Знак\; равно\; 1\; \{\backslash \; Displaystyle\; \{\backslash \; б\; egin\; \{align\}\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; 0\}\; H\_\; \{1-X\}\; \{\backslash \; text\; \{не\; определено\}\}\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; 1\}\; H\_\; \{1-X\}\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; H\_\; \{1-X\}\; =\; 0\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; H\_\; \{1-X\}\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; H\_\; \{1-X\}\; =\; 1\; \backslash \; end\; \{align\}\}\}$

Хотя оба H X и H 1-X являются асимметричными, в случае, когда оба параметра равны α = β, гармонические средние равны: H X = H 1-X. Это равенство следует из следующей симметрии, отображаемой между обоими гармоническими средними:

$H\; X\; (B\; (\alpha ,\; \beta ))\; =\; H\; 1\; -\; X\; (B\; (\beta ,\; \alpha )),\; если\; \alpha ,\; \beta >1.\; \{\backslash \; Displaystyle\; H\_\; \{X\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; H\_\; \{1-X\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\; \{\backslash \; text\; \{if\}\}\; \backslash \; альфа,\; \backslash \; бета>1.\}$

Меры статистической дисперсии

Дисперсия

дисперсия (второй момент, сосредоточенный на среднем) бета-случайная величина X с ограничениями α и β:

$var\; \; (X)\; =\; E\; \; [(X\; -\; \mu )\; 2]\; =\; \alpha \; \beta \; (\alpha \; +\; \beta )\; 2\; (\alpha \; +\; \beta \; +\; 1)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; operatorname\; \{E\}\; [(X-\; \backslash \; mu)\; ^\; \{2\}]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; \backslash \; beta\}\; \{(\backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{2\}\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\}\}$

Если в приведенном выше выражении указать α = β, получим

$var\; \; (X)\; =\; 1\; 4\; (2\; \beta \; +\; 1),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \{\backslash \; frac\; \{1\}\; \{4\; (2\; \backslash \; beta\; +1)\}\},\}$

показывает, что для α = β дисперсия монотонно уменьшается по мере увеличения α = β. α = β = 0 в этом выражении находимой максимальной дисперсии var (X) = 1/4, которая возникает только при приближении к пределу при α = β = 0.

Бета-распределение также может быть параметризовано в терминах его среднего μ (0 < μ < 1) and sample size ν = α + β (ν>0) (см. Раздел ниже под названием «Среднее значение и размер выборки»):

$\alpha \; =\; \mu \; \nu ,\; где\; \nu \; =\; (\alpha \; +\; \beta )>0\; \beta \; =\; (1\; -\; \mu )\; \nu ,\; где\; \nu \; =\; (\alpha \; +\; \beta )>0.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; alpha\; =\; \backslash \; mu\; \backslash \; nu,\; \{\backslash \; text\; \{where\}\}\; \backslash \; nu\; =\; (\backslash \; alpha\; +\; \backslash \; beta)>0\; \backslash \backslash \backslash \; beta\; =\; (1-\; \backslash \; mu)\; \backslash \; ню,\; \{\backslash \; текст\; \{где\}\}\; \backslash \; ню\; =\; (\backslash \; альфа\; +\; \backslash \; бета)>0.\; \backslash \; end\; \{align\}\}\}$

Использование Эти параметры, можно выразить дисперсию в терминах среднего μ и размера выборки следующим образом:

$var\; \; (X)\; =\; \mu \; (1\; -\; \mu )\; 1\; +\; \nu \; \{\backslash \; displaystyle\; \backslash \; OperatorName\; \{var\}\; (\; X)\; =\; \{\backslash \; frac\; \{\backslash \; mu\; (1-\; \backslash \; mu)\}\; \{1+\; \backslash \; nu\}\}\}$

Время ν = (α + β)>0, должно следовать, что var (X) < μ(1 − μ).

Для симметричного распределения среднее значение находится в середине распределения, μ = 1/2, и поэтому:

$var\; \; (X)\; =\; 1\; 4\; (1\; +\; \nu ),\; если\; \mu \; =\; 1\; 2\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\; \}\; (X)\; =\; \{\backslash \; frac\; \{1\}\; \{4\; (1+\; \backslash \; nu)\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; mu\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\}$

Кроме того, следующие пределы (с приближением к пределу только приведенных выше выражений) могут быть получены из приведенных выше выражений:

$lim\; \beta \; \to \; 0\; var\; \; (X)\; =\; lim\; \alpha \; \to \; 0\; var\; \; (X)\; =\; lim\; \beta \; \to \; \infty \; var\; \; (X)\; =\; lim\; \alpha \; \to \; \infty \; var\; \; (X)\; =\; lim\; \nu \; \to \; \infty \; var\; \; (X)\; =\; lim\; \mu \; \to \; 0\; var\; \; (X)\; =\; lim\; \mu \; \to \; 1\; var\; \; (X)\; знак\; равно\; 0\; lim\; \nu \; \to \; 0\; var\; \; (X)\; =\; \mu \; (1\; -\; \mu )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\; \}\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\; \}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; to\; 1\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; 0\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; \backslash \; mu\; (1-\; \backslash \; mu)\; \backslash \; end\; \{выровнено\}\}$

Геометрическая дисперсия и ковариация

логарифм геометрической дисперсии по сравнению с α и β логарифм геометрической дисперсии по сравнению с α и β

Логарифм геометрической дисперсии, ln (var GX) распределения со случайной величиной X - второй момент логарифма X с центром на среднем геометрическом значении X, ln (G X):

$ln\; \; var\; GX\; =\; E\; \; [(ln\; \; X\; -\; ln\; \; GX)\; 2]\; =\; E\; \; [(ln\; \; X\; -\; E\; \; [ln\; \; X])\; 2]\; =\; E\; \; [(ln\; \; X)\; 2]\; -\; (\dots \; \; [пер\; \; Икс])\; 2\; знак\; равно\; вар\; \; [пер\; \; Икс]\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; пер\; \backslash \; о\; peratorname\; \{var\}\; \_\; \{GX\}\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [(\backslash \; ln\; X-\; \backslash \; ln\; G\_\; \{X\})\; ^\; \{2\}\; \backslash \; right]\; \backslash \backslash \; =\; \backslash \; operatorname\; \{E\}\; [(\backslash \; ln\; X-\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; ln\; X])\; ^\; \{2\}\; \backslash \; right]\; \backslash \backslash \; =\; \backslash \; operatorname\; \{E\; \}\; \backslash \; left\; [(\backslash \; ln\; X)\; ^\; \{2\}\; \backslash \; right]\; -\; (\backslash \; operatorname\; \{E\}\; [\backslash \; ln\; X])\; ^\; \{2\}\; \backslash \backslash \; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; X]\; \backslash \; end\; \{\; align\}\}\}$

и, следовательно, геометрическая дисперсия составляет:

$var\; GX\; =\; e\; var\; \; [ln\; \; X]\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; \_\; \{GX\}\; =\; e\; ^\; \{\backslash \; operatorname\; \{var\}\; [\backslash \; ln\; X]\}\}$

В Fisher матрица, кривизна логарифма функции правдоподобия, логарифм геометрической дисперсии отраженной переменной 1 - X и логарифм информации геометрической ковариации между X и 1 - X:

$ln ⁡ var G (1 - X) = E ⁡ [(ln ⁡ (1 - X) - ln ⁡ G 1 - X) 2] = E ⁡ [(ln ⁡ (1 - X) - E ⁡ [ln ⁡ (1 - X)]) 2] = E ⁡ [(ln ⁡ (1 - X)) 2] - (E ⁡ [ln ⁡ (1 - X)]) 2 = var ⁡ [ln ⁡ (1 - X)] var G ( 1 - X) = e var ⁡ [ln ⁡ (1 - X)] ln ⁡ cov GX, 1 - X = E ⁡ [(ln ⁡ X - ln ⁡ GX) (ln ⁡ (1 - X) - ln ⁡ G 1 - X)] = E ⁡ [(ln ⁡ X - E ⁡ [ln ⁡ X]) (ln ⁡ (1 - X) - E ⁡ [ln ⁡ (1 - X)])] = E ⁡ [ln ⁡ X ln ⁡ (1 - X)] - E ⁡ [ln ⁡ X] E ⁡ [ln ⁡ (1 - X)] = cov ⁡ [пер ⁡ Икс, пер ⁡ (1 - Икс)] cov GX, (1 - X) = е cov ⁡ [пер ⁡ X, пер ⁡ (1 - X)] {\ displaystyle {\ begin {выровнено} \ ln \ operatorname {var_ {G (1-X)}} = \ operatorname {E} [(\ ln (1-X) - \ ln G_ {1-X}) ^ {2}] \\ = \ operatorname {E} [(\ ln (1-X) - \ operatorname {E} [\ ln (1-X)]) ^ {2}] \\ = \ operatorname {E} [(\ ln (1-X)) ^ {2}] - (\ operatorname {E} [\ ln (1- X)]) ^ {2} \\ = \ operatorname {var} [\ ln (1-X)] \\ \\\ OperatorName {var_ {G (1-X)}} = e ^ {\ OperatorName {var} [\ ln (1-X)]} \\ \\\ ln \ operatorname {cov_ {G {X, 1- X}}} = \ operatorname {E} [(\ ln X- \ ln G_ {X}) (\ ln (1-X) - \ ln G_ {1-X})] \\ = \ operatorname {E} [(\ ln X- \ operatorname {E} [\ ln X]) (\ ln (1-X) - \ operatorname {E} [\ ln (1-X)])] \\ = \ operatorname {E} \ left [ \ ln X \ ln (1-X) \ right] - \ operatorname {E} [\ ln X] \ operatorname {E} [\ ln (1-X)] \\ = \ operatorname {cov} [\ ln X, \ ln (1-X)] \\ \\\ operatorname {cov} _ {G {X, (1-X)}} = e ^ {\ operatorname {cov} [\ ln X, \ ln (1-X)]} \ end {align}}}$

Для бета-распределения логарифмические моменты более высокого порядка могут быть получены путем использования представления бета-распределения как пропорции двух гамма-распределений и дифференцирования через интеграл. Они могут быть выражены через полигамма-функции высокого порядка. См. Раздел «Другие моменты, Моменты преобразованных случайных величин, Моменты логарифмически преобразованных случайных величин». дисперсия логарифмических чисел и ковариация ln X и ln (1 - X):

$var\; \; [ln\; \; X]\; =\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; X]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}$

$var\; \; [пер\; \; (1\; -\; Икс)]\; знак\; равно\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; альфа\; +\; \backslash \; бета)\}$

$cov\; \; [пер\; \; X,\; пер\; \; (1\; -\; X)]\; =\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; [\backslash \; ln\; X,\; \backslash \; ln\; (1-X)]\; =\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}$

где тригамма-функция, обозначается ψ 1 (α), является вторым из полигамма-функций и определяется как производная от дигамма-функции :

$\psi \; 1\; (\alpha )\; =\; d\; 2\; ln\; \; \Gamma \; (\alpha )\; d\; \alpha \; 2\; =\; d\; \psi \; (\alpha )\; d\; \alpha .\; \{\backslash \; Displaystyle\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{d\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{d\; \backslash ,\; \backslash \; psi\; (\backslash \; alpha)\}\; \{d\; \backslash \; alpha\}\}.\}$

Следовательно,

$ln\; \; var\; GX\; =\; var\; \; [ln\; \; X]\; =\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\; \backslash \; displaystyle\; \backslash \; ln\; \backslash \; operatorname\; \{var\}\; \_\; \{GX\}\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; X]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}$

$пер\; \; вар\; G\; (1\; -\; Икс)\; =\; вар\; \; [пер\; \; (1\; -\; Икс)]\; =\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; ln\; \backslash \; operatorname\; \{var\}\; \_\; \{\; G\; (1-X)\}\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}$

$пер\; \; cov\; GX,\; 1\; -\; Икс\; =\; cov\; \; [пер\; \; X,\; пер\; \; (1\; -\; X)]\; =\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; ln\; \backslash \; operatorname\; \{cov\}\; \_\; \{GX,\; 1-\; X\}\; =\; \backslash \; operatorname\; \{cov\}\; [\backslash \; ln\; X,\; \backslash \; ln\; (1-X)]\; =\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}$

На прилагаемых графиках показаны логарифмические геометрические отклонения и логарифм геометрическая ковариация в зависимости от параметров формы α и β. Графики показывают, что логарифмические геометрические отклонения и логарифмические геометрические ковариации близки к нулю для параметров формы α и β, превышающие 2, и что значения логарифмических геометрических отклонений быстро возрастают для значений параметров α и β меньше единицы. Геометрические отклонения журнала положительны для всех значений параметров формы. Логарифмическая геометрическая ковариация отрицательна для всех параметров формы и больших отрицательных значений для α и β меньше единицы.

Ниже приведены пределы с одним конечным параметром (ненулевым), и другой приближается к этому пределу:

$lim α → 0 ln ⁡ var GX = lim β → 0 ln ⁡ var G (1 - X) = ∞ lim β → 0 ln ⁡ var GX = lim α → ∞ ln ⁡ var GX = lim α → 0 ln ⁡ var G (1 - X) = lim β → ∞ ln ⁡ var G (1 - X) = lim α → ∞ ln ⁡ cov GX, (1 - X) = lim β → ∞ ln ⁡ cov GX, (1 - X) = 0 lim β → ∞ ln ⁡ var GX = ψ 1 (α) lim α → ∞ ln ⁡ var G (1 - X) = ψ 1 (β) lim α → 0 ln ⁡ cov GX, (1 - X) = - ψ 1 (β) lim β → 0 ln ⁡ cov GX, (1 - X) = - ψ 1 (α) {\ Displaystyle {\ begin {align} \ lim _ {\ alpha \ to 0} \ ln \ operatorname {var} _ {GX} = \ lim _ {\ beta \ to 0} \ ln \ operatorname { var} _ {G (1-X)} = \ infty \\ \ lim _ {\ beta \ to 0} \ ln \ operatorname {var} _ {GX} = \ lim _ {\ alpha \ to \ infty} \ ln \ operatorname {var} _ {GX} = \ lim _ {\ alpha \ to 0} \ ln \ operatorname {var} _ {G (1-X)} = \ lim _ {\ beta \ to \ infty} \ ln \ operatorname {var} _ {G (1-X)} = \ lim _ {\ alpha \ to \ infty} \ ln \ operatorname {cov } _ {GX, (1-X)} = \ lim _ {\ beta \ to \ infty} \ ln \ operatorname {cov} _ {GX, (1-X)} = 0 \\ \ lim _ {\ beta \ to \ infty} \ ln \ operatorname {var} _ {GX} = \ psi _ {1} (\ alpha) \\ \ lim _ {\ alpha \ to \ infty} \ ln \ operatorname {var} _ {G (1-X)} = \ psi _ {1} (\ beta) \\ \ lim _ {\ alpha \ to 0} \ ln \ operatorname {cov} _ {GX, (1-X)} = - \ psi _ {1} (\ beta) \\ \ lim _ {\ beta \ to 0} \ ln \ operatorname {cov} _ {GX, (1-X)} = - \ psi _ {1} ( \ alpha) \ end {align}}}$

Пределы с двумя изменяемыми ограничениями:

$lim α → ∞ (lim β → ∞ ln ⁡ var GX) = lim β → ∞ (lim α → ∞ ln ⁡ var G (1 - X)) = lim α → ∞ (lim β → 0 ln ⁡ cov GX, (1 - X)) = lim β → ∞ (lim α → 0 ln ⁡ cov GX, (1 - X)) = 0 lim α → ∞ (lim β → 0 ln ⁡ var GX) = lim β → ∞ (lim α → 0 ln ⁡ var G (1 - X)) = ∞ lim α → 0 (lim β → 0 ln ⁡ cov GX, (1 - Икс)) = lim β → 0 (lim α → 0 ln ⁡ cov GX, (1 - X)) Знак равно - ∞ {\ Displaystyle {\ begin {align} \ lim _ {\ alpha \ to \ infty} (\ lim _ {\ beta \ to \ infty} \ l n \ operatorname {var} _ {GX}) = \ lim _ {\ beta \ to \ infty} (\ lim _ {\ alpha \ to \ infty} \ ln \ operatorname {var} _ {G (1-X) }) = \ lim _ {\ alpha \ to \ infty} (\ lim _ {\ beta \ to 0} \ ln \ operatorname {cov} _ {GX, (1-X)}) = \ lim _ {\ beta \ to \ infty} (\ lim _ {\ alpha \ to 0} \ ln \ operatorname {cov} _ {GX, (1-X)}) = 0 \\ \ lim _ {\ alpha \ to \ infty} (\ lim _ {\ beta \ to 0} \ ln \ operatorname {var} _ {GX}) = \ lim _ {\ beta \ to \ infty} (\ lim _ {\ alpha \ to 0} \ ln \ operatorname {var} _ {G (1-X)}) = \ infty \\ \ lim _ {\ alpha \ to 0} (\ lim _ {\ beta \ to 0} \ ln \ operatorname {cov} _ {GX, (1-X)}) = \ lim _ {\ beta \ to 0} (\ lim _ {\ alpha \ to 0} \ ln \ operatorname {cov} _ {GX, (1-X)}) = - \ infty \ end {выровнено}}}$

Хотя и ln (var GX), и ln (var G (1 - X)) асимметричны, когда параметры формы равны, α = β, один имеет: ln (var GX) = ln (var G (1-X)). Это равенство следует из следующей симметрии, отображаемой между двумя логарифмическими геометрическими дисперсиями:

$ln\; \; var\; G\; X\; \; (B\; (\alpha ,\; \beta ))\; =\; ln\; \; var\; G\; (1\; -\; X)\; \; (B\; (\beta ,\; \alpha )).\; \{\backslash \; displaystyle\; \backslash \; ln\; \backslash \; operatorname\; \{var\}\; \_\; \{GX\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; \backslash \; ln\; \backslash \; operatorname\; \{var\}\; \_\; \{G\; (1-X)\}\; (\backslash \; mathrm\; \{B\; \}\; (\backslash \; beta,\; \backslash \; alpha)).\}$

Лог-геометрическая ковариация симметрична:

$ln\; \; cov\; GX,\; (1\; -\; X)\; \; (B\; (\alpha ,\; \beta ))\; =\; ln\; \; cov\; GX,\; (1\; -\; Икс)\; \; (В\; (\beta ,\; \alpha ))\; \{\backslash \; Displaystyle\; \backslash \; ln\; \backslash \; operatorname\; \{cov\}\; \_\; \{GX,\; (1-X)\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; альфа,\; \backslash \; бета))\; =\; \backslash \; ln\; \backslash \; operatorname\; \{cov\}\; \_\; \{GX,\; (1-X)\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

Среднее абсолютное отклонение от среднего

Отношение абсолютного среднего отклонения. в Std.Dev. для бета-распределения с α и β в диапазоне от 0 до 5 Отношение среднего абсолютного отклонения. в Std.Dev. для бета-распределения со средним 0 ≤ μ ≤ 1 и размером выборки 0 < ν ≤ 10

Среднее отклонение вокруг среднего для бета-распределения с регулируемой формы α и β составляет:

$E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; Знак\; равно\; 2\; \alpha \; \alpha \; \beta \; \beta \; B\; (\alpha ,\; \beta )\; (\alpha \; +\; \beta )\; \alpha \; +\; \beta \; +\; 1\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; \{\backslash \; frac\; \{2\; \backslash \; alpha\; ^\; \{\backslash \; alpha\}\; \backslash \; beta\; ^\; \{\backslash \; beta\}\}\; \{\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; (\backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{\backslash \; альфа\; +\; \backslash \; бета\; +1\}\}\}\}$

Среднее абсолютное отклонение около среднего - это более надежная оценка из статистической дисперсии, чем стандартное отклонение для бета -распределений с хвостами и точками перегиба на каждой стороне моды, бета (α, β) с α, β>2, так как оно зависит от линейных (абсолютных) отклонений, а не от квадратичных отклонений от среднего. Таким образом, влияние очень большого отклонения от среднего значения не так сильно взвешено.

Используя приближение Стирлинга к гамма-функции, Н.Л.Джонсон и С.Котц получил следующее приближение для значений параметров формы больше единицы (относительная погрешность для этого приближения составляет всего -3,5% при α = β = 1 и уменьшается до нуля при α → ∞, β → ∞):

$среднее\; значение\; абс.\; разработчик\; от\; среднего\; стандартного\; отклонения\; =\; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; var\; \; (X)\; \approx \; 2\; \pi \; (1\; +\; 7\; 12\; (\alpha \; +\; \beta )\; -\; 1\; 12\; \alpha \; -\; 1\; 12\; \beta ),\; если\; \alpha ,\; \beta >1.\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровненный\}\; \{\backslash \; frac\; \{\backslash \; text\; \{означает\; абс.\; разработчик\; от\; среднего\}\}\; \{\backslash \; text\; \{стандартное\; отклонение\}\}\}\; =\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\}\; \{\backslash \; sqrt\; \{\backslash \; operatorname\; \{var\}\; (X)\}\}\}\; \backslash \backslash \; \backslash \; приблизительно\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\}\}\}\; \backslash \; left\; (1\; +\; \{\backslash \; frac\; \{7\}\; \{12\; (\backslash \; alpha\; +\; \backslash \; beta)\}\}\; \{\}\; -\; \{\backslash \; frac\; \{1\}\; \{12\; \backslash \; alpha\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{12\; \backslash \; beta\}\}\; \backslash \; right),\; \{\backslash \; text\; \{\; если\}\}\; \backslash \; alpha,\; \backslash \; beta>1.\; \backslash \; end\; \{align\}\}\}$предел α → ∞, β → ∞, отношение среднего абсолютного отклонения к стандартному отклонению (для бета-распределения) становится равным относительно тех же мер для нормального распределения: $2\; \pi \; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\}\}\}\}$. Для α = β = 1 это соотношение равно $3\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{3\}\}\; \{2\}\}\}$, так что от α = β = 1 до α, β → ∞ отношение уменьшается на 8,5%. Для α = β = 0 стандартное отклонение в точности равно среднему абсолютному отклонению около среднего значения. с α = β = 0 до α = β = 1 и на 25% с α = β = 0 до α, β → ∞. Однако для искаженных бета-распределений, таких что α → 0 или β → 0, отношение стандартного отклонения к среднему абсолютному отклонению приближается к бесконечности (хотя каждое из них в отдельно сти стремится к нулю), потому что среднее отклонение приближается к нулю быстрее, чем стандартное отклонение.

Использование параметризации в терминах среднего μ и размера выборки ν = α + β>0:

α = μν, β = (1 − μ) ν

один может выразить среднее абсолютное отклонение от среднего в терминах среднего μ и размера выборки ν следующим образом:

$E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; 2\; \mu \; \mu \; \nu \; (1\; -\; \mu )\; (1\; -\; \mu )\; \nu \; \nu \; B\; (\mu \; \nu ,\; (1\; -\; \mu )\; \nu )\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{E\}\; [|\; XE\; [X]\; |]\; =\; \{\backslash \; гидроразрыва\; \{2\; \backslash \; mu\; ^\; \{\backslash \; mu\; \backslash \; nu\}\; (1-\; \backslash \; mu)\; ^\; \{(1-\; \backslash \; mu)\; \backslash \; nu\}\}\; \{\backslash \; nu\; \backslash \; mathrm\; \{B\}\; (\backslash \; mu\; \backslash \; nu,\; (1-\; \backslash \; mu)\; \backslash \; nu)\}\}\}$

Для симметричного распределения среднее значение находится в середине распределения, μ = 1/2, и поэтому:

$E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; 2\; 1\; -\; \nu \; \nu \; B\; (\nu \; 2,\; \nu \; 2)\; =\; 2\; 1\; -\; \nu \; \Gamma \; (\nu )\; \nu \; (\Gamma \; (\nu \; 2))\; 2\; lim\; \nu \; \to \; 0\; (lim\; \mu \; \to \; 1\; 2\; E\; \; [|\; X\; -\; E\; [X]\; |])\; знак\; равно\; 1\; 2\; lim\; \nu \; \to \; \infty \; (lim\; \mu \; \to \; 1\; 2\; E\; \; [|\; X\; -\; E\; [X]\; |])\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; \{\backslash \; frac\; \{2\; ^\; \{1-\; \backslash \; nu\}\}\; \{\backslash \; nu\; \backslash \; mathrm\; \{B\}\; (\{\backslash \; tfrac\; \{\backslash \; nu\}\; \{2\}\},\; \{\backslash \; tfrac\; \{\backslash \; nu\}\; \{2\; \}\})\}\}\; =\; \{\backslash \; frac\; \{2\; ^\; \{1-\; \backslash \; nu\}\; \backslash \; Gamma\; (\backslash \; nu)\}\; \{\backslash \; nu\; (\backslash \; Gamma\; (\{\backslash \; tfrac\; \{\backslash \; nu\}\; \{2\}\}))\; ^\; \{2\}\; \}\}\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; 0\}\; \backslash \; left\; (\backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; to\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; \backslash \; справа)\; =\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; \backslash \; infty\}\; \backslash \; left\; (\backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; to\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; OperatorName\; \{E\}\; [|\; XE\; [X]\; |]\; \backslash \; right)\; =\; 0\; \backslash \; end\; \{align\}\}\}$

Кроме того, следующие ограничения (только для указанной переменной приближается к пределу) могут быть получены из приведенных выше выражений :

$lim\; \beta \; \to \; 0\; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; lim\; \alpha \; \to \; 0\; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; 0\; lim\; \beta \; \to \; \infty \; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; lim\; \alpha \; \to \; \infty \; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; 0\; lim\; \mu \; \to \; 0\; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; lim\; \mu \; \to \; 1\; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; 0\; lim\; \nu \; \to \; 0\; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; \mu \; (1\; -\; \mu )\; lim\; \nu \; \to \; \infty \; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; lim\_\; \{\backslash \; beta\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; 0\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; 0\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; \backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; в\; 1\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; 0\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; \{\backslash \; sqrt\; \{\backslash \; mu\; (1-\; \backslash \; mu)\}\}\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{E\}\; [|\; XE\; [X]\; |]\; =\; 0\; \backslash \; end\; \{align\}\}\}$

Средняя абсолютная разница

Средняя абсолютная разница для бета-распределения:

$MD\; =\; \int \; 0\; 1\; \int \; 0\; 1\; f\; (x;\; \alpha ,\; \beta )\; f\; (y;\; \alpha ,\; \beta )\; |\; х\; -\; у\; |\; dxdy\; знак\; равно\; (4\; \alpha \; +\; \beta )\; В\; (\alpha \; +\; \beta ,\; \alpha \; +\; \beta )\; В\; (\alpha ,\; \alpha )\; В\; (\beta ,\; \beta )\; \{\backslash \; Displaystyle\; \backslash \; mathrm\; \{MD\}\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; \backslash ,\; f\; (y;\; \backslash \; alpha,\; \backslash \; beta)\; \backslash ,\; |\; xy\; |\; \backslash ,\; dx\; \backslash ,\; dy\; =\; \backslash \; left\; (\{\backslash \; frac\; \{4\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{B\; (\backslash \; alpha\; +\; \backslash \; beta,\; \backslash \; alpha\; +\; \backslash \; beta)\}\; \{B\; (\backslash \; alpha,\; \backslash \; alpha)\; B\; (\backslash \; beta,\; \backslash \; beta)\}\}\}$

Коэффициент Джини для бета-распределения составляет половину относительной средней средней разницы:

$G\; =\; (2\; \alpha )\; B\; (\alpha \; +\; \beta ,\; \alpha \; +\; \beta )\; В\; (\alpha ,\; \alpha )\; В\; (\beta ,\; \beta )\; \{\backslash \; Displaystyle\; \backslash \; mathrm\; \{G\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{2\}\; \{\backslash \; alpha\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{B\; (\backslash \; alpha\; +\; \backslash \; beta,\; \backslash \; alpha\; +\; \backslash \; beta)\}\; \{B\; (\backslash \; alpha,\; \backslash \; alpha)\; B\; (\backslash \; beta,\; \backslash \; beta)\}\}\}$

Асимметрия

Асимметрия для бета-распределения как функция дисперсии и среднего

Асимметрия (третий момент с центра в среднем, нормированный на степени дисперсии 3/2) бета-распределения составляет

$\gamma \; 1\; =\; E\; \; [(X\; -\; \mu )\; 3]\; (var\; \; (X))\; 3/2\; =\; 2\; (\beta \; -\; \alpha )\; \alpha \; +\; \beta \; +\; 1\; (\alpha \; +\; \beta \; +\; 2)\; \alpha \; \beta .\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{1\}\; =\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{E\}\; [(X-\; \backslash \; mu)\; ^\; \{3\}]\}\; \{(\backslash \; operatorname\; \{var\}\; (X))\; ^\; \{3/2\}\}\; \}\; =\; \{\backslash \; frac\; \{2\; (\backslash \; beta\; -\; \backslash \; alpha)\; \{\backslash \; sqrt\; \{\backslash \; alpha\; +\; \backslash \; beta\; +1\}\}\}\; \{(\backslash \; alpha\; +\; \backslash \; beta\; +2)\; \{\backslash \; sqrt\; \{\backslash \; alpha\; \backslash \; beta\}\}\}\}\}\; \}.\}$

Допуская α = β в приведенном выше выражении, получаем γ 1 = 0, еще раз обработ, что для α = β распределение симметрично и, следовательно, асимметрия соответствует нулю. Положительный перекос (вправо) для α < β, negative skew (left-tailed) for α>β.

Использование параметров в терминах среднего μ и размера выборки ν = α + β:

$\alpha \; =\; \mu \; \nu ,\; где\; \nu \; =\; (\alpha \; +\; \beta )>0\; \beta \; =\; (1\; -\; \mu )\; \nu ,\; где\; \nu \; =\; (\alpha \; +\; \beta )>0.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; alpha\; \{\}\; =\; \backslash \; mu\; \backslash \; nu,\; \{\backslash \; text\; \{where\}\}\; \backslash \; nu\; =\; (\backslash \; alpha\; +\; \backslash \; beta)>0\; \backslash \backslash \backslash \; beta\; \{\}\; =\; (1-\; \backslash \; mu)\; \backslash \; nu,\; \{\backslash \; text\; \{where\}\}\; \backslash \; nu\; =\; (\backslash \; alpha\; +\; \backslash \; beta)>0.\; \backslash \; end\; \{align\}\}\}$

один можно выразить асимметрию через среднее значение μ и размер выборки ν следующим образом:

$\gamma \; 1\; =\; E\; \; [(X\; -\; \mu )\; 3]\; (var\; \; (X))\; 3/2\; =\; 2\; (1-2\; \mu )\; 1\; +\; \nu \; (2\; +\; \nu )\; \mu \; (1\; -\; \mu ).\; \{\backslash \; Displaystyle\; \backslash \; gamma\; \_\; \{1\}\; =\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{E\}\; [(X-\; \backslash \; mu)\; ^\; \{3\}]\}\; \{(\backslash \; operatorname\; \{\; var\}\; (X))\; ^\; \{3/2\}\}\}\; =\; \{\backslash \; frac\; \{2\; (1-2\; \backslash \; mu)\; \{\backslash \; sqrt\; \{1+\; \backslash \; nu\}\}\}\; \{(2+\; \backslash \; nu)\; \{\backslash \; sqrt\; \{\backslash \; mu\; (1-\; \backslash \; mu)\}\}\}\}.\}$

Асимметрия также может быть выражена только через дисперсию var и среднее значение μ следующим образом:

Прилагаемый график асимметрии, как функции дисперсии и среднего показывает, что максимальная дисперсия (1/4) сочетается с нулевой асимметрией и условием симметрии (μ = 1/2), и что максимальный асимметрия (положительная или отрицательная бесконечность) возникает, когда среднее значение находится на одном конце или другом, так что «масса» распределения вероятностей сосредоточена на концах (минимальная дисперсия).

Следующее выражение для квадрата асимметрии с точки зрения размера выборки ν = α + β и дисперсии var полезно для оценки моментов параметров четырех:

$(\gamma \; 1)\; 2\; знак\; равно\; (E\; \; [(X\; -\; \mu )\; 3])\; 2\; (вар\; \; (Икс))\; 3\; знак\; равно\; 4\; (2\; +\; \nu )\; 2\; (1\; вар\; -\; 4\; (1\; +\; \nu ))\; \{\backslash \; displaystyle\; (\backslash \; gamma\; \_\; \{1\})\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{(\backslash \; operatorname\; \{E\}\; [(X-\; \backslash \; mu)\; ^\; \{3\}])\; ^\; \{2\}\}\; \{(\backslash \; operatorname\; \{var\}\; (X))\; ^\; \{3\}\}\}\; =\; \{\backslash \; frac\; \{4\}\; \{(2+\; \backslash \; nu)\; ^\; \{2\}\}\}\; \{\backslash \; bigg\; (\}\; \{\backslash \; frac\; \{1\}\; \{\backslash \; text\; \{var\}\}\}\; -\; 4\; (1+\; \backslash \; nu)\; \{\backslash \; bigg)\}\}$

Это выражение дает нулевую асимметрию для α = β, поскольку в этом случае (см. раздел «Дисперсия»): $var\; =\; 1\; 4\; (1\; +\; правильно\; \nu )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; =\; \{\backslash \; frac\; \{1\}\; \{4\; (1+\; \backslash \; nu)\}\}\}$.

Для симметричного случая (α = β) асимметрия = 0 во всем диапазоне, и следующие ограничения:

$lim\; \alpha \; =\; \beta \; \to \; 0\; \gamma \; 1\; =\; lim\; \alpha \; =\; \beta \; \to \; \infty \; \gamma \; 1\; =\; lim\; \nu \; \to \; 0\; \gamma \; 1\; =\; lim\; \nu \; \to \; \infty \; \gamma \; 1\; =\; lim\; \mu \; \to \; 1\; 2\; \gamma \; 1\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; 0\}\; \backslash \; gamma\; \_\; \{1\}\; =\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; t\; o\; \backslash \; infty\}\; \backslash \; gamma\; \_\; \{1\}\; =\; \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; 0\}\; \backslash \; gamma\; \_\; \{1\}\; =\; \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; \backslash \; infty\}\; \backslash \; gamma\; \_\; \{1\}\; =\; \backslash \; lim\; \_\; \{\; \backslash \; mu\; \backslash \; to\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; gamma\; \_\; \{1\}\; =\; 0\}$

Для асимметричных случаев (α ≠ β) следующие пределы (только указанная переменная приближается к пределу) могут быть получены из приведенных выше выражений:

$lim α → 0 γ 1 = lim μ → 0 γ 1 = ∞ lim β → 0 γ 1 = lim μ → 1 γ 1 = - ∞ lim α → ∞ γ 1 = - 2 β, lim β → 0 (lim α → ∞ γ 1) = - ∞, lim β → ∞ (lim α → ∞ γ 1) = 0 lim β → ∞ γ 1 = 2 α, lim α → 0 (lim β → ∞ γ 1) = ∞, lim α → ∞ (lim β → ∞ γ 1) = 0 lim ν → 0 γ 1 = 1-2 μ μ (1 - μ), lim μ → 0 (lim ν → 0 γ 1) = ∞, lim μ → 1 (lim ν → 0 γ 1) знак равно - ∞ {\ Displaystyle {\ begin {align} \ lim _ {\ alpha \ to 0} \ gamma _ {1} = \ lim _ {\ mu \ в 0} \ gamma _ {1} = \ infty \\ \ lim _ {\ beta \ to 0} \ gamma _ {1} = \ lim _ {\ mu \ to 1} \ gamma _ {1} = - \ infty \\ \ lim _ {\ alpha \ to \ infty} \ gamma _ {1} = - {\ frac {2} {\ sqrt {\ beta}}}, \ quad \ lim _ {\ be ta \ to 0} (\ lim _ {\ alpha \ to \ infty} \ gamma _ {1}) = - \ infty, \ quad \ lim _ {\ beta \ to \ infty} (\ lim _ {\ alpha \ to \ infty} \ gam ma _ {1}) = 0 \\ \ lim _ {\ beta \ to \ infty} \ gamma _ {1} = {\ frac {2} {\ sqrt {\ alpha}}}, \ quad \ lim _ {\ alpha \ to 0} (\ lim _ {\ beta \ to \ infty} \ gamma _ {1}) = \ infty, \ quad \ lim _ {\ alpha \ to \ infty} ( \ lim _ {\ beta \ to \ infty} \ gamma _ {1}) = 0 \\ \ lim _ {\ nu \ to 0} \ gamma _ {1} = {\ frac {1-2 \ mu} {\ sqrt {\ mu (1- \ mu)}}}, \ quad \ lim _ {\ mu \ to 0} (\ lim _ {\ nu \ to 0} \ gamma _ {1}) = \ infty, \ quad \ lim _ {\ mu \ to 1} (\ lim _ {\ nu \ to 0} \ gamma _ {1}) = - \ infty \ end {align}}}$

эксцесс

чрезмерный эксцесс Для бета-распределения как функция распределения и среднего

Бета-распределение было в акустическом анализе для оценки повреждений зубчатых колес, поскольку как сообщается, эксцесс бета-распределения является хорошим индикатором состояния зубчатого колеса. Эксцесс также использовался, чтобы отличить сейсмический сигнал, создаваемый шагами человека, от других сигналов. Люди или другие цели, движущиеся по земле, генерируют непрерывные сигналы в виде сейсмических волн, можно разделять разные цели на основе генерируемых ими сейсмических волн. Эксцесс чувствителен к импульсным сигналам, поэтому он более чувствителен к сигналу, создаваемомуому сигналу человека, чем другие сигналы, генерируемые транспортными средствами, ветром, шумом и т. Д. К сожалению, обозначения эксцесса не стандартизированы. Кенни и Кепинг используют символ γ 2 для избыточного эксцесса, но Абрамовиц и Стегун используют другую терминологию. Во избежание путаницы между эксцессом (четвертый момент с центром в среднем, нормированный квадратом дисперсии) и избыточным эксцессом при использовании символов они будут записаны следующим образом:

$избыточный\; эксцесс\; =\; эксцесс\; -\; 3\; =\; E\; \; [(X\; -\; \mu )\; 4]\; (\; var\; \; (X))\; 2\; -\; 3\; =\; 6\; [\alpha \; 3\; -\; \alpha \; 2\; (2\; \beta \; -\; 1)\; +\; \beta \; 2\; (\beta \; +\; 1)\; -\; 2\; \alpha \; \beta \; (\beta \; +\; 2)]\; \alpha \; \beta \; (\alpha \; +\; \beta \; +\; 2)\; (\alpha \; +\; \beta \; +\; 3)\; =\; 6\; [(\alpha \; -\; \beta )\; 2\; (\alpha \; +\; \beta \; +\; 1)\; -\; \alpha \; \beta \; (\alpha \; +\; \beta \; +\; 2)]\; \alpha \; \beta \; (\alpha \; +\; \beta \; +\; 2)\; (\alpha \; +\; \beta \; +\; 3).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; \{\backslash \; text\; \{kurtosis\}\}\; -\; 3\; \backslash \backslash \; =\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{E\}\; [(X-\; \backslash \; mu)\; ^\; \{\; 4\}]\}\; \{(\backslash \; operatorname\; \{var\}\; (X))\; ^\; \{2\}\}\}\; -\; 3\; \backslash \backslash \; =\; \{\backslash \; frac\; \{6\; [\backslash \; alpha\; ^\; \{3\}\; -\; \backslash \; alpha\; ^\; \{2\}\; (2\; \backslash \; beta\; -1)\; +\; \backslash \; beta\; ^\; \{2\}\; (\backslash \; beta\; +1)\; -2\; \backslash \; alpha\; \backslash \; beta\; (\backslash \; beta\; +2)]\}\; \{\backslash \; alpha\; \backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; +2)\; (\backslash \; alpha\; +\; \backslash \; beta\; +3)\}\}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{6\; [(\backslash \; alpha\; -\; \backslash \; beta)\; ^\; \{2\}\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\; -\; \backslash \; alpha\; \backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; +2)]\; \}\; \{\backslash \; alpha\; \backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; +2)\; (\backslash \; alpha\; +\; \backslash \; beta\; +3)\}\}.\; \backslash \; end\; \{align\}\}\}$

Если положить α = β в приведенном выше выражении, получится

$избыточный\; эксцесс\; =\; -\; 6\; 3\; +\; 2\; \alpha ,\; если\; \alpha \; =\; \beta \; \{\backslash \; displaystyle\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; -\; \{\backslash \; frac\; \{6\}\; \{3\; +\; 2\; \backslash \; alpha\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha\; =\; \backslash \; beta\}$.

Следовательно, для симметричных бета-распределений избыточный эксцесс отрицательный, возрастая от минимального значения −2 в пределе при {α = β} → 0 и приближаясь к максимальному значению нуля при {α = β} → ∞. Значение −2 - это минимальное значение избыточного эксцесса, которого может когда-либо достичь любое распределение (не только бета-распределения, но и любое распределение любого возможного типа). Это минимальное значение достигается, когда вся плотность вероятности полностью сосредоточена на каждом конце x = 0 и x = 1, и ничего между ними нет: двухточечное распределение Бернулли с равной вероятностью 1/2 на каждом конце (подбрасывание монеты: дальнейшее обсуждение см. в разделе ниже «Эксцесс, ограниченный квадратом асимметрии»). Описание эксцесса как меры «потенциальных выбросов» (или «потенциально редких, экстремальных значений») распределения вероятностей является правильным для всех распределений, включая бета-распределение. В редких случаях в бета-распределении могут встречаться экстремальные значения, тем выше его эксцесс; в противном случае эксцесс будет меньше. Для α ≠ β, перекос бета-распределений, избыточный эксцесс может достичь неограниченных положительных значений (особенно для α → 0 для конечного β или для β → 0 для конечного α), потому что эта сторона, противоположная моде, будет давать случайные экстремальные значения. Минимальный процесс имеет место, когда плотность массы одинаково сконцентрирована на каждом конце (и, следовательно, среднее значение находится в центре), и между концами нет плотности массы вероятности.

Использование параметров в терминах среднего μ и размера выборки ν = α + β:

$\alpha \; =\; \mu \; \nu ,\; где\; \nu \; =\; (\alpha \; +\; \beta )>0\; \beta \; =\; (1\; -\; \mu )\; \nu ,\; где\; \nu \; =\; (\alpha \; +\; \beta )>0.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; alpha\; \{\}\; =\; \backslash \; mu\; \backslash \; nu,\; \{\backslash \; text\; \{where\}\}\; \backslash \; nu\; =\; (\backslash \; alpha\; +\; \backslash \; beta)>0\; \backslash \backslash \backslash \; beta\; \{\}\; =\; (1-\; \backslash \; mu)\; \backslash \; nu,\; \{\backslash \; text\; \{where\}\}\; \backslash \; nu\; =\; (\backslash \; alpha\; +\; \backslash \; beta)>0.\; \backslash \; end\; \{align\}\}\}$

один может выразить избыточный эксцесс через среднее значение μ и размер выборки ν следующим образом:

$избыточный\; эксцесс\; =\; 6\; 3\; +\; \nu \; ((1-2\; \mu )\; 2\; (1\; +\; \nu )\; \mu \; (1\; -\; \mu )\; (2\; +\; \nu )\; -\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; \{\backslash \; frac\; \{6\}\; \{3+\; \backslash \; nu\}\}\; \{\backslash \; bigg\; (\}\; \{\backslash \; frac\; \{(1-2\; \backslash \; mu)\; ^\; \{2\}\; (1+\; \backslash \; nu)\}\; \{\backslash \; mu\; (1-\; \backslash \; mu)\; (2+\; \backslash \; nu)\}\}\; -\; 1\; \{\backslash \; bigg)\}\}$

Избыточный эксцесс также может быть выражен с помощью следующих двух параметров: дисперсия var и размер выборки ν следующим образом:

и, с точки зрения дисперсия var и среднее μ следующим образом:

График избыточного эксцесса как функции дисперсии и среднего показывает, что минимальное значение и збыточного эксцесса s (−2, что является минимально возможным избыточным эксцесса для любого положения) имеет отношение с максимальной величиной дисперсии (1/4) и условием симметрии: среднее значение, имеющееся в средней точке (μ = 1/2). Это происходит для симметричного случая α = β = 0 с нулевой асимметрией. В пределе это 2-точечное распределение Бернулли с равной вероятностью 1/2 для каждой дельта-функции Дирака конец x = 0 и x = 1 и нулевой вероятностью везде. (Подбрасывание монеты: одна грань монеты x = 0, другая сторона - x = 1.) Дисперсия максимальна, потому что распределение является бимодальным, и между двумя режимами (шипами) на каждом конце ничего нет. Избыточный эксцесс минимален: плотность вероятности «масса» равна нулю в среднем и сосредоточена на двух пиках на каждом конце. Избыточный эксцесс достигает минимально возможного значения (для любого распределения), когда функция плотности вероятности имеет два пика на каждом конце: он двухпиковым, и между ничего ними нет.

С другой стороны, график показывает, что для крайних случаев перекоса, когда среднее значение находится около одного или другого конца (μ = 0 или μ = 1), дисперсия близка к нулю, избыточный эксцесс быстро приближается к бесконечности, когда среднее значение распределения приближается к одному из концов.

В качестве альтернативы избыточный эксцесс может быть выражен только с помощью следующих двух параметров: квадрата асимметрии и размера выборки следующим образом:

Из этого последнего выражения можно получить те же самые пределы, опубликованные почти столетие назад Карлом Пирсоном в его статье, для бета-распределения (см. ниже раздел под названием «Эксцесс, ограниченный квадратом асимметрии»). Установив α + β = ν = 0 в приведенном выше выражении, можно получить нижнюю границу Пирсона (значения асимметрии и избыточного эксцесса ниже границы (избыточный эксцесс + 2 - асимметрия = 0) не могут иметь место ни для какого распределения, и, следовательно, Карл Пирсон уместно назвал область ниже этой границы «невозможной областью»). Предел α + β = ν → ∞ определяет верхнюю границу Пирсона.

$lim\; \nu \; \to \; 0\; избыточный\; эксцесс\; =\; (асимметрия)\; 2\; -\; 2\; lim\; \nu \; \to \; \infty \; избыточный\; эксцесс\; =\; 3\; 2\; (асимметрия)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; 0\}\; \{\; \backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; (\{\backslash \; text\; \{skewness\}\})\; ^\; \{2\}\; -2\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; nu\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; \{\backslash \; tfrac\; \{\; 3\}\; \{2\}\}\; (\{\backslash \; text\; \{skewness\}\})\; ^\; \{2\}\; \backslash \; end\; \{align\}\}\}$

следовательно:

Значения ν = α + β, такие, что ν находится в диапазоне от нуля до бесконечности, 0 < ν < ∞, span the whole region of the beta distribution in the plane of excess kurtosis versus squared skewness.

Для симметричного случая (α = β), применяются следующие ограничения:

$lim\; \alpha \; =\; \beta \; \to \; 0\; избыточный\; эксцесс\; =\; -\; 2\; lim\; \alpha \; =\; \beta \; \to \; \infty \; избыточный\; эксцесс\; =\; 0\; lim\; \mu \; \to \; 1\; 2\; избыточный\; эксцесс\; =\; -\; 6\; 3\; +\; \nu \; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; 0\}\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; -\; 2\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; 0\; \backslash \backslash \; \backslash \; lim\; \_\; \{\backslash \; mu\; \backslash \; to\; \{\backslash \; frac\; \{1\}\; \{2\}\; \}\}\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; =\; -\; \{\backslash \; frac\; \{6\}\; \{3+\; \backslash \; nu\}\}\; \backslash \; end\; \{align\}\}\}$

Для н есимметричных случаев (α ≠ β) могут быть получены следующие пределы (с приближением к пределу только характеристик) из приведенных выше выражений:

$lim α → 0 избыточный эксцесс = lim β → 0 избыточный эксцесс = lim μ → 0 избыточный курто sis = lim μ → 1 избыточный эксцесс = ∞ lim α → ∞ избыточный эксцесс = 6 β, lim β → 0 (lim α → ∞ избыточный эксцесс) = ∞, lim β → ∞ (lim α → ∞ избыточный эксцесс) = 0 lim β → ∞ избыточный эксцесс = 6 α, lim α → 0 (lim β → ∞ избыточный эксцесс) = ∞, lim α → ∞ (lim β → ∞ избыточный эксцесс) = 0 lim ν → 0 избыточный эксцесс = - 6 + 1 μ (1 - μ), lim μ → 0 (lim ν → 0 избыточный эксцесс) = ∞, lim μ → 1 (lim ν → 0 избыточный эксцесс) = ∞ {\ displaystyle {\ begin {align} \ lim _ { \ alpha \ to 0} {\ text {избыточный эксцесс}} = \ lim _ {\ beta \ to 0} {\ text {избыточный эксцесс}} = \ lim _ {\ mu \ to 0} {\ text {избыточный эксцесс }} = \ lim _ {\ mu \ to 1} {\ text {избыточный эксцесс}} = \ infty \\ \ lim _ {\ alpha \ to \ infty} {\ text {избыточный ный ный эксцесс}} = {\ frac {6} {\ beta}}, {\ text {}} \ lim _ {\ beta \ to 0} (\ lim _ {\ alpha \ to \ infty} {\ text { избыточный эксцесс}}) = \ infty, {\ text {}} \ lim _ {\ beta \ to \ infty} (\ lim _ {\ alpha \ to \ infty} {\ text {избыточный эксцесс}}) = 0 \ \ \ lim _ {\ beta \ to \ infty} {\ text {избыточный эксцесс}} = {\ frac {6} {\ alpha}}, {\ text {}} \ lim _ {\ alpha \ to 0} (\ lim _ {\ beta \ to \ infty} {\ text {избыточный эксцесс}}) = \ infty, {\ text {}} \ lim _ {\ alpha \ to \ infty} (\ lim _ {\ beta \ to \ infty} {\ text {избыточный эксцесс}}) = 0 \\ \ lim _ {\ nu \ to 0} {\ text {избыточный эксцесс}} = - 6 + {\ frac {1} {\ mu ( 1 - \ mu)}}, {\ text {}} \ lim _ {\ mu \ to 0} (\ lim _ {\ nu \ to 0} {\ text {избыточный эксцесс}}) = \ infty, {\ text {}} \ lim _ {\ mu \ to 1} (\ lim _ {\ nu \ to 0} {\ text {избыточный эксцесс}}) = \ infty \ end {align}}}$

Характеристическая функция

Re (характерная функция) симметричный случай α = β в диапазоне от 25 до 0 Re (характерная функция) симметричный случай α = β в диапазоне от 0 до 25 Re (характерная функция) β = α + 1/2; α в диапазоне от 25 до 0 Re (Характерная функция) α = β + 1/2; β в диапазоне от 25 до 0 Re (Характерная функция) α = β + 1/2; β в диапазоне от 0 до 25

Характеристическая функция представляет собой преобразование Фурье функции плотности вероятности. Характеристическая функция бета-распределения является конфлюэнтная гипергеометрическая функция Куммера (первого рода):

$\phi \; X\; (\alpha ;\; \beta ;\; t)\; =\; E\; \; [eit\; X]\; =\; \int \; 0\; 1\; eitxf\; (x;\; \alpha ,\; \beta )\; dx\; =\; 1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; it)\; =\; \sum \; n\; =\; 0\; \infty \; \alpha \; (n)\; (it)\; n\; (\alpha \; +\; \beta )\; (n)\; n!\; Знак\; равно\; 1\; +\; \sum \; К\; знак\; равно\; 1\; \infty \; (\prod \; г\; =\; 0\; К\; -\; 1\; \alpha \; +\; г\; \alpha \; +\; \beta \; +\; г)\; (я\; т)\; К\; К!\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; varphi\; \_\; \{X\}\; (\backslash \; alpha;\; \backslash \; beta;\; t)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{itX\}\; \backslash \; right]\; \backslash \backslash \; =\; \backslash \; int\; \_\; \{\; 0\}\; ^\; \{1\}\; e\; ^\; \{itx\}\; f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; dx\; \backslash \backslash \; =\; \{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; it)\; \backslash !\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; alpha\; ^\; \{(n)\}\; (it)\; ^\; \{n\}\}\; \{(\backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{(n)\; \}\; n!\}\}\; \backslash \backslash \; =\; 1+\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (\backslash \; prod\; \_\; \{r\; =\; 0\}\; ^\; \{k-1\}\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; r\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; +\; r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{(it)\; ^\; \{k\}\}\; \{k!\}\}\; \backslash \; end\; \{align\}\}\}$

где

$x\; (n)\; =\; x\; (Икс\; +\; 1)\; (Икс\; +\; 2)\; \cdots \; (Икс\; +\; N\; -\; 1)\; \{\backslash \; Displaystyle\; х\; ^\; \{(п)\}\; =\; х\; (х\; +\; 1)\; (х\; +\; 2)\; \backslash \; cdots\; (х\; +\; п-1)\}$

- это возрастающий факториал, также называемый «символом Поххаммера». Значение характеристической функции для t = 0 равно единице:

$\phi \; X\; (\alpha ;\; \beta ;\; 0)\; =\; 1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; 0)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (\backslash \; alpha;\; \backslash \; beta;\; 0)\; =\; \{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; 0)\; =\; 1\}$.

Кроме того, действующая и мнимая части характерной функции имеют следующие симметрии относительно начала измерения t :

$Re\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; it)]\; =\; Re\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; -\; it)]\; \{\backslash \; displaystyle\; \{\backslash \; textrm\; \{Re\}\}\; \backslash \; left\; [\{\; \}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; it)\; \backslash \; right]\; =\; \{\backslash \; textrm\; \{Re\}\}\; \backslash \; left\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; -it)\; \backslash \; right]\}$

$Im\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; it)]\; =\; -\; Im\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; -\; оно)]\; \{\backslash \; displaystyle\; \{\backslash \; textrm\; \{Im\}\}\; \backslash \; left\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; it)\; \backslash \; right]\; =\; -\; \{\backslash \; textrm\; \{Im\}\}\; \backslash \; left\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; -it)\; \backslash \; right]\}$

Симметричный случай α = β упрощает типическую функцию бета-распределения до функции Бесселя, поскольку в частном случае α + β = 2α конфлюэнтная гипергеометрическая функция ction (первый вид) сводится к функции Бесселя (модифицированной функции Бесселя первого рода $I\; \alpha \; -\; 1\; 2\; \{\backslash \; displaystyle\; I\; \_\; \{\backslash \; alpha\; -\; \{\backslash \; frac\; \{1\}\}\; \{2\}\}\}\}$) с использованием второго преобразования Куммера следующим образом:

$1\; F\; 1\; (\alpha ;\; 2\; \alpha ;\; i\; t)\; знак\; равно\; e\; i\; t\; 2\; 0\; F\; 1\; (;\; \alpha \; +\; 1\; 2;\; (i\; t)\; 2\; 16)\; =\; e\; i\; t\; 2\; (i\; t\; 4)\; 1\; 2\; -\; \alpha \; \Gamma \; (\alpha \; +\; 1\; 2)\; I\; \alpha \; -\; 1\; 2\; (i\; t\; 2).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; 2\; \backslash \; alpha;\; it)\; =\; e\; ^\; \{\backslash \; frac\; \{it\}\; \{2\}\}\; \{\}\; \_\; \{0\}\; F\_\; \{1\}\; \backslash \; left\; (;\; \backslash \; alpha\; +\; \{\backslash \; tfrac\; \{1\}\; \{2\}\};\; \{\backslash \; frac\; \{(it)\; ^\; \{2\}\}\; \{16\}\}\; \backslash \; right)\; \backslash \backslash \; =\; e\; ^\; \{\backslash \; frac\; \{\; it\}\; \{2\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{it\}\; \{4\}\}\; \backslash \; right)\; ^\; \{\{\backslash \; frac\; \{1\}\; \{2\}\}\; -\; \backslash \; alpha\}\; \backslash \; Gamma\; \backslash \; left\; (\backslash \; alpha\; +\; \{\backslash \; tfrac\; \{\; 1\}\; \{2\}\}\; \backslash \; right)\; I\; \_\; \{\backslash \; alpha\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{it\}\; \{2\}\}\; \backslash \; right).\; \backslash \; End\; \{align\}\}\}$

На прилагаемых графиках действующая часть (Re) характерной функции бета-распределения отображается для симметричного (α = β) и асимметричного (α ≠ β) случаях..

Другие моменты

Функция момента создания

Отсюда также следует, что функция создания момента равна

$MX\; (\alpha ;\; \beta ;\; t)\; =\; E\; \; [et\; X]\; =\; \int \; 0\; 1\; etxf\; (x;\; \alpha ,\; \beta )\; dx\; =\; 1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; t)\; =\; \sum \; n\; =\; 0\; \infty \; \alpha \; (n)\; (\alpha \; +\; \beta )\; (n)\; ТНН!\; Знак\; равно\; 1\; +\; \sum \; К\; знак\; равно\; 1\; \infty \; (\prod \; г\; =\; 0\; К\; -\; 1\; \alpha \; +\; г\; \alpha \; +\; \beta \; +\; г)\; т\; К\; К!\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; M\_\; \{X\}\; (\backslash \; alpha;\; \backslash \; beta;\; t)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{tX\}\; \backslash \; right]\; \backslash \backslash \; [4pt]\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; e\; ^\; \{tx\}\; f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; \backslash ,\; dx\; \backslash \backslash \; [4pt]\; =\; \{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; t)\; \backslash \backslash \; [4pt]\; =\; \backslash \; sum\; \_\; \{n\; =\; 0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; alpha\; ^\; \{(n)\}\}\; \{(\backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{(n)\; \}\}\}\; \{\backslash \; frac\; \{t\; ^\; \{n\}\}\; \{n!\}\}\; \backslash \backslash \; [4pt]\; =\; 1+\; \backslash \; sum\; \_\; \{k\; =\; 1\}\; ^\; \{\backslash \; infty\}\; \backslash \; left\; (\backslash \; prod\; \_\; \{r\; =\; 0\; \}\; ^\; \{k-1\}\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; r\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; +\; r\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{t\; ^\; \{k\}\}\; \{k!\}\}\; \backslash \; end\; \{выравнивается\}\}\; \}$

В частности, M X (α; β; 0) = 1.

Высшие моменты

Используя функцию , производящую момент, k-й исходный момент задается множителем

$\prod \; r\; =\; 0\; k\; -\; 1\; \alpha \; +\; r\; \alpha \; +\; \beta \; +\; r\; \{\backslash \; displaystyle\; \backslash \; prod\; \_\; \{r\; =\; 0\}\; ^\; \{k-\; 1\}\; \{\; \backslash \; frac\; \{\backslash \; alpha\; +\; r\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; +\; r\}\}\}$

умножение члена (экспоненциального ряда) $(tkk!)\; \{\backslash \; Displaystyle\; \backslash \; left\; (\{\backslash \; frac\; \{t\; ^\; \{k\}\; \}\; \{k!\}\}\; \backslash \; right)\}$в ряду прои зводящей функции момента

$E\; \; [X\; k]\; =\; \alpha \; (k)\; (\alpha \; +\; \beta )\; (К)\; знак\; равно\; \prod \; р\; знак\; равно\; 0\; K\; -\; 1\; \alpha \; +\; р\; \alpha \; +\; \beta \; +\; р\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{E\; \}\; [X\; ^\; \{k\}]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; ^\; \{(k)\}\}\; \{(\backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{(k)\}\}\}\; =\; \backslash \; prod\; \_\; \{r\; =\; 0\}\; ^\; \{k\; -\; 1\}\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; r\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; +\; r\}\}\}$

где (x) - символ Поххаммера, представляющий возрастающий факториал. Его также можно записать в рекурсивной форме как

$E\; \; [X\; k]\; =\; \alpha \; +\; k\; -\; 1\; \alpha \; +\; \beta \; +\; k\; -\; 1\; E\; \; [X\; k\; -\; 1].\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [X\; ^\; \{k\}]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; k-1\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; +\; k-1\}\}\; \backslash \; operatorname\; \{E\}\; [X\; ^\; \{k-\; 1\}].\}$

С момента, когда производящая функция $MX\; (\alpha ;\; \beta ;\; \cdot )\; \{\backslash \; displaystyle\; M\_\; \{X\}\; (\backslash \; alpha;\; \backslash \; beta;\; \backslash \; cdot)\}$имеет положительный радиус сходимости, бета-распределение определяет его моменты.

Моменты преобразованных случайных величин

Моменты линейно преобразованных, произведенных и инвертированных случайных величин

Также можно показать следующие ожидания для преобразованной случайной величины, где случайная величина X является бета-распределенной функцией α и β: X ~ Beta (α, β). Ожидаемое значение значения 1 - X является зеркальной симметричной ожидаемого на основе X:

$E\; \; [1\; -\; X]\; =\; \beta \; \alpha \; +\; \beta \; E\; \; [X\; (1\; -\; X)]\; =\; E\; \; [(1\; -\; Икс)\; Икс\; ]\; знак\; равно\; \alpha \; \beta \; (\alpha \; +\; \beta )\; (\alpha \; +\; \beta \; +\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{E\}\; [1-X]\; =\; \{\backslash \; frac\; \{\backslash \; beta\}\; \{\backslash \; alpha\; +\; \backslash \; бета\}\}\; \backslash \backslash \; \backslash \; operatorname\; \{E\}\; [X\; (1-X)]\; =\; \backslash \; operatorname\; \{E\}\; [(1-X)\; X]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; \backslash \; beta\}\; \{(\backslash \; alpha\; +\; \backslash \; beta)\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\}\}\; \backslash \; end\; \{align\}\}\}$

Из-за зеркальной симметрии функции плотности вероятности бета-распределения дисперсии, основанные на числа X и 1 - X идентичны, а ковариация на X ( 1 - X является отрицательной величиной дисперсии:

$var\; \; [(1\; -\; X)]\; =\; var\; \; [X]\; =\; -\; cov\; \; [X,\; (1\; -\; Икс)]\; знак\; равно\; \alpha \; \beta \; (\alpha \; +\; \beta )\; 2\; (\; \alpha \; +\; \beta \; +\; 1)\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{var\}\; [(1-X)]\; =\; \backslash \; operatorname\; \{var\}\; [X]\; =\; -\; \backslash \; operatorname\; \{cov\}\; [X,\; (1-X)]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; \backslash \; beta\}\; \{(\backslash \; alpha\; +\; \backslash \; beta)\; ^\; \{2\}\; (\backslash \; alpha\; +\; \backslash \; beta\; +1)\}\}\}$

Это ожидаемые значения для инвертированных переме нных (они связаны с гармоническим средним s, см. раздел «Среднее гармоническое»):

$E\; \; [1\; X]\; =\; \alpha \; +\; \beta \; -\; 1\; \alpha \; -\; 1,\; если\; \alpha >1,\; E\; \; [1\; 1\; -\; X]\; =\; \alpha \; +\; \beta \; -\; 1\; \beta \; -\; 1,\; если\; \beta >1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{X\}\}\; \backslash \; right]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\; \{\backslash \; альфа\; -\; 1\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha>1\; \backslash \backslash \; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\; \{\backslash \; beta\; -1\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; beta>1\; \backslash \; end\; \{align\}\}\}$

Следующее преобразование путем деления ее X на зеркальное X / (1 - X) приводит к «инвертированному бета-распределения» или простого бета-распределения (также известное как бета-распределение второго типа или Тип VI Пирсона ):

$E\; \; [X\; 1\; -\; X]\; =\; \alpha \; \beta \; -\; 1,\; если\; \beta >1\; E\; \; [1\; -\; XX]\; =\; \beta \; \alpha \; -\; 1,\; если\; \alpha >1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{\backslash \; beta\; -1\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; beta>1\; \backslash \backslash \; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1-X\}\; \{X\}\}\; \backslash \; right]\; =\; \{\backslash \; frac\; \{\backslash \; beta\}\; \{\backslash \; alpha\; -1\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha>1\; \backslash \; end\; \{align\}\}\}$

Варианты преобразованных чисел могут быть получены интегрированным, так как ожидаемые значения вторых моментов сосредоточены на соответствующие значения:

$var\; \; [1\; X]\; =\; E\; \; [(1\; X\; -\; EE\; [1\; X]])\; 2]\; =\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{X\}\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{X\}\}\; -\; \backslash \; ope\; ratorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{X\}\}\; \backslash \; right]\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\; =\}$

$var\; \; [1\; -\; XX]\; =\; E\; \; [(1\; -\; XX\; -\; E\; \; [1\; -\; XX])\; 2]\; =\; \beta \; (\alpha \; +\; \beta \; -\; 1)\; (\alpha \; -\; 2)\; (\alpha \; -\; 1)\; 2,\; если\; \alpha >2\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; \backslash \; left\; [\{\backslash \; frac\; \{1-X\}\; \{X\}\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{1-X\}\; \{X\}\}\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\; -X\}\; \{X\}\}\; \backslash \; right]\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\; =\; \{\backslash \; frac\; \{\backslash \; beta\; (\backslash \; alpha\; +\; \backslash \; beta\; -1)\}\; \{(\backslash \; alpha\; -2)\; (\backslash \; alpha\; -1)\; ^\; \{2\}\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha>2\}$

Следующая вариация деление измененного X на ее зеркальное отображение (X / (1-X) дает дисперсию« инвертированного бета-распределения »или простое бета-распределения (также известный как бета-распределение второго типа или Тип VI Пирсона ):

$var\; \; [1\; 1\; -\; X]\; =\; E\; \; [(1\; 1\; -\; X\; -\; E\; \; [1\; 1\; -\; X\; ])\; 2]\; =\; var\; \; [X\; 1\; -\; X]\; =\; \{\backslash \; disp\; Laystyle\; \backslash \; имя\; оператора\; \{var\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right]\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{var\}\; \backslash \; left\; [\{\backslash \; fr\; ac\; \{X\}\; \{\; 1-X\}\}\; \backslash \; right]\; =\}$

$E\; \; [(X\; 1\; -\; X\; -\; E\; \; [X\; 1\; -\; X])\; 2]\; =\; \alpha \; (\alpha \; +\; \beta \; -\; 1)\; (\beta \; -\; 2)\; (\beta \; -\; 1)\; 2,\; если\; \beta >2\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{X\}\; \{1-X\}\}\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{X\}\; \{\; 1-X\}\}\; \backslash \; right]\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; (\backslash \; alpha\; +\; \backslash \; beta\; -1)\}\; \{(\backslash \; beta\; -2)\; (\backslash \; beta\; -\; 1)\; ^\; \{\; 2\}\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; beta>2\}$

Ковариации:

$cov\; \; [1\; X,\; 1\; 1\; -\; X]\; =\; cov\; \; [1\; -\; XX,\; X\; 1\; -\; X]\; =\; cov\; \; [1\; X,\; X\; 1\; -\; X]\; =\; cov\; co\; [1\; -\; XX,\; 1\; 1\; -\; X]\; =\; \alpha \; +\; \beta \; -\; 1\; (\alpha \; -\; 1)\; (\beta \; -\; 1),\; если\; \alpha ,\; \beta >1\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{cov\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}]\; \{X\}\},\; \{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{cov\}\; \backslash \; left\; [\{\backslash \; frac\; \{1-X\}\; \{X\}\},\; \{\backslash \; frac\; \{X\}\; \{1\; -X\}\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{cov\}\; \backslash \; left\; [\{\backslash \; frac\; \{1\}\; \{X\}\},\; \{\backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{cov\}\; \backslash \; left\; [\{\backslash \; frac\; \{1-X\}\; \{X\}\},\; \{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right]\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\; \{(\backslash \; alpha\; -1)\; (\; \backslash \; beta\; -1)\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha,\; \backslash \; beta>1\}$

Эти ожидания и отклонения системе в четырехпараметрической информационной матрице Fisher (раздел под названием« Информация Fisher »,« четыре различных »)

Моменты логарифмически преобразованные случайные величины

График logit (X) = ln (X / (1-X)) (вертикальная ось) относительно X в области от 0 до 1 (горизонтальная ось). Логит-преобразование интересны, так как они обычно преобразуют различные формы (включая J-образные) в (обычно наклонные) колоколообразные формы по логит-переменным, и они могут удалять конечные сингулярности по исходной переменной

Ожидаемые значения для логарифмических преобразований оценки максимального правдоподобия, см. Раздел «Оценка параметров, максимальная вероятность» ниже) обсуждаются в этом разделе. Следующие логарифмические линейные преобразования к средним геометрическим G X и G (1-X) (см. Раздел «Среднее геометрическое»):

$E\; \; [ln\; \; (X)\; ]\; =\; \psi \; (\alpha )\; -\; \psi \; (\alpha \; +\; \beta )\; =\; -\; E\; \; [ln\; \; (1\; X)],\; E\; \; [ln\; \; (1\; -\; X)]\; =\; \psi \; (\beta )\; -\; \psi \; (\alpha \; +\; \beta )\; =\; -\; E\; \; [ln\; \; (1\; 1\; -\; X)].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{E\}\; [\backslash \; ln\; (X)]\; =\; \backslash \; psi\; (\backslash \; alpha)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{X\}\}\; \backslash \; right)\; \backslash \; right],\; \backslash \backslash \backslash \; имя\; оператора\; \{E\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; psi\; (\backslash \; beta)\; -\; \backslash \; psi\; (\; \backslash \; альфа\; +\; \backslash \; бета)\; =\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right)\; \backslash \; right].\; \backslash \; end\; \{align\}\}\}$

Где дигамма-функция ψ (α) определяется как логарифмическая производная от гамма-функции :

$\psi \; (\alpha )\; знак\; равно\; d\; пер\; \; \Gamma \; (\alpha )\; d\; \alpha \; \{\backslash \; displaystyle\; \backslash \; psi\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{d\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{d\; \backslash \; alpha\}\}\}$

преобразование логита интересны, поскольку они обычно преобразовывать различные формы (в том числе J-образные) в (обычно наклонные) колоколообразные плотности по логит-переменным, и они могут удалять концевые сингулярности по исходной переменной:

$E\; \; [ln\; \; (\; X\; 1\; -\; X)]\; =\; \psi \; (\alpha )\; -\; \psi \; (\beta )\; =\; E\; \; [ln\; \; (X)]\; +\; E\; \; [ln\; \; (1\; 1\; -\; X)],\; E\; \; [ln\; \; (1\; -\; XX)\; ]\; =\; \psi \; (\beta )\; -\; \psi \; (\alpha )\; =\; -\; E\; \; [ln\; (X\; 1\; -\; X)].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; psi\; (\backslash \; alpha)\; -\; \backslash \; psi\; (\backslash \; beta)\; =\; \backslash \; operatorname\; \{E\}\; [\backslash \; ln\; (X)]\; +\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right)\; \backslash \; right],\; \backslash \backslash \backslash \; имя\; оператора\; \{E\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1-X\}\; \{X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; psi\; (\backslash \; beta)\; -\; \backslash \; psi\; (\backslash \; alpha)\; =\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right)\; \backslash \; right].\; \backslash \; end\; \{align\}\}\}$

Джонсон рассмотрел распределение logit - преобразованная переменная ln (X / 1 - X), включая ее производящую функцию момента и приближения для больших значений параметров. Это преобразование расширяет конечный носитель [0, 1] на основе исходного X до бесконечного носителя в обоих направлениях вещественной прямой (−∞, + ∞).

Логарифмические моменты более высокого порядка могут быть получены путем использования представления бета-распределения как пропорции двух гамма-распределений и дифференцирования через интеграл. Они могут быть выражены через полигамма-функции более высокого порядка следующим образом:

$E\; \; [ln\; 2\; \; (X)]\; =\; (\psi \; (\alpha )\; -\; \psi \; (\alpha \; +\; \beta ))\; 2\; +\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta ),\; E\; \; [ln\; 2\; \; (1\; -\; X)]\; =\; (\psi \; (\beta )\; -\; \psi \; (\alpha \; +\; \beta ))\; 2\; +\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta ),\; E\; \; [ln\; \; (X)\; ln\; \; (1\; -\; X)]\; =\; (\psi \; (\alpha )\; -\; \psi \; (\alpha \; +\; \beta ))\; (\psi \; (\beta )\; -\; \psi \; (\alpha \; +\; \beta ))\; -\; \psi \; 1\; (\alpha \; +\; \beta ).\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; OperatorName\; \{E\}\; \backslash \; left\; [\backslash \; ln\; ^\; \{2\}\; (X)\; \backslash \; right]\; =\; (\backslash \; psi\; (\backslash \; alpha)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta))\; ^\; \{2\}\; +\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta),\; \backslash \backslash \backslash \; имя\; оператора\; \{E\}\; \backslash \; left\; [\backslash \; ln\; ^\; \{2\}\; (1-X)\; \backslash \; right]\; =\; (\backslash \; psi\; (\backslash \; beta)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta))\; ^\; \{2\}\; +\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; бета),\; \backslash \backslash \backslash \; имя\; оператора\; \{E\}\; \backslash \; left\; [\backslash \; ln\; (X)\; \backslash \; ln\; (1-X)\; \backslash \; right]\; =\; (\backslash \; psi\; (\backslash \; alpha)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta))\; (\backslash \; psi\; (\backslash \; beta)\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta))\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta).\; \backslash \; end\; \{align\}\}\}$

, следовательно, дисперсия логарифмических чисел и ковариация ln (X) и ln (1 - X) составляют:

$cov ⁡ [ln ⁡ (X), ln ⁡ (1 - X)] = E ⁡ [ln ⁡ (X) ln ⁡ (1 - X)] - E ⁡ [ln ⁡ (X)] E ⁡ [ln ⁡ (1 - X) ] = - ψ 1 (α + β) var ⁡ [ln ⁡ X] = E ⁡ [ln 2 ⁡ (X)] - (E ⁡ [ln ⁡ (X)]) 2 = ψ 1 (α) - ψ 1 (α + β) = ψ 1 (α) + cov ⁡ [ln ⁡ (X), ln ⁡ (1 - X)] var ⁡ [ln ⁡ (1 - X)] = E ⁡ [ln 2 ⁡ (1 - X)] - (E ⁡ [ln ⁡ (1 - X)]) 2 = ψ 1 (β) - ψ 1 (α + β) = ψ 1 (β) + cov ⁡ [пер ⁡ (Икс), пер ⁡ (1 - Икс)] {\ displaystyle {\ begin {выровнено} \ operatorname {cov} [\ ln (X), \ ln (1-X)] = \ operatorname {E} \ left [\ ln (X) \ ln (1-X) \ right] - \ operatorname {E} [\ ln (X)] \ operatorname {E} [\ ln (1-X)] = - \ psi _ {1} (\ alpha + \ beta) \\ \\\ OperatorName {var} [\ ln X] = \ operatorname {E} [\ ln ^ {2} (X)] - (\ operatorname {E} [\ ln (X)]) ^ {2} \\ = \ psi _ {1} (\ alpha) - \ psi _ {1} (\ alpha + \ beta) \\ = \ psi _ {1} (\ alpha) + \ operatorname { cov} [\ ln (X), \ ln (1-X)] \\ \\\ OperatorName {var} [\ ln (1-X)] = \ operatorname {E} [\ ln ^ {2} (1 -X)] - (\ operatorname {E} [\ ln (1-X)]) ^ {2} \\ = \ psi _ {1} (\ beta) - \ psi _ {1} (\ alpha + \ beta) \\ = \ psi _ {1} (\ beta) + \ operatorname {cov} [\ ln (X), \ ln (1-X)] \ end {align}}}$

где тригамма-функция, обозначенная ψ 1 (α), является второй из функций полигаммы, и определяется как производная функция дигамма :

$\psi \; 1\; (\alpha )\; знак\; равно\; d\; 2\; пер\; \; \Gamma \; (\alpha )\; d\; \alpha \; 2\; =\; d\; \psi \; (\alpha )\; d\; \alpha \; \{\backslash \; Displaystyle\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{d\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{d\; \backslash \; psi\; (\backslash \; alpha)\}\; \{d\; \backslash \; alpha\}\}\}$.

Дисперсия и ковариация логарифмически преобразованных чисел X и (1 - X) в общем случае различны, потому что логарифмическое преобразование разрушает зеркальную симметрию исходных чисел X и (1 - X), поскольку логарифм приближается к отрицательной бесконечности для тип, стремящейся к нулю.

Эти логарифмические дисперсии и ковариация являются элементами матрицы информации Фишера для бета-распределения. Они также являются мерой кривизны логарифмической функции правдоподобия (см. Раздел об оценке максимального правдоподобия).

Дисперсия логарифмических обратных переменных идентична дисперсиям логарифмических переменных:

$var\; \; [ln\; \; (1\; X)]\; =\; var\; \; [ln\; \; (X)]\; =\; \psi \; 1\; (\; \alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta ),\; var\; \; [ln\; \; (1\; 1\; -\; X)]\; =\; var\; \; [ln\; \; (1\; -\; X)]\; =\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta ),\; cov\; \; [ln\; \; (1\; X),\; ln\; \; (1\; 1\; -\; X)]\; =\; cov\; \; [ln\; \; (X),\; ln\; \; (1\; -\; X)]\; =\; -\; \psi \; 1\; (\alpha \; +\; \beta ).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{var\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (X)]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta),\; \backslash \backslash \backslash \; operatorname\; \{var\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{\; 1-X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; бета),\; \backslash \backslash \backslash \; operatorname\; \{cov\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{X\}\}\; \backslash \; right),\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{1-X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; operatorname\; \{cov\}\; [\backslash \; ln\; (X),\; \backslash \; ln\; (1-X)]\; =\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta).\; \backslash \; end\; \{выравнивается\}\}\}$

Отсюда также следует, что дисперсии преобразованных переменных logit равны:

$var\; \; [ln\; \; (X\; 1\; -\; X)]\; =\; var\; \; [ln\; \; (1\; -\; XX)]\; =\; -\; cov\; \; [пер\; \; (Икс\; 1\; -\; Икс),\; пер\; \; (1\; -\; XX)]\; =\; \psi \; 1\; (\alpha )\; +\; \psi \; 1\; (\beta )\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{var\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\; \backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; operatorname\; \{var\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1-X\}\; \{X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; -\; \backslash \; operatorname\; \{cov\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right),\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{1-X\}\; \{X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; +\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\}$

Количество информации (энтропия)

Учитывая бета-распределенную случайную величину, X ~ Beta (α, β), дифференциальная энтропия X - (измеряется в натс ), ожидаемое значение отрицательного логарифма функции плотности вероятности :

$h\; (X)\; =\; E\; \; [-\; ln\; \; (f\; (x;\; \alpha ,\; \beta ))]\; =\; \int \; 0\; 1\; -\; f\; (x;\; \alpha ,\; \beta )\; ln\; \; (f\; (x;\; \alpha ,\; \beta ))\; dx\; =\; ln\; \; (B\; (\alpha ,\; \beta ))\; -\; (\alpha \; -\; 1)\; \psi \; (\alpha )\; -\; (\beta \; -\; 1)\; \psi \; (\beta )\; +\; (\alpha \; +\; \beta \; -\; 2)\; \psi \; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; h\; (X)\; =\; \backslash \; operatorname\; \{E\}\; [-\; \backslash \; ln\; (f\; (x;\; \backslash \; alpha,\; \backslash \; beta))]\; \backslash \backslash \; [4pt]\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; -f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; \backslash \; ln\; (f\; (x;\; \backslash \; альфа,\; \backslash \; бета))\; \backslash ,\; dx\; \backslash \backslash \; [4pt]\; =\; \backslash \; ln\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; -\; (\backslash \; alpha\; -1)\; \backslash \; psi\; (\backslash \; alpha)\; -\; (\backslash \; beta\; -\; 1)\; \backslash \; psi\; (\backslash \; beta)\; +\; (\backslash \; alpha\; +\; \backslash \; beta\; -2)\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\; \backslash \; end\; \{align\}\}\}$

где f (x; α, β) - функция плотности вероятности бета-распределения:

$f\; (x;\; \alpha ,\; \beta )\; =\; 1\; B\; (\alpha ,\; \beta )\; x\; \alpha \; -\; 1\; (1\; -\; x)\; \beta \; -\; 1\; \{\backslash \; displaystyle\; f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; x\; ^\; \{\backslash \; alpha\; -1\}\; (1-x)\; ^\; \{\backslash \; beta\; -1\}\}$

Дигамма-функция ψ появляется в формуле для дифференциальной энтропии как следствие интегральной формулы Эйлера для гармонических чисел, которая следует из интеграла:

$\int \; 0\; 1\; 1\; -\; Икс\; \alpha \; -\; 1\; 1\; -\; xdx\; знак\; равно\; \psi \; (\alpha )\; -\; \psi \; (1)\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \{\backslash \; frac\; \{1-x\; ^\; \{\backslash \; alpha\; -1\}\}\; \{1-x\}\}\; \backslash ,\; dx\; =\; \backslash \; psi\; (\backslash \; alpha)\; -\; \backslash \; psi\; (1)\}$

дифференциальная энтропия бета-распределения отрицательна для всех зна чений α и β больше нуля, за исключением α = β = 1 (для которых значения бета-распределения совпадают с равномерным распределением ), где дифференциальная энтропия достигает своего максимального нулевого значения. Следует ожидать, что максимальная энтропия должна иметь место, когда бета-распределение становится равным равномерному распределению, поскольку неопределенность максимальна, когда все возможные события равновероятны.

Для α или β, приближающихся к нулю, дифференциальная энтропия приближается к своему минимальному значению отрицательной бесконечности. Для (любого или обоих) α или β, приближающихся к нулю, существует максимальная степень порядка: вся плотность вероятности сосредоточена на концах, а плотность вероятности равна нулю в точках, расположенных между концами. Точно так же для (любого или обоих) α или β, приближающихся к бесконечности, дифференциальная энтропия приближается к своему минимальному значению отрицательной бесконечности и максимальной величине порядка. Если либо α, либо β приближается к бесконечности (а другое - конечно), вся плотность вероятности сосредоточена в конце, а плотность вероятности равна нулю везде. Если оба параметра формы равны (симметричный случай), α = β, и они приближаются к бесконечности одновременно, плотность вероятности становится пиковой (дельта-функция Дирака ), сосредоточенной в середине x = 1/2, и следовательно, есть 100% вероятность в середине x = 1/2 и нулевая вероятность везде.

(непрерывный случай) дифференциальная энтропия была введена Шенноном в его оригинальной статье (где он назвал ее «энтропией непрерывного распределения») в качестве заключительной части той же статьи, где он определил дискретная энтропия. С тех пор известно, что дифференциальная энтропия может отличаться от бесконечно малого предела дискретной энтропии на бесконечное смещение, поэтому дифференциальная энтропия может быть отрицательной (как и для бета-распределения). Что действительно важно, так это относительное значение энтропии.

Учитывая две бета-распределенные случайные величины, X 1 ~ Beta (α, β) и X 2 ~ Beta (α ′, β ′), перекрестная энтропия равна (измеряется в натсах)

$H\; (X\; 1,\; X\; 2)\; =\; \int \; 0\; 1\; -\; f\; (x;\; \alpha ,\; \beta )ln\; \; (f\; (x;\; \alpha \; \prime ,\; \beta \; \prime ))\; dx\; =\; ln\; \; (B\; (\alpha \; \prime ,\; \beta \; \prime ))\; -\; (\alpha \; \prime \; -\; 1)\; \psi \; (\alpha )\; -\; (\beta \; \prime \; -\; 1)\; \psi \; (\beta )\; +\; (\alpha \; \prime \; +\; \beta \; \prime \; -\; 2)\; \psi \; (\alpha \; +\; \beta ).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; H\; (X\_\; \{1\},\; X\_\; \{2\})\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; -f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; \backslash \; ln\; (f\; (x\; ;\; \backslash \; alpha\; \text{'},\; \backslash \; beta\text{'}))\; \backslash ,\; dx\; \backslash \backslash \; [4pt]\; =\; \backslash \; ln\; \backslash \; left\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha\; \text{'},\; \backslash \; beta\text{'})\; \backslash \; right)\; -\; (\backslash \; alpha\; \text{'}-1)\; \backslash \; psi\; (\backslash \; alpha)\; -\; (\backslash \; beta\; \text{'}-1)\; \backslash \; psi\; (\backslash \; beta)\; +\; (\backslash \; alpha\text{'}\; +\; \backslash \; beta\; \text{'}-2)\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta).\; \backslash \; end\; \{align\}\}\}$

Перекрестная энтропия использовалась в качестве метрики ошибки для измерения расстояния между двумя гипотезами. Его абсолютное значение минимально, когда два распределения идентичны. Это информационная мера, наиболее тесно связанная с логарифмической максимальной вероятностью (см. Раздел «Оценка параметров. Оценка максимального правдоподобия»)).

Относительная энтропия, или расхождение Кульбака – Лейблера DKL(X1|| X 2), является мерой неэффективности предположения, что распределение равно X 2 ~ Beta (α ′, β ′), когда распределение действительно X 1 ~ Бета (α, β). Он определяется следующим образом (измеряется в натсах).

$DKL (X 1 | | X 2) = ∫ 0 1 f (x; α, β) ln ⁡ (f (x; α, β) f (x; α ′, β ′)) dx = (∫ 0 1 f (x; α, β) ln ⁡ (f (x; α, β)) dx) - (∫ 0 1 f (x; α, β) ln ⁡ (f (x; α ′, β ′)) dx) = - h (X 1) + H (X 1, X 2) = ln ⁡ (B (α ′, β ′) B (α, β)) + (α - α ′) ψ (α) + (β - β ′) ψ (β) + (α ′ - α + β ′ - β) ψ (α + β). {\ displaystyle {\ begin {align} D _ {\ mathrm {KL}} (X_ {1} || X_ {2}) = \ int _ {0} ^ {1} f (x; \ alpha, \ beta) \ ln \ left ({\ frac {f (x; \ alpha, \ beta)} {f (x; \ alpha ', \ beta')}} \ right) \, dx \\ [4pt] = \ left (\ int _ {0} ^ {1} f (x; \ alpha, \ beta) \ ln (f (x; \ alpha, \ beta)) \, dx \ right) - \ left (\ int _ { 0} ^ {1} f (x; \ alpha, \ beta) \ ln (f (x; \ alpha ', \ beta')) \, dx \ right) \\ [4pt] = - h (X_ { 1}) + H (X_ {1}, X_ {2}) \\ [4pt] = \ ln \ left ({\ frac {\ mathrm {B} (\ alpha ', \ beta')} {\ mathrm {B} (\ alpha, \ beta)}} \ right) + (\ alpha - \ alpha ') \ psi (\ alpha) + (\ beta - \ beta') \ psi (\ beta) + (\ alpha ' - \ alpha + \ beta '- \ beta) \ psi (\ alpha + \ beta). \ end {align}}}$

Относительная энтропия, или расхождение Кульбака – Лейблера, всегда не -отрицательный. Далее следуют несколько числовых примеров:

• X1~ Beta (1, 1) и X 2 ~ Beta (3, 3); D KL(X1|| X 2) = 0,598803; D KL(X2|| X 1) = 0,267864; h (X 1) = 0; h (X 2) = -0,267864
• X1~ бета (3, 0,5) и X 2 ~ бета (0,5, 3); D KL(X1|| X 2) = 7,21574; D KL(X2|| X 1) = 7,21574; h (X 1) = -1,10805; h (X 2) = −1,10805.

Дивергенция Кульбака – Лейблера не является симметричной D KL(X1|| X 2) ≠ D KL(X2|| X 1) для случая, когда отдельные бета-распределения Beta (1, 1) и Beta (3, 3) симметричны, но имеют разные энтропии h (X 1) ≠ h (X 2). Величина дивергенции Кульбака зависит от направления движения: идет ли переход от более высокой (дифференциальной) энтропии к более низкой (дифференциальной) энтропии или наоборот. В приведенном выше числовом примере дивергенция Кульбака измеряет неэффективность предположения, что распределение является (колоколообразным) бета (3, 3), а не (равномерным) бета (1, 1). Энтропия h для бета (1, 1) выше, чем энтропия h для бета (3, 3), потому что равномерное распределение Beta (1, 1) имеет максимальное количество беспорядка. Дивергенция Кульбака более чем в два раза выше (0,598803 вместо 0,267864) при измерении в направлении уменьшения энтропии: направлении, которое предполагает, что (однородное) бета (1, 1) распределение является (колоколообразным) бета (3, 3), а не наоборот. В этом ограниченном смысле дивергенция Кульбака соответствует второму закону термодинамики.

Дивергенция Кульбака – Лейблера симметрична D KL(X1|| X 2) = D KL(X2|| X 1) для искаженных случаев Beta (3, 0.5) и Beta (0.5, 3), которые имеют равную дифференциальную энтропию h (X 1) = h (X 2).

Условие симметрии:

$DKL\; (X\; 1\; |\; |\; X\; 2)\; =\; DKL\; (X\; 2\; |\; |\; X\; 1),\; если\; h\; (X\; 1)\; =\; h\; (X\; 2),\; для\; (с\; перекосом)\; \alpha \; \ne \; \beta \; \{\backslash \; Displaystyle\; D\; \_\; \{\backslash \; mathrm\; \{KL\}\}\; (X\_\; \{1\}\; ||\; X\_\; \{2\})\; =\; D\; \_\; \{\backslash \; mathrm\; \{KL\}\}\; (X\_\; \{2\}\; ||\; X\_\; \{1\}),\; \{\backslash \; text\; \{if\}\}\; h\; (X\_\; \{1\})\; =\; h\; (X\_\; \{2\}),\; \{\backslash \; text\; \{for\; (skewed)\}\}\; \backslash \; alpha\; \backslash \; neq\; \backslash \; beta\}$

следует из приведенных выше определений и зеркального симметрия f (x; α, β) = f (1 − x; α, β), которой обладает бета-распределение.

Взаимосвязь между статистическими показателями

Среднее значение, мода и отношение медианы

Если 1 < α < β then mode ≤ median ≤ mean. Expressing the mode (only for α, β>1) и средним соответствие в терминах α и β:

$\alpha \; -\; 1\; \alpha \; +\; \beta \; -\; 2\; \le \; медиана\; \le \; \alpha \; \alpha \; +\; \beta ,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}\; \backslash \; leq\; \{\backslash \; text\; \{median\}\}\; \backslash \; leq\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\},\}$

Если 1 < β < α then the order of the inequalities are reversed. For α, β>1, абсолютное расстояние между средним значением и медианой меньше 5% расстояния между максимальным и минимальными значениями x. С другой стороны, абсолютное расстояние между средним значением и модой может достичь 50% расстояния между максимальным и минимальным значениями x для (патологического ) случая α = 1 и β = 1. (для этих значений бета-распределение приближается к равномерному распределению, а дифференциальная энтропия приближается к своему максимальному значению и, следовательно, к максимальному «порядку»).

Например, для α = 1.0001 и β = 1.00000001:

• режим = 0,9999; PDF (режим) = 1.00010
• среднее значение = 0.500025; PDF (среднее значение) = 1,00003
• медиана = 0,500035; PDF (медиана) = 1,00003
• среднее значение - режим = -0,499875
• среднее значение - медиана = -9,65538 × 10

(где PDF означает значение функции плотности вероятности )

Среднее, геометрическое среднее и гармоническое среднее соотношение

: Среднее, среднее, геометрическое среднее и гармоническое среднее для бета-распределения с 0 < α = β < 5

Это известно из неравенства средних арифметических и геометрических, что среднее геометрическое ниже среднего. Точно так же гармоническое среднее ниже среднего геометрического. На прилагаемом графике показано, что для α = β и среднее, и медиана точно равны 1/2, независимо от значения α = β, и мода также равна 1/2 для α = β>1, однако геометрические и гармонические средние меньше 1/2, и они приближаются к этому значению только асимптотически при α = β → ∞.

эксцесс, ограниченный квадратом асимметрии

Бета-распределение параметров α и β в зависимости от избыточного эксцесса и квадрата асимметрии

Как отмечено Fe ller, в системе Пирсона бета-плотность вероятности отображается как тип I (любое различие между бета-распределением и распределением Пирсона типа I является только поверхностным и не имеет значения для следующего обсуждения взаимосвязи между эксцессом и асимметрией). Карл Пирсон показал в таблице 1 своей статьи, опубликованной в 1916 году, график с эксцессом в качестве вертикальной оси (ордината ) и квадратом асимметрия в качестве горизонтальной оси (абсцисса ), на которой отображено несколько распределений. Область, занятая бета-распределением, ограничена следующими двумя линиями в плоскости (асимметрия, эксцесс) или (асимметрия, избыточный эксцесс) плоскости :

или, что то же самое,

(в то время, когда не было мощных цифровых компьютеров), Карл Пирсон точно вычислил дальнейшие границы, например, отделение «U-образного» распределения от «J-образного». Нижняя граничная линия (избыточный эксцесс + 2 - асимметрия = 0) образована наклонными "U-образными" бета-распределениями с обоими значениями параметров формы α и β, близкими к нулю. Верхняя граничная линия (избыточный эксцесс - (3/2) асимметрия = 0) создается чрезвычайно искаженными распределениями с очень большими значениями одного из параметров и очень маленькими значениями другого параметра. Карл Пирсон показал, что эта верхняя граничная линия (избыточный эксцесс - (3/2) асимметрия = 0) также является пересечением с распределением Пирсона III, которое имеет неограниченную поддержку в одном направлении (в сторону положительной бесконечности), и может быть колоколообразной или J-образной формы. Его сын, Эгон Пирсон, показал, что область (в плоскости эксцесса / квадрата асимметрии) занята бета-распределением (эквивалентно распределением Пирсона I) по мере приближения к этой границе (избыточный эксцесс - (3 / 2) асимметрия = 0) используется совместно с нецентральным распределением хи-квадрат. Карл Пирсон (Pearson 1895, pp. 357, 360, 373–376) также показал, что гамма-распределение является распределением типа III Пирсона. Следовательно, эта граничная линия для распределения Пирсона типа III известна как гамма-линия. (Это можно показать из того факта, что избыточный эксцесс гамма-распределения равен 6 / k, а квадрат асимметрии равен 4 / k, следовательно (избыточный эксцесс - (3/2) асимметрия = 0) идентично удовлетворяется гамма-распределением независимо от значения параметра «k»). Позже Пирсон заметил, что распределение хи-квадрат является частным случаем типа III Пирсона и также разделяет эту граничную линию (как это очевидно из того факта, что для распределения хи-квадрат избыточный эксцесс составляет 12 / k, а квадрат асимметрии равен 8 / k, следовательно (избыточный эксцесс - (3/2) асимметрия = 0) одинаково удовлетворяется независимо от значения параметра «k»). Этого и следовало ожидать, поскольку распределение хи-квадрат X ~ χ (k) является частным случаем гамма-распределения с параметризацией X ~ Γ (k / 2, 1/2), где k - положительное целое число, определяющее «число степеней свободы» распределения хи-квадрат.

Пример бета-распределения около верхней границы (избыточный эксцесс - (3/2) асимметрия = 0) задается как α = 0,1, β = 1000, для которого соотношение (избыточный эксцесс) / ( асимметрия) = 1,49835 приближается к верхнему пределу 1,5 снизу. Пример бета-распределения около нижней границы (избыточный эксцесс + 2 - асимметрия = 0) дается выражением α = 0,0001, β = 0,1, для которого выражение (избыточный эксцесс + 2) / (асимметрия) = 1,01621 приближается к нижний предел 1 сверху. В бесконечно малом пределе как для α, так и для β, симметрично приближающихся к нулю, избыточный эксцесс достигает минимального значения при −2. Это минимальное значение находится в точке, в которой нижняя граничная линия пересекает вертикальную ось (ордината ). (Однако в исходной диаграмме Пирсона ордината представляет собой эксцесс, а не избыточный эксцесс, и он увеличивается вниз, а не вверх).

Значения асимметрии и избыточного эксцесса ниже нижней границы (избыточный эксцесс + 2 - асимметрия = 0) не могут иметь место ни для какого распределения, и поэтому Карл Пирсон соответственно назвал область ниже этой границы «невозможный регион». Граница этой «невозможной области» определяется (симметричной или наклонной) бимодальным U-образным распределением ионы, для которых параметры α и β приближаются к нулю, и, следовательно, вся плотность вероятности сосредоточена на концах: x = 0, 1 и практически ничего между ними. При возможности при α ≈ β ≈ 0 плотность вероятности сосредоточена на двух концах x = 0 и x = 1, эта «невозможная граница» определяется двухточечным распределением: вероятность может принимать только 2 значения (Бернулли распределение ), одно с вероятностью p, а другое с вероятностью q = 1 - p. Для случаев, проявляющихся к этой предельной границе с симметрией α = β, асимметрия ≈ 0, избыточный эксцесс ≈ −2 (это самый низкий избыточный эксцесс, возможный для распределения), и вероятности p ≈ q ≈ 1/2. Для случаев, приближающихся к этой предельной границе с асимметрией, избыточный эксцесс ≈ −2 + асимметрия, вероятность вероятности сконцентрирована больше на одном конце, чем на другом конце (практически ничего между ними), с вероятностями $p\; =\; \beta \; \alpha \; +\; \beta \; \{\backslash \; displaystyle\; p\; =\; \{\backslash \; tfrac\; \{\backslash \; beta\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\}$на левом конце x = 0 и $q\; =\; 1\; -\; p\; =\; \alpha \; \alpha \; +\; \beta \; \{\backslash \; displaystyle\; q\; =\; 1-p\; =\; \{\backslash \; tfrac\; \{\backslash \; alpha\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\}$на правом конце x = 1.

Симметрия

Все утверждения зависит от α, β>0

• Функция плотности вероятности симметрия отражения

$f\; (x;\; \alpha ,\; \beta )\; =\; f\; (1\; -\; x;\; \beta ,\; \alpha )\; \{\backslash \; displaystyle\; f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\; =\; f\; (1-x;\; \backslash \; beta,\; \backslash \; alpha)\}$

• Кумулятивная функция распределения симметрия отражения плюс унитарное смещение

$F\; (Икс;\; \alpha ,\; \beta )\; знак\; равно\; Я\; Икс\; (\alpha ,\; \beta )\; =\; 1\; -\; F\; (1\; -\; Икс;\; \beta ,\; \alpha )\; =\; 1\; -\; Я\; 1\; -\; Икс\; (\beta ,\; \alpha )\; \{\backslash \; Displaystyle\; F\; (х;\; \backslash \; альфа,\; \backslash \; beta)\; =\; I\_\; \{x\}\; (\backslash \; alpha,\; \backslash \; beta)\; =\; 1-F\; (1-x;\; \backslash \; beta,\; \backslash \; alpha)\; =\; 1-I\_\; \{1-x\}\; (\backslash \; beta,\; \backslash \; alpha)\}$

• Режим симметрия отражения плюс унитарная трансляционная

$мода\; \; (B\; (\alpha ,\; \beta ))\; =\; 1\; -\; мода\; \; (В\; (\beta ,\; \alpha )),\; если\; В\; (\beta ,\; \alpha )\; \ne \; В\; (1,\; 1)\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{mode\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; 1-\; \backslash \; operatorname\; \{mode\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha)),\; \{\backslash \; text\; \{if\}\}\; \backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha)\; \backslash \; neq\; \backslash \; mathrm\; \{B\}\; (1,1)\}$

• Медиансимметрия отражения плюс унитарная перевод

$медиана\; \; (B\; (\alpha ,\; \beta ))\; =\; 1\; -\; медиана\; \; (B\; (\beta ,\; \alpha ))\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{median\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; 1-\; \backslash \; operatorname\; \{median\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• Среднее симметрия отражения плюс унитарное смещение

$\mu \; (B\; (\alpha ,\; \beta ))\; знак\; равно\; 1\; -\; \mu \; (В\; (\beta ,\; \alpha ))\; \{\backslash \; Displaystyle\; \backslash \; му\; (\; \backslash \; mathrm\; \{B\}\; (\backslash \; альфа,\; \backslash \; бета))\; =\; 1-\; \backslash \; му\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• Каждое геометрическое среднее индивидуально асимметрично, следующая симметрия имеющая между средним ге ометрическим на основе X и средним геометрическим на основе его отражения (1-X)

$G\; Икс\; (В\; (\alpha ,\; \beta ))\; знак\; равно\; г\; (1\; -\; Икс)\; (В\; (\beta ,\; \alpha ))\; \{\backslash \; Displaystyle\; G\_\; \{X\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; альфа,\; \backslash \; бета))\; =\; G\; \_\; \{(1\; -X)\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• Гармоническое означает, что каждый из них индивидуально асимметричен, следующий симметрия применяется между гармоническим средним на основе X и гармоническим средним на основе его отражение (1-X)

$HX\; (B\; (\alpha ,\; \beta ))\; Знак\; равно\; ЧАС\; (1\; -\; Икс)\; (В\; (\beta ,\; \alpha )),\; если\; \alpha ,\; \beta >1\; \{\backslash \; Displaystyle\; H\_\; \{X\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; альфа,\; \backslash \; бета))\; =\; H\; \_\; \{(\; 1-X)\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha,\; \backslash \; beta>1\}$.

• Вариациясимметрия

$\alpha var\; \; (B\; (,\; \beta ))\; знак\; равно\; вар\; \; (В\; (\beta ,\; \alpha ))\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; \backslash \; operatorname\; \{var\}\; (\backslash \; mathrm\; \{\; B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• Геометрические отклонения индивидуально асимметрична, между логарифмической геометрической дисперсией используется следующая симметрия на основе X и логарифмической геометрической дисперсии на основе его отражения (1-X)

$пер\; \; (вар\; GX\; \; (B\; (\alpha ,\; \beta )))\; =\; пер\; \; (вар\; G\; (1\; -\; Икс)\; \; (В\; (\beta ,\; \alpha )))\; \{\backslash \; displaystyle\; \backslash \; ln\; (\backslash \; operatorname\; \{var\_\; \{GX\}\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)))\; =\; \backslash \; ln\; (\backslash \; operatorname\; \{var\_\; \{G\; (1-X)\}\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha)))\}$

• Геометрическая ковариация симметрия

$ln\; \; cov\; GX,\; (1\; -\; X)\; \; (B\; (\alpha ,\; \beta ))\; знак\; равно\; пер\; \; cov\; GX,\; (1\; -\; X)\; \; (B\; (\beta ,\; \alpha ))\; \{\backslash \; Displaystyle\; \backslash \; ln\; \backslash \; OperatorName\; \{cov\_\; \{GX,\; (1-X)\}\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; \backslash \; ln\; \backslash \; operatorname\; \{cov\_\; \{GX,\; (1-\; X)\}\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• Среднее абсолютное отклонение вокруг средней симметрии

$E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; (B\; (\alpha ,\; \beta ))\; =\; E\; \; [|\; X\; -\; E\; [X]\; |\; ]\; (В\; (\beta ,\; \alpha ))\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{E\}\; [|\; XE\; [X]\; |]\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; \backslash \; OperatorName\; \{E\}\; [|\; XE\; [X]\; |]\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• асимметрияасимметрия

$асимметрия\; \; (B\; (\alpha ,\; \beta ))\; =\; -\; асимметрия\; \; (\; В\; (\beta ,\; \alpha ))\; \{\backslash \; Displaystyle\; \backslash \; OperatorName\; \{skewness\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; -\; \backslash \; operatorname\; \{skewness\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\; \}$

• Чрезмерный эксцесс симметрия

$избыточный\; эксцесс\; (B\; (\alpha ,\; \beta ))\; =\; избыточный\; эксцесс\; (B\; (\beta ,\; \alpha ))\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; (\backslash \; mathrm\; \{B\; \}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; \{\backslash \; text\; \{избыточный\; эксцесс\}\}\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• Характеристическая функция симметрия вещественной части (относительно начала "t")

$Re\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; it)]\; =\; Re\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; -\; it)]\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{\; Re\}\}\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; it)]\; =\; \{\backslash \; text\; \{Re\}\}\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; -it)]\}$

• Характеристическая функция кососимметрия из Мнимая номинальная t (относительно начала анализа «t»)

$Im\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; оно)]\; =\; -\; Им\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; -\; оно)]\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{Im\}\}\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; it)]\; =\; -\; \{\backslash \; text\; \{Im\}\}\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; -it)]\}$

• Характеристическая функция симметрия Абсолютное значение (относительно источника "t")

$Abs\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; it)]\; =\; Abs\; [1\; F\; 1\; (\alpha ;\; \alpha \; +\; \beta ;\; -\; оно)]\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{Abs\}\}\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; it)]\; =\; \{\backslash \; text\; \{Abs\}\}\; [\{\}\; \_\; \{1\}\; F\_\; \{1\}\; (\backslash \; alpha;\; \backslash \; alpha\; +\; \backslash \; beta;\; -it)]\}$

• Дифференциальная энтропия симметрия

$h\; (B\; (\alpha ,\; \beta ))\; =\; h\; (B\; (\beta ,\; \alpha ))\; \{\; \backslash \; displaystyle\; h\; (\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta))\; =\; h\; (\backslash \; mathrm\; \{B\}\; (\backslash \; beta,\; \backslash \; alpha))\}$

• Относительная энтропия (также называется Дивергенция Кульбака - Лейблера ) симметрия

$DKL\; (X\; 1\; |\; |\; X\; 2)\; =\; DKL\; (X\; 2\; |\; |\; X\; 1),\; если\; h\; (X\; 1)\; =\; h\; (X\; 2),\; для\; (перекошено)\; \alpha \; \ne \; \beta \; \{\backslash \; Displaystyle\; D\; \_\; \{\backslash \; mathrm\; \{KL\}\}\; (X\_\; \{1\}\; ||\; X\_\; \{2\})\; =\; D\; \_\; \{\backslash \; mathrm\; \{KL\}\}\; (X\_\; \{2\}\; ||\; X\_\; \{1\}),\; \{\backslash \; text\; \{я\; f\}\}\; h\; (X\_\; \{1\})\; =\; h\; (X\_\; \{2\})\; \{\backslash \; text\; \{,\; для\; (перекос)\}\}\; \backslash \; alpha\; \backslash \; neq\; \backslash \; beta\}$

• Фишер информационная матрица симметрия

$I\; i,\; j\; =\; I\; j,\; i\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{i,\; j\}\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{j,\; i\}\}$

Геометрия функции плотности вероятности

Точки перегиба

Расположение точки перегиба в зависимости от α и β, показывающие области с одной точкой перегиба Расположение точки перегиба по сравнению с α и β, показывающее область с двумя точками перегиба

Для параметров формы α и β функция плотности вероятности имеет точек перегиба, в которых кривизна меняет знак. Положение этих точек перегиба может быть полезно в качестве меры дисперсии или разброса распределения.

Определение следующей величины:

$\kappa \; =\; (\alpha \; -\; 1)\; (\beta \; -\; 1)\; \alpha \; +\; \beta \; -\; 3\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; \backslash \; kappa\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{\backslash \; \backslash \; \backslash \; frac\; \{(\backslash \; alpha\; -1)\; (\backslash \; beta\; -1)\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -3\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}\}$

Точки перегиба в зависимости от значений параметров α и β, как показано ниже:

• (α>2, β>2) Распределение имеет колокола (симметрично при α = β и скошено равно в противном случае) с двумя точками перегиба,

$x\; =\; режим\; \pm \; \kappa \; =\; \alpha \; -\; 1\; \pm \; (\alpha \; -\; 1)\; (\beta \; -\; 1)\; \alpha \; +\; \beta \; -\; 3\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; text\; \{mode\}\}\; \backslash \; pm\; \backslash \; kappa\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\; \backslash \; pm\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{(\backslash \; alpha\; -1)\; (\backslash \; beta\; -1)\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -3\}\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\; \}\}\}$

• (α = 2, β>2) Распределение одномодальное, с положительным перекосом, с правым хвостом, с одной точкой перегиба, расположенной справа от моды:

$x\; =\; режим\; +\; \kappa \; Знак\; равно\; 2\; \beta \; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; text\; \{mode\}\}\; +\; \backslash \; kappa\; =\; \{\backslash \; frac\; \{2\}\; \{\backslash \; beta\}\}\}$

• (α>2, β = 2) Распреде ление одномодальное, с отрицательным перекосом, левостороннее, с одна точка перегиба, расположенная слева от режима:

$x\; =\; mode\; -\; \kappa \; =\; 1-2\; \alpha \; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; text\; \{mode\}\}\; -\; \backslash \; kappa\; =\; 1-\; \{\backslash \; frac\; \{2\}\; \{\backslash \; alpha\}\}\}$

• (1 < α < 2, β>2, α +β>2) Распределение одномодальное, с положительным перекосом, с правым хвостом, с одной точка перегиба, расположен справа от режима:

$x\; =\; mode\; +\; \kappa \; =\; \alpha \; -\; 1\; +\; (\alpha \; -\; 1)\; (\beta \; -\; 1)\; \alpha \; +\; \beta \; -\; 3\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; x\; =\; \{\; \backslash \; text\; \{mode\}\}\; +\; \backslash \; kappa\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\; +\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{(\backslash \; alpha\; -1)\; (\backslash \; beta\; -1)\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -3\}\}\}\; \}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}\}$

• (0 < α < 1, 1 < β < 2) The distribution has a mode at the left end x = 0 and it is positively skewed, right-tailed. There is одна точка перегиба, расположенная справа от режима:

$x\; =\; \alpha \; -\; 1\; +\; (\alpha \; -\; 1)\; (\beta \; -\; 1)\; \alpha \; +\; \beta \; -\; 3\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\; +\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{(\backslash \; alpha\; -1)\; (\backslash \; beta\; -1)\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -3\}\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}$

• (α>2, 1 < β < 2) The distribution is unimodal negatively skewed, left-tailed, with одна точка перегиба, расположенная слева от режима:

$x\; =\; режим\; -\; \kappa \; =\; \alpha \; -\; 1\; -\; (\alpha \; -\; 1)\; (\beta \; -\; 1)\; \alpha \; +\; \beta \; -\; 3\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; text\; \{mode\}\}\; -\; \backslash \; kappa\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\; -\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\; (\backslash \; alpha\; -1)\; (\backslash \; beta\; -1)\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -3\}\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}\}$

• (1 < α < 2, 0 < β < 1) The distribution has a mode at the right end x=1 and it is negatively skewed, left-tailed. There is одна точка перегиба, расположенная слева от режима:

$x\; =\; \alpha \; -\; 1\; -\; (\alpha \; -\; 1)\; (\beta \; -\; 1)\; \alpha \; +\; \beta \; -\; 3\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; x\; =\; \{\backslash \; frac\; \{\backslash \; alpha\; -1\; -\; \{\; \backslash \; sqrt\; \{\backslash \; frac\; \{(\backslash \; alpha\; -1)\; (\backslash \; beta\; -1)\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -3\}\}\}\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}\}$

В оставшейся части нет точек перегиба (симметричные и перекошенные) области: U-образная: (α, β < 1) upside-down-U-shaped: (1 < α < 2, 1 < β < 2), reverse-J-shaped (α < 1, β>2) или J-образная: (α>2, β < 1)

На прилагаемых графиках показано расположение точек перегиба (показано вертикально, от 0 до 1) по сравнению с α и β (горизонтальные оси от 0 до 5). Есть большие разрезы на поверхностях, пересекающие линии α = 1, β = 1, α = 2 и β = 2, потому что при этих значениях бета-распределение изменяется с 2-х мод на 1-моду на отсутствие моды.

Формы

PDF для симметричного бета-распределения в зависимости от x и α = β от 0 до 30 PDF для симметричного бета-распределения в зависимости от x и α = β от 0 до 2 PDF для искаженного бета-распределения в зависимости от x и β = 2,5α от 0 до 9 PDF для искаженного бета-распределения в зависимости от x и β = 5,5α от 0 до 9 PDF для Функция искаженного бета-распределения в зависимости от x и β = 8α от 0 до 10

Функция бета-распределения может принимать разные формы в зависимости от параметров двух параметров α и β. Способность бета-распределения такое большое разнообразие форм (с использованием всего двух параметров) частично отвечает за то, что оно принимает широкое применение для моделирования реальных измерений:

Симметричный (α = β)

• функция плотности равна симметричный примерно 1/2 (синие и бирюзовые графики).
• медиана = среднее значение = 1/2.
• асимметрия = 0.
• дисперсия = 1 / (4 (2α + 1))
• α = β < 1
  • U-образный (синий график).
  • бимодальный: левый режим = 0, правый режим = 1, анти-режим = 1/2
  • 1/12 < var(X) < 1/4
  • −2 < excess kurtosis(X) < −6/5
  • α = β = 1 / 2 - распределение арксинуса
    • var (X) = 1/8
    • избыточный эксцесс (X) = −3/2
    • CF = Rinc (t)
  • α = β → 0 является двухточечным распределением Бернулли с равной вероятностью 1/2 в каждой дельта-функции Дирака end x = 0 и x = 1 и нулевая вероятность везде. Подбрасывание монеты: одна грань монеты имеет x = 0, а другая грань - x = 1.
    • $lim\; \alpha \; =\; \beta \; \to \; 0\; var\; \; (X)\; =\; 1\; 4\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; бета\; \backslash \; к\; 0\}\; \backslash \; OperatorName\; \{var\}\; (X)\; =\; \{\backslash \; tfrac\; \{1\}\; \{4\}\}\}$
    • $lim\; \alpha \; =\; \beta \; \to \; 0\; эксцесс\; \; (X)\; =\; -\; 2\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; 0\}\; \backslash \; operatorname\; \{extra\; \backslash \; kurtosis\}\; (X)\; =\; -\; 2\}$более низкое значение, чем это, невозможно для любого распределения.
    • разницаая энтропия приближается к минимальному значению -∞
• α = β = 1
  • равномерное [0, 1] распределение
  • без режима
  • var (X) = 1/12
  • избыточный эксцесс (X) = −6/5
  • (где-либо еще отрицательный) дифференциальная энтропия достигает своего максимальное значение нуля
  • CF = Sinc (t)
• α = β>1
  • симметричный одномодальный
  • режим = 1/2.
  • 0 < var(X) < 1/12
  • −6 / 5 < excess kurtosis(X) < 0
  • α = β = 3/2 - полуэллиптическое [0, 1] распределение, см.: распределение полукругов Вигнера
    • var (X) = 1/16.
    • избыточный эксцесс (X) = −1
    • CF = 2 Jinc (t)
  • α = β = 2 - параболическое [0, 1] распределение
    • var (X) = 1/20
    • избыточный эксцесс (X) = −6/7
    • CF = 3 Tinc (t)
  • α = β>2 имеет форму колокола с точками перегиба, расположенными по обеим сторонам от моды
    • 0 < var(X) < 1/20
    • −6/7 < excess kurtosis(X) < 0
  • α = β → ∞ - это 1-точечное вырожденное распределение с всплеском дельта-функции Дирака в средней точке x = 1/2 с вероятностью 1, и нулевая вероятность везде. 100% вероятность (абсолютная уверенность) сосредоточена в единственной точке x = 1/2.
    • $lim\; \alpha \; знак\; равно\; \beta \; \to \; \infty \; var\; \; (X)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{var\}\; (X)\; =\; 0\}$
    • $lim\; \alpha \; =\; \beta \; \to \; \infty \; избыточный\; эксцесс\; \; (Икс)\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{\backslash \; alpha\; =\; \backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; \backslash \; operatorname\; \{избыточный\; \backslash \; эксцесс\}\; (X)\; =\; 0\}$
    • дифференциальная энтропия приближается к минимальному значению -∞

Перекос (α ≠ β)

Функция плотности перекос. Обмен значениями параметров дает зеркальное отображение (обратное) исходной кривой, некоторые более сильные случаи:

• α < 1, β < 1
  • U-образная
  • Положительный перекос для бимодального α < β, negative skew for α>β.
  • : левый режим = 0, правый режим = 1, анти-режим = $\alpha \; -\; 1\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{\backslash \; alpha\; -1\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}\}$
  • 0 < median < 1.
  • 0 < var(X) < 1/4
• α>1, β>1
  • унимодальный (пурпурный и голубой графики),
  • Положительный перекос для режима α < β, negative skew for α>β.
  • $=\; \alpha \; -\; 1\; \alpha \; +\; \beta \; -\; 2\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{mode\}\}\; =\; \{\backslash \; tfrac\; \{\backslash \; alpha\; -1\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; -2\}\}\}$
  • 0 < median < 1
  • 0 < var(X) < 1/12
• α < 1, β ≥ 1
  • обратная J-образная форма с правым хвостом,
  • положительно перекошенная,
  • строго убывающий, выпуклый
  • режим = 0
  • 0 < median < 1/2.
  • (максимальная дисперсия при возникновении $\alpha \; =\; -\; 1\; +\; 5\; 2,\; \beta \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \{\backslash \; tfrac\; \{-1)\; +\; \{\backslash \; sqrt\; \{\; 5\}\}\}\; \{2\}\},\; \backslash \; beta\; =\; 1\}$или α = Φ, конъюгат золотого сечения )
• α ≥ 1, β < 1
  • J- образный с левым хвостом,
  • отрицательно скошенный,
  • строго возрастающий, выпуклый
  • режим = 1
  • 1/2 < median < 1
  • (максимальная ошибка возникает при $\alpha \; =\; 1,\; \beta \; =\; -\; 1\; +\; 5\; 2\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 1,\; \backslash \; beta\; =\; \{\backslash \; tfrac\; \{-1\; +\; \{\backslash \; sqrt\; \{5\}\}\}\; \{2\}\}\}$или β = Φ конъюгатого сечения )
• α = 1, β>1
  • положительно перекошен,
  • строго убывает (красный график),
  • перевернут (зеркальное отображение) степенная функция [0,1] распределение
  • среднее значение = 1 / (β + 1)
  • медиана = 1 - 1/2
  • режим = 0
  • α = 1, 1 < β < 2
    • вогнутый
    • 
    • 1/18 < var(X) < 1/12.
  • α = 1, β = 2
    • прямая линия с наклоном −2, правое - треугольное распределение с прямым углом на левом конце, при x = 0
    • $median\; =\; 1\; -\; 1\; 2\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{median\}\}\; =\; 1\; -\; \{\backslash \; tfrac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\}\}\}$
    • var (X) = 1/18
  • α = 1, β>2
    • обратная J-образная форма с правым хвостом,
    • выпуклый
    • 
    • 0 < var(X) < 1/18
• α>1, β = 1
  • отрицательно смещен,
  • стр ого возрастает (зеленый график),
  • степенная функция [0, 1] распределение
  • среднее значение = α / (α + 1)
  • медиана = 1/2
  • режим = 1
  • 2>α>1, β = 1
    • вогнутый
    • 
    • 1/18 < var(X) < 1/12
  • α = 2, β = 1
    • прямая линия с наклоном +2, распределение вправо - треугольник с прямым углом на правом конце, при x = 1
    • $медиана\; =\; 1\; 2\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{median\}\}\; =\; \{\; \backslash \; tfrac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\}\}\}$
    • var (X) = 1/18
  • α>2, β = 1
    • J-образный с левым хвостом, выпуклый
    • 
    • 0 < var(X) < 1/18

Связанные распределения

Преобразования

• Если X ~ Beta (α, β), то 1 - X ~ Beta (β, α) зеркальное изображение симметрия
• Если X ~ Beta (α, β), то $X\; 1\; -\; X\; \sim \; \beta \; \prime \; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{X\}\; \{1-X\}\}\; \backslash \; sim\; \{\backslash \; beta\; ^\; \{\text{'}\}\}\; (\backslash \; alpha,\; \backslash \; beta)\}$. бета-простое распределение, также называемое «бета-распределение второго рода».
• Если X ~ Beta (α, β), то $1\; X\; -\; 1\; \sim \; \beta \; \prime \; (\beta ,\; \alpha )\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{X\}\}\; -\; 1\; \backslash \; sim\; \{\backslash \; beta\; ^\; \{\text{'}\}\}\; (\backslash \; beta,\; \backslash \; alpha)\}$.
• Если X ~ Beta (n / 2, m / 2) тогда $m\; X\; n\; (1\; -\; X)\; \sim \; F\; (n,\; m)\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{mX\}\; \{n\; (1-X)\}\}\; \backslash \; sim\; F\; (n,\; m)\}$(при n>0 и m>0), F-распределение Фишера – Снедекора.
• Если $X\; \sim \; Beta\; \; (1\; +\; \lambda \; m\; -\; min\; max\; -\; min,\; 1\; +\; \lambda \; max\; -\; m\; max\; -\; min)\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Beta\}\; \backslash \; left\; (1+\; \backslash \; lambda\; \{\backslash \; tfrac\; \{m-\; \backslash \; min\}\; \{\backslash \; max\; -\; \backslash \; min\}\},\; 1+\; \backslash \; lambda\; \{\backslash \; tfrac\; \{\; \backslash \; max\; -m\}\; \{\backslash \; max\; -\; \backslash \; min\}\}\; \backslash \; right)\}$затем min + X (max - min) ~ PERT (min, max, m, λ), где PERT обозначает Распределение PERT, используемое в анализе PERT, и m = наиболее вероятное значение. Традиционно λ = 4 в PERT-анализе.
• Если X ~ Beta (1, β), то X ~ Распределение Кумарасвами с параметрами (1, β)
• Если X ~ Beta (α, 1), то X ~ Распределение Кумарасвами с параметрами (α, 1)
• Если X ~ Beta (α, 1), то −ln (X) ~ Exponential (α)

Особые и предельные случаи

Пример восьми реализаций случайного блуждания в одном измерении, начиная с 0: вероятность для времени последнего посещения источника распределяется как бета (1/2, 1/2) Бета (1/2, 1/2): распределение арксинуса плотность вероятности было предложено Гарольдом Джеффрисом для представления неопределенности для Бернулли или биномиальное распределение в байесовском выводе, и теперь обычно обозначается как Jeffreys Prior : p (1 - p). Это распределение также появляется в нескольких случайных блужданиях фундаментальных теоремах

• Beta (1, 1) ~ U (0, 1).
• Если X ~ Beta (3/2, 3/2) и r>0, то 2rX - r ~ распределение полукругов Вигнера.
• Beta (1/2, 1/2) эквивалентно распределению арксинусов. Это распределение также является априорной вероятностью Джеффри для биномиальных распределений Бернулли и биномиальных распределений. Плотность вероятности арксинуса - это распределение, которое фигурирует в нескольких фундаментальных теоремах о случайных блужданиях. При справедливом подбрасывании монеты случайное блуждание вероятность для времени последнего посещения источника распределяется как (U-образное) распределение арксинусов. В игре с честным подбрасыванием монеты для двух игроков считается, что игрок идет впереди, если случайное блуждание (начавшееся в исходной точке) происходит выше исходной точки. Наиболее вероятное количество раз, когда данный игрок будет лидировать в игре длиной 2N, не равно N. Напротив, N - это наименее вероятное количество раз, когда игрок будет лидировать. Наиболее вероятное количество раз в отведении равно 0 или 2N (согласно распределению арксинусов ).
• $lim\; n\; \to \; \infty \; n\; Beta\; \; (1,\; n)\; =\; Exponential\; \; (1)\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; n\; \backslash \; operatorname\; \{Beta\}\; (1,\; n)\; =\; \backslash \; operatorname\; \{Exponential\}\; (1)\}$экспоненциальное распределение.
• $lim\; n\; \to \; \infty \; n\; Beta\; \; (k,\; n)\; =\; гамма\; \; (к,\; 1)\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{n\; \backslash \; to\; \backslash \; infty\}\; n\; \backslash \; operatorname\; \{Beta\}\; (k,\; n)\; =\; \backslash \; operatorname\; \{Gamma\}\; (k,\; 1)\}$гамма-распределение.

Получено из других распределений

• k-й упорядоченная статистика выборки размера n из равномерного распределения является бета-случайной величиной, U (k) ~ Beta (k, n + 1 − k).
• Если X ~ Gamma (α, θ) и Y ~ Gamma (β, θ) независимы, тогда $XX\; +\; Y\; \sim \; Beta\; \; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{X\}\; \{X\; +\; Y\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{Beta\}\; (\backslash \; alpha,\; \backslash \; beta)\; \backslash ,\}$.
• Если $X\; \sim \; \chi \; 2\; (\alpha )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; chi\; ^\; \{2\}\; (\backslash \; alpha)\; \backslash ,\}$и $Y\; \sim \; \chi \; 2\; (\beta )\; \{\backslash \; displaystyle\; Y\; \backslash \; sim\; \backslash \; chi\; ^\; \{2\}\; (\backslash \; beta)\; \backslash ,\}$независимы, тогда $XX\; +\; Y\; \sim \; Beta\; \; (\alpha \; 2,\; \beta \; 2)\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{X\}\; \{X\; +\; Y\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{Beta\}\; (\{\; \backslash \; tfrac\; \{\backslash \; alpha\}\; \{2\}\},\; \{\backslash \; tfrac\; \{\backslash \; beta\}\; \{2\}\})\}$.
• Если X ~ U (0, 1) и α>0, то X ~ Beta (α, 1). Распределение степенной функции.
• Если $X\; \sim \; Binom\; \; (k;\; n;\; p)\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Binom\}\; (k;\; n;\; p)\}$, затем $Икс\; (n\; +\; 1)\; \sim \; Бета\; \; (\alpha ,\; \beta )\; \{\backslash \; Displaystyle\; \{X\; (n\; +\; 1)\}\; \backslash \; sim\; \backslash \; OperatorName\; \{Beta\}\; (\backslash \; alpha,\; \backslash \; beta)\}$для дискретных значений n и k, где $\alpha \; =\; k\; +\; 1\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; k\; +\; 1\}$и $\beta \; =\; n\; -\; k\; +\; 1\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; n-k\; +\; 1\}$.

Комбинация с другими распределениями

• X ~ Beta (α, β) и Y ~ F (2β, 2α), затем $Pr\; (X\; \le \; \alpha \; \alpha \; +\; \beta \; x)\; =\; Pr\; (Y\; \ge \; Икс)\; \{\backslash \; Displaystyle\; \backslash \; Pr\; (X\; \backslash \; Leq\; \{\backslash \; tfrac\; \{\backslash \; alpha\}\; \{\backslash \; alpha\; +\; \backslash \; beta\; x\}\})\; =\; \backslash \; Pr\; (Y\; \backslash \; geq\; x)\; \backslash ,\}$для все x>0.

Составление с другими распределениями

• Если p ~ Beta (α, β) и X ~ Bin (k, p), то X ~ бета-биномиальное распределение
• Если p ~ Beta (α, β) и X ~ NB (r, p), затем X ~ бета-отрицательное биномиальное распределение

Обобщения

• Обобщение на несколько переменных, то есть многомерное бета-распределение, называется р-н Дирихле Ибутион. Одномерные маргиналы распределения Дирихле имеют бета-распределение. Бета-распределение сопряжено с биномиальным распределением и распределением Бернулли точно так же, как распределение Дирихле сопряжено с полиномиальным распределением и категориальным распределением..
• Распределение Пирсона типа I идентично бета-распределению (за исключением произвольного сдвига и масштабирования, которые также могут быть выполнены с помощью четырехпараметрической параметризации бета-распределения).
• $Бета\; \; (\alpha ,\; \beta )\; знак\; равно\; lim\; \delta \; \to \; 0\; N\; на\; C\; entral\; B\; eta\; (\alpha ,\; \beta ,\; \delta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Beta\}\; (\backslash \; alpha,\; \backslash \; beta)\; =\; \backslash \; lim\; \_\; \{\backslash \; delta\; \backslash \; to\; 0\}\; \{\; \backslash \; rm\; \{NonCentralBeta\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; \backslash \; delta)\}$нецентральное бета-распределение
• обобщенное бета-распределение - это семейство распределений с пятью параметрами который имеет бета-распределение как частный случай.
• Матрица бета-распределение переменных - это распределение для положительно определенных матриц.

.

Статистический вывод

Оценка параметра

Метод моментов

Два неизвестных параметра

Два неизвестных параметра ($(\alpha \; ^,\; \beta \; ^)\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{\; \backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\})\}$бета-распределения, поддерживаемого в интервале [0,1]), можно оценить, используя метод моментов, с первыми двумя моментами (выборочное среднее и выборочная дисперсия) следующим образом. Пусть:

$выборочное\; среднее\; (X)\; =\; x\; ¯\; =\; 1\; N\; \sum \; i\; =\; 1\; NX\; i\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{sample\; mean\; (X)\}\}\; =\; \{\backslash \; bar\; \{x\}\}\; =\; \{\backslash \; frac\; \{1\; \}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; X\_\; \{i\}\}$

быть выборочным средним, оценкой и

$выборочной\; дисперсией\; (X)\; =\; v\; ¯\; =\; 1\; N\; -\; 1\; \sum \; я\; знак\; равно\; 1\; N\; (Икс\; я\; -\; x\; ¯)\; 2\; \{\backslash \; Displaystyle\; \{\backslash \; text\; \{образец\; дисперсии\; (X)\}\}\; =\; \{\backslash \; bar\; \{v\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{N-1\}\; \}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; (X\_\; \{i\}\; -\; \{\backslash \; bar\; \{x\}\})\; ^\; \{2\}\}$

- выборочная оценка дисперсии. метод моментов оценки параметров:

$\alpha \; ^\; =\; x\; ¯\; (x\; ¯\; (1\; -\; x\; ¯)\; v\; ¯\; -\; 1),\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\; \}\; =\; \{\backslash \; bar\; \{x\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\{\backslash \; bar\; \{x\}\}\; (1\; -\; \{\backslash \; bar\; \{x\}\})\}\; \{\backslash \; bar\; \{v\}\}\}\; -\; 1\; \backslash \; right),\}$если

$\beta \; ^\; =\; (1\; -\; x\; ¯)\; (x\; ¯\; (1\; -\; x\; ¯)\; v\; ¯\; -\; 1),\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; =\; (1\; -\; \{\backslash \; bar\; \{x\}\})\; \backslash \; left\; (\{\backslash \; frac\; \{\{\backslash \; bar\; \{x\}\}\; (1\; -\; \{\backslash \; bar\; \{x\}\})\}\; \{\backslash \; bar\; \{v\}\}\}\; -\; 1\; \backslash \; right),\}$if

Когда требуется распределение в известном интервале, отличном от [0, 1] со случайной величиной X, скажем [a, c] со случайной величиной Y, затем замените $x\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{x\}\}\}$на $y\; ¯\; -\; ac\; -\; a,\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\{\backslash \; bar\; \{y\}\}\; -\; a\}\; \{ca\}\},\}$и $v\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{v\}\}\}$с $v\; Y\; ¯\; (c\; -\; a)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; bar\; \{v\_\; \{Y\}\}\}\; \{(ca)\; ^\; \{2\}\}\}\}$в приведенной выше паре уравнений для параметров формы (см. «Альтернативные параметризации, четыре параметра »ниже)., где:

$выбор\; очное\; среднее\; (Y)\; знак\; равно\; Y\; ¯\; =\; 1\; N\; \sum \; я\; =\; 1\; NY\; я\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{образец\; среднего\; (Y)\}\}\; =\; \{\backslash \; bar\; \{y\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; Y\_\; \{i\}\}$

$выборочная\; дисперсия\; (Y)\; =\; v\; Y\; ¯\; =\; 1\; N\; -\; 1\; \sum \; i\; =\; 1\; N\; (Y\; i\; -\; y\; ¯)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{sample\; дисперсия\; (Y)\}\}\; =\; \{\backslash \; bar\; \{v\_\; \{Y\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{N-1\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; (Y\_\; \{i\}\; -\; \{\backslash \; bar\; \{y\}\})\; ^\; \{2\}\}$

Четыре неизвестных параметра

Решения для оценки параметров в зависимости от (выборки) избыточного эксцесса и (выборки) квадрата асимметрии Бета-распределение

Все четыре параметра ($\alpha \; ^,\; \beta \; ^,\; a\; ^,\; c\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\},\; \{\backslash \; hat\; \{a\}\},\; \{\backslash \; hat\; \{c\}\}\}$бета-распределения, поддерживаемого в интервале [a, c] - см. Раздел «Альтернативные параметризации, четыре параметра» -), можно оценить, используя метод моментов, разработанный Карлом Пирсоном, приравнивая значения выборки и генеральной совокупности первых четырех центральных моментов (среднее значение, дисперсия, асимметрия и избыточный эксцесс). Избыточный эксцесс выражался в квадрате асимметрии, а размер выборки ν = α + β (см. Предыдущий раздел «эксцесс» ) следующим образом:

Это уравнение можно использовать для определения размера выборки ν = α + β в терминах квадрата асимметрии и избыточный эксцесс следующим образом:

$\nu \; ^\; =\; \alpha \; ^\; +\; \beta \; ^\; =\; 3\; (избыточный\; эксцесс\; в\; выборке)\; -\; (асимметрия\; выборки)\; 2\; +\; 2\; 3\; 2\; (асимметрия\; выборки)\; 2\; -\; (избыточный\; эксцесс\; в\; выборке)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; nu\}\}\; =\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; =\; 3\; \{\backslash \; frac\; \{(\{\backslash \; text\; \{образец\; избыточного\; эксцесса\}\})\; -\; (\{\backslash \; text\; \{образец\; асимметрии\}\; \})\; ^\; \{2\}\; +2\}\; \{\{\backslash \; frac\; \{3\}\; \{2\}\}\; (\{\backslash \; text\; \{образец\; асимметрии\}\})\; ^\; \{2\}\; -\; \{\backslash \; text\; \{(пример\; избыточного\; эксцесса)\}\}\}\}\}$

Это отношение (умноженное на коэффициент 3) между ранее выведенными границами предела для бета-распределения в пространстве (как первоначально было сделано Карлом Пирсоном), определенным с координатами квадрат t асимметрия по одной оси и избыточный эксцесс по другой оси (см. предыдущий раздел под названием «Эксцесс, ограниченный квадратом асимметрии»):

Случай нулевой асимметрии может быть решен немедленно, потому что для нулевой асимметрии, α = β и, следовательно, ν = 2α = 2β, поэтому α = β = ν / 2

$\alpha \; ^\; =\; \beta \; ^\; =\; \nu \; ^\; 2\; =\; 3\; 2\; (избыточный\; эксцесс\; образца)\; +\; 3\; -\; (избыточный\; эксцесс\; образца)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; =\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; =\; \{\backslash \; frac\; \{\backslash \; hat\; \{\backslash \; nu\}\}\; \{2\}\}\; =\; \{\backslash \; frac\; \{\{\backslash \; frac\; \{3\}\; \{2\}\}\; (\; \{\backslash \; text\; \{образец\; избыточного\; эксцесса\}\})\; +\; 3\}\; \{-\; \{\backslash \; text\; \{(пример\; избыточного\; эксцесса)\}\}\}\}\}$

(избыточный эксцесс отрицателен для бета-распределение с нулевой асимметрией в диапазоне от -2 до 0, так что $\nu \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; nu\}\}\}$- и, следовательно, параметры формы образца - положительны, в диапазоне от нуля, когда параметры формы приближаются к нулю, а избыточный эксцесс приближается к -2, до бесконечности, когда параметры формы стремятся к бесконечности, а избыточный эксцесс пр иближается к нулю).

Для ненулевой асимметрии выборки необходимо решить систему двух связанных уравнений. Поскольку асимметрия и избыточный эксцесс не зависят от параметров $a\; ^,\; c\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{a\}\},\; \{\backslash \; hat\; \{c\}\}\}$, параметры $\alpha \; ^,\; \beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$можно однозначно определить на основе асимметрии образца и избыточного эксцесса образца путем решения связанные уравнения с двумя известными переменными (асимметрия образца и избыточный эксцесс образца) и двумя неизвестными ( параметрами формы):

$(перекос\; образца)\; 2\; =\; 4\; (\beta \; ^\; -\; \alpha \; ^)\; 2\; (1\; +\; \alpha \; ^\; +\; \beta \; ^)\; \alpha \; ^\; \beta \; ^\; (2\; +\; \alpha \; ^\; +\; \beta \; ^)\; 2\; \{\backslash \; displaystyle\; (\{\backslash \; text\; \{пример\; перекоса\}\})\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{4\; (\{\backslash \; шляпа\; \{\backslash \; beta\}\}\; -\; \{\backslash \; hat\; \{\backslash \; alpha\}\})\; ^\; \{2\}\; (1\; +\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\}\; \{\{\backslash \; hat\; \{\backslash \; alpha\}\; \}\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; (2\; +\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\; ^\; \{2\}\}\}\}$

$избыточный\; эксцесс\; выборки\; =\; 6\; 3\; +\; \alpha \; ^\; +\; \beta \; ^\; ((2\; +\; \alpha \; ^\; +\; \beta \; ^)\; 4\; (примерная\; асимметрия)\; 2-1)\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{образец\; избыточного\; эксцесса\}\}\; =\; \{\backslash \; frac\; \{6\}\; \{3\; +\; \{\backslash \; hat\; \{\backslash \; alpha\}\; \}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{(2\; +\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}))\}\; \{4\}\}\; (\{\backslash \; text\; \{примерная\; асимметрия\}\})\; ^\; \{2\}\; -1\; \backslash \; right)\}$

, в результате получается следующее решение:

$\alpha \; ^,\; \beta \; ^\; =\; \nu \; ^\; 2\; (1\; \pm \; 1\; 1\; +\; 16\; (\nu \; ^\; +\; 1)\; (\nu \; ^\; +\; 2)\; 2\; (перекос\; образца)\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; =\; \{\backslash \; frac\; \{\backslash \; hat\; \{\backslash \; nu\}\}\; \{2\}\}\; \backslash \; left\; (1\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1\; +\; \{\backslash \; frac\; \{16\; (\{\backslash \; hat\; \{\backslash \; nu\}\}\; +\; 1)\}\; \{\; (\{\backslash \; hat\; \{\backslash \; nu\}\}\; +\; 2)\; ^\; \{2\}\; (\{\backslash \; text\; \{sample\; skewness\}\})\; ^\; \{2\}\}\}\}\}\; \backslash \; right)\}$

Где нужно взять следующие решения: $\alpha \; ^>\beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}>\{\backslash \; hat\; \{\backslash \; beta\}\}\}$для (отрицательной) асимметрии образца <0 и для (положительного) перекоса образца>0.

На прилагаемом графике эти два решения показаны в виде границ с горизонтальными осями (избыточный эксцесс образца) и (квадрат асимметрии образца) и формы в качестве вертикальной оси. Поверхности ограничены условием, что избыточный эксцесс образца должен быть ограничен квадратом асимметрии образца, как указано в приведенном выше уравнении. Две поверхности встречаются у правого края, определяемого нулевым перекосом. Вдоль этого правого края оба параметра равны, и распределение имеет симметричную U-образную форму для α = β < 1, uniform for α = β = 1, upside-down-U-shaped for 1 < α = β < 2 and bell-shaped for α = β>2. Поверхности также встречаются на переднем (нижнем) крае, определяемом линией «невозможной границы» (избыточный эксцесс + 2 - асимметрия = 0). Вдоль этой передней (нижней) границы обоих вариантов формы приближаются к нулю, а плотность им больше сосредоточена на одном конце, чем на конце (практически между ничего), с вероятностями $p\; =\; \beta \; \alpha \; +\; \beta \; \{\backslash \; displaystyle\; p\; =\; \{\backslash \; tfrac\; \{\backslash \; beta\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\}$на левом конце x = 0 и $q\; =\; 1\; -\; p\; =\; \alpha \; \alpha \; +\; \beta \; \{\backslash \; displaystyle\; q\; =\; 1\; -p\; =\; \{\backslash \; tfrac\; \{\backslash \; alpha\}\; \{\backslash \; alpha\; +\; \backslash \; beta\}\}\}$на правом конце x = 1. Две поверхности расходятся дальше по направлению к заднему краю. На этой задней кромке параметры поверхности сильно отличаются друг от друга. Как было принято, например, Боуменом и Шентоном, выборка в окрестности линии (избыточный эксцесс в выборке - (3/2) (асимметрия выборки) = 0) (J-образная часть заднего края, где встречается синий бежевый), «опасно близок к хаосу », потому что на этой линии знаменатель приведенного выше выражения для оценки ν = α + β становится равным нулю и, следовательно, ν приближается к бесконечности по мере приближения к этой линии. Боуман и Шентон пишут, что «параметры высших моментов (эксцесс и асимметрия) чрезвычайно хрупки (около этой линии). Однако среднее значение и стандартное отклонение довольно надежны». Таким образом, проблема заключается в случае оценки четырех параметров для очень асимметричных распределений, так что избыточный эксцесс приближается к квадрату асимметрии (3/2). Эта граничная линия образована чрезвычайно искаженными распределениями с очень большими значениями одного из параметров и очень маленькими значениями другого параметра. См. Раздел под названием «Эксцесс, ограниченный квадратом асимметрии» для получения числового примера и дополнительных комментариев об этой граничной линии заднего края (примерный эксцесс - (3/2) (выборочная асимметрия) = 0). Как заметил сам Карл Пирсон, эта проблема может не иметь большого практического значения, поскольку эта проблема возникает только для сильно искаженных J-образных (или зеркальных J-образных) распределений с очень разными значениями параметров формы, которые вряд ли будут часто встречаться в практика). Обычные косоугольные распределения, которые встречаются на практике, не имеют этой проблемы оценки параметров.

Остальные два параметра $a\; ^,\; c\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{a\}\},\; \{\backslash \; hat\; \{c\}\}\}$могут быть определены с использованием выборочного среднего и выборочная дисперсия с использованием множества уравнений. Один из альтернативных вариантов - вычислить диапазон интервала поддержки $(c\; ^\; -\; a\; ^)\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\}$на основе выборки дисперсия и выборочный эксцесс. Для этой цели можно решить в терминах диапазона $(c\; ^\; -\; a\; ^)\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\}$, уравнение, выражающее избыточный эксцесс через дисперсию выборки, и размер выборки ν (см. разделы «Эксцесс» и «Альтернативные параметризации, четыре параметра»):

$эксцесс\; выборки\; =\; 6\; (3\; +\; \nu \; ^)\; (\; 2\; +\; \nu \; ^)\; ((c\; ^\; -\; a\; ^)\; 2\; (выборочная\; дисперсия)\; -\; 6-5\; \nu \; ^)\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{выборочный\; эксцесс\}\}\; =\; \{\backslash \; frac\; \{6\}\; \{(3\; +\; \{\backslash \; шляпа\; \{\backslash \; nu\}\})\; (2\; +\; \{\backslash \; hat\; \{\backslash \; nu\}\})\}\}\; \{\backslash \; bigg\; (\}\; \{\backslash \; frac\; \{(\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\; ^\; \{2\; \}\}\; \{\backslash \; text\; \{(образец\; дисперсии)\}\}\}\; -\; 6-5\; \{\backslash \; hat\; \{\backslash \; nu\}\}\; \{\backslash \; bigg)\}\}$

, чтобы получить:

$(c\; ^\; -\; a\; ^)\; =\; (sample\; дисперсия)\; 6\; +\; 5\; \nu \; ^\; +\; (2\; +\; \nu \; ^)\; (3\; +\; \nu \; ^)\; 6\; (выборка\; избыточного\; эксцесса)\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\; =\; \{\backslash \; sqrt\; \{\backslash \; text\; \{(образец\; дисперсии)\}\}\}\; \{\backslash \; sqrt\; \{6\; +\; 5\; \{\backslash \; hat\; \{\backslash \; nu\}\}\; +\; \{\backslash \; frac\; \{(2\; +\; \{\backslash \; hat\; \{\backslash \; nu\}\})\; (3\; +\; \{\backslash \; hat\; \{\; \backslash \; nu\}\})\}\; \{6\}\}\; \{\backslash \; text\; \{(пример\; избыточного\; эксцесса)\}\}\}\}\}$

Другой альтернативой является вычисление диапазона интервала поддержки $(c\; ^\; -\; a\; ^)\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\}$на основе дисперсии выборки и асимметрии выборки. Для этой цели можно решить в терминах диапазона $(c\; ^\; -\; a\; ^)\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\}$, уравнение, выражающее квадрат асимметрии через дисперсию выборки и размер выборки ν (см. разделы «Асимметрия» и «Альтернативные параметризации, четыре параметра»):

$(асимметрия\; выборки)\; 2\; =\; 4\; (2\; +\; \nu \; ^)\; 2\; ((c\; ^\; -\; a\; ^)\; 2\; (выборочная\; дисперсия)\; -\; 4\; (1\; +\; \nu \; ^))\; \{\backslash \; displaystyle\; (\{\backslash \; text\; \{sample\; skewness\}\})\; ^\; \{2\}\; =\; \{\backslash \; frac\; \{4\}\; \{(\; 2\; +\; \{\backslash \; hat\; \{\backslash \; nu\}\})\; ^\; \{2\}\}\}\; \{\backslash \; bigg\; (\}\; \{\backslash \; frac\; \{(\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\; ^\; \{2\}\}\; \{\backslash \; text\; \{(выборочная\; дисперсия)\}\}\}\; -\; 4\; (1\; +\; \{\backslash \; hat\; \{\backslash \; nu\}\})\; \{\backslash \; bigg)\}\}$

для получения:

$(c\; ^\; -\; a\; ^)\; =\; (выборочная\; дисперсия)\; 2\; (2\; +\; \nu \; ^)\; 2\; (асимметрия\; выборки)\; 2\; +\; 16\; (1\; +\; \nu \; ^)\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\})\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{\backslash \; text\; \{(образец\; отклонения)\}\}\}\; \{2\}\}\; \{\backslash \; sqrt\; \{(2\; +\; \{\backslash \; hat\; \{\backslash \; nu\}\})\; ^\; \{2\}\; (\{\backslash \; text\; \{образец\; отклонения\}\})\; ^\; \{2\}\; +16\; (\; 1\; +\; \{\backslash \; hat\; \{\backslash \; nu\}\})\}\}\}$

Остающийся параметр может быть определен из выборочного среднего и ранее полученных параметров: $(c\; ^\; -\; a\; ^),\; \alpha \; ^,\; \nu \; ^\; знак\; равно\; \alpha \; ^\; +\; \beta \; ^\; \{\backslash \; displaystyle\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\}),\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; nu\}\}\; =\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$:

$a\; ^\; =\; (выборочное\; среднее)\; -\; (\alpha \; ^\; \nu \; ^)\; (c\; ^\; -\; a\; ^)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{a\; \}\}\; =\; (\{\backslash \; text\; \{sample\; mean\}\})\; -\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; \{\backslash \; hat\; \{\backslash \; nu\}\}\}\; \backslash \; right)\; (\{\backslash \; hat\; \{c\}\}\; -\; \{\; \backslash \; hat\; \{a\}\})\}$

и, наконец, $c\; ^\; =\; (c\; ^\; -\; a\; ^)\; +\; a\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{c\}\}\; =\; (\{\backslash \; hat\; \{c\; \}\}\; -\; \{\backslash \; hat\; \{a\}\})\; +\; \{\backslash \; hat\; \{a\}\}\}$.

В приведенных выше формулах можно использовать, например, как оценки моментов выборки:

$среднее значение выборки = y ¯ = 1 N ∑ i = 1 NY i дисперсия выборки = v ¯ Y = 1 N - 1 ∑ i = 1 N (Y i - y ¯) 2 асимметрия выборки = G 1 = N (N - 1) (N - 2) ∑ i = 1 N (Y i - y ¯) 3 v ¯ Y 3 2 избыточного эксцесса выборки = G 2 = N (N + 1) (N - 1) (N - 2) (N - 3) ∑ i = 1 N (Y я - Y ¯) 4 v ¯ Y 2 - 3 (N - 1) 2 (N - 2) (N - 3) {\ displaystyle {\ begin {align} {\ text {sample mean}} = { \ overline {y}} = {\ frac {1} {N}} \ sum _ {i = 1} ^ {N} Y_ {i} \\ {\ text {образец дисперсии}} = {\ overline {v }} _ {Y} = {\ frac {1} {N-1}} \ sum _ {i = 1} ^ {N} (Y_ {i} - {\ overline {y}}) ^ {2} \\ {\ text {образец асимметрия}} = G_ {1} = {\ frac {N} {(N-1) (N-2)}} {\ frac {\ sum _ {i = 1} ^ {N} (Y_ {i} - {\ overline {y}}) ^ {3}} {{\ overline {v}} _ {Y} ^ {\ frac {3} {2}}}} \\ {\ text {образец избыточного эксцесса}} = G_ {2} = {\ frac {N (N + 1)} {(N-1) (N-2) (N-3)}} {\ frac {\ sum _ {i = 1} ^ { N} (Y_ {i} - {\ overline {y}}) ^ {4}} {{\ overline {v}} _ {Y} ^ {2}}} - {\ frac {3 (N-1) ^ {2}} {(N-2) (N-3)}} \ end {align}}}$

Оценки G 1 для асимметрии выборки и G 2 для выборочного эксцесса использовались DAP / SAS, PSPP / SPSS, и Excel. Однако они не используются BMDP и (согласно) они не использовались MINITAB в 1998 году. Фактически, Джоанес и Гилл в своем исследовании 1998 года пришли к выводу, что оценки асимметрии и эксцесса использованные в BMDP и в MINITAB (в то время) имели меньшую дисперсию и среднеквадратичную ошибку в нормальных выборках, но оценки асимметрии и эксцесса, используемые в DAP / SAS, PSPP / SPSS, а именно G 1 и G 2, имели меньшую среднеквадратичную ошибку в выборках из очень искаженного распределения. Именно по этой причине мы прописали «асимметрию выборки» и т. Д. В приведенной выше формулах, чтобы явно указать, что пользователь должен выбрать лучшую оценку в соответствии с рассматриваемой проблемой, как лучшую оценку асимметрии и эксцесса. зависит от величины перекоса (как показано Джоанесом и Гиллом).

Максимальное правдоподобие

Два неизвестных параметра

Макс (совместное логарифмическое правдоподобие / N) для максимумов бета-распределения при α = β = 2 Макс (совместное логарифмическое правдоподобие / N) для Максимумы бета-распределения при α = β ∈ {0,25,0,5,1,2,4,6,8}

Как и в случае значение размера правдоподобия для гамма -распределения, оценки правдоподобия для бета-распределения не имеют общего решения в замкнутой форме для произвольных значений параметров. Если X 1,..., X N являются независимыми случайными величинами, каждая из которых имеет бета-распределение, функция совместного правдоподобия для N iid наблюдений будет :

$ln\; L\; (\alpha ,\; \beta \; \mid \; X)\; =\; \sum \; i\; =\; 1\; N\; ln\; \; (L\; i\; (\alpha ,\; \beta \; \mid \; X\; i))\; =\; \sum \; i\; =\; 1\; N\; ln\; \; (f\; (X\; i;\; \alpha ,\; \beta ))\; =\; \sum \; i\; =\; 1\; N\; ln\; \; (X\; i\; \alpha \; -\; 1\; (1\; -\; X\; i)\; \beta \; -\; 1\; B\; (\alpha ,\; \beta ))\; =\; (\alpha \; -\; 1)\; \sum \; i\; =\; 1\; N\; ln\; \; (X\; i)\; +\; (\beta \; -\; 1)\; \sum \; я\; знак\; равно\; 1\; N\; пер\; \; (1\; -\; Икс\; я)\; -\; N\; пер\; \; В\; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; ln\; \backslash ,\; \{\backslash \; mathcal\; \{L\}\}\; (\; \backslash \; альфа,\; \backslash \; beta\; \backslash \; mid\; X)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; mathcal\; \{L\}\}\; \_\; \{i\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X\_\; \{i\; \})\; \backslash \; справа)\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \backslash \; left\; (f\; (X\_\; \{i\};\; \backslash \; alpha,\; \backslash \; beta)\; \backslash \; right)\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{\; i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{X\_\; \{i\}\; ^\; \{\backslash \; alpha\; -1\}\; (1-X\_\; \{i\})\; ^\; \{\backslash \; beta\; -1\}\}\; \{\backslash \; mathrm\; \{B\})\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; \backslash \; right)\; \backslash \backslash \; =\; (\backslash \; alpha\; -1)\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (X\_\; \{i\})\; +\; (\backslash \; beta\; -1)\; \backslash \; сумма\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (1-X\_\; \{i\})\; -\; N\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; \backslash \; end\; \{align\}\}\}$

Нахождение максимума параметр формы включает в себя принятие частной производной по этому параметру и установка выражения равной формы нулю, что дает оценку максимальное правдоподобия параметров формы:

$\partial \; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; \partial \; \alpha \; =\; \sum \; i\; =\; 1\; N\; ln\; \; Икс\; я\; -\; N\; \partial \; пер\; \; В\; (\alpha ,\; \beta )\; \partial \; \alpha \; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; X\_\; \{i\}\; -N\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\; =\; 0\}$

$\partial \; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; \partial \; \beta \; =\; \sum \; я\; знак\; равно\; 1\; N\; пер\; \; (1\; -\; Икс\; я)\; -\; N\; \partial \; пер\; \; В\; (\alpha ,\; \beta )\; \partial \; \beta \; =\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; альфа,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{\backslash \; partial\; \backslash \; beta\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (1-X\_\; \{i\})\; -\; N\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; mathrm\; \{\; B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; beta\}\}\; =\; 0\}$

где:

$\partial \; ln\; \; B\; (\alpha ,\; \beta )\; \partial \; \alpha \; =\; -\; \partial \; ln\; \; \Gamma \; (\alpha \; +\; \beta )\; \partial \; \alpha \; +\; \partial \; ln\; \; \Gamma \; (\alpha )\; \partial \; \alpha \; +\; \partial \; ln\; \; \Gamma \; (\beta )\; \partial \; \alpha \; =\; -\; \psi \; (\alpha \; +\; \beta )\; +\; \psi \; (\alpha )\; +\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; частичный\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha\; +\; \backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\; +\; \{\backslash \; frac\; \{\backslash \; частично\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\; =\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\; +\; \backslash \; psi\; (\backslash \; alpha)\; +0\}$

$\partial \; ln\; \; B\; (\alpha ,\; \beta )\; \partial \; \beta \; =\; -\; \partial \; ln\; \; \Gamma \; (\alpha \; +\; \beta )\; \partial \; \beta \; +\; \partial \; ln\; \; \Gamma \; (\alpha )\; \partial \; \beta \; +\; \partial \; пер\; \; \Gamma \; (\beta )\; \partial \; \beta \; знак\; равно\; -\; \psi \; (\alpha \; +\; \beta )\; +\; 0\; +\; \psi \; (\beta )\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; beta\}\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha\; +\; \backslash \; beta)\; \}\; \{\backslash \; partial\; \backslash \; beta\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{\backslash \; partial\; \backslash \; beta\}\}\; +\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; beta\}\}\; =\; -\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\; +0+\; \backslash \; psi\; (\backslash \; beta)\}$

так как дигамма-функция, обозначенная ψ (α), определяется как логарифмическая производная от гамма-функции :

$\psi \; (\alpha )\; знак\; равно\; \partial \; пер\; \Gamma \; (\alpha )\; \partial \; \alpha \; \{\backslash \; displaystyle\; \backslash \; psi\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\}$

значения с нулевой наклонной касательной действительно является максимумом (не точкой перевала или минимумом), необходимо также удовлетворить условию что кривизна отрицательная. Это означает, что вторая отрицательная производная по параметрам формыательна

используя предыдущие уравнения, это эквивалентно:

$\partial \; 2\; пер\; \; В\; (\alpha ,\; \beta )\; \partial \; \alpha \; 2\; знак\; равно\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )>0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\; \{\backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)>0\}$

$\partial \; 2\; пер\; \; В\; (\alpha ,\; \beta )\; \partial \; \beta \; 2\; знак\; равно\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta )>0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; альфа,\; \backslash \; бета)\}\; \{\; \backslash \; partial\; \backslash \; beta\; ^\; \{2\}\}\}\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)>0\}$

, где тригамма-функция, обозначенная ψ 1 (α), является второй из функций полигаммы, и определяется как производная функция digamma :

$\psi \; 1\; (\alpha )\; =\; \partial \; 2\; ln\; \; \Gamma \; (\alpha )\; \partial \; \alpha \; 2\; =\; \partial \; \psi \; (\alpha )\; \partial \; \alpha .\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{\backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; \backslash ,\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash ,\; \backslash \; psi\; (\backslash \; alpha)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}.\}$

Эти условия эквивалентны утверждению, что дисперсии логарифмически преобразованных переменных положительны, поскольку:

$var\; \; [ln\; \; (X)]\; знак\; равно\; E\; \; [пер\; 2\; \; (X)]\; -\; (E\; \; [пер\; \; (X)])\; 2\; =\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (X)]\; =\; \backslash \; operatorname\; \{E\}\; [\backslash \; ln\; ^\; \{2\}\; (X)]\; -\; (\backslash \; operatorname\; \{E\}\; [\backslash \; ln\; (X)])\; ^\; \{2\}\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}$

$var\; \; [ln\; \; (1\; -\; X)]\; =\; E\; \; [ln\; 2\; \; (1\; -\; X)]\; -\; (E\; \; [пер\; \; (1\; -\; Икс)])\; 2\; знака\; равно\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; operatorname\; \{E\}\; [\backslash \; ln\; ^\; \{2\}\; (1-X)]\; -\; (\backslash \; operatorname\; \{E\}\; [\backslash \; ln\; (1-X)])\; ^\; \{2\}\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}$

должно быть условием максимальной отрицательной кривизны эквивалентно утверждениям:

$var\; \; [l\; n\; \; (X)]>0\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (X)]>0\}$

$вар\; \; [пер\; \; (1\; -\; X)]>0\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\; ln\; (1-X)]>0\}$

В качестве альтернативы условием максимальной отрицательной кривизны является также эквивалентно заявлению, что следующие логарифми производственные от геометрических средних GX(и G GXX) положительны, поскольку:

$\psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; знак\; равно\; \partial \; пер\; GX\; \partial \; \alpha >0\; \{\backslash \; displaystyle\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; G\_\; \{X\}\}\; \{\backslash \; partial\; \backslash \; alpha\}\}>0\}$

$\psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; =\; \partial \; ln\; \; G\; (1\; -\; X)\; \partial \; \beta >0\; \{\backslash \; Стиль\; отображения\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; G\; \_\; \{(1-X)\}\}\; \{\backslash \; partial\; \backslash \; beta\}\; \}>0\}$

Хотя эти наклоны действительно положительные, другие наклоны отрицательные:

наклоны среднего и медианы относительно α и β демонстрируют сходное поведение знака.

<7763>Из условий, что в максимуме частная производная по параметру формы равна нулю, мы получаем следующие системы связанных логических уравнений значения максимального правдоподобия (для средних правдоподобий), необходимо инвертировать, чтобы получить (неизвестные) оценки параметров формы $\alpha \; ^,\; \beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$в терминах (известного) среднего логарифмов выборок X 1,..., X N:

$E\; ^\; [ln\; \; (X)]\; =\; \psi \; (\alpha \; ^)\; -\; \psi \; (\alpha \; ^\; +\; \beta \; ^)\; =\; 1\; N\; \sum \; i\; =\; 1\; N\; ln\; \; X\; i\; =\; ln\; \; G\; ^\; XE\; ^\; [ln\; \; (1\; -\; X)]\; =\; \psi \; (\beta \; ^)\; -\; \psi \; (\alpha \; ^\; +\; \beta \; ^)\; =\; 1\; N\; \sum \; я\; знак\; равно\; 1\; N\; пер\; \; (1\; -\; Икс\; я)\; =\; пер\; \; G\; ^\; (1\; -\; Икс)\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; hat\; \{\backslash \; operatorname\; \{E\}\}\}\; [\backslash \; ln\; (X)]\; =\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\})\; -\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; X\_\; \{i\}\; =\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\; \backslash \backslash \; \{\backslash \; hat\; \{\backslash \; operatorname\; \{E\}\}\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; beta\}\})\; -\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{я\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (1-X\_\; \{i\})\; =\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\; \backslash \; end\; \{align\}\}\}$

где мы распознаем $log\; \; G\; ^\; X\; \{\backslash \; displaystyle\; \backslash \; log\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\}$как логарифм выборки среднего геометрического и $log\; \; G\; ^\; (1\; -\; X)\; \{\backslash \; displaystyle\; \backslash \; log\; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\}$как логарифм выборки среднего геометрического на основе (1 - X), изображение X. Для $\alpha \; ^\; =\; \beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; =\; \{\backslash \; hat\; \{\; \backslash \; beta\}\}\}$следует, что $G\; ^\; X\; Знак\; равно\; G\; ^\; (1\; -\; X)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\; =\; \{\backslash \; hat\; \{G\}\; \}\; \_\; \{(1-X)\}\}$.

$G\; ^\; X\; =\; \prod \; i\; =\; 1\; N\; (Икс\; я)\; 1\; /\; NG\; ^\; (1\; -\; Икс)\; знак\; равно\; \prod \; я\; знак\; равно\; 1\; N\; (1\; -\; Икс\; я)\; 1\; /\; N\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; (X\_\; \{i\})\; ^\; \{1\; /\; N\}\; \backslash \backslash \; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; (1-X\_\; \{i\})\; ^\; \{1\; /\; N\}\; \backslash \; end\; \{align\}\}\}$

Эти связанные уравнения, содержащие дигамма-функции оценок параметров фо рмы $\alpha \; ^,\; \beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$должны решаться численными методами, как это было сделано, например, Бекман и др. Gnanadesikan et al. дают численные решения для нескольких случаев. Н.Л.Джонсон и С.Котц предполагают, что для «слишком малых» оценок параметров формы $\alpha \; ^,\; \beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\; \}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$, логарифмическое приближение к дигамма-функции $\psi \; (\alpha \; ^)\approx \; ln\; \; (\alpha \; ^\; -\; 1\; 2)\; \{\backslash \; displaystyle\; \backslash \; psi\; (\{\; \backslash \; hat\; \{\backslash \; alpha\}\})\; \backslash \; приблизительно\; \backslash \; ln\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\})\}$может получить получение начальных значений для итерационного решения, поскольку уравнения, полученные в результате этого приближения, могут быть решены точно:

$ln\; \; \alpha \; ^\; -\; 1\; 2\; \alpha \; ^\; +\; \beta \; ^\; -\; 1\; 2\; \approx \; ln\; \; G\; ^\; X\; \{\backslash \; displaystyle\; \backslash \; ln\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{\backslash \; alpha\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \{\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\}\; \backslash \; приблизительно\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\}$

$ln\; \; \beta \; ^\; -\; 1\; 2\; \alpha \; ^\; +\; \beta \; ^\; -\; 1\; 2\; \approx \; ln\; \; G\; ^\; (1\; -\; X)\; \{\backslash \; displaystyle\; \backslash \; ln\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{\backslash \; beta\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \{\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \}\}\; \backslash \; приблизительно\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\}$

что приводит к следующему для начальных значений (параметров формы оценки в терминах среднего геометрического) для решения итеративного решения:

$\alpha \; ^\; \approx \; 1\; 2\; +\; G\; ^\; X\; 2\; (1\; -\; G\; ^\; X\; -\; G\; ^\; (1\; -\; X)),\; если\; \alpha \; ^>1\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; \backslash \; приблизительно\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\}\; \{2\; (\; 1\; -\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\; -\; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\})\}\}\; \{\backslash \; text\; \{if\}\}\; \{\backslash \; hat\; \{\backslash \; alpha\}\}>1\}$

$\beta \; ^\; \approx \; 1\; 2\; +\; G\; ^\; (1\; -\; X)\; 2\; (1\; -\; G\; ^\; X\; -\; G\; ^\; (1\; -\; X)),\; если\; \beta \; ^>1\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; \backslash \; приблизительно\; \{\; \backslash \; tfrac\; \{1\}\; \{2\}\}\; +\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\}\; \{2\; (1\; -\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\; -\; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1\; -X)\})\}\}\; \{\backslash \; text\; \{if\}\}\; \{\backslash \; hat\; \{\backslash \; beta\}\}>1\}$

В качес тве альтернативы оценки, использованные методом моментов, можно вместо этого использовать в качестве начальных значений для итеративного уравнения уравнения, связанные с максимальным правдоподобием, в терминах дигамма-функций.

Если требуется распределение в известном интервале, отличном от [0, 1], со случайной величиной X, скажем, [a, c] со случайной величиной Y, тогда замените ln (X i) в первом уравнении с

$ln\; \; Y\; i\; -\; ac\; -\; a,\; \{\backslash \; displaystyle\; \backslash \; ln\; \{\backslash \; frac\; \{Y\_\; \{i\}\; -a\}\; \{ca\}\},\}$

и замените ln (1 - X i) во втором уравнении с

$ln\; \; c\; -\; Y\; ic\; -\; a\; \{\backslash \; displaystyle\; \backslash \; ln\; \{\backslash \; frac\; \{c-Y\_\; \{i\}\}\; \{ca\}\}\}$

(см. Раздел «Альтернативные параметры, четыре варианта» ниже).

Если известен один из параметров формы, проблема значительно упрощается. Следующее преобразование logit можно использовать для определения неизвестного параметра формы (для случаев с перекосом, таких как $\alpha \; ^\; \ne \; \beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; \backslash \; neq\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$в противном случае, если симметричны, оба -равных известных известны, если известен один):

$E\; ^\; [ln\; \; (X\; 1\; -\; X)]\; =\; \psi \; (\alpha \; ^)\; -\; \psi \; (\beta \; ^)\; знак\; равно\; 1\; N\; \sum \; я\; знак\; равно\; 1\; N\; пер\; \; Икс\; я\; 1\; -\; Икс\; я\; =\; пер\; \; G\; ^\; X\; -\; пер\; \; (G\; ^\; (1\; -\; X))\; \{\backslash \; Displaystyle\; \{\backslash \; шляпа\; \{\backslash \; имя\; оператора\; \{E\}\}\}\; \backslash \; left\; [\backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right)\; \backslash \; right]\; =\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\})\; -\; \backslash \; psi\; (\{\; \backslash \; hat\; \{\backslash \; beta\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \{\backslash \; frac\; \{X\_\; \{i\}\}\; \{1-X\_\; \{i\}\}\; \}\; =\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\; -\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\; \backslash \; right)\}$

Этот логит преобразование - это логарифм преобразования, которое делит переменную X на ее зеркальное отображение (X / (1 - X), что приводит к «инвертированному бета-распределению» или простому бета-распределению (также известному как бета-распределение второго типа или Тип VI Пирсона ) с поддержкой [0, + ∞). Как ранее обсуждалось в разделе «Моменты логарифмически преобразованных случайных величин», преобразование logit $ln\; \; X\; 1\; -\; X\; \{\backslash \; displaystyle\; \backslash \; ln\; \{\backslash \; frac\; \{X\}\; \{1-X\}\}\}$, изученный Джонсоном, расширяет конечную опору [0, 1] на основе исходной переменной X до бесконечной опоры в обоих направлениях действительной прямой (−∞, + ∞).

Если, например, $\beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$известен, неизвестный параметр $\alpha \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\}$может быть получена в терминах обратной дигамма-функции правой части этого уравнения:

$\psi \; (\alpha \; ^)\; =\; 1\; N\; \sum \; i\; =\; 1\; N\; ln\; \; Икс\; я\; 1\; -\; Икс\; я\; +\; \psi \; (\beta \; ^)\; \{\backslash \; Displaystyle\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \{\backslash \; frac\; \{X\_\; \{i\}\}\; \{1-X\_\; \{i\}\}\}\; +\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; beta\}\})\}$

$\alpha \; ^\; =\; (Обратная\; дигамма)\; [ln\; \; G\; ^\; X\; -\; пер\; \; G\; ^\; (1\; -\; Икс)\; +\; \psi \; (\beta \; ^)]\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; =\; (\backslash \; operatorname\; \{Inversedigamma\})\; [\backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\; -\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\; +\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; beta\}\})]\}$

В частности, если один из параметров формы имеет значение, равное единице, например, для $\beta \; ^\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; =\; 1\}$(распределение степенной функции с ограниченной поддержкой [0,1]), используя тождество ψ ( x + 1) = ψ (x) + 1 / x в уравнении $\psi \; (\alpha \; ^)\; -\; \psi \; (\alpha \; ^\; +\; \beta \; ^)\; =\; ln\; \; G\; ^\; X\; \{\backslash \; displaystyle\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; аль\; pha\}\})\; -\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\; =\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\}$, максимум Оценка правдоподобия для неизвестного параметра $\alpha \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\}$, точно:

$\alpha \; ^\; =\; -\; 1\; 1\; N\; \sum \; i\; =\; 1\; N\; ln\; \; Икс\; я\; =\; -\; 1\; пер\; \; G\; ^\; Икс\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\; N\}\; \backslash \; ln\; X\_\; \{i\}\}\}\; =\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\}\}\}$

У бета-версии есть поддержка [0, 1], поэтому , и, следовательно, $(-\; ln\; \; G\; ^\; X)>0\; \{\backslash \; displaystyle\; (-\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\})>0\}$, следовательно, $а\; ^>0.\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}>0.\}$

В заключение, оценки максимального правдоподобия параметров формы бета-распределения (в целом) являются сложной функцией выборки среднее геометрическое и выборки среднее геометрическое на основе (1-X), зеркальное отображение X. Может возникнуть вопрос, необходима ли дисперсия (в дополнение к среднему) для оцените два параметра формы с помощью метода моментов, почему дисперсия (логарифмическая или геометрическая) не требуется для оценки двух параметров формы с помощью метода максимального правдоподобия, для которого достаточно только геометрических средних? Ответ заключается в том, что среднее значение не дает много информации в виде среднего геометрического. Для бета-распределения с равными параметрами формы α = β среднее равно точно 1/2, незави симо от значения параметров формы, и поэтому re независимо от величины статистической дисперсии (дисперсии). С другой стороны, среднее геометрическое бета-распределения с равными параметрами формы α = β зависит от значения параметров формы и, следовательно, содержит больше информации. Кроме того, среднее геометрическое бета-распределения не удовлетворяет условиям симметрии, которым удовлетворяет среднее значение, поэтому, используя как среднее геометрическое, основанное на X, так и среднее геометрическое на основе (1 - X), метод максимального правдоподобия может обеспечить наилучшие оценки для обоих параметров α = β, без необходимости использования дисперсии.

Можно выразить совместное логарифмическое правдоподобие для N iid наблюдений с помощью достаточной статистики (выборочные геометрические средние) следующим образом:

$ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; =\; (\alpha \; -\; 1)\; ln\; \; G\; ^\; X\; +\; (\beta \; -\; 1)\; ln\; \; G\; ^\; (1\; -\; X)\; -\; ln\; \; B\; (\alpha ,\; \beta ).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\}\}\; =\; (\backslash \; alpha\; -1)\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\; \}\; +\; (\backslash \; beta\; -1)\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{(1-X)\}\; -\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta).\}$

Мы можем построить соединение log правдоподобия на N наблюдений для фиксированных значений выборочных геометрических средних, чтобы увидеть поведение функции правдоподобия как функцию параметров формы α и β. На таком графике оценки параметров формы $\alpha \; ^,\; \beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$соответствуют максимумам функция правдоподобия. См. Прилагаемый график, который показывает, что все функции правдоподобия пересекаются при α = β = 1, что соответствует значениям параметров формы, которые дают максимальную энтропию (максимальная энтропия возникает для параметров формы, равных единице: равномерное распределение). Из графика видно, что функция правдоподобия дает резкие пики для значений оценок параметров формы, близких к нулю, но что для значений оценок параметров формы больше единицы функция правдоподобия становится довольно плоской с менее определенными пиками. Очевидно, что метод оценки параметра максимального правдоподобия для бета-распределения становится менее приемлемым для больших значений средств оценки параметров формы, поскольку неопределенность в определении пика увеличивается с увеличением значения средств оценки параметров формы. К такому же выводу можно прийти, заметив, что выражение для кривизны функции правдоподобия выражается в геометрической дисперсии

$\partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; \partial \; \alpha \; 2\; =\; -\; var\; \; [ln\; \; Икс]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{\backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; -\; \backslash \; имя\; оператора\; \{var\}\; [\backslash \; ln\; X]\}$

$\partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; \partial \; \beta \; 2\; =\; -\; var\; \; [ln\; \; (1\; -\; X)]\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{\backslash \; partial\; \backslash \; beta\; ^\; \{2\}\}\}\; =\; -\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)\; ]\}$

Эти отклонения (и, следовательно, кривизна) намного больше при малых значениях параметра формы α и β. Однако для значений параметров формы α, β>1 отклонения (и, следовательно, кривизны) выравниваются. Эквивалентно этот результат следует из границы Крамера – Рао, поскольку компоненты матрицы информации Фишера для бета-распределения являются этими логарифмическими дисперсиями. Граница Крамера – Рао утверждает, что дисперсия любой несмещенной оценки $\alpha \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\}$α ограничено обратной величиной информации Фишера :

$var\; (\alpha \; ^)\; \ge \; 1\; var\; \; [ln\; \; X]\; \ge \; 1\; \psi \; 1\; (\alpha \; ^)\; -\; \psi \; 1\; (\alpha \; ^\; +\; \beta \; ^)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{var\}\; (\{\backslash \; hat\; \{\backslash \; alpha\}\})\; \backslash \; geq\; \{\backslash \; frac\; \{1\}\; \{\backslash \; operatorname\; \{var\}\; [\backslash \; ln\; X]\}\}\; \backslash \; geq\; \{\backslash \; frac\; \{1\}\; \{\backslash \; psi\; \_\; \{1\}\; (\{\backslash \; hat\; \{\backslash \; alpha\}\})\; -\; \backslash \; psi\; \_\; \{1\}\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\}\}\}$

$var\; (\beta \; ^)\; \ge \; 1\; вар\; \; [пер\; (1\; -\; X)]\; \ge \; 1\; \psi \; 1\; (\beta \; ^)\; -\; \psi \; 1\; (\alpha \; ^\; +\; \beta \; ^)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{var\}\; (\{\backslash \; hat\; \{\backslash \; beta\; \}\})\; \backslash \; geq\; \{\backslash \; frac\; \{1\}\; \{\backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\}\}\; \backslash \; geq\; \{\backslash \; frac\; \{1\}\; \{\backslash \; psi\; \_\; \{1\}\; (\{\backslash \; hat\; \{\backslash \; beta\; \}\})\; -\; \backslash \; psi\; \_\; \{1\}\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\}\}\}$

, поэтому дисперсия оценок увеличивается с увеличением α и β, поскольку логарифмические отклонения уменьшаются.

Также можно выразить совместное логарифмическое правдоподобие для N iid наблюдений в терминах дигамма-функции выражений для логарифмов выборочных геометрических средних следующим образом:

$ln\; L\; (\alpha ,\; \beta \; X)\; N\; =\; (\alpha \; -\; 1)\; (\psi \; (\alpha \; ^)\; -\; \psi \; (\alpha \; ^\; +\; \beta \; ^))\; +\; (\beta \; -\; 1)\; (\psi \; (\beta \; ^)\; -\; \psi \; (\alpha \; ^\; +\; \beta \; ^))\; -\; пер\; \; В\; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; ln\; \backslash ,\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\}\}\; =\; (\backslash \; альфа\; -1)\; (\backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\})\; -\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}))\; +\; (\backslash \; beta\; -1)\; (\backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; beta\}\})\; -\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}))\; -\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}$

это выражение идентично отрицанию кросс-энтропии (см. Раздел «Количество информации (энтропия)»). Следовательно, нахождение максимума совместной логарифмической вероятности параметров формы на N iid наблюдений идентично нахождению минимума кросс-энтропии для бета-распределения как функции параметров формы.

$ln\; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; =\; -\; H\; =\; -\; h\; -\; DKL\; =\; -\; ln\; \; B\; (\alpha ,\; \beta )\; +\; (\alpha \; -\; 1)\; \psi \; (\alpha \; ^)\; +\; (\beta \; -\; 1)\; \psi \; (\; \beta \; ^)\; -\; (\alpha \; +\; \beta \; -\; 2)\; \psi \; (\alpha \; ^\; +\; \beta \; ^)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; ln\; \backslash ,\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\; \}\}\; =\; -\; H\; =\; -h-D\; \_\; \{\backslash \; mathrm\; \{KL\}\}\; =\; -\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; +\; (\backslash \; alpha\; -1)\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\; \})\; +\; (\backslash \; beta\; -1)\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; beta\}\})\; -\; (\backslash \; alpha\; +\; \backslash \; beta\; -2)\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\; \})\}$

с перекрестной энтропией, определенной следующим образом:

$H\; =\; \int \; 0\; 1\; -\; f\; (X;\; \alpha \; ^,\; \beta \; ^)\; ln\; \; (f\; (X;\; \alpha ,\; \beta ))\; d\; X\; \{\backslash \; displaystyle\; H\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; -f\; (X;\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\})\; \backslash \; ln\; (f\; (X;\; \backslash \; alpha,\; \backslash \; beta))\; \backslash ,\; \{\backslash \; rm\; \{d\}\}\; X\}$

Четыре неизвестных параметра

Процедура аналогична той, которая используется в случае двух неизвестных параметров. Если Y 1,..., Y N являются независимыми случайными величинами, каждая из которых имеет бета-распределение с четырьмя параметрами, функция совместного логарифмического правдоподобия для N iid наблюдений равно:

$ln\; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; =\; \sum \; i\; =\; 1\; N\; ln\; L\; i\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y\; i)\; =\; \sum \; i\; =\; 1\; N\; ln\; f\; (Y\; i\; ;\; \alpha ,\; \beta ,\; a,\; c)\; =\; \sum \; i\; =\; 1\; N\; ln\; (Y\; i\; -\; a)\; \alpha \; -\; 1\; (c\; -\; Y\; i)\; \beta \; -\; 1\; (c\; -\; a)\; \alpha \; +\; \beta \; -\; 1\; B\; (\alpha ,\; \beta )\; =\; (\alpha \; -\; 1)\; \sum \; i\; =\; 1\; N\; ln\; \; (Y\; i\; -\; a)\; +\; (\beta \; -\; 1)\; \sum \; i\; =\; 1\; N\; ln\; \; (c\; -\; Y\; i)\; -\; N\; ln\; \; B\; (\alpha ,\; \beta )\; -\; N\; (\alpha \; +\; \beta \; -\; 1)\; пер\; \; (с\; -\; а)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; пер\; \backslash ,\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; альфа,\; \backslash \; бета,\; а,\; с\; \backslash \; середина\; Y)\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \backslash ,\; \{\backslash \; mathcal\; \{L\}\}\; \_\; \{i\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y\_\; \{i\})\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \backslash ,\; f\; (Y\_\; \{i\};\; \backslash \; alpha,\; \backslash \; beta,\; a,\; c)\; \backslash \backslash \; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \backslash ,\; \{\backslash \; frac\; \{(Y\_\; \{i\}\; -a)\; ^\; \{\backslash \; alpha\; -1\}\; (c-Y\_\; \{i\})\; ^\; \{\backslash \; beta\; -1\}\}\; \{(ca)\; ^\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; \backslash \backslash \; =\; (\backslash \; alpha\; -1)\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (Y\_\; \{i\}\; -a)\; +\; (\backslash \; beta\; -1)\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (c-Y\_\; \{i\})\; -\; N\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; -N\; (\backslash \; alpha\; +\; \backslash \; beta\; -\; 1)\; \backslash \; ln\; (ca)\; \backslash \; конец\; \{align\}\}\}$

Нахождение максимума по параметру формы включает в себя взятие частной производной по параметру формы и установку выражения равным нулю, что дает оценку максимального правдоподобия параметров формы :

$\partial \; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \alpha \; =\; \sum \; i\; =\; 1\; N\; ln\; \; (Y\; i\; -\; a)\; -\; N\; (-\; \psi \; (\alpha \; +\; \beta )\; +\; \psi \; (\alpha )).)\; -\; N\; пер\; \; (с\; -\; а)\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; alpha\; \}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (Y\_\; \{i\}\; -a)\; -N\; (-\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\; +\; \backslash \; psi\; (\backslash \; alpha))\; -\; N\; \backslash \; ln\; (ca)\; =\; 0\}$

$\partial \; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \beta \; =\; \sum \; i\; =\; 1\; N\; ln\; \; (c\; -\; Y\; i)\; -\; N\; (-\; \psi \; (\alpha \; +\; \beta )\; +\; \psi \; (\beta ))\; -\; N\; пер\; \; (с\; -\; а)\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; гидроразрыва\; \{\backslash \; partial\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; альфа,\; \backslash \; бета,\; а,\; с\; \backslash \; середина\; Y)\}\; \{\backslash \; partial\; \backslash \; beta\}\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (c-Y\_\; \{i\})\; -\; N\; (-\; \backslash \; psi\; (\backslash \; alpha\; +\; \backslash \; beta)\; +\; \backslash \; psi\; (\backslash \; beta))\; -N\; \backslash \; ln\; (ca)\; =\; 0\}$

$\partial \; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; a\; =\; -\; (\alpha \; -\; 1)\; \sum \; i\; =\; 1\; N\; 1\; Y\; i\; -\; a\; +\; N\; (\alpha \; +\; \beta \; -\; 1)\; 1\; с\; -\; a\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; гидроразрыва\; \{\backslash \; partial\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; m\; id\; Y)\}\; \{\backslash \; partial\; a\}\}\; =\; -\; (\backslash \; alpha\; -1)\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{1\}\; \{Y\_\; \{i\}\; -a\}\}\; \backslash ,\; +\; N\; (\; \backslash \; alpha\; +\; \backslash \; beta\; -1)\; \{\backslash \; frac\; \{1\}\; \{ca\}\}\; =\; 0\}$

$\partial \; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; с\; \mid \; Y)\; \partial \; c\; знак\; равно\; (\beta \; -\; 1)\; \sum \; я\; Знак\; равно\; 1\; N\; 1\; с\; -\; Y\; я\; -\; N\; (\alpha \; +\; \beta \; -\; 1)\; 1\; с\; -\; a\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; c\}\}\; =\; (\backslash \; beta\; -1)\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{1\}\; \{c-Y\_\; \{i\}\}\}\; \backslash ,\; -\; N\; (\backslash \; alpha\; +\; \backslash \; beta\; -1)\; \{\backslash \; frac\; \{1\}\; \{ca\}\}\; =\; 0\}$

эти уравнения можно пересмотреть - представлены в следующей форме четырех систем связанных уравнений (первые два уравнения являются средними геометрическими, а вторые два уравнения - средними гармоническими) в терминах оценок правдоподобия для четырех параметров $\alpha \; ^,\; \beta \; ^,\; a\; ^,\; c\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\},\; \{\backslash \; hat\; \{a\}\},\; \{\backslash \; hat\; \{c\}\}\}$:

$1\; N\; \sum \; i\; =\; 1\; N\; пер\; \; Y\; я\; -\; a\; ^\; c\; ^\; -\; a\; ^\; =\; \psi \; (\alpha \; ^)\; -\; \psi \; (\alpha \; ^\; +\; \beta \; ^)\; =\; пер\; \; G\; ^\; X\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; \{\backslash \; fr\; ac\; \{Y\_\; \{i\}\; -\; \{\backslash \; hat\; \{a\}\}\}\; \{\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\}\}\}\; =\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\})\; -\; \backslash \; psi\; (\; \{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\; =\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{X\}\}$

$1\; N\; \sum \; i\; =\; 1\; N\; ln\; \; с\; ^\; -\; Y\; ic\; ^\; -\; a\; ^\; =\; \psi \; (\beta \; ^)\; -\; \psi \; (\alpha \; ^\; +\; \beta \; ^)\; =\; пер\; \; G\; ^\; 1\; -\; X\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\; N\}\; \backslash \; ln\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{c\}\}\; -\; Y\_\; \{i\}\}\; \{\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\}\}\}\; =\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; beta\}\; \})\; -\; \backslash \; psi\; (\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\})\; =\; \backslash \; ln\; \{\backslash \; hat\; \{G\}\}\; \_\; \{1-X\}\}$

$1\; 1\; N\; \sum \; я\; знак\; равно\; 1\; N\; c\; ^\; -\; a\; ^\; Y\; я\; -\; a\; ^\; =\; \alpha \; ^\; -\; 1\; \alpha \; ^\; +\; \beta \; ^\; -\; 1\; =\; H\; ^\; X\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\{\backslash \; frac\; \{1\}\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\}\}\; \{Y\_\; \{i\}\; -\; \{\backslash \; hat\; \{a\}\}\}\}\}\}\; =\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{\backslash \; alpha\}\}\; -\; 1\}\; \{\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; -\; 1\}\}\; =\; \{\backslash \; hat\; \{H\}\}\; \_\; \{X\}\}$

$1\; 1\; N\; \sum \; я\; знак\; равно\; 1\; N\; c\; ^\; -\; a\; ^\; c\; ^\; -\; Y\; я\; =\; \beta \; ^\; -\; 1\; \alpha \; ^\; +\; \beta \; ^\; -\; 1\; =\; H\; ^\; 1\; -\; X\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\{\; \backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \{\backslash \; frac\; \{\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\}\}\; \{\{\backslash \; hat\; \{c\}\}\; -\; Y\_\; \{i\}\}\}\}\}\; =\; \{\backslash \; f\; rac\; \{\{\backslash \; hat\; \{\backslash \; beta\}\}\; -\; 1\}\; \{\{\backslash \; hat\; \{\backslash \; alpha\}\}\; +\; \{\backslash \; hat\; \{\backslash \; beta\}\}\; -\; 1\}\}\; =\; \{\backslash \; hat\; \{H\}\}\; \_\; \{1-X\}\}$

с образцом геометрических средств:

$G\; ^\; X\; =\; \prod \; i\; =\; 1\; N\; (Y\; i\; -\; a\; ^\; c\; ^\; -\; a\; ^)\; 1\; N\; \{\backslash \; Displaystyle\; \{\backslash \; шляпа\; \{G\}\}\; \_\; \{X\}\; =\; \backslash \; prod\; \_\; \{я\; =\; 1\}\; ^\; \{N\}\; \backslash \; left\; (\{\backslash \; frac\; \{Y\_\; \{i\}\; -\; \{\backslash \; hat\; \{a\}\}\}\; \{\{\backslash \; hat\; \{c\}\}\; -\; \{\backslash \; hat\; \{a\}\}\}\}\; \backslash \; справа)\; ^\; \{\backslash \; frac\; \{1\}\; \{N\}\}\}$

$G\; ^\; (1\; -\; X)\; =\; \prod \; я\; =\; 1\; N\; (c\; ^\; -\; Y\; ic\; ^\; -\; a\; ^)\; 1\; N\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\; G\}\}\; \_\; \{(1-X)\}\; =\; \backslash \; prod\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; left\; (\{\backslash \; frac\; \{\{\backslash \; hat\; \{c\}\}\; -\; Y\_\; \{i\}\}\; \{\{\backslash \; hat\; \{c\; \}\}\; -\; \{\backslash \; hat\; \{a\}\}\})\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{N\}\}\}$

Параметры $a\; ^,\; c\; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{a\}\},\; \{\backslash \; hat\; \{c\}\}\}$вложены в выражении среднего геометрического нелинейным (в степени 1 / N). Это исключает, как правило, решение в замкнутой форме даже для приближения начального значения для целей итераций. Одна альтернатива - использовать в качестве начальных значений для итерации значения, полученным методом решения моментов для четырехпараметрического случая. Кроме выражения для гармонических средних качественных показателей хорошего качества только для $\alpha \; ^,\; \beta \; ^>1\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; alpha\}\},\; \{\backslash \; hat\; \{\backslash \; beta\}\}>1\}$, что исключает максимальное вероятностное решение для параметров Информационная матрица Фишера для случая с четырьмя событиями положительно определенная только для α, β>2 (для дальнейшего обсуждения см. раздел, посвященный информации Фишера. матрица, четырехпараметрический случай) Для колоколообразных (симметричных или несимметричных) бета-распределений, точками перегиба, предусмотренных по обе стороны от режима.>α = 2: E ⁡ [- 1 N ∂ 2 ln ⁡ L (α, β, a, c ∣ Y) ∂ a 2] = I a, a {\ displaysty le \ alpha = 2: \ quad \ operatorname {E} \ left [- {\ frac {1 } {N}} {\ frac {\ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ mid Y)} {\ partial a ^ {2}}} \ справа] = {\ mathcal {I}} _ {a, a}}

$\beta \; =\; 2:\; E\; \; [-\; 1\; N\; \partial \; 2\; пер\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; c\; 2]\; =\; I\; c,\; c\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; 2:\; \backslash \; quad\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{\; L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; c\; ^\; \{2\}\}\}\; \backslash \; right]\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{c,\; c\}\}$

$\alpha \; Знак\; равно\; 2:\; E\; \; [-\; 1\; N\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \alpha \; \partial \; a]\; =\; я\; \alpha ,\; a\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 2:\; \backslash \; quad\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; alpha\; \backslash \; partial\; a\}\}\; \backslash \; right]\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; a\}\}$

$\beta \; =\; 1:\; E\; \; [-\; 1\; N\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \beta \; \partial \; c]\; знак\; равно\; I\; \beta ,\; c\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; 1:\; \backslash \; quad\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [-\; \{\backslash \; fr\; ac\; \{1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; beta\; \backslash \; partial\; c\; \}\}\; \backslash \; righ\; t]\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; c\}\}$

(для fu Дальнейшее обсуждение см. в разделе, посвященном информационной матрице Фишера). Таким образом, невозможно строго выполнить оценку максимального правдоподобия для некоторых хорошо известных распределений, принадлежащих к семейству четырехпараметрических бета-распределений, таких как равномерное распределение (Beta (1, 1, a, c)) и распределение арксинусов (Beta (1/2, 1/2, a, c)). Н.Л.Джонсон и С.Коц игнорируют уравнения для гармонических средних и вместо этого предлагают: «Если a и c неизвестны, требуются оценки максимального правдоподобия a, c, α и β., вышеупомянутая процедура (для случая двух неизвестных параметров с преобразованием X как X = (Y - a) / (c - a)) может быть повторена с использованием последовательности пробных значений a и c до тех пор, пока пара (a, c) для которого максимальная вероятность (при заданных a и c) максимально велика »(где для ясности их обозначения для параметров были переведены в настоящие обозначения).

Информационная матрица Фишера

Пусть случайная величина X имеет плотность вероятности f (x; α). Частная производная по параметру (неизвестному и подлежащему оценке) α логарифмической функции правдоподобия называется оценкой. Второй момент оценки называется информацией Фишера :

$I\; (\alpha )\; =\; E\; \; [(\partial \; \partial \; \alpha \; ln\; \; L\; (\alpha \; \mid \; X))\; 2],\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\; \}\; (\backslash \; alpha)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; alpha\}\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha\; \backslash \; mid\; X)\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right],\}$

ожидание для оценки равно нулю, поэтому информация Фишера также является вторым моментом, сосредоточенным на среднем значении оценки: дисперсия оценки.

Если log функция правдоподобия дважды дифференцируема по параметру α и при определенных условиях регулярности, то информация Фишера также может быть записана следующим образом (что часто является более удобным форму для расчетов):

$I\; (\alpha )\; =\; -\; E\; \; [\partial \; 2\; \partial \; \alpha \; 2\; ln\; \; (L\; (\alpha \; \mid \; X))].\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; (\backslash \; alpha)\; =\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\}\; \{\backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; \backslash \; ln\; (\{\; \backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha\; \backslash \; mid\; X))\; \backslash \; right].\}$

Таким образом, информация Фишера является отрицательным значением математического ожидания второй производной относительно параметра α log функция правдоподобия. Следовательно, информация Фишера является мерой кривизны логарифмической функции правдоподобия α. Низкая кривизна (и, следовательно, высокий радиус кривизны ), более плоская кривая логарифмической функции правдоподобия имеет низкую информацию Фишера; в то время как кривая логарифмической функции правдоподобия с большой кривизной (и, следовательно, с низким радиусом кривизны ) имеет высокую информацию Фишера. Когда информационная матрица Фишера вычисляется на основе оценок параметров («наблюдаемая информационная матрица Фишера»), это эквивалентно замене истинной логарифмической поверхности правдоподобия приближением ряда Тейлора, взятого до квадратичных членов. Слово информация в контексте информации Fisher относится к информации о параметрах. Такая информация, как: оценка, достаточность и свойства дисперсии оценщиков. Граница Крамера – Рао утверждает, что инверсия информации Фишера является нижней границей дисперсии любой оценки параметра α:

$var\; \; [\alpha \; ^]\; \ge \; 1\; I\; (\alpha ).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{var\}\; [\{\backslash \; hat\; \{\backslash \; alpha\}\}]\; \backslash \; geq\; \{\backslash \; frac\; \{1\}\; \{\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; alpha)\}\}.\}$

Точность, с которой оценка параметра α ограничена информацией Фишера логарифмической функции правдоподобия. Информация Фишера является мерой минимальной ошибки, связанной с оценкой параметра распределения, и ее можно рассматривать как меру разрешающей способности эксперимента, необходимой для различения двух альтернативных гипотез о параметре.

Когда есть N параметров

$[\theta \; 1\; \theta \; 2\dots \; \theta \; N],\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; theta\; \_\; \{1\}\; \backslash \backslash \backslash \; theta\; \_\; \{2\}\; \backslash \backslash \backslash \; dots\; \backslash \backslash \backslash \; theta\; \_\; \{N\}\; \backslash \; end\; \{bmatrix\}\},\}$

, тогда информация Фишера принимает форму положительной полуопределенной симметричной матрицы размером N × N , информационной матрицы Фишера, с типичной элемент:

$(I\; (\theta ))\; i,\; j\; =\; E\; \; [(\partial \; \partial \; \theta \; i\; ln\; \; L)\; (\partial \; \partial \; \theta \; j\; ln\; L)].\; \{\backslash \; displaystyle\; \{(\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; theta))\}\; \_\; \{i,\; j\}\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; theta\; \_\; \{\; i\}\}\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; right)\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; partial\}\; \{\backslash \; partial\; \backslash \; theta\; \_\; \{j\}\}\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; \backslash \; right)\; \backslash \; right].\}$

При определенных условиях регулярности информационная матрица Фишера также может быть записана в следующей форме, которая часто более удобна для вычислений:

$(I\; (\theta ))\; i,\; j\; =\; -\; E\; \; [\; \partial \; 2\; \partial \; \theta \; i\; \partial \; \theta \; j\; ln\; \; (L)].\; \{\backslash \; displaystyle\; \{(\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; theta))\}\; \_\; \{i,\; j\}\; =\; -\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\}\; \{\backslash \; partial\; \backslash \; theta\; \_\; \{i\}\; \backslash ,\; \backslash \; partial\; \backslash \; theta\; \_\; \{j\}\}\}\; \backslash \; ln\; (\{\backslash \; mathcal\; \{L\}\})\; \backslash \; right]\; \backslash ,.\}$

С X 1,..., X Niid случайных величин, может быть построен N-мерный «ящик» со сторонами X 1,..., X N. Коста и Ковер показывают, что дифференциальная энтропия (Шеннона) h (X) связана с объемом типичного набора (имеющего энтропию образца, близкую к истинной энтропии), в то время как информация Фишера связана с поверхностью этого типичного набора.

Два параметра

Для X 1,..., X N независимых случайных величин, каждая из которых имеет бета-структуру, параметризованное значение формы α и β, функция совместной логарифмического правдоподобия для N iid наблюдений составляет:

$ln\; \; (L\; (\alpha ,\; \beta \; \mid \; X))\; =\; (\alpha \; -\; 1)\; \sum \; i\; =\; 1\; N\; ln\; \; X\; я\; +\; (\beta \; -\; 1)\; \sum \; я\; знак\; равно\; 1\; N\; пер\; \; (1\; -\; Икс\; я)\; -\; N\; пер\; \; В\; (\alpha ,\; \beta )\; \{\backslash \; Displaystyle\; \backslash \; пер\; (\{\backslash \; mathcal\; \{L\}\}\; (\backslash \; альфа,\; \backslash \; бета\; \backslash \; mid\; X))\; =\; (\backslash \; alpha\; -1)\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; X\_\; \{i\}\; +\; (\backslash \; beta\; -1)\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (1-X\_\; \{i\})\; -\; N\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}$

поэтому Совместная логарифмическая функция правдоподобия на N iid наблюдений:

$1\; N\; ln\; \; (L\; (\alpha ,\; \beta \; \mid \; X))\; =\; (\alpha \; -\; 1)\; 1\; N\; \sum \; i\; =\; 1\; N\; ln\; \; X\; i\; +\; (\beta \; -\; 1)\; 1\; N\; \sum \; я\; знак\; равно\; 1\; N\; пер\; \; (1\; -\; Икс\; я)\; -\; пер\; \; В\; (\alpha ,\; \beta )\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; ln\; (\{\backslash \; mathcal\; \{L\}\}\; (\backslash \; альфа,\; \backslash \; бета\; \backslash \; середина\; X))\; =\; (\backslash \; альфа\; -1)\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; X\_\; \{i\}\; +\; (\backslash \; beta\; -1)\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (1-X\_\; \{i\})\; -\; \backslash ,\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}$

Для случая с двумя диагональными данными Фишера состоит из 4 компонентов: 2 и 2 внешних. Информационная матрица Фишера симметрична, один из этих недиагональных компонентов. Таким образом, информационная матрица Фишера имеет 3 независимых компонента (2 диагональных и 1 недиагональный).

Арьял и Надараджа рассчитали информационную матрицу Фишера для четырехпараметрического случая, из которого двухпараметрический случай может быть получен следующим образом:

$-\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; \partial \; \alpha \; 2\; =\; var\; \; [ln\; \; (X)]\; =\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; =\; I\; \alpha ,\; \alpha \; =\; E\; \; [-\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; \partial \; \alpha \; 2]\; знак\; равно\; пер\; \; вар\; GX\; \{\backslash \; Displaystyle\; -\; \{\backslash \; гидроразрыва\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\; \backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (X)]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; alpha\}\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\; \backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; \backslash \; right]\; =\; \backslash \; ln\; \backslash \; operatorname\; \{var\}\; \_\; \{GX\}\}$

$-\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; \partial \; \beta \; 2\; =\; var\; \; [ln\; \; (1\; -\; X)]\; =\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; =\; I\; \beta ,\; \beta \; =\; E\; \; [-\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; \partial \; \beta \; 2]\; =\; пер\; \; вар\; г\; (1\; -\; Икс)\; \{\backslash \; Displaystyle\; -\; \{\backslash \; гидроразрыва\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; альфа,\; \backslash \; бета\; \backslash \; середина\; X)\}\; \{N\; \backslash ,\; \backslash \; partial\; \backslash \; бета\; ^\; \{2\}\}\}\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; psi\; \_\; \{1\; \}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; \backslash \; beta\}\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\; \backslash \; partial\; \backslash \; beta\; ^\; \{2\}\}\}\; \backslash \; right]\; =\; \backslash \; ln\; \backslash \; operatorname\; \{var\}\; \_\; \{\; G\; (1-X)\}\}$

$-\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; \partial \; \alpha \; \partial \; \beta \; =\; cov\; \; [ln\; \; X,\; ln\; \; (1\; -\; X)]\; =\; -\; \psi \; 1\; (\; \alpha \; +\; \beta )\; знак\; равно\; I\; \alpha ,\; \beta \; знак\; равно\; E\; \; [-\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta \; \mid \; X)\; N\; \partial \; \alpha \; \partial \; \beta ]\; =\; ln\; \; cov\; GX,\; (1\; -\; X)\; \{\backslash \; displaystyle\; -\; \{\; \backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\; \backslash ,\; \backslash \; partial\; \backslash \; alpha\; \backslash ,\; \backslash \; partial\; \backslash \; beta\}\}\; =\; \backslash \; operatorname\; \{cov\; \}\; [\backslash \; ln\; X,\; \backslash \; ln\; (1-X)]\; =\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; beta\}\; =\; \backslash \; operatorname\; \{E\; \}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta\; \backslash \; mid\; X)\}\; \{N\; \backslash ,\; \backslash \; partial\; \backslash \; alpha\; \backslash ,\; \backslash \; partial\; \backslash \; beta\}\; \}\; \backslash \; right]\; =\; \backslash \; ln\; \backslash \; operatorname\; \{co\; v\}\; \_\; \{G\; \{X,\; (1-X)\}\}\}$

Электронная информационная матрица Фишера симметрична

$I\; \alpha ,\; \beta \; =\; I\; \beta ,\; \alpha \; =\; ln\; \; cov\; GX,\; (1\; -\; Икс)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; beta\}\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; \backslash \; alpha\}\; =\; \backslash \; ln\; \backslash \; operatorname\; \{cov\}\; \_\; \{ГРАММ\; \{X,\; (1-X)\; \}\}\}$

Информационные компоненты Фишера равны логарифмической геометрической дисперсии и логарифмической геометрической ковариации. Следовательно, они могут быть выражены как тригамма-функции, обозначенные ψ 1 (α), вторая из полигамма-функций, определенные как производная функции дигамма :

$\psi \; 1\; (\alpha )\; =\; d\; 2\; ln\; \; \Gamma \; (\alpha )\; \partial \; \alpha \; 2\; =\; \partial \; \psi \; (\alpha )\; \partial \; \alpha .\; \{\backslash \; Displaystyle\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; =\; \{\backslash \; frac\; \{d\; ^\; \{2\}\; \backslash \; ln\; \backslash \; Gamma\; (\backslash \; alpha)\}\; \{\backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; \backslash ,\; \{\backslash \; frac\; \{\; \backslash \; partial\; \backslash \; psi\; (\backslash \; alpha)\}\; \{\backslash \; partial\; \backslash \; alpha\}\}.\}$

Эти производные также выводятся в разделе «Оценка параметров», «Максимальное правдоподобие», «Два неизвестных расписания» и на графиках log функции правдоподобия также показаны в этом разделе. Раздел под названием «Геометрическая дисперсия и ковариация» содержит графики и дальнейшее описание компонентов информационной системы Фишера: логарифмической геометрической формы дисперсии и логарифмической формы ковариации как функции параметров α и β. Раздел «Другие моменты», «Моменты преобразованных случайных величин», «Моменты логарифмически преобразованных случайных величин» содержит формулы для моментов логарифмически преобразованных случайных величин. Изображения для информационных компонентов Фишера $I\; \alpha ,\; \alpha ,\; I\; \beta ,\; \beta \; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; alpha\},\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; \backslash \; beta\; \}\}$и $I\; \alpha ,\; \beta \; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; beta\}\}$показаны в разделе «Геометрические дисперсия».

Определитель информационной системы Фишера представляет интерес (например, для вычислений априорной вероятности Джеффриса). Из выражений для отдельных компонентов информационной матрицы Фишера следует, что определитель (симметричной) информационной системы Фишера для бета-распределения равен:

$det (I (α, β)) = I α, α I β, β - I α, β I α, β = (ψ 1 (α) - ψ 1 (α + β)) (ψ 1 (β) - ψ 1 (α + β)) - (- ψ 1 (α + β)) (- ψ 1 (α + β)) = ψ 1 (α) ψ 1 (β) - (ψ 1 (α) + ψ 1 (β)) ψ 1 (α + β) lim α → 0 det (I (α, β)) = lim β → 0 det (I (α, β)) = ∞ lim α → ∞ det (I (α, β)) = lim β → ∞ det (I (α, β)) = 0 {\ Displaystyle { \ begin {выровнен} \ det ({\ mathcal {I}} (\ alpha, \ beta)) = {\ mathcal {I}} _ {\ alpha, \ alpha} {\ mathcal {I}} _ {\ beta, \ beta} - {\ mathcal {I}} _ {\ alpha, \ beta} {\ mathcal {I}} _ {\ alpha, \ beta} \\ [4pt] = (\ psi _ {1} (\ alpha) - \ psi _ {1} (\ alpha + \ beta)) (\ psi _ {1} (\ beta) - \ psi _ {1} (\ alpha + \ beta)) - (- \ psi _ {1} (\ alpha + \ beta)) (- \ psi _ {1} (\ alpha + \ beta)) \\ [4pt] = \ psi _ {1} (\ альфа) \ psi _ {1 } (\ beta) - (\ psi _ {1} (\ alpha) + \ psi _ {1} (\ be ta)) \ psi _ {1} (\ alp ha + \ beta) \\ [4pt] \ lim _ {\ alpha \ to 0} \ det ({\ mathcal {I}} (\ alpha, \ beta)) = \ lim _ {\ beta \ to 0} \ det ({\ mathcal {I}} (\ alpha, \ beta)) = \ infty \\ [4pt] \ lim _ {\ alpha \ to \ infty} \ det ({\ mathcal {I}} (\ alpha, \ beta)) = \ lim _ {\ beta \ to \ infty} \ det ({\ mathcal {I}} (\ alpha, \ beta)) = 0 \ end {align}}}$

От критерий Сильвестра (проверка, все ли диагональные элементы положительны), из следует, что информационная матрица Фишера для условия с двумя точками положительно-определенная (при стандартном условии, что параметры формы равны положительные α>0 и β>0).

Четыре параметра

Информация Фишера I (a, a) для α = β по сравнению с диапазоном (c - a) и показателем степени α = β Информация Фишера I (α, a) для α = β, в зависимости от диапазона (c - a) показателя степени α = β

Если Y 1,..., Y N являются независимыми случайными величинами, каждая из которых имеет бета-распределение с четырьмя параметрами: показатели α и β, а также минимум (диапазон распределения) и c (максимум распределения) (раздел «Альтернативные параметры», «Четыре параметра») с плотностью вероятности функция :

$f\; (y;\; \alpha ,\; \beta ,\; a,\; c)\; =\; f\; (x;\; \alpha ,\; \beta )\; c\; -\; a\; =\; (y\; -\; ac\; -\; a)\; \alpha \; -\; 1\; (c\; -\; yc\; -\; a)\; \beta \; -\; 1\; (c\; -\; а)\; B\; (\alpha ,\; \beta )\; =\; (y\; -\; a)\; \alpha \; -\; 1\; (c\; -\; y)\; \beta \; -\; 1\; (c\; -\; a)\; \alpha \; +\; \beta \; -\; 1\; B\; (\alpha ,\; \beta ).\; \{\backslash \; displaystyle\; f\; (y;\; \backslash \; alpha,\; \backslash \; beta,\; a,\; c)\; =\; \{\backslash \; frac\; \{f\; (x;\; \backslash \; alpha,\; \backslash \; beta)\}\; \{ca\}\}\; =\; \{\backslash \; frac\; \{\backslash \; left\; (\{\backslash \; frac\; \{ya\; \}\; \{ca\}\}\; \backslash \; right)\; ^\; \{\backslash \; alpha\; -1\}\; \backslash \; left\; (\{\backslash \; frac\; \{cy\}\; \{ca\}\}\; \backslash \; right)\; ^\; \{\backslash \; beta\; -1\}\}\; \{(ca)\; B\; (\backslash \; alpha,\; \backslash \; beta)\}\}\; =\; \{\backslash \; frac\; \{(ya)\; ^\; \{\backslash \; alpha\; -1\}\; (cy)\; ^\; \{\backslash \; beta\; -1\}\}\; \{(ca)\; ^\; \{\backslash \; alpha\; +\; \backslash \; beta\; -1\}\; B\; (\backslash \; alpha,\; \backslash \; beta)\}\}.\}$

совместная логарифмическая функция правдоподобия для N iid наблюдений:

$1\; N\; ln\; \; (L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y))\; =\; \alpha \; -\; 1\; N\; \sum \; i\; =\; 1\; N\; ln\; \; (Y\; i\; -\; a)\; +\; \beta \; -\; 1\; N\; \sum \; i\; =\; 1\; N\; ln\; \; (c\; -\; Y\; i)\; -\; ln\; \; B\; (\alpha ,\; \beta )\; -\; (\alpha \; +\; \beta \; -\; 1)\; ln\; \; (\; с\; -\; а)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; ln\; (\{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y))\; =\; \{\backslash \; frac\; \{\backslash \; альфа\; -\; 1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (Y\_\; \{i\}\; -a)\; +\; \{\backslash \; frac\; \{\backslash \; beta\; -1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{N\}\; \backslash \; ln\; (c-Y\_\; \{i\})\; -\; \backslash \; ln\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\; -\; (\backslash \; alpha\; +\; \backslash \; beta\; -1)\; \backslash \; ln\; (ca)\}$

Для случая с четырьмя включенной информацией Фишера состоит из 4 * 4 = 16 компонентов. Он имеет 12 недиагональных компонентов = (всего 4 × 4 - 4 диагональных). Информационная матрица Фишера симметрична, половина этих компонентов (12/2 = 6) независимы. Следовательно, информационная матрица Фишера имеет 6 независимых недиагональных + 4 диагональных = 10 независимых компонентов. Ариал и Надараджа рассчитали информационную матрицу Фишера для четырехпараметрического случая следующим образом:

$-\; 1\; N\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \alpha \; 2\; =\; var\; \; [ln\; \; (X)]\; =\; \psi \; 1\; (\alpha )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; =\; I\; \alpha ,\; \alpha \; =\; E\; \; [-\; 1\; N\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \alpha \; 2]\; =\; ln\; \; (var\; GX)\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\; \backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (X)]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\; \backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; alpha\}\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{\; L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; alpha\; ^\; \{2\}\}\}\; \backslash \; right]\; =\; \backslash \; ln\; (\backslash \; operatorname\; \{var\_\; \{GX\}\})\}$

$-\; 1\; N\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \beta \; 2\; =\; var\; \; [ln\; \; (1\; -\; X)]\; =\; \psi \; 1\; (\beta )\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; =\; Я\; \beta ,\; \beta \; знак\; равно\; Е\; \; [-\; 1\; N\; \partial \; 2\; пер\; \; L\; (\alpha ,\; \beta ,\; a,\; с\; \mid \; Y)\; \partial \; \beta \; 2]\; =\; пер\; \; (вар\; G\; (1\; -\; X))\; \{\backslash \; Displaystyle\; -\; \{\backslash \; гидроразрыва\; \{\; 1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; beta\; ^\; \{2\}\}\}\; =\; \backslash \; operatorname\; \{var\}\; [\backslash \; ln\; (1-X)]\; =\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; \backslash \; beta\}\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\; -\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; beta\; ^\; \{2\}\}\}\; \backslash \; right]\; =\; \backslash \; ln\; (\backslash \; operatorname\; \{var\_\; \{G\; (1-X)\}\})\}$

$-\; 1\; N\; \partial \; 2\; ln\; \; L\; (\alpha ,\; \beta ,\; a,\; c\; \mid \; Y)\; \partial \; \alpha \; \partial \; \beta \; =\; cov\; \; [ln\; \; X,\; (1\; -\; X)]\; =\; -\; \psi \; 1\; (\alpha \; +\; \beta )\; =\; I\; \alpha ,\; \beta \; =\; E\; \; [-\; 1\; N\; \partial \; 2\; пер\; L\; (\alpha ,\; \beta ,\; a,\; с\; \mid \; Y)\; \partial \; \alpha \; \partial \; \beta ]\; знак\; равно\; пер\; \; (cov\; GX,\; (1\; -\; X))\; \{\backslash \; displaystyle\; -\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; alpha\; \backslash ,\; \backslash \; partial\; \backslash \; beta\}\}\; =\; \backslash \; operatorname\; \{cov\}\; [\backslash \; ln\; X,\; (1-X)]\; =\; -\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\; =\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; beta\}\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [-\; \{\backslash \; frac\; \{1\}\; \{N\}\; \}\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (\backslash \; alpha,\; \backslash \; beta,\; a,\; c\; \backslash \; mid\; Y)\}\; \{\backslash \; partial\; \backslash \; a\; lpha\; \backslash ,\; \backslash \; partial\; \backslash \; beta\}\}\; \backslash \; right]\; =\; \backslash \; ln\; (\backslash \; operatorname\; \{cov\}\; \_\; \{G\; \{X,\; (1-X)\}\})\}$

В приведенных выше выражениях использование X вместо Y в выражениях var [ln (X)] = ln (var GX) это не ошибка. Выражения в терминах логарифмической геометрической дисперсии и логарифмической геометрической ковариации возникают как функции двухпараметрической параметра параметров X ~ Beta (α, β), поскольку при взятии частных производственных по показателям (α, β) в четырехпараметрическом случае, можно получить те же выражения, что и для случая Эти члены четырехпараметрической информационной матрицы не зависят от минимума и максимума диапазона распределения. Единственный ненулевой член при двойном дифференцировании логарифмической функции правдоподобия относительно показателей α и β - это вторая производная логарифма бета-функции: ln (B (α, β)). Этот член не зависит от минимума и максимума c диапазона распределения. Двойное дифференцирование этого члена приводит к тригамма-функциям. Разделы «Максимальное правдоподобие», «Два неизвестных события» и «Четыре неизвестных события» также показывают этот факт.

Информация Fisher для N i.i.d. Образца в N раз больше индивидуальной информации Fisher (уравнение 11.279, стр. 394 из Cover and Thomas). (Арьял и Надараджа использует одно наблюдение, N = 1, для следующих компонентов информации Фишера, что приводит к результату же, что и рассмотрение производных логарифма правдоподобия на N наблюдений. Кроме того, ниже ошибочное выражение для $I\; a,\; a\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{a,\; a\}\}$в Aryal и Nadarajah было исправлено.)

$α>2: E ⁡ [- 1 N ∂ 2 ln ⁡ L ( α, β, a, c ∣ Y) ∂ a 2] = I a, a = β (α + β - 1) (α - 2) (c - a) 2 β>2: E ⁡ [- 1 N ∂ 2 ln ⁡ L (α, β, a, c ∣ Y) ∂ c 2] = I c, c = α (α + β - 1) (β - 2) (c - a) 2 E ⁡ [- 1 N ∂ 2 ln ⁡ L (α, β, a, c ∣ Y) ∂ a ∂ c] = I a, c = (α + β - 1) (c - a) 2 α>1: E ⁡ [- 1 N ∂ 2 ln ⁡ L (α, β, a, c ∣ Y) ∂ α ∂ a] = I α, a = β (α - 1) (c - a) E ⁡ [- 1 N ∂ 2 ln ⁡ L ( α, β, a, c ∣ Y) ∂ α ∂ c] = I α, c = 1 (c - a) E ⁡ [- 1 N ∂ 2 ln ⁡ L (α, β, a, c ∣ Y) ∂ β ∂ a] = I β, a = - 1 (c - a) β>1: E ⁡ [- 1 N ∂ 2 ln ⁡ L (α, β, a, c ∣ Y) ∂ β ∂ c] знак равно Я β, с знак равно - α (β - 1) (с - а) {\ displaystyle {\ begin {align} \ alpha>2: \ q uad \ operatorname {E} \ left [- {\ frac {1} {N}} {\ frac {\ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ середина Y)} {\ partial a ^ {2}}} \ right] = {\ mathcal {I}} _ {a, a} = {\ frac {\ beta (\ alpha + \ beta -1)} { (\ alpha -2) (ca) ^ {2}}} \\\ beta>2: \ quad \ operatorname {E} \ left [- {\ frac {1} {N}} {\ frac {\ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ mid Y)} {\ partial c ^ {2}}} \ right] = {\ mathcal {I}} _ {c, c} = {\ frac {\ alpha (\ alpha + \ beta -1)} {(\ beta -2) (ca) ^ {2}}} \\\ имя оператора {E} \ left [- { \ frac {1} {N}} {\ frac {\ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ mid Y)} {\ partial a \, \ partial c}} \ right] = {\ mathcal {I}} _ {a, c} = {\ frac {(\ alpha + \ beta -1)} {(ca) ^ {2}}} \\\ alpha>1: \ quad \ operatorname {E} \ left [- {\ frac {1} {N}} {\ frac {\ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ mid Y)} {\ partial \ alpha \, \ partial a}} \ right] = {\ mathcal {I}} _ {\ alpha, a} = { \ frac {\ beta} {(\ alpha -1) (ca)}} \\ \ operatorname {E} \ left [- {\ frac {1} {N}} {\ frac {\ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ mid Y)} {\ partial \ alpha \, \ partial c}} \ right] = {\ mathcal {I}} _ {\ alpha, c} = {\frac {1} {(ca)}} \\\ OperatorName {E} \ left [- {\ frac {1} {N}} {\ frac { \ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ mid Y)} {\ partial \ beta \, \ partial a}} \ right] = {\ mathcal {I}} _ {\ beta, a} = - {\ frac {1} {(ca)}} \\\ beta>1: \ quad \ operatorname {E} \ left [- {\ frac {1} { N}} {\ frac {\ partial ^ {2} \ ln {\ mathcal {L}} (\ alpha, \ beta, a, c \ mid Y)} {\ partial \ beta \, \ partial c}} \ right] = {\ mathcal {I}} _ {\ beta, c} = - {\ frac {\ alpha} {(\ beta -1) (ca)}} \ end {выравнивается}}}$

Два нижних диагональных элемента информационной матрицы Фишера относительно параметра "a" (минимум диапазона распределения): $I\; a,\; a\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{a,\; a\}\}$, и в отношении параметра " c "(максимум диапазона распределения): $I\; c,\; c\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{c,\; c\}\}$определены только для показателей степени α>2 и β>2 соответственно. Компонент информационной матрицы Фишера $I\; a,\; a\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{a,\; a\}\}$для минимального "a" приближается к бесконечности для степени α, приближающейся к 2 сверху, а компонент информационной матрицы Фишера $I\; c,\; c\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{c,\; c\}\}$для максимального значения «c» приближается к бесконечности для показателя β, приближающегося к 2 сверху.

Информационная матрица Фишера для случая с четырьмя параметрами не зависит от отдельных значений минимального «а» и максимального «с», а только от общего диапазона (с-а). Более того, компоненты информационной матрицы Фишера, которые зависят от дальности (c-a), зависят только через ее обратную величину (или квадрат обратной), так что информация Фишера уменьшается с увеличением дальности (c-a).

На прилагаемых изображениях показаны информационные компоненты Фишера $I\; a,\; a\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{a,\; a\}\}$и $I\; \alpha ,\; a\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; a\}\}$. Изображения для информационных компонентов Фишера $I\; \alpha ,\; \alpha \; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; \backslash \; alpha\}\}$и $I\; \beta ,\; \beta \; \{\backslash \; displaystyle\; \{\; \backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; \backslash \; beta\}\}$показаны в разделе «Геометрическая дисперсия». Все эти информационные компоненты Фишера выглядят как бассейн, «стенки» которого расположены при низких значениях параметров.

Следующие компоненты информации Фишера бета-распределения с четырьмя параметрами могут быть выражены в терминах двухпараметров: X ~ бета (α, β) ожидания преобразованного отношения ((1-X) / X) и его зеркального изображения (X / (1-X)), масштабированного по диапазону (c − a), что может быть полезно для интерпретации:

$I\; \alpha ,\; a\; =\; E\; \; [1\; -\; XX]\; c\; -\; a\; =\; \beta \; (\alpha \; -\; 1)\; (c\; -\; a),\; если\; \alpha >1\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; a\}\; =\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{1-X\}\; \{X\}\}\; \backslash \; right]\}\; \{ca\}\}\; =\; \{\backslash \; frac\; \{\backslash \; beta\}\; \{(\backslash \; alpha\; -1)\; (ca)\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; alpha>1\}$

$I\; \beta ,\; c\; =\; -\; E\; \; [X\; 1\; -\; X]\; c\; -\; a\; =\; -\; \alpha \; (\beta \; -\; 1)\; (c\; -\; a),\; если\; \beta >1\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; c\; \}\; =\; -\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{E\}\; \backslash \; left\; [\{\backslash \; frac\; \{X\}\; \{1-X\}\}\; \backslash \; right]\}\; \{ca\}\}\; =\; -\; \{\backslash \; frac\; \{\backslash \; alpha\}\; \{(\backslash \; beta\; -1)\; (ca)\}\}\; \{\backslash \; text\; \{if\}\}\; \backslash \; beta>1\}$

Это также ожидаемые значения «инвертированного бета-распределения» или основного бета-распределения (также известного как бета-распределение второго типа или Тип VI Пирсона ) и его зеркальное отображение, масштабированное по диапазону (c - a).

Кроме того, следующие компоненты информации Фишера могут быть выражены в терминах гармонической (1 / X) дисперсии или дисперсии на основе преобразованных в отношение переменных ((1-X) / X) следующим образом:

$α>2: I a, a = var ⁡ [1 X] (α - 1 c - a) 2 = var ⁡ [1 - XX] (α - 1 c - a) 2 = β (α + β - 1) (α - 2) (c - a) 2 β>2: I c, c = var ⁡ [1 1 - X] (β - 1 c - a) 2 = var ⁡ [X 1 - X] (β - 1 c - a) 2 = α (α + β - 1) (β - 2) (c - a) 2 I a, c = cov ⁡ [1 X, 1 1 - X] (α - 1) (β - 1) (c - a) 2 = cov ⁡ [1 - XX, X 1 - X] (α - 1) (β - 1) (c - a) 2 = (α + β - 1) (c - a) 2 {\ displaystyle {\ begin {align} \ alpha>2: \ quad {\ mathcal {I}} _ {a, a} = \ operatorname {var} \ left [{\ frac {1} {X}} \ right] \ left ({\ frac {\ alpha -1} {ca}} \ right) ^ {2} = \ operatorname {var} \ left [{\ frac {1-X} {X}} \ right] \ left ({\ frac {\ alpha -1} {ca}} \ right) ^ {2} = {\ frac {\ beta (\ alpha + \ beta -1)} {(\ alpha -2) (ca) ^ {2}}} \\\ beta>2: \ quad {\ mathcal {I}} _ {c, c} = \ operat orname {var} \ left [{\ frac {1} {1 -X}} \ right] \ left ({\ frac {\ beta -1} {ca}} \ right) ^ {2} = \ operatorname {var} \ left [{\ frac {X} {1-X} } \ right] \ left ({\ frac {\ beta -1} {ca}} \ right) ^ {2} = {\ frac {\ alpha (\ alpha + \ beta -1)} {(\ beta -2) (ca) ^ {2}}} \\ {\ mathcal {I}} _ {a, c} = \ operatorname {cov} \ left [{\ frac {1} {X}}, {\ frac { 1} {1-X}} \ right] {\ frac {(\ alpha -1) (\ beta -1)} {(ca) ^ {2}}} = \ operatorname {cov} \ left [{\ frac {1-X} {X}}, {\ frac {X} {1-X}} \ right] {\ frac {(\ alpha -1) (\ beta -1)} {(ca) ^ {2} }} = {\ frac {(\ alpha + \ beta -1)} {(ca) ^ {2}}} \ end {align}}}$

См. раздел« Моменты линейно преобразованные, произведенные и инвертированные случайные величины »для этих ожиданий.

Определитель информационной матрицы Фишера представляет интерес (например, для вычисления априорной вероятности Джеффриса). Из выражений для отдельных компонентов следует, что определитель (симметричной) информационной матрицы Фишера для бета-распределения с четырьмя параметрами равен:

$det (I (α, β, a, c)) = - I a, c 2 I α, a I α, β + I a, a I a, c I α, c I α, β + I a, c 2 I α, β 2 - I a, a I c, c I α, β 2 - I a, c I α, a I α, c I β, a + I a, c 2 I α, α I β, a + 2 I c, c I α, a I α, β I β, a - 2 I a, c I α, c I α, β I β, a + I α, c 2 I β, a 2 - I c, c I α, α I β, a 2 + I a, c I α, a 2 I β, c - I a, a I a, c I α, α I β, c - I a, c I α, a I α, β I β, c + I a, a I α, c I α, β I β, c - I α, a I α, c I β, a I β, c + I a, c I α, α I β, a I β, c - I c, c I α, a 2 I β, β + 2 I a, c I α, a I α, c I β, β - I a, a I α, c 2 I β, β - I a, c 2 I α, α I β, β + I a, a I c, c I α, α I β, β, если α, β>2 {\ displaystyle {\ begin {align} \ det ({\ mathcal {I}} (\ alpha, \ beta, a, c)) = {} - {\ mathcal {I}} _ {a, c} ^ {2} {\ mathcal {I}} _ {\ alpha, a} {\ mathcal {I}} _ {\ alpha, \ beta} + {\ mathcal {I}} _ {a, a} {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ {\ alpha, c} {\ mathcal {I}} _ {\ alpha, \ beta} + {\ mathcal {I}} _ {a, c} ^ {2} {\ mathcal {I}} _ {\ alpha, \ beta} ^ {2} - {\ mathcal {I}} _ { a, a} {\ mathcal {I}} _ {c, c} {\ mathcal {I}} _ {\ alpha, \ beta} ^ {2} \\ {} - {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ {\ alpha, a} {\ mathcal {I}} _ {\ alpha, c} {\ mathcal {I}} _ {\ beta, a} + {\ mathcal {I}} _ {a, c} ^ {2} {\ mathcal {I}} _ {\ alpha, \ alpha} {\ mathcal {I}} _ {\ beta, a} +2 {\ mathcal { I}} _ {c, c} {\ mathcal {I}} _ {\ alpha, a} {\ mathcal {I}} _ {\ alpha, \ beta} {\ mathcal {I}} _ {\ beta, a} \\ {} - 2 {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ {\ alpha, c} {\ mathcal {I}} _ {\ alpha, \ beta } {\ mathcal {I}} _ {\ beta, a} + {\ mathcal {I}} _ {\ alpha, c} ^ {2} {\ mathcal {I}} _ {\ beta, a} ^ { 2} - {\ mathcal {I}} _ {c, c} {\ mathcal {I}} _ {\ alpha, \ alpha} {\ mathcal {I}} _ {\ beta, a} ^ {2} + {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ {\ alpha, a} ^ {2} {\ mathcal {I}} _ {\ beta, c} \\ {} - {\ mathcal {I}} _ {a, a} {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ {\ alpha, \ alpha} {\ mathcal {I}} _ {\ beta, c} - {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ { \ alpha, a} {\ mathcal {I}} _ {\ alpha, \ beta} {\ mathcal {I}} _ {\ beta, c} + {\ mathcal {I}} _ {a, a} {\ mathcal {I}} _ {\ alpha, c} {\ mathcal {I}} _ {\ alpha, \ beta} {\ mathcal {I}} _ {\ beta, c} \\ {} - {\ mathcal {I}} _ {\ alpha, a} {\ mathcal {I}} _ {\ alpha, c} {\ mathcal {I}} _ {\ beta, a} {\ mathcal {I}} _ {\ beta, c} + {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ {\ alpha, \ alpha} {\ mathcal {I}} _ {\ beta, a} {\ mathcal { I}} _ {\ beta, c} - {\ mathcal {I}} _ {c, c} {\ mathcal {I}} _ {\ alpha, a} ^ {2} {\ mathcal {I}} _ {\ beta, \ beta} \\ {} + 2 {\ mathcal {I}} _ {a, c} {\ mathcal {I}} _ {\ alpha, a} {\ mathcal {I}} _ { \ alpha, c} {\ mathcal {I}} _ {\ beta, \ beta} - {\ mathcal {I}} _ {a, a} {\ mathcal {I}} _ {\ alpha, c} ^ { 2} {\ mathcal {I}} _ {\ beta, \ beta} - {\ mathcal {I}} _ {a, c} ^ {2} {\ mathcal {I}} _ {\ alpha, \ alpha} {\ mathcal {I}} _ {\ b eta, \ beta} + {\ mathcal {I}} _ {a, a} {\ mathcal {I}} _ {c, c} {\ mathcal {I}} _ {\ alpha, \ alpha} {\ mathcal {I}} _ {\ beta, \ beta} {\ text {if}} \ alpha, \ beta>2 \ end {align}}}$

Используя критерий Сильвестра (проверка, все ли диагональные элементы положительны), и поскольку диагональные компоненты $I\; a,\; a\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{a,\; a\}\}$и $I\; c,\; c\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{c,\; c\}\}$имеют особенности при α = 2 и β = 2, из этого следует, что информационная матрица Фишера для случая с четырьмя положительно особенными для α>2 и β>2. Формула-распределений (симметричная или несимметричная) формула колокола, отсюда следует, что информационная матрица. Таким образом, важные распределения, принадлежащие семейству четырехпараметрического бета-распределения, такие какболическое распределение (Beta (2,2, a, c)) и равномерное распределение (Beta (1,1, a, c))) имеют информационные компоненты Фишера ($I\; a,\; a,\; I\; c,\; c,\; I\; \alpha ,\; a,\; I\; \beta ,\; c\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{a,\; a\},\; \{\backslash \; mathcal\; \{\; I\}\}\; \_\; \{c,\; c\},\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; alpha,\; a\},\; \{\backslash \; mathcal\; \{I\}\}\; \_\; \{\backslash \; beta,\; c\}\}$), которые в случае четырех параметров (хотя их информационные компоненты Фишера все параметры для случая двух параметров). Четырехпараметрическое полуокружное распределение Вигнера (бета (3 / 2,3 / 2, a, c)) и арксинусное распределение (бета (1 / 2,1 / 2, a, c)) имеют отрицательные детерминанты информации Фишера для четырехпараметрического случая.

Байесовский вывод

$B\; eta\; (1,\; 1)\; \{\backslash \; displaystyle\; Beta\; (1,1)\}$: равномерное распределение плотности вероятности было предложено Томас Байес, чтобы предотвратить игнорирование априорных вероятностей в байесовском выводе. Он не показывает состояние полного незнания, а состояние знания, в котором мы наблюдали по крайней мере один успех и одну неудачу, и поэтому у нас есть предварительное знание, что оба состояния являются физически возможно.

Использование бета-распределений в байесовском выводе связано с тем, что они обеспечивают семейство сопряженных априорных распределений вероятностей для биномиального (включая Бернулли ) и геометрические распределения. Область бета-распределения можно рассматривать как вероятность, и на самом деле распределение используется для описания значений вероятности p:

$P\; (p;\; \alpha ,\; \beta )\; =\; p\; \alpha \; -\; 1\; (1\; -\; p)\; \beta \; -\; 1\; B\; (\alpha ,\; \beta ).\; \{\backslash \; Displaystyle\; P\; (p;\; \backslash \; alpha,\; \backslash \; beta)\; =\; \{\backslash \; frac\; \{p\; ^\; \{\backslash \; alpha\; -1\}\; (1-p)\; ^\; \{\backslash \; beta\; -1\}\}\; \{\backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}\}.\}$

Примерами бета-распределений, используемых в априорных вероятностях представления игнорирования значений предшествующих параметров в байесовском выводе, являются бета (1,1), бета (0,0) и бета (1/2, 1/2).

.

Правило преемственности

Классическим применением бета-распределения правило преемственности, введенное в 18 веке Пьером-Симоном Лапласом в курсе лечения проблемы восхода солнца. В нем указано, что, учитывая его успех в n условно независимых испытаниях Бернулли с вероятностью p, оценка значения в следующем испытании составляет $s\; +\; 1\; n\; +\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{s\; +\; 1\}\; \{n\; +\; 2\}\}\}$. Эта оценка представляет собой ожидаемое значение апостериорного распределения по p, а именно Beta (s + 1, n - s + 1), которое задается правилами Байеса, если решена однородная априорная вероятность по p (т. Е. Beta (1, 1)), а затем принесло успехи в испытаниях. Правило преемственности Лапласа подверглось критике со стороны выдающих ученых. Р. Т. Кокс описал применение Лапласом правил преемственности к проблеме восход солнца (стр. 89) как «пародию на правильное использование этого принципа». Кейнс замечает (Ch.XXX, p. 382), «действительно, это настолько глупая теорема, что принимать ее во внимание дискредитировано». Карл Пирсон показал, что вероятность того, что следующие (n + 1) испытания будут успешными после успехов в испытаниях, составляет всего 50%, что было сочтено такими учеными, как Джеффрис, слишком низким и неприемлемым представлением научного процесса. экспериментов для проверки предложенного научного закона. Как Джеффрис (стр. 128) (с указанием CD Broad ) - преемственность Лапласа - высокая вероятность успеха (n + 1) / (n + 2)) в следующем испытании, но только умеренная вероятность (50 %) того, что следующая выборка (n + 1) сопоставимого размера будет столь же успешной. Как указывает Перкс, «правило преемственности трудно принять. Оно присваивает вероятность следующего испытания, что подразумевает предположение, что фактический пробег является средним пробегом, и что мы всегда находимся в конце среднего пробега. Казалось бы, более разумным было предположить, что мы находимся в середине среднего прогона. Ясно, что имеет высокое значение высокого уровня вероятностей, если они должны соответствовать разумному мнению ». Эти проблемы с правилами преемственности Лапласа побудили Холдейна, Перкса, Джеффриса и других искать другие формы априорной вероятности (см. Следующий раздел , озаглавленный «Байесовский вывод» ). По словам Джейнса, основная проблема с правилами преемственности состоит в том, что оно недействительно, когда s = 0 или s = n (см. правило преемственности для анализа его действительности).

Байесовская априорная вероятность (бета (1,1))

Бета-распределение достигает максимальной дифференциальной энтропии для бета (1,1): равномерная плотность вероятности для все значения в области распределения имеют одинаковую плотность. Это равномерное распределение Бета (1,1) было предложено («с большим сомнением») Томасом Байесом в качестве априорного распределения вероятностей, чтобы выразить незнание правильного априорного распределения. Это предварительное распределение было принято (по-видимому, из его работ, без каких-либо сомнений) Пьером-Симоном Лапласом, и поэтому оно было также известно как «правило Байеса-Лапласа» или «правило Лапласа». «обратной вероятности » в публикациях первой половины 20 века. В конце 19-го и начале 20-го века ученые осознали, что предположение о равномерной «равной» плотности вероятности зависит от фактических функций (например, от того, какая шкала наиболее подходит - линейной или логарифмической) и используемых параметризаций.. В частности, особого внимания требует поведение вблизи концов распределений с конечной опорой (например, вблизи x = 0 для распределения с начальной опорой при x = 0). Кейнс (Ch.XXX, p. 381) подверг критике использование равномерной априорной вероятности Байеса (Beta (1,1)), согласно которой все значения между нулем и единицей равновероятны, следующим образом: «Таким образом, опыт, если он что-то показывает, показывает, что наблюдается очень заметная группировка статистических отношений в окрестностях нуля и единицы, отношений для положительных теорий и корреляций между положительными качествами в окрестности нуля, а также для отрицательных теорий и корреляций между отрицательными качествами в окрестности единство. "

априорная вероятность Холдейна (бета (0,0))

$B\; эта\; (0,\; 0)\; \{\backslash \; displaystyle\; Beta\; (0,0)\}$: априорная вероятность Холдейна Вероятность, выражающая полное игнорирование предшествующей информации, когда мы даже не уверены, физически ли возможно, чтобы эксперимент закончился успехом или неудачей. При α, β → 0 бета-распределение приближается к двухточечному распределению Бернулли со всей плотностью вероятности, сосредоточенной на каждом конце, в точках 0 и 1, и ничего между ними. Подбрасывание монеты: одна грань монеты имеет значение 0, а другая сторона - 1.

Бета (0,0) распределение было предложено J.B.S. Холдейн, который предположил, что априорная вероятность,представляющая полную неопределенность, должна быть пропорциональна p (1 − p). Функцию p (1 − p) можно рассматривать как предел числителя бета-распределения, поскольку оба параметра формы стремятся к нулю: α, β → 0. Бета-функция (в знаменателе бета-распределения) стремится к бесконечности для оба параметра стремятся к нулю, α, β → 0. Следовательно, p (1 − p), деленное на бета-функцию, приближается к 2-точечному распределению Бернулли с равной вероятностью 1/2 на каждом конце, при 0 и 1, и ничего между ними, поскольку α, β → 0. Подбрасывание монеты: одна грань монеты находится в положении 0, а другая сторона - в 1. Априорное распределение вероятностей Холдейна Beta (0,0) - это "неправильный предыдущий ", потому что его интегрирование (от 0 до 1) не может строго сходиться к 1 из-за особенностей на каждом конце. Однако это не проблема для вычисления апостериорных вероятностей, если размер выборки не очень мал. Кроме того, Зеллнер указывает, что по шкале логарифм шансов (преобразование логит ln (p / 1-p)) априор Холдейна является равномерно плоским априорном. Тот факт, что равномерная априорная вероятность на logit преобразованной переменной ln (p / 1 − p) (с областью (-∞, ∞)) эквивалентна априорной вероятности Холдейна в области [0, 1] на это указывал Гарольд Джеффрис в первом издании (1939 г.) его книги «Теория вероятностей» (стр. 123). Джеффрис пишет: «Конечно, если мы доведем правило Байеса-Лапласа до крайностей, мы придем к результатам, которые не соответствуют чьему-либо образу мышления. Правило (Холдейна) dx / (x (1 − x)) заходит слишком далеко наоборот. Это привело бы к выводу, что если выборка относится к одному типу в отношении некоторого свойства, существует вероятность 1, что все население принадлежит к этому типу ". Тот факт, что «единообразие» зависит от параметризации, побудил Джеффриса искать форму априорной модели, которая была бы инвариантной при различных параметризациях.

априорная вероятность Джеффриса (бета (1 / 2,1 / 2) для распределения Бернулли или для биномиального распределения)

априорная вероятность Джеффри для бета-распределения: квадратный корень из определителя матрицы информации Фишера : $det\; (I\; (\alpha ,\; \beta ))\; =\; \psi \; 1\; (\alpha )\; \psi \; 1\; (\beta )\; -\; (\psi \; 1\; (\alpha )\; +\; \psi \; 1\; (\beta ))\; \psi \; 1\; (\alpha \; +\; \beta )\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; sqrt\; \{\backslash \; det\; (\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; alpha,\; \backslash \; beta))\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; (\backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; +\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta))\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}\}\}$является функцией тригамма-функции ψ1параметров формы α, β плотности апостериорного бета с образцами, имеющими успех = "s", отказ = "f" из s / (s + f) = 1/2 и s + f = {3,10,50} на основе 3 различных априорных функций вероятности: Холдейна (бета (0,0), Джеффриса (бета (1 / 2,1 / 2)) и Байеса (Бета (1,1)). Изображение показывает, что существует небольшая разница между апостериорными значениями для апостериорных при размере выборки 50 (с более выраженным пиком около p = 1/2). Значительные различия проявляются для очень малых размеров выборки 3 Плотность апостериорного бета с успешными образцами = "s", неудача = "f" из s / (s + f) = 1/4, и s + f ∈ {3,10,50}, на основе трех различных априорных функций вероятности: Холдейна (бета (0,0), Джеффриса (бета (1 / 2,1 / 2)) и Байеса (бета (1, 1)). Изображение показывает, что существует небольшая разница между апостерическими значениями для апостериорной выборки с размером выборки 50 (с более выраженным пиком p = 1/4). = 3, в этом вырожденном и маловероятном случае априор Холдейна дает обратную J-образную форму с модой при p = 0 вместо p = 1/4. Если имеется достаточно данных выборки , три априорных значения Байеса (бета (1, 1)), Джеффриса (бета (1 / 2,1 / 2)) и Холдейна (бета (0,0)) должны дать аналогичную апостериорную вероятность плотности. Апостериорные плотности бета с образцами имея успех = s, неудача = f из s / (s + f) = 1/4 и s + f ∈ {4,12,40}, на основе трех различных априорных функций вероятности: Холдейна (бета (0,0), Джеффри (бета (1/2, 1/2)) и Байеса (бета (1,1)). Изображение показывает, что существует небольшая разница между апостериорными значениями для апостериорной выборки при размере выборки 40 ( Значительные различия проявляются для очень малых размеров выборки

Гарольд Джеффрис использовать использовать неинформативную априорную вероятностную меру, которая должна быть инвариантной при повторной параметры : пропорциональной квадратному корню из определитель матрицы информации Фишера. Для распределения Бернулли это можно показать следующим образом: для монеты, которая является «орлом» с вероятностью p ∈ [0, 1] и является «решкой» с вероятностью 1 - p, для данного (H, T) ∈ {(0,1), (1,0)} вероятнос ть равна p (1 - p). Времена T = 1 - H, распределение Бернулли равно p (1 - p). Рассматривая p как единственный параметр, следует, что вероятность распределения Бернулли равна

$ln\; \; L\; (p\; \mid \; H)\; =\; H\; ln\; \; (p)\; +\; (1\; -\; H)\; ln\; \; (1\; -\; p).\; \{\backslash \; displaystyle\; \backslash \; ln\; \{\backslash \; mathcal\; \{L\}\}\; (p\; \backslash \; mid\; H)\; =\; H\; \backslash \; ln\; (p)\; +\; (1-H)\; \backslash \; ln\; (1-p).\}$

Информационная матрица Фишера имеет только один компонент (это скаляр, потому что есть только один параметр: p), поэтому:

$I\; (p)\; =\; E\; [(ddp\; ln\; \; (L\; (p\; \mid \; H)))\; 2]\; =\; E\; [(H\; p\; -\; 1\; -\; H\; 1\; -\; p)\; 2]\; =\; p\; 1\; (1\; -\; p)\; 0\; (1\; p\; -\; 0\; 1\; -\; p)\; 2\; +\; p\; 0\; (1\; -\; p)\; 1\; (0\; p\; -\; 1\; 1\; -\; p)\; 2\; =\; 1\; р\; (1\; -\; р).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \{\backslash \; sqrt\; \{\{\backslash \; mathcal\; \{I\}\}\; (p)\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; operatorname\; \{E\}\; \backslash !\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{d\}\; \{dp\}\}\; \backslash \; ln\; (\{\backslash \; mathcal\; \{L\}\}\; (p\; \backslash \; mid\; H))\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; sqrt\; \{\backslash \; operatorname\; \{E\}\; \backslash !\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; frac\; \{H\}\; \{p\}\}\; -\; \{\backslash \; frac\; \{1-H\}\; \{1-p\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; sqrt\; \{p\; ^\; \{1\}\; (1-p)\; ^\; \{0\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{p\}\}\; -\; \{\backslash \; frac\; \{0\}\; \{1-p\}\}\; \backslash \; right)\; ^\; \{2\; \}\; +\; p\; ^\; \{0\}\; (1-p)\; ^\; \{1\}\; \backslash \; left\; (\{\backslash \; frac\; \{0\}\; \{p\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{1-p\}\}\; \backslash \; right)\; ^\; \{2\}\}\; \}\; \backslash \backslash \; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{p\; (1-p)\}\}\}.\; \backslash \; end\; \{align\}\}\}$

Аналогично, для биномиального распределения с n Бернулли испытывает, можно показать, что

$I\; (p)\; =\; np\; (1\; -\; p).\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{\{\backslash \; mathcal\; \{I\}\}\; (p)\}\}\; =\; \{\backslash \; frac\; \{\backslash \; sqrt\; \{n\}\}\; \{\backslash \; sqrt\; \{p\; (1-p)\}\}\}.\}$

Таким образом, для Бернулли и биномиальных распределений, до Джеффри пропорционально $1\; p\; (1\; -\; p)\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; frac\; \{1\}\; \{\; \backslash \; sqrt\; \{p\; (1-p)\}\}\}\}$, что оказывается пропорциональным бета-распределению с переменными областями x = p и возможной формой α = β = 1/2, распределение арксинуса :

$B\; eta\; (1\; 2,\; 1\; 2)\; =\; 1\; \pi \; p\; (1\; -\; p).\; \{\backslash \; displaystyle\; Beta\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\},\; \{\backslash \; tfrac\; \{1\}\; \{2\}\})\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; \{\backslash \; sqrt\; \{p\; (1-p)\}\}\}\; \}.\}$

Следующая часть будет показана, что нормализируется константа для априорной Джеффри несущественна для окончательного результата, потому что нормализируется константа сокращается в теореме Байеса для апостериорной вероятности. Следовательно, бета (1 / 2,1 / 2) используется как априор Джеффри для Бернулли, так и для биномиального распределения. Как показано в следующем разделе, при использовании этого выражения как априорной вероятности, умноженной на правдоподобие в теореме Байеса, апостериорная вероятность оказывается бета-распределением. Однако важно понимать, что априор Джеффриса пропорционален $1\; p\; (1\; -\; p)\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{p\; (1-p)\}\}\}\}$для распределения Бернулли и биномиального распределения, но не для бета-распределения. Априор Джеффри для бета-распределения определяет определителем информации Фишера для бета-распределения, которое, как показано в разделе под названием «Информационная матрица Фишера», является функцией тригамма-функции ψ1параметров формы α и β следующим образом:

$det\; (I\; (\alpha ,\; \beta ))\; =\; \psi \; 1\; (\alpha )\; \psi \; 1\; (\beta )\; -\; (\psi \; 1\; (\alpha )\; +\; \psi \; 1\; (\beta ))\; \psi \; 1\; (\alpha \; +\; \beta )\; lim\; \alpha \; \to \; 0\; det\; (I\; (\alpha ,\; \beta ))\; =\; lim\; \beta \; \to \; 0\; det\; (I\; (\alpha ,\; \beta ))\; =\; \infty \; lim\; \alpha \; \to \; \infty \; det\; (I\; (\alpha ,\; \beta ))\; =\; lim\; \beta \; \to \; \infty \; Det\; (я\; (\alpha ,\; \beta ))\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \{\backslash \; sqrt\; \{\backslash \; det\; (\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; alpha,\; \backslash \; beta))\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; psi\; \_\; \{\; 1\}\; (\backslash \; alpha)\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta)\; -\; (\backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha)\; +\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; beta))\; \backslash \; psi\; \_\; \{1\}\; (\backslash \; alpha\; +\; \backslash \; beta)\}\}\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; 0\}\; \{\backslash \; sqrt\; \{\backslash \; det\; (\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; alpha,\; \backslash \; beta))\}\}\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; в\; 0\}\; \{\backslash \; sqrt\; \{\backslash \; det\; (\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; alpha,\; \backslash \; beta))\}\}\; =\; \backslash \; infty\; \backslash \backslash \backslash \; lim\; \_\; \{\backslash \; alpha\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; sqrt\; \{\backslash \; det\; (\; \{\backslash \; mathcal\; \{I\}\}\; (\backslash \; alpha,\; \backslash \; beta))\}\}\; =\; \backslash \; lim\; \_\; \{\backslash \; beta\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; sqrt\; \{\backslash \; det\; (\{\backslash \; mathcal\; \{I\}\}\; (\backslash \; альфа,\; \backslash \; бета))\}\}\; =\; 0\; \backslash \; конец\; \{выровнено\}\}$

Как обсуждалось ранее, априор Джеффри для распределения Бернулли и биномиального распределения пропорционален арксинусному распределению Бета (1 / 2,1 / 2), одномерной кривой, которая выглядит как бассейн в виде функции распределения Бернулли и биномиального распределения. Стенки бассейна образованы приближением p к сингулярности на концах p → 0 и p → 1, где Beta (1 / 2,1 / 2) стремится к бесконечности. Джеффрис априор для бета-распределения представляет собой двумерную поверхность (встроенную в трехмерное пространство), которая выглядит как бассейн, только две из его стенок встречаются в части α = β = 0 (и отсутствуют две стенки), как функция параметров формы α и β бета-распределения. Две смежные стенки этой двумерной поверхности образованы формируются формы α и β, приближающиеся к сингулярным функциям (тригамма-функции) при α, β → 0. У нее нет стенок для α, β → ∞, потому что в этом случае Определитель информационной матрицы Фишера для бета -распределения стремится к нулю.

В следующем разделе будет показана априорная вероятность априорной вероятности (при умножении на биномиальную функцию правдоподобия), которые являются промежуточными между результатами апостериорной вероятности априорных вероятностей Холдейна и Байеса.

Априор Джеффри может быть трудно получить аналитически, а в некоторых случаях его просто не существует (даже для простых функций распределения такого как асимметричное треугольное распределение ). Бергер, Бернардо и Сан в статье 2009 года определили эталонное априорное распределение вероятностей (в отличие от априорного Джеффри) существует для асимметричного треугольного распределения. Они не могут получить выражение в своей замкнутой форме для априорной ссылки, что она идеально соответствует (собственному) априорному

$Beta\; \; (1\; 2,\; 1\; 2)\; \sim \; 1\; \theta \; (1\; -\; \theta )\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{Beta\}\; (\{\backslash \; tfrac\; \{1\}\; \{2\}\},\; \{\backslash \; tfrac\; \{1\}\; \{2\}\})\; \backslash \; sim\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{\backslash \; theta\; (1-\; \backslash \; theta)\}\}\; \}\}$

где θ - переменная вершины для асимметричного треугольного распределения с опорой [0, 1] (соответствующие следующие значения параметров в статье Википедии о треугольном распределении : вершина c = θ, левый конец a = 0 и правый конец b = 1). Бергер и др. также приводят эвристический аргумент, что Бета (1 / 2,1 / 2) действительно может быть точной априорной Бергера - Бернардо - Сан для асимметричного треугольного распределения. Следовательно, бета (1 / 2,1 / 2) не только априор Джеффриса для распределений Бернулли и биномиальных распределений, но также, по-видимому, является эталоном Бергера – Бернардо – Сан для асимметричного треугольного распределения (для которого априор Джеффриса не Существуют), распределение, используемое в управлении проектами, и PERT анализ для описания стоимости и продолжительности задач проекта.

Кларк и Бэррон доказывают, что среди непрерывных положительных априоров Джеффрис априор (если он существует) асимптотически максимизирует взаимную информацию Шеннона между выборкой размера n и параметром, и поэтому Джеффрис априор является самый неинформативный априор (измерение информации как информации Шеннона). Доказательство основывается на исследовании расхождения Кульбака – Лейблера между функциями плотности вероятности для случайных величин iid.

Влияние различных вариантов априорной вероятности на апостериорное бета-распределение

Если выборки взяты из совокупности случайной величины X, что приводит к s успехам и f неудачам в "n" Бернулли испытывает n = s + f, затем функцию правдоподобия для параметров s и f при x = p (обозначение x = p в приведенных ниже выражениях подчеркнет, что область x обозначает значение параметра p в биномиальном распределении) является следующим биномиальным распределением :

$L\; (s,\; f\; \mid \; x\; =\; p)\; =\; (s\; +\; fs)\; xs\; (1\; -\; x)\; f\; =\; (ns)\; xs\; (\; 1\; -\; х)\; н\; -\; с.\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{L\}\}\; (s,\; f\; \backslash \; mid\; x\; =\; p)\; =\; \{s\; +\; f\; \backslash \; choose\; s\}\; x\; ^\; \{s\}\; (1-x)\; ^\; \{f\}\; =\; \{n\; \backslash \; choose\; s\}\; x\; ^\; \{s\}\; (1-x)\; ^\; \{ns\}.\}$

Если представления о априорной вероятности информации достаточно хорошо аппроксимируются бета-распределением с параметрами α Prior и β Prior, то:

$PriorProbability\; (x\; =\; p;\; \alpha \; Prior,\; \beta \; Prior)\; =\; x\; \alpha \; Prior\; -\; 1\; (1\; -\; x)\; \beta \; Prior\; -\; 1\; B\; (\alpha \; Prior,\; \beta \; Prior)\; \{\backslash \; displaystyle\; \{\backslash \; operatorname\; \{PriorProbability\}\}\; (x\; =\; p;\; \backslash \; alpha\; \backslash \; operatorname\; \{Prior\},\; \backslash \; beta\; \backslash \; operatorname\; \{Prior\})\; =\; \{\backslash \; frac\; \{x\; ^\; \{\backslash \; alpha\; \backslash \; operatorname\; \{Prior\}\; -1\}\; (1-x)\; ^\; \{\backslash \; beta\; \backslash \; operatorname\; \{Prior\}\; -1\}\}\; \{\backslash \; mathrm\; \{B\}\; (\backslash \; alpha\; \backslash \; operatorname\; \{Prior\},\; \backslash \; beta\; \backslash \; operatorname\; \{Prior\})\}\}\}$

Согласно теореме Байеса для непрерывного пространства событий, апостериорная вероятность дается как произведение априорной вероятности и функции правдоподобия (с учетом свидетельства s и f = n - s), нормализованных так, чтобы площадь под кривой равнялась один след ующим образом:

$апостериорная вероятность ⁡ (x = p ∣ s, n - s) = PriorProbability ⁡ (x = p; α Prior, β Prior) L (s, f ∣ x = p) ∫ 0 1 Prior Вероятность ⁡ (x = p; α Prior, β Prior) L (s, f ∣ x = p) dx = (ns) xs + α Приор - 1 (1 - x) n - s + β Приор - 1 / B (α Приор, β Приор) ∫ 0 1 ((ns) xs + α Приор - 1 (1 - x) n - s + β Приор - 1 / B (α Prior, β Prior)) dx = xs + α Prior - 1 (1 - x) n - s + β Prior - 1 ∫ 0 1 (xs + α Prior - 1 (1 - x) n - s + β Prior - 1) dx = xs + α Prior - 1 (1 - x) n - s + β Prior - 1 B (s + α Prior, n - s + β Prior). {\ displaystyle {\ begin {align} \ operatorname {posteriorprobability} (x = p \ mid s, ns) \\ [6pt] = {} {\ frac {\ operatorname {PriorProbability} (x = p; \ alpha \ operatorname {Prior}, \ beta \ operatorname {Prior}) {\ mathcal {L}} (s, f \ mid x = p)} {\ int _ {0} ^ {1} \ operatorname {PriorProbability} (x = p; \ alpha \ operatorname {Prior}, \ beta \ operatorname {Prior}) {\ mathcal {L}} (s, f \ mid x = p) dx}} \\ [6pt] = {} {\ frac {{n \ choose s} x ^ {s + \ alpha \ operatorname {Prior} -1} (1-x) ^ {n-s + \ beta \ operatorname {Prior} -1} / \ mathrm {B} (\ alpha \ operatorname {Prior}, \ beta \ operatorname {Prior})} {\ int _ {0} ^ {1} \ left ({n \ choose s} x ^ {s + \ alpha \ operatorname {Prior} -1} (1-x) ^ {n-s + \ beta \ operatorname {Prior} -1} / \ mathrm {B} (\ alpha \ operatorname {Prior}, \ beta \ operatorname {Prior}) \ right) dx}} \ \ [6pt] = {} {\ frac {x ^ {s + \ alpha \ operatorname {Prior} -1} (1-x) ^ {n-s + \ beta \ operatorname {Prior} -1}} {\ int _ {0} ^ { 1} \ left (x ^ {s + \ alpha \ operatorname {Prior} -1} (1-x) ^ {n-s + \ beta \ operatorname {Prior} -1} \ right) dx} } \\ [6pt] = {} {\ frac {x ^ {s + \ alpha \ operator имя {Приор} -1} (1-x) ^ {n-s + \ beta \ operatorname {Prior} -1}} {\ mathrm {B} (s + \ alpha \ operatorname {Prior}, n-s + \ beta \ operatorname {Prior})}}. \ end {align}}}$

Биномиальный коэффициент

$(s\; +\; fs)\; =\; (ns)\; =\; (s\; +\; f)!\; с!\; е!\; =\; п!\; с!\; (н-с)!\; \{\backslash \; displaystyle\; \{s\; +\; f\; \backslash \; choose\; s\}\; =\; \{n\; \backslash \; choose\; s\}\; =\; \{\backslash \; frac\; \{(s\; +\; f)!\}\; \{s!\; f!\}\}\; =\; \{\backslash \; frac\; \{n!\}\; \{s!\; (ns)!\}\}\}$

появляется как в числителе, так и в знаменателе апостериорной вероятности, и он не зависит от переменной интегрирования x, следовательно, он сокращается и не имеет отношения к окончательному результату. Точно так же нормализующий коэффициент для априорной вероятности, бета-функция B (αPrior, βPrior) отменяется, и это не имеет значения для окончательного результата. Такой же результат апостериорной вероятности может быть получен, если использовать ненормированный априор

$x\; \alpha \; Prior\; -\; 1\; (1\; -\; x)\; \beta \; Prior\; -\; 1\; \{\backslash \; displaystyle\; x\; ^\; \{\backslash \; alpha\; \backslash \; operatorname\; \{Prior\}\; -1\}\; (\; 1-x)\; ^\; \{\backslash \; beta\; \backslash \; operatorname\; \{Prior\}\; -1\}\}$

, потому что все нормализующие множители сокращаются. Некоторые авторы (включая самого Джеффриса), таким образом, используют ненормализованную априорную формулу, поскольку константа нормализации сокращается. Числитель апостериорной вероятности оказывается просто (ненормированным) произведением априорной вероятности и функции правдоподобия, а знаменатель - ее интегралом от нуля до единицы. Бета-функция в знаменателе B (s + α Prior, n - s + β Prior) появляется как нормировочная константа, чтобы гарантировать, что полная апостериорная вероятность равна единице.

Отношение s / n количества успешных испытаний к общему количеству испытаний является достаточной статистикой в биномиальном случае, что актуально для следующих результатов.

Для априорной вероятности Байеса (Beta (1,1)) апостериорная вероятность равна:

Для Jeffreys 'ранее вероятность (бета (1 / 2,1 / 2)), апостериорная вероятность равна:

и для Haldane априорная вероятность (Бета (0,0)), апостериорная вероятность равна:

Из приведенных выше выражений следует, что для s / n = 1/2) все три вышеупомянутые априорные вероятности приводят к идентичное расположение для апостериорной вероятности, среднее значение = режим = 1/2. Для s / n < 1/2, the mean of the posterior probabilities, using the following priors, are such that: mean for Bayes prior>среднее значение для априорного Джеффри>среднее для априорного значения Холдейна. Для s / n>1/2 порядок этих неравенств меняется на противоположный, так что априорная вероятность Холдейна дает наибольшее апостериорное среднее. Априорная вероятность Холдейна Beta (0,0) приводит к апостериорной плотности вероятности со средним значением (ожидаемым значением для вероятности успеха в «следующем» испытании), идентичным отношению s / n количества успехов к общему количеству. испытаний. Таким образом, априор Холдейна дает апостериорную вероятность с ожидаемым значением в следующем испытании, равным максимальной вероятности. Априорная вероятность Байеса Beta (1,1) приводит к апостериорной плотности вероятности с модой, идентичной отношению s / n (максимальное правдоподобие).

В случае, если 100% испытаний были успешными s = n, априорная вероятность Байеса Beta (1,1) приводит к апостериорному ожидаемому значению, равному правилу последовательности (n + 1) / (n + 2), в то время как предыдущая бета-версия Холдейна (0,0) дает апостериорное ожидаемое значение 1 (абсолютная уверенность в успехе в следующем испытании). Априорная вероятность Джеффри дает апостериорное ожидаемое значение, равное (n + 1/2) / (n + 1). Перкс (стр. 303) указывает: «Это обеспечивает новое правило преемственности и выражает« разумную »позицию, которую следует занять, а именно: после непрерывной серии n успехов мы предполагаем вероятность следующего испытания, эквивалентную предположению что мы примерно на полпути к средней пробежке, т. е. что мы ожидаем неудачи один раз за (2n + 2) испытаний. Правило Байеса – Лапласа подразумевает, что мы приближаемся к концу средней пробежки или что мы ожидаем неудачи один раз в (n + 2) испытаниях. Сравнение явно свидетельствует в пользу нового результата (то, что теперь называется приором Джеффри) с точки зрения «разумности» ».

И наоборот, в случае, если 100% испытаний закончились неудачей ( s = 0), априорная вероятность Байеса Beta (1,1) приводит к апостериорному ожидаемому значению успеха в следующем испытании, равному до 1 / (n + 2), в то время как предшествующая бета-версия Холдейна (0,0) дает апостериорное ожидаемое значение успеха в следующем испытании, равное 0 (абсолютная уверенность в неудаче в следующем испытании). Априорная вероятность Джеффри приводит к апостериорному ожидаемому значению успеха в следующем испытании, равному (1/2) / (n + 1), на что Перкс (стр. 303) указывает: «это гораздо более отдаленный результат, чем результат Байеса. -Результат Лапласа 1 / (n + 2) ".

Джейнс ставит под сомнение (для унифицированного априорного бета (1,1)) использование этих формул для случаев s = 0 или s = n, поскольку интегралы не сходятся (бета (1,1) неправильный априор для s = 0 или s = n). На практике условия 0

Как отмечалось в разделе о правиле последовательности, К. Пирсон показал, что после n успехов в n попытках апостериорная вероятность (на основе распределения Байеса-Бета (1,1) как априорная вероятность) того, что следующие (n + 1) испытания будут успешными, равна 1/2 независимо от значения n. Основываясь на бета-распределении Холдейна (0,0) как априорной вероятности, эта апостериорная вероятность равна 1 (абсолютная уверенность в том, что после n успехов в n испытаниях все следующие (n + 1) испытания будут успешными). Перкс (стр. 303) показывает, что для так называемых апоров Джеффри эта вероятность равна ((n + 1/2) / (n + 1)) ((n + 3/2) / (n + 2))... (2n + 1/2) / (2n + 1), что для n = 1, 2, 3 дает 15/24, 315/480, 9009/13440; быстро приближается к предельному значению $1/2\; =\; 0.70710678\dots \; \{\backslash \; displaystyle\; 1\; /\; \{\backslash \; sqrt\; \{2\}\}\; =\; 0.70710678\; \backslash \; ldots\}$, когда n стремится к бесконечности. Перкс отмечает, что то, что сейчас известно как априор Джеффри: «явно более« разумно », чем либо результат Байеса-Лапласа, либо результат альтернативного правила (Холдейна), отвергнутого Джеффрисом, который дает определенность как вероятность. Он явно обеспечивает намного лучшее соответствие с процессом индукции. Является ли он «абсолютно» разумным для этой цели, то есть достаточно ли он велик, без абсурдности достижения единства, - это вопрос, который должны решать другие. Но необходимо понимать, что результат зависит от предположения о полном безразличии и отсутствии знаний до проведения эксперимента по отбору проб ».

Ниже приведены дисперсии апостериорного распределения, полученные с помощью этих трех априорных распределений вероятностей:

для априорной вероятности Байеса (Beta (1,1)), апостериорная дисперсия:

$дисперсия\; =\; (n\; -\; s\; +\; 1)\; (s\; +\; 1)\; (3\; +\; n)\; (2\; +\; n)\; 2,\; что\; для\; s\; =\; n\; 2\; приводит\; к\; дисперсии\; =\; 1\; 12\; +\; 4\; n\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{variance\}\}\; =\; \{\backslash \; frac\; \{(n-s\; +\; 1)\; (s\; +\; 1)\}\; \{(3\; +\; n)\; (2\; +\; n)\; ^\; \{2\}\}\},\; \{\backslash \; text\; \{который\; для\; \}\}\; s\; =\; \{\backslash \; frac\; \{n\}\; \{2\}\}\; \{\backslash \; text\; \{приводит\; к\; отклонению\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{12\; +\; 4n\}\}\}$

для Джеффриса априорная вероятность (бета (1 / 2,1 / 2)), апостериорная дисперсия составляет:

$дисперсия\; =\; (n\; -\; s\; +\; 1\; 2)\; (s\; +\; 1\; 2)\; (2\; +\; n)\; (1\; +\; n)\; 2,\; что\; для\; s\; =\; n\; 2\; приводит\; к\; var\; =\; 1\; 8\; +\; 4\; n\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{variance\}\}\; =\; \{\backslash \; frac\; \{(n-s\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\})\; (s\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\})\}\; \{(2\; +\; n)\; (1\; +\; n)\; ^\; \{2\}\}\},\; \{\backslash \; text\; \{который\; для\}\}\; s\; =\; \{\backslash \; frac\; \{n\}\; \{2\}\}\; \{\backslash \; text\; \{приводит\; к\; var\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{8\; +\; 4n\}\}\}$

и для априорной вероятности Холдейна (бета (0,0)) апостериорная дисперсия составляет:

$дисперсия\; =\; (n\; -\; s)\; s\; (1\; +\; n)\; n\; 2,\; что\; для\; s\; =\; n\; 2\; приводит\; к\; дисперсии\; =\; 1\; 4\; +\; 4\; n\; \{\backslash \; displaystyle\; \{\backslash \; text\; \{variance\}\}\; =\; \{\backslash \; frac\; \{(ns)\; s\}\; \{(1+\; n)\; n\; ^\; \{2\}\}\},\; \{\backslash \; text\; \{который\; для\}\}\; s\; =\; \{\backslash \; frac\; \{n\}\; \{2\}\}\; \{\backslash \; text\; \{приводит\; к\; дисперсии\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{4\; +\; 4n\; \}\}\}$

Итак, как заметил Силви, для больших n дисперсия мала и, следовательно, апостериорное распределение сильно концентрировано, тогда как предполагаемое априорное распределение было очень размытым. Это согласуется с тем, на что можно было бы надеяться, поскольку смутные априорные знания преобразуются (посредством теоремы Байеса) в более точные апостериорные знания посредством информативного эксперимента. Для малых n априорные результаты Haldane Beta (0,0) дают наибольшую апостериорную дисперсию, тогда как априорные результаты Bayes Beta (1,1) дают более концентрированные апостериорные отклонения. Предварительная бета-версия Джеффри (1 / 2,1 / 2) дает апостериорную дисперсию между двумя другими. По мере увеличения n дисперсия быстро уменьшается, так что апостериорная дисперсия для всех трех априорных значений сходится примерно к одному и тому же значению (приближаясь к нулевой дисперсии при n → ∞). Вспоминая предыдущий результат о том, что априорная вероятность Бета (0,0) Холдейна приводит к апостериорной плотности вероятности со средним значением (ожидаемым значением для вероятности успеха в следующем «испытании»), идентичным отношением s / n количества успехов к общему количеству испытаний, из приведенного выше выражения следует, что также предварительная бета Холдейна (0,0) приводит к апостериорной дисперсии, идентичной дисперсии, выраженной в терминах макс. оценка правдоподобия s / n и размер выборки (в разделе «Дисперсия»):

$дисперсия\; =\; \mu \; (1\; -\; \mu )\; 1\; +\; \nu \; =\; (n\; -\; s)\; s\; (1\; +\; n)\; n\; 2\; \{\backslash \; displaystyle\; \{\backslash \; текст\; \{дисперсия\}\}\; =\; \{\backslash \; frac\; \{\backslash \; mu\; (1-\; \backslash \; mu)\}\; \{1+\; \backslash \; nu\}\}\; =\; \{\backslash \; frac\; \{(ns)\; s\}\; \{(1\; +\; n)\; n\; ^\; \{2\}\}\}\}$

со средним значением μ = s / n и выборки ν = n.

В байесовском выводе использование предшествующего распределения Бета (αPrior, βPrior) перед биномиальным распределением эквивалентным добавлением (αPrior - 1) псевдонаблюдений за «успехом» и (βPrior - 1) псевдонаблюдения «неудач» относительно фактического количества ожидаемых успехов и неудач, оценка результатов биномиального распределения по доле успехов как для реального, так и для псевдонаблюдений. Единообразный априорный бета (1,1) не пере (или вычитает) какие-либо псевдо-наблюдения, поскольку для бета (1,1) следует, что (αPrior - 1) = 0 и (βPrior - 1) = 0. Априор Холдейна Бета (0,0) вычитает по одному псевдонаблюдению из каждого, а предыдущая бета Джеффри (1 / 2,1 / 2) вычитает 1/2 псевдонаблюдения успеха и равное количество неудач. Это вычитание имеет эффект сглаживания апостерического распределения. Если доля успехов не составляет 50% (s / n 1/2), значения αPrior и βPrior меньше 1 (и, следовательно, отрицательные (αPrior - 1) и (βPrior - 1)) благоприятствуют разреженности, т. Е. Распределения, в которых параметр p ближе к 0 или 1. Фактически, αPrior и βPrior между 0 и 1 при совместной работе функционируют как параметр концентрации.

На прилагаемых графиках показаны апостериорные функции плотности вероятности для размеров выборки n. ∈ {3,10,50}, успехи s ∈ {n / 2, n / 4} и бета (αPrior, βPrior) ∈ {Beta (0,0), Beta (1 / 2,1 / 2), Beta ( 1,1)}. Также имели место случаи для n = {4,12,40}, успеха s = {n / 4} и Beta (αPrior, βPrior) ∈ {Beta (0,0), Beta (1 / 2,1 / 2)., Бета (1,1)}. Первый график показывает симметричные случаи для успехов s ∈ {n / 2} со средним значением = mode = 1/2, а второй график показывает искаженные случаи s ∈ {n / 4}. Изображения показывают, что существует небольшая разница между апостериорными значениями для апостериорного исследования с размером выборки 50 (представляет собой более выраженным пиком около p = 1/2). Значительные различия для очень малых размеров выборки (в частности, для более плоского распределения для вырожденного случая размера выборки = 3). Таким образом, искаженные случаи с успехом = {n / 4} демонстрируют больший эффект от выбора априорного критерия при небольшом размере выборки, чем симметричные случаи. Для симметричного распределения априорное бета-распределение Байеса (1,1) дает наиболее "пиковые" и самые высокие апостериорные распределения, а априорное бета-распределение Холдейна (0,0) дает наиболее плоское и наименьшее пиковое распределение. Между ними находится предыдущая бета-версия Jeffreys (1/2, 1/2). Для почти симметричных, но не слишком перекошенных распределений эффект априорных значений аналогичен. Для очень небольшого размера выборки (в данном случае для размера выборки 3) и асимметричного распределения (в этом примере для s ∈ {n / 4}) априор Холдейна может привести к обратному J-образному распределению с сингулярностью на левый конец. Однако это происходит только в вырожденных случаях (в этом примере n = 3 и, следовательно, s = 3/4 < 1, a degenerate value because s should be greater than unity in order for the posterior of the Haldane prior to have a mode located between the ends, and because s = 3/4 is not an integer number, hence it violates the initial assumption of a binomial distribution for the likelihood) and it is not an issue in generic cases of reasonable sample size (such that the condition 1 < s < n − 1, necessary for a mode to exist between both ends, is fulfilled).

В главе 12 (стр. 385) своей книги Джейнс утверждает, что Холдейн предшествовал бета-версии (0, 0) предварительное состояние знания о полном незнании, когда мы даже не уверены, физически возможно, чтобы эксперимент привел к успеху или неудаче, в то время как байесовский (унифицированный) априорный бета (1,1), если каждый знает, что возможны оба бинарных исхода. Джейнс заявляет: «интерпретирующий предшествующий алгоритм Байеса-Лапласа (бета (1,1)) как описывающий не состояние полного невежества, а состояние знания, в котором мы наблюдали один успех и один неудача... Хотя бы один успех и одну неудачу, тогда мы узнаем, что эксперимент является истинным бинарным экспериментом в смысле физических возможностей ». Джейнс специально не обсуждает предыдущую бета-версию Джеффриса (1 / 2,1 / 2) (Обсуждение Джейнсом« Приора Джеффриса »на стр. 181, 423 иорный в главе 12 книги Джейнса вместо этого упомянутый неподходящий, не-ни преобразованный, предшествующий "1 / p dp", введенный Джеффрисом в издании его книги 1939 года, как он представил то, что теперь известно как апри инвариант Джеффриса: квадратный корень из определителя информационной матрицы Фишера. «1 / p» является априорным инвариантом Джеффриса (1946) для экспоненциального распределения, а не для распределений Бернулли или биномиальных распределений). Однако из вышеприведенного обсуждения следует, что бета Джеффриса (1 / 2,1 / 2) предшествует состоянию знаний, промежуточному между бета-версией Холдейна (0,0) и бета-версией Байеса (1,1).

Аналогичным образом Карл Пирсон в своей книге 1892 года Грамматика науки (стр. 144 издания 1900 г.) утверждал, что байесовская (бета (1,1) форма Пирсон писал: «Это не меньшее, единственное предположение, которое мы, кажется, сделали, - это то, что мы ничего». природа, рутина и аномия (от греческого ανομία, а именно: a- «без» и nomos «закон») должны рассматриваться как соответствующие вероятности возникновения. оно включает в себя знание о природе, которое мы не обладаем. Мы используем наш опыт построения и действия монет в целом, чтобы утверждать, что орел и решка равноверны, но мы не имеем права утверждать перед опытом, что, поскольку мы ничего не знаем о природа, распорядок и нарушение равновероятны. ашем невежестве мы должны рассмотреть, прежде чем испытать, что natu Он может состоять из всех процедур, всех аномалий (безнормальности) или их смеси в любых пропорциях, и все они равновероятны. Какая из этих конституций после опыта наиболее вероятной, должна явноеть от того, каким был этот опыт ».

Если имеется достаточно данных выборки, а апостериорная вероятностная мода не находится одной из крайностей области (x = 0 или x = 1), три априора Байеса (бета (1,1)), Джеффриса (бета (1 / 2,1 / 2)) и Холдейна (бета (0, 0)) должны давать аналогичные плотности апостериорной вероятности. В противном случае, как указывает Гельман и др. (Стр. 65), «если доступно так мало данных, что выбор неинформативного априорного распределения имеет значение, необходимо указать соответствующую информацию в предварительном распределении», или, как указывает Бергер (стр. 125), «когда разные разумные априорные значения имеют разные разные» ответы, можно ли утверждать, что существует один ответ? Не лучше ли признать, что существует научная неопределенность, а вывод зависит от предшествующих убеждений? »

.

Возникновение и применение

Статистика заказов

Бета-распределение имеет важное применение в теории порядка . Основной результат состоит в том, что распределение k-го наименьшего из выборки размера n из непрерывного равномерного распределения имеет бета-распределение. Этот результат суммируется как:

$U\; (k)\; \sim \; Beta\; \; (k,\; n\; +\; 1\; -\; k).\; \{\backslash \; displaystyle\; U\; \_\; \{(k)\}\; \backslash \; sim\; \backslash \; operatorname\; \{Beta\}\; (k,\; n\; +\; 1-k).\}$

Из этого и применения теории, относящейся к интегральному преобразованию вероятностей, можно получить распределение любой статистики отдельного порядка из непрерывного распределения.

Субъективная логика

В стандартной логике признания либо истинными, либо ложными. В отличие от этого, субъективная логика предполагает, что люди не могут определять с абсолютной точностью. Уверенность в том, является ли утверждением о реальном мире абсолютно верным или ложным. В субъективной логике апостериорные оценки вероятности двоичных событий могут быть представлены бета-распределениями.

Вейвлет-анализ

A вейвлет является волнообразным колебание с амплитудой , которое начинается с нуля, увеличивается, а снова уменьшается до нуля. Обычно это можно представить как «кратковременное колебание», которое быстро затухает. Вейвлеты Программу извлечения информации из различных типов данных, включая, но не ограничиваясь, аудиосигналы и изображения. Таким образом, вейв использует специально созданные для того, чтобы получить свойства, которые делают их полезными для обработки сигналов. Вейвлеты локализованы как по времени, так и по частоте, тогда как стандартное преобразование Фурье локализовано только по частотам. Таким образом, стандартные преобразования Фурье применимы только к стационарным процессам, а вейвлеты применимы к не- стационарным процессам. Непрерывные вейвлеты могут быть построены на основе бета-распределения. Бета-вейвлеты можно рассматривать как мягкую разновидность которые вейвлетов Хаара, форма точно настраивает установленные формы α и β.

Управление проектом: моделирование стоимости и расписания

Бета-рейтинг может быть для моделирования событий, которые имеют место в пределах интервала, определяемого минимальным и максимальным числом. По этой причине бета-распределение - вместе с треугольным распределением - широко используется в PERT, метод критического пути (CPM), Совместное моделирование графика затрат (JCSM) и системы управления проектами / контроля для описания времени до завершения и стоимости задачи. В управлении проектами широко используются стенографические вычисления для оценки среднего и стандартного отклонения бета-распределения:

$\mu \; (X)\; =\; a\; +\; 4\; b\; +\; c\; 6\; \sigma \; (\; Икс)\; =\; с\; -\; a\; 6\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mu\; (X)\; =\; \{\backslash \; frac\; \{a\; +\; 4b\; +\; c\}\; \{6\}\}\; \backslash \backslash \backslash \; sigma\; (X)\; =\; \{\backslash \; frac\; \{\; ca\}\; \{6\}\}\; \backslash \; end\; \{align\}\}\}$

где a - минимум, c - максимум, а b - наиболее вероятное значение (режим для α>1 и β>1).

Приведенная выше оценка для mean $\mu \; (X)\; =\; a\; +\; 4\; b\; +\; c\; 6\; \{\backslash \; displaystyle\; \backslash \; mu\; (X)\; =\; \{\backslash \; frac\; \{a\; +\; 4b\; +\; c\}\; \{6\}\}\}$известен как PERT трехточечная оценка и является точным для любого из следующих значений β (для произвольного α в пределах этих диапазонов):

β = α>1 (симметричный случай) с стандартным отклонением $\sigma \; (X)\; =\; c\; -\; a\; 2\; 1\; +\; 2\; \alpha \; \{\backslash \; displaystyle\; \backslash \; sigma\; (X)\; =\; \{\backslash \; frac\; \{ca\}\; \{2\; \{\backslash \; sqrt\; \{1\; +\; 2\; \backslash \; alpha\}\}\}\}\}$, асимметрия = 0, и избыточный эксцесс = $-\; 6\; 3\; +\; 2\; \alpha \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{-6\}\; \{3\; +\; 2\; \backslash \; alpha\}\}\}$

или

β = 6 - α для 5>α>1 (наклонный случай) со стандартным отклонением

$\sigma \; (Икс)\; знак\; равно\; (с\; -\; а)\; \alpha \; (6\; -\; \alpha )\; 6\; 7,\; \{\backslash \; displaystyle\; \backslash \; sigma\; (X)\; =\; \{\backslash \; frac\; \{(ca)\; \{\backslash \; sqrt\; \{\backslash \; alpha\; (6-\; \backslash \; alpha)\}\; \}\}\; \{6\; \{\backslash \; sqrt\; \{7\}\}\}\},\}$

асимметрия = $(3\; -\; \alpha )\; 7\; 2\; \alpha \; (6\; -\; \alpha )\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{(3-\; \backslash \; альфа)\; \{\backslash \; sqrt\; \{7\}\}\}\; \{2\; \{\backslash \; sqrt\; \{\backslash \; alpha\; (6-\; \backslash \; alpha)\}\}\}\}\}$и избыточный эксцесс = $21\; \alpha \; (6\; -\; \alpha )\; -\; 3\; \{\backslash \; Displaystyle\; \{\backslash \; гидроразрыва\; \{21\; \}\; \{\backslash \; alpha\; (6-\; \backslash \; alpha)\}\}\; -\; 3\}$

Приведенная выше оценка для стандартного отклонения σ (X) = (c - a) / 6 точна для любого из следующих значения α и β:

α = β = 4 (симметричный) с асимметрией, = 0 и избыточным эксцессом = −6/11.

β = 6 - α и $\alpha \; =\; 3\; -\; 2\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 3\; -\; \{\backslash \; sqrt\; \{2\}\}\}$(правосторонний, положительный перекос) с перекосом $=\; 1\; 2\; \{\backslash \; displaystyle\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\}\}\}\}$и избыточный эксцесс = 0

β = 6 - α и $\alpha \; =\; 3\; +\; 2\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; 3\; +\; \{\backslash \; sqrt\; \{2\}\}\}$(левосторонний, отрицательный перекос) с перекосом $=\; -\; 1\; 2\; \{\backslash \; displaystyle\; =\; \{\backslash \; frac\; \{-1\}\; \{\backslash \; sqrt\; \{2\}\}\}\}$и избыточный эксцесс = 0

В противном случае они могут быть плохой аппроксимацией для бета-распределений с другими значениями α и β, демонстрируя средние ошибки 40% в среднем и 549% в дисперсии.

Вычислительные методы

Создание бета -распределенные случайные величины

Если X и Y независимы, с $X\; \sim \; \Gamma \; (\alpha ,\; \theta )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; Gamma\; (\backslash \; alpha,\; \backslash \; theta)\}$и $Y\; \sim \; \Gamma \; (\beta ,\; \theta )\; \{\backslash \; displaystyle\; Y\; \backslash \; sim\; \backslash \; Gamma\; (\backslash \; beta,\; \backslash \; theta)\}$, затем

$XX\; +\; Y\; \sim \; B\; (\alpha ,\; \beta ).\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{X\}\; \{X\; +\; Y\}\}\; \backslash \; sim\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta).\}$

Итак, один из алгоритмов генерации бета-вариаций - это генерировать $XX\; +\; Y\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{X\}\; \{X\; +\; Y\}\}\}$, где X - гамма-вариация с параметрами (α, 1), а Y - независимая гамма-вариация с параметры (β, 1). Фактически, здесь $XX\; +\; Y\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{X\}\; \{X\; +\; Y\}\}\}$и $X\; +\; Y\; \{\backslash \; displaystyle\; X\; +\; Y\}$независимы, и $X\; +\; Y\; \sim \; \Gamma \; (\alpha \; +\; \beta ,\; \theta )\; \{\backslash \; displaystyle\; X\; +\; Y\; \backslash \; sim\; \backslash \; Gamma\; (\backslash \; alpha\; +\; \backslash \; beta,\; \backslash \; theta)\}$. Если $Z\; \sim \; \Gamma \; (\gamma ,\; \theta )\; \{\backslash \; displaystyle\; Z\; \backslash \; sim\; \backslash \; Gamma\; (\backslash \; gamma,\; \backslash \; theta)\}$и $Z\; \{\backslash \; displaystyle\; Z\}$не зависит от $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$, тогда $X\; +\; YX\; +\; Y\; +\; Z\; \sim \; B\; (\alpha \; +\; \beta ,\; \gamma )\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{X\; +\; Y\}\; \{X\; +\; Y\; +\; Z\}\}\; \backslash \; sim\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha\; +\; \backslash \; beta,\; \backslash \; gamma)\}$и $X\; +\; YX\; +\; Y\; +\; Z\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{X\; +\; Y\}\; \{X\; +\; Y\; +\; Z\}\}\}$не зависит от $XX\; +\; Y\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{X\}\; \{X\; +\; Y\}\}\}$. Это показывает, что произведение независимых $B\; (\alpha ,\; \beta )\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta)\}$и $B\; (\alpha \; +\; \beta ,\; \gamma )\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha\; +\; \backslash \; beta,\; \backslash \; gamma)\}$случайные величины - это a $B\; (\alpha ,\; \beta \; +\; \gamma )\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{B\}\; (\backslash \; alpha,\; \backslash \; beta\; +\; \backslash \; gamma)\}$случайная величина.

Кроме того, статистика k-го порядка из n равномерно распределенных переменных равна $B\; (k,\; n\; +\; 1\; -\; k)\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{B\; \}\; (k,\; n\; +\; 1-k)\}$, поэтому альтернативой, если α и β являются малыми целыми числами, является генерация α + β - 1 однородной переменной и выбор α-го наименьшего значения.

Другой способ создания бета-распределения - это модель урны Pólya. Согласно этому методу, один запуск с «урной» с использованием α «bl Отметьте« шары и β »белые шары и проведите равномерную розыгрыш с заменой. При каждой попытке добавлен дополнительный шар в соответствии с цветом последнего выпавшего шара.

Также можно использовать выбор с обратным преобразованием.

История

Карл Пирсон проанализировал бета- распределение как решение Тип I распределений Пирсона

Первое систематическое современное обсуждение бета-распределения, вероятно, связано с Карлом Пирсоном FRS (27 марта 1857 г. - 27 апреля 1936 г.), влиятельный англичанин математик, которому приписывают создание дисциплин математической. В статьях Пирсона бета-формула сформулировано как решениедифференциального уравнения: Распределение Пирсона типа I, обычное Полностью идентичен, за исключением произвольного сдвига и масштабирования (бета-распределения и распределения Пирсона типа I всегда можно выровнять путем правильного выбора параметров). Фактически, в нескольких английских книгах и журналах статьях за несколько десятилетий до Второй мировой войны было принято называть бета-распределением типа I Пирсона. Уильям П. Элдертон (1877–1962) в своей монографии 1906 года «Частотные кривые и корреляция» далее анализирует бета-распределение как распределение типа I Пирсона, включая полное обсуждение метода моментов для случая четырех параметров., и диаграммы (что Элдертон называет) U-образной, J-образной, скрученной J-образной формы, формы «треуголка», горизонтальных и наклонных прямых ящиков. Элдертон написал: «Я в основном в долгу перед профессором Пирсоном, но это такая задолженность, за которую невозможно выразить официальную благодарность». Элдертон в своей монографии 1906 года предоставляет впечатляющий объем информации о бета-распределении, включая уравнения для происхождения, распределения в качестве режима, а также для других распределений Пирсона: типов с I по VII. Элдертон также включил ряд приложений, включая одно («II») по бета- и гамма-функциям. В более поздних изданиях Элдертон добавил уравнения происхождения, определенных в качестве среднего, и анализ распределений Пирсона с VIII по XII.

Как отмечают Боуман и Шентон, «Фишер и Пирсон разошлись во мнениях относительно подхода к оценке (фактора), в частности, в отношении (метода Пирсона) моментов и (метода Фишера) максимальной вероятности в случае бета-распределения»., Согласно Боуману и Шентону, «случай, когда модель типа I (бета-распределение) оказалась в центре споров, было чистой случайностью». Рональд Фишер ( 17 февраля 1890 г. - 29 июля 1962 г.) был одним из гигантов статистики в первой половине 20-го века, и его давний публичный конфликт с Карлом Пирсоном можно проследить в некоторых статьях. Бета-распределения и критики Фишером метода моментов Пирсона как произвольного см. Статью Пирсона «Метод моментов и метод максимального правдоподобия» (опубликованная через три года после его выхода на пенсию из Университетского колледжа). разделена между Фишером и сыном Пирсона Эгоном), в котором Пирсон пишет: «Я читал (статья Кошая в Журнале Королевского статистического общества, 1933 г.), которая, насколько мне известно, является единственным случаем в настоящее время опубликовано о методе профессора Фишера. К моему удивлению, этот метод зависит от сначала расчета констант частоты кривой с помощью метода моментов, а затем наложения на них, что Фишер называет "методом правдоподобия" дальнейшее приближение для получения того, что он использует, он, таким образом, получит «более эффективные значения» констант кривой ».

Трактат Дэвида и Эдвардса по истории статистики цитирует первое современное рассмотрение бета-распределения в 1911 году с использованием обозначения бета, которое стало стандартным благодаря Коррадо Джини, итальянцу статистик, демограф и социолог, разработавшие коэффициент Джини. Н.Л.Джонсон и С.Коц в своей всеобъемлющей и очень информативной монографии о ведущих исторических личностях в статистических науках называют Коррадо Джини «ранним байесовским... который занимался проблемой выявления параметров начального бета-распределения, выделяя методы, которые предвосхитили появление так называемого эмпирического байесовского подхода ». Байес в посмертной статье, опубликованной в 1763 году Ричардом Прайсом, получил бета-распределение как плотность вероятности успеха в испытаниях Бернулли (см. Раздел «Приложения, байесовский вывод» "в этой статье), но в статье не анализируются какие-либо моменты бета-распределения и не обсуждаются какие-либо его свойства.

Ссылки

Внешние ссылки

Викискладе есть носители, связанные с Бета-распределением.

• «Бета-распределением» Фионой Маклахлан, Wolfram Demonstrations Project, 2007.
• Бета-распространение - Обзор и пример, xycoon.com
• Бета-распространение, brighton-webs.co.uk
• Видео о бета-распространении, exstrom.com
• , Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик У. «Бета-распределение». MathWorld.
• Статистика Гарвардского университета 110 Лекция 23 «Бета-распространение», профессор Джо Блитцштейн