Случайная величина

Переменная, представляющая случайное явление

В вероятности и статистике, случайная величина, случайная величина, случайная переменная или стохастическая переменная неформально описывается как переменная, значения которой зависят от результатов случайное явление. Формальная математическая обработка случайных величин - тема теории вероятностей. В этом контексте под случайной величиной понимается измеримая функция, определенная в вероятностном пространстве, которая отображает пространство выборки на действительные числа.

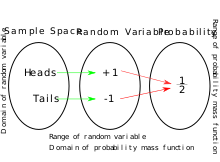
Этот график показывает, как случайная величина является функцией от всех возможных результатов до реальных значений. Он также показывает, как случайная величина используется для определения функций вероятности и массы.

Возможные значения случайной величины могут представлять возможные результаты еще не проведенного эксперимента или возможные результаты прошлого эксперимента, который уже существовал. значение является неопределенным (например, из-за неточных измерений или квантовой неопределенности ). Они также могут концептуально представлять либо результаты «объективно» случайного процесса (такого как бросание кубика), либо «субъективную» случайность, являющуюся результатом неполного знания величины. Значение вероятностей, приписываемых потенциальным значениям случайной величины, не является частью самой теории вероятностей, а вместо этого связано с философскими аргументами по интерпретации вероятности. Математика работает одинаково, независимо от конкретной интерпретации.

В качестве функции случайная величина должна быть измеримой, что позволяет назначать вероятности наборам ее потенциальных значений. Часто результаты зависят от некоторых физических переменных, которые нельзя предсказать. Например, при подбрасывании справедливой монеты конечный результат орла или решки зависит от неопределенных физических условий, поэтому наблюдаемый результат является неопределенным. Монета могла зацепиться за трещину в полу, но такая возможность исключается из рассмотрения.

область случайной величины называется пространством выборки. Он интерпретируется как набор возможных исходов случайного явления. Например, в случае подбрасывания монеты рассматриваются только два возможных исхода, а именно орел или решка.

Случайная величина имеет распределение вероятностей, которое определяет вероятность борелевских подмножеств ее диапазона. Случайные переменные могут быть дискретными, то есть принимать любое из указанного конечного или счетного списка значений (имеющего счетный диапазон), наделенного функцией вероятностной массы что характерно для распределения вероятностей случайной величины; или непрерывный, принимающий любое числовое значение в интервале или совокупности интервалов (имеющих неисчислимый диапазон) с помощью функции плотности вероятности, которая является характеристикой распределения вероятностей случайной величины; или их смесь.

Две случайные величины с одинаковым распределением вероятностей могут отличаться по своей связи или независимости от других случайных величин. Реализации случайной величины, то есть результаты случайного выбора значений в соответствии с функцией распределения вероятностей переменной, называются случайными переменными.

• 1 Определение
  • 1.1 Стандартный случай
  • 1.2 Расширения
• 2 Функции распределения
• 3 Примеры
  • 3.1 Дискретная случайная величина
    • 3.1.1 Бросок монеты
    • 3.1.2 Бросок кости
  • 3.2 Непрерывная случайная величина
  • 3.3 Смешанный тип
• 4 Теоретико-мерное определение
  • 4.1 Случайные величины с действительным знаком
• 5 Моменты
• 6 Функции случайных величин
  • 6.1 Пример 1
  • 6.2 Пример 2
  • 6.3 Пример 3
  • 6.4 Пример 4
• 7 Некоторые свойства
• 8 Эквивалентность случайных величин
  • 8.1 Равенство в распределении
  • 8.2 Почти гарантированное равенство
  • 8.3 Равенство
• 9 Сходимость
• 10 См. Также
• 11 Ссылки
  • 11.1 Встроенные ссылки
  • 11.2 Литература
• 12 Внешние ссылки

A случайная величина - это измеримая функция $X:\; \Omega \; \to \; E\; \{\backslash \; стиль\; отображения\; X\; \backslash \; двоеточие\; \backslash \; Omega\; \backslash \; to\; E\}$из набора возможных результатов $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$до измеримого пространства $E\; \{\backslash \; Displaystyle\; E\}$. Техническое аксиоматическое определение требует, чтобы $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$было пространством выборки тройки вероятностей $(\Omega ,\; F,\; P)\; \{\backslash \; displaystyle\; (\; \backslash \; Omega,\; \{\backslash \; mathcal\; \{F\}\},\; \backslash \; operatorname\; \{P\})\}$(см. Определение из теории меры). Случайная величина часто обозначается заглавными римскими буквами, например $X\; \{\backslash \; displaystyle\; X\}$, $Y\; \{\backslash \; displaystyle\; Y\}$, $Z\; \{\backslash \; displaystyle\; Z\}$, $T\; \{\; \backslash \; displaystyle\; T\}$.

Вероятность того, что $X\; \{\backslash \; displaystyle\; X\}$примет значение в измеримом наборе $S\; \subseteq \; E\; \{\backslash \; displaystyle\; S\; \backslash \; substeq\; E\}$записывается как

$P\; \; (X\; \in \; S)\; =\; P\; \; (\{\omega \; \in \; \Omega \; \mid \; X\; (\omega )\; \in \; S\})\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{P\}\; (X\; \backslash \; in\; S)\; =\; \backslash \; operatorname\; \{P\}\; (\backslash \; \{\backslash \; omega\; \backslash \; in\; \backslash \; Omega\; \backslash \; mid\; X\; (\backslash \; omega)\; \backslash \; in\; S\; \backslash \})\}$

Стандартный случай

Во многих случаях $X\; \{\backslash \; displaystyle\; X\}$имеет вещественное значение, т. Е. $E\; =\; R\; \{\backslash \; displaystyle\; E\; =\; \backslash \; mathbb\; \{R\}\}$. В некоторых контекстах термин случайный элемент (см. расширения) используется для обозначения случайной величины не этой формы.

Когда изображение (или диапазон) $X\; \{\backslash \; displaystyle\; X\}$является счетным, случайная величина называется дискретная случайная величина, и ее распределение является дискретным распределением вероятностей, то есть может быть описано с помощью функции массы вероятности, которая присваивает вероятность каждому значению в изображении $Х\; \{\backslash \; Displaystyle\; X\}$. Если изображение бесконечно бесконечно (обычно это интервал ), то $X\; \{\backslash \; displaystyle\; X\}$называется непрерывной случайной величиной . В частном случае, когда это абсолютно непрерывный, его распределение может быть описано с помощью функции плотности вероятности, которая присваивает вероятности интервалам; в частности, каждая отдельная точка обязательно должна иметь нулевую вероятность для абсолютно непрерывной случайной величины. Не все непрерывные случайные величины абсолютно непрерывны, распределение смеси является одним из таких контрпримеров; такие случайные величины не могут быть описаны плотностью вероятности или функцией массы вероятности.

Любая случайная величина может быть описана ее кумулятивной функцией распределения, которая описывает вероятность того, что случайная величина будет меньше или равна определенному значению.

Расширения

Термин «случайная величина» в статистике традиционно ограничивается случаем вещественных значений ($E\; =\; R\; \{\backslash \; displaystyle\; E\; =\; \backslash \; mathbb\; \{R\}\}$). В этом случае структура действительных чисел позволяет определять такие величины, как ожидаемое значение и дисперсия случайной величины, ее кумулятивная функция распределения, и моменты его распределения.

Однако приведенное выше определение действительно для любого измеримого пространства $E\; \{\backslash \; displaystyle\; E\}$значений. Таким образом, можно рассматривать случайные элементы других наборов $E\; \{\backslash \; displaystyle\; E\}$, например случайные логические значения, категориальные значения, сложными числа, векторы, матрицы, последовательности, деревья, наборы, фигур, коллекторы и функции. Затем можно конкретно указать случайную переменную типа type $E\; \{\backslash \; displaystyle\; E\}$или $E\; \{\backslash \; displaystyle\; E\}$-значная случайная величина.

Эта более общая концепция случайного элемента особенно полезна в таких дисциплинах, как теория графов, машинное обучение, естественный язык. обработка и другие области в дискретной математике и информатике, где часто интересуют моделирование случайных вариаций нечисловых структур данных. В некоторых случаях, тем не менее, удобно представлять каждый элемент $E\; \{\backslash \; displaystyle\; E\}$, используя одно или несколько действительных чисел. В этом случае случайный элемент может дополнительно быть представлен как вектор вещественных случайных величин (все они определены в одном и том же базовом вероятностном пространстве $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$, что позволяет различным случайным величинам коварировать ). Например:

• Случайное слово может быть представлено как случайное целое число, которое служит индексом в словаре возможных слов. В качестве альтернативы его можно представить как случайный индикаторный вектор, длина которого равна размеру словаря, где единственными значениями положительной вероятности являются $(1\; 0\; 0\; 0\; \cdots )\; \{\backslash \; displaystyle\; (1\; \backslash \; 0\; \backslash \; 0\; \backslash \; 0\; \backslash \; \backslash \; cdots)\}$, $(0\; 1\; 0\; 0\; \cdots )\; \{\backslash \; displaystyle\; (0\; \backslash \; 1\; \backslash \; 0\; \backslash \; 0\; \backslash \; \backslash \; cdots)\}$, $(0\; 0\; 1\; 0\; \cdots )\; \{\backslash \; displaystyle\; (0\; \backslash \; 0\; \backslash \; 1\; \backslash \; 0\; \backslash \; \backslash \; cdots)\}$, а позиция 1 указывает слово.
• Случайное предложение заданной длины $N\; \{\backslash \; displaystyle\; N\}$может быть представлен как вектор из $N\; \{\backslash \; displaystyle\; N\}$случайных слов.
• A случайный граф на $N\; \{\backslash \; displaystyle\; N\}$заданном вершины могут быть представлены как матрица случайных величин $N\; \times \; N\; \{\backslash \; displaystyle\; N\; \backslash \; times\; N\}$, значения которой задают матрицу смежности случайного графа.
• A случайная функция $F\; \{\backslash \; displaystyle\; F\}$может быть представлена ​​как набор случайных величин $F\; (x)\; \{\backslash \; displaystyle\; F\; (x)\}$, задавая значения функции при различных s указывает $x\; \{\backslash \; displaystyle\; x\}$в области определения функции. $F\; (x)\; \{\backslash \; displaystyle\; F\; (x)\}$- обычные случайные величины с действительным знаком при условии, что функция является действительной. Например, случайный процесс является случайной функцией времени, случайный вектор - случайной функцией некоторого набора индексов, например $1,\; 2,\dots ,\; n\; \{\backslash \; displaystyle\; 1,2,\; \backslash \; ldots,\; n\}$и random field представляет собой случайную функцию для любого набора (обычно времени, пространства или дискретного набора).

Если случайная величина $X:\; \Omega \; \to \; R\; \{\backslash \; displaystyle\; X\; \backslash \; двоеточие\; \backslash \; Omega\; \backslash \; to\; \backslash \; mathbb\; \{R\}\}$определена в вероятностном пространстве $(\Omega ,\; F,\; P)\; \{\backslash \; displaystyle\; (\backslash \; Omega,\; \{\backslash \; mathcal\; \{F\}\},\; \backslash \; operatorname\; \{P\})\}$задано, мы можем задать такие вопросы, как "Насколько вероятно, что значение $X\; \{\backslash \; displaystyle\; X\}$равно 2? ". Это то же самое, что вероятность события $\{\omega :\; X\; (\omega )\; =\; 2\}\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; omega:\; X\; (\backslash \; omega)\; =\; 2\; \backslash \}\; \backslash ,\; \backslash !\}$, которое часто записывается как $P\; (X\; =\; 2)\; \{\backslash \; displaystyle\; P\; (X\; =\; 2)\; \backslash ,\; \backslash !\}$или $p\; X\; (2)\; \{\backslash \; displaystyle\; p\_\; \{X\; \}\; (2)\}$для краткости.

Запись всех этих вероятностей выходных диапазонов действительной случайной величины $X\; \{\backslash \; displaystyle\; X\}$дает распределение вероятностей для $X\; \{\backslash \; Displaystyle\; X\}$. Распределение вероятностей "забывает" о конкретном вероятностном пространстве, используемом для определения $X\; \{\backslash \; displaystyle\; X\}$, и записывает только вероятности различных значений $X\; \{\backslash \; displaystyle\; X\}$. Такое распределение вероятностей всегда можно уловить с помощью его кумулятивной функции распределения

$FX\; (x)\; =\; P\; \; (X\; \le \; x)\; \{\backslash \; displaystyle\; F\_\; \{X\}\; (x)\; =\; \backslash \; operatorname\; \{P\}\; (X\; \backslash \; leq\; x)\}$

, а также иногда с использованием функции плотности вероятности, $p\; X\; \{\backslash \; displaystyle\; p\_\; \{X\}\}$. В терминах теории меры мы используем случайную величину $X\; \{\backslash \; displaystyle\; X\}$, чтобы «продвинуть» меру $P\; \{\backslash \; displaystyle\; P\}$на $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$до меры $p\; X\; \{\backslash \; displaystyle\; p\_\; \{X\}\}$на $R\; \{\; \backslash \; Displaystyle\; \backslash \; mathbb\; \{R\}\}$. Базовое вероятностное пространство $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$- это техническое устройство, используемое для гарантии существования случайных величин, иногда для их построения, и для определения таких понятий, как корреляция и зависимость. или независимость на основе совместного распределения двух или более случайных величин в одном вероятностном пространстве. На практике часто пространство $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$полностью удаляется и просто ставится мера на $R\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\}$, который присваивает меру 1 всей действительной прямой, т. е. работает с распределениями вероятностей вместо случайных величин. См. Статью о функциях квантилей для более полной разработки.

Дискретная случайная величина

В эксперименте человек может быть выбран случайным образом, и одной случайной величиной может быть рост человека. Математически случайная величина интерпретируется как функция, которая сопоставляет человека с ростом человека. Со случайной величиной связано распределение вероятностей, которое позволяет вычислить вероятность того, что высота находится в любом подмножестве возможных значений, таких как вероятность того, что высота составляет от 180 до 190 см, или вероятность того, что высота либо меньше более 150 или более 200 см.

Другой случайной величиной может быть количество детей человека; это дискретная случайная величина с неотрицательными целыми числами. Он позволяет вычислять вероятности для отдельных целочисленных значений - функции массы вероятности (PMF) - или для наборов значений, включая бесконечные наборы. Например, интересующим событием может быть «четное количество детей». Как для конечных, так и для бесконечных наборов событий их вероятности могут быть найдены путем сложения PMF элементов; то есть вероятность четного числа детей равна бесконечной сумме $PMF\; \; (0)\; +\; PMF\; \; (2)\; +\; PMF\; \; (4)\; +\; \cdots \; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{PMF\}\; (0)\; +\; \backslash \; operatorname\; \{PMF\}\; (2)\; +\; \backslash \; operatorname\; \{PMF\}\; (4)\; +\; \backslash \; cdots\}$.

В таких примерах, как эти, пространство выборки часто подавляется, так как это математически сложно описать, а возможные значения случайных величин затем рассматриваются как пространство выборки. Но когда две случайные величины измеряются в одном и том же пространстве выборки результатов, например, рост и количество детей, вычисляемых для одних и тех же случайных людей, легче отслеживать их взаимосвязь, если признается, что приходят и рост, и количество детей. от одного и того же случайного человека, например, чтобы можно было задать вопросы о том, коррелированы ли такие случайные величины или нет.

Если $\{an\},\; \{bn\}\; \{\backslash \; textstyle\; \backslash \; \{a\_\; \{n\}\; \backslash \},\; \backslash \; \{b\_\; \{n\}\; \backslash \}\}$- счетные наборы действительных чисел, $bn>0\; \{\backslash \; textstyle\; b\_\; \{n\}>0\}$и $\sum \; nbn\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{n\}\; b\_\; \{n\}\; =\; 1\}$, затем $F\; =\; \sum \; nbn\; \delta \; an\; \{\backslash \; displaystyle\; F\; =\; \backslash \; sum\; \_\; \{n\}\; b\_\; \{n\}\; \backslash \; delta\; \_\; \{a\_\; \{n\}\}\}$- дискретная функция распределения. Здесь $\delta \; t\; (Икс)\; знак\; равно\; 0\; \{\backslash \; displaystyle\; \backslash \; delta\; \_\; \{t\}\; (x)\; =\; 0\}$для , $\delta \; t\; (x)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; delta\; \_\; \{t\}\; (x)\; =\; 1\}$для $x\; \ge \; t\; \{\backslash \; displaystyle\; x\; \backslash \; geq\; t\}$. Возьмем, например, перечисление всех рациональных чисел как $\{an\}\; \{\backslash \; displaystyle\; \backslash \; \{a\_\; \{n\}\; \backslash \}\}$, получается дискретная функция распределения, которая не является ступенчатой ​​функцией или кусочной константой.

Подбрасывание монеты

Возможные результаты для одного подбрасывание монеты можно описать пробелом $\Omega \; =\; \{\; орла,\; решка\}\; \{\backslash \; displaystyle\; \backslash \; Omega\; =\; \backslash \; \{\{\backslash \; text\; \{head\}\},\; \{\backslash \; text\; \{tails\}\}\; \backslash \}\}$. Мы можем ввести случайную величину с действительным знаком $Y\; \{\backslash \; displaystyle\; Y\}$, которая моделирует выплату в 1 доллар за успешную ставку на решку следующим образом:

$Y\; (\omega )\; =\; \{1,\; если\; \omega \; =\; орла,\; 0,\; если\; \omega \; =\; решка.\; \{\backslash \; displaystyle\; Y\; (\backslash \; omega)\; =\; \{\backslash \; begin\; \{case\}\; 1,\; \{\backslash \; text\; \{if\}\}\; \backslash \; omega\; =\; \{\backslash \; text\; \{head\}\},\; \backslash \backslash \; [6pt]\; 0,\; \{\backslash \; text\; \{if\}\; \}\; \backslash \; omega\; =\; \{\backslash \; text\; \{tails\}\}.\; \backslash \; end\; \{cases\}\}\}$

Если монета является честной монетой, Y имеет функцию массы вероятности $е\; Y\; \{\backslash \; displaystyle\; f\_\; \{Y\}\}$определяется выражением:

$f\; Y\; (y)\; =\; \{1\; 2,\; если\; y\; =\; 1,\; 1\; 2,\; если\; y\; =\; 0,\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; \{\backslash \; begin\; \{cases\}\; \{\backslash \; tfrac\; \{1\}\; \{2\}\},\; \{\backslash \; text\; \{if\}\}\; y\; =\; 1,\; \backslash \backslash \; [6pt]\; \{\backslash \; tfrac\; \{1\}\; \{2\}\; \},\; \{\backslash \; text\; \{if\}\}\; y\; =\; 0,\; \backslash \; end\; \{cases\}\}\}$

Бросок кубиков

Если пробел представляет собой набор возможных чисел, брошенных на двух кубиках, и интересующая случайная величина представляет собой сумму S чисел на двух игральных костях, тогда S представляет собой дискретную случайную величину, распределение которой описывается функцией массы вероятности , построенной здесь как высота столбцов изображения.

Случайная величина может также может использоваться для описания процесса бросания игральных костей и возможных результатов. Наиболее очевидное представление для случая двух игральных костей - взять набор пар чисел n 1 и n 2 из {1, 2, 3, 4, 5, 6} (представляющие числа на двух кубиках) как пробел. Общее количество выпавших чисел (сумма чисел в каждой паре) тогда является случайной величиной X, заданной функцией, которая преобразует пару в сумму:

$X\; ((n\; 1,\; n\; 2))\; =\; n\; 1\; +\; n\; 2\; \{\backslash \; displaystyle\; X\; ((n\_\; \{1\},\; n\_\; \{2\}))\; =\; n\_\; \{1\}\; +\; n\_\; \{2\}\}$

и (если кости справедливые ) имеет вероятностную массу функция ƒ X определяется как:

$f\; X\; (S)\; =\; min\; (S\; -\; 1,\; 13\; -\; S)\; 36,\; для\; S\; \in \; \{2,\; 3,\; 4,\; 5,\; 6,\; 7,\; 8,\; 9,\; 10,\; 11,\; 12\}\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (S)\; =\; \{\backslash \; frac\; \{\backslash \; min\; (S-1,13-S)\}\; \{36\}\},\; \{\backslash \; text\; \{for\}\}\; S\; \backslash \; in\; \backslash \; \{2,3,4,5,6,7,8,9,10,11,12\; \backslash \}\}$

Непрерывная случайная величина

Формально непрерывная случайная величина - это случайная величина, чья кумулятивная функция распределения везде непрерывна. Нет «пробелов », которые соответствовали бы числам, которые имеют конечную вероятность появления. Вместо этого непрерывные случайные величины почти никогда не принимают точно заданное значение c (формально $\forall \; c\; \in \; R:\; Pr\; (X\; =\; c)\; =\; 0\; \{\backslash \; textstyle\; \backslash \; forall\; c\; \backslash \; in\; \backslash \; mathbb\; \{R\; \}:\; \backslash ;\; \backslash \; Pr\; (X\; =\; c)\; =\; 0\}$), но существует положительная вероятность того, что его значение будет лежать в определенных интервалах, которые могут быть сколь угодно малыми. Непрерывные случайные величины обычно допускают функции плотности вероятности (PDF), которые характеризуют их CDF и меры вероятности ; такие распределения также называются абсолютно непрерывными ; но некоторые непрерывные распределения являются сингулярным или сочетанием абсолютно непрерывной части и особой части.

Примером непрерывной случайной величины может служить счетчик, который может выбирать горизонтальное направление. Тогда значения, принимаемые случайной величиной, являются направлениями. Мы могли бы представить эти направления в виде севера, запада, востока, юга, юго-востока и т. Д. Однако обычно удобнее сопоставить пространство выборки со случайной величиной, которая принимает значения, которые являются действительными числами. Это можно сделать, например, сопоставив направление с пеленгом в градусах по часовой стрелке от севера. Затем случайная переменная принимает значения, которые являются действительными числами из интервала [0, 360), причем все части диапазона «равновероятны». В этом случае X = угол поворота. Любое действительное число имеет нулевую вероятность быть выбранным, но положительная вероятность может быть присвоена любому диапазону значений. Например, вероятность выбора числа в [0, 180] составляет ⁄ 2. Вместо того чтобы говорить о функции массы вероятности, мы говорим, что плотность вероятности X равна 1/360. Вероятность подмножества [0, 360) может быть вычислена путем умножения меры набора на 1/360. В общем, вероятность набора для данной непрерывной случайной величины может быть вычислена путем интегрирования плотности по данному набору.

Более формально, для любого интервала $I\; =\; [a,\; b]\; =\; \{x\; \in \; R:\; a\; \le \; x\; \le \; b\}\; \{\backslash \; textstyle\; I\; =\; [a,\; b]\; =\; \backslash \; \{x\; \backslash \; in\; \backslash \; mathbb\; \{R\}:\; a\; \backslash \; leq\; x\; \backslash \; leq\; b\; \backslash \}\}$, случайная величина $XI\; \sim \; U\; \; (I)\; =\; U\; \; [a,\; b]\; \{\backslash \; displaystyle\; X\_\; \{I\}\; \backslash \; sim\; \backslash \; operatorname\; \{U\}\; (I)\; =\; \backslash \; operatorname\; \{U\}\; [a,\; b]\}$называется «непрерывной однородной случайной величиной» (CURV), если вероятность того, что он принимает значение в подынтервале , зависит только от длины подынтервала. Это означает, что вероятность того, что $XI\; \{\backslash \; displaystyle\; X\_\; \{I\}\}$попадет в любой подинтервал $[c,\; d]\; \subseteq \; [a,\; b]\; \{\backslash \; displaystyle\; [c,\; d]\; \backslash \; substeq\; [a,\; b]\}$пропорционально длине подынтервала, то есть, если a ≤ c ≤ d ≤ b, у него

$Pr\; (XI\; \in \; [c,\; d])\; =\; d\; -\; cb\; -\; a\; Pr\; (XI\; \in \; I)\; =\; d\; -\; cb\; -\; a\; \{\backslash \; displaystyle\; \backslash \; Pr\; \backslash \; left\; (X\_\; \{I\}\; \backslash \; in\; [c,\; d]\; \backslash \; right)\; =\; \{\backslash \; frac\; \{dc\}\; \{ba\}\}\; \backslash \; Pr\; \backslash \; left\; (X\_\; \{I\}\; \backslash \; in\; I\; \backslash \; right)\; =\; \{\backslash \; frac\; \{dc\}\; \{ba\}\}\}$

где последнее равенство является результатом аксиома унитарности вероятности. Дается функция плотности вероятности кривой $X\; \sim \; U\; \; [a,\; b]\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{U\}\; [a,\; b]\}$индикаторной функцией своего интервала поддержки, нормированного на длину интервала:

$f\; X\; (x)\; =\; \{1\; b\; -\; a,\; a\; \le \; x\; \le \; b\; 0,\; в\; противном\; случае.\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; begin\; \{case\}\; \backslash \; displaystyle\; \{1\; \backslash \; over\; ba\},\; a\; \backslash \; leq\; x\; \backslash \; leq\; b\; \backslash \backslash \; 0,\; \{\backslash \; text\; \{else\}\}.\; \backslash \; end\; \{case\; \}\}\}$Особый интерес представляет равномерное распределение на единичном интервале $[0,\; 1]\; \{\backslash \; displaystyle\; [0,1]\}$. Образцы любого желаемого распределения вероятностей $D\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{D\}\}$могут быть созданы путем вычисления функции квантиля для $D\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{D\}\}$на случайно сгенерированном числе, равномерно распределенном на единичном интервале. При этом используются свойства кумулятивных функций распределения, которые являются объединяющей структурой для всех случайных величин.

Смешанный тип

A смешанная случайная величина - это случайная величина, кумулятивная функция распределения которой не является ни кусочно-постоянной (дискретная случайная величина), ни везде -непрерывный. Его можно реализовать как сумму дискретной случайной величины и непрерывной случайной величины; в этом случае CDF будет средневзвешенным значением CDF компонентных переменных.

Пример случайной переменной смешанного типа будет основан на эксперименте, в котором подбрасывается монета и вертушка вращается только в том случае, если в результате подбрасывания монеты выпали решки. Если результат - решка, X = -1; в противном случае X = значение счетчика, как в предыдущем примере. Существует вероятность ⁄ 2 того, что эта случайная величина будет иметь значение -1. Другие диапазоны значений будут иметь половину вероятностей последнего примера.

В большинстве случаев каждое распределение вероятностей на действительной прямой представляет собой смесь дискретной части, единственной части и абсолютно непрерывной части; см. теорему Лебега о разложении § Уточнение. Дискретная часть сосредоточена на счетном множестве, но это множество может быть плотным (как множество всех рациональных чисел).

Наиболее формальное, аксиоматическое определение случайной величины связано с теорией меры. Непрерывные случайные переменные определяются с помощью наборов чисел, а также функций, которые отображают такие наборы на вероятности. Из-за различных трудностей (например, парадокса Банаха – Тарского ), которые возникают, если такие множества недостаточно ограничены, необходимо ввести так называемую сигма-алгебру для ограничения возможных множеств. по которым могут быть определены вероятности. Обычно используется такая особая сигма-алгебра, борелевская σ-алгебра, которая позволяет определять вероятности для любых наборов, которые могут быть получены либо непосредственно из непрерывных интервалов чисел, либо с помощью конечного или счетно бесконечное число объединений и / или пересечений таких интервалов.

Теоретико-мерное определение выглядит следующим образом.

Пусть $(\Omega ,\; F,\; P)\; \{\backslash \; displaystyle\; (\backslash \; Omega,\; \{\backslash \; mathcal\; \{F\}\},\; P)\}$будет вероятностным пространством и $(E,\; E)\; \{\backslash \; displaystyle\; (E,\; \{\backslash \; mathcal\; \{E\}\})\}$a измеримое пространство. Тогда $(E,\; E)\; \{\backslash \; displaystyle\; (E,\; \{\backslash \; mathcal\; \{E\}\})\}$-значная случайная величина является измеримой функцией $X:\; \Omega \; \to \; E\; \{\backslash \; displaystyle\; X\; \backslash \; двоеточие\; \backslash \; Omega\; \backslash \; to\; E\}$, что означает, что для каждого подмножества $B\; \in \; E\; \{\backslash \; displaystyle\; B\; \backslash \; in\; \{\backslash \; mathcal\; \{E\}\}\}$, его прообраз $X\; -\; 1\; (B)\; \in \; F\; \{\backslash \; displaystyle\; X\; ^\; \{-\; 1\}\; (B)\; \backslash \; in\; \{\backslash \; mathcal\; \{F\}\}\}$где $X\; -\; 1\; (B)\; =\; \{\omega :\; X\; (\omega )\; \in \; B\}\; \{\backslash \; displaystyle\; X\; ^\; \{-\; 1\}\; (B)\; =\; \backslash \; \{\backslash \; omega:\; X\; (\backslash \; omega)\; \backslash \; in\; B\; \backslash \}\}$. Это определение позволяет нам измерить любое подмножество $B\; \in \; E\; \{\backslash \; displaystyle\; B\; \backslash \; in\; \{\backslash \; mathcal\; \{E\}\}\}$в целевом пространстве, глядя на его прообраз, который по предположению измерим.

В более интуитивных терминах член $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$является возможным результатом, членом $F\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{F\; \}\}\}$- измеримое подмножество возможных результатов, функция $P\; \{\backslash \; displaystyle\; P\}$дает вероятность каждого такого измеримого подмножества, $E\; \{\backslash \; displaystyle\; E\}$представляет набор значений, которые может принимать случайная величина (например, набор действительных чисел), и член $E\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\}$- это «хорошо управляемое» (измеримое) подмножество $E\; \{\backslash \; displaystyle\; E\}$(тех, для которых может быть определена вероятность). Тогда случайная величина представляет собой функцию от любого результата к количеству, так что результаты, ведущие к любому полезному подмножеству величин для случайной величины, имеют четко определенную вероятность.

Когда $E\; \{\backslash \; displaystyle\; E\}$является топологическим пространством, тогда наиболее распространенным выбором является σ-алгебра $E\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{E\}\}\}$- это борелевская σ-алгебра $B\; (E)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{B\}\}\; (\; E)\}$, которая представляет собой σ-алгебру, сгенерированную совокупностью всех открытых множеств в $E\; \{\backslash \; displaystyle\; E\}$. В таком случае случайная величина со значением $(E,\; E)\; \{\backslash \; displaystyle\; (E,\; \{\backslash \; mathcal\; \{E\}\})\}$называется $E\; \{\backslash \; displaystyle\; E\}$-значная случайная величина . Более того, когда пробел $E\; \{\backslash \; displaystyle\; E\}$является действительной линией $R\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\}$, тогда такой вещественный случайная величина называется просто случайной величиной .

случайными величинами с действительными значениями

В этом случае пространство наблюдения - это набор действительных чисел. Напомним, $(\Omega ,\; F,\; P)\; \{\backslash \; displaystyle\; (\backslash \; Omega,\; \{\backslash \; mathcal\; \{F\}\},\; P)\}$- это вероятностное пространство. Для реального пространства наблюдения функция $X:\; \Omega \; \to \; R\; \{\backslash \; displaystyle\; X\; \backslash \; двоеточие\; \backslash \; Omega\; \backslash \; rightarrow\; \backslash \; mathbb\; \{R\}\}$является случайной величиной с действительным знаком, если

$\{\; \omega :\; X\; (\omega )\; \le \; r\}\; \in \; F\; \forall \; r\; \in \; R.\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; omega:\; X\; (\backslash \; omega)\; \backslash \; leq\; r\; \backslash \}\; \backslash \; in\; \{\backslash \; mathcal\; \{F\}\}\; \backslash \; qquad\; \backslash \; forall\; r\; \backslash \; in\; \backslash \; mathbb\; \{R\}.\}$

Это определение является частным случаем из вышеперечисленного, поскольку набор $\{(-\; \infty ,\; r]:\; r\; \in \; R\}\; \{\backslash \; displaystyle\; \backslash \; \{(-\; \backslash \; infty,\; r]:\; r\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; \backslash \}\}$порождает борелевскую σ-алгебру на множестве действительных чисел, и достаточно проверить измеримость на любом порождающем множестве. Здесь мы можем доказать измеримость на этом порождающем множестве, используя тот факт, что $\{\omega :\; X\; (\omega )\; \le \; г\}\; знак\; равно\; Икс\; -\; 1\; ((-\; \infty ,\; r])\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; omega:\; X\; (\backslash \; omega)\; \backslash \; leq\; r\; \backslash \}\; =\; X\; ^\; \{-\; 1\}\; ((-\; \backslash \; infty,\; r])\}$.

Распределение вероятностей случайной величины часто характеризуется небольшим количеством параметров, которые также имеют практическую интерпретацию.Например, часто достаточно знать, каково ее «среднее значение». Это зафиксировано математической концепцией ожидаемого значения случайной величины, обозначаемой $E\; \; [X]\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [X]\}$, и также называется первый момент. В общем, $E\; \; [f\; (X)]\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [f\; (X)]\}$не равно $f\; (E\; \; [X])\; \{\backslash \; displaystyle\; f\; (\backslash \; operatorname\; \{E\}\; [X])\}$. Как только "среднее значение" известно, можно спросить, насколько далеко от этого среднего значения обычно находятся значения $X\; \{\backslash \; displaystyle\; X\}$, вопрос, на который отвечает дисперсия и стандартное отклонение случайной величины. $E\; \; [X]\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [X]\}$можно интуитивно рассматривать как среднее значение, полученное из бесконечной совокупности, члены которой являются частными оценками $X\; \{\backslash \; displaystyle\; X\}$.

Математически это известно как (обобщенная) проблема моментов : для данного класса случайных величин $X\; \{\backslash \; displaystyle\; X\}$найдите коллекцию $\{fi\}\; \{\backslash \; displaystyle\; \backslash \; \{f\_\; \{i\}\; \backslash \}\}$таких функций, что ожидаемые значения $E\; \; [fi\; (X)]\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [f\_\; \{i\}\; (X)]\}$полностью охарактеризовать распределение случайной величины $X\; \{\backslash \; displaystyle\; X\}$.

Моменты могут только быть определенным для действительных функций от случайных величин (или комплексных значений и т. д.). Если случайная величина сама имеет действительное значение, то могут быть взяты моменты самой переменной, которые эквивалентны моментам тождественной функции $f\; (X)\; =\; X\; \{\backslash \; displaystyle\; f\; (X)\; =\; X\}$случайной величины. Однако даже для случайных величин с ненастоящими значениями могут быть взяты моменты действительных функций этих переменных. Например, для категориальной случайной величины X, которая может принимать номинальные значения «красный», «синий» или «зеленый», функция с действительным знаком $[X\; =\; зеленый]\; \{\backslash \; displaystyle\; [X\; =\; \{\backslash \; text\; \{green\}\}]\}$можно построить; здесь используется скобка Айверсона, и он имеет значение 1, если $X\; \{\backslash \; displaystyle\; X\}$имеет значение «зеленый», в противном случае - 0. Затем можно определить ожидаемое значение и другие моменты этой функции.

Новая случайная величина Y может быть определена с помощью применения действительной измеримой по Борелю функции $g:\; R\; \to \; R\; \{\backslash \; displaystyle\; g\; \backslash \; двоеточие\; \backslash \; mathbb\; \{R\}\; \backslash \; rightarrow\; \backslash \; mathbb\; \{R\}\}$к результатам вещественной случайной величины $X\; \{\backslash \; displaystyle\; X\; \}$. То есть $Y\; =\; g\; (X)\; \{\backslash \; displaystyle\; Y\; =\; g\; (X)\}$. кумулятивная функция распределения для $Y\; \{\backslash \; displaystyle\; Y\}$тогда равна

$F\; Y\; (y)\; =\; P\; \; (g\; (X)\; \le \; y).\; \{\backslash \; displaystyle\; F\_\; \{Y\}\; (y)\; =\; \backslash \; operatorname\; \{P\}\; (g\; (X)\; \backslash \; leq\; y).\}$

Если функция $g\; \{\backslash \; displaystyle\; g\}$обратима ( т.е. существует $h\; =\; g\; -\; 1\; \{\backslash \; displaystyle\; h\; =\; g\; ^\; \{-\; 1\}\}$, где $h\; \{\backslash \; displaystyle\; h\}$равно $g\; \{\backslash \; displaystyle\; g\}$'s обратная функция ) и либо увеличивается, либо уменьшается, тогда предыдущее отношение может быть расширено для получения

$FY\; (\; y)\; =\; P\; \; (g\; (X)\; \le \; y)\; =\; \{P\; \; (X\; \le \; h\; (y))\; =\; FX\; (h\; (y)),\; если\; h\; =\; g\; -\; 1\; возрастает,\; P\; \; (X\; \ge \; h\; (y))\; =\; 1\; -\; FX\; (h\; (y)),\; если\; h\; =\; g\; -\; 1\; убывает.\; \{\backslash \; displaystyle\; F\_\; \{Y\}\; (y)\; =\; \backslash \; operatorname\; \{P\}\; (g\; (X)\; \backslash \; leq\; y)\; =\; \{\backslash \; begin\; \{cases\}\; \backslash \; operatorname\; \{P\}\; (X\; \backslash \; leq\; h\; (y))\; =\; F\_\; \{X\; \}\; (h\; (y)),\; \{\backslash \; text\; \{if\}\}\; h\; =\; g\; ^\; \{-\; 1\}\; \{\backslash \; text\; \{возрастание\}\},\; \backslash \backslash \backslash \backslash \backslash \; имя\; оператора\; \{P\}\; (X\; \backslash \; geq\; h\; (y))\; =\; 1-F\_\; \{X\}\; (h\; (y)),\; \{\backslash \; text\; \{if\}\}\; h\; =\; g\; ^\; \{-\; 1\}\; \{\backslash \; text\; \{уменьшение\}\}.\; \backslash \; End\; \{cases\}\}\}$

С помощью те же гипотезы обратимости $g\; \{\backslash \; displaystyle\; g\}$, предполагая также дифференцируемость, связь между функциями плотности вероятности может быть найдена путем дифференцирования обоих стороны приведенного выше выражения по отношению к $y\; \{\backslash \; displaystyle\; y\}$, чтобы получить

$f\; Y\; (y)\; =\; f\; X\; (h\; (y))\; |\; d\; h\; (y)\; d\; y\; |.\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; f\_\; \{X\}\; \{\backslash \; bigl\; (\}\; h\; (y)\; \{\backslash \; bigr)\}\; \backslash \; left\; |\; \{\backslash \; frac\; \{dh\; (y)\}\; \{dy\}\}\; \backslash \; right\; |.\}$

Если нет обратимости $g\; \{\backslash \; displaystyle\; g\}$, но каждый $y\; \{\backslash \; displaystyle\; y\}$допускает не более чем счетное количество корней ( то есть конечное или счетное бесконечное число $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$таких, что $y\; =\; g\; (xi)\; \{\backslash \; displaystyle\; y\; =\; g\; (x\_\; \{i\; \})\}$), то предыдущая связь между функциями плотности вероятности может быть обобщена с помощью

$f\; Y\; (y)\; =\; \sum ,\; если\; X\; (gi\; -\; 1\; (y))\; |\; d\; g\; i\; -\; 1\; (y)\; d\; y\; |\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; \backslash \; sum\; \_\; \{i\}\; f\_\; \{X\}\; (g\_\; \{i\}\; ^\; \{-\; 1\}\; (y))\; \backslash \; left\; |\; \{\backslash \; frac\; \{dg\_\; \{i\}\; ^\; \{-\; 1\; \}\; (y)\}\; \{dy\}\}\; \backslash \; right\; |\}$

где $xi\; =\; gi\; -\; 1\; (y)\; \{\backslash \; displaystyle\; x\_\; \{i\}\; =\; g\_\; \{i\}\; ^\; \{-\; 1\}\; (y)\}$, согласно теореме об обратной функции. Формулы для плотностей не требуют увеличения $g\; \{\backslash \; displaystyle\; g\}$.

В теории измерения, аксиоматический подход к вероятности, если случайная величина $X\; \{\backslash \; displaystyle\; X\}$на $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$и измеримая функция по Борелю $g:\; R\; \to \; R\; \{\backslash \; displaystyle\; g\; \backslash \; двоеточие\; \backslash \; mathbb\; \{R\}\; \backslash \; rightarrow\; \backslash \; mathbb\; \{R\}\}$, тогда $Y\; =\; g\; (X)\; \{\backslash \; displaystyle\; Y\; =\; g\; (X)\}$также является случайной величиной на $\Omega \; \{\backslash \; displaystyle\; \backslash \; Omega\}$, поскольку композиция измеримых функций также измерима. (Однако это не обязательно верно, если $g\; \{\backslash \; displaystyle\; g\}$измеримо по Лебегу.) Та же процедура, которая позволила выйти из вероятностного пространства $(\Omega ,\; P)\; \{\backslash \; displaystyle\; (\backslash \; Omega,\; P)\}$до $(R,\; d\; FX)\; \{\backslash \; displaystyle\; (\backslash \; mathbb\; \{R\},\; dF\_\; \{X\})\}$можно использовать для получения распределения $Y\; \{\backslash \; displaystyle\; Y\}$.

Пример 1

Пусть $X\; \{\backslash \; displaystyle\; X\}$будет действительным -значная, непрерывная случайная величина и пусть $Y\; =\; X\; 2\; \{\backslash \; displaystyle\; Y\; =\; X\; ^\; \{2\}\}$.

$FY\; (y)\; =\; P\; \; (X\; 2\; \le \; y).\; \{\backslash \; displaystyle\; F\_\; \{Y\}\; (y)\; =\; \backslash \; operatorname\; \{P\}\; (X\; ^\; \{2\}\; \backslash \; leq\; y).\}$

Если , то $P\; (X\; 2\; \le \; y)\; =\; 0\; \{\; \backslash \; displaystyle\; P\; (X\; ^\; \{2\}\; \backslash \; leq\; y)\; =\; 0\}$, поэтому

If $y\; \ge \; 0\; \{\backslash \; displaystyle\; y\; \backslash \; geq\; 0\}$, тогда

$P\; \; (X\; 2\; \le \; y)\; =\; P\; \; (|\; X\; |\; \le \; y)\; =\; P\; \; (-\; y\; \le \; X\; \le \; y),\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{\; P\}\; (X\; ^\; \{2\}\; \backslash \; leq\; y)\; =\; \backslash \; operatorname\; \{P\}\; (|\; X\; |\; \backslash \; leq\; \{\backslash \; sqrt\; \{y\}\})\; =\; \backslash \; operatorname\; \{P\}\; (-\; \{\backslash \; sqrt\; \{y\}\}\; \backslash \; leq\; X\; \backslash \; leq\; \{\backslash \; sqrt\; \{y\}\}),\}$

поэтому

$FY\; (y)\; =\; FX\; (y)\; -\; FX\; (-\; y),\; если\; y\; \ge \; 0.\; \{\backslash \; displaystyle\; F\_\; \{Y\}\; (y)\; =\; F\_\; \{X\}\; (\{\backslash \; sqrt\; \{y\}\})\; -\; F\_\; \{X\}\; (-\; \{\backslash \; sqrt\; \{y\}\})\; \backslash \; qquad\; \{\backslash \; hbox\; \{if\}\}\; \backslash \; quad\; y\; \backslash \; geq\; 0.\}$

Пример 2

Предположим, $X\; \{\backslash \; displaystyle\; X\}$- случайная величина с кумулятивным распределением

$FX\; (x)\; =\; P\; (X\; \le \; x)\; =\; 1\; (1\; +\; e\; -\; х)\; \theta \; \{\backslash \; displaystyle\; F\_\; \{X\}\; (x)\; =\; P\; (X\; \backslash \; leq\; x)\; =\; \{\backslash \; frac\; \{1\}\; \{(1\; +\; e\; ^\; \{-\; x\})\; ^\; \{\backslash \; theta\}\}\}\}$

где $\theta >0\; \{\backslash \; displaystyle\; \backslash \; theta>0\}$- фиксированный параметр. Рассмотрим случайную величину $Y\; =\; l\; o\; g\; (1\; +\; e\; -\; X).\; \{\backslash \; displaystyle\; Y\; =\; \backslash \; mathrm\; \{log\}\; (1\; +\; e\; ^\; \{-\; X\}).\}$Тогда

$FY\; (y)\; =\; P\; (Y\; \le \; y)\; =\; P\; (log\; (1\; +\; e\; -\; X)\; \le \; y)\; =\; P\; (X\; \ge \; -\; log\; (ey\; -\; 1)).\; \{\backslash \; displaystyle\; F\_\; \{Y\}\; (y)\; =\; P\; (Y\; \backslash \; leq\; y)\; =\; P\; (\backslash \; mathrm\; \{log\}\; (1\; +\; e\; ^\; \{-\; X\})\; \backslash \; leq\; y)\; =\; P\; (X\; \backslash \; geq\; -\; \backslash \; mathrm\; \{log\}\; (\; e\; ^\; \{y\}\; -1)).\; \backslash ,\}$

Последнее выражение может быть вычислено в терминах кумулятивного распределения $X,\; \{\backslash \; displaystyle\; X,\}$итак

$FY\; (y)\; =\; 1\; -\; FX\; (-\; log\; \; (ey\; -\; 1))\; =\; 1\; -\; 1\; (1\; +\; e\; log\; \; (ey\; -\; 1))\; \theta \; =\; 1\; -\; 1\; (1\; +\; ey\; -\; 1)\; \theta \; =\; 1\; -\; е\; -\; у\; \theta .\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; F\_\; \{Y\}\; (y)\; =\; 1-F\_\; \{X\}\; (-\; \backslash \; log\; (e\; ^\; \{y\}\; -1))\; \backslash \backslash \; [5pt]\; =\; 1\; -\; \{\backslash \; frac\; \{1\}\; \{(1\; +\; e\; ^\; \{\backslash \; log\; (e\; ^\; \{y\}\; -1)\})\; ^\; \{\backslash \; theta\}\}\}\; \backslash \backslash \; [5pt]\; =\; 1\; -\; \{\backslash \; frac\; \{1\}\; \{(1\; +\; e\; ^\; \{y\}\; -1)\; ^\; \{\backslash \; theta\}\}\}\; \backslash \backslash \; [5pt]\; =\; 1-e\; ^\; \{-\; y\; \backslash \; theta\}.\; \backslash \; end\; \{align\}\}\}$

что является кумулятивным распределением функция (CDF) экспоненциального распределения.

Пример 3

Предположим, что $X\; \{\backslash \; displaystyle\; X\}$- случайная величина с стандартное нормальное распределение, плотность которого равна

$f\; X\; (x)\; =\; 1\; 2\; \pi \; e\; -\; x\; 2/2.\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; e\; ^\; \{-\; x\; ^\; \{2\}\; /\; 2\}.\}$

Рассмотрим случайную величину $Y\; =\; Х\; 2.\; \{\backslash \; displaystyle\; Y\; =\; X\; ^\; \{2\}.\}$Мы можем найти плотность, используя приведенную выше формулу для замены переменных:

$f\; Y\; (y)\; =\; \sum \; if\; X\; (gi\; -\; 1\; (\; у))\; |\; d\; g\; i\; -\; 1\; (y)\; d\; y\; |.\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; \backslash \; sum\; \_\; \{i\}\; f\_\; \{X\}\; (g\_\; \{i\}\; ^\; \{-\; 1\}\; (y))\; \backslash \; left\; |\; \{\backslash \; frac\; \{dg\_\; \{i\}\; ^\; \{-\; 1\; \}\; (y)\}\; \{dy\}\}\; \backslash \; right\; |.\}$

В этом случае изменение не монотонно, потому что каждое значение $Y\; \{\backslash \; displaystyle\; Y\}$имеет два соответствующих значения $X\; \{\backslash \; displaystyle\; X\}$(одно положительное и отрицательное). Однако из-за симметрии обе половины будут преобразовываться одинаково, т.е.

$f\; Y\; (y)\; =\; 2\; f\; X\; (g\; -\; 1\; (y))\; |\; d\; g\; -\; 1\; (y)\; d\; y\; |.\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; 2f\_\; \{X\}\; (g\; ^\; \{-\; 1\}\; (y))\; \backslash \; left\; |\; \{\backslash \; frac\; \{dg\; ^\; \{-\; 1\}\; (y)\}\; \{dy\}\}\; \backslash \; right\; |.\}$

Обратное преобразование:

$x\; =\; g\; -\; 1\; (y)\; =\; y\; \{\backslash \; displaystyle\; x\; =\; g\; ^\; \{-\; 1\}\; (y)\; =\; \{\backslash \; sqrt\; \{y\}\}\}$

и его производная равна

$dg\; -\; 1\; (y)\; dy\; =\; 1\; 2\; y.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dg\; ^\; \{-\; 1\}\; (y)\}\; \{dy\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \{\backslash \; sqrt\; \{y\}\}\}\}.\}$

Тогда

$f\; Y\; (y)\; знак\; равно\; 2\; 1\; 2\; \pi \; e\; -\; y\; /\; 2\; 1\; 2\; y\; =\; 1\; 2\; \pi \; ye\; -\; y\; /\; 2.\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; 2\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; e\; ^\; \{-\; y\; /\; 2\}\; \{\backslash \; frac\; \{1\}\; \{2\; \{\backslash \; sqrt\; \{y\}\; \}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; y\}\}\}\; e\; ^\; \{-\; y\; /\; 2\}.\}$

Это распределение хи-квадрат с одним степень свободы.

Пример 4

Предположим, $X\; \{\backslash \; displaystyle\; X\}$- случайная величина с нормальным распределением, плотность которой равна

$f\; X\; (x)\; =\; 1\; 2\; \pi \; \sigma \; 2\; e\; -\; (x\; -\; \mu )\; 2\; /\; (2\; \sigma \; 2).\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; \backslash \; sigma\; ^\; \{2\}\}\}\}\; e\; ^\; \{-\; (x-\; \backslash \; mu)\; ^\; \{2\}\; /\; (2\; \backslash \; sigma\; ^\; \{2\})\}.\}$

Рассмотрим случайную величину $Y\; =\; X\; 2.\; \{\backslash \; displaystyle\; Y\; =\; X\; ^\; \{2\}.\}$Мы можем найти плотность, используя приведенную выше формулу для замены переменных:

$f\; Y\; (y)\; =\; \sum \; if\; X\; (gi\; -\; 1\; (\; у))\; |\; d\; g\; i\; -\; 1\; (y)\; d\; y\; |.\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; \backslash \; sum\; \_\; \{i\}\; f\_\; \{X\}\; (g\_\; \{i\}\; ^\; \{-\; 1\}\; (y))\; \backslash \; left\; |\; \{\backslash \; frac\; \{dg\_\; \{i\}\; ^\; \{-\; 1\; \}\; (y)\}\; \{dy\}\}\; \backslash \; right\; |.\}$

В этом случае изменение не монотонное, потому что каждое значение $Y\; \{\backslash \; displaystyle\; Y\}$имеет два соответствующих значения $X\; \{\backslash \; displaystyle\; X\}$(одно положительное и отрицательное). В отличие от предыдущего примера, в этом случае, однако, нет симметрии, и мы должны вычислить два различных члена:

$f\; Y\; (y)\; =\; f\; X\; (g\; 1\; -\; 1\; (y))\; |\; d\; g\; 1\; -\; 1\; (y)\; d\; y\; |\; +\; f\; X\; (g\; 2\; -\; 1\; (y))\; |\; d\; g\; 2\; -\; 1\; (y)\; d\; y\; |.\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; f\_\; \{X\}\; (g\_\; \{1\}\; ^\; \{-\; 1\}\; (y))\; \backslash \; left\; |\; \{\backslash \; frac\; \{dg\_\; \{1\}\; ^\; \{-\; 1\}\; (y)\}\; \{\; dy\}\}\; \backslash \; right\; |\; +\; f\_\; \{X\}\; (g\_\; \{2\}\; ^\; \{-\; 1\}\; (y))\; \backslash \; left\; |\; \{\backslash \; frac\; \{dg\_\; \{2\}\; ^\; \{-\; 1\}\; (y)\}\; \{dy\}\}\; \backslash \; right\; |.\}$

Обратное преобразование:

$x\; =\; g\; 1,\; 2\; -\; 1\; (y)\; =\; \pm \; y\; \{\backslash \; displaystyle\; x\; =\; g\_\; \{1,2\}\; ^\; \{-\; 1\}\; (y)\; =\; \backslash \; pm\; \{\backslash \; sqrt\; \{y\}\}\}$

и его производная

$dg\; 1,\; 2\; -\; 1\; (y)\; dy\; =\; \pm \; 1\; 2\; y.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{dg\_\; \{1,2\}\; ^\; \{-\; 1\}\; (y)\}\; \{dy\}\}\; =\; \backslash \; pm\; \{\backslash \; frac\; \{1\}\; \{2\; \{\backslash \; sqrt\; \{y\}\}\}\}.\}$

Тогда

$f\; Y\; (y)\; =\; 1\; 2\; \pi \; \sigma \; 2\; 1\; 2\; y\; (e\; -\; (y\; -\; \mu )\; 2\; /\; (2\; \sigma \; 2)\; +\; e\; -\; (-\; y\; -\; \mu )\; 2\; /\; (2\; \sigma \; 2)).\; \{\backslash \; displaystyle\; f\_\; \{Y\}\; (y)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\; \backslash \; sigma\; ^\; \{2\}\}\}\}\; \{\backslash \; frac\; \{1\}\; \{2\; \{\backslash \; sqrt\; \{y\}\}\}\}\; (e\; ^\; \{-\; (\{\backslash \; sqrt\; \{y\}\}\; -\; \backslash \; mu)\; ^\; \{2\}\; /\; (2\; \backslash \; sigma\; ^\; \{2\})\}\; +\; e\; ^\; \{-\; (-\; \{\backslash \; sqrt\; \{y\}\}\; -\; \backslash \; mu)\; ^\; \{2\}\; /\; (2\; \backslash \; sigma\; ^\; \{2\})\}).\}$

Это нецентральное распределение хи-квадрат с одной степенью свободы.

• Вероятностное распределение суммы двух независимых случайных величин представляет собой свертку каждого из их распределений.
• Распределения вероятностей не являются векторным пространством - они не замыкаются под линейными комбинациями, поскольку они не сохраняют неотрицательность или полный интеграл 1 - но они закрываются под выпуклой комбинацией, таким образом образуя выпуклое подмножество пространства функций (или мер).

Существует несколько различных смыслов, в которых случайные величины могут считаться эквивалентными. Две случайные величины могут быть равными, почти наверняка или равными по распределению.

В порядке возрастания силы точное определение этих понятий эквивалентности дается ниже.

Равенство в распределении

Если пространство выборки является подмножеством вещественной линии, случайные величины X и Y равны в распределении (обозначается $X\; =\; d\; Y\; \{\backslash \; displaystyle\; X\; \{\; \backslash \; stackrel\; \{d\}\; \{=\}\}\; Y\}$), если они имеют одинаковые функции распределения:

$P\; \; (X\; \le \; x)\; =\; P\; \; (Y\; \le \; x)\; для\; всех\; x.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{P\}\; (X\; \backslash \; leq\; x)\; =\; \backslash \; operatorname\; \{P\}\; (Y\; \backslash \; leq\; x)\; \backslash \; quad\; \{\backslash \; text\; \{для\; всех\}\}\; x.\}$

Чтобы быть равными в распределении, случайные величины нет необходимости определять в одном и том же вероятностном пространстве. Две случайные величины, имеющие равные производящие функции момента, имеют одинаковое распределение. Это обеспечивает, например, полезный метод проверки равенства некоторых функций независимых, одинаково распределенных (IID) случайных величин. Однако функция создания момента существует только для распределений, которые имеют определенное преобразование Лапласа.

Почти наверняка равенство

Две случайные величины X и Y равны почти наверняка (обозначено $X\; =\; as\; Y\; \{\backslash \; displaystyle\; X\; \backslash ;\; \{\backslash \; stackrel\; \{\backslash \; text\; \{as\}\}\; \{=\}\}\; \backslash ;\; Y\}$) тогда и только тогда, когда вероятность того, что они различны, равна ноль :

$P\; \; (X\; \ne \; Y)\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{P\}\; (X\; \backslash \; neq\; Y)\; =\; 0.\}$

Для всех практических целей теории вероятностей это понятие эквивалентности так же сильно, как фактическое равенство. Ему соответствует следующее расстояние:

$d\; \infty \; (X,\; Y)\; =\; ess\; \; sup\; \omega \; |\; X\; (\omega )\; -\; Y\; (\omega )\; |,\; \{\backslash \; displaystyle\; d\; \_\; \{\backslash \; infty\}\; (X,\; Y)\; =\; \backslash \; operatorname\; \{ess\}\; \backslash \; sup\; \_\; \{\backslash \; omega\}\; |\; X\; (\backslash \; omega)\; -Y\; (\backslash \; omega)\; |,\}$

где "ess sup" представляет существенную верхнюю грань в смысле теории меры.

Равенство

Наконец, две случайные величины X и Y равны, если они равны как функции на их измеримом пространстве :

$X\; (\omega )\; =\; Y\; (\omega )\; для\; всех\; \omega .\; \{\backslash \; displaystyle\; X\; (\backslash \; omega)\; =\; Y\; (\backslash \; omega)\; \backslash \; qquad\; \{\backslash \; hbox\; \{for\; all\}\}\; \backslash \; omega.\}$

Это понятие обычно наименее полезно в теории вероятностей, поскольку на практике и в теории лежащее в основе пространство измерений в эксперименте редко описывается явным образом или даже может быть охарактеризовано.

Важной темой математической статистики является получение результатов сходимости для определенных последовательностей случайных величин; например, закон больших чисел и центральная предельная теорема.

. Существуют различные смыслы, в которых последовательность $X\; n\; \{\backslash \; displaystyle\; X\_\; \{n\}\}$случайных величин может сходиться к случайной величине $X\; \{\backslash \; displaystyle\; X\}$. Они объясняются в статье о сходимости случайных величин.

• Математический портал

• Алеаторизм
• Алгебра случайных величин
• Событие (теория вероятностей)
• Многомерная случайная величина
• Парные независимые случайные величины
• Наблюдаемая переменная
• Случайный элемент
• Случайная функция
• Случайная мера
• Генератор случайных чисел производит случайное значение
• Случайный вектор
• Случайность
• Случайный процесс
• Взаимосвязи между распределениями вероятностей

Встроенные цитаты

Литература

• , Энциклопедия математики, EMS Press, 2001 [1994]
• Цукерман, Моше (2014), Введение в теорию массового обслуживания и стохастические модели телетрафика (PDF)
• Цукерман, Моше (2014), Основные темы вероятностей (PDF)