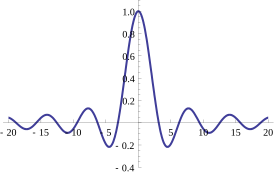
Характеристическая функция (теория вероятностей)

Характеристическая функция однородной случайной величины U (–1,1). Эта функция является действительной, потому что она соответствует случайной величине, симметричной относительно начала координат; однако характеристические функции обычно могут быть комплексными.

В теории вероятностей и статистике, характеристическая функция любого вещественного случайная величина полностью определяет ее распределение вероятностей. Если случайная величина допускает функцию плотности вероятности, то характеристическая функция представляет собой преобразование Фурье функции плотности вероятности. Таким образом, он обеспечивает альтернативный способ получения аналитических результатов по сравнению с работой напрямую с функциями плотности вероятности или кумулятивными функциями распределения. Особенно простые результаты получены для характеристических функций распределений, определяемых взвешенными суммами случайных величин.

В дополнение к одномерным распределениям, характеристические функции могут быть определены для векторных или матричных случайных величин, а также могут быть расширены на более общие случаи.

Характеристическая функция всегда существует, когда рассматривается как функция действительного аргумента, в отличие от функции создания момента. Существуют связи между поведением характеристической функции распределения и свойствами распределения, такими как наличие моментов и существование функции плотности.

• 1 Введение
• 2 Определение
• 3 Обобщения
• 4 Примеры
• 5 Свойства
  • 5.1 Непрерывность
  • 5.2 Формулы обращения
  • 5.3 Критерии для характеристических функций
• 6 Использование
  • 6.1 Основные операции с распределениями
  • 6.2 Моменты
  • 6.3 Анализ данных
  • 6.4 Пример
• 7 Целые характеристические функции
• 8 Понятия, связанные с данным
• 9 См. Также
• 10 Примечания
• 11 Ссылки
  • 11.1 Цитаты
  • 11.2 Источники
• 12 Внешние ссылки

Характеристическая функция предоставляет альтернативный способ описания случайной величины. Аналогично функции кумулятивного распределения ,

$FX\; (x)\; =\; E\; \; [1\; \{X\; \le \; x\}]\; \{\backslash \; displaystyle\; F\_\; \{X\}\; (x)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; mathbf\; \{1\; \}\; \_\; \{\backslash \; \{X\; \backslash \; leq\; x\; \backslash \}\}\; \backslash \; right]\}$

(где 1{X ≤ x} - это индикаторная функция - она ​​равна 1, когда X ≤ x, и ноль в противном случае), который полностью определяет поведение и свойства распределения вероятностей случайной величины X, характеристическая функция,

$\phi \; X\; (t)\; =\; E\; \; [eit\; X],\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{itX\}\; \backslash \; right],\}$

также полностью определяет поведение и свойства распределения вероятностей случайной величины X. Эти два подходы эквивалентны в том смысле, что, зная одну из функций, всегда можно найти другую, но они дают разные идеи для понимания свойств случайной величины. Однако в отдельных случаях могут быть различия в том, могут ли эти функции быть представлены в виде выражений, включающих простые стандартные функции.

Если случайная величина допускает функцию плотности , то характеристической функцией является ее двойственный в том смысле, что каждая из них является преобразованием Фурье другого. Если случайная величина имеет функцию , генерирующую момент $MX\; (t)\; \{\backslash \; displaystyle\; M\_\; \{X\}\; (t)\}$, то область определения характеристической функции может быть продолжен на комплексную плоскость, причем

$\phi \; X\; (-\; it)\; =\; MX\; (t).\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (-\; it)\; =\; M\_\; \{X\}\; (t).\}$

Однако обратите внимание, что характеристическая функция распределения всегда существует, даже если функция плотности вероятности или функция создания момента - нет.

Подход характеристической функции особенно полезен при анализе линейных комбинаций независимых случайных величин: в классическом доказательстве центральной предельной теоремы используются характеристические функции и теорема Леви о непрерывности. Другое важное приложение - теория разложимости случайных величин.

Для скалярной случайной величины X характеристическая функция определяется как ожидаемое значение числа e, где i - мнимая единица, а t ∈ R - аргумент характеристической функции:

$\{\phi \; X:\; R\; \to \; C\; \phi \; X\; (t)\; =\; E\; \; [eit\; X]\; =\; \int \; R\; eitxd\; FX\; (x)\; знак\; равно\; \int \; R\; eitxf\; X\; (x)\; dx\; =\; \int \; 0\; 1\; eit\; QX\; (p)\; dp\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{cases\}\; \backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; \backslash !:\; \backslash \; Mathbb\; \{R\}\; \backslash \; to\; \backslash \; mathbb\; \{C\}\; \backslash \backslash \backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{itX\}\; \backslash \; right]\; =\; \backslash \; int\; \_\; \{\backslash \; mathbb\; \{R\}\}\; e\; ^\; \{itx\; \}\; \backslash ,\; dF\_\; \{X\}\; (x)\; =\; \backslash \; int\; \_\; \{\backslash \; mathbb\; \{R\}\}\; e\; ^\; \{itx\}\; f\_\; \{X\}\; (x)\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; e\; ^\; \{\; itQ\_\; \{X\}\; (p)\}\; \backslash ,\; dp\; \backslash \; end\; \{ases\}\}\}$

Здесь F X - это кумулятивная функция распределения X, а интеграл представляет собой Риман – Стилтьес род. Если случайная величина X имеет функцию плотности вероятности fX, то характеристической функцией является ее преобразование Фурье с изменением знака в комплексной экспоненте, и последняя формула в скобках действительна. Q X (p) - это обратная кумулятивная функция распределения X, также называемая функцией квантиля X. Это соглашение для констант, появляющихся в определении характеристической функции, отличается от обычного соглашение для преобразования Фурье. Например, некоторые авторы определяют φ X (t) = Ee, что по сути является изменением параметра. В литературе можно встретить и другие обозначения: $p\; ^\; \{\backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; hat\; \{p\}\}\}$как характеристическая функция для вероятностной меры p, или $f\; ^\; \{\; \backslash \; displaystyle\; \backslash \; scriptstyle\; \{\backslash \; hat\; \{f\}\}\}$как характеристическая функция, соответствующая плотности f.

Понятие характеристических функций обобщается на многомерные случайные величины и более сложные случайные элементы. Аргумент характеристической функции всегда будет принадлежать непрерывному двойственному элементу пространства, в котором случайная величина X принимает свои значения. Для общих случаев такие определения перечислены ниже:

• Если X - k-мерный случайный вектор, то для t ∈ R

$\phi \; X\; (t)\; =\; E\; \; [exp\; \; (it\; TX)\; ],\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; exp\; (it\; ^\; \{T\}\; \backslash !\; X)\; \backslash \; right],\}$

где $t\; T\; \{\; \backslash \; textstyle\; t\; ^\; \{T\}\}$- это транспонирование матрицы $t\; \{\backslash \; textstyle\; t\}$,

• Если X ak × p-мерное случайное матрица, тогда для t ∈ R

$\phi \; X\; (t)\; =\; E\; \; [exp\; \; (i\; tr\; \; (t\; TX))],\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; \backslash \; operatorname\; \{\; E\}\; \backslash \; left\; [\backslash \; exp\; \backslash \; left\; (i\; \backslash \; operatorname\; \{tr\}\; (t\; ^\; \{T\}\; \backslash !\; X)\; \backslash \; right)\; \backslash \; right],\}$

где $tr\; \; (\cdot )\; \{\backslash \; textstyle\; \backslash \; operatorname\; \{tr\}\; (\backslash \; cdot)\}$- оператор трассировки,

• Если X - комплексная случайная величина, то для t ∈ C

$\phi \; Икс\; (T)\; знак\; равно\; Е\; \; [ехр\; \; (я\; Re\; \; (t\; ¯\; X))],\; \{\backslash \; Displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (т)\; =\; \backslash \; OperatorName\; \{E\}\; \backslash \; left\; [\backslash \; exp\; \backslash \; left\; (я\; \backslash \; operatorname\; \{Re\}\; \backslash \; left\; (\{\backslash \; overline\; \{t\}\}\; X\; \backslash \; right)\; \backslash \; right)\; \backslash \; right],\}$

где $t\; ¯\; \{\backslash \; textstyle\; \{\backslash \; overline\; \{t\}\}\}$- комплексное сопряжение из $t\; \{\backslash \; textstyle\; t\}$и $Re\; \; (z)\; \{\backslash \; textstyle\; \backslash \; operatorname\; \{Re\}\; (\; z)\}$- действительная часть комплексного числа $z\; \{\backslash \; textstyle\; z\}$,

• Если X - k-мерный комплексный случайный вектор, тогда для t ∈ C

$\phi \; X\; (t)\; =\; E\; \; [exp\; \; (i\; Re\; \; (t\; \ast \; X))],\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; exp\; (я\; \backslash \; OperatorName\; \{Re\}\; (t\; ^\; \{*\}\; \backslash !\; X))\; \backslash \; right],\}$

где $t\; \ast \; \{\backslash \; textstyle\; t\; ^\; \{*\}\}$- сопряженное транспонирование матрицы $t\; \{\backslash \; textstyle\; t\}$,

• Если X (s) является случайным процессом, то для всех функций t (s), таких что интеграл $\int \; р\; t\; (s)\; X\; (s)\; ds\; \{\backslash \; textstyle\; \backslash \; int\; \_\; \{\backslash \; mathbb\; \{R\}\}\; t\; (s)\; X\; (s)\; \backslash ,\; \backslash \; mathrm\; \{d\}\; s\}$сходится для почти всех реализаций X

$\phi \; X\; (t)\; =\; E\; \; [exp\; \; (i\; \int \; R\; t\; (s)\; X\; (s)\; ds)].\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [\backslash \; exp\; \backslash \; left\; (i\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; t\; (s)\; X\; (s)\; \backslash ,\; ds\; \backslash \; right)\; \backslash \; right].\}$

Распределение	Характеристическая функция φ (t)
Вырожденная δa	$eita\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; e\; ^\; \{ita\}\}$
Бернулли Берн (p)	$1\; -\; p\; +\; peit\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; 1-p\; +\; pe\; ^\; \{it\}\}$
Биномиальное B (n, p)	$(\; 1\; -\; p\; +\; peit)\; n\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; (1-p\; +\; pe\; ^\; \{it\})\; ^\; \{n\}\}$
Отрицательный бином NB (r, p)	$(1\; -\; п\; 1\; -\; peit)\; r\; \{\backslash \; displaystyle\; \backslash ,\; \{\backslash \; biggl\; (\}\; \{\backslash \; frac\; \{1-p\}\; \{1-pe\; ^\; \{i\; \backslash ,\; t\}\}\}\; \{\backslash \; biggr)\}\; ^\; \{\backslash !\; r\}\}$
Пуассон Пуа (λ)	$e\; \lambda \; (eit\; -\; 1)\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; E\; ^\; \{\backslash \; lambda\; (e\; ^\; \{it\}\; -1)\}\}$
Равномерное (непрерывное) U (a, b)	$eitb\; -\; eitait\; (b\; -\; a)\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; \{\backslash \; Frac\; \{e\; ^\; \{itb\}\; -e\; ^\; \{ita\}\}\; \{it\; (ba)\}\}\; \}$
Равномерное (дискретное) DU (a, b)	$eait\; -\; e\; (b\; +\; 1)\; it\; (b\; -\; a\; +\; 1)\; (1\; -\; eit)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{e\; ^\; \{ait\}\; -e\; ^\; \{(b\; +\; 1)\; it\}\}\; \{(b-a\; +\; 1)\; (1-e\; ^\; \{it\})\}\}\}$
Лаплас L (μ, b)	$eit\; \mu \; 1\; +\; b\; 2\; T\; 2\; \{\backslash \; Displaystyle\; \backslash !\; \backslash ,\; \{\backslash \; frac\; \{e\; ^\; \{it\; \backslash \; mu\}\}\; \{1\; +\; b\; ^\; \{2\}\; t\; ^\; \{2\}\}\}\}$
Нормальный N (μ, σ)	$eit\; \mu \; -\; 1\; 2\; \sigma \; 2\; t\; 2\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; e\; ^\; \{it\; \backslash \; mu\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; sigma\; ^\; \{2\}\; t\; ^\; \{2\}\}\}$
Хи-квадрат χk	$(1-2\; it)\; -\; k\; /\; 2\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; (1-2it)\; ^\; \{-\; k\; /\; 2\}\}$
Коши C (μ, θ)	$eit\; \mu \; -\; \theta \; |\; т\; |\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; e\; ^\; \{it\; \backslash \; mu\; -\; \backslash \; theta\; |\; t\; |\}\}$
Гамма Γ (k, θ)	$(1\; -\; it\; \theta )\; -\; k\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; (1-it\; \backslash \; theta)\; ^\; \{-\; k\}\}$
Экспоненциальная Exp (λ)	$(1\; -\; it\; \lambda \; -\; 1)\; -\; 1\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; (1-it\; \backslash \; lambda\; ^\; \{-\; 1\})\; ^\; \{-\; 1\}\}$
Геометрический Gf (p). (количество отказов)	$p\; 1\; -\; eit\; (1\; -\; p)\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; \{\backslash \; frac\; \{p\}\; \{1-e\; ^\; \{it\}\; (1-p)\}\}\}$
Геометрический Gt (p). (количество испытаний)	$pe\; -\; it\; -\; (1\; -\; p)\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; \{\backslash \; Frac\; \{p\}\; \{e\; ^\; \{-\; it\}\; -\; (1-p)\}\}\}$
Многомерный нормальный N(μ, Σ)	$et\; T\; (i\; \mu \; -\; 1\; 2\; \Sigma \; t)\; \{\backslash \; displaystyle\; e\; ^\; \{\backslash \; mathbf\; \{t\}\; ^\; \{\backslash \; mathrm\; \{T\}\}\; \backslash \; left\; (i\; \{\backslash \; boldsymbol\; \{\backslash \; mu\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \backslash \; mathbf\; \{t\}\; \backslash \; right)\}\}$
Многомерный Коши Многопараметрический Коши (μ, Σ)	$eit\; T\; \mu \; -\; t\; T\; \Sigma \; t\; \{\backslash \; displaystyle\; \backslash !\; \backslash ,\; E\; ^\; \{i\; \backslash \; mathbf\; \{t\}\; ^\; \{\backslash \; mathrm\; \{T\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; mu\}\}\; -\; \{\backslash \; sqrt\; \{\backslash \; mathbf\; \{t\}\; ^\; \{\backslash \; mathrm\; \{T\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \backslash \; mathbf\; \{t\}\}\}\}\; \}$

Оберхеттингер (1973) предоставляет обширные таблицы характеристических функций.

• Характеристическая функция Функция вещественнозначной случайной величины всегда существует, поскольку она является интегралом ограниченной непрерывной функции по пространству, мера конечна.
• Характеристическая функция равномерно непрерывна на всем пространстве
• Оно не обращается в нуль в области около нуля: φ (0) = 1.
• Оно ограничено: | φ (t) | ≤ 1.
• Это эрмитово : φ (−t) = φ (t). В частности, характеристическая функция симметричной (относительно начала координат) случайной величины является действительной и даже.
• Существует биекция между распределениями вероятностей и характеристическими функциями.. То есть для любых двух случайных величин X 1, X 2 обе имеют одинаковое распределение вероятностей тогда и только тогда, когда $\phi \; X\; 1\; =\; \phi \; X\; 2\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\_\; \{1\}\}\; =\; \backslash \; varphi\; \_\; \{X\_\; \{2\}\}\}$.
• Если случайная величина X имеет моменты до k-го порядка, то характеристическая функция φ X k раз непрерывно дифференцируемо на всей действительной прямой. В этом случае

$E\; \; [X\; k]\; =\; i\; -\; k\; \phi \; X\; (k)\; (0).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [X\; ^\; \{k\}]\; =\; i\; ^\; \{-\; k\}\; \backslash \; varphi\; \_\; \{X\}\; ^\; \{(k)\}\; (0).\}$

• Если характеристическая функция φ X имеет k-ю производную в нуле, тогда случайная величина X имеет все моменты до k, если k четное, но только до k - 1, если k нечетное.

$\phi \; X\; (k)\; (\; 0)\; знак\; равно\; ik\; E\; \; [Икс\; К]\; \{\backslash \; Displaystyle\; \backslash \; varphi\; \_\; \{X\}\; ^\; \{(k)\}\; (0)\; =\; я\; ^\; \{k\}\; \backslash \; OperatorName\; \{E\}\; [X\; ^\; \{k\}]\}$

• Если X 1,..., X n - независимые случайные величины, а a 1,..., a n - некоторые константы, то характеристическая функция линейной комбинации X i равна

$\phi \; a\; 1\; X\; 1\; +\; \cdots \; +\; an\; X\; n\; (t)\; =\; \phi \; X\; 1\; (a\; 1\; t)\; \Phi \; X\; n\; (муравей).\; \{\backslash \; Displaystyle\; \backslash \; varphi\; \_\; \{a\_\; \{1\}\; X\_\; \{1\}\; +\; \backslash \; cdots\; +\; a\_\; \{n\}\; X\_\; \{n\}\}\; (t)\; =\; \backslash \; varphi\; \_\; \{X\_\; \{1\}\}\; (a\_\; \{1\}\; t)\; \backslash \; cdots\; \backslash \; varphi\; \_\; \{X\_\; \{n\}\}\; (a\_\; \{n\}\; t).\}$

Один конкретный случай - это сумма двух независимых случайных величин X 1 и X 2 в в этом случае

$\phi \; X\; 1\; +\; X\; 2\; (t)\; =\; \phi \; X\; 1\; (t)\; \cdot \; \phi \; X\; 2\; (t).\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\_\; \{1\}\; +\; X\_\; \{2\}\}\; (t)\; =\; \backslash \; varphi\; \_\; \{X\_\; \{1\}\}\; (t)\; \backslash \; cdot\; \backslash \; varphi\; \_\; \{X\_\; \{2\}\}\; (t).\}$

• Поведение хвоста характеристической функции определяет гладкость соответствующей функции плотности.
• Пусть случайная величина $Y\; =\; a\; X\; +\; b\; \{\backslash \; displaystyle\; Y\; =\; aX\; +\; b\}$быть линейным преобразованием случайной величины $X\; \{\backslash \; displaystyle\; X\}$. Характеристическая функция $Y\; \{\backslash \; displaystyle\; Y\}$равна $\phi \; Y\; (t)\; =\; eitb\; \phi \; X\; (at)\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{Y\}\; (t)\; =\; e\; ^\; \{itb\}\; \backslash \; varphi\; \_\; \{X\}\; (at)\}$. Для случайных векторов $X\; \{\backslash \; displaystyle\; X\}$и $Y\; =\; AX\; +\; B\; \{\backslash \; displaystyle\; Y\; =\; AX\; +\; B\}$(где A - постоянная матрица и B - постоянный вектор), мы имеем $\phi \; Y\; (t)\; =\; eit\; \top \; B\; \phi \; X\; (A\; \top \; t)\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{Y\}\; (t)\; =\; e\; ^\; \{it\; ^\; \{\backslash \; top\}\; B\; \}\; \backslash \; varphi\; \_\; \{X\}\; (A\; ^\; \{\backslash \; top\}\; t)\}$.

Непрерывность

Установленное выше взаимное соответствие между распределениями вероятностей и характеристическими функциями последовательно непрерывно. То есть всякий раз, когда последовательность функций распределения F j (x) сходится (слабо) к некоторому распределению F (x), соответствующая последовательность характеристических функций φ j (t) будет также сходятся, и предел φ (t) будет соответствовать характеристической функции закона F. Более формально это сформулировано как

теорема Леви о непрерывности : Последовательность X j n-переменных случайных величин сходится в распределении к случайной величине X тогда и только тогда, когда последовательность φ Xjсходится поточечно к функции φ, которая является непрерывной в начале координат. Тогда φ является характеристической функцией X.

Эта теорема часто используется для доказательства закона больших чисел и центральной предельной теоремы.

Формулы обращения

Между кумулятивными функциями распределения и характеристическими функциями существует взаимно однозначное соответствие, поэтому можно найти одну из этих функций, если мы знаем другую. Формула в определении характеристической функции позволяет нам вычислить φ, когда мы знаем функцию распределения F (или плотность f). Если, с другой стороны, мы знаем характеристическую функцию φ и хотим найти соответствующую функцию распределения, то можно использовать одну из следующих теорем обращения .

Теорема . Если характеристическая функция φ X является интегрируемой, то F X абсолютно непрерывна, и, следовательно, X имеет функцию плотности вероятности. В одномерном случае (т.е. когда X имеет скалярное значение) функция плотности задается как

$f\; X\; (x)\; =\; F\; X\; \prime \; (x)\; =\; 1\; 2\; \pi \; \int \; R\; e\; -\; i\; t\; x\; \phi \; X\; (t)\; d\; t.\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; F\_\; \{X\}\; \text{'}(x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; e\; ^\; \{-\; itx\}\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash ,\; dt.\}$

В многомерном случае это

$f\; X\; (x)\; =\; 1\; (2\; \pi )\; n\; \int \; R\; ne\; -\; i\; (t\; \cdot \; x)\; \phi \; X\; (t)\; \lambda \; (dt)\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{(2\; \backslash \; pi)\; ^\; \{n\}\}\}\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\; ^\; \{n\}\}\; e\; ^\; \{-i\; (t\; \backslash \; cdot\; x)\}\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash \; lambda\; (dt)\}$

где $t\; \cdot \; x\; \{\backslash \; textstyle\; t\; \backslash \; cdot\; x\}$- скалярное произведение.

PDF - это производная Радона – Никодима распределения μ X по мере Лебега λ:

$f\; X\; (x)\; =\; d\; \mu \; X\; d\; \lambda \; (x).\; \{\backslash \; displaystyle\; f\_\; \{X\}\; (x)\; =\; \{\backslash \; frac\; \{d\; \backslash \; mu\; \_\; \{X\}\}\; \{d\; \backslash \; lambda\}\}\; (x).\}$

Теорема (Леви) . Если φ X является характеристической функцией функции распределения F X, две точки < b are such that {x | a < x < b} is a задают непрерывность из μ X (в одномерном случае это условие эквивалентно непрерывности F X в точках a и b), то

• Если X скалярный:

$FX\; (b)\; -\; FX\; (a)\; =\; 1\; 2\; \pi \; lim\; T\; \to \; \infty \; \int \; -\; T\; +\; T\; e\; -\; ita\; -\; e\; -\; itбит\; \phi \; X\; (t)\; dt.\; \{\backslash \; displaystyle\; F\_\; \{X\}\; (b)\; -F\_\; \{X\}\; (a)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; lim\; \_\; \{T\; \backslash \; to\; \backslash \; infty\}\; \backslash \; int\; \_\; \{-\; T\}\; ^\; \{\; +\; T\}\; \{\backslash \; frac\; \{e\; ^\; \{-\; ita\}\; -e\; ^\; \{-\; itb\}\}\; \{it\}\}\; \backslash ,\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash ,\; dt.\}$

Эту формулу можно изменить в форме, более удобной для численных расчетов, как

$F\; (x\; +\; h)\; -\; F\; (x\; -\; h)\; 2\; h\; =\; 1\; 2\; \pi \; \int \; -\; \infty \; \infty \; sin\; \; hthte\; -\; itx\; \phi \; X\; (t)\; dt.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{F\; (x\; +\; h)\; -F\; (xh)\}\; \{2h\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\; \backslash \; frac\; \{\backslash \; sin\; ht\}\; \{ht\}\}\; e\; ^\; \{-\; itx\}\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash ,\; dt.\}$

Для случайной величины, ограниченной снизу, можно получить $F\; (b)\; \{\backslash \; displaystyle\; F\; (b)\}$, взяв $a\; \{\backslash \; displaystyle\; a\}$так, чтобы $F\; (a)\; =\; 0.\; \{\backslash \; displaystyle\; F\; (a)\; =\; 0.\}$В противном случае, если случайная величина не ограничена снизу, предел для $a\; \to \; -\; \infty \; \{\backslash \; displaystyle\; a\; \backslash \; to\; -\; \backslash \; infty\}$дает $F\; (b)\; \{\backslash \; displaystyle\; F\; (b)\}$, но численно непрактично.

• Если X - векторная случайная величина:

Теорема . Если a (возможно) является атомом X (в одномерном случае это означает точку разрыва F X), то

• Если X скалярный:

$FX\; (a)\; -\; FX\; (a\; -\; 0)\; знак\; равно\; lim\; T\; \to \; \infty \; 1\; 2\; T\; \int \; -\; T\; +\; T\; e\; -\; ita\; \phi \; X\; (t)\; dt\; \{\backslash \; displaystyle\; F\_\; \{X\}\; (a)\; -F\_\; \{X\}\; (a-0)\; =\; \backslash \; lim\; \_\; \{T\; \backslash \; to\; \backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{2T\}\}\; \backslash \; int\; \_\; \{-\; T\}\; ^\; \{+\; T\}\; e\; ^\; \{-\; ita\}\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash ,\; dt\}$

• Если X - векторная случайная величина:

$\mu \; X\; (\{a\})\; =\; lim\; T\; 1\; \to \; \infty \; \cdots \; lim\; T\; n\; \to \; \infty \; (\prod \; k\; =\; 1\; n\; 1\; 2\; T\; k)\; \int \; [-\; T\; 1,\; T\; 1]\; \times \; \cdots \; \times \; [-\; T\; n,\; T\; п]\; е\; -\; я\; (T\; \cdot \; a)\; \phi \; Икс\; (T)\; \lambda \; (dt)\; \{\backslash \; Displaystyle\; \backslash \; му\; \_\; \{X\}\; (\backslash \; \{a\; \backslash \})\; =\; \backslash \; lim\; \_\; \{T\_\; \{1\}\; \backslash \; to\; \backslash \; infty\}\; \backslash \; cdots\; \backslash \; lim\; \_\; \{T\_\; \{n\}\; \backslash \; to\; \backslash \; infty\}\; \backslash \; left\; (\backslash \; prod\; \_\; \{k\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{1\}\; \{2T\_\; \{k\}\}\}\; \backslash \; right)\; \backslash \; int\; \backslash \; limits\; \_\; \{[-T\_\; \{1\},\; T\_\; \{1\}]\; \backslash \; times\; \backslash \; dots\; \backslash \; times\; [-T\_\; \{n\},\; T\_\; \{n\}]\}\; e\; ^\; \{-\; i\; (t\; \backslash \; cdot\; a)\}\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash \; lambda\; (dt)\}$

Теорема (Гиль-Пелаес) . Для одномерной случайной величины X, если x является точкой непрерывности F X, то

$FX\; (x)\; =\; 1\; 2\; -\; 1\; \pi \; \int \; 0\; \infty \; Im\; \; [e\; -\; itx\; \phi \; X\; (t)\; ]\; tdt.\; \{\backslash \; displaystyle\; F\_\; \{X\}\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; -\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{0\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{Im\}\; [e\; ^\; \{-\; itx\}\; \backslash \; varphi\; \_\; \{X\}\; (t)]\}\; \{t\}\}\; \backslash ,\; dt.\}$

где мнимая часть комплексного числа $z\; \{\backslash \; displaystyle\; z\}$задается как $I\; m\; (z)\; =\; (z\; -\; z\; \ast )\; /\; 2\; i\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{Im\}\; (z)\; =\; (zz\; ^\; \{*\})\; /\; 2i\}$. Интеграл может быть не интегрируемым по Лебегу ; например, когда X - это дискретная случайная величина, которая всегда равна 0, она становится интегралом Дирихле.

Доступны формулы обращения для многомерных распределений.

Критерии для характеристических функций

Множество всех характеристических функций замыкается при выполнении определенных операций:

• A выпуклая линейная комбинация $\sum \; nan\; \phi \; n\; (t)\; \{\backslash \; textstyle\; \backslash \; sum\; \_\; \{n\}\; a\_\; \{n\}\; \backslash \; varphi\; \_\; \{n\}\; (t)\}$(с $an\; \ge \; 0,\; \sum \; nan\; =\; 1\; \{\backslash \; textstyle\; a\_\; \{n\}\; \backslash \; geq\; 0,\; \backslash \; \backslash \; sum\; \_\; \{n\}\; a\_\; \{n\; \}\; =\; 1\}$) конечного или счетного числа характеристических функций также является характеристической функцией.
• Произведение конечного числа характеристических функций также является характеристической функцией. То же самое верно и для бесконечного произведения при условии, что оно сходится к функции, непрерывной в начале координат.
• Если φ - характеристическая функция, а α - действительное число, то $\phi \; ¯\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{\backslash \; varphi\}\}\}$, Re (φ), | φ | и φ (αt) также являются характеристическими функциями.

Хорошо известно, что любое неубывающее càdlàg функция F с пределами F (−∞) = 0, F (+ ∞) = 1 соответствует кумулятивной функции распределения некоторой случайной величины. Также есть интерес найти аналогичные простые критерии, когда заданная функция φ может быть характеристической функцией некоторой случайной величины. Центральным результатом здесь является теорема Бохнера, хотя ее полезность ограничена, поскольку главное условие теоремы, неотрицательная определенность, очень трудно проверить. Существуют и другие теоремы, например, Хинчина, Матиаса или Крамера, хотя их применение столь же сложно. С другой стороны, теорема Поли дает очень простое условие выпуклости, которое является достаточным, но не необходимым. Характеристические функции, удовлетворяющие этому условию, называются типом Пойи.

Теорема Бохнера. Произвольная функция φ: R→ Cявляется характеристической функцией некоторой случайной величины тогда и только тогда, когда φ положительно определена, непрерывна в начале координат, и если φ (0) = 1.

критерий Хинчина . Комплекснозначная абсолютно непрерывная функция φ с φ (0) = 1 является характеристической функцией тогда и только тогда, когда она допускает представление

$\phi \; (t)\; =\; \int \; R\; g\; (t\; +\; \theta )\; g\; (\theta )\; ¯\; d\; \theta .\; \{\backslash \; displaystyle\; \backslash \; varphi\; (t)\; =\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; g\; (t\; +\; \backslash \; theta)\; \{\backslash \; overline\; \{g\; (\backslash \; theta)\}\}\; \backslash ,\; d\; \backslash \; theta.\}$

Теорема Матиаса . Вещественнозначная четная непрерывная абсолютно интегрируемая функция φ с φ (0) = 1 является характеристической функцией тогда и только тогда, когда

$(-\; 1)\; n\; (\int \; R\; \phi \; (pt)\; e\; -\; t\; 2\; /\; 2\; ЧАС\; 2\; N\; (t)\; dt)\; \ge \; 0\; \{\backslash \; displaystyle\; (-1)\; ^\; \{n\}\; \backslash \; left\; (\backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; \backslash \; varphi\; (pt)\; e\; ^\; \{-\; t\; ^\; \{2\}\; /\; 2\}\; H\_\; \{2n\}\; (t)\; \backslash ,\; dt\; \backslash \; right)\; \backslash \; geq\; 0\}$

для n = 0,1,2,... и всех p>0. Здесь H 2n обозначает многочлен Эрмита степени 2n.

Теорема Поли может быть использована для построения примера двух случайных величин, характеристические функции которых совпадают на конечном интервале, но различны в другом месте.

Теорема Поли . Если $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$является вещественной, четной, непрерывной функцией, которая удовлетворяет условиям

• $\phi \; (0)\; =\; 1\; \{\backslash \; displaystyle\; \backslash \; varphi\; (0)\; =\; 1\; \}$,
• $\phi \; \{\backslash \; displaystyle\; \backslash \; varphi\}$равно выпуклый для $t>0\; \{\backslash \; displaystyle\; t>0\}$,
• $\phi \; (\infty )\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; varphi\; (\backslash \; infty)\; =\; 0\}$,

, тогда φ (t) является характеристической функцией абсолютно непрерывного распределения, симметричного относительно 0.

Из-за теорема непрерывности, характеристические функции используются в наиболее часто встречающемся доказательстве центральной предельной теоремы. Основной метод, используемый при выполнении вычислений с характеристической функцией, - это распознавание функции как характеристической функции конкретной распределение.

Основные манипуляции с распределениями

Характеристика функции особенно полезны для работы с линейными функциями от независимых случайных величин. Например, если X 1, X 2,..., X n представляет собой последовательность независимых (и не обязательно одинаково распределенных) случайных величин, и

$S\; N\; =\; \sum \; я\; =\; 1\; nai\; X\; i,\; \{\backslash \; displaystyle\; S\_\; \{n\}\; =\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; a\_\; \{i\}\; X\_\; \{i\},\; \backslash ,\; \backslash !\}$

где a i - константы, тогда характеристическая функция для S n задается как

$\phi \; S\; n\; (t)\; =\; \phi \; X\; 1\; (a\; 1\; t)\; \phi \; X\; 2\; (a\; 2\; t)\; \cdots \; \phi \; Икс\; N\; (муравей)\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{S\_\; \{n\}\}\; (t)\; =\; \backslash \; varphi\; \_\; \{X\_\; \{1\}\}\; (a\_\; \{1\}\; t)\; \backslash \; varphi\; \_\; \{X\_\; \{2\}\}\; (a\_\; \{2\}\; t)\; \backslash \; cdots\; \backslash \; varphi\; \_\; \{X\_\; \{n\}\}\; (a\_\; \{n\}\; t)\; \backslash ,\; \backslash !\}$

В частности, φ X + Y (t) = φ X (t) φ Y (t). Чтобы убедиться в этом, запишите определение характеристической функции:

$\phi \; X\; +\; Y\; (t)\; =\; E\; \; [eit\; (X\; +\; Y)]\; =\; E\; \; [eit\; X\; eit\; Y]\; =\; E\; \; [eit\; X]\; E\; \; [eit\; Y]\; знак\; равно\; \phi \; Икс\; (T)\; \phi \; Y\; (T)\; \{\backslash \; Displaystyle\; \backslash \; varphi\; \_\; \{X\; +\; Y\}\; (t)\; =\; \backslash \; OperatorName\; \{E\}\; \backslash \; left\; [e\; ^\; \{it\; (X\; +\; Y)\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{itX\}\; e\; ^\; \{itY\}\; \backslash \; right]\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{itX\}\; \backslash \; right]\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{itY\}\; \backslash \; right]\; =\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash \; varphi\; \_\; \{Y\}\; (t)\}$

Независимость X и Y требуется для установления равенства третьего и четвертого выражений.

Другой особый случай, представляющий интерес для одинаково распределенных случайных величин, - это когда i = 1 / n и тогда S n является выборочным средним. В этом случае, написав X вместо среднего,

$\phi \; X\; ¯\; (t)\; =\; \phi \; X\; (tn)\; n\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{\backslash \; overline\; \{X\}\}\; (t)\; =\; \backslash \; varphi\; \_\; \{X\}\; \backslash \; !\; \backslash \; left\; (\{\backslash \; tfrac\; \{t\}\; \{n\}\}\; \backslash \; right)\; ^\; \{n\}\}$

Моменты

Характеристические функции также могут использоваться для поиска моментов случайного переменная. При условии, что момент n существует, характеристическая функция может быть дифференцирована n раз и

$E\; \; [X\; n]\; =\; i\; -\; n\; \phi \; X\; (n)\; (0)\; =\; i\; -\; n\; [dndtn\; \phi \; X\; (t)]\; t\; Знак\; равно\; 0\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [X\; ^\; \{n\}\; \backslash \; right]\; =\; i\; ^\; \{-\; n\}\; \backslash ,\; \backslash \; varphi\; \_\; \{X\}\; ^\; \{(n)\}\; (0)\; =\; i\; ^\; \{-\; n\}\; \backslash ,\; \backslash \; left\; [\{\backslash \; frac\; \{d\; ^\; \{n\}\}\; \{dt\; ^\; \{n\}\}\}\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash \; right]\; \_\; \{t\; =\; 0\}\; \backslash ,\; \backslash !\}$

Например, предположим, что X имеет стандартное распределение Коши. Тогда φ X (t) = e. Это не дифференцируемое при t = 0, что показывает, что распределение Коши не имеет ожидания. Кроме того, характеристическая функция выборочного среднего X n независимых наблюдений имеет характеристическую функцию φ X (t) = (e) = e, используя результат из предыдущего раздела. Это характерная функция стандартного распределения Коши: таким образом, выборочное среднее имеет то же распределение, что и сама генеральная совокупность.

Логарифм характеристической функции - это производящая функция кумулянта, которая полезна для поиска кумулянтов ; некоторые вместо этого определяют кумулянтную производящую функцию как логарифм функции создания момента и называют логарифм характеристической функции второй кумулянтной производящей функцией.

Анализ данных

Характеристические функции могут использоваться как часть процедур для подгонки распределений вероятностей к выборкам данных. Случаи, когда это обеспечивает практически осуществимый вариант по сравнению с другими возможностями, включают подгонку устойчивого распределения, поскольку выражения для плотности в закрытой форме недоступны, что затрудняет реализацию оценки максимального правдоподобия. Доступны процедуры оценки, которые сопоставляют теоретическую характеристическую функцию с эмпирической характеристической функцией , рассчитанной на основе данных. Полсон и др. (1975) и Heathcote (1977) предоставляют некоторые теоретические основы для такой процедуры оценки. Кроме того, Yu (2004) описывает применение эмпирических характеристических функций для соответствия моделям временных рядов, где процедуры правдоподобия нецелесообразны.

Пример

гамма-распределение с параметром масштаба θ и параметром формы k имеет характеристическую функцию

$(1\; -\; \theta \; i\; t)\; -\; k.\; \{\backslash \; displaystyle\; (1-\; \backslash \; theta\; \backslash ,\; i\; \backslash ,\; t)\; ^\; \{-\; k\}.\}$

Теперь предположим, что у нас есть

$X\; \sim \; \Gamma \; (k\; 1,\; \theta )\; и\; Y\; \sim \; \Gamma \; (k\; 2,\; \theta )\; \{\backslash \; displaystyle\; X\; ~\; \backslash \; sim\; \backslash \; Gamma\; (k\_\; \{1\},\; \backslash \; theta)\; \{\backslash \; t\_dv\; \{and\}\}\; Y\; \backslash \; sim\; \backslash \; Gamma\; (k\_\; \{2\},\; \backslash \; theta)\; \backslash ,\}$

с X и Y независимы друг от друга, и мы хотим знать, каково распределение X + Y. Характеристические функции:

$\phi \; X\; (t)\; =\; (1\; -\; \theta \; it)\; -\; k\; 1,\; \phi \; Y\; (t)\; =\; (1\; -\; \theta \; it)\; -\; k\; 2\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; (1-\; \backslash \; theta\; \backslash ,\; i\; \backslash ,\; t)\; ^\; \{-\; k\_\; \{1\}\},\; \backslash ,\; \backslash \; qquad\; \backslash \; varphi\; \_\; \{Y\}\; (t)\; =\; (1-\; \backslash \; theta\; \backslash ,\; i\; \backslash ,\; t)\; ^\; \{\; -k\_\; \{2\}\}\}$

что в силу независимости и основных свойств характеристической функции приводит к

$\phi \; X\; +\; Y\; (t)\; =\; \phi \; X\; (t)\; \phi \; Y\; (t)\; =\; (1\; -\; \theta \; it)\; -\; k\; 1\; (1\; -\; \theta \; it)\; -\; k\; 2\; =\; (1\; -\; \theta \; it)\; -\; (k\; 1\; +\; k\; 2).\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\; +\; Y\}\; (t)\; =\; \backslash \; varphi\; \_\; \{X\}\; (t)\; \backslash \; varphi\; \_\; \{Y\}\; (t)\; =\; (1-\; \backslash \; theta\; \backslash ,\; i\; \backslash ,\; t)\; ^\; \{-\; k\_\; \{1\}\}\; (1-\; \backslash \; theta\; \backslash ,\; i\; \backslash ,\; t)\; ^\; \{-\; k\_\; \{2\}\}\; =\; \backslash \; left\; (1-\; \backslash \; theta\; \backslash ,\; i\; \backslash ,\; t\; \backslash \; right)\; ^\; \{-\; (k\_\; \{1\}\; +\; k\_\; \{2\})\}.\}$

Это характеристическая функция параметра масштаба гамма-распределения θ и параметра формы k 1 + k 2, поэтому мы заключаем

$X\; +\; Y\; \sim \; \Gamma \; (k\; 1\; +\; k\; 2,\; \theta )\; \{\backslash \; displaystyle\; X\; +\; Y\; \backslash \; sim\; \backslash \; Gamma\; (k\_\; \{1\}\; +\; k\_\; \{2\},\; \backslash \; theta)\; \backslash ,\}$

Результат может быть расширен к n независимым гамма-распределенным случайным величинам с одинаковым масштабным параметром, и мы получаем

$\forall \; i\; \in \; \{1,\dots ,\; n\}:\; X\; i\; \sim \; \Gamma \; (ki,\; \theta )\; \Rightarrow \; \sum \; i\; =\; 1\; n\; X\; i\; \sim \; \Gamma \; (\sum \; i\; =\; 1\; nki,\; \theta ).\; \{\backslash \; displaystyle\; \backslash \; forall\; i\; \backslash \; in\; \backslash \; \{1,\; \backslash \; ldots,\; n\; \backslash \}:\; X\_\; \{i\}\; \backslash \; sim\; \backslash \; Gamma\; (k\_\; \{i\},\; \backslash \; theta)\; \backslash \; qquad\; \backslash \; Rightarrow\; \backslash \; qquad\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; X\_\; \{i\}\; \backslash \; sim\; \backslash \; Gamma\; \backslash \; left\; (\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; k\_\; \{i\},\; \backslash \; theta\; \backslash \; right).\}$

Как определено выше, аргумент характеристической функции рассматривается как действительное число: однако некоторые аспекты теории характеристических функций расширяются за счет расширения определения на комплексную плоскость с помощью аналитического продолжения, в случаях где это возможно.

Понятия, связанные с данным, включают функцию создания момента и функцию создания вероятности. Характеристическая функция существует для всех распределений вероятностей. Это не так для функции создания момента.

Характеристическая функция тесно связана с преобразованием Фурье : характеристическая функция функции плотности вероятности p (x) представляет собой комплексно-сопряженное элемента непрерывное преобразование Фурье функции p (x) (согласно обычному соглашению; см. непрерывное преобразование Фурье - другие соглашения ).

$\phi \; Икс\; (t)\; =\; ⟨eit\; X⟩\; =\; \int \; R\; eitxp\; (x)\; dx\; =\; (\int \; R\; e\; -\; itxp\; (x)\; dx)\; ¯\; =\; P\; (t)\; ¯,\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; \backslash \; langle\; e\; ^\; \{itX\}\; \backslash \; rangle\; =\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; e\; ^\; \{itx\}\; p\; (x)\; \backslash ,\; dx\; =\; \{\backslash \; overline\; \{\backslash \; left\; (\backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; e\; ^\; \{-\; itx\}\; p\; (x)\; \backslash ,\; dx\; \backslash \; right)\}\}\; =\; \{\backslash \; overline\; \{P\; (t)\}\},\}$

где P (t) обозначает непрерывный Фурье преобразовать функции плотности вероятности p (x). Аналогично, p (x) может быть восстановлен из φ X (t) с помощью обратного преобразования Фурье:

$p\; (x)\; =\; 1\; 2\; \pi \; \int \; R\; eitx\; P\; (t)\; dt\; =\; 1\; 2\; \pi \; \int \; R\; eitx\; \phi \; X\; (t)\; ¯\; dt.\; \{\backslash \; displaystyle\; p\; (x)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; e\; ^\; \{itx\}\; P\; (t)\; \backslash ,\; dt\; =\; \{\backslash \; frac\; \{1\}\; \{\; 2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{\backslash \; mathbf\; \{R\}\}\; e\; ^\; \{itx\}\; \{\backslash \; overline\; \{\backslash \; varphi\; \_\; \{X\}\; (t)\}\}\; \backslash ,\; dt.\}$

Действительно, даже когда случайная величина не имеет плотности, характеристическую функцию можно рассматривать как преобразование Фурье меры, соответствующей случайной величине.

Другая связанная концепция - это представление распределений вероятностей как элементов воспроизводящего гильбертова пространства ядра посредством встраивания распределений в ядро. Эту структуру можно рассматривать как обобщение характеристической функции при конкретном выборе функции ядра .

• Субзависимость, более слабое условие, чем независимость, которое определяется в терминах характеристических функций.
• Кумулянт, член кумулянтных функций, которые являются журналами характеристических функций.

Цитаты

Источники

• , Энциклопедия математики, EMS Press, 2001 [1994]