 Временной ряд: случайные данные плюс тренд, с наиболее подходящей линией и различными примененными фильтрами
Временной ряд: случайные данные плюс тренд, с наиболее подходящей линией и различными примененными фильтрами A временной ряд - это ряд точек данных, проиндексированных (или перечисленных, или графически отображенных) в порядке времени. Чаще всего временной ряд представляет собой последовательность , взятую в последовательные равноотстоящие моменты времени. Таким образом, это последовательность данных дискретного времени. Анализ временных рядов может быть полезен, чтобы увидеть, как данный актив, ценная бумага или экономическая переменная изменяется с течением времени. Примерами временных рядов являются высоты океанских приливов, количество солнечных пятен и дневное значение закрытия промышленного индекса Доу-Джонса.
. Временные ряды очень часто строятся с помощью запустить диаграммы (временная линейная диаграмма ). Временные ряды используются в статистике, обработке сигналов, распознавании образов, эконометрике, математических финансах, прогноз погоды, прогноз землетрясений, электроэнцефалография, техника управления, астрономия, техника связи, и в основном в любой области прикладной науки и инженерии, которая включает временные измерения.
Анализ временных рядов включает методы анализа данных временных рядов с целью извлечения значимой статистики и других характеристик данных. Прогнозирование временных рядов - это использование модели для прогнозирования будущих значений на основе ранее наблюдаемых значений. Хотя регрессионный анализ часто используется для проверки теории о том, что текущие значения одного или нескольких независимых временных рядов влияют на текущее значение другого временного ряда, этот тип анализа временных рядов не называется «анализ временных рядов», который фокусируется на сравнении значений одного временного ряда или нескольких зависимых временных рядов в разные моменты времени. Прерванный временной ряд анализ - это анализ вмешательств на одном временном ряду.
Данные временных рядов имеют естественный временной порядок. Это отличает анализ временных рядов от перекрестных исследований, в которых нет естественного упорядочения наблюдений (например, объяснение заработной платы людей ссылкой на их соответствующий уровень образования, где данные отдельных лиц могут быть введены в Любой заказ). Анализ временных рядов также отличается от анализа пространственных данных, где наблюдения обычно относятся к географическому местоположению (например, учет цен на жилье по местоположению, а также внутренних характеристик домов). Стохастическая модель для временного ряда, как правило, будет отражать тот факт, что наблюдения, близкие друг к другу во времени, будут более тесно связаны, чем наблюдения дальше друг от друга. Кроме того, модели временных рядов часто используют естественное одностороннее упорядочение времени, так что значения для данного периода будут выражаться как производные некоторым образом из прошлых значений, а не из будущих значений (см. обратимость времени.)
Анализ временных рядов может применяться к вещественным, непрерывным данным, дискретным числовым данным или дискретным символьным данным. данные (т. е. последовательности символов, таких как буквы и слова на английском языке ).
Методы анализа временных рядов можно разделить на два класса: методы частотной области и методы временной области. К первым относятся спектральный анализ и вейвлет-анализ ; последние включают автокорреляционный и кросс-корреляционный анализ. Во временной области корреляция и анализ могут выполняться аналогично фильтру с использованием масштабированной корреляции, тем самым уменьшая необходимость работы в частотной области.
Кроме того, методы анализа временных рядов можно разделить на параметрические и непараметрические методы. Параметрические подходы предполагают, что лежащий в основе стационарный случайный процесс имеет определенную структуру, которая может быть описана с использованием небольшого количества параметров (например, с использованием авторегрессии или модель скользящего среднего ). В этих подходах задача состоит в оценке параметров модели, описывающей случайный процесс. Напротив, непараметрические подходы явно оценивают ковариацию или спектр процесса, не предполагая, что процесс имеет какую-либо конкретную структуру.
Методы анализа временных рядов также можно разделить на линейный и нелинейный, а также одномерный и многомерный.
Временной ряд - это один из типов данных панели . Панельные данные - это общий класс, многомерный набор данных, тогда как набор данных временных рядов - это одномерная панель (как и набор поперечных сечений ). Набор данных может демонстрировать характеристики как панельных данных, так и данных временных рядов. Один из способов узнать - спросить, что отличает одну запись данных от других. Если ответом является поле временных данных, то это кандидат на набор данных временного ряда. Если для определения уникальной записи требуется поле данных о времени и дополнительный идентификатор, не связанный со временем (студенческий билет, символ акций, код страны), то это кандидат на данные панели. Если различие заключается в не-временном идентификаторе, то набор данных является кандидатом на набор перекрестных данных.
Есть несколько типов мотивации и анализа данных, доступных для временных рядов, которые подходят для различных целей.
В контексте статистики, эконометрики, количественных финансов, сейсмологии, метеорология и геофизика. Основная цель анализа временных рядов - прогнозирование. В контексте обработки сигналов, техники управления и техники связи он используется для обнаружения сигнала и оценки. В контексте интеллектуального анализа данных, распознавания образов и машинного обучения анализ временных рядов может использоваться для кластеризации, классификации, запрос по содержанию, обнаружение аномалий, а также прогнозирование.
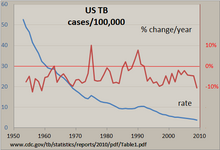 Заболеваемость туберкулезом США 1953-2009 гг.
Заболеваемость туберкулезом США 1953-2009 гг. Самый простой способ проверить регулярный временной ряд вручную - с линейной диаграммой , такой как та, которая показана для туберкулеза в Соединенных Штатах, сделанной с помощью программы для работы с электронными таблицами. Количество случаев было стандартизовано по ставке на 100 000 и рассчитано процентное изменение этой ставки за год. Линия, которая почти неуклонно опускается, показывает, что заболеваемость туберкулезом снижалась на протяжении многих лет, но процентное изменение этого показателя варьировалось на целых +/- 10% с «всплесками» в 1975 году и примерно в начале 1990-х годов. Использование обеих вертикальных осей позволяет сравнивать два временных ряда на одном графике.
Другие методы включают:
Аппроксимация кривой - это процесс построения кривой или математической функции, которая имеет лучше всего подходит для серии данных точек, возможно, с учетом ограничений. Аппроксимация кривой может включать либо интерполяцию, где требуется точное соответствие данным, либо сглаживание, при котором строится «сглаженная» функция, которая приблизительно соответствует данным. Связанная с этим тема - регрессионный анализ, который больше фокусируется на вопросах статистического вывода, таких как степень неопределенности в кривой, которая соответствует данным, наблюдаемым со случайными ошибками. Подгонянные кривые можно использовать в качестве вспомогательных средств для визуализации данных, для определения значений функции, когда данные недоступны, и для суммирования взаимосвязей между двумя или более переменными. Экстраполяция означает использование подобранной кривой за пределами диапазона наблюдаемых данных и подвержен степени неопределенности, поскольку он может отражать метод, использованный для построения кривой, в той же степени, в какой он отражает наблюдаемые данные.
Построение экономических временных рядов включает оценку некоторых компонентов для некоторых дат путем интерполяции между значениями («контрольными показателями») для более ранних и более поздних дат. Интерполяция - это оценка неизвестной величины между двумя известными величинами (исторические данные) или вывод об отсутствующей информации из доступной информации («чтение между строк»). Интерполяция полезна, когда данные, окружающие отсутствующие данные, доступны и известны их тенденции, сезонность и долгосрочные циклы. Это часто делается с использованием связанных рядов, известных на все соответствующие даты. В качестве альтернативы используется полиномиальная интерполяция или сплайн-интерполяция, когда кусочно полиномиальные функции вписываются во временные интервалы, так что они плавно сочетаются друг с другом. Другая проблема, которая тесно связана с интерполяцией, - это аппроксимация сложной функции простой функцией (также называемая регрессией ). Основное различие между регрессией и интерполяцией состоит в том, что полиномиальная регрессия дает один полином, который моделирует весь набор данных. Однако сплайн-интерполяция дает кусочно-непрерывную функцию, состоящую из множества полиномов для моделирования набора данных.
Экстраполяция - это процесс оценки за пределами исходного диапазона наблюдения значения переменной на основе ее взаимосвязи с другой переменной. Это похоже на интерполяцию, которая производит оценки между известными наблюдениями, но экстраполяция подвержена большей неопределенности и более высокому риску получения бессмысленных результатов.
В общем, задача аппроксимации функции требует от нас выбрать функцию среди четко определенного класса, которая близко соответствует («аппроксимирует») целевой функции. в зависимости от задачи. Можно выделить два основных класса задач аппроксимации функций: во-первых, для известных целевых функций теория приближений - это ветвь численного анализа, которая исследует, как определенные известные функции (например, специальные функции ) могут быть аппроксимированы определенным классом функций (например, многочленами или рациональными функциями ), которые часто имеют желаемые свойства (недорогие вычисления, непрерывность, интеграл и ограничение значения и т. д.).
Во-вторых, целевая функция, назовем ее g, может быть неизвестна; вместо явной формулы предоставляется только набор точек (временной ряд) вида (x, g (x)). В зависимости от структуры домена и кодомена g могут применяться несколько методов аппроксимации g. Например, если g - операция над действительными числами, методы интерполяции, экстраполяции, регрессионного анализа и можно использовать подгонку кривой. Если codomain (диапазон или целевой набор) g является конечным набором, вместо этого вы имеете дело с проблемой классификации. Связанная с этим проблема аппроксимации временных рядов в режиме онлайн состоит в том, чтобы суммировать данные за один проход и построить приблизительное представление, которое может поддерживать различные запросы временных рядов с пределами наихудшего случая ошибки.
В некоторой степени различные проблемы (регрессия, классификация, аппроксимация пригодности ) получили единое рассмотрение в теории статистического обучения., где они рассматриваются как контролируемое обучение проблемы.
В статистике, прогноз является частью статистического вывода. Один конкретный подход к такому выводу известен как прогнозирующий вывод, но прогнозирование может выполняться в рамках любого из нескольких подходов к статистическому выводу. Действительно, одно из описаний статистики заключается в том, что она обеспечивает средство передачи знаний об выборке совокупности всему населению и другим связанным популяциям, что не обязательно совпадает с прогнозированием во времени. Когда информация передается во времени, часто в определенные моменты времени, процесс известен как прогнозирование.
Назначение шаблона временного ряда для конкретная категория, например, определение слова на основе серии движений руки на языке жестов.
Этот подход основан на гармоническом анализе и фильтрации сигналов в частотной области с использованием преобразования Фурье и оценка спектральной плотности, разработка которой была значительно ускорена во время Второй мировой войны математиком Норбертом Винером, инженерами-электриками Рудольфом Э. Кальманом, Деннис Габор и другие для фильтрации сигналов от шума и прогнозирования значений сигналов в определенный момент времени. См. фильтр Калмана, теория оценки и цифровая обработка сигналов
Разделение временного ряда на последовательность сегментов. Часто временной ряд может быть представлен как последовательность отдельных сегментов, каждый из которых имеет свои характерные свойства. Например, аудиосигнал конференц-связи можно разделить на части, соответствующие времени, в течение которого говорил каждый человек. При сегментации временных рядов цель состоит в том, чтобы идентифицировать граничные точки сегмента во временном ряду и охарактеризовать динамические свойства, связанные с каждым сегментом. К этой проблеме можно подойти, используя обнаружение точки изменения, или моделируя временные ряды как более сложную систему, такую как линейная система марковского скачка.
Модели для данных временных рядов могут иметь множество форм и представлять различные случайные процессы. При моделировании вариаций уровня процесса три широких класса практического значения: модели авторегрессии (AR), интегрированные (I) модели и скользящее среднее (MA). модели. Эти три класса линейно зависят от предыдущих точек данных. Комбинация этих идей дает модели авторегрессионного скользящего среднего (ARMA) и авторегрессионного интегрированного скользящего среднего (ARIMA). Модель авторегрессионного дробно интегрированного скользящего среднего (ARFIMA) обобщает первые три. Расширения этих классов для работы с векторными данными доступны под заголовком многомерных моделей временных рядов, а иногда предшествующие аббревиатуры расширяются за счет включения начальной буквы «V» для «вектора», как в VAR для векторной авторегрессии .. Дополнительный набор расширений этих моделей доступен для использования в тех случаях, когда наблюдаемые временные ряды управляются некоторыми «вынуждающими» временными рядами (которые могут не иметь причинного воздействия на наблюдаемые ряды): отличие от многомерного случая состоит в том, что серия принуждения может быть детерминированной или находиться под контролем экспериментатора. В этих моделях аббревиатуры дополняются финальной буквой «X», означающей «экзогенный».
Нелинейная зависимость уровня ряда от предыдущих точек данных представляет интерес, отчасти из-за возможности создания хаотического временного ряда. Однако, что более важно, эмпирические исследования могут указать на преимущество использования прогнозов, полученных на основе нелинейных моделей, по сравнению с прогнозами, полученными на основе линейных моделей, как, например, в нелинейных авторегрессионных экзогенных моделях. Дополнительные ссылки на нелинейный анализ временных рядов: (Kantz and Schreiber) и (Abarbanel)
Среди других типов моделей нелинейных временных рядов есть модели для представления изменений дисперсии во времени (гетероскедастичность ). Эти модели представляют авторегрессионную условную гетероскедастичность (ARCH), и набор содержит большое количество разнообразных представлений (GARCH, TARCH, EGARCH, FIGARCH, CGARCH и т. Д.). Здесь изменения в изменчивости связаны с недавними прошлыми значениями наблюдаемых рядов или предсказываются ими. Это контрастирует с другими возможными представлениями локально изменяющейся изменчивости, где изменчивость может быть смоделирована как управляемая отдельным изменяющимся во времени процессом, как в дважды стохастической модели.
в недавней работе по безмодельному анализу, методы, основанные на вейвлет-преобразовании (например, локальные стационарные вейвлеты и нейронные сети, разложенные по вейвлетам) получили признание. Методы многоуровневого (часто называемого множественным разрешением) разлагают данный временной ряд, пытаясь проиллюстрировать временную зависимость в нескольких масштабах. См. Также Мультифрактал с марковским переключением (MSMF) для моделирования эволюции волатильности.
A Скрытая марковская модель (HMM) - это статистическая марковская модель, в которой моделируемая система считается марковским процессом с ненаблюдаемыми (скрытыми) состояниями. HMM можно рассматривать как простейшую динамическую байесовскую сеть. Модели HMM широко используются в распознавании речи для преобразования временного ряда произнесенных слов в текст.
Для анализа временных рядов используется ряд различных обозначений. Обычная нотация, определяющая временной ряд X, который индексируется натуральными числами, записывается как
Другое распространенное обозначение:
где T - набор индексов.
Есть два набора условий, при которых строится большая часть теории:
Однако идеи стационарности должны быть расширены, чтобы учесть две важные идеи: строгая стационарность и стационарность второго порядка. И модели, и приложения могут быть разработаны при каждом из этих условий, хотя модели в последнем случае можно рассматривать как частично определенные.
Кроме того, может применяться анализ временных рядов, если ряды сезонно стационарны или нестационарны. Ситуации, когда амплитуды частотных составляющих изменяются со временем, можно разрешить с помощью частотно-временного анализа, который использует частотно-временное представление временного ряда или сигнала.
Инструменты для исследования данных временных рядов включают:
Показатели временных рядов или характеристики, которые можно использовать для временных рядов классификации или регрессионного анализа :
Временные ряды можно визуализировать с помощью двух категорий диаграмм: перекрывающихся диаграмм и отдельных диаграмм. Перекрывающиеся диаграммы отображают все временные ряды в одном макете, в то время как отдельные диаграммы представляют их на разных макетах (но выровнены для целей сравнения)
| На Викискладе есть материалы, связанные с Временные ряды. |