
 Пояснения к показателю Ляпунова
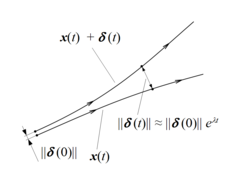
Пояснения к показателю Ляпунова В математике, то показатель Ляпунова или Ляпунова характеристический показатель из динамической системы является величиной, которая характеризует скорость разделения, бесконечно близких траекторий. Количественно две траектории в фазовом пространстве с начальным вектором разделения расходятся (при условии, что расходимость можно рассматривать в рамках линеаризованного приближения) со скоростью, определяемой выражением
где - показатель Ляпунова.
Скорость отрыва может быть разной для разных ориентаций вектора начального отрыва. Таким образом, имеется спектр показателей Ляпунова, равный по численности размерности фазового пространства. Обычно наибольший показатель называют максимальным показателем Ляпунова (MLE), поскольку он определяет понятие предсказуемости динамической системы. Положительный MLE обычно рассматривается как указание на то, что система хаотична. (при выполнении некоторых других условий, например компактности фазового пространства). Обратите внимание, что произвольный начальный вектор разделения обычно будет содержать некоторую составляющую в направлении, связанном с MLE, и из-за экспоненциальной скорости роста влияние других показателей со временем будет стираться.
Экспонента названа в честь Александра Ляпунова.
Максимальный показатель Ляпунова можно определить следующим образом:
Предел гарантирует справедливость линейного приближения в любое время.
Для системы с дискретным временем (карты или итерации с фиксированной точкой) для орбиты, начинающейся с этого, это означает:
 Ведущий вектор Ляпунова.
Ведущий вектор Ляпунова. Для динамической системы с уравнением эволюции в n -мерном фазовом пространстве спектр показателей Ляпунова
в общем, зависит от отправной точки. Однако нас обычно интересует аттрактор (или аттракторы) динамической системы, и обычно с каждым аттрактором связан один набор показателей. Выбор начальной точки может определить, на каком аттракторе окажется система, если их больше одного. (Для гамильтоновых систем, не имеющих аттракторов, это не проблема.) Показатели Ляпунова описывают поведение векторов в касательном пространстве фазового пространства и определяются из матрицы Якоби
этот якобиан определяет эволюцию касательных векторов, заданных матрицей, через уравнение
с начальным условием. Матрица описывает, как небольшое изменение в точке распространяется до конечной точки. Лимит
определяет матрицу (условия существования предела даются теоремой Оселедца ). Показатели Ляпунова определяются собственными значениями.
Набор показателей Ляпунова будет одинаковым почти для всех начальных точек эргодической компоненты динамической системы.
Чтобы ввести показатель Ляпунова, рассмотрим фундаментальную матрицу (например, для линеаризации вдоль стационарного решения в непрерывной системе фундаментальная матрица состоит из линейно независимых решений первого приближения системы. Сингулярные значения матрицы равны квадратные корни из собственных значений матрицы.Наибольший показатель Ляпунова имеет вид
А. М. Ляпунов доказал, что если система первого приближения регулярна (например, все системы с постоянными и периодическими коэффициентами регулярны) и ее наибольший показатель Ляпунова отрицателен, то решение исходной системы асимптотически устойчиво по Ляпунову. Позже О. Перрон заявил, что требование регулярности первого приближения является существенным.
В 1930 году О. Перрон построил пример системы второго порядка, в которой первое приближение имеет отрицательные показатели Ляпунова вдоль нулевого решения исходной системы, но в то же время это нулевое решение исходной нелинейной системы является неустойчивым по Ляпунову. Кроме того, в некоторой окрестности этого нулевого решения почти все решения исходной системы имеют положительные показатели Ляпунова. Также можно построить обратный пример, в котором первое приближение имеет положительные показатели Ляпунова вдоль нулевого решения исходной системы, но в то же время это нулевое решение исходной нелинейной системы устойчиво по Ляпунову. Эффект обращения знаков показателей Ляпунова решений исходной системы и системы первого приближения с одинаковыми начальными данными впоследствии был назван эффектом Перрона.
Контрпример Перрона показывает, что наибольший отрицательный показатель Ляпунова, как правило, не указывает на стабильность, и что наибольший положительный показатель Ляпунова, как правило, не указывает на хаос.
Следовательно, нестационарная линеаризация требует дополнительного обоснования.
Если система консервативна (т. Е. Отсутствует диссипация ), элемент объема фазового пространства останется неизменным вдоль траектории. Таким образом, сумма всех показателей Ляпунова должна быть равна нулю. Если система диссипативна, сумма показателей Ляпунова отрицательна.
Если система является потоком и траектория не сходится к одной точке, один показатель всегда равен нулю - показатель Ляпунова, соответствующий собственному значению с собственным вектором в направлении потока.
Спектр Ляпунова можно использовать для оценки скорости производства энтропии, фрактальной размерности и размерности Хаусдорфа рассматриваемой динамической системы. В частности, из знания спектра Ляпунова можно получить так называемую размерность Ляпунова (или размерность Каплана – Йорка ), которая определяется следующим образом:
где - максимальное целое число, при котором сумма наибольших показателей все еще неотрицательна. представляет собой верхнюю границу информационного измерения системы. Более того, сумма всех положительных показателей Ляпунова дает оценку энтропии Колмогорова – Синая согласно теореме Песина. Наряду с широко используемыми численными методами оценки и вычисления размерности Ляпунова существует эффективный аналитический подход, основанный на прямом методе Ляпунова со специальными функциями типа Ляпунова. Показатели Ляпунова ограниченной траектории и ляпуновская размерность аттрактора инвариантны относительно диффеоморфизма фазового пространства.
Мультипликативный обратная наибольшего показателя Ляпунова иногда называют в литературе как время ляпуновской, и определяет характерное электронное -folding время. Для хаотических орбит время Ляпунова будет конечным, тогда как для обычных орбит оно будет бесконечным.
 Точки внутри и снаружи множества Мандельброта раскрашены показателем Ляпунова.
Точки внутри и снаружи множества Мандельброта раскрашены показателем Ляпунова. Как правило, вычисление показателей Ляпунова, как определено выше, не может быть выполнено аналитически, и в большинстве случаев приходится прибегать к численным методам. Ранний пример, который также представляет собой первую демонстрацию экспоненциального расхождения хаотических траекторий, был проведен Р. Х. Миллером в 1964 году. В настоящее время наиболее часто используемая численная процедура оценивает матрицу, основанную на усреднении нескольких приближений определения предела за конечное время.
Один из наиболее часто используемых и эффективных численных методов вычисления спектра Ляпунова для гладкой динамической системы основан на периодической ортонормировке Грама – Шмидта векторов Ляпунова, чтобы избежать смещения всех векторов в направлении максимального расширения.
Для расчета показателей Ляпунова по ограниченным экспериментальным данным были предложены различные методы. Однако применение этих методов сопряжено с множеством трудностей, и к таким проблемам следует подходить осторожно. Основная трудность заключается в том, что данные не полностью исследуют фазовое пространство, скорее, они ограничены аттрактором, который имеет очень ограниченное (если вообще есть) распространение по определенным направлениям. Эти более тонкие или более единичные направления в наборе данных связаны с более отрицательными показателями. Было показано, что использование нелинейных отображений для моделирования эволюции малых смещений от аттрактора значительно улучшает возможность восстановления спектра Ляпунова при условии, что данные имеют очень низкий уровень шума. Также исследовалась особенность данных и их связь с более отрицательными показателями.
В то время как (глобальный) показатель Ляпунова дает меру общей предсказуемости системы, иногда представляет интерес оценка локальной предсказуемости вокруг точки x 0 в фазовом пространстве. Это может быть сделано через собственные значения в якобиевой матрице J 0 ( х 0). Эти собственные значения также называются локальными показателями Ляпунова. (Предупреждение: в отличие от глобальных показателей эти локальные показатели не инвариантны при нелинейном изменении координат).
Этот термин обычно используется в отношении синхронизации хаоса, в которой две системы связаны, обычно однонаправленно, так что существует система привода (или ведущая) и система ответа (или ведомая). Условные показатели - это показатели системы отклика с системой привода, рассматриваемой просто как источник (хаотического) сигнала возбуждения. Синхронизация происходит, когда все условные показатели отрицательны.