Кластерный анализ

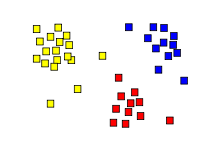
Задача группировки объектов так, чтобы объекты в одной группе (или кластере) были более похожи друг на друга, чем на те в других кластерах Результат кластерного анализа, показанный в виде раскрашивания квадратов в три кластера.

Кластерный анализ или кластеризация - это задача группировки объектов набора таких, объектов в одной группе (называемой кластером ) похожи (в некотором смысле) друг на друга, чем на объекты в других группах (кластерах). Это основная задача исследовательского общего анализа данных и метод статистического анализа данных, используемых во многих областях, включая распознавание образов, анализ изображений, поиск информации, биоинформатика, сжатие данных, компьютерная графика и машина обучение.

Сам по себе кластерный анализ - это не какой-то конкретный алгоритм, общая задача, которую необходимо решить. Это может быть достигнуто с помощью различных алгоритмов, которые значительно различаются по своему пониманию того, что составляет кластер и как их эффективно находить. Популярные понятия кластеров включают группы с небольшими расстояниями между элементами кластера, плотными областями пространства данных, интервалами или конкретными статистическими распределениями. Таким образом, кластеризацию можно сформулировать как задачу многоцелевой оптимизации. Соответствующий алгоритм кластеризации и параметры параметров (включая такие параметры, как функция расстояния для использования, порог плотности или количество ожидаемых кластеров) зависят от индивидуального набора данных и предполагаемого использования результатов, достижения. Кластерный анализ как таковой - это не автоматическая задача, а итеративный процесс обнаружения знаний или интерактивной многоцелевой оптимизации, которая включает себя в испытания и неудачи. Часто бывает необходимо изменить предварительную обработку данных и параметров модели, пока результат не достигает желаемых свойств.

Помимо термина кластеризация, существует ряд терминов с похожим расположением, включая автоматическую классификацию, числовую таксономию, ботриологию (от греческого βτρυς «виноград»), типологический анализ и выявление сообществ. Тонкие различия часто заключаются в использовании результатов: если при интеллектуальном анализе данных интерес представляют результирующие группы, то при классификации интерес представляет результирующая различительная способность.

Кластерный анализ зародился в антропологии Драйвером и Крёбером в 1932 году и введен в психологию Джозефом Зубином в 1938 году и Робертом Трайоном в 1939 году и широко использовался Кеттелла начиная с 1943 г. для классификации черт личности в психологии.

• 1 Определение
• 2 Алгоритмы
  • 2.1 Кластеризация на основе подключений (иерархическая кластеризация)
  • 2.2 Центроид- кластеризация на основе
  • 2.3 Кластеризация на основе распределения
  • 2.4 Кластеризация на основе плотности
  • 2.5 Кластеризация на основе сетки
  • 2.6 Последние разработки
• 3 Оценка и оценка
  • 3.1 Внутренняя оценка
  • 3.2 Внешняя оценка
  • 3.3 Кластерная тенденция
• 4 Приложения
  • 4.1 Биология, вычислительная биология и биоинформатика
  • 4.2 Медицина
  • 4.3 Бизнес и маркетинг
  • 4.4 Всемирная паутина
  • 4.5 Информатика
  • 4.6 Социальные
  • 4.7 Другое
• 5 См.
  • 5.1 Специализированные типы кластерного анализа
  • 5.2 Методы, используемые также в кластерном анализе
  • 5.3 Проекция и предварительная обработка данных
  • 5.4 Другое
• 6 Ссылки

Понятие «Кластер» не может быть точно определено, что является одним из причин, по которому существуют так много алгоритмов кластеризации. Есть общий знаменатель: группа объектов данных. Однако разные исследователи используют разные кластерные модели, и для каждой из этих кластерных моделей могут быть предложены разные алгоритмы. Понятие кластера, найденное различными алгоритмами, значительно различается по своим свойствам. Понимание этих «кластерных моделей» является ключом к пониманию различных алгоритмов. Типичные модели кластеров включают:

• модели связности: например, иерархическая кластеризация строит модели на основе удаленной связи.
• модели Centroid: например, алгоритм k-средних представляет каждый кластер одним среднимом.
• Модели распределения: кластеры моделируются с использованием статистических распределений, таких как многомерные нормальные распределения, используются алгоритмом максимизации ожидания.
• Модели плотности: например, DBSCAN и ОПТИКА определяют кластеры как связанные плотные области в пространственных данных.
• Модели подпространств: в бикластеризации (также известный как совместная кластеризация или двухрежимная кластеризация), кластеры моделируются как члены кластера, так и атрибутами.
• Групповые модели: некоторые алгоритмы не предоставляют уточненную модель для своих результатов, а просто группировку информации.
• Модели на основе графиков: клика, то есть подмножество узлов в графе, такое что накануне Если два узла в подмножестве соединены ребром, это можно рассматривать как прототип кластера. Ослабление требований к полному соединению (часть ребер может отсутствовать) известны как квазиклики, как в алгоритме кластеризации HCS.
• Модели подписанного графа: каждый путь в знаковый граф знак из произведений знаков на ребрах. Согласно предположениям теории баланса, ребра могут менять знак и приводить к бифуркации графа. Более слабая «аксиома кластеризации» (ни один цикл не имеет ровно одно отрицательное ребро) дает результаты с более чем двумя кластерами или подграфами только с положительными ребрами.
• Нейронные модели: наиболее известная неконтролируемая нейронная сеть - это самоорганизующаяся карта, и эти модели обычно можно охарактеризовать как аналогичные одним или нескольким из вышеперечисленных моделей и других моделей подпространства, нейронная сеть, реализуют форму анализа основных компонентов или анализа независимых компонентов.

«Кластеризация» - это, по сути, набор таких кластеров, обычно используются все объекты в наборе данных. Кроме того, он может указывать отношения кластеров друг к другу, например иерархию кластеров, встроенных друг в друга. Кластеризацию можно примерно разделить на:

• Жесткая кластеризация: каждый объект принадлежит кластеру или нет.
• Мягкая кластеризация (также: нечеткая кластеризация ): каждый объект принадлежит каждому кластеру в определенной степени (например, вероятность принадлежности к кластеру)

Возможны также более тонкие различия, например:

• Строгая кластеризация секционирования: каждый объект принадлежит ровно одному кластеру
• Строгая кластеризация секционирования с выбросами: объекты также могут принадлежать ни одному кластеру и выбросу выбросами
• Перекрывающаяся кластеризация (также: альтернативная кластеризация, многовидовая кластеризация) : объекты могут принадлежать более чем одному кластеру; обычно включает кластеры
• Иерархическая кластеризация: объекты, которые принадлежат подчиненному кластеру, также принадлежат родительскому кластеру
• Кластеризация подпространства : при перекрывающейся кластеризации в однозначно определенном подпространстве кластеры не ожидаются для перекрытия

Как указано выше, алгоритмы кластеризации можно разделить на категории на основе их модели кластера. В следующем обзоре будут представлены наиболее известные примеры алгоритмов кластеризации, как возможно, существует более 100 опубликованных алгоритмов кластеризации. Не все модели для своих кластеров, поэтому их нелегко разделить на категории. Обзор алгоритмов, объясненных в Википедии, можно найти в списке статистических алгоритмов.

Не существует объективно «правильного» алгоритма кластеризации, но, как было принято, «кластеризация находится в поле зрения смотрящего». Наиболее подходящий алгоритм кластеризации для конкретной задачи часто следует выбрать экспериментально, если нет математической причины предпочесть одну модель кластера другая. Алгоритм, используется для одного типа модели, обычно не работает на одном типе модели, который содержит радикально другой тип модели. Например, k-means не может найти невыпуклые кластеры.

Кластеризация на основе подключения (иерархическая кластеризация)

Кластеризация на основе подключения, также известная как иерархическая кластеризация, основана на идее о том, что объекты больше связаны с близкими соседями объектами, чем с объектами, находящимися дальше. Эти алгоритмы соединяют «объекты» в «кластеры» в зависимости от их расстояния. Кластер можно описать в основном максимальным расстоянием, установленным для частей кластера. На разных расстояниях будут формироваться разные кластеры, которые могут быть представлены с помощью дендрограммы, которая объясняет, откуда взялось общее название «иерархическая кластеризация »: эти алгоритмы не обеспечивают единого разделения набора данных, но вместо этого специальную иерархию кластеров, сливаются друг с другом с помощью специальных инструкций. В дендрограмме ось Y отмечает расстояние, на котором кластеры сливаются, а объекты размещаются вдоль оси x, так что кластеры не смешиваются.

Кластеризация на основе связности - это целое семейство методов, которые различаются способами расстоянияний. Помимо обычного выбора функций выбора, пользователю также необходимо выбрать критерий связи (поскольку кластер состоит из нескольких объектов, есть несколько условий для вычисления расстояния) для использования. Популярные варианты как известны одинарная кластеризация (минимальное расстояние до объекта), полная связка кластеризация (максимальное расстояние до объекта) и UPGMA или WPGMA («Метод невзвешенной или взвешенной парной группы со средним арифметическим», также известный как кластеризация средних связей). Кроме того, иерархическая кластеризация может быть агломеративной (начиная с отдельных элементов и их в кластеры) или разделяющей (начиная с полного набора и разделяя его на разделы).

Эти методы производят не уникальное разбиение набора данных, иерархию, из которой пользователю по-прежнему следует выбирать подходящие кластеры. Они не очень устойчивы к выбросам, которые либо проявляются как дополнительные кластеры, либо даже вызывают слияние других кластеров (известное как «явление сцепления», в частности, с кластеризацией с одной связью ). В общем случае сложность составляет $O\; (n\; 3)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{O\}\}\; (n\; ^\; \{3\})\}$для агломеративной кластеризации и $O\; (2\; n\; -\; 1)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{O\}\}\; (2\; ^\; \{n-1\})\}$для делительной кластеризации, что делает их слишком медленными для больших наборов данных. Для некоторых случаев известны оптимальные эффективные методы (сложности $O\; (n\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; mathcal\; \{O\}\}\; (n\; ^\; \{2\})\}$): SLINK для одиночного соединения и CLINK для кластеризации полного связывания. В сообществе эти методы интеллектуального анализа данных эти методы признаны устаревшими системами анализа, но часто устаревшими. Однако новые методы создания вдохновения для многих более поздних методов.

• Примеры кластеризации связей
• 

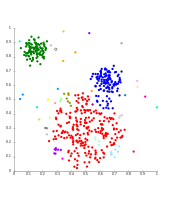
  Одинарная связь по гауссовским данным. В 35 кластерах самый большой кластер начинает фрагментироваться на более мелкие части, в то время как раньше он все еще был связан со вторым по величине из-за эффекта одноканальности.

• 

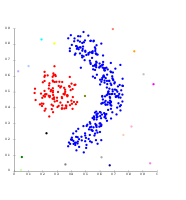
  Одинарное соединение на кластерах на основе плотности. Извлечено 20 кластеров, большинство из которых содержат одиночные элементы, как кластеризация связей не имеет понятия «шум».

Кластеризация на основе центроидов

При кластеризации на основе центроидов кластеры представлены центральным вектором, который не обязательно может быть членом набора данных. Когда количество кластеров фиксировано на k, кластеризация k-средних дает формальное определение как задачу оптимизации: найти k центров кластеров и назначить объекты ближайшего центру кластера, так что квадраты расстояний от кластера свернут.

Сама проблема оптимизации, как известно, является NP-сложной, и поэтому общий подход заключается в поиске только приблизительных решений. Особенно хорошо хорошо приближенным методом является алгоритм Ллойда, часто называемый просто «алгоритм k-средних» (хотя другой алгоритм представил это название ). Однако он находит только локальный оптимум и обычно запускается несколько раз с разными случайными инициализациями. Вариации k-средних часто включают такие оптимизации, как выбор лучшего из нескольких прогонов, но также ограничение центроидов улучшения данных (k-medoids ), выбор медианы (кластеризация k- медианы ), выбирая начальные центры менее случайным образом (k-means ++ ) или разрешая нечеткое назначение кластеров (нечеткие c-means ).

Большинство алгоритмов типа k-means требуют заранее указать количество кластеров - k -, что считается одним из самых больших недостатков этих алгоритмов. Кроме того, алгоритмы предпочитают кластеры одинакового размера, так как они всегда присваивают объект ближайшему центроиду. Это часто приводит к неправильной обрезке границ кластеров (что неудивительно, алгоритм оптимизирует кластеры кластеров, а не границы кластеров).

K-средство обладает рядом теоретических свойств. Во-первых, он разбивает пространство данных на данные, известную как диаграмма Вороного. Во-втором он концептуально близок к классификации ближайшего соседа и поэтому популярен в машинном обучении. В-третьих, его можно рассматривать как кластеризацию на основе модели, вариант алгоритма Ллойда - как вариант алгоритма максимизации ожидания для этой модели, обсуждаемой ниже.

• Примеры кластеризации k-средних
• 

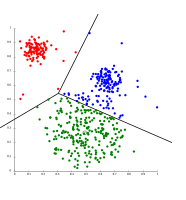
  k-средство разделяет данные в ячейках Вороного, что предполагает наличие кластеров одинакового размера (здесь)

• 

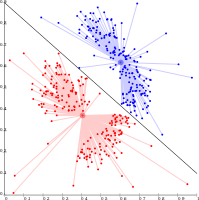
  k-средство может представлять кластеры на основе плотности

Центроидные кластеры такие задачи, как k-средства и k-medoids, являются частными случаями некомпенсированной метрической задачи размещения оборудования, канонической проблемы в сообществах исследователей операций и вычислительной геометрии. Задача состоит в том, чтобы найти основные складские места для оптимального обслуживания заданного набора потребителей. Можно рассматривать «склады» как центроиды кластера, а «местоположения потребителей» - как данные, вызываие кластеризации. Это позволяет применить разработанные алгоритмические решения из литературы по размещению объектов рассматриваемого в настоящее время задаче кластеризации на основе центроидов.

Кластеризация на основе распределения

Модель кластеризации, наиболее связанная со статистикой, основанная на моделях распределения. Затем кластеры можно легко определить как объекты, принадлежащие, скорее всего, к одному и тому же распределению. Удобным свойством этот метод является то, что он очень похож на способ создания набора искусственных данных: выборки случайных объектов из распределения.

Хотя теоретические основы этих методов превосходна, они страдают одной ключевой проблемой, известной как переоснащение, если не наложены ограничения на сложность модели. Более сложная модель обычно лучше объясняет данные, что затрудняет выбор подходящей сложности модели.

Один известный метод известен как модели смеси Гаусса (с использованием алгоритма максимизации ожидания ). Здесь набор данных обычно моделируется с фиксированным (во избежание переобучения) гауссовых распределений, которые инициализируются случайным образом и параметры которых итеративно оптимизируются для лучшего соответствия набору данных. Это сведется к локальному оптимуму, поэтому несколько прогонов могут дать результаты разные. Чтобы получить кластеризацию, объектам часто присваивается гауссово распределение, которое они, скорее всего, принадлежат; для мягких кластеров в этом нет необходимости.

Кластеризация на основе распределения создает сложные модели для кластеров, которые могут фиксировать корреляцию и зависимость между атрибутами. Однако эти алгоритмы ложатся дополнительным бременем на пользователя: для многих реальных наборов данных может не быть четко определенной математической модели (например, если предположить, что распределение Гаусса является довольно сильным допущением для данных).

• Примеры кластеризации гауссовской модели смеси
• 

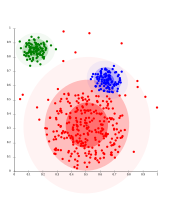
  Для данных с распределением по Гауссу, EM работает хорошо, поскольку он использует гауссианы для моделирования кластеров

• 

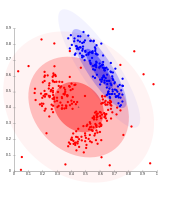
  Кластеры на основе плотности не могут быть смоделированы с использованием распределений Гаусса

Кластеризация на основе плотности

При кластеризации на основе плотности кластеры определяются как области с более высокой плотностью, чем остальная часть набора данных. Объекты в разреженных областях, необходимые для разделения кластеров, обычно считаются шумовыми и граничными точками.

Самый популярный метод кластеризации на основе плотности - DBSCAN. В отличие от многих более новых методов, он имеет четко определенную кластерную модель, называемую «плотность-достижимость». Подобно кластеризации на основе связей, она основана на соединении точек в пределах определенных пороговых значений расстояния. Однако он соединяет только точки, удовлетворяющие критерию плотности, в исходном варианте, определяемом как минимальное количество других объектов в пределах этого радиуса. Кластер состоит из всех связанных плотностью объектов (которые могут образовывать кластер произвольной формы в отличие от многих других методов) плюс все объекты, которые находятся в пределах диапазона этих объектов. Еще одним интересным свойством DBSCAN является то, что его сложность довольно низкая - для него требуется линейное количество запросов диапазона в базе данных - и что он обнаружит практически одинаковые результаты (это детерминированный для точек ядра и шума, но не для пограничных точек) в каждом прогоне, поэтому нет необходимости запускать его несколько раз. ОПТИКА - это обобщение DBSCAN, которое устраняет необходимость выбора подходящего значения для параметра диапазона $\epsilon \; \{\backslash \; displaystyle\; \backslash \; varepsilon\}$и дает иерархический результат, связанный с этим из кластеризации связей. DeLi-Clu, Density-Link-Clustering объединяет идеи из однокомпонентной кластеризации и OPTICS, полностью устраняя параметр $\epsilon \; \{\backslash \; displaystyle\; \backslash \; varepsilon\}$и предлагая улучшения производительности сверх ОПТИКА с использованием индекса R-tree.

Ключевым недостатком DBSCAN и OPTICS является то, что они ожидают некоторого падения плотности для обнаружения границ кластера. На наборах данных, например, с перекрывающимися распределениями Гаусса - обычным вариантом использования искусственных данных - границы кластера, созданные этими алгоритмами, часто будут выглядеть произвольно, поскольку плотность кластера непрерывно уменьшается. На наборе данных, состоящем из смесей гауссиан, эти алгоритмы почти всегда уступают таким методам, как EM-кластеризация, которые могут точно моделировать данные такого типа.

Среднее смещение - это подход к кластеризации, при которомкаждый объект перемещается в область с наибольшей плотностью в его окрестностях, на основе плотности ядра. В конце концов объекты сходятся к локальным максимумам плотности. Подобно кластеризации k-средних, эти «аттракторы плотности» могут служить данным набора, но средний сдвиг может обнаруживать кластеры произвольной формы, аналогичные DBSCAN. Из-за дорогостоящей итерационной процедуры и оценки плотности среднего обычно медленнее, чем DBSCAN или k-Means. Кроме применимости алгоритма среднего сдвига к многомерным данным затруднена из-за негладкого поведения оценки плотности ядра, что приводит к чрезмерной фрагментации хвостов кластера.

• Примеры кластеризации на основе плотности
• 

  На основе кластеризации плотности с помощью DBSCAN.

• 

  DBSCAN предполагает наличие проблем кластеров с одинаковой плотностью и может иметь с разделением соседних кластеров

• 

  ОПТИКА - DBSCAN, улучшающий обработку кластеров с разной плотностью

На основе сетки кластеризация

Метод на основе сетки используется для многомерного набора данных. В этом методе мы создаем сеточную структуру, и выполняется процедура на сетках (также известных как ячейки). Метод на основе быстрых и имеет низкую вычислительную сложность. Существует два типа методов кластеризации на основе сетки: STING и CLIQUE. В алгоритме кластеризации на основе сети используются следующие шаги:

1. Разделение пространства данных на конечное число ячеек.
2. Произвольно выбрать 'c', где c не следует переходить заранее.
3. Вычислить плотность c
4. Если плотность c больше пороговой плотности
   1. Пометьте ячейку c как новый кластер
   2. Рассчитайте плотность всех соседей 'c'
   3. Если плотность соседней ячейки больше, чем пороговая плотность, плотность ячейки в кластер и повторяйте шаги 4.2 и 4.3, пока не будет соседа. с плотностью выше пороговой.
5. Повторяйте шаги 2, 3 и 4, пока не пройдете все ячейки.
6. Стоп.

Последние разработки

В последние годы были предприняты значительные усилия было вложено в улучшение реализации алгоритмов. Среди них - CLARANS (Ng and Han, 1994) и BIRCH (Zhang et al., 1996). В связи с недавней необходимостью обрабатывать все большие и большие наборы данных (также известные как большие данные ), желание обменять семантическое сгенерированных кластеров на производительность растет. Это привело к развитию методов предварительной кластеризации, таких как кластеризация навеса, которые могут обрабатывать наборы данных, но полученные «кластеры» предоставили лишь грубое предварительное разбиение набора данных для последующего анализа с существующими более медленными методами, такими как кластеризация k-средних.

Для большой размерности из используемых методов многие методы не работают из-за проклятия размерности, которое отображает функции расстояния проблематичны в многомерныхх. Это привело к появлению новых алгоритмов кластеризации для данных большой размерности, которые сосредоточены на кластеризации подпространств (где используются только некоторые атрибуты, а модели кластеров включают соответствующие атрибуты для кластера) и корреляционная кластеризация, которая также ищет произвольно повернутые («коррелированные») кластеры подпространств, которые можно смоделировать, задав корреляцию их атрибутов. Примерами таких алгоритмов кластеризации являются CLIQUE и SUBCLU.

. Идеи из методов кластеризации на основе плотности (в частности, семейство алгоритмов DBSCAN / OPTICS ) были адаптированы для подпространства кластеризация (HiSC, иерархическая кластеризация подпространств и DiSH) и корреляционная кластеризация (HiCO, иерархическая корреляционная кластеризация, 4C с использованием «корреляционной связности» и ERiC, исследующие иерархические корреляционные кластеры на основе плотности).

Было предложено несколько различных систем кластеризации, основанных на взаимной информации. Один из них - вариант метрики информации Марины Мейла; другой обеспечение иерархическую кластеризацию. Используя генетические алгоритмы, можно оптимизировать широкий спектр различных функций, включая взаимную информацию. Кроме того, распространение иммунений, недавнее развитие информатики и статистической физики, создание к созданию новых типов алгоритмов кластеризации.

Оценка (или «проверка») результатов кластеризации так же сложна, как и сама кластеризация. Популярные подходы включают в себя «внутреннюю» оценку, где кластеризацию сводят к единому баллу качества, «внешнюю» оценку, где кластеризацию сравнивают с существующей «предлагаемой» классификацией, «ручную» оценку экспертом-человеком и «косвенную» "оценку путем оценки полезности кластеризации

Внутренние меры оценки страдают, заключаются в том, что они включают функции, которые сами по себе могут рассматриваться как цель кластеризации. Например, можно кластеризовать набор данных по коэффициенту Silhouette; Используя такую ​​внутреннюю меру для оценки, можно сравнить схожесть задач оптимизации, не обязательно, насколько полезна кластеризация.

Внешняя оценка имеет аналогичные: если у нас есть такие метки «наземной истины», то нам не нужно будет кластеризоваться; й, метки отражают только одно возможное разделение набора данных, что не означает, что не существует другой стороны, даже лучшей стороны кластеризации.

Таким образом, ни один из этих подходов не может в конечном итоге судить о фактическом качестве кластеризации, но для этого нужна человеческая оценка, которая очень субъективна. Тем не менее, такая статистика может быть весьма информативной при выявлении кластеров, но не следует отказываться от субъективной оценки.

Внутренняя оценка

Когда результат кластеризации оценивается на основе данных, которые сами были кластеризованы, это называется внутренней оценкой. Эти методы обычно присваивают лучший алгоритм алгоритма, который создает кластеры с высоким результатом внутри кластера и низким результатом между кластерами. Одним из недостатков использования внутренних критериев является создание высоких баллов по внутреннему критерию. Кроме того, эта оценка смещена в сторону алгоритмов, использующих одну и ту же модель кластера. Например, кластеризация k-средним естественным образом оптимизирует расстояние до объектов, а критерий критерия, основанный на расстоянии, скорее всего, переоценит результирующую кластеризацию.

Следовательно, меры внутренней оценки лучше всего подходят для ситуаций, когда один алгоритм работает лучше, чем другой, но это не должно означать, что один алгоритм дает более достоверные результаты, чем другой. Валидность, измеряемая индексом, зависит от утверждения, что такая структура существует в наборе данных. Алгоритм, для каких-то моделей, не имеет шансов, если набор данных содержит радикально другой набор моделей или если измеряет радикально другой критерий. Например, кластеризация k-средних может найти только выпуклые кластеры, некоторые оценочные индексы предполагают выпуклые кластеры. В наборе данных с невыпуклыми кластерами нецелесообразно использование k-средних, ни критерия оценки, предполагающего выпуклость.

Существует более десятка внутренних мер оценки, обычно основанных на интуиции, элементы в одном кластере должны быть более похожи, чем элементы в разных кластерах. Например, для оценки качества алгоритмов кластеризации по внутреннему критерию можно использовать следующие методы:

• индекс Дэвиса - Болдина

индекс Дэвиса - Болдина можно рассчитать по следующей формуле:

$DB\; знак\; 1\; N\; \sum \; я\; знак\; равно\; 1\; Н\; макс.\; J\; \ne \; я\; (\sigma \; я\; +\; \sigma \; jd\; (ci,\; cj))\; \{\backslash \; displaystyle\; DB\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash \; max\; \_\; \{j\; \backslash \; neq\; i\; \}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; sigma\; \_\; \{i\}\; +\; \backslash \; sigma\; \_\; \{j\}\}\; \{d\; (c\_\; \{i\},\; c\_\; \{j\})\}\}\; \backslash \; right)\}$

, где n - количество кластеров, $ci\; \{\backslash \; displaystyle\; c\_\; \{i\}\}$- центроид кластера $i\; \{\backslash \; displaystyle\; i\}$, $\sigma \; i\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{i\; \}\}$- среднее расстояние от всех элементов в кластере $i\; \{\backslash \; displaystyle\; i\}$до центроида. $ci\; \{\backslash \; displaystyle\; c\_\; \{i\}\}$и $d\; (ci,\; cj)\; \{\backslash \; displaystyle\; d\; (c\_\; \{i\},\; c\_\; \{j\})\}$- расстояние между центроидами $ci\; \{\backslash \; displaystyle\; c\_\; \{i\}\}$и $cj\; \{\backslash \; displaystyle\; c\_\; \{j\}\}$. Низкое межкластерное сходство, низкий уровень индекса Дэвиса-Боулдина, алгоритм кластеризации, который создает набор кластеров с наименьшим Дэвиса - Болдина считается лучшим алгоритмом на основе этого критерия.

• Индекс Данна

Индекс Данна направлен на выявление плотных и хорошо разделенных кластеров. Он определен как отношение минимального расстояния между кластерами к максимальному расстоянию внутри кластера. Для каждого раздела кластера индекс можно рассчитать по следующей формуле:

где d (i, j) представляет собой расстояние между кластерами i и j, а d '(k) измеряет внутрикластерное расстояние кластера k. Межкластерное расстояние d (i, j) между двумя кластерами может быть любым числом мер расстояния, расстоянием между центроидами кластеров. Точно такое же расстояние d '(k) внутри кластера может быть измерено различными способами, например, максимальное расстояние между любым парой элементов в кластере k. Этот критерий критерий ищет кластеры с высоким внутрикластным сходством и низким межкластерным сходством, более желательными алгоритмы, тысячей кластеры с высоким индексом Данна.

• Коэффициент длины

Коэффициент силуэта контрастирует со средним расстоянием до элементов в одном и том же кластере со средним расстоянием до элементов в других кластерах. Объекты с высокими значениями положения хорошо сгруппированными. Этот хорошо работает с кластеризацией k-средних средних, а также используется для определения оптимального количества кластеров.

Внешняя оценка

При внешней оценке результатов кластеризации оцениваются на основе данных, которые не использовались для кластеризации., например известные метки классов и внешние тесты. Такие тесты состоят из набора классических элементов. Таким образом, наборы тестов можно рассматривать как золотой стандарт для оценки. Эти методы оценки позволяют измерить, насколько близка кластеризация к заранее определенным тестовым классам. Обсуждалось, подходит ли это для реальных данных или только для синтетических наборов данных с фактической истиной, поскольку классы могут содержать внутреннюю структуру, присутствующие атрибуты могут не допускать разделения кластеров или классы могут содержать аномалии. Кроме того, с точки зрения открытия знаний предполагаемым результатом не обязательно может быть предполагаемым результатом. В специальном сценарии ограниченной кластеризации, где метаинформация (например, метаинформация) уже используется в процессе кластеризации, удержание информации для целей оценки нетривиально.

Ряд показателей адаптирован из вариантов, использования для оценки задач классификации. Вместо подсчета количества раз, когда класс был правильно назначен одной точке данных (известный как истинных положительных результатов ), такие показатели подсчета пар оценивают, является ли каждая пара точек данных, которая действительно находится в одном кластере, предполагается, что они находятся в одном кластере.

Как и в случае внутренней оценки, существует несколько внешних показателей оценки, например:

• Чистота : Чистота - это мера того, в какой степени кластеры содержат один класс. Его расчет можно представить следующим образом: для каждого кластера подсчитайте количество точек данных из наиболее распространенного класса в указанном кластере. Теперь возьмите сумму по всем кластерам и разделите на общее количество точек данных. Формально, учитывая некоторый набор кластеров $M\; \{\backslash \; displaystyle\; M\}$и некоторый набор классов $D\; \{\backslash \; displaystyle\; D\}$, оба разделяют $N\; \{\; \backslash \; displaystyle\; N\}$точки данных, чистота может быть определена как:

$1\; N\; \sum \; m\; \in \; M\; max\; d\; \in \; D\; |\; м\; \cap \; д\; |\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{N\}\}\; \backslash \; sum\; \_\; \{m\; \backslash \; in\; M\}\; \backslash \; max\; \_\; \{d\; \backslash \; in\; D\}\; \{|\; m\; \backslash \; cap\; d\; |\}\}$

Эта мера не наказывает наличие много кластеров, и большее количество кластеров облегчит получение высокой чистоты. Оценка чистоты 1 всегда возможна, если каждая точка данных помещается в отдельный кластер. Кроме того, чистота не подходит для несбалансированных данных, где даже плохо работающие алгоритмы кластеризации дадут высокую чистоту. Например, если набор данных размером 1000 состоит из двух классов, один из которых содержит 999 точек, а другой - 1 точку, тогда каждый возможный раздел будет иметь чистоту не менее 99,9%.

• Индекс Rand ( William M. Rand 1971)

Индекс Rand вычисляет, насколько кластеры (возвращаемые алгоритмом кластеризации) похожи на эталонные классификации. Его можно вычислить по следующей формуле:

$RI\; =\; TP\; +\; TNTP\; +\; FP\; +\; FN\; +\; TN\; \{\backslash \; displaystyle\; RI\; =\; \{\backslash \; frac\; \{TP\; +\; TN\}\; \{TP\; +\; FP\; +\; FN\; +\; TN\}\}\}$

где $TP\; \{\backslash \; displaystyle\; TP\}$- количество истинных положительных результатов, $TN\; \{\backslash \; displaystyle\; TN\}$- количество истинных отрицательных результатов, $FP\; \{\backslash \; displaystyle\; FP\}$- количество ложных срабатываний, а $FN\; \{\backslash \; displaystyle\; FN\}$- количество ложноотрицательные. Подсчитываемые здесь экземпляры - это количество правильных попарных назначений. То есть $TP\; \{\backslash \; displaystyle\; TP\}$- это количество пар точек, которые сгруппированы вместе в прогнозируемом разделе и в разделе основной достоверности $FP\; \{\backslash \; displaystyle\; FP\}$- это количество пар точек, которые сгруппированы вместе в прогнозируемом разделе, но не в разделе основной достоверности и т. д. Если набор данных имеет размер N, затем $TP\; +\; TN\; +\; FP\; +\; FN\; =\; (N\; 2)\; \{\backslash \; displaystyle\; TP\; +\; TN\; +\; FP\; +\; FN\; =\; \{\backslash \; binom\; \{N\}\; \{2\}\}\}$.

Одна проблема с Индекс Rand состоит в том, что ложные срабатывания и ложноотрицательные имеют одинаковый вес. Это может быть нежелательной характеристикой для некоторых приложений кластеризации. F-мера решает эту проблему, так же как и скорректированный на случайность скорректированный индекс Рэнда.

• F-мера

F-мера может исправить для уравновешивания вклада ложных отрицательных результатов посредством взвешивания отзыв с помощью программы $\beta \; \ge \; 0\; \{\backslash \; displaystyle\; \backslash \; beta\; \backslash \; geq\; 0\}$. Пусть precision и recall (обе меры внешней оценки сами по себе) используемым следующим образом:

$P\; =\; TPTP\; +\; FP\; \{\; \backslash \; displaystyle\; P\; =\; \{\backslash \; frac\; \{TP\}\; \{TP\; +\; FP\}\}\}$

$R\; =\; TPTP\; +\; FN\; \{\backslash \; displaystyle\; R\; =\; \{\backslash \; frac\; \{TP\}\; \{TP\; +\; FN\}\}\}$

где $P\; \{\backslash \; displaystyle\; P\}$- это точность скорости, а $R\; \{\backslash \; displaystyle\; R\}$- отзыв. Мы можем вычислить F-меру, используя следующую формулу:

$F\; \beta \; =\; (\beta \; 2\; +\; 1)\; \cdot \; P\; \cdot \; R\; \beta \; 2\; \cdot \; P\; +\; R\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; beta\}\; =\; \{\backslash \; frac\; \{(\backslash \; бета\; ^\; \{2\}\; +1)\; \backslash \; cdot\; P\; \backslash \; cdot\; R\}\; \{\backslash \; beta\; ^\; \{2\}\; \backslash \; cdot\; P\; +\; R\}\}\}$

Когда $\beta \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; 0\}$, $F\; 0\; =\; P\; \{\backslash \; Displaystyle\; F\_\; \{0\}\; =\; P\}$. Другими словами, отзыв не влияет на F-меру, когда $\beta \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; 0\}$и увеличивает $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$выделяется увеличивающийся вес для отзыва в последнем F.

Также $TN\; \{\backslash \; displaystyle\; TN\}$не принимается во внимание счет и может изменяться от 0 и выше без ограничения.

• Индекс Жаккара

Индекс Жаккара используется для количественной оценки сходства двух ассеты данных. Индекс Жаккард принимает значения от 0 до 1. Индекс 1 означает, что два набора, индекс 0 указывает, что наборы данных не имеют общих элементов. Индекс Жаккара определяет следующую формулой:

$J\; (A,\; B)\; =\; |\; A\; \cap \; B\; |\; |\; A\; \cup \; B\; |\; =\; TPTP\; +\; FP\; +\; FN\; \{\backslash \; displaystyle\; J\; (A,\; B)\; =\; \{\backslash \; frac\; \{|\; A\; \backslash \; cap\; B\; |\}\; \{|\; A\; \backslash \; cup\; B\; |\}\}\; =\; \{\backslash \; frac\; \{TP\}\; \{TP\; +\; FP\; +\; FN\}\}\}$

Это просто количество уникальных элементов, общих для обоих наборов, деленное на общее количество уникальных элементов в обоих наборах.

Также $TN\; \{\backslash \; displaystyle\; TN\}$не учитывается и может неограниченно изменяться от 0 вверх.

• Индекс кости

Симметричная мера игральной кости удваивает вес на $TP\; \{\backslash \; displaystyle\; TP\}$, при этом $TN\; \{\backslash \; displaystyle\; TN\}$:

$DSC\; =\; 2\; TP\; 2\; TP\; +\; FP\; +\; FN\; \{\backslash \; displaystyle\; DSC\; =\; \{\backslash \; frac\; \{2TP\}\; \{2TP\; +\; FP\; +\; FN\}\}\}$

• индекс Фаулкса - Маллоуса (EB Fowlkes CL Mallows, 1983)

Индекс Фаулкса - Мэллоуса вычисляет сходство между кластерами, возвращаемыми алгоритмами кластеризации, и эталонными классификациями. Чем выше значение индекса Фаулкса - Маллоуса, тем более похожи кластеры и эталонные классификации. Его можно вычислить по формуле:

$FM\; =\; TPTP\; +\; FP\; \cdot \; TPTP\; +\; FN\; \{\backslash \; Displaystyle\; FM\; =\; \{\backslash \; sqrt\; \{\{\backslash \; frac\; \{TP\}\; \{TP\; +\; FP\}\}\; \backslash \; cdot\; \{\backslash \; frac\; \{TP\}\; \{TP\; +\; FN\}\}\}\}\}$

где $TP\; \{\backslash \; displaystyle\; TP\}$- количество истинных положительных результатов, $FP\; \{\backslash \; displaystyle\; FP\}$- количество ложных срабатываний, а $FN\; \{\backslash \; displaystyle\; FN\}$- количество ложных отрицательных результатов. Индекс $FM\; \{\backslash \; displaystyle\; FM\}$- это среднее геометрическое для точности и вспомнить $P\; \{\backslash \; displaystyle\; P\}$и $R\; \{\backslash \; displaystyle\; R\}$, поэтому они также известны как G-мера, а F-мера - их среднее гармоническое значение. Кроме того, точность и отзыв также известные как индексы Уоллеса $BI\; \{\backslash \; displaystyle\; B\; ^\; \{I\}\}$и $BII\; \{\backslash \; displaystyle\; B\; ^\; \{II\}\}$. Нормализованные версии вероятности отзыва, точности и G-меры соответствуют Информированность, Маркированность и Корреляция Мэтьюза и сильно связаны с Каппа.

• взаимная информация - это теоретико-информационная мера того, сколько информации распределяется между кластеризацией и типификацией, которая может проявлять нелинейное сходство между двумя кластерами. Нормализованная взаимная информация - это пониженное смещение для различных номеров кластеров.
• Матрица неточностей

Матрица неточностей может установка для быстрой визуализации результатов алгоритма классификации (или кластеризации). Он показывает, насколько кластер отличается от кластера золотого стандарта.

Кластерная тенденция

Чтобы измерить кластерную тенденцию, нужно измерить, в какой степени кластеры существуют в данных, вызываих кластеризации, и может быть выполнено в качестве начального теста перед попыткой кластеризации. Один из способов сделать это - сравнить данные со случайными данными. В среднем случайные данные не должны иметь кластеров.

• Статистика Хопкинса

Существует несколько формулировок статистики Хопкинса. Типичный из них следующий. Пусть $X\; \{\backslash \; displaystyle\; X\}$будет набором $n\; \{\backslash \; displaystyle\; n\}$точек данных в $d\; \{\backslash \; displaystyl\; e\; d\}$пространственное пространство. Рассмотрим случайную выборку (без замены) из $m\; \ll \; n\; \{\backslash \; displaystyle\; m\; \backslash \; ll\; n\}$точек с элементами $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$. Также сгенерируйте набор $Y\; \{\backslash \; displaystyle\; Y\}$из $m\; \{\backslash \; displaystyle\; m\}$равномерно распределенных точек данных. Теперь определите две меры расстояния: $ui\; \{\backslash \; displaystyle\; u\_\; \{i\}\}$как расстояние $yi\; \in \; Y\; \{\backslash \; displaystyle\; y\_\; \{i\}\; \backslash \; in\; Y\}$от ближайшего соседа в X и $wi\; \{\backslash \; displaystyle\; w\_\; \{i\}\}$как расстояние $xi\; \in \; X\; \{\backslash \; displaystyle\; x\_\; \{i\}\; \backslash \; in\; X\}$от его ближайшего к X. Затем мы определяем статистику Хопкинса как:

$H\; =\; \sum \; i\; =\; 1\; muid\; \sum \; i\; =\; 1\; muid\; +\; \sum \; i\; =\; 1\; mwid,\; \{\backslash \; displaystyle\; H\; =\; \{\backslash \; frac\; \{\backslash \; sum\; \_\; \{i\; =\; 1\; \}\; ^\; \{m\}\; \{u\_\; \{i\}\; ^\; \{d\}\}\}\; \{\backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{m\}\; \{u\_\; \{i\}\; ^\; \{d\}\}\; +\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{\; m\}\; \{w\_\; \{i\}\; ^\; \{d\}\}\}\}\; \backslash ,,\}$

Согласно этому определению, однородные случайные данные должны иметь значения, близкие к 0,5, кластеризованные данные должны иметь тенденцию, чтобы иметь значения, близкие к 1.

Однако данные, содержащие только один гауссиан, также будут иметь оценку, близкую к 1, поскольку эта статистика измеряет отклонение от равномерного распределения, а не мультимодальность, что делает эту статистику в отношении ст епени бесполезен в применении (реальные данные никогда не являются единообразными).

Биология, com Предполагаемая биология и биоинформатика

Растение и животное экология

Кластерный анализ используется для описания и пространственного и временного сравнения сообществ (сообществ) организмов в гетерогенной среде. Он также используется в систематике растений для создания искусственных филогений или кластеров организмов (особей) вида, рода или более высокого уровня, которые разделяют ряд атрибутов.

Транскриптомика

Кластеризация используется для создания групп генов со связанными паттернами экспрессии (также известными как коэкспрессированные гены), как в алгоритме кластеризации HCS. Часто такие группы включают функционально связанные белки, такие как ферменты для конкретного пути или гены, которые совместно регулируются. Высокопроизводительные эксперименты с использованием теговируемой последовательности (EST) или микипов ДНК могут быть мощным инструментом аннотации генома - общих элементов геномики.

Анализ последовательностей

Кластеризация последовательностей используется для группировки гомологичных последовательностей в семейства генов. Это очень важное понятие в биоинформатике и эволюционной биологии в целом. См. Эволюцию посредством дупликации генов.

Показатели генотипирования платформ

Для автоматического генотипов используются алгоритмы кластеризации.

Генетическая кластеризация человека

Развитие генетических данных используются в кластеризации для структуры населения.

Медицина

Медицинская визуализация

На ПЭТ-сканированиях можно использовать кластерный анализ для различных типов тканей в трехмерном изображении для множества различных целей.

Анализ антимикробной активности

Кластерный анализ можно использовать для анализа паттернов устойчивости к антибиотикам, для классификации антимикробных соединений в соответствии с их механизмом действия, для классификации антибиотиков в соответствии с их антибактериальной активностью.

IMRT-сегментация

Кластеризация может разделить карты потока на отдельные области для преобразования в доставляемые поля в лучевой терапии на основе MLC.

Бизнес и маркетинг

Исследование рынка

Кластерный анализ исследований широко используется в исследованиях рынка при работе с многомерными данными из опросов и тестовых панелей. Исследователи рынка используют кластерный анализ для разделения совокупности из потребителей на сегменты рынка и лучшего понимания отношений между группами / потребителей272>клиентов, а также для использования в различных сегментации рынка, позиционирование продукта, разработка нового продукта и выбор тестовых рынков.

Группировка товаров

Кластеризацию можно использовать для группировки всех товаров, доступных в Интернете, в набор уникальных товаров. Например, все товары на eBay могут быть сгруппированы в уникальные товары (eBay не имеет концепции SKU ).

World Wide Web

Анализ социальных сетей

В исследовании социальные сети, кластеризация программных группировок поиска сообществ внутри больших групп людей.

Группировка результатов поиска

В процессе группировки групп файлов и веб-сайтов, кластеризация может для создания релевантного набора Результаты поиска по сравнению с обычными поисковыми системами, такими как Google. В настоящее время существует ряд веб-инструментов кластеризации, таких как Clusty. Каждое отдельное использование соответствует уникальному кластеру результатов, что позволяет алгоритму ранжирования возвращать исчерпывающие результа. ты. путем выбора лучшего результата из каждого кластера.

Оптимизация скользящей карты

Карта фотографий Flickr и другие сайты карт используют кластеризацию, чтобы уменьшить количество маркеров на карте. Это ускоряет работу и уменьшает количество визуального беспорядка.

Информатика

Эволюция программного обеспечения

Кластеризация программного обеспечения, благодаря уменьшению унаследованных свойств кода за счет реформирования функций, которые стали рассредоточенными. Это форма реструктуризации и, следовательно, способ профилактического обслуживания.

Сегментация изображения

Кластеризация местная область для разделения цифрового изображения на отдельные для обнаружение границ или распознавание объектов.

Эволюционные алгоритмы

Кластеризация может использовать различные ниш в популяции эволюционного алгоритма, чтобы репродуктивные возможности быть распределены более равномерно среди видов или подвиды.

Рекомендательные системы

Рекомендуемые системы разработаны, чтобы рекомендовать новые товары на основе вкусов пользователя. Иногда они используют алгоритмы кластеризации для прогнозирования предпочтений пользователя на основе предпочтений других пользователей в кластере пользователя.

Методы Монте-Карло с цепью Маркова

Кластеризация часто используется для определения местоположения и характеристики экстремумов в целевом распределении.

Обнаружение аномалий

Аномалии / выбросы обычно - явно или неявно - в отношении структуры кластеризации в данных.

Обработка естественного языка

Кластеризация может устранить проблему лексической двусмысленности.

Социальные наука

Анализ преступности

Кластерный анализ можно использовать для используемых областей, где имеется больше случаев различных видов преступлений. Выявив эти области отдельные или «горячие точки», где подобное преступление произошло в течение определенного периода времени.

Интеллектуальный анализ образовательных данных

Кластерный анализ, например, используется для использования группы школ или учащихся со схожими характеристиками.

Типологии

На основе данных опросов проектов, которые используются исследовательским центром Pew Research Center, используют кластерный анализ для определения типов мнений, привычек и демографических характеристик, могут быть полезны в политике и маркетинге.

Другое

Полевая робототехника

Алгоритмы кластеризации используются для ситуационной осведомленности роботов, чтобы отслеживать объекты и использовать выбросы в данных датчиков.

Математическая химия

Найти структурное поведение и т. д., например, 3000 химических соединений были сгрупп в пространстве 90 топологических индексов.

Климатология

Чтобы найти погодные режимы или предпочтительные атмосферные модели давления на уровне моря.

Финансы

Кластерный анализ был использован для кластеризации запасов по секторам.

Нефтяная геология

Кластерный анализ используется для восстановления недостающих данных о керне забоя или недостающих каротажных кривых для оценки свойств коллектора.

Геохимия

Кластеризация химических свойств в разных местах пробы.

На Викискладе есть средства массовой информации, связанные с Кластерный анализ.

Специализированные типы кластерного анализа

• Автоматические алгоритмы кластеризации
• Сбалансированная кластеризация
• Кластеризация многомерных данных
• Концептуальная кластеризация
• Консенсусная кластеризация
• кластерная кластеризация
• Обнаружение сообщества
• Кластеризация потока данных
• Кластеризация HCS
• Кластеризация последовательностей
• Спектральная кластеризация

Методы, используемые в кластерном анализе

• Искусственная нейронная сеть (ANN)
• Поиск ближайшего соседа
• Анализ компонентов соседства
• Анализ скрытых классов
• Распространение сходства

Данные проецирование и предварительная обработка

• Уменьшение размеров
• Прин анализ компонентов cipal
• Многомерное масштабирование

Другое

• Моделирование с взвешиванием по кластерам
• Проклятие размерности
• Определение количества клас теров в наборе данных
• Параллельные координаты
• Анализ структурированных данных