UPGMA

редактировать

Метод агломеративной иерархической кластеризации

UPGMA (метод невзвешенной парной группы со средним арифметическим ) является простой агломеративный (восходящий) метод иерархической кластеризации. Этот метод обычно приписывается Sokal и Michener.

. Метод UPGMA аналогичен его взвешенному варианту, методу WPGMA.

Обратите внимание, что невзвешенный член указывает, что все расстояния вносят равный вклад в каждое вычисленное среднее значение, и не относится к математике, с помощью которой оно достигается. Таким образом, простое усреднение в WPGMA дает взвешенный результат, а пропорциональное усреднение в UPGMA дает невзвешенный результат (см. Рабочий пример).

Содержание

1 Алгоритм
2 Рабочий пример
- 2.1 Первый шаг
- 2.2 Второй этап
- 2.3 Третий этап
- 2.4 Заключительный этап
- 2.5 Дендрограмма UPGMA
- 2.6 Сравнение с другими связями
3 Использование
4 Сложность времени
5 См. Также
6 Ссылки
7 Внешние ссылки

Алгоритм

Алгоритм UPGMA строит корневое дерево (дендрограмма ), которое отражает структуру, представленную в попарной матрице сходства (или матрица несходства ). На каждом шаге ближайшие два кластера объединяются в кластер более высокого уровня. Расстояние между любыми двумя кластерами $A {\ displaystyle {\ mathcal {A }}}$ ${\ mathcal {A}}$ и $B {\ displaystyle {\ mathcal {B}}}$ ${\ mathcal {B}}$ , каждый размером (т. Е. мощность ) $| A | {\ displaystyle {| {\ mathcal {A}} |}}$ ${\ displaystyle {| {\ mathcal {A}} |}}$ и $| B | {\ displaystyle {| {\ mathcal {B}} |}}$ ${\ displaystyle {| {\ mathcal {B}} |}}$ , принимается как среднее всех расстояний $d (x, y) {\ displaystyle d (x, y)}$ $d (x, y)$ между парами объектов $x {\ displaystyle x}$ $x$ в $A {\ displaystyle {\ mathcal {A}}}$ ${\ mathcal {A}}$ и $y { \ displaystyle y}$ $y$ в $B {\ displaystyle {\ mathcal {B}}}$ ${\ mathcal {B}}$ , то есть среднее расстояние между элементами каждого кластера:

1 | А | ⋅ | B | ∑ Икс ∈ A ∑ Y ∈ B d (x, y) {\ displaystyle {1 \ over {| {\ mathcal {A}} | \ cdot | {\ mathcal {B}} |}} \ sum _ {x \ in {\ mathcal {A}}} \ sum _ {y \ in {\ mathcal {B}}} d (x, y)}

{1 \ over {| {\ mathcal {A }} | \ cdot | {\ mathcal {B}} |}} \ sum _ {{x \ in {\ mathcal {A}}}} \ sum _ {{y \ in {\ mathcal {B}}}} d (Икс, Y)

Другими словами, на каждом шаге кластеризации обновленное расстояние между объединенными кластерами $A ∪ B {\ displaystyle {\ mathcal {A}} \ cup {\ mathcal {B}}}$ ${ \ displaystyle {\ mathcal {A}} \ cup {\ mathcal {B}}}$ и новый кластер $X {\ displaystyle X}$ $X$ дается пропорциональным усреднением $d A, X {\ displaystyle d _ {{\ mathcal {A}}, X}}$ ${\ displaystyle d _ {{\ mathcal {A}}, X}}$ и $d B, X {\ displaystyle d_ {{\ mathcal {B}}, X}}$ ${\ displaystyle d _ {{\ mathcal {B}}, X}}$ расстояния:

$d (A ∪ B), X = | А | ⋅ d A, X + | B | ⋅ d B, X | А | + | B | {\ displaystyle d _ {({\ mathcal {A}} \ cup {\ mathcal {B}}), X} = {\ frac {| {\ mathcal {A}} | \ cdot d _ {{\ mathcal {A} }, X} + | {\ mathcal {B}} | \ cdot d _ {{\ mathcal {B}}, X}} {| {\ mathcal {A}} | + | {\ mathcal {B}} |} }}$ ${\ Displaystyle d _ {({\ mathcal {A}} \ cup {\ mathcal {B}}), X} = {\ frac {| {\ mathcal {A} } | \ cdot d _ {{\ mathcal {A}}, X} + | {\ mathcal {B}} | \ cdot d _ {{\ mathcal {B}}, X}} {| {\ mathcal {A}} | + | {\ mathcal {B}} |}}}$

Алгоритм UPGMA создает корневые дендрограммы и требует допущения о постоянной скорости - то есть, он принимает ультраметрическое дерево, в котором расстояния от корня до каждого конца ветви равны. Когда подсказки представляют собой молекулярные данные (например, ДНК, РНК и белок ), взятые одновременно, предположение ультраметричности становится эквивалентным для предположения о молекулярных часах.

Рабочий пример

Этот рабочий пример основан на JC69 матрице генетических расстояний, вычисленной на основе выравнивания последовательности 5S рибосомной РНК из пяти бактерий: Bacillus subtilis ( $a {\ displaystyle a}$ $a$ ), Bacillus stearothermophilus ( $b {\ displaystyle b}$ $b$ ), Lactobacillus viridescens ( $c {\ displaystyle c}$ $c$ ), Acholeplasma modicum ( $d {\ displaystyle d}$ $d$ ) и Micrococcus luteus ( $e {\ displaystyle e}$ $е$ ).

Первый шаг

Первая кластеризация

Предположим, что у нас есть пять элементов $(a, b, c, d, e) {\ displaystyle (a, b, c, d, e)}$ $(a, b, c, d, e)$ и следующая матрица $D 1 {\ displaystyle D_ {1}}$ $D_{1}$ попарных расстояний между ними:

	a	b	c	d	e
a	0	17	21	31	23
b	17	0	30	34	21
c	21	30	0	28	39
d	31	34	28	0	43
e	23	21	39	43	0

В этом примере $D 1 (a, b) = 17 {\ displaystyle D_ {1} (a, b) = 17}$ ${\ displaystyle D_ {1} (a, b) = 17}$ - наименьшее значение $D 1 {\ displaystyle D_ {1}}$ $D_{1}$ , поэтому мы объединяем элементы $a {\ displaystyle a}$ $a$ и $b {\ displaystyle b }$ $b$ .

Оценка длины первой ветви

Пусть $u {\ displaystyle u}$ $u$ обозначает узел, к которому $a {\ displaystyle a}$ $a$ и $b {\ displaystyle b}$ $b$ теперь подключены. Установка $δ (a, u) = δ (b, u) = D 1 (a, b) / 2 {\ displaystyle \ delta (a, u) = \ delta (b, u) = D_ {1} (a, b) / 2}$ ${\ displaystyle \ delta (a, u) = \ delta (b, u) = D_ {1} (a, b) / 2}$ гарантирует, что элементы $a {\ displaystyle a}$ $a$ и $b {\ displaystyle b}$ $b$ равноудалены из $u {\ displaystyle u}$ $u$ . Это соответствует ожиданиям гипотезы ультраметричности. Ветви, соединяющие $a {\ displaystyle a}$ $a$ и $b {\ displaystyle b}$ $b$ с $u {\ displaystyle u}$ $u$ тогда длина $δ (a, u) = δ (b, u) = 17/2 = 8,5 {\ displaystyle \ delta (a, u) = \ delta (b, u) = 17/2 = 8,5}$ ${\ displaystyle \ delta ( a, u) = \ delta (b, u) = 17/2 = 8,5}$ (см. Окончательную дендрограмму)

Первое обновление матрицы расстояний

Затем мы переходим к обновлению исходной матрицы расстояний $D 1 {\ displaystyle D_ {1}}$ $D_{1}$ в новую матрицу расстояний $D 2 {\ displaystyle D_ {2}}$ $D_ {2}$ (см. Ниже), размер уменьшен на одну строку и один столбец из-за кластеризации $a {\ displaystyle a}$ $a$ с $b {\ displaystyle b}$ $b$ . Значения, выделенные жирным шрифтом в $D 2 {\ displaystyle D_ {2}}$ $D_ {2}$ , соответствуют новым расстояниям, вычисленным с помощью усреднения расстояний между каждым элементом первого кластера $(a, b) {\ displaystyle (a, b)}$ $(a, b)$ и каждый из оставшихся элементов:

$D 2 ((a, b), c) = (D 1 (a, c) × 1 + D 1 (b, c) × 1) / (1 + 1) = (21 + 30) / 2 = 25,5 {\ displaystyle D_ {2} ((a, b), c) = (D_ {1} ( a, c) \ раз 1 + D_ {1} (b, c) \ times 1) / (1 + 1) = (21 + 30) /2=25,5}$ ${\ displaystyle D_ {2} ((a, b), c) = (D_ {1} (a, c) \ times 1 + D_ { 1} (b, c) \ раз 1) / (1 + 1) = (21 + 30) /2=25.5}$

$D 2 ((a, b), d) знак равно (D 1 (a, d) + D 1 (b, d)) / 2 = (31 + 34) / 2 = 32,5 {\ displaystyle D_ {2} ((a, b), d) = ( D_ {1} (a, d) + D_ {1} (b, d)) / 2 = (31 + 34) /2=32.5}$ ${\ displaystyle D_ {2} ((a, b), d) = (D_ {1} (a, d) + D_ { 1} (b, d)) / 2 = (31 + 34) /2=32.5}$

$D 2 ((a, b), e) = (D 1 (a, e) + D 1 (b, e)) / 2 = (23 + 21) / 2 = 22 {\ displaystyle D_ {2} ((a, b), e) = (D_ {1} ( a, e) + D_ {1} (b, e)) / 2 = (23 + 21) / 2 = 22}$ ${\ displaystyle D_ {2} ((a, b), e) = (D_ {1} (a, e) + D_ {1} (b, e)) / 2 = ( 23 + 21) / 2 = 22}$

Значения, выделенные курсивом в $D 2 {\ displaystyle D_ {2}}$ На $D_ {2}$ обновление матрицы не влияет, поскольку они соответствуют расстояниям между элементами, не участвующими в первом кластере.

Второй шаг

Вторая кластеризация

Теперь мы повторяем три предыдущих шага, начиная с новой матрицы расстояний $D 2 {\ displaystyle D_ {2}}$ $D_ {2}$

	(a, b)	c	d	e
(a, b)	0	25,5	32,5	22
c	25,5	0	28	39
d	32,5	28	0	43
e	22	39	43	0

Здесь $D 2 ((a, b), е) = 22 {\ displaystyle D_ {2} ((a, b), e) = 22}$ ${\ displaystyle D_ {2} ((a, b), e) = 22}$ - наименьшее значение из $D 2 {\ displaystyle D_ {2}}$ $D_ {2}$ , поэтому мы объединяем кластер $(a, b) {\ displaystyle (a, b)}$ $(a, b)$ и элемент $e {\ displaystyle e}$ $е$ .

Оценка длины второй ветви

Пусть $v {\ displaystyle v}$ $v$ обозначает узел, к которому $(a, b) {\ displaystyle (a, b)}$ $(a, b)$ и $e {\ displaystyle e}$ $е$ теперь подключены. Из-за ограничения ультраметричности ветви, соединяющие $a {\ displaystyle a}$ $a$ или $b {\ displaystyle b}$ $b$ с $v {\ displaystyle v}$ $v$ и $e {\ displaystyle e}$ $е$ to $v {\ displaystyle v}$ $v$ равны и имеют следующую длину: $δ (a, v) знак равно δ (b, v) знак равно δ (e, v) = 22/2 = 11 {\ displaystyle \ delta (a, v) = \ delta (b, v) = \ delta (e, v) = 22/2 = 11}$ ${\ displaystyle \ delta (a, v) = \ delta (b, v) = \ delta (e, v) = 22/2 = 11}$

Вычисляем недостающую длину ветви: $δ (u, v) = δ (e, v) - δ (a, u) = δ (e, v) - δ (б, и) знак равно 11-8,5 = 2,5 {\ Displaystyle \ дельта (и, v) = \ дельта (е, v) - \ дельта (а, и) = \ дельта (е, v) - \ дельта ( b, u) = 11-8,5 = 2,5}$ ${\ displaystyle \ дельта (и, v) = \ дельта (е, v) - \ дельта (а, и) = \ дель та (е, v) - \ дельта (b, u) = 11-8,5 = 2,5}$ (см. окончательную дендрограмму)

Обновление матрицы второго расстояния

Затем мы переходим к обновлению $D 2 {\ displaystyle D_ {2}}$ $D_ {2}$ в новую матрицу расстояний $D 3 {\ displaystyle D_ {3}}$ $D_ {3}$ (см. Ниже), уменьшенную на одну строку и один столбец из-за кластеризации $(a, б) {\ displaystyle (a, b)}$ $(a, b)$ с $e {\ displaystyle e }$ $е$ . Значения, выделенные жирным шрифтом в $D 3 {\ displaystyle D_ {3}}$ $D_ {3}$ , соответствуют новым расстояниям, вычисленным с помощью пропорционального усреднения :

$D 3 (((a, b), e), c) = (D 2 ((a, b), c) × 2 + D 2 (e, c) × 1) / (2 + 1) = (25,5 × 2 + 39 × 1) / 3 = 30 { \ Displaystyle D_ {3} (((a, b), e), c) = (D_ {2} ((a, b), c) \ times 2 + D_ {2} (e, c) \ times 1) / (2 + 1) = (25,5 \ times 2 + 39 \ times 1) / 3 = 30}$ ${\ displaystyle D_ {3} (((a, b), e), c) = (D_ {2} (( а, б), в) \ раз 2 + D_ {2} (д, в) \ раз 1) / (2 + 1) = (25,5 \ раз 2 + 39 \ раз 1) / 3 = 30}$

Благодаря этому пропорциональному среднему, вычисление этого нового расстояния учитывает больший размер $( a, b) {\ displaystyle (a, b)}$ $(a, b)$ кластер (два элемента) по отношению к $e {\ displaystyle e}$ $е$ (один элемент). Аналогично:

$D 3 (((a, b), e), d) = (D 2 ((a, b), d) × 2 + D 2 (e, d) × 1) / (2 + 1) = (32,5 × 2 + 43 × 1) / 3 = 36 {\ displaystyle D_ {3} (((a, b), e), d) = (D_ {2} ((a, b), d) \ times 2 + D_ {2} (e, d) \ times 1) / (2 + 1) = (32,5 \ times 2 + 43 \ times 1) / 3 = 36}$ ${\ displaystyle D_ {3} (((a, b), e), d) = (D_ {2} ((a, b), d) \ times 2 + D_ {2} (e, d) \ times 1) / (2 + 1) = (32,5 \ times 2 + 43 \ times 1) / 3 = 36}$

Следовательно, пропорциональное усреднение дает равный вес к начальным расстояниям матрицы $D 1 {\ displaystyle D_ {1}}$ $D_{1}$ . Это причина того, почему метод невзвешен не по отношению к математической процедуре, а по отношению к начальным расстояниям.

Третий шаг

Третья кластеризация

Мы снова повторяем три предыдущих шага, начиная с обновленной матрицы расстояний $D 3 {\ displaystyle D_ {3}}$ $D_ {3}$ .

	((a, b), e)	c	d
((a, b), e)	0	30	36
c	30	0	28
d	36	28	0

Здесь $D 3 (c, d) = 28 {\ displaystyle D_ {3} (c, d) = 28}$ ${\ displaystyle D_ {3} (c, d) = 28}$ - наименьшее значение $D 3 {\ displaystyle D_ {3}}$ $D_ {3}$ , поэтому мы соединяем элементы $c {\ displaystyle c}$ $c$ и $d {\ displaystyle d}$ $d$ .

Оценка длины третьей ветви

Пусть $w {\ displaystyle w}$ $w$ обозначает узел, к которому $c {\ displaystyle c}$ $c$ и $d {\ displaystyle d}$ $d$ теперь соединены. Ветви, соединяющие $c {\ displaystyle c}$ $c$ и $d {\ displaystyle d}$ $d$ с $w {\ displaystyle w}$ $w$ тогда длина $δ (c, w) = δ (d, w) = 28/2 = 14 {\ displaystyle \ delta (c, w) = \ delta (d, w) = 28/2 = 14}$ ${\ displaystyle \ delta (c, w) = \ delta (d, w) = 28/2 = 14}$ (см. Финальную дендрограмму)

Третье обновление матрицы расстояний

Необходимо обновить одну запись, учитывая, что два элемента $c {\ displaystyle c}$ $c$ и $d {\ displaystyle d}$ $d$ каждый имеет вклад $1 {\ displaystyle 1}$ $1$ в среднее вычисление :

$D 4 ((c, d), ((a, b), e)) = (D 3 (c, ((a, b), e)) × 1 + D 3 (d, ((a, b), e)) × 1) / (1 + 1) = (30 × 1 + 36 × 1) / 2 = 33 {\ displaystyle D_ {4} ((c, d), ((a, b), e)) = (D_ {3} (c, ((a, b), e)) \ times 1 + D_ {3} (d, ((a, b), e)) \ times 1) / (1 + 1) = (30 \ times 1 +36 \ times 1) / 2 = 33}$ ${\ displaystyle D_ {4} ((c, d), ((a, b), e)) = (D_ {3} (c, ((a, b), e)) \ times 1 + D_ {3} (d, ((a, b), e)) \ times 1) / (1 + 1) = (30 \ times 1 +36 \ times 1) / 2 = 33}$

Заключительный шаг

Заключительная матрица $D 4 {\ displaystyle D_ {4}}$ $D_ {4}$ :

	( (a, b), e)	(c, d)
((a, b), e)	0	33
(c, d)	33	0

Итак, мы объединить кластеры $((a, b), e) {\ displaystyle ((a, b), e)}$ ${\ displaystyle ((a, b), e)}$ и $(c, d) {\ displaystyle (c, d) }$ ${\ displaystyle (c, d)}$ .

Пусть $r {\ displaystyle r}$ $r$ обозначает (корневой) узел, к которому $((a, b), e) {\ displaystyle ((a, b), e)}$ ${\ displaystyle ((a, b), e)}$ и $(c, d) {\ displaystyle (c, d)}$ ${\ displaystyle (c, d)}$ теперь соединены. Ветви, соединяющие $((a, b), e) {\ displaystyle ((a, b), e)}$ ${\ displaystyle ((a, b), e)}$ и $(c, d) {\ displaystyle (c, d)} От$ ${\ displaystyle (c, d)}$ до $r {\ displaystyle r}$ $r$ тогда имеют длины:

$δ (((a, b), e), r) = δ ((c, d), r) знак равно 33/2 = 16,5 {\ displaystyle \ delta (((a, b), e), r) = \ delta ((c, d), r) = 33/2 = 16,5}$ ${\ Displaystyle \ де lta (((a, b), e), r) = \ delta ((c, d), r) = 33/2 = 16,5}$

Вычисляем две оставшиеся длины ветвей:

$δ (v, r) = δ (((a, b), e), r) - δ (e, v) = 16,5 - 11 = 5,5 {\ displaystyle \ delta (v, r) = \ delta (((a, b), e), r) - \ delta (e, v) = 16,5-11 = 5,5}$ ${\ displaystyle \ delta (v, r) = \ delta (((a, b), e), г) - \ дельта (е, v) = 16,5-11 = 5,5}$

$δ (w, r) = δ ( (с, d), г) - δ (с, вес) знак равно 16,5 - 14 = 2,5 {\ Displaystyle \ дельта (ш, г) = \ дельта ((с, г), г) - \ дельта (с, ш) = 16.5-14 = 2.5}$ ${\ displaystyle \ delta (w, r) = \ delta ((c, d), r) - \ delta (c, w) = 16,5–14 = 2,5}$

Дендрограмма UPGMA

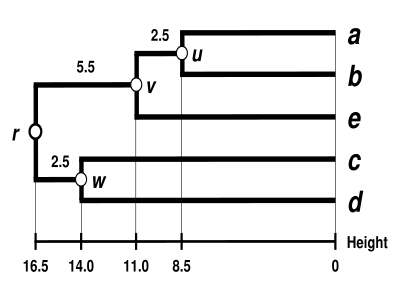
Дендрограмма завершена. Он ультраметрический, потому что все подсказки (от $a {\ displaystyle a}$ $a$ до $e {\ displaystyle e}$ $е$ ) находятся на одинаковом расстоянии от $r {\ displaystyle r }$ $r$ :

$δ (a, r) = δ (b, r) = δ (e, r) = δ (c, r) = δ (d, r) = 16,5 {\ displaystyle \ delta (a, r) = \ delta (b, r) = \ delta (e, r) = \ delta (c, r) = \ delta (d, r) = 16.5}$ ${\ displaystyle \ delta (a, r) = \ delta (b, r) = \ delta (e, r) = \ delta (c, r) = \ дельта (d, r) = 16,5}$

Следовательно, корень дендрограммы лежит на $r {\ displaystyle r}$ $r$ , самый глубокий узел.

Сравнение с другими связями

Альтернативные схемы связи включают кластеризацию одиночных связей, кластеризацию полной связи и кластеризацию средних связей WPGMA. Реализация другой связи - это просто вопрос использования другой формулы для расчета межкластерных расстояний на этапах обновления матрицы расстояний в вышеупомянутом алгоритме. Полная кластеризация по связям позволяет избежать недостатка альтернативного метода кластеризации с одной связью - так называемого явления сцепления, когда кластеры, сформированные с помощью кластеризации с одной связью, могут быть принудительно объединены из-за того, что отдельные элементы находятся близко друг к другу, даже если многие элементы в каждом кластеры могут быть очень далеки друг от друга. Полное сцепление имеет тенденцию находить компактные кластеры примерно равных диаметров.

Сравнение дендрограмм, полученных разными методами кластеризации из одной и той же матрицы расстояний.

Одинарная кластеризация.	Кластеризация с полной связью.	Средняя кластеризация связей: WPGMA.	Средняя кластеризация сцепления: UPGMA.

Использует

В экологии это один из самых популярных методов классификации единиц выборки (например, участков растительности) на основе их попарного сходства в соответствующих переменных дескриптора (таких как видовой состав). Например, его использовали для понимания трофического взаимодействия между морскими бактериями и простейшими.
В биоинформатике UPGMA используется для создания фенетических деревья (фенограммы). Первоначально UPGMA был разработан для использования в исследованиях электрофореза белков, но в настоящее время наиболее часто используется для создания направляющих деревьев для более сложных алгоритмов. Этот алгоритм, например, используется в процедурах выравнивания последовательностей, поскольку он предлагает один порядок, в котором последовательности будут выравниваться. Действительно, направляющее дерево нацелено на группировку наиболее похожих последовательностей, независимо от их скорости эволюции или филогенетического сходства, и это как раз и является целью UPGMA
В филогенетике UPGMA предполагает постоянную скорость эволюции (гипотеза молекулярных часов ) и что все последовательности были взяты в одно и то же время, и не является хорошо зарекомендовавшим себя методом вывода взаимосвязей, если это предположение не было проверено и оправдано для используемого набора данных. Обратите внимание, что даже в условиях «строгой синхронизации» последовательности, выбранные в разное время, не должны приводить к ультраметрическому дереву.

Временная сложность

Тривиальная реализация алгоритма для построения дерева UPGMA имеет $O (n 3) {\ displaystyle O (n ^ {3})}$ $O (n ^ {3})$ временная сложность, а использование кучи для каждого кластера, чтобы сохранить расстояние от другого кластера, сокращает его время до $O (n 2 журнал ⁡ n) {\ displaystyle O (n ^ {2} \ log n)}$ $O (n ^ 2 \ log n)$ . Фионн Муртаг представил некоторые другие подходы для особых случаев, временной алгоритм $O (k 3 kn 2) {\ displaystyle O (k3 ^ {k} n ^ {2})}$ ${\ displaystyle O (k3 ^ {k} n ^ {2})}$ Дэя и Эдельсбруннера. для k-мерных данных, которые оптимальны $O (n 2) {\ displaystyle O (n ^ {2})}$ $O (n ^ {2})$ для постоянного k, а другой $O (n 2) {\ displaystyle O (n ^ {2})}$ $O (n ^ {2})$ алгоритм для ограниченного ввода, когда «агломеративная стратегия удовлетворяет свойству сводимости».

См. также

Ссылки

Внешние ссылки