Распределение Коши

Распределение вероятностей

Коши

Функция плотности вероятности . Фиолетовая кривая - стандартное распределение Коши
Накопительная функция распределения
Параметры	$x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\; \backslash !\}$местоположение (действительное ). $\gamma >0\; \{\backslash \; displaystyle\; \backslash \; gamma>0\}$масштаб (реальный)
Поддержка	$x\; \in \; (-\; \infty ,\; +\; \infty )\; \{\backslash \; displaystyle\; \backslash \; displaystyle\; x\; \backslash \; in\; (-\; \backslash \; infty,\; +\; \backslash \; infty)\; \backslash !\}$
PDF	$1\; \pi \; \gamma \; [\; 1\; +\; (Икс\; -\; Икс\; 0\; \gamma )\; 2]\; \{\backslash \; Displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; \backslash \; gamma\; \backslash ,\; \backslash \; left\; [1+\; \backslash \; left\; (\{\backslash \; frac\; \{x-x\_\; \{0\}\}\; \{\backslash \; гамма\})\; \}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\}\}\; \backslash !\}$
CDF	$1\; \pi \; arctan\; \; (x\; -\; x\; 0\; \gamma )\; +\; 1\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\; \}\; \backslash \; arctan\; \backslash \; left\; (\{\backslash \; frac\; \{x-x\_\; \{0\}\}\; \{\backslash \; gamma\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash !\; \}$
Квантиль	$x\; 0\; +\; \gamma \; загар\; \; [\pi \; (F\; -\; 1\; 2)]\; \{\backslash \; displaystyle\; x\_\; \{0\}\; +\; \backslash \; gamma\; \backslash ,\; \backslash \; tan\; [\backslash \; pi\; (F\; -\; \{\backslash \; tfrac\; \{1\}\; \{\; 2\}\})]\}$
Среднее	неопределенное
Медианное	$x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\; \backslash !\}$
Режим	$x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\; \backslash \; !\}$
Дисперсия	undefined
Асимметрия	undefined
Пример. эксцесс	undefined
Энтропия	$log\; \; (4\; \pi \; \gamma )\; \{\backslash \; displaystyle\; \backslash \; log\; (4\; \backslash \; pi\; \backslash \; gamma)\; \backslash !\}$
MGF	не существует
CF	$exp\; \; (Икс\; 0\; это\; -\; \gamma \; |\; t\; |)\; \{\backslash \; displaystyle\; \backslash \; displaystyle\; \backslash \; exp\; (x\_\; \{0\}\; \backslash ,\; i\; \backslash ,\; t-\; \backslash \; gamma\; \backslash ,\; |\; t\; |)\; \backslash !\}$
информация Фишера	$1\; 2\; \gamma \; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; gamma\; ^\; \{2\}\}\}\}$

Распределение Коши, названное в честь Огюстена Коши, является непрерывным распределением вероятностей. Это также известно, особенно физиков, как распределение Лоренца (после Хендрика Лоренца ), распределение Коши - Лоренца, Функция Лоренца (ian), или распределение Брейта - Вигнера . Распределение Коши $f\; (x;\; x\; 0,\; \gamma )\; \{\backslash \; displaystyle\; f\; (x;\; x\_\; \{0\},\; \backslash \; gamma)\}$- это распределение x-точки пересечения луча, выходящего из $(x\; 0,\; \gamma )\; \{\backslash \; displaystyle\; (x\_\; \{0\},\; \backslash \; gamma)\}$с равномерно распределенным углом. Это также распределение отношений двух независимых нормально распределенных случайных величин с нулевым средним.

Распределение Коши часто используется в качестве канонического примера «патологического » распределения, поскольку его ожидаемое значение и его дисперсия не является (но см. § Объяснение неопределенных моментов ниже). Распределение Коши не имеет конечных моментов порядка больше или равного единице; существуют только дробные абсолютные моменты. Распределение Коши не имеет функции , производящей момент.

В математике оно используется вместе с ядром Пуассона, которое является фундаментальным решением для уравнение Лапласа в верхней полуплоскости .

Это одно из немногих распределений, которое стабильно имеет функцию плотности вероятности, которая может быть выражена аналитически, другими являются нормальное распределение и распределение Леви.

• 1
• 2 Характеристика
  • 2.1 Функция плотности вероятности
  • 2.2 Кумулятивная функция История распределения
  • 2.3 Энтропия
• 3 Дивергенция Кульбака-Лейблера
• 4 Свойства
  • 4.1 Характеристическая функция
• 5 Объяснение неопределенных моментов
  • 5.1 Среднее
  • 5.2 Меньшие моменты
  • 5.3 Высшие моменты
  • 5.4 Моменты усеченных распределений
• 6 Оценка параметров
• 7 Общее распределение Коши
• 8 Свойства преобразования
• 9 Мера Леви
• 10 Связанные распределения
• 11 R элятивистское распределение Брейта - Вигнера
• 12 Возникновение и применение
• 13 См. также
• 14 Ссылки
• 15 Внешние ссылки

Оценка среднего и стандартного отклонения по выборкам из распределения Коши (внизу) не сходится с большим количеством выборок, как в нормальном распределении ( вверху). Скачки могут быть сколь угодно большими, как видно на графиках внизу. (Щелкните, чтобы развернуть)

Функции сучались функции распределения Коши из математики в 17 веке, но в контексте и под названием ведьмы Агнеси. Несмотря на название, первый явный анализ свойств распределения Коши был опубликован французским математиком Пуассоном в 1824 году, и Коши стал ассоциироваться с ним только во время академических споров в 1853 году. Таким образом, название распределения является случаем закона эпонимии Стиглера. Пуассон заметил, что если брать среднее значение наблюдений, следующая за таким распределением, то средняя ошибка сходится к какому-либо конечному наблюдению. Таким образом, использование Лапласом центральной предельной теоремы с таким распределением было неуместным, поскольку предполагало конечное среднее значение и дисперсию. Несмотря на это, Пуассон не должен считать этот вопрос важным, в отличие от Бьенайме, который был вовлечь Коши в долгий спор по этому поводу.

Функция плотности вероятности

Распределение Коши имеет плотность плотности вероятности (PDF)

$f\; (x;\; x\; 0,\; \gamma )\; Знак\; равно\; 1\; \pi \; \gamma \; [1\; +\; (x\; -\; x\; 0\; \gamma )\; 2]\; =\; 1\; \pi \; \gamma \; [\gamma \; 2\; (x\; -\; x\; 0)\; 2\; +\; \gamma \; 2],\; \{\backslash \; displaystyle\; f\; (x;\; x\_\; \{0\},\; \backslash \; gamma)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; \backslash \; gamma\; \backslash \; left\; [1+\; \backslash \; left\; (\{\backslash \; frac\; \{x-x\_\; \{0\}\}\; \{\backslash \; gamma\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\}\}\; =\; \{\; 1\; \backslash \; over\; \backslash \; pi\; \backslash \; gamma\}\; \backslash \; left\; [\{\backslash \; gamma\; ^\; \{2\}\; \backslash \; over\; (x-x\_\; \{0\})\; ^\; \{2\}\; +\; \backslash \; gamma\; ^\; \{2\}\}\; \backslash \; right],\}$

где $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$- параметр местоположения, определяющий местоположение пика распределения, а $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$- это параметр масштаба , определяет полуширину на полувысоте (HWHM), альтернативно $2\; \gamma \; \{\backslash \; displaystyle\; 2\; \backslash \; gamma\}$составляет полную ширину на половине значений (FWHM). $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$также равен половине межквартирного размаха и иногда называется вероятной ошибкой. Огюстен-Луи Коши использовал такую ​​функцию плотности в 1827 году с бесконечно малым параметр масштаба, определяя то, что теперь будет называться дельта-функции Дирака.

Максимальное значение или амплитуда PDF-файла Коши: $1\; \pi \; \gamma \; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; \backslash \; gamma\}\}\}$, расположенный в $x\; =\; x\; 0\; \{\backslash \; displaystyle\; x\; =\; x\_\; \{0\}\}$.

Иногда бывает удобно выразить PDF через комплексный параметр $\psi \; =\; x\; 0\; +\; i\; \gamma \; \{\backslash \; displaystyle\; \backslash \; psi\; =\; x\_\; \{0\}\; +\; i\; \backslash \; gamma\}$

$f\; (Икс;\; \psi )\; знак\; равно\; 1\; \pi \; Im\; (1\; x\; -\; \psi )\; =\; 1\; \pi \; Re\; (-\; ix\; -\; \psi )\; \{\backslash \; displaystyle\; f\; (x;\; \backslash \; psi)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash ,\; \{\backslash \; textrm\; \{\; Im\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{x-\; \backslash \; psi\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash ,\; \{\backslash \; textrm\; \{Re\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{\; -i\}\; \{x-\; \backslash \; psi\}\}\; \backslash \; right)\}$

Особый случай, когда $x\; 0\; =\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\; =\; 0\}$и $\gamma \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; 1\}$называется стандартным распределением Коши с функцией плотности вероятности

$f\; (x;\; 0,\; 1)\; =\; 1\; \pi \; (1\; +\; х\; 2).\; \{\backslash \; displaystyle\; f\; (x;\; 0,1)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; (1\; +\; x\; ^\; \{2\})\}\}.\; \backslash !\}$

В физике трехпараметрическая функция Лоренца часто используется:

$f\; (x;\; x\; 0,\; \gamma ,\; I)\; =\; I\; [1\; +\; (x\; -\; x\; 0\; \gamma )\; 2]\; =\; I\; [\gamma \; 2\; (x\; -\; икс\; 0)\; 2\; +\; \gamma \; 2],\; \{\backslash \; displaystyle\; f\; (x;\; x\_\; \{0\},\; \backslash \; gamma,\; I)\; =\; \{\backslash \; frac\; \{I\}\; \{\backslash \; left\; [1+\; \backslash \; left\; (\{\backslash \; frac\; \{x-x\_\; \{\; 0\}\}\; \{\backslash \; gamma\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right]\}\}\; =\; I\; \backslash \; left\; [\{\backslash \; gamma\; ^\; \{2\}\; \backslash \; over\; (x-x\_\; \{0\})\; ^\; \{2\}\; +\; \backslash \; gamma\; ^\; \{2\}\}\; \backslash \; right],\}$

где $I\; \{\backslash \; displaystyle\; I\}$- высота пика. Указанная трехпараметрическая функция не является функцией плотности вероятности, поскольку она не интегрируется до 1, за исключением особого случая, когда $I\; =\; 1\; \pi \; \gamma .\; \{\backslash \; displaystyle\; I\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; \backslash \; gamma\}\}.\; \backslash !\}$

Кумулятивная функция распределения

кумулятивная функция распределения распределения Коши:

$F\; (x;\; x\; 0,\; \gamma )\; =\; 1\; \pi \; arctan\; \; (x\; -\; x\; 0\; \gamma )\; +\; 1\; 2\; \{\backslash \; displaystyle\; F\; (x;\; x\_\; \{0\},\; \backslash \; gamma)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; arctan\; \backslash \; left\; (\{\backslash \; frac\; \{x-x\_\; \{0\}\}\; \{\backslash \; gamma\; \}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}$

и функция квантиля (обратный cdf ) распределения Коши равен

$Q\; (p;\; x\; 0,\; \gamma )\; =\; x\; 0\; +\; \gamma \; tan\; \; [\pi \; (p\; -\; 1\; 2)].\; \{\backslash \; displaystyle\; Q\; (p;\; x\_\; \{0\},\; \backslash \; gamma)\; =\; x\_\; \{0\}\; +\; \backslash \; gamma\; \backslash ,\; \backslash \; tan\; \backslash \; left\; [\backslash \; pi\; \backslash \; left\; (p\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; right)\; \backslash \; right].\}$

Отсюда следует, что первый и третий квартили равны $(x\; 0\; -\; \gamma ,\; x\; 0\; +\; \gamma )\; \{\backslash \; displaystyle\; (x\_\; \{0\}\; -\; \backslash \; gamma,\; x\_\; \{0\}\; +\; \backslash \; gamma))\}$, и, следовательно, межквартильный размах равенство $2\; \gamma \; \{\backslash \; displaystyle\; 2\; \backslash \; gamma\}$.

Для стандартного распределения кумулятивная функция распределения упрощается до функция арктангенса $arctan\; \; (x)\; \{\backslash \; displaystyle\; \backslash \; arctan\; (x)\}$:

$F\; (x;\; 0,\; 1)\; =\; 1\; \pi \; arctan\; \; (x)\; +\; 1\; 2\; \{\backslash \; displaystyle\; F\; (x;\; 0,\; 1)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; arctan\; \backslash \; left\; (x\; \backslash \; right)\; +\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}$

Энтропия

Энтропия распределения Коши определяется выражением:

$H\; (\gamma )\; =\; -\; \int \; -\; \infty \; \infty \; f\; (x;\; x\; 0,\; \gamma )\; log\; \; (f\; (x;\; x\; 0,\; \gamma ))\; dx\; =\; log\; \; (4\; \pi \; \gamma )\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{align\}\; H\; (\backslash \; gamma)\; =\; -\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; f\; (x;\; x\_\; \{0\},\; \backslash \; gamma)\; \backslash \; log\; (f\; (x;\; x\_\; \{0\},\; \backslash \; gamma))\; \backslash ,\; dx\; \backslash \backslash \; [6pt]\; =\; \backslash \; log\; (4\; \backslash \; pi\; \backslash \; gamma)\; \backslash \; end\; \{align\}\}\}$

Производственная квантильная функция , квантильная функция плотности для распределения Коши:

$Q\; \prime \; (p;\; \gamma )\; =\; \gamma \; \pi \; sec\; 2\; [\pi \; (p\; -\; 1\; 2)].\; \{\backslash \; displaystyle\; Q\; \text{'}(p;\; \backslash \; gamma)\; =\; \backslash \; gamma\; \backslash ,\; \backslash \; pi\; \backslash ,\; \{\backslash \; sec\}\; ^\; \{2\}\; \backslash \; left\; [\backslash \; pi\; \backslash \; left\; (p\; -\; \{\backslash \; tfrac\; \{1\}\; \{2\}\}\; \backslash \; right)\; \backslash \; верно].\; \backslash !\}$

дифференциальная энтропия распределение может быть определено в терминах его квантильной плотности, а именно:

$H\; (\gamma )\; =\; \int \; 0\; 1\; log\; (Q\; \prime \; (п;\; \gamma ))\; dp\; знак\; равно\; журнал\; \; (4\; \pi \; \gamma )\; \{\backslash \; Displaystyle\; H\; (\backslash \; gamma)\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{1\}\; \backslash \; log\; \backslash ,\; (Q\; \text{'}(p;\; \backslash \; gamma))\; \backslash ,\; \backslash \; mathrm\; \{d\}\; p\; =\; \backslash \; log\; (4\; \backslash \; pi\; \backslash \; gamma)\}$

Распределение Коши - это максимальная вероятности энтропии для случайной переменной $X\; \{\backslash \; displaystyle\; X\}$для которого

$E\; \; [журнал\; \; (1\; +\; (X\; -\; x\; 0)\; 2\; /\; \gamma \; 2)]\; =\; журнал\; \; 4\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [\backslash \; log\; (1+\; (X-\; x\_\; \{0\})\; ^\; \{2\}\; /\; \backslash \; gamma\; ^\; \{2\})]\; =\; \backslash \; log\; 4\}$

или альтернативный вариант для случайной переменной $X\; \{\backslash \; displaystyle\; X\}$для что

$E\; \; [log\; \; (\; 1\; +\; (X\; -\; x\; 0)\; 2)]\; =\; 2\; log\; \; (1\; +\; \gamma ).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [\backslash \; log\; (1+\; (X-x\_\; \{0\})\; ^\; \{2\})]\; =\; 2\; \backslash \; log\; (1+\; \backslash \; gamma).\}$

В стандартной форме это Максимальная вероятность энтропии для случайной переменной $X\; \{\backslash \; displaystyle\; X\}$, для которой

$E\; [ln\; \; (1\; +\; X\; 2)]\; =\; ln\; \; 4.\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; \backslash !\; \backslash \; left\; [\backslash \; ln\; (1\; +\; X\; ^\; \{2\})\; \backslash \; right]\; =\; \backslash \; ln\; 4.\}$

.

Дивергенция Кульбака-Лейблера между двумя распределениями Коши имеет следующую симметричную формулу замкнутой формы:

$KL\; (pl\; 1,\; s\; 1:\; pl\; 2,\; s\; 2)\; =\; log\; \; (s\; 1\; +\; s\; 2)\; 2\; +\; (l\; 1\; -\; l\; 2)\; 2\; 4\; с\; 1\; с\; 2.\; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{KL\}\; \backslash \; left\; (p\_\; \{l\_\; \{1\},\; s\_\; \{1\}\}:\; p\_\; \{l\_\; \{2\},\; s\_\; \{2\}\}\; \backslash \; right)\; =\; \backslash \; log\; \{\backslash \; frac\; \{\backslash \; left\; (s\_\; \{1\}\; +\; s\_\; \{2\}\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; left\; (l\_\; \{1\}\; -l\_\; \{2\}\; \backslash \; right)\; ^\; \{2\}\}\; \{4s\_\; \{1\}\; s\_\; \{2\}\}\}.\}$

Распределение Коши представляет собой распределение, для которого среднее, дисперсия или более высокие моменты. Его режим и медиана хорошо и оба Равны $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$.

Когда $U\; \{\backslash \; displaystyle\; U\}$и $V\; \{\backslash \; displaystyle\; V\}$- две независимые нормально распределенные случайные величины с ожидаемого числа 0 и дисперсия 1, то отношение $U\; /\; V\; \{\backslash \; displaystyle\; U\; /\; V\}$имеет стандартное распределение Коши.

Если $\Sigma \; \{\backslash \; displaystyle\; \backslash \; Sigma\}$является $p\; \times \; p\; \{\backslash \; displaystyle\; p\; \backslash \; times\; p\}$положительно-полуопределенная матрица ковариаций со строго положительными диагональными элементами, то для независимо и одинаково распределенных $X,\; Y\; \sim \; N\; (0,\; \Sigma )\; \{\backslash \; displaystyle\; X,\; Y\; \backslash \; sim\; N\; (0,\; \backslash \; Sigma)\}$и любой случайный $p\; \{\backslash \; displaystyle\; p\}$-вектор $w\; \{\backslash \; displaystyle\; w\}$независимо от $X\; \{\backslash \; displaystyle\; X\}$и $Y\; \{\backslash \; displaystyle\; Y\}$такие, что $w\; 1\; +\; \cdots \; +\; wp\; =\; 1\; \{\backslash \; displaystyle\; w\_\; \{1\}\; +\; \backslash \; cdots\; +\; w\_\; \{p\}\; =\; 1\}$и $wi\; \ge \; 0,\; i\; =\; 1,\dots ,\; p,\; \{\backslash \; displaystyle\; w\_\; \{i\}\; \backslash \; geq\; 0,\; i\; =\; 1,\; \backslash \; ldots,\; p,\}$(определяя категориальное распределение ), выполняется

$\sum \; j\; =\; 1\; pwj\; X\; j\; Y\; j\; \sim \; C\; auchy\; (0,\; 1).\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{j\; =\; 1\}\; ^\; \{p\}\; w\_\; \{j\}\; \{\backslash \; frac\; \{X\_\; \{j\}\}\; \{Y\_\; \{j\}\}\}\; \backslash \; sim\; \backslash \; mathrm\; \{Cauchy\}\; (0,1).\}$

Если $X\; 1,\dots ,\; X\; n\; \{\backslash \; displaystyle\; X\_\; \{1\},\; \backslash \; ldots,\; X\_\; \{n\}\}$являются независимыми и одинаково распределенными случайными величинами, каждой со стандартным распределением Коши, то выборочное среднее $(X\; 1\; +\; \cdots \; +\; X\; n)\; /\; n\; \{\backslash \; displaystyle\; (X\_\; \{1\}\; +\; \backslash \; cdots\; +\; X\_\; \{n\})\; /\; n\}$имеет такое же стандартное распределение Коши. Чтобы убедиться, что это так, вычислите качественную функцию выборочного среднего:

$\phi \; X\; ¯\; (t)\; =\; E\; [ei\; X\; ¯\; t]\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{\backslash \; overline\; \{X\}\}\; (\; t)\; =\; \backslash \; mathrm\; \{E\}\; \backslash \; left\; [e\; ^\; \{i\; \{\backslash \; overline\; \{X\}\}\; t\}\; \backslash \; right]\}$

где $X\; ¯\; \{\backslash \; displaystyle\; \{\backslash \; overline\; \{X\}\}\}$- выборочное среднее. Этот пример показывает, что гипотеза конечной дисперсии в центральной предельной теореме не может быть отброшена. Это также пример обобщенной версии центральной предельной теоремы, которая характерна для всех стабильных распределений, частным случаем которых является распределение Коши.

Распределение Коши - это бесконечно делимое распределение вероятностей. Это также строго стабильное распределение.

Стандартное распределение Коши совпадает с t-распределением Стьюдента с одной степенью свободы.

Как и все стабильные распределения, семейство масштаба местоположения, к которому принадлежат Коши, замкнуто при линейных преобразованиях с действительными коэффициентами. Кроме того, распределение Коши закрывается при дробно-линейных преобразованиях с действующими коэффициентами. В этой связи см. параметры распределений Коши Маккаллахом.

Характеристическая функция

Пусть $X\; \{\backslash \; displaystyle\; X\}$обозначает распределенную случайную категорию Коши. характерная функция распределение Коши определяется как

$\phi \; X\; (t;\; x\; 0,\; \gamma )\; =\; E\; \; [ei\; X\; t]\; =\; \int \; -\; \infty \; \infty \; f\; (x;\; x\; 0,\; \gamma )\; eixtdx\; =\; eix\; 0\; t\; -\; \gamma \; |\; т\; |.\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t;\; x\_\; \{0\},\; \backslash \; gamma)\; =\; \backslash \; operatorname\; \{E\}\; \backslash \; left\; [e\; ^\; \{iXt\}\; \backslash \; right]\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\; \}\; f\; (x;\; x\_\; \{0\},\; \backslash \; gamma)\; e\; ^\; \{ixt\}\; \backslash ,\; dx\; =\; e\; ^\; \{ix\_\; \{0\}\; t-\; \backslash \; gamma\; |\; t\; |\}.\}$

что является просто Фурье преобразовать плотность вероятности. Первоначальная плотность вероятности может быть выражена через характеристическую функцию, по существу, с помощью обратного преобразования Фурье:

$f\; (x;\; x\; 0,\; \gamma )\; =\; 1\; 2\; \pi \; \int \; -\; \infty \; \infty \; \phi \; X\; (t;\; x\; 0,\; \gamma )\; е\; -\; ixtdt\; \{\backslash \; displaystyle\; f\; (x;\; x\_\; \{0\},\; \backslash \; gamma)\; =\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; pi\}\}\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \backslash \; varphi\; \_\; \{X\}\; (\; t;\; x\_\; \{0\},\; \backslash \; gamma)\; e\; ^\; \{-\; ixt\}\; \backslash ,\; dt\; \backslash !\}$

n-й момент распределения - это n-я производная характеристическая функция, вычисленная при $t\; =\; 0\; \{\backslash \; displaystyle\; t\; =\; 0\}$. Обратите внимание, что характерная функция не дифференцируема в начале координат: это соответствует тому факту, что распределение Коши не имеет четко определенных моментов выше, чем нулевой момент.

Среднее

Если распределение вероятностей имеет функция плотности $f\; (x)\; \{\backslash \; displaystyle\; f\; (x)\}$, тогда среднее значение, если оно существует, дается как

$\int \; -\; \infty \; \infty \; xf\; (x)\; dx.\; (1)\; \{\backslash \; Displaystyle\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; xf\; (x)\; \backslash ,\; dx.\; \backslash \; Qquad\; \backslash \; qquad\; (1)\; \backslash !\}$

Мы можем оценить этот двусторонний несобственный интеграл путем вычисления суммы двух односторонних несобственных интегралов. То есть

$\int \; a\; \infty \; x\; f\; (x)\; d\; x\; +\; \int \; -\; \infty \; a\; x\; f\; (x)\; d\; x.\; (2)\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{a\}\; ^\; \{\backslash \; infty\}\; xf\; (x)\; \backslash ,\; dx\; +\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{a\}\; xf\; (x)\; \backslash ,\; dx.\; \backslash \; Qquad\; \backslash \; qquad\; (2)\; \backslash !\}$

для произвольного действительного числа $a\; \{\backslash \; displaystyle\; a\}$.

Для существования интеграла (даже в виде бесконечного значения), хотя бы один из членов этой суммы должен быть конечным, или оба должны быть бесконечными и иметь один и тот же знак. В случае распределения Коши оба члена в этой сумме (2) бесконечны и имеют противоположный знак. Следовательно, (1) не определено, как и среднее значение.

Обратите внимание, что главное значение Коши среднего значения распределения Коши равно

$lim\; a\; \to \; \infty \; \int \; -\; aaxf\; (x)\; dx,\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{a\; \backslash \; to\; \backslash \; infty\}\; \backslash \; int\; \_\; \{-\; a\}\; ^\; \{a\}\; xf\; (x)\; \backslash ,\; dx,\; \backslash !\}$

который равен нулю. С другой стороны, соответствующий интеграл

$lim\; a\; \to \; \infty \; \int \; -\; 2\; aaxf\; (x)\; dx,\; \{\backslash \; displaystyle\; \backslash \; lim\; \_\; \{a\; \backslash \; to\; \backslash \; infty\}\; \backslash \; int\; \_\; \{-\; 2a\}\; ^\; \{a\}\; xf\; (x)\; \backslash ,\; dx,\; \backslash !\}$

не равно нулю, что легко увидеть, вычислив интеграл. Это снова показывает, что среднее (1) не может существовать.

Различные результаты теории вероятностей относительно ожидаемых значений, такие как строгий закон больших чисел, не выполняются для распределения Коши.

Меньшие моменты

Определены абсолютные моменты для $p\; \in \; (-\; 1,\; 1)\; \{\backslash \; displaystyle\; p\; \backslash \; in\; (-1,1)\}$. Для $X\; \sim \; C\; a\; u\; c\; час\; Y\; (0,\; \gamma )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; mathrm\; \{Cauchy\}\; (0,\; \backslash \; gamma)\}$мы имеем

$E\; \; [|\; X\; |\; p]\; =\; \gamma \; p\; s\; e\; c\; (\pi \; p\; /\; 2).\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{E\}\; [|\; X\; |\; ^\; \{p\}]\; =\; \backslash \; gamma\; ^\; \{p\}\; \backslash \; mathrm\; \{sec\}\; (\backslash \; pi\; p\; /\; 2).\}$

Высшие моменты

Распределение Коши не имеет конечных моментов любого порядка. Некоторые из более высоких исходных моментов действительно существуют и имеют значение бесконечности, например, необработанный второй момент:

$E\; \; [X\; 2]\; \propto \; \int \; -\; \infty \; \infty \; x\; 2\; 1\; +\; x\; 2\; dx\; =\; \int \; -\; \infty \; \infty \; 1-1\; 1\; +\; x\; 2\; dx\; знак\; равно\; \int \; -\; \infty \; \infty \; dx\; -\; \int \; -\; \infty \; \infty \; 1\; 1\; +\; x\; 2\; dx\; =\; \int \; -\; \infty \; \infty \; dx\; -\; \pi \; =\; \infty .\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; operatorname\; \{E\}\; [X\; ^\; \{2\}]\; \backslash \; propto\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{x\; ^\; \{2\}\}\; \{1+\; x\; ^\; \{2\}\}\}\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; 1\; -\; \{\backslash \; frac\; \{1\}\; \{1\; +\; x\; ^\; \{2\}\}\}\; \backslash ,\; dx\; \backslash \backslash \; [8pt]\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; dx-\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; \{\backslash \; frac\; \{1\}\; \{1\; +\; x\; ^\; \{2\}\}\}\; \backslash ,\; dx\; =\; \backslash \; int\; \_\; \{-\; \backslash \; infty\}\; ^\; \{\backslash \; infty\}\; dx-\; \backslash \; pi\; =\; \backslash \; infty.\; \backslash \; end\; \{align\}\}\}$

Изменив формулу, можно увидеть, что второй момент по сути является бесконечным интегралом константы (здесь 1). Более высокие даже мощные необработанные моменты также будут оцениваться до бесконечности. Однако сырые моменты с нечетной нечеткой нечеткой нечеткой, что отличается от хорошей со скоростью бесконечности. Необработанные моменты с нечетной степенью не достижимой оценки, поскольку их значения по существу эквивалентны $\infty \; -\; \infty \; \{\backslash \; displaystyle\; \backslash \; infty\; -\; \backslash \; infty\}$, поскольку две половины интеграла расходятся и имеют противоположные знаки. Первый необработанный момент - это среднее значение, которого, как ни странно, не существует. (См. Также обсуждение выше по этому поводу.) Это, в свою очередь, означает, что все центральные моменты и стандартизованные моменты не используются, поскольку все они основаны на среднем значении. Дисперсия - которая является вторым центральным моментом - также не (несмотря на то, что необработанный второй момент имеет размерность).

Результаты для высших моментов следуют из неравенства Гёльдера, которое подразумевает, что более высокие моменты (или половины моментов) расходятся, если более низкие.

Моменты усеченных распределений

Рассмотрим усеченное распределение, определенное ограничение стандартного распределения Коши интервалом [-10, 10]. Такое усеченное распределение имеет все моменты (и центральная предельная теорема применима к i.i.d. наблюдения из него); тем не менее, почти для всех практических целей оно ведет себя как распределение Коши.

Параметры распределения Коши не соответствуют среднему значению и дисперсии, попытка оценить параметры Коши с использованием выбора среднего и выборочной дисперсии не увенчается успехом. Например, если i.i.d. выборка размера n берется из распределения Коши, можно вычислить выборочное среднее как:

$x\; ¯\; =\; 1\; n\; \sum \; i\; =\; 1\; nxi\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{x\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{n\}\}\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; x\_\; \{i\}\}$

Хотя примерные значения $xi\; \{\backslash \; displaystyle\; x\_\; \{i\}\}$будут сосредоточены вокруг центральное значение $x\; 0\; \{\; \backslash \; displaystyle\; x\_\; \{0\}\}$, среднее значение выборки будет становиться все более изменчивым по мере увеличения числа наблюдений из-за увеличения вероятности обнаружения точек выборки с большим абсолютным значением. Фактически, распределение выборочного среднего будет равно распределению самих наблюдений; то есть выборочное среднее большой выборки не лучше (или хуже) для оценки $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$, чем любое отдельное наблюдение из выборки. Точно так же расчет дисперсии выборки приведет к тому, что значения будут расти по мере увеличения количества наблюдений.

Таким образом, более надежные средства оценки центрального значения $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$и параметра масштабирования $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$необходимы. Один из простых методов - взять среднее значение выборки в качестве оценки $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$и половину выборки межквартильного размаха в качестве оценки. из $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$. Были разработаны другие, более точные и надежные методы. Например, усеченное среднее средних 24% выборки статистика заказов дает оценку для $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$, что более эффективно, чем использование медианы выборки или полного среднего значения выборки. Однако из-за толстых хвостов распределения Коши эффективность средства оценки снижается, если используется более 24% выборки.

Максимальное правдоподобие также можно использовать для оценки параметры $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$и $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$. Однако это имеет тенденцию усложняться тем фактом, что для этого требуется найти корни многочлена высокой степени, и может быть несколько корней, которые представляют локальные максимумы. Кроме того, хотя оценка максимального правдоподобия является асимптотически эффективной, она относительно неэффективна для небольших выборок. Функция логарифма правдоподобия для распределения Коши для размера выборки $n\; \{\backslash \; displaystyle\; n\}$:

$\ell \; ^\; (x\; 0,\; \gamma \; \mid \; x\; 1,\dots ,\; xn)\; =\; -\; n\; журнал\; \; (\gamma \; \pi )\; -\; \sum \; я\; знак\; равно\; 1\; N\; журнал\; \; (1\; +\; (xi\; -\; x\; 0\; \gamma )\; 2)\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; ell\}\}\; (\backslash !\; x\_\; \{0\},\; \backslash \; gamma\; \backslash \; mid\; x\_\; \{1\},\; \backslash \; dotsc,\; x\_\; \{n\})\; =\; -\; n\; \backslash \; log\; (\backslash \; gamma\; \backslash \; pi)\; -\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \backslash \; log\; \backslash \; left\; (1+\; \backslash \; left\; (\{\backslash \; frac\; \{\; x\_\; \{i\}\; -x\_\; \{0\}\}\; \{\backslash \; gamma\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; right)\}$

Максимизация функции правдоподобия журнала относительно $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$и $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$дает следующую систему уравнений:

$\sum \; i\; =\; 1\; nxi\; -\; x\; 0\; \gamma \; 2\; +\; (xi\; -\; x\; 0)\; 2\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{x\_\; \{i\}\; -x\_\; \{0\}\}\; \{\backslash \; gamma\; ^\; \{2\}\; +\; \backslash \; left\; (x\_\; \{i\}\; -\; \backslash !\; x\_\; \{0\}\; \backslash \; right)\; ^\; \{2\}\}\}\; =\; 0\}$

$\sum \; я\; =\; 1\; n\; (xi\; -\; x\; 0)\; 2\; \gamma \; 2\; +\; (xi\; -\; x\; 0)\; 2\; -\; n\; 2\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; сумма\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; left\; (x\_\; \{i\}\; -x\_\; \{0\}\; \backslash \; right)\; ^\; \{2\}\}\; \{\backslash \; gamma\; ^\; \{2\}\; +\; \backslash \; left\; (x\_\; \{i\}\; -x\_\; \{0\}\; \backslash \; right)\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{n\}\; \{2\}\}\; =\; 0\}$

Обратите внимание, что

$\sum \; i\; =\; 1\; n\; (xi\; -\; x\; 0)\; 2\; \gamma \; 2\; +\; (xi\; -\; x\; 0)\; 2\; \{\backslash \; displaystyl\; e\; \backslash \; sum\; \_\; \{i\; =\; 1\}\; ^\; \{n\}\; \{\backslash \; frac\; \{\backslash \; left\; (x\_\; \{i\}\; -x\_\; \{0\}\; \backslash \; right)\; ^\; \{2\}\}\; \{\backslash \; gamma\; ^\; \{2\}\; +\; \backslash \; left\; (x\_\; \{\; i\}\; -x\_\; \{0\}\; \backslash \; right)\; ^\; \{2\}\}\}$

является монотонной функцией в $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$и что решение $\gamma \; \{\; \backslash \; displaystyle\; \backslash \; gamma\}$должен удовлетворять

$min\; |\; x\; i\; -\; x\; 0\; |\; \le \; \gamma \; \le \; max\; |\; x\; i\; -\; x\; 0\; |.\; \{\backslash \; displaystyle\; \backslash \; min\; |\; x\_\; \{i\}\; -x\_\; \{0\}\; |\; \backslash \; leq\; \backslash \; gamma\; \backslash \; leq\; \backslash \; max\; |\; x\_\; \{i\}\; -x\_\; \{0\}\; |.\}$

Решение только для $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$требует решения многочлена степени $2\; n\; -\; 1\; \{\backslash \; displaystyle\; 2n-1\}$и решения только для $\gamma \; \{\backslash \; displaystyle\; \backslash ,\; \backslash !\; \backslash \; gamma\}$требует решения полинома степени $2\; n\; \{\backslash \; displaystyle\; 2n\}$. Следовательно, независимо от того, выполняется ли решение для одного параметра или для обоих параметров одновременно, обычно требуется численное решение на компьютере. Преимущество оценки максимального правдоподобия - асимптотическая эффективность; оценка $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$с использованием выборочной медианы лишь примерно на 81% асимптотически эффективна, чем оценка $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$по максимальной вероятности. Среднее значение усеченной выборки с использованием статистики среднего порядка 24% составляет около 88% как асимптотически эффективный показатель $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$как оценка максимального правдоподобия. Когда метод Ньютона используется для поиска решения для оценки максимального правдоподобия, статистика среднего порядка 24% может использоваться в качестве начального решения для $x\; 0\; \{\backslash \; displaystyle\; x\_\; \{0\}\}$.

Форму можно оценить с помощью медианы абсолютных значений, поскольку для местоположения 0 переменные Коши $X\; \sim \; C\; auchy\; (0,\; \gamma )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; mathrm\; \{Cauchy\}\; (0,\; \backslash \; gamma)\}$, $медиана\; (|\; X\; |)\; =\; \gamma \; \{\backslash \; displaystyle\; \backslash \; mathrm\; \{median\}\; (|\; X\; |)\; =\; \backslash \; gamma\}$параметр формы.

A случайный вектор $X\; =\; (X\; 1,\dots ,\; X\; k)\; T\; \{\backslash \; displaystyle\; X\; =\; (X\_\; \{1\},\; \backslash \; ldots,\; X\_\; \{k\}))\; ^\; \{T\}\}$называется многомерным распределением Коши, если каждая линейная комбинация его компонентов $Y\; =\; a\; 1\; X\; 1\; +\; \cdots \; +\; ak\; X\; k\; \{\backslash \; displaystyle\; Y\; =\; a\_\; \{1\; \}\; X\_\; \{1\}\; +\; \backslash \; cdots\; +\; a\_\; \{k\}\; X\_\; \{k\}\}$имеет распределение Коши. То есть для любого постоянного вектора $a\; \in \; R\; k\; \{\backslash \; displaystyle\; a\; \backslash \; in\; \backslash \; mathbb\; \{R\}\; ^\; \{k\}\}$случайная величина $Y\; =\; a\; TX\; \{\backslash \; displaystyle\; Y\; =\; a\; ^\; \{T\}\; X\}$должно иметь одномерное распределение Коши. Характеристическая функция многомерного распределения Коши определяется выражением:

$\phi \; X\; (t)\; =\; eix\; 0\; (t)\; -\; \gamma \; (t),\; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{X\}\; (t)\; =\; e\; ^\; \{ix\_\; \{\; 0\}\; (t)\; -\; \backslash \; gamma\; (t)\},\; \backslash !\}$

где $x\; 0\; (t)\; \{\backslash \; displaystyle\; x\_\; \{0\}\; (t)\}$и $\gamma \; (t)\; \{\backslash \; displaystyle\; \backslash \; gamma\; (t)\}$- вещественные функции с $x\; 0\; (t)\; \{\backslash \; displaystyle\; x\_\; \{0\}\; (t)\}$a однородной функцией от первая степень и $\gamma \; (t)\; \{\backslash \; displaystyle\; \backslash \; gamma\; (t)\}$положительная однородная функция первой степени. Более формально:

$x\; 0\; (a\; t)\; =\; a\; x\; 0\; (t),\; \{\backslash \; displaystyle\; x\_\; \{0\}\; (at)\; =\; ax\_\; \{0\}\; (t),\}$

$\gamma \; (a\; t)\; =\; |\; а\; |\; \gamma \; (t),\; \{\backslash \; displaystyle\; \backslash \; gamma\; (at)\; =\; |\; а\; |\; \backslash \; gamma\; (t),\}$

для всех $t\; \{\backslash \; displaystyle\; t\}$.

Примером двумерного распределения Коши может быть задается по формуле:

$f\; (x,\; y;\; x\; 0,\; y\; 0,\; \gamma )\; =\; 1\; 2\; \pi \; [\gamma \; ((x\; -\; x\; 0)\; 2\; +\; (y\; -\; y\; 0)\; 2\; +\; \gamma \; 2)\; 3/2].\; \{\backslash \; displaystyle\; f\; (x,\; y;\; x\_\; \{0\},\; y\_\; \{0\},\; \backslash \; gamma)\; =\; \{1\; \backslash \; over\; 2\; \backslash \; pi\}\; \backslash \; left\; [\{\backslash \; gamma\; \backslash \; over\; ((x-x\_\; \{0\})\; ^\; \{\; 2\}\; +\; (y-y\_\; \{0\})\; ^\; \{2\}\; +\; \backslash \; gamma\; ^\; \{2\})\; ^\; \{3/2\}\}\; \backslash \; right].\}$

Обратите внимание, что в этом примере, хотя и нет аналога в ковариационную матрицу $x\; \{\backslash \; displaystyle\; x\}$и $y\; \{\backslash \; displaystyle\; y\}$не статистически независимы.

Мы также можем написать эта формула для комплексной переменной. Тогда функция плотности вероятности комплексного Коши равна:

$f\; (z;\; z\; 0,\; \gamma )\; =\; 1\; 2\; \pi \; [\gamma \; (|\; z\; -\; z\; 0\; |\; 2\; +\; \gamma \; 2)\; 3/2].\; \{\backslash \; displaystyle\; f\; (z;\; z\_\; \{0\},\; \backslash \; gamma)\; =\; \{1\; \backslash \; over\; 2\; \backslash \; pi\}\; \backslash \; left\; [\{\backslash \; gamma\; \backslash \; over\; (|\; z-z\_\; \{0\}\; |\; ^\; \{2\}\; +\; \backslash \; gamma\; ^\; \{\; 2\})\; ^\; \{3/2\}\}\; \backslash \; right].\}$

Аналогично одномерной плотности, многомерная плотность Коши также связана с многомерным распределением Стьюдента. Они эквивалентны, когда параметр степеней свободы равен единице. Плотность распределения Стьюдента измерения $k\; \{\backslash \; displaystyle\; k\}$с одной степенью свободы принимает следующий вид:

$f\; (x;\; \mu ,\; \Sigma ,\; k)\; =\; \Gamma \; (1\; +\; k\; 2)\; \Gamma \; (1\; 2)\; \pi \; k\; 2\; |\; \Sigma \; |\; 1\; 2\; [1\; +\; (x\; -\; \mu )\; T\; \Sigma \; -\; 1\; (x\; -\; \mu )]\; 1\; +\; k\; 2.\; \{\backslash \; displaystyle\; f\; (\{\backslash \; mathbf\; \{x\}\};\; \{\backslash \; mathbf\; \{\backslash \; mu\}\},\; \{\backslash \; mathbf\; \{\backslash \; Sigma\}\},\; k)\; =\; \{\backslash \; frac\; \{\backslash \; Gamma\; \backslash \; left\; (\{\backslash \; frac\; \{1\; +\; k\; \}\; \{2\}\}\; \backslash \; right)\}\; \{\backslash \; Gamma\; (\{\backslash \; frac\; \{1\}\; \{2\}\})\; \backslash \; pi\; ^\; \{\backslash \; frac\; \{k\}\; \{2\}\}\; \backslash \; left\; |\; \{\backslash \; mathbf\; \{\backslash \; Sigma\}\}\; \backslash \; right\; |\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; [1\; +\; (\{\backslash \; mathbf\; \{x\}\}\; -\; \{\backslash \; mathbf\; \{\backslash \; mu\}\})\; ^\; \{T\}\; \{\backslash \; mathbf\; \{\backslash \; Sigma\}\}\; ^\; \{-\; 1\}\; (\{\backslash \; mathbf\; \{x\}\}\; -\; \{\backslash \; mathbf\; \{\backslash \; mu\}\})\; \backslash \; right]\; ^\; \{\backslash \; frac\; \{1\; +\; k\}\; \{2\}\}\}\}.\}$

Свойства и детали для этой плотности могут можно получить, рассматривая его как частный случай многомерной плотности Стьюдента.

• Если $X\; \sim \; Коши\; \; (x\; 0,\; \gamma )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (x\_\; \{0\},\; \backslash \; gamma)\; \backslash ,\}$затем $К\; Икс\; +\; \ell \; \sim \; Коши\; (Икс\; 0\; К\; +\; \ell ,\; \gamma \; |\; К\; |)\; \{\backslash \; displaystyle\; kX\; +\; \backslash \; ell\; \backslash \; sim\; \{\backslash \; textrm\; \{Cauchy\}\}\; (x\_\; \{0\}\; k\; +\; \backslash \; ell,\; \backslash \; gamma\; |\; k\; |)\}$
• Если $X\; \sim \; Cauchy\; \; (x\; 0,\; \gamma \; 0)\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (x\_\; \{0\},\; \backslash \; gamma\; \_\; \{0\})\; \backslash ,\}$и $Y\; \sim \; Коши\; \; (x\; 1,\; \gamma \; 1)\; \{\backslash \; displaystyle\; Y\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (x\_\; \{1\},\; \backslash \; gamma\; \_\; \{1\})\; \backslash ,\}$независимы, тогда $X\; +\; Y\; \sim \; Cauchy\; \; (x\; 0\; +\; x\; 1,\; \gamma \; 0\; +\; \gamma \; 1)\; \{\backslash \; displaystyle\; X\; +\; Y\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (x\_\; \{0\}\; +\; x\_\; \{1\},\; \backslash \; gamma\; \_\; \{0\}\; +\; \backslash \; gamma\; \_\; \{1\})\; \backslash ,\}$и $X\; -\; Y\; \sim \; Cauchy\; \; (x\; 0\; -\; x\; 1,\; \gamma \; 0\; +\; \gamma \; 1)\; \{\backslash \; displaystyle\; XY\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (x\_\; \{0\}\; -x\_\; \{1\},\; \backslash \; gamma\; \_\; \{0\}\; +\; \backslash \; gamma\; \_\; \{1\})\; \backslash ,\}$
• Если $X\; \sim \; Коши\; \; (0,\; \gamma )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (0,\; \backslash \; gamma)\; \backslash ,\}$, затем $1\; X\; \sim \; Cauchy\; \; (0,\; 1\; \gamma )\; \{\backslash \; displaystyle\; \{\backslash \; tfrac\; \{1\}\; \{X\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{C\; auchy\}\; (0,\; \{\backslash \; tfrac\; \{1\}\; \{\backslash \; gamma\}\})\; \backslash ,\}$
• Параметризация МакКуллахом распределений Коши : выражение распределения Коши через один комплексный параметр $\psi \; =\; x\; 0\; +\; я\; \gamma \; \{\backslash \; displaystyle\; \backslash \; psi\; =\; x\_\; \{0\}\; +\; i\; \backslash \; gamma\}$, определить $X\; \sim \; Cauchy\; \; (\psi )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (\backslash \; psi)\}$для обозначения $X\; \sim \; Cauchy\; \; (x\; 0,\; |\; \gamma \; |)\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (x\_\; \{0\},\; |\; \backslash \; gamma\; |)\}$. Если $Икс\; \sim \; Коши\; \; (\psi )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (\backslash \; psi)\}$, то:

$a\; X\; +\; bc\; X\; +\; d\; \sim \; Cauchy\; \; (a\; \psi \; +\; bc\; \psi \; +\; d)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{aX\; +\; b\}\; \{cX\; +\; d\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; \backslash \; left\; (\{\backslash \; frac\; \{a\; \backslash \; psi\; +\; b\}\; \{c\; \backslash \; psi\; +\; d\; \}\}\; \backslash \; right)\}$

где $a\; \{\backslash \; displaystyle\; a\}$, $b\; \{\backslash \; displaystyle\; b\}$, $c\; \{\backslash \; displaystyle\; c\}$и $d\; \{\backslash \; displaystyle\; d\}$- действительные числа.

• Используя то же соглашение, что и выше, если $X\; \sim \; Cauchy\; \; (\psi )\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (\backslash \; psi)\}$, то:

$X\; -\; я\; Икс\; +\; я\; \sim \; CCauchy\; \; (\psi \; -\; я\; \psi \; +\; я)\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{Xi\}\; \{X\; +\; i\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{CCauchy\}\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; psi\; -i\}\; \{\; \backslash \; psi\; +\; i\}\}\; \backslash \; right)\}$

где $CCauchy\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{CCauchy\}\}$- круговое распределение Коши.

Распределение Коши - это стабильное распределение индекса 1. Представление Леви – Хинчина такого устойчивого распределения параметра $\gamma \; \{\backslash \; displaystyle\; \backslash \; gamma\}$задается для $X\; \sim \; Stable\; \; (\gamma ,\; 0,\; 0)\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \backslash \; operatorname\; \{Stable\}\; (\backslash \; gamma,\; 0,0)\; \backslash ,\}$по :

$E\; \; (\; eix\; X)\; =\; exp\; \; (\; \int \; R\; (\; eixy\; -\; 1)\; \Pi \; \gamma \; (\; dy))\; \{\backslash displaystyle\; \backslash operatorname\; \{E\}\; \backslash left(e^\{ixX\}\backslash right)=\backslash exp\; \backslash \; left(\backslash int\; \_\{\backslash mathbb\; \{R\}\; \}(e^\{ixy\}-1)\backslash Pi\; \_\{\backslash gamma\; \}(dy)\backslash right)\}$

where

and $c\; 1,\; \gamma ,\; c\; 2,\; \gamma \; \{\backslash displaystyle\; c\_\{1,\backslash gamma\; \},c\_\{2,\backslash gamma\; \}\}$can be expressed explicitly. In the case $\gamma \; =\; 1\; \{\backslash displaystyle\; \backslash gamma\; =1\}$of the Cauchy distribution, one has $c\; 1,\; \gamma \; =\; c\; 2,\; \gamma \; \{\backslash displaystyle\; c\_\{1,\backslash gamma\; \}=c\_\{2,\backslash gamma\; \}\}$.

This last representation is a consequence of the formula

$|\; х\; |\; =\; \int \; R\; (\; 1\; -\; e\; i\; x\; y)\; d\; y\; y\; 2\; \{\backslash displaystyle\; |x|=\backslash int\; \_\{\backslash mathbb\; \{R\}\; \}(1-e^\{ixy\})\backslash ,\{\backslash frac\; \{dy\}\{y^\{2\}\}\}\}$

• $Cauchy\; \; (\; 0,\; 1)\; \sim \; t\; (\; d\; f\; =\; 1)\; \{\backslash displaystyle\; \backslash operatorname\; \{Cauchy\}\; (0,1)\backslash sim\; \{\backslash textrm\; \{t\}\}(\backslash mathrm\; \{df\}\; =1)\backslash ,\}$Student's t distribution
• $Cauchy\; \; (\; \mu ,\; \sigma )\; \sim \; t\; (\; d\; f\; =\; 1)\; (\; \mu ,\; \sigma )\; \{\backslash displaystyle\; \backslash operatorname\; \{Cauchy\}\; (\backslash mu,\backslash sigma)\backslash sim\; \{\backslash textrm\; \{t\}\}\_\{(\backslash mathrm\; \{df\}\; =1)\}(\backslash mu,\backslash sigma)\backslash ,\}$non-standardized Student's t distribution
• If $X,\; Y\; \sim \; N\; (\; 0,\; 1)\; X,\; Y\; \{\backslash displaystyle\; X,Y\backslash sim\; \{\backslash textrm\; \{N\}\}(0,1)\backslash ,X,Y\}$independent, then $X\; Y\; \sim \; Cauchy\; (\; 0,\; 1)\; \{\backslash displaystyle\; \{\backslash tfrac\; \{X\}\{Y\}\}\backslash sim\; \{\backslash textrm\; \{Cauchy\}\}(0,1)\backslash ,\}$
• If $X\; \sim \; U\; (\; 0,\; 1)\; \{\backslash displaystyle\; X\backslash sim\; \{\backslash textrm\; \{U\}\}(0,1)\backslash ,\}$then $tan\; \; (\; \pi \; (\; X\; -\; 1\; 2))\; \sim \; Cauchy\; (\; 0,\; 1)\; \{\backslash displaystyle\; \backslash tan\; \backslash left(\backslash pi\; \backslash left(X-\{\backslash tfrac\; \{1\}\{2\}\}\backslash right)\backslash right)\backslash sim\; \{\backslash textrm\; \{Cauchy\}\}(0,1)\backslash ,\}$
• If $X\; \sim \; L\; o\; g\; -\; C\; a\; u\; c\; h\; y\; \; (\; 0,\; 1)\; \{\backslash displaystyle\; X\backslash sim\; \backslash opera\; torname\; \{Log-Cauchy\}\; (0,1)\}$then $ln\; \; (\; X)\; \sim \; Cauchy\; (\; 0,\; 1)\; \{\backslash displaystyle\; \backslash ln(X)\backslash sim\; \{\backslash textrm\; \{Cauchy\}\}(0,1)\}$
• If $X\; \sim \; Cauchy\; \; (\; x\; 0,\; \gamma )\; \{\backslash displaystyle\; X\backslash sim\; \backslash operatorname\; \{Cauchy\}\; (x\_\{0\},\backslash gamma)\}$then $1\; X\; \sim \; Cauchy\; \; (\; x\; 0\; x\; 0\; 2\; +\; \gamma \; 2,\; \gamma \; x\; 0\; 2\; +\; \gamma \; 2)\; \{\backslash displaystyle\; \{\backslash tfrac\; \{1\}\{X\}\}\backslash sim\; \backslash operatorname\; \{Cauchy\}\; \backslash left(\{\backslash tfrac\; \{x\_\{0\}\}\{x\_\{0\}^\{2\}+\backslash gamma\; ^\{2\}\}\},\{\backslash tfrac\; \{\backslash gamma\; \}\{x\_\{0\}^\{2\}+\backslash gamma\; ^\{2\}\}\}\backslash right)\}$
• The Cauchy distribution is a limiting case of a Pearson distribution of type 4
• The Cauchy distribution is a special case of a Pearson distribution of type 7.
• The Cauchy distribution is a stable distribution : if $X\; \sim \; Stable\; (\; 1,\; 0,\; \gamma ,\; \mu )\; \{\backslash displaystyle\; X\backslash sim\; \{\backslash textrm\; \{Stable\}\}(1,0,\backslash gamma,\backslash mu)\}$, then $X\; \sim \; Cauchy\; \; (\; \mu ,\; \gamma )\; \{\backslash displaystyle\; X\backslash sim\; \backslash operatorname\; \{Cauchy\}\; (\backslash mu,\backslash gamma)\}$.
• The Cauchy distribution is a singular limit of a hyperbolic distribution
• The wrapped Cauchy distribution, taking values on a circle, is derived from the Cauchy distribution by wrapping it around the circle.
• If $X\; \sim \; N\; (\; 0,\; 1)\; \{\backslash displaystyle\; X\backslash sim\; \{\backslash textrm\; \{N\}\}(0,1)\}$, $Z\; \sim \; I\; nverse\; -\; G\; amma\; \; (1/2,\; s\; 2/2)\; \{\backslash \; displaystyle\; Z\; \backslash \; sim\; \backslash \; operatorname\; \{Inverse-Gamma\}\; (1/2,\; s\; ^\; \{2\}\; /\; 2)\}$, затем $Y\; =\; \mu \; +\; XZ\; \sim \; Коши\; \; (\mu ,\; s)\; \{\backslash \; displaystyle\; Y\; =\; \backslash \; mu\; +\; X\; \{\backslash \; sqrt\; \{Z\}\}\; \backslash \; sim\; \backslash \; operatorname\; \{Cauchy\}\; (\backslash \; mu,\; s)\}$. Для половинных распределений Коши это соотношение выполняется, если положить $X\; \sim \; N\; (0,\; 1)\; I\; \{X>=\; 0\}\; \{\backslash \; displaystyle\; X\; \backslash \; sim\; \{\backslash \; textrm\; \{N\}\}\; (0,1)\; I\; \backslash \; \{\; X>=\; 0\; \backslash \}\}$.

В ядерной и физике частиц, энергетический профиль резонанс описывается релятивистским распределением Брейта – Вигнера, а распределение Коши - (нерелятивистским) распределением Брейта – Вигнера.

• В спектроскопия, распределение Коши описывает форму спектральных линий, которые подвержены однородному уширению, в котором все атомы взаимодействуют одинаково с диапазоном частот, содержащимся в Форма линии. Многие механизмы вызывают однородное уширение, в первую очередь столкновительное уширение. Lifeti me или естественное уширение также приводит к форме линии, описываемой распределением Коши.

• Применения распределения Коши или его преобразования можно найти в полях, работающих с экспоненциальным ростом. В статье Уайта 1958 года была получена тестовая статистика для оценок $\beta \; ^\; \{\backslash \; displaystyle\; \{\backslash \; hat\; \{\backslash \; beta\}\}\}$для уравнения $xt\; +\; 1\; =\; \beta \; xt\; +\; \epsilon \; t.\; +\; 1,\; \beta >1\; \{\backslash \; displaystyle\; x\_\; \{t\; +\; 1\}\; =\; \backslash \; beta\; \{x\}\; \_\; \{t\}\; +\; \backslash \; varepsilon\; \_\; \{t\; +\; 1\},\; \backslash \; beta>1\}$и где оценка за правдоподобеньших квадратов найдена с использованием обычных

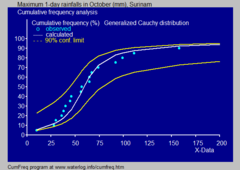
Дневные осадки с использованием CumFreq, см. также аппроксимация распределения

• Распределение Коши часто представляет собой распределение Распределение. Классическая ссылка на это называется проблемой маяка Чайки и как в приведенном выше разделе как распределение Брейта - Вигнера в физике элемента. ентарных частиц.

• В гидрологии распределены Коши применяемые к экстремальным явлениям, как годовые максимальные однодневные осадки и сток реки. Синий рисунок иллюстрирует пример подгонки распределения Коши к ранжированным месячным максимальным однодневным осадкам, также 90% доверительный пояс, основанный на биноми распределении. Данные о дождевых осадках представлены с помощью , где представлены позиции как часть кумулятивного частотного анализа.

• Выражение для мнимой части комплексной электрической диэлектрической проницаемости согласно модели Лоренца распределением Коши..

• В дополнительном распределении к модели толстых хвостов в вычислительных финансах, Коши распределения можно использовать для моделирования VAR (значение с риском ), производя много большая вероятность экстремального риска, чем распределение Гаусса.

• полет Леви и процесс Леви
• процесс Коши
• стабильный процесс
• наклонное распределение

• , Энциклопедия математики, EMS Press, 2001 [1994]
• Раннее использование: статья о распределении Коши содержит некоторую историческую информацию.
• Вайсштейн, Эрик У. "Распределение Коши". MathWorld.
• Научная библиотека GNU - Справочное руководство
• Отношения нормальных чисел Джорджа Марсалья