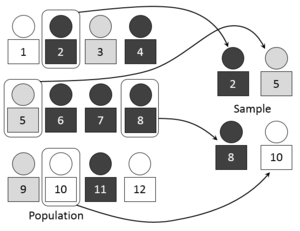
 Визуальное представление выбора простой случайной выборки
Визуальное представление выбора простой случайной выборки В статистика и методология количественного исследования, выборка - это набор людей или объектов, собранных или выбранных из статистической совокупности с помощью определенной процедуры. Элементы выборки известны как точки выборки, единицы выборки или наблюдения. Задуманный как набор данных, образец часто обозначается заглавными римскими буквами, например 
Как правило, население очень велико, поэтому проведение переписи или полное перечисление всех особей в совокупности непрактично или невозможно. Выборка обычно представляет собой подмножество управляемого размера. Собираются выборки, и по выборкам вычисляется статистика, так что можно сделать выводы или экстраполяции из выборки в генеральную совокупность.
Выборка может быть взята из генеральной совокупности без замены (т. Е. Ни один элемент не может быть выбран более одного раза в одной и той же выборке), и в этом случае это подмножество из население ; или с заменой (т. е. элемент может появляться несколько раз в одной выборке), в этом случае это мультиподмножество.
A полная выборка - это набор объектов из родительской совокупности, включающий все такие объекты, которые удовлетворяют набору четко определенных критериев отбора. Например, полная выборка австралийских мужчин ростом выше 2 м будет состоять из списка всех австралийских мужчин ростом выше 2 м. Но сюда не входят немецкие мужчины, высокие австралийские женщины или люди ростом ниже 2 м. Поэтому для составления такой полной выборки требуется полный список родительской популяции, включая данные о росте, поле и национальности для каждого члена этой родительской популяции. В случае человеческих популяций такой полный список вряд ли существует (человеческое население исчисляется миллиардами). Но такие полные образцы часто доступны в других дисциплинах, таких как набор игроков в крупной спортивной лиге, даты рождения членов парламента или полный ограниченный по величине список астрономических объектов.
несмещенная (репрезентативная) выборка - это набор объектов, выбранных из полной выборки с использованием процесса выбора, который не зависит от свойств объектов. Например, объективная выборка австралийских мужчин ростом выше 2 м может состоять из случайной выборки из 1% австралийских мужчин выше 2 м. Но человек, выбранный из списка избирателей, может быть непредвзятым, поскольку, например, мужчины в возрасте до 18 лет не будут включены в список избирателей. В астрономическом контексте объективная выборка может состоять из той части полной выборки, для которой доступны данные, при условии, что доступность данных не зависит от свойств отдельных источников.
Лучший способ избежать необъективной или нерепрезентативной выборки - выбрать случайную выборку, также известную как вероятностная выборка. Случайная выборка определяется как выборка, в которой каждый отдельный член совокупности имеет известный ненулевой шанс быть выбранным в качестве части выборки. Несколько типов случайных выборок: простые случайные выборки, систематические выборки, стратифицированные случайные выборки и кластерные случайные выборки.
Выборка, которая не является random называется неслучайной выборкой или неслучайной выборкой. Некоторыми примерами неслучайных выборок являются удобные образцы, оценочные образцы, целевые образцы, квотные образцы, образцы снежного кома, а в квази-методах Монте-Карло.
В математических терминах, учитывая распределение вероятностей F, случайную выборку длины n (где n может быть любым положительным целым числом) представляет собой набор реализаций n независимых, одинаково распределенных (iid ) случайных величин с распределением F.
Выборка конкретно представляет результаты из n экспериментов, в которых измеряется одно и то же количество. Например, если мы хотим оценить средний рост представителей определенной популяции, мы измеряем рост n человек. Каждое измерение берется из распределения вероятностей F, характеризующего совокупность, поэтому каждая измеренная высота 


