Стратифицированная выборка

Стратифицированная случайная выборка

В статистике, стратифицированная выборка представляет собой метод отбора проб из популяции, которая может быть секционированной в подгруппы.

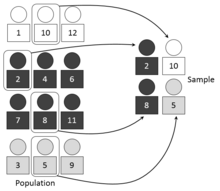Пример стратифицированной выборки

В статистических обследованиях, когда субпопуляции в общей популяции различаются, может быть полезно провести выборку каждой субпопуляции ( страты) независимо. Стратификация - это процесс разделения членов популяции на однородные подгруппы перед выборкой. Страты должны определять разделение населения. То есть, он должен быть исчерпывающим и взаимоисключающим : каждый элемент совокупности должен быть отнесен к одной и только одной страте. Затем в каждом слое применяется простая случайная выборка. Цель состоит в том, чтобы повысить точность выборки за счет уменьшения ошибки выборки. Он может производить взвешенное среднее, которое имеет меньшую вариабельность, чем среднее арифметическое из более простой случайной выборке населения.

В вычислительной статистике стратифицированная выборка - это метод уменьшения дисперсии, когда методы Монте-Карло используются для оценки статистики населения по известной совокупности.

• 1 Пример
• 2 Стратегии стратифицированной выборки
• 3 преимущества
• 4 Недостатки
• 5 Средняя и стандартная ошибка
• 6 Распределение размера выборки
• 7 См. Также
• 8 ссылки
• 9 Дальнейшее чтение

Предположим, что нам нужно оценить среднее количество голосов за каждого кандидата на выборах. Предположим, что в стране 3 города: в городе A 1 миллион заводских рабочих, в городе B 2 миллиона служащих, а в городе C 3 миллиона пенсионеров. Мы можем выбрать случайную выборку размером 60 для всего населения, но есть некоторая вероятность того, что полученная случайная выборка плохо сбалансирована по этим городам и, следовательно, является смещенной, вызывая значительную ошибку в оценке (когда интересующий результат имеет различное распределение по интересующему параметру между городами). Вместо этого, если мы выберем случайную выборку из 10, 20 и 30 из городов A, B и C соответственно, тогда мы сможем произвести меньшую ошибку в оценке для того же общего размера выборки. Этот метод обычно используется, когда популяция не является однородной группой.

1. Пропорциональное распределение использует долю выборки в каждой страте, которая пропорциональна доле всего населения. Например, если популяция состоит из всего n особей, из которых m мужчин и f женщин (и где m + f = n), то относительный размер двух выборок ( x 1 = m / n мужчин, x 2 = ж / п самки) должна отражать эту пропорцию.
2. Оптимальное распределение (или непропорциональное распределение). Доля выборки каждой страты пропорциональна как пропорции (как указано выше), так и стандартному отклонению распределения переменной. Большие выборки берутся в стратах с наибольшей изменчивостью, чтобы получить наименьшую возможную общую дисперсию выборки.

Реальным примером использования стратифицированной выборки может быть политический опрос. Если респондентам необходимо отразить разнообразие населения, исследователь будет специально стремиться включить участников из различных групп меньшинств, таких как раса или религия, исходя из их пропорциональности к общей численности населения, как указано выше. Таким образом, стратифицированное обследование может претендовать на то, чтобы быть более репрезентативным для населения, чем обследование простой случайной выборки или систематической выборки.

Причины использования стратифицированной выборки вместо простой случайной выборки включают:

1. Если измерения внутри слоев имеют более низкое стандартное отклонение (по сравнению с общим стандартным отклонением в генеральной совокупности), стратификация дает меньшую ошибку в оценке.
2. Для многих приложений измерения становятся более управляемыми и / или более дешевыми, когда совокупность сгруппирована по стратам.
3. Когда желательно иметь оценки параметров совокупности для групп внутри совокупности - стратифицированная выборка подтверждает, что у нас достаточно выборок из интересующих слоев.

Если плотность населения сильно различается в пределах региона, стратифицированная выборка гарантирует, что оценки могут быть сделаны с одинаковой точностью в различных частях региона и что сравнения субрегионов могут быть выполнены с одинаковой статистической мощностью. Например, в Онтарио при обследовании, проводимом по всей провинции, может использоваться более крупная фракция выборки на менее населенном севере, поскольку разница в численности населения между севером и югом настолько велика, что фракция выборки, основанная на выборке провинции в целом, может привести к сбор лишь нескольких данных с севера.

Стратифицированная выборка бесполезна, когда совокупность не может быть полностью разделена на непересекающиеся подгруппы. Было бы неправильным применением этого метода сделать размеры выборки подгрупп пропорциональными количеству данных, доступных от подгрупп, вместо того, чтобы масштабировать размеры выборки до размеров подгрупп (или их дисперсий, если известно, что они значительно различаются, например, с помощью F Test ). Считается, что данные, представляющие каждую подгруппу, имеют одинаковую важность, если предполагаемые различия между ними требуют стратифицированной выборки. Если дисперсии подгрупп значительно различаются и данные необходимо стратифицировать по дисперсии, невозможно одновременно сделать размер выборки каждой подгруппы пропорциональным размеру подгруппы в общей совокупности. Чтобы узнать об эффективном способе разделения ресурсов выборки между группами, которые различаются по средствам, дисперсии и стоимости, см. «Оптимальное распределение». Проблема стратифицированной выборки в случае неизвестных априорных классов (соотношение субпопуляций во всей популяции) может иметь пагубное влияние на выполнение любого анализа набора данных, например классификации. В этом отношении можно использовать минимаксный коэффициент выборки, чтобы сделать набор данных устойчивым в отношении неопределенности в базовом процессе генерации данных.

Объединение подстратов для обеспечения адекватных чисел может привести к парадоксу Симпсона, когда тенденции, которые действительно существуют в разных группах данных, исчезают или даже меняются местами при объединении групп.

Среднее значение и дисперсия стратифицированной случайной выборки определяются как:

${\ displaystyle {\ bar {x}} = {\ frac {1} {N}} \ sum _ {h = 1} ^ {L} N_ {h} {\ bar {x_ {h}}}}$

${\ displaystyle s _ {\ bar {x}} ^ {2} = \ sum _ {h = 1} ^ {L} \ left ({\ frac {N_ {h}} {N}} \ right) ^ {2 } \ left ({\ frac {N_ {h} -n_ {h}} {N_ {h}}} \ right) {\ frac {s_ {h} ^ {2}} {n_ {h}}}}$

куда,

${\ Displaystyle L =}$ количество слоев

${\ Displaystyle N =}$ сумма всех размеров страты

${\ displaystyle N_ {h} =}$ размер пласта ${\ displaystyle h}$

${\ displaystyle {\ bar {x_ {h}}} =}$ выборочное среднее по страте ${\ displaystyle h}$

${\ displaystyle n_ {h} =}$ количество наблюдений в страте ${\ displaystyle h}$

${\ displaystyle s_ {h} =}$ стандартное отклонение выборки страты ${\ displaystyle h}$

Обратите внимание, что член ( -) / (), который равен (1 - /), является поправкой на конечную популяцию и должен быть выражен в «единицах выборки». Вышеупомянутая поправка на конечную популяцию дает: ${\ displaystyle N_ {h}}$${\ displaystyle n_ {h}}$${\ displaystyle N_ {h}}$${\ displaystyle n_ {h}}$${\ displaystyle N_ {h}}$ ${\ displaystyle N_ {h}}$

${\ displaystyle s _ {\ bar {x}} ^ {2} = \ sum _ {h = 1} ^ {L} \ left ({\ frac {N_ {h}} {N}} \ right) ^ {2 } {\ frac {s_ {h} ^ {2}} {n_ {h}}}}$

где = / - вес населения страты. ${\ displaystyle w_ {h}}$${\ displaystyle N_ {h}}$${\ displaystyle N}$${\ displaystyle h}$

Для стратегии пропорционального распределения размер выборки в каждой страте берется пропорционально размеру страты. Предположим, что в компании есть следующие сотрудники:

• мужчин, полная занятость: 90
• мужчин, неполный рабочий день: 18
• женщина, полная занятость: 9
• женщины, неполный рабочий день: 63
• всего: 180

и нас просят взять выборку из 40 сотрудников, разделенных по вышеуказанным категориям.

Первый шаг - вычислить процентное соотношение каждой группы от общей суммы.

• % мужчин, работающих полный рабочий день = 90 ÷ 180 = 50%
• % мужчин, неполный рабочий день = 18 ÷ 180 = 10%
• % женщин, работающих полный рабочий день = 9 ÷ 180 = 5%
• % женщин, неполный рабочий день = 63 ÷ 180 = 35%

Это говорит нам о том, что из нашей выборки из 40,

• 50% (20 человек) должны быть мужчинами, работающими полный рабочий день.
• 10% (4 человека) должны быть мужчинами, работающими неполный рабочий день.
• 5% (2 человека) должны составлять женщины, работающие полный рабочий день.
• 35% (14 человек) должны составлять женщины, работающие неполный рабочий день.

Еще один простой способ без вычисления процента - это умножить размер каждой группы на размер выборки и разделить на общую численность населения (размер всего персонала):

• мужчины, полный рабочий день = 90 × (40 ÷ 180) = 20
• мужчины, неполный рабочий день = 18 × (40 ÷ 180) = 4
• женщины, дневная форма = 9 × (40 ÷ 180) = 2
• женщины, неполный рабочий день = 63 × (40 ÷ 180) = 14

• Опрос общественного мнения
• Многоступенчатый отбор проб
• Статистический бенчмаркинг
• Размер стратифицированной выборки
• Стратификация (клинические испытания)

• Сэрндал, Карл-Эрик; и другие. (2003). «Стратифицированная выборка». Выборка обследования с помощью модели. Нью-Йорк: Спрингер. С. 100–109. ISBN   0-387-40620-4.