Выпуклость в экономике

Выпуклость - важная тема в экономике . В модели Эрроу – Дебре из общего экономического равновесия агенты имеют выпуклые наборы бюджета и выпуклые предпочтения : при равновесных ценах бюджет гиперплоскость поддерживает наилучшую достижимую кривую безразличия. функция прибыли - это выпуклое сопряжение функции стоимости. Выпуклый анализ - стандартный инструмент для анализа экономики учебников. Невыпуклые явления в экономике изучались с помощью негладкого анализа, который обобщает выпуклый анализ.

• 1 Предварительные сведения
  • 1.1 Реальные векторные пространства
  • 1.2 Выпуклые множества
  • 1.3 Выпуклая оболочка
• 2 Двойственность: пересекающиеся полупространства
  • 2.1 Поддерживающая теорема о гиперплоскости
  • 2.2 Экономика
• 3 Невыпуклость
  • 3.1 Негладкий анализ
• 4 См. Также
• 5 Примечания
• 6 Ссылки

Экономика зависит от следующих определений и результатов из выпуклой геометрии.

вещественных векторных пространств

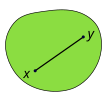A выпуклого множества покрывает отрезок линии, соединяющий любые две его точки. 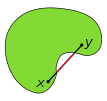Невыпуклый набор не может покрыть точку в некотором отрезке, соединяющем два из своих Сегменты линии тест выпуклость.

A реальное векторное пространство двух измерений может иметь декартову систему координат, в котором каждая точка определяется списком из двух действительных чисел, называемых «координатами», которые условно обозначается x и y. Две точки на декартовой плоскости могут быть сложены по координатам

(x1, y 1) + (x 2, y 2) = (x 1+x2, y 1+y2);

далее точка может быть умножена на каждое действительное число λ по координатам

λ (x, y) = (λx, λy).

В более общем смысле, любое реальное векторное пространство (конечной) размерности D можно рассматривать как набор всех возможных списков действительных чисел D {(v 1, v 2,..., V D)} вместе с двумя операциями : сложение вектора и умножение на действительное число.Для конечномерных векторных пространств каждая операция сложения векторов и умножения действительных чисел может быть определена по координатам, следуя примеру декартовой плоскости.

Выпуклые множества

В выпуклая оболочка красного набора, каждая синяя точка представляет собой выпуклую комбинацию некоторых красных точек.

В реальном векторном пространстве набор определяется как выпуклый если для каждой пары его точек каждая точка на отрезке , соединяющее их, покрыто множеством. Например, твердый куб выпуклый; однако все, что является полым или помятым, например форма полумесяца, не является выпуклым. Тривиально, пустое множество выпукло.

Более формально множество Q является выпуклым, если для всех точек v 0 и v 1 в Q и для каждого действительного числа λ в блоке интервал [0,1], точка

(1 - λ) v 0 + λv 1

является членом Q.

Согласно математической индукции, множество Q является выпуклым тогда и только тогда, когда каждая выпуклая комбинация членов Q также принадлежит Q. По определению, выпуклая комбинация индексированного подмножества {v 0, v 1,..., v D } векторного пространства - любое средневзвешенное значение λ0v0+ λ 1v1+... + λ DvDдля некоторого индексированного набора неотрицательных действительных чисел {λ d }, удовлетворяющего уравнению λ0+ λ 1 +... + λ D = 1.

Определение выпуклого множества подразумевает, что пересечение двух выпуклых множеств является выпуклым множеством. В более общем смысле, пересечение семейства выпуклых множеств является выпуклым множеством.

Выпуклая оболочка

Для каждого подмножества Q реального векторного пространства его выпуклая оболочка Conv (Q) - это минимальное выпуклое множество, которое содержит Q. Таким образом, Conv (Q) является пересечением всех выпуклых множеств, которые покрывают Q. Выпуклая оболочка множества может быть эквивалентно определена как множество всех выпуклых комбинаций точек в Q.

A выпуклое множество $S\; \{\backslash \; displaystyle\; S\}$(розового цвета), опорная гиперплоскость $S\; \{\backslash \; displaystyle\; S\}$(пунктирная линия) и полупространство, ограниченное гиперплоскостью, содержащей $S\; \{\backslash \; displaystyle\; S\}$(светло-синим).

Поддержка гиперплоскости - это концепция в геометрии. Гиперплоскость делит пространство на два полупространства. Гиперплоскость поддерживает set $S\; \{\backslash \; displaystyle\; S\}$в реальном n-пространстве $R\; n\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\}$, если он соответствует обоим из следующих условий:

• $S\; \{\backslash \; displaystyle\; S\}$полностью содержится в одном из два замкнутых полупространства, определяемые гиперплоскостью
• $S\; \{\backslash \; displaystyle\; S\}$, имеют по крайней мере одну точку на гиперплоскости.

Здесь замкнутое полупространство полупространство, включающее гиперплоскость.

Поддерживающая теорема о гиперплоскости

Выпуклое множество может иметь более одной поддерживающей гиперплоскости в данной точке на его границе.

Эта теорема утверждает, что если $S\; \{\backslash \; displaystyle\; S\}$- замкнутое выпуклое множество в $R\; n,\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{n\},\}$и $x\; \{\backslash \; displaystyle\; x\}$- точка на границе из $S,\; \{\backslash \; displaystyle\; S,\}$тогда существует поддерживающая гиперплоскость, содержащая $х.\; \{\backslash \; displaystyle\; x.\}$

Гиперплоскость в теореме может быть не уникальной, как показано на втором рисунке справа. Если замкнутое множество $S\; \{\backslash \; displaystyle\; S\}$не является выпуклым, утверждение теоремы неверно во всех точках на границе $S,\; \{\backslash \; displaystyle\; S,\}$, как показано на третьем рисунке справа.

Опорная гиперплоскость, содержащая заданную точку на границе $S\; \{\backslash \; displaystyle\; S\}$, может не существовать, если $S\; \{\backslash \; displaystyle\; S\}$не выпуклый.

Экономика

Потребитель предпочитает вектор товаров (Q x, Q y) другим доступным векторам. При этом оптимальном векторе бюджетная линия поддерживает кривую безразличия I2.

Оптимальная корзина товаров возникает там, где выпуклый набор предпочтений потребителя поддерживается бюджетным ограничением, поскольку показано на схеме. Если набор предпочтений является выпуклым, то набор оптимальных решений потребителя представляет собой выпуклое множество, например, уникальную оптимальную корзину (или даже линейный сегмент оптимальных корзин).

Для простоты предположим, что предпочтения потребителя можно описать с помощью функции полезности, которая является непрерывной функцией, что подразумевает, что наборы предпочтений являются закрытыми. (Значение термина «замкнутое множество» объясняется ниже, в подразделе, посвященном приложениям оптимизации.)

Когда предпочтения потребителей имеют вогнутости, линейные бюджеты не должны поддерживать равновесие: потребители могут прыгать между распределениями.

Если набор предпочтений невыпуклый, то некоторые цены создают бюджет, поддерживающий два различных оптимальных решения о потреблении. Например, мы можем представить, что для зоопарков лев стоит столько же, сколько орел, и, кроме того, бюджета зоопарка хватит на одного орла или одного льва. Можно также предположить, что смотритель зоопарка считает любое животное равноценным. В этом случае зоопарк покупал либо одного льва, либо одного орла. Конечно, современный зоотехник не захочет покупать половину орла и половину льва (или грифона )! Таким образом, предпочтения современного зоопарка невыпуклые: хранитель зоопарка предпочитает иметь любое животное, а не любую их строго выпуклую комбинацию.

Невыпуклые множества были включены в теории общего экономического равновесия, сбоев рыночного механизма и государственной экономики. Эти результаты описаны в учебниках для выпускников по микроэкономике, теории общего равновесия, теории игр, математической экономике и прикладной математике (для экономистов). Результаты леммы Шепли – Фолкмана устанавливают, что невыпуклости совместимы с приблизительным равновесием на рынках с большим количеством потребителей; эти результаты также применимы к производственной экономике с большим количеством мелких фирм.

в «олигополиях » (на рынках доминируют несколько производителей), особенно в «монополиях »(на рынках доминирует один производитель), неравномерность остается важной. Обеспокоенность по поводу того, что крупные производители используют рыночную власть, фактически положила начало литературе о невыпуклых наборах, когда Пьеро Сраффа писал о фирмах с растущей отдачей от масштаба в 1926 году, после чего Гарольд Хотеллинг писал о ценообразовании по предельным затратам в 1938 году. И Сраффа, и Хотеллинг осветили рыночную власть производителей без конкурентов, что явно стимулировало создание литературы по вопросам предложения в экономике. Невыпуклые наборы возникают также с экологическими товарами (и другими внешними факторами ), с информационной экономикой и с фондовыми рынками (и другими неполные рынки ). Такие приложения продолжали мотивировать экономистов к изучению невыпуклых множеств.

Негладкий анализ

Экономисты все чаще изучали невыпуклые множества с помощью негладкого анализа, который обобщает выпуклый анализ. «Невыпуклость в [как] производстве, так и в потреблении... требовала математических инструментов, выходящих за рамки выпуклости, и дальнейшее развитие должно было ждать изобретения негладкого исчисления» (например, Фрэнсис Кларк локально Липшиц исчисление), как описано в Rockafellar Wets (1998) и Мордухович (2006), в соответствии с Khan (2008). Brown (1995, pp. 1967–1968) harvtxt error: no target: CITEREFBrown1995 (help ) писал, что «основным методологическим нововведением в анализе общего равновесия фирм с правилами ценообразования» было «внедрение методов негладкого анализа как [синтез] глобального анализа (дифференциальная топология) и [из] выпуклого анализа ». Согласно Брауну (1995, стр. 1966) harvtxt error: no target: CITEREFBrown1995 (help ), «негладкий анализ расширяет локальную аппроксимацию многообразий касательными плоскостями [и расширяет ] аналогичное приближение выпуклых множеств касательными конусами к множествам, "которые могут быть негладкими или невыпуклыми. Экономисты также использовали алгебраическую топологию.

• Выпуклая двойственность

• Блюм, Лоуренс Э. (2008c). «Выпуклость». В Durlauf, Steven N.; Блюм, Лоуренс Э. (ред.). Новый экономический словарь Пэлгрейва (второе изд.). Пэлгрейв Макмиллан. С. 225–226. doi : 10.1057 / 9780230226203.0315. ISBN 978-0-333-78676-5. CS1 maint: ref = harv (ссылка )
• Блюм, Лоуренс Э. (2008cp «Выпуклое программирование». In Durlauf, Steven N.; Блюм, Лоуренс E (ред.). Новый экономический словарь Palgrave (второе издание). Palgrave Macmillan. С. 220–225. doi : 10.1057 / 9780230226203.0314. ISBN 978-0-333-78676-5. Проверьте значения даты в: | year =() CS1 maint: ref = harv (link )
• Блюм, Лоуренс Э. (2008d). «Двойственность». In Durlauf, Steven N.; Блюм, Лоуренс E (ред.). Новый экономический словарь Пэлгрейва (второе изд.). Palgrave Macmillan. Pp. 551– 555. doi : 10.1057 / 9780230226203.0411. ISBN 978-0-333-78676-5. CS1 maint: ref = harv (ссылка )
• Crouzeix, J.-P. (2008). «Квазивогнутость». In Durlauf, Steven N.; Blume, Lawrence E (ред.). Новый экономический словарь Пэлгрейва (второе изд.). Palgrave Macmillan. pp. 815–816. doi : 10.1057 / 9780230226203.1375. ISBN 978-0-333-78676-5. CS1 maint: ref = harv (link )
• Diewert, WE (1982). "12 Двойственность подходы к микроэкономической теории ". В Эрроу, Кеннет Джозеф ; Intriligator, Майкл Д. (ред.). Справочник по математической экономике, Том II . Справочники по экономике. 1 . Амстердам: North-Holland Publishing Co., стр. 535–599. doi : 10.1016 / S1573-4382 (82) 02007-4. ISBN 978-0-444-86127-6. MR 0648778. CS1 maint: ref = harv (ссылка )
• Грин, Джерри; Хеллер, Уолтер П. (1981). «1 Математический анализ и выпуклость с приложениями к экономике». В Эрроу, Кеннет Джозеф ; Intriligator, Майкл Д. (ред.). Справочник по математической экономике, Том I . Справочники по экономике. 1 . Амстердам: North-Holland Publishing Co., стр. 15–52. doi : 10.1016 / S1573-4382 (81) 01005-9. ISBN 978-0-444-86126-9. MR 0634800. CS1 maint: ref = harv (link )
• Luenberger, David G. Microeconom ic Theory, McGraw-Hill, Inc., New York, 1995.
• Mas-Colell, A. (1987). «Невыпуклость» (PDF). В Итуэлле, Джон; Милгейт, Мюррей; Ньюман, Питер (ред.). Новый Палгрейв: экономический словарь (первое издание). Пэлгрейв Макмиллан. С. 653–661. doi : 10.1057 / 9780230226203.3173. ISBN 9780333786765. CS1 maint: ref = harv (ссылка )
• Ньюман, Питер (1987c). «Выпуклость». In Eatwell, John; Milgate, Murray; Newman, Peter (ред.). New Palgrave: A Dictionary of Economics (первое издание). Palgrave Macmillan. P. 1. doi : 10.1057 / 9780230226203.2282. ISBN 9780333786765. CS1 maint: ref = harv (ссылка )
• Ньюман, Питер (1987d). «Двойственность». В Eatwell, John; Milgate, Murray; Newman, Peter (ред.). New Palgrave: A Dictionary of Economics (первое издание).). Palgrave Macmillan. Стр. 1. doi : 10.1057 / 9780230226203.2412. ISBN 9780333786765. CS1 maint: ref = harv (link )
• Rockafellar, R. Tyrrell (1997). Выпуклый анализ. Вехи Принстона в математике (Перепечатка серии математических исследований Принстона 1979 г. 28 изд.). Princeton, Нью-Джерси: Princeton University Press. ISBN 978-0-691-01586-6. MR 0274683. CS1 maint: ref = harv (ссылка ).
• Шнайдер, Рольф (1993). Выпуклые тела: теория Брунна – Минковского. Энциклопедия математики и ее приложений. 44 . Кембридж: Издательство Кембриджского университета. С. xiv + 490. doi : 10.1017 / CBO9780511526282. ISBN 978-0-521-35220-8. MR 1216521. CS1 maint: ref = harv (ссылка )