Разложение по сингулярным числам

Разложение матрицы

Иллюстрация разложения по сингулярным числам UΣV вещественной матрицы 2 × 2 M.

• Вверху: Действие M, обозначенное его действием на единичный диск D и два канонических единичных вектора e 1 и e 2.
• Слева: Действие V, вращение, на D, e 1 и e 2.
• Внизу: Действие Σ, масштабирование сингулярными значениями σ 1 по горизонтали и σ 2 по вертикали.
• Справа: Действие U, другое вращение.

В линейная алгебра, разложение по сингулярным числам (SVD ) - это факторизация вещественного или комплексная матрица, которая обобщает собственное разложение квадратной нормальной матрицы на любую $m\; \times \; n\; \{\backslash \; displaystyle\; m\; \backslash \; times\; n\}$матрица через расширение полярного разложения.

В частности, сингулярная val ue разложение $m\; \times \; n\; \{\backslash \; displaystyle\; m\; \backslash \; times\; n\}$вещественной или комплексной матрицы $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$является факторизацией формы $U\; \Sigma \; V\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\; \backslash \; Sigma\; V\; ^\; \{*\}\}\}$, где $U\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\}$- это $m\; \times \; m\; \{\backslash \; displaystyle\; m\; \backslash \; times\; m\}$вещественная или комплексная унитарная матрица, $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\; \}$- это $m\; \times \; n\; \{\backslash \; displaystyle\; m\; \backslash \; times\; n\}$прямоугольная диагональная матрица с неотрицательными действительными числами по диагонали, и $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$- это $n\; \times \; n\; \{\backslash \; displaystyle\; n\; \backslash \; times\; n\}$вещественная или комплексная унитарная матрица. Если $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$реально, $U\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\}$и $VT\; =\; V\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\; ^\; \{T\}\}\; =\; \backslash \; mathbf\; \{V\; ^\; \{*\}\}\}$- вещественные ортогональные матрицы.

диагональные элементы $\sigma \; i\; =\; \Sigma \; ii\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{i\}\; =\; \backslash \; Sigma\; \_\; \{ii\}\}$из $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$известны как сингулярные значения из $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$. Количество ненулевых особых значений равно рангу для $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$. Столбцы $U\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\}$и столбцы $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$называются лево-сингулярные векторы и правые сингулярные векторы из $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$соответственно.

SVD не уникален. Всегда можно выбрать разложение так, чтобы сингулярные значения $\Sigma \; i\; i\; \{\backslash \; displaystyle\; \backslash \; Sigma\; \_\; \{ii\}\}$располагались в порядке убывания. В этом случае $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$(но не всегда U и V ) однозначно определяется M.

Термин иногда относится к компактному SVD, аналогичному разложению $M\; =\; U\; \Sigma \; V\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{U\; \backslash \; Sigma\; V\; ^\; \{*\}\}\}$, в котором $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$представляет собой квадратную диагональ размером $r\; \times \; r\; \{\backslash \; displaystyle\; r\; \backslash \; times\; r\}$, где $r\; \le \; min\; \{m,\; n\}\; \{\backslash \; displaystyle\; r\; \backslash \; leq\; \backslash \; min\; \backslash \; \{m,\; n\; \backslash \}\}$- это ранг M, и имеет только ненулевые особые значения. В этом варианте $U\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\}$представляет собой $m\; \times \; r\; \{\backslash \; displaystyle\; m\; \backslash \; times\; r\}$полуунитарную матрицу и $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$- это $n\; \times \; r\; \{\backslash \; displaystyle\; n\; \backslash \; times\; r\}$полуунитарная матрица, такая что $U\; *\; U\; =\; V\; *\; V\; =\; I\; r\; \times \; r\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\; ^\; \{*\}\; U\}\; =\; \backslash \; mathbf\; \{V\; ^\; \{*\}\; V\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{r\; \backslash \; times\; r\}\; \}$.

Математические приложения SVD включают вычисление псевдообратной матрицы, аппроксимацию матрицы и определение ранга, диапазона и нулевого пространства матрицы. SVD также чрезвычайно полезен во всех областях науки, инженерии и статистики, таких как обработка сигналов, аппроксимация методом наименьших квадратов данные и управление процессом.

• 1 Интуитивная интерпретация
  • 1.1 Вращение, масштабирование координат и отражение
  • 1.2 Особые значения как полуоси эллипса или эллипсоида
  • 1.3 Столбцы U и V являются ортонормированными основаниями
  • 1.4 Геометрическое значение
• 2 Пример
• 3 SVD и спектральное разложение
  • 3.1 Сингулярные значения, сингулярные векторы и их связь с SVD
  • 3.2 Связь с разложением по собственным значениям
• 4 Приложения SVD
  • 4.1 Псевдообратная
  • 4.2 Решение однородных линейных уравнений
  • 4.3 Полная минимизация методом наименьших квадратов
  • 4.4 Диапазон, нулевое пространство и ранг
  • 4.5 Аппроксимация матрицы низкого ранга
  • 4.6 Разделимые модели
  • 4.7 Ближайшая ортогональная матрица
  • 4.8 Алгоритм Кабша
  • 4.9 Обработка сигналов
  • 4.10 Другие примеры
• 5 Доказательства существования
  • 5.1 Ba sed по спектральной теореме
  • 5.2 На основе вариационной характеристики
• 6 Расчет SVD
  • 6.1 Численный подход
  • 6.2 Аналитический результат 2 × 2 SVD
• 7 Уменьшенные SVD
  • 7.1 Тонкий SVD
  • 7.2 Компактный SVD
  • 7.3 Усеченный SVD
• 8 Нормы
  • 8.1 Нормы Ky Fan
  • 8.2 Норма Гильберта – Шмидта
• 9 Вариации и обобщения
  • 9.1 Представление Mode-k
  • 9.2 Тензорный SVD
  • 9.3 Масштабно-инвариантный SVD
  • 9.4 HOSVD функций - численная реконструкция - преобразование модели TP
  • 9.5 Ограниченные операторы в гильбертовых пространствах
  • 9.6 Сингулярные числа и компактные операторы
• 10 История
• 11 См. Также
• 12 Примечания
• 13 Ссылки
• 14 Внешние ссылки

Анимированная иллюстрация SVD реальной двумерной матрицы сдвига M. Сначала мы видим единичный диск синим цветом вместе с двумя каноническими единичными векторами. Затем мы видим действия M, который искажает диск в виде эллипса. SVD раскладывает M на три простых преобразования: начальное вращение V, масштабирование $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$по осям координат и окончательный поворот U . Длины σ 1 и σ 2 полуосей эллипса являются сингулярными значениями для M, а именно Σ1,1 и Σ2,2.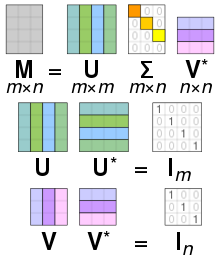 Визуализация матричных умножений при разложении по сингулярным числам

Вращение, масштабирование координат и отражение

В специальном случай, когда M является вещественной квадратной матрицей размером m × m, матрицы U и V могут быть выбраны как действительные m × m матрицы тоже. В этом случае «унитарный» означает то же самое, что и «ортонормированный ». Затем, интерпретируя обе унитарные матрицы, а также диагональную матрицу, резюмированную здесь как A, как линейное преобразование x→Axпространства R, матрицы U и V представляют вращения или отражение пространства, а $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$представляет собой масштабирование каждой координаты xiна коэффициент σ i. Таким образом, SVD-декомпозиция разбивает любое обратимое линейное преобразование R на композицию трех геометрических преобразований : вращение или отражение (V ), за которым следует покоординатное масштабирование ($\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$), за которым следует другое вращение или отражение (U ).

В частности, если M имеет положительный определитель, тогда U и V могут быть выбраны как отражения или оба поворота. Если определитель отрицательный, ровно один из них должен быть отражением. Если определитель равен нулю, каждый может быть независимо выбран как принадлежащий к любому типу.

Если матрица M является действительной, но не квадратной, а именно m × n с m ≠ n, ее можно интерпретировать как линейное преобразование из R в Р . Тогда U и V могут быть выбраны для поворота на R и R соответственно; и $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$, помимо масштабирования первого $min\; \{m,\; n\}\; \{\backslash \; displaystyle\; \backslash \; min\; \backslash \; \{m,\; n\; \backslash \}\}$координаты, также расширяет вектор нулями, т.е. удаляет конечные координаты, чтобы превратить R в R.

особые значения как полуоси эллипса или эллипсоида

Как показано на рисунке сингулярные значения можно интерпретировать как величину полуосей эллипса в 2D. Эту концепцию можно обобщить на n-мерное евклидово пространство, где сингулярные значения любой квадратной матрицы n × n рассматриваются как величина полуоси n-мерного эллипсоид. Точно так же сингулярные значения любой матрицы m × n можно рассматривать как величину полуоси n-мерного эллипсоида в m-мерном пространстве, например, как эллипс в (наклонной) 2D плоскости. в трехмерном пространстве. Особые значения кодируют величину полуоси, а сингулярные векторы кодируют направление. Подробнее см. ниже.

Столбцы U и V являются ортонормированными основаниями

Поскольку U и V унитарны, столбцы каждого из них образуют набор ортонормированные векторы, которые можно рассматривать как базисные векторы. Матрица M отображает базисный вектор Viна растянутый единичный вектор σ iUi. По определению унитарной матрицы то же самое верно для их сопряженных транспозиций U и V, за исключением того, что геометрическая интерпретация сингулярных значений как отрезков теряется. Короче говоря, столбцы U, U, Vи V являются ортонормированными основаниями. Когда $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$является нормальной матрицей, Uи V уменьшаются до унитарной, используемой для диагонализации $M\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{M\}\}$. Однако, когда $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$не является нормальным, но все же диагонализуемым, его собственное разложение и разложение по сингулярным числам различны.

Геометрическое значение

Поскольку U и V являются унитарными, мы знаем, что столбцы U1,..., UmU дает ортонормированный базис K, а столбцы V1,..., VnV дают ортонормированный базис K (с учетом к стандартным скалярным произведениям на этих пространствах).

линейное преобразование

$\{T:\; K\; n\; \to \; K\; mx\; \mapsto \; M\; x\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{cases\}\; T:\; K\; ^\; \{n\}\; \backslash \; в\; K\; ^\; \{m\}\; \backslash \; \backslash \; x\; \backslash \; mapsto\; \backslash \; mathbf\; \{M\}\; x\; \backslash \; end\; \{ases\}\}\}$

имеет особенно простое описание этих ортонормированных базисов:

$T\; (V\; i)\; =\; \sigma \; i\; U\; i,\; i\; =\; 1,\dots ,\; мин\; (м,\; п),\; \{\backslash \; displaystyle\; T\; (\backslash \; mathbf\; \{V\}\; \_\; \{i\})\; =\; \backslash \; sigma\; \_\; \{i\}\; \backslash \; mathbf\; \{U\}\; \_\; \{i\},\; \backslash \; qquad\; i\; =\; 1,\; \backslash \; ldots,\; \backslash \; min\; (m,\; n),\}$

где σ i - i-я диагональная запись в $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$, и T (Vi) = 0 для i>min (m, n).

Таким образом, геометрическое содержание теоремы SVD можно резюмировать следующим образом: для любого линейного отображения T: K → K можно найти ортонормированные базисы K и K такие, что T отображает i-й базисный вектор K на неотрицательное кратное i-го базисного вектора K, и отправляет оставшиеся базисные векторы в ноль. По отношению к этим базам отображение T поэтому представляется диагональной матрицей с неотрицательными действительными диагональными элементами.

Чтобы получить более наглядный вид сингулярных значений и факторизации SVD - по крайней мере, при работе с реальными векторными пространствами - рассмотрите сферу S радиуса один в R . Линейное отображение T отображает эту сферу на эллипсоид в R . Ненулевые особые значения - это просто длины полуосей этого эллипсоида. Особенно, когда n = m, и все сингулярные значения различны и отличны от нуля, SVD линейного отображения T может быть легко проанализировано как последовательность трех последовательных ходов: рассмотрим эллипсоид T (S) и, в частности, его оси; затем рассмотрите направления в R, отправленные T на эти оси. Эти направления оказываются взаимно ортогональными. Сначала примените изометрию V, посылая эти направления на оси координат R . На втором ходу примените эндоморфизм D, диагонализованный вдоль осей координат и растягивающий или сжимающий в каждом направлении, используя длины полуосей T (S) в качестве коэффициентов растяжения. Затем композиция D∘ Vотправляет единичную сферу на эллипсоид, изометричный T (S). Чтобы определить третий и последний ход U, примените изометрию к этому эллипсоиду, чтобы перенести его на T (S). Как легко проверить, композиция U∘ D∘ Vсовпадает с T.

Рассмотрим матрицу 4 × 5

$M\; =\; [1\; 0\; 0\; 0\; 2\; 0\; 0\; 3\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 0\; 2\; 0\; 0\; 0]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; 0\; 2\; \backslash \backslash \; 0\; 0\; 3\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 0\; \backslash \backslash \; 0\; 2\; 0\; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\}$

Разложение по единственному числу этой матрицы задается формулой U$\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$V

$U = [0 - 1 0 0 - 1 0 0 0 0 0 0 - 1 0 0 - 1 0] Σ = [ 3 0 0 0 0 0 5 0 0 0 0 0 2 0 0 0 0 0 0 0] V ∗ = [0 0 - 1 0 0 - 0,2 0 0 0 - 0,8 0 - 1 0 0 0 0 0 0 1 0 - 0,8 0 0 0 0,2] {\ displaystyle {\ begin {align} \ mathbf {U} = {\ begin {bmatrix} \ color {Green} 0 \ color {Blue} -1 \ color {Cyan} 0 \ color { Изумруд} 0 \\\ цвет {зеленый} -1 \ цвет {синий} 0 \ цвет {голубой} 0 \ цвет {изумруд} 0 \\\ цвет {зеленый} 0 \ цвет {синий} 0 \ цвет {голубой} 0 \ color {Emerald} -1 \\\ color {Green} 0 \ color {Blue} 0 \ color {Cyan} -1 \ color {Emerald} 0 \ end {bmatrix}} \\ [6pt] {\ boldsymbol {\ Sigma}} = {\ begin {bmatrix} 3 0 0 0 \ color {Gray} {\ mathit {0}} \\ 0 {\ sqrt {5}} 0 0 \ co lor {Серый} {\ mathit {0}} \\ 0 0 2 0 \ color {Серый} {\ mathit {0}} \\ 0 0 0 \ color {Красный} \ mathbf {0} \ color {Серый} {\ mathit {0 }} \ end {bmatrix}} \\ [6pt] \ mathbf {V} ^ {*} = {\ begin {bmatrix} \ color {Violet} 0 \ color {Violet} 0 \ color {Violet} -1 \ color {Violet} 0 \ color {Violet} 0 \\\ color {Plum} - {\ sqrt {0.2}} \ color {Plum} 0 \ color {Plum} 0 \ color {Plum} 0 \ color {Plum} - {\ sqrt {0.8}} \\\ color {Magenta} 0 \ color {Magenta} -1 \ color {Magenta} 0 \ color {Magenta} 0 \ color {Magenta} 0 \\\ color {Orchid} 0 \ color {Orchid} 0 \ color {Orchid} 0 \ color {Orchid} 1 \ color {Orchid} 0 \\\ color {Purple} - {\ sqrt {0.8}} \ color {Purple} 0 \ color {Purple} 0 \ color {Purple} 0 \ color {Purple} {\ sqrt {0.2}} \ end {bmatrix}} \ end {align}}}$

Матрица масштабирования $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\; \}\}$равен нулю за пределами диагонали (серый курсив), а один диагональный элемент равен нулю (красный жирный шрифт). Кроме того, поскольку матрицы U и V являются унитарными, умножение на их соответствующие сопряженные транспозиции дает матриц идентичности, как показано ниже. В этом случае, поскольку U и V являются вещественными, каждая из них является ортогональной матрицей .

$UU\; \ast \; =\; [1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 1]\; =\; I\; 4\; VV\; \ast \; =\; [1\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0\; 0\; 0\; 1]\; =\; I\; 5\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\; \}\; \backslash \; mathbf\; \{U\}\; \backslash \; mathbf\; \{U\}\; ^\; \{*\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 1\; 0\; 0\; \backslash \backslash \; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 1\; \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{4\}\; \backslash \; \backslash \; [6pt]\; \backslash \; mathbf\; \{V\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; 1\; 0\; 0\; 0\; 0\; \backslash \backslash \; 0\; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 1\; 0\; 0\; 0\; \backslash \backslash \; 0\; 0\; 0\; 1\; 0\; \backslash \backslash \; 0\; 0\; 0\; 0\; 1\; \backslash \; end\; I\; \backslash \; mathbf\}\; =\; \}\; \_\; \{5\}\; \backslash \; end\; \{align\}\}\}$

Это конкретное разложение по сингулярным числам не является уникальным. Выбор $V\; \{\backslash \; displaystyle\; V\}$так, чтобы

$V\; \ast \; =\; [0\; 1\; 0\; 0\; 0\; 0\; 0\; 1\; 0\; 0\; 0,2\; 0\; 0\; 0\; 0,8\; 0,4\; 0\; 0\; 0,5\; -\; 0,1\; -\; 0,4\; 0\; 0\; 0,5\; 0,1]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; color\; \{Violet\}\; 0\; \backslash \; color\; \{Violet\}\; 1\; \backslash \; color\; \{Violet\}\; 0\; \backslash \; color\; \{Violet\}\; 0\; \backslash \; color\; \{Violet\; \}\; 0\; \backslash \backslash \backslash \; color\; \{Plum\}\; 0\; \backslash \; color\; \{Plum\}\; 0\; \backslash \; color\; \{Plum\}\; 1\; \backslash \; color\; \{Plum\}\; 0\; \backslash \; color\; \{Plum\}\; 0\; \backslash \backslash \backslash \; color\; \{Magenta\}\; \{\backslash \; sqrt\; \{0.2\}\}\; \backslash \; color\; \{Magenta\}\; 0\; \backslash \; color\; \{Magenta\}\; 0\; \backslash \; color\; \{Magenta\}\; 0\; \backslash \; color\; \{Magenta\}\; \{\backslash \; sqrt\; \{0.8\}\}\; \backslash \backslash \backslash \; color\; \{Orchid\}\; \{\backslash \; sqrt\; \{0.4\}\}\; \backslash \; color\; \{Orchid\}\; 0\; \backslash \; color\; \{Orchid\}\; 0\; \backslash \; color\; \{Orchid\}\; \{\backslash \; sqrt\; \{0.5\}\}\; \backslash \; color\; \{Orchid\}\; -\; \{\backslash \; sqrt\; \{0.1\}\}\; \backslash \backslash \backslash \; color\; \{Purple\}\; -\; \{\backslash \; sqrt\; \{0.4\}\}\; \backslash \; color\; \{Purple\}\; 0\; \backslash \; color\; \{Purple\}\; 0\; \backslash \; color\; \{Purple\}\; \{\backslash \; sqrt\; \{0.5\}\}\; \backslash \; color\; \{Purple\}\; \{\backslash \; sqrt\; \{0.1\}\}\; \backslash \; end\; \{bmatrix\}\}\}$

также является допустимым единственным числом ценностная декомпозиция.

Сингулярные значения, сингулярные векторы и их связь с SVD

Неотрицательное действительное число σ является сингулярным значение для M тогда и только тогда, когда существуют векторы единичной длины $u\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{u\}\}\}$в K и $v\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{v\}\}\}$в K такое, что

$M\; v\; \to \; =\; \sigma \; u\; \to \; и\; M\; \ast \; u\; \to \; =\; \sigma \; v\; \to .\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; \{\backslash \; vec\; \{v\}\}\; =\; \backslash \; sigma\; \{\backslash \; vec\; \{u\}\}\; \backslash ,\; \{\backslash \; text\; \{and\}\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \{\backslash \; vec\; \{u\}\}\; =\; \backslash \; sigma\; \{\backslash \; vec\; \{v\}\}.\}$

Векторы $u\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{u\}\}\}$и $v\; \to \; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{v\}\}\}$называются лево-сингулярными и право-сингулярными векторами для σ соответственно.

В любом разложении по сингулярным числам

$M\; =\; U\; \Sigma \; V\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{U\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\; \}\}$

диагональные элементы $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$равны сингулярным значениям M . Первые столбцы p = min (m, n) в U и V являются, соответственно, левыми и правыми сингулярными векторами для соответствующих сингулярных значений. Следовательно, из приведенной выше теоремы следует, что:

• Матрица m × n M имеет не более p различных сингулярных значений.
• Всегда можно найти унитарный базис Uдля K с подмножеством базисных векторов, охватывающих лево-сингулярные векторы каждого сингулярного значения M.
• . Всегда можно найти унитарный базис V для K с подмножеством базисных векторов, охватывающих правые сингулярные векторы каждого сингулярного значения M.

Особое значение, для которого мы можем найти два левых (или правых) сингулярных вектора, которые являются линейно независимыми, называется вырожденным. Если $u\; \to \; 1\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{u\}\}\; \_\; \{1\}\}$и $u\; \to \; 2\; \{\backslash \; displaystyle\; \{\backslash \; vec\; \{u\}\}\; \_\; \{2\}\}$- это два сингулярных вектора слева, которые соответствуют сингулярному значению σ, тогда любая нормализованная линейная комбинация двух векторов также является сингулярным вектором слева, соответствующим сингулярному значению σ. Аналогичное утверждение верно и для правых сингулярных векторов. Количество независимых левых и правых сингулярных векторов совпадает, и эти особые векторы появляются в одних и тех же столбцах U и V, соответствующих диагональным элементам $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$все с одинаковым значением σ.

В качестве исключения левый и правый сингулярные векторы сингулярного значения 0 включают все единичные векторы в ядре и коядре, соответственно, в M, которое по теореме ранг – недействительность не может быть той же размерности, если m ≠ n. Даже если все сингулярные значения отличны от нуля, если m>n, то коядро нетривиально, и в этом случае U дополняется m - n ортогональными векторами из коядра. Наоборот, если m < n, then V дополняется n - m ортогональными векторами из ядра. Однако, если сингулярное значение 0 существует, дополнительные столбцы U или V уже появляются как левый или правый сингулярные векторы.

Невырожденные сингулярные значения всегда имеют уникальные лево- и правые сингулярные векторы с точностью до умножения на единичный фазовый множитель e (для реального случая с точностью до знака). Следовательно, если все сингулярные значения квадратной матрицы M невырождены и не равны нулю, то ее разложение по сингулярным значениям будет уникальным с точностью до умножения столбца U на коэффициент единичной фазы и одновременное умножение соответствующего столбца V на тот же коэффициент единичной фазы. В общем, SVD уникален до произвольных унитарных преобразований, применяемых единообразно к векторам-столбцам обоих U и V, охватывающих подпространства каждого сингулярного значения, и вплоть до произвольных унитарных преобразований на векторы U и V, охватывающие ядро ​​и коядро, соответственно, M.

Связь с разложением по собственным значениям

Разложение по сингулярным значениям является очень общим в том смысле, что его можно применить к любой матрице размера m × n, тогда как разложение по собственным значениям можно применить только к диагонализуемым матрицам. Тем не менее, эти два разложения связаны.

Для SVD M, как описано выше, выполняются следующие два соотношения:

$M\; \ast \; M\; =\; V\; \Sigma \; \ast \; U\; \ast \; U\; \Sigma \; V\; \ast \; =\; V\; (\Sigma \; \ast \; \Sigma )\; V\; *\; MM\; *\; знак\; равно\; U\; \Sigma \; V\; *\; V\; \Sigma \; *\; U\; *\; =\; U\; (\Sigma \; \Sigma \; *)\; U\; *\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{V\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; ^\; \{*\}\; \backslash \; mathbf\; \{U\}\; ^\; \{*\}\; \backslash ,\; \backslash \; mathbf\; \{U\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; =\; \backslash \; mathbf\; \{V\}\; (\{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; ^\; \{*\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\})\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; \backslash \backslash \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{M\}\; ^\; \{\; *\}\; =\; \backslash \; mathbf\; \{U\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; \backslash ,\; \backslash \; mathbf\; \{V\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; ^\; \{*\}\; \backslash \; mathbf\; \{U\}\; ^\; \{*\}\; =\; \backslash \; mathbf\; \{U\}\; (\{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; ^\; \{*\})\; \backslash \; mathbf\; \{U\}\; ^\; \{*\}\; \backslash \; end\; \{align\}\}\}$

Правые части этих соотношений описывают разложения левых частей на собственные значения. Следовательно:

• Столбцы V (правые сингулярные векторы) являются собственными векторами из MM.
• . Столбцы U (лево-сингулярные векторы) являются собственные векторы MM.
• Ненулевые элементы $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$(ненулевые особые значения) являются квадратными корнями ненулевого собственные значения из MMили MM.

В частном случае, когда M является нормальной матрицей, которая поопределению должна быть квадратная, спектральная теорема говорит, что он может быть единственно диагонализован с использованием базиса собственных векторов, так что его можно записать M= УДУ для унитарной матрицы U и диагональная матрица D . Когда M также является положительно полуопределенным, разложение M= UDU является также разложением по сингулярным числам. В противном случае его можно преобразовать в SVD, переместив фазу каждого σ в либо на соответствующее ему Vi, либо Ui. Естественная связь SVD с ненормальными матрицами осуществляется теоремы о полярном разложении : M= SR, где S= U$\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$Uположительно полуопределено и нормальный, а R= UVунитарный.

Таким образом, за исключением положительных полуопределенных нормальных матриц, разложение по собственным значениям и SVD для M, хотя и связаны, различаются: различаются: разложение по собственным значениям M= UDU, где U не обязательно унитарен и D не обязательно положительно полуопределен, тогда как SVD - это M= U$\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$V, где $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$- диагональные и положительно полуопределенные, а U и V - унитарные матрицы, которые не обязательно связаны, кроме как через матрицу M . Хотя только исправные квадратные матрицы имеют разложение по собственному значению, любая матрица $m\; \times \; n\; \{\backslash \; displaystyle\; m\; \backslash \; times\; n\}$SVD.

Псевдообратная

Разложение по сингулярным числам может быть приложение для вычисления псевдообратной матрицы. (Различные варианты используют разные обозначения для псевдообратной матрицы; здесь мы используем.) Действительно, псевдообратная матрица M с разложением по сингулярным значениям M= UΣVравно

M= VΣU

, где Σ - этодообратное Значение Σ, которое формируется заменой каждого ненулевого диагонального элемента его обратным и транспонированием полученной матрицы. Псевдообратная функция - это один из способов линейных наименьших квадратов.

Решение однородных линейных соотношений

Набор однородных линейных уравнений может быть записан как Ax= 0для матриц A и вектор х . Типичная ситуация состоит в том, что A известно и необходимо определить ненулевое значение x, которое удовлетворяет уравнению. Такой x принадлежит нулевому пространству A и иногда называется (правым) нулевым вектором A . Вектор x можно охарактеризовать как правый сингулярный вектор, соответствующему сингулярному значению A, равному нулю. Это наблюдение означает, что если A представляет собой квадратную матрицу и не имеет исчезающего сингулярного значения, уравнение не имеет ненулевого x в качестве решения. Это также означает, что при наличии нескольких вариантов любая линейная комбинация соответствующих правых сингулярных векторов является допустимым решением. Аналогично определению (правого) нулевого вектора ненулевой x, удовлетворяющий xA= 0, с x, обозначающим сопряженное обозначение x, является левым нулевым вектором A.

Минимизация наименьших квадратов

A Всего наименьших квадратов Задача относится к определению вектора x, который минимизирует 2-норму дату Ax при ограничении || x || = 1. Решением оказывается правый сингулярный вектор A, соответствующему наименьшему сингулярному значению.

Диапазон, пустое пространство и ранг

Другое применение SVD состоит в том, что обеспечивает явное представление диапазона диапазона и пустого пространства в матрица М . Право-сингулярные стандарты, соответствующие исчезающим сингулярным значениям M, охватывают нулевое пространство M и лево-сингулярные стандарты, соответствующие ненулевым сингулярным значениям M охватывают диапазон M . Например, в приведенном выше примере пустое пространство занято двумя последними строками V, а диапазон - первыми тремя столбцами U.

. Как следствие, ранг из M равенство количеству ненулевых сингулярных значений, которое совпадает с ненулевых диагональных элементов в $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$. В числовой шкале линейной алгебре могут быть введены различные ранговые матрицы, так как ошибка округления может привести к небольшому, но ненулевым сингулярным значениям в матрице с недостаточным рангом. Предполагается, что единичные значения за значительным промежутком численно эквивалентны нулю.

Аппроксимация матрицы низкого ранга

В некоторых практических приложениях необходимо решить аппроксимации матрицы M другой матрицей $M\; ~\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{\backslash \; mathbf\; \{M\; \}\}\}\}$, считается усеченным, имеющим определенный ранг r. В случае, если аппроксимация на основе минимизации нормы Фробениуса разницы между M и $M\; ~\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{\backslash \; mathbf\; \{M\}\}\}\}$при ограничении $ранг\; \; (M\; ~)\; =\; r\; \{\backslash \; displaystyle\; \backslash \; operatorname\; \{rank\}\; \backslash \; left\; (\{\backslash \; tilde\; \{\backslash \; mathbf\; \{M\}\}\}\; \backslash \; right)\; =\; r\}$, оказывается, что решение задается SVD M, а именно

$M\; ~\; =\; U\; \Sigma \; ~\; V\; \ast ,\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{\backslash \; mathbf\; \{M\}\}\}\; =\; \backslash \; mathbf\; \{U\}\; \{\backslash \; тильда\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\},\}$

где $\Sigma \; ~\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\}\}$- это та же матрица, что и $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$, за исключением того, что она содержит только r наибольших сингулярных значений (остальные сингулярные значения заменяются нулем). Это известно как теорема Эккарта - Юнга, поскольку она была доказана этим двумя авторами в 1936 году (хотя позже выяснилось, что она известна более ранним авторам; см. Стюарт 1993).

Разделимые модели

SVD можно рассматривать как разложение матрицы на взвешенную упорядоченную сумму разделимых матриц. Под разделимой мы подразумеваем, что матрица A может быть записана как внешнее произведение векторов A= u⊗ v, или, в координатах, $A\; ij\; =\; uivj\; \{\backslash \; displaystyle\; A\_\; \{ij\; \}\; =\; u\_\; \{i\}\; v\_\; \{j\}\}$. В частности, матрица M может быть разложена как

$M\; =\; \sum \; i\; A\; i\; =\; \sum \; i\; \sigma \; i\; U\; i\; \otimes \; V\; i.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; sum\; \_\; \{i\}\; \backslash \; mathbf\; \{A\}\; \_\; \{i\}\; =\; \backslash \; sum\; \_\; \{i\}\; \backslash \; sigma\; \_\; \{i\}\; \backslash \; mathbf\; \{U\}\; \_\; \{i\}\; \backslash \; otimes\; \backslash \; mathbf\; \{V\}\; \_\; \{i\}.\}$

Здесь Uiи Vi- это i-й столбец соответствующий матриц SVD, σ i - упорядоченные сингулярные значения, и каждый Aiотделимо. SVD можно использовать для нахождения разделения фильтра изображения обработки на отдельные горизонтальные и вертикальные фильтры. Обратите внимание, что количество ненулевых σ i - это внимание в точности ранг матрицы.

Разделимые модели часто возникают в биологических системах, и SVD-факторизация полезна для анализа таких систем. Например, некоторые восприимчивые поля простых клеток визуальной области V1 могут хорошо использовать с помощью фильтра Габора в пространственной области, умноженного на функцию модуляции во временной области. Таким образом, данный линейный фильтр, оцениваемый, например, посредством обратной корреляции, можно переставить два пространственных измерения в одно измерение, таким образом, получая двумерный фильтр (пространство, время), который может быть разложен с помощью SVD. Тогда первый столбец U в SVD-факторизации представляет собой Габор, а первый столбец V представляет модуль времени (или наоборот). Затем можно определить индекс отделимости

$\alpha \; =\; \sigma \; 1\; 2\; \sum \; я\; \sigma \; я\; 2,\; \{\backslash \; displaystyle\; \backslash \; alpha\; =\; \{\backslash \; frac\; \{\backslash \; sigma\; \_\; \{1\}\; ^\; \{2\}\}\; \{\backslash \; sum\; \_\; \{i\}\; \backslash \; sigma\; \_\; \{i\}\; ^\; \{2\}\}\},\}$

, которая представляет собой долю степени в матрице M, которая учитывается первой разделяемой матрицей в разложении.

Ближайшая ортогональная матрица

Можно использовать SVD квадратной матрицы A для определения ортогональной матрицы O, ближайшей к A . Точность подгонки измеряется нормой Фробениуса из O− A. Решением является продукт UV . Это интуитивно понятно, потому что ортогональная матрица будет иметь разложение UIV, где I - единичная матрица, так что если A= U$\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$V, то произведение A= UVсводится к замене единичных значений на единицу. Эквивалентно, решение представляет собой унитарную матрицу R= UVполярного разложения M= RP= P'Rв любом порядке растяжения и вращения, как описано выше.

Похожая проблема с интересными приложениями формы - это ортогональная проблема Прокруста, которая в нахождении ортогональной матрицы O, которая наиболее точно отображает А в В . В частности,

$O\; =\; argmin\; \Omega \; \Vert \; A\; \Omega \; -\; B\; \Vert \; F\; при\; условии\; \Omega \; T\; \Omega \; =\; I,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{O\}\; =\; \{\backslash \; underset\; \{\backslash \; Omega\}\; \{\backslash \; operatorname\; \{argmin\}\}\}\; \backslash \; |\; \backslash \; mathbf\; \{A\}\; \{\backslash \; boldsymbol\; \{\backslash \; Omega\}\}\; -\; \backslash \; mathbf\; \{B\}\; \backslash \; |\; \_\; \{F\}\; \backslash \; quad\; \{\backslash \; text\; \{при\; условии\}\}\; \backslash \; quad\; \{\backslash \; boldsymbol\; \{\backslash \; Omega\}\}\; ^\; \{\backslash \; textf\; \{T\}\}\; \{\backslash \; boldsymbol\; \{\backslash \; Omega\}\}\; =\; \backslash \; mathbf\; \{I\},\}$

где $\Vert \; \cdot \; \Vert \; F\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; cdot\; \backslash \; |\; \_\; \{F\}\}$обозначает норму Фробениуса.

Эта проблема эквивалентна поиску ближайшей ортогональной матрицы к заданной матрице M= AB.

Алгоритм Кабша

Алгоритм Кабша (называемый проблемой Вахбы в других областях) использует SVD для вычисления оптимального поворота (относительно минимизации наименьших квадратов), который выровняет набор точек с соответствующим набором точек. Среди прочего, он используется для сравнения структур молекул.

Обработка сигналов

SVD и псевдоинверсия были успешно применены к обработке сигналов, обработке изображений и больших данных ( например, при обработке геномных сигналов).

Другие примеры

SVD также широко применяется для изучения линейных обратных задач и полезен при анализе методов регуляризации например, Тихонова. Он широко используется в статистике, где он связан с анализом главных компонентов и с анализом соответствия, а также в обработке сигналов и распознавании образов <562.>. Он также используется в модальном анализе только для вывода, где немасштабированные формы колебаний могут быть определены из сингулярных векторов. Еще одно использование - скрытое семантическое индексирование при обработке текста на естественном языке.

В обычных численных вычислениях с участием линейных или линеаризованных систем существует универсальная константа, которая характеризует регулярность или особенность проблемы, которая является «числом обусловленности» системы $\kappa :\; =\; \sigma \; max\; /\; \sigma \; min\; \{\backslash \; displaystyle\; \backslash \; kappa:\; =\; \backslash \; sigma\; \_\; \{\backslash \; text\; \{max\}\}\; /\; \backslash \; sigma\; \_\; \{\backslash \; text\; \{min\}\}\}$. Он часто контролирует частоту появления ошибок или скорость сходимости данной вычислительной схемы в таких системах.

SVD также играет решающую роль в области квантовой информации в форме, которую часто называют как разложение Шмидта. С его помощью состояния двух квантовых систем естественным образом разлагаются, обеспечивая необходимое и достаточное условие для их запутанности : если ранг $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$матрица больше единицы.

Одно из применений SVD к довольно большим матрицам - это численный прогноз погоды, где методы Ланцоша используются для оценки наиболее линейно быстро растущих нескольких возмущений центрального численного прогноз погоды на заданный начальный период времени; то есть сингулярные векторы, соответствующие наибольшим сингулярным значениям линеаризованного пропагатора для глобальной погоды за этот интервал времени. Выходными сингулярными векторами в этом случае являются целые погодные системы. Затем эти возмущения пропускаются через полную нелинейную модель для генерации ансамблевого прогноза , позволяющего справиться с некоторой неопределенностью, которая должна допускаться в отношении текущего центрального прогноза.

SVD также применялся для моделирования сокращенного порядка. Целью моделирования пониженного порядка является уменьшение количества степеней свободы в сложной системе, которую необходимо моделировать. SVD был объединен с радиальными базисными функциями для интерполяции решений трехмерных задач нестационарного потока.

Интересно, что SVD использовался для улучшения моделирования формы гравитационных волн с помощью наземного гравитационно-волнового интерферометра. АЛИГО. SVD может помочь повысить точность и скорость генерации сигналов для поддержки поиска гравитационных волн и обновления двух различных моделей сигналов.

Декомпозиция по сингулярным значениям используется в рекомендательных системах для прогнозирования оценок пользователей. Распределенные алгоритмы были разработаны с целью вычисления SVD на кластерах обычных машин.

Другая реализация кода алгоритма рекомендации Netflix SVD (третий оптимальный алгоритм в конкурсе, проводимом Netflix, чтобы найти лучшую совместную фильтрацию методы прогнозирования пользовательских оценок фильмов на основе предыдущих обзоров) на платформе Apache Spark доступны в следующем репозитории GitHub, реализованном Александросом Иоаннидисом. Оригинальный алгоритм SVD, который в этом случае выполняется параллельно, поощряет пользователей веб-сайта GroupLens, консультируясь с предложениями по мониторингу новых фильмов, адаптированными к потребностям каждого пользователя.

СВД низкого ранга применялась для обнаружения горячих точек на основе пространственно-временных данных с применением для обнаружения болезни вспышки. Комбинация SVD и SVD более высокого порядка также применялась для обнаружения событий в реальном времени из сложных потоков данных (многомерные данные с пространственными и временными измерениями) в Наблюдение за заболеваниями.

Собственное значение λ матрицы M характеризуется алгебраическим использованием M u = λu. Когда M равно эрмитовскому, также доступна вариационная характеристика. Пусть M будет действительной симметричной матрицей размера n × n . Определите

$\{f:\; R\; n\; \to \; R\; f\; (x)\; =\; x\; TM\; x\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{cases\}\; f:\; \backslash \; mathbb\; \{R\}\; ^\; \{n\}\; \backslash \; to\; \backslash \; mathbb\; \{R\}\; \backslash \backslash \; f\; (\; x)\; =\; x\; ^\; \{\backslash \; textf\; \{T\}\}\; \backslash \; mathbf\; \{M\}\; x\; \backslash \; end\; \{ases\}\}$

Согласно теореме об экстремальных значениях, эта непрерывная функция использует максимума при некотором u, когда ограничен единичной сферой {|| х || = 1}. По теореме о множителях Лагранжа u обязательно удовлетворяет

$\nabla \; x\; TM\; x\; -\; \lambda \; \cdot \; \nabla \; x\; T\; x\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; x\; ^\; \{\backslash \; textf\; \{T\}\}\; \backslash \; mathbf\; \{M\}\; x\; -\; \backslash \; lambda\; \backslash \; cdot\; \backslash \; nabla\; x\; ^\; \{\backslash \; textf\; \{T\}\}\; x\; =\; 0\}$

для некоторого действительного числа λ. Символ набла, ∇, является оператором del (дифференцирование по x). Используя симметрию M, получаем

$\nabla \; x\; T\; M\; x\; -\; \lambda \; \cdot \; \nabla \; x\; T\; x\; =\; 2\; (M\; -\; \lambda \; I)\; x.\; \{\backslash \; displaystyle\; \backslash \; nabla\; x\; ^\; \{\backslash \; textf\; \{T\}\}\; \backslash \; mathbf\; \{M\}\; x-\; \backslash \; lambda\; \backslash \; cdot\; \backslash \; nabla\; x\; ^\; \{\backslash \; textf\; \{T\}\}\; x\; =\; 2\; (\backslash \; mathbf\; \{M\}\; -\; \backslash \; lambda\; \backslash \; mathbf\; \{I\})\; x.\}$

Следовательно, M u = λu, поэтому u является собственным вектором единичной длины M . Для каждого собственного вектора v единичной длины элемента M его собственное значение равно f (v), поэтому λ является наибольшим значением длины M . То же вычисление, выполненное с ортогональным дополнением к u, дает следующее по величине собственное значение и так далее. Сложный эрмитов случай аналогичен; там f (x) = x * M x - вещественная функция от 2n вещественного числа.

Особые значения похожи в том, что они могут быть алгебраически или на основе вариационных принципов. Хотя, в отличие от случая собственных значений, эрмитичность или симметрия M больше не требуется.

В этом разделе приводятся эти два аргумента в использовании функций разложения по сингулярным числам.

На основе спектральной теоремы

Пусть $M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\}$будет комплексной матрицей размера m × n. <Времен313>M ∗ M {\ displaystyle \ mathbf {M} ^ {*} \ mathbf {M}}является положительно полуопределенным и эрмитовым, по спектральной теореме, существует унитарная матрица размер n × n $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$такая, что

$V\; \ast \; M\; \ast \; MV\; =\; D\; ¯\; =\; [D\; 0\; 0\; 0],\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; =\; \{\backslash \; bar\; \{\backslash \; mathbf\; \{D\}\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{D\}\; 0\; \backslash \backslash \; 0\; 0\; \backslash \; end\; \{bmatrix\}\},\}$

где $D\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{D\}\}$диагональный и положительно определенный размер $\ell \; \times \; \ell \; \{\; \backslash \; displaystyle\; \backslash \; ell\; \backslash \; times\; \backslash \; ell\}$, где $\ell \; \{\backslash \; displaystyle\; \backslash \; ell\}$количество ненулевых собственных значений $M\; \ast \; M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\; \}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\}$(который можно показать для проверки $\ell \; \le \; min\; (n,\; m)\; \{\backslash \; displaystyle\; \backslash \; ell\; \backslash \; leq\; \backslash \; min\; (n,\; m)\}$). Обратите внимание, что $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$здесь по определению матрицы, $i\; \{\backslash \; displaystyle\; i\}$-й столбец $i\; \{\backslash \; displaystyle\; i\}$-й собственный вектор $M\; \ast \; M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\}$, соответствующее собственное значение $D\; ¯\; ii\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{\backslash \; mathbf\; \{D\}\}\}\; \_\; \{ii\}\}$. Кроме того, $j\; \{\backslash \; displaystyle\; j\}$-й столбец $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$для $j>\ell \; \{\backslash \; displaystyle\; j>\backslash \; ell\}$, является собственным вектором $M\; \ast \; M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\}$с собственным значением <3j13>D ¯ = 0 { \ displaystyle {\ bar {\ mathbf {D}}} _ {jj} = 0}. Это можно выразить записью $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$как $V\; =\; [V\; 1\; V\; 2]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\; \}\}\}$, где столбцы $V\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\}$и $V\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\}$, следовательно, содержат собственные конструкции $M\; \ast \; M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\}$, соответствующие нену левым и нулевым собственным значениям соответственно. Использование th переписывает $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$, уравнение принимает следующий вид:

$[V\; 1\; \ast \; V\; 2\; \ast ]\; M\; \ast \; M\; [V\; 1\; V\; 2]\; =\; [\; V\; 1\; *\; M\; *\; MV\; 1\; V\; 1\; *\; M\; *\; MV\; 2\; V\; 2\; *\; M\; *\; MV\; 1\; V\; 2\; *\; M\; *\; MV\; 2]\; =\; [D\; 0\; 0\; 0].\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; \backslash \backslash \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\}\; \backslash \; end\; \{bmatrix\}\}\; \backslash \; mathbf\; \{M\}\; ^\; \{\; *\}\; \backslash \; mathbf\; \{M\}\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; \backslash \backslash \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{\; V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{D\}\; 0\; \backslash \backslash \; 0\; 0\; \backslash \; end\; \{bmatrix\}\}.\}$

Отсюда следует, что

$V\; 1\; \ast \; M\; \ast \; MV\; 1\; =\; D,\; V\; 2\; \ast \; M\; \ast \; MV\; 2\; =\; 0.\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; =\; \backslash \; mathbf\; \{D\; \},\; \backslash \; quad\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; =\; \backslash \; mathbf\; \{0\}.\}$

Кроме того, второе уравнение подразумевает $MV\; 2\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; \backslash \; m\; athbf\; \{V\}\; \_\; \{2\}\; =\; \backslash \; mathbf\; \{0\}\}$. Наконец, унитарность $V\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\}$переводится в терминах $V\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\}$и $V\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\}$, в следующих условиях:

$V\; 1\; *\; V\; 1\; =\; I\; 1,\; V\; 2\; *\; В\; 2\; знак\; равно\; I\; 2,\; В\; 1\; В\; 1\; *\; +\; В\; 2\; В\; 2\; *\; =\; I\; 12,\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{1\},\; \backslash \backslash \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{2\},\; \backslash \backslash \backslash \; mathbf\; \{\; V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; +\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\}\; =\; \backslash \; mathbf\; \{I\}\; \_\; \{12\},\; \backslash \; end\; \{align\}\}\}$

где нижние индексы в матрицах идентичности используются для обозначения того, что они имеют разные размеры.

Давайте теперь определим

$U\; 1\; =\; MV\; 1\; D\; -\; 1\; 2.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\; =\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{D\}\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}.\}$

Тогда

$U\; 1\; D\; 1\; 2\; V\; 1\; \ast \; =\; MV\; 1\; D\; -\; 1\; 2\; D\; 1\; 2\; V\; 1\; \ast \; =\; M\; (I\; -\; V\; 2\; V\; 2\; \ast )\; =\; M\; -\; (MV\; 2)\; V\; 2\; \ast \; =\; M,\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\; \backslash \; mathbf\; \{D\}\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; =\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{D\}\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; mathbf\; \{\; D\}\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; =\; \backslash \; mathbf\; \{M\}\; (\backslash \; mathbf\; \{I\}\; -\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\})\; =\; \backslash \; mathbf\; \{M\}\; -\; (\backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\})\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; ^\; \{*\}\; =\; \backslash \; mathbf\; \{M\},\}$

, поскольку $MV\; 2\; =\; 0.\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; =\; \backslash \; mathbf\; \{0\}.\}$Это также можно рассматривать как непосредственное следствие факта, что $MV\; 1\; V\; 1\; *\; =\; М\; \{\backslash \; Displaystyle\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\; \}\; =\; \backslash \; mathbf\; \{M\}\}$. Обратите внимание, как это эквивалентно наблюдению, если $\{vi\}\; i\; =\; 1\; l\; \{\backslash \; displaystyle\; \backslash \; \{\{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{i\}\; \backslash \}\; \_\; \{i\; =\; 1\}\; ^\; \{l\}\}$- это набор собственных векторов $M\; \ast \; M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\}$, соответствующим ненулевым собственным значениям, тогда $\{M\; vi\}\; i\; =\; 1\; l\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; mathbf\; \{M\}\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{i\}\; \backslash \}\; \_\; \{i\; =\; 1\}\; ^\; \{l\}\}$- это набор ортогональных векторов, а $\{\lambda \; -\; 1/2\; M\; vi\}\; i\; =\; 1\; l\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; lambda\; ^\; \{-\; 1/2\}\; \backslash \; mathbf\; \{M\}\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{i\; \}\; \backslash \}\; \_\; \{i\; =\; 1\}\; ^\; \{l\}\}$набор (обычно неполный) ортонормированных векторов. Это соответствует матричному формализму, используемому выше, обозначающему $V\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\}$матрицу, столбцы которой равны $\{vi\}\; i\; =\; 1\; l\; \{\; \backslash \; displaystyle\; \backslash \; \{\{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{i\}\; \backslash \}\; \_\; \{i\; =\; 1\}\; ^\; \{l\}\}$, с $V\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\}$матрица, столбцы которой являются собственными векторами $M\; \ast \; M\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; math\; bf\; \{M\}\}$которая исчезает собственное значение и $U\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\}$матрица, столбцы которой являются векторами $\{\lambda \; -\; 1/2\; M\; vi\}\; i\; =\; 1\; l\; \{\backslash \; displaystyle\; \backslash \; \{\backslash \; lambda\; ^\; \{-\; 1/2\}\; \backslash \; mathbf\; \{M\}\; \{\backslash \; boldsymbol\; \{v\}\}\; \_\; \{i\}\; \backslash \}\; \_\; \{i\; =\; 1\}\; ^\; \{l\}\}$.

Мы видим, что это почти желаемый результат, за исключением того, что $U\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\}$и $V\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \}$в общем случае не унитарны, поскольку они могут не быть квадратными. Однако мы знаем, что количество строк $U\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\}$не меньше количества столбцов, поскольку размеры $D\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{D\}\}$не больше, чем $m\; \{\backslash \; displaystyle\; m\}$и $n\; \{\backslash \; displaystyle\; n\}$. Кроме того, поскольку

$U\; 1\; *\; U\; 1\; =\; D\; -\; 1\; 2\; V\; 1\; *\; M\; *\; MV\; 1\; D\; -\; 1\; 2\; =\; D\; -\; 1\; 2\; DD\; -\; 1\; 2\; =\; I\; 1,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{\; 1\}\; ^\; \{*\}\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\; =\; \backslash \; mathbf\; \{D\}\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; \backslash \; mathbf\; \{D\}\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; =\; \backslash \; mathbf\; \{D\}\; ^\; \{-\; \{\; \backslash \; frac\; \{1\}\; \{2\}\}\}\; \backslash \; mathbf\; \{D\}\; \backslash \; mathbf\; \{D\}\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\; =\; \backslash \; mathbf\; \{I\_\; \{1\}\},\}$

столбцы в $U\; 1\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\}$являются ортонормированными и могут быть расширены до ортонормированного базиса. Это означает, что мы можем выбрать $U\; 2\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\}\; \_\; \{2\}\}$так, чтобы $U\; =\; [U\; 1\; U\; 2]\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{U\; \}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\; \backslash \; mathbf\; \{U\}\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\}$унитарен.

Для V1у нас уже есть V2, чтобы сделать его унитарным. Теперь определите

$\Sigma \; =\; [[D\; 1\; 2\; 0\; 0\; 0]\; 0],\; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{D\}\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; 0\; \backslash \backslash \; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\},\}$

где дополнительные нулевые строки добавляются или удаляются для создания количество нулевых строк равно количеству столбцов U2, и, следовательно, общие размеры $\Sigma \; \{\backslash \; displaystyle\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\}$равны $m\; \times \; п\; \{\backslash \; Displaystyle\; м\; \backslash \; раз\; п\}$. Тогда

$[U\; 1\; U\; 2]\; [[D\; 1\; 2\; 0\; 0\; 0]\; 0]\; [V\; 1\; V\; 2]\; \ast \; =\; [U\; 1\; U\; 2]\; [D\; 1\; 2\; V\; 1\; \ast \; 0]\; =\; U\; 1\; D\; 1\; 2\; V\; 1\; *\; знак\; равно\; M,\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\; \backslash \; mathbf\; \{U\}\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; \{\backslash \; begin\; \{\; bmatrix\}\; \backslash \; mathbf\; \{\}\; D\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; 0\; \backslash \backslash \; 0\; 0\; \backslash \; end\; \{bmatrix\}\}\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{V\}\; \_\; \{\; 1\}\; \backslash \; mathbf\; \{V\}\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; ^\; \{*\}\; =\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\; \backslash \; mathbf\; \{U\}\; \_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\; \{\backslash \; begin\; \{bmatrix\}\; \backslash \; mathbf\; \{D\}\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; \backslash \backslash \; 0\; \backslash \; end\; \{bmatrix\}\}\; =\; \backslash \; mathbf\; \{U\}\; \_\; \{1\}\; \backslash \; mathbf\; \{D\}\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; mathbf\; \{V\}\; \_\; \{1\}\; ^\; \{*\}\; =\; \backslash \; mathbf\; \{M\},\}$

который является желаемый результат:

$M\; =\; U\; \Sigma \; V\; \ast .\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{U\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}.\}$

Обратите внимание, что аргумент может начинаться с диагонализации MM а не MM(это прямо показывает, что MM и MMимеют одинаковые ненулевые собственные значения).

На основе вариационной характеристики

Особые значения также могут быть охарактеризованы как максимумы uMv, рассматриваемые как функция u и v, над определенными подпространствами. Сингулярные векторы - это значения u и v, где достигаются эти максимумы.

Пусть M обозначает матрицу m × n с действительными элементами. Пусть S будет единицей $(k\; -\; 1)\; \{\backslash \; displaystyle\; (k-1)\}$-sphere in $R\; k\; \{\backslash \; displaystyle\; \backslash \; mathbb\; \{R\}\; ^\; \{k\}\}$, и положим $\sigma \; (u,\; v)\; =\; u\; TM\; v,\; u\; \in \; S\; m\; -\; 1,\; v\; \in \; S\; n\; -\; 1.\; \{\backslash \; displaystyle\; \backslash \; sigma\; (\backslash \; mathbf\; \{u\},\; \backslash \; mathbf\; \{v\})\; =\; \backslash \; mathbf\; \{u\}\; ^\; \{\backslash textf\; \{T\}\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{v\},\; \backslash \; qquad\; \backslash \; mathbf\; \{u\}\; \backslash \; in\; S\; ^\; \{m-1\},\; \backslash \; mathbf\; \{v\}\; \backslash \; in\; S\; ^\; \{n-1\}.\}$

Рассмотрим функцию σ, ограниченную на S × S. Поскольку и S, и S компактны, их изделие также компактно. Кроме того, поскольку σ непрерывно, оно достигает наибольшего значения по крайней мере для одной пары векторов u ∈ S и v ∈ S. Это наибольшее значение обозначается σ 1, а соответствующие векторы обозначены u1и v1. Поскольку σ 1 является наибольшим значением σ (u, v), оно должно быть неотрицательным. Если бы он был отрицательным, изменение знака u1или v1сделало бы его положительным и, следовательно, больше.

Утверждение. u1, v1- левый и правый сингулярные векторы M с соответствующим сингулярным значением σ 1.

Доказательство. Подобно случаю собственных значений, по предположению, два вектора удовлетворяют критерию Лагранжа уравнение множителя:

$\nabla \; \sigma \; =\; \nabla \; u\; TM\; v\; -\; \lambda \; 1\; \cdot \; \nabla \; u\; T\; u\; -\; \lambda \; 2\; \cdot \; \nabla \; v\; T\; v\; \{\backslash \; displaystyle\; \backslash \; nabla\; \backslash \; sigma\; =\; \backslash \; nabla\; \backslash \; mathbf\; \{u\}\; ^\; \{\backslash textf\; \{T\; \}\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{v\}\; -\; \backslash \; lambda\; \_\; \{1\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; mathbf\; \{u\}\; ^\; \{\backslash textf\; \{T\}\}\; \backslash \; mathbf\; \{u\}\; -\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; cdot\; \backslash \; nabla\; \backslash \; mathbf\; \{v\}\; ^\; \{\backslash textf\; \{T\}\}\; \backslash \; mathbf\; \{v\}\}$

После некоторой алгебры это становится

$M\; v\; 1\; =\; 2\; \lambda \; 1\; u\; 1\; +\; 0\; MT\; u\; 1\; =\; 0\; +\; 2\; \lambda \; 2\; v\; 1\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{v\}\; \_\; \{1\}\; =\; 2\; \backslash \; lambda\; \_\; \{1\}\; \backslash \; mathbf\; \{u\}\; \_\; \{1\}\; +0\; \backslash \backslash \; \backslash \; mathbf\; \{M\}\; ^\; \{\backslash textf\; \{T\}\}\; \backslash \; mathbf\; \{u\}\; \_\; \{1\}\; =\; 0\; +\; 2\; \backslash \; lambda\; \_\; \{2\}\; \backslash \; mathbf\; \{v\}\; \_\; \{1\}\; \backslash \; end\; \{align\}\}\}$

Умножив первое уравнение слева на $u\; 1\; T\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{u\}\; \_\; \{1\}\; ^\; \{\backslash textf\; \{T\}\}\}$и второе уравнение слева на $v\; 1\; T\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{v\}\; \_\; \{1\}\; ^\; \{\backslash textf\; \{T\}\}\}$и таки нг || и || = || v || = 1 дает

$\sigma \; 1\; =\; 2\; \lambda \; 1\; =\; 2\; \lambda \; 2.\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{1\}\; =\; 2\; \backslash \; lambda\; \_\; \{1\}\; =\; 2\; \backslash \; lambda\; \_\; \{2\}.\}$

Подставляя это в пару уравнений выше, мы получаем

$M\; v\; 1\; =\; \sigma \; 1\; U\; 1\; MT\; U\; 1\; знак\; равно\; \sigma \; 1\; v\; 1\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; mathbf\; \{M\}\; \backslash \; mathbf\; \{v\}\; \_\; \{1\}\; =\; \backslash \; sigma\; \_\; \{1\}\; \backslash \; mathbf\; \{u\}\; \_\; \{1\}\; \backslash \backslash \backslash \; mathbf\; \{M\}\; ^\; \{\backslash textf\; \{T\}\}\; \backslash \; mathbf\; \{u\}\; \_\; \{1\}\; =\; \backslash \; sigma\; \_\; \{1\}\; \backslash \; mathbf\; \{v\}\; \_\; \{1\}\; \backslash \; end\; \{align\}\}\}$

Это доказывает утверждение.

Больше сингулярных векторов и сингулярных значений можно найти, максимизируя σ (u, v) по сравнению с нормализованным u, v, которые ортогональны u1и v1соответственно.

Переход от действительного числа к комплексному аналогичен случаю собственных значений.

Разложение по сингулярным значениям может быть вычислено с использованием следующих наблюдений:

• Лево-сингулярные векторы M представляют собой набор ортонормированные собственные векторы из MM.
• Право-сингулярные векторы M представляют собой набор ортонормированных собственных векторов MM.
• неотрицательных сингулярных значений M (находится на диагональных элементах $\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$) - квадратные корни неотрицательных собственных значений обоих MMи MM.

Численный подход

SVD матрицы M обычно вычисляется с помощью двухэтапной процедуры. На первом этапе матрица сокращается до двунаправленной матрицы. Это требует O (mn) операций с плавающей запятой (flop), предполагая, что m ≥ n. Второй шаг - вычислить SVD двухдиагональной матрицы. Этот шаг может быть выполнен только с помощью итеративного метода (как и в случае с алгоритмами собственных значений ). Однако на практике достаточно вычислить SVD с определенной точностью, как машина эпсилон. Если эта точность считается постоянной, то второй шаг занимает O (n) итераций, каждая из которых стоит O (n) провалов. Таким образом, первый этап более дорогой, а общая стоимость составляет O (млн) операций (Trefethen Bau III 1997, Lecture 31).

Первый шаг может быть выполнен с использованием отражений Хаусхолдера за 4 млн - 4n / 3 флопов, предполагая, что нужны только сингулярные значения, а не сингулярные векторы. Если m намного больше, чем n, то предпочтительно сначала уменьшить матрицу M до треугольной матрицы с помощью QR-разложения , а затем использовать отражения Хаусхолдера для дальнейшего уменьшения матрицы до двухдиагональной формы. ; общая стоимость составляет 2 млн + 2 тыс. операций (Trefethen Bau III 1997, Лекция 31).

Второй шаг может быть выполнен с помощью варианта QR-алгоритма для вычисления собственных значений, который впервые был описан Golub Kahan (1965) harvtxt error : несколько целей (2 ×): CITEREFGolubKahan1965 (справка ). Подпрограмма DBDSQR LAPACK реализует этот итерационный метод с некоторыми изменениями, чтобы охватить случай, когда особые значения очень малы (Demmel Kahan 1990). Вместе с первым шагом с использованием отражений Хаусхолдера и, при необходимости, QR-разложения, это формирует процедуру DGESVD для вычисления разложения по сингулярным значениям.

Тот же алгоритм реализован в Научной библиотеке GNU (GSL). GSL также предлагает альтернативный метод, использующий односторонний на шаге 2 (GSL Team 2007). Этот метод вычисляет SVD двухдиагональной матрицы путем решения последовательности задач SVD 2 × 2, аналогично тому, как алгоритм собственных значений Якоби решает последовательность методов собственных значений 2 × 2 (Golub Van Loan 1996, §8.6.3). Еще один метод для шага 2 использует идею алгоритмов собственных значений «разделяй и властвуй» (Trefethen Bau III 1997, Lecture 31).

Существует альтернативный способ, в котором явно не используется разложение по собственным значениям. Обычно проблема сингулярных чисел матрицы M преобразуется в эквивалентную симметричную задачу на собственные значения, такую ​​как M M, MMили

$(O\; M\; M\; \ast \; O).\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{pmatrix\}\; \backslash \; mathbf\; \{O\}\; \backslash \; mathbf\; \{M\}\; \backslash \backslash \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{O\}\; \backslash \; end\; \{pmatrix\}\}.\}$

Подходы которые используют разложение по собственным значениям, основаны на алгоритме QR, который хорошо разработан, чтобы быть стабильным и быстрым. Обратите внимание, что сингулярные значения являются действительными, а правые и левые сингулярные векторы не требуются для формирования преобразований подобия. Можно итеративно переключаться между QR-разложением и LQ-разложением, чтобы найти действительные диагональные эрмитовы матрицы. Разложение QR дает M⇒ QR, а разложение LQ для R дает R⇒ LP. Таким образом, на каждой итерации у нас есть M⇒ QLP, обновляем M⇐ Lи повторяем ортогонализации. В конце концов, эта итерация между QR-разложением и LQ-разложением дает левую и правую унитарные сингулярные матрицы. Этот подход нельзя легко ускорить, поскольку алгоритм QR может иметь спектральные сдвиги или дефляцию. Это связано с тем, что метод сдвига нелегко определить без использования преобразований подобия. Однако этот итеративный подход очень просто реализовать, поэтому он является хорошим выбором, когда скорость не имеет значения. Этот метод также дает представление о том, как чисто ортогональные / унитарные преобразования могут получить SVD.

Аналитический результат 2 × 2 SVD

Сингулярные значения матрицы 2 × 2 могут быть найдены аналитически. Пусть матрица имеет вид $M\; =\; z\; 0\; I\; +\; z\; 1\; \sigma \; 1\; +\; z\; 2\; \sigma \; 2\; +\; z\; 3\; \sigma \; 3\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; z\_\; \{0\}\; \backslash \; mathbf\; \{I\}\; +\; z\_\; \{1\}\; \backslash \; sigma\; \_\; \{1\}\; +\; z\_\; \{2\}\; \backslash \; sigma\; \_\; \{2\}\; +\; z\_\; \{3\}\; \backslash \; sigma\; \_\; \{3\}\}$

где $zi\; \in \; C\; \{\backslash \; displaystyle\; z\_\; \{i\}\; \backslash \; in\; \backslash \; mathbb\; \{C\}\}$- комплексные числа, которые параметризуют матрицу, I - единичная матрица, а $\sigma \; i\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{i\}\}$обозначают матрицы Паули. Тогда его два сингулярных значения равны

$σ ± = | z 0 | 2 + | z 1 | 2 + | z 2 | 2 + | z 3 | 2 ± (| z 0 | 2 + | z 1 | 2 + | z 2 | 2 + | z 3 | 2) 2 - | z 0 2 - z 1 2 - z 2 2 - z 3 2 | 2 = | z 0 | 2 + | z 1 | 2 + | z 2 | 2 + | z 3 | 2 ± 2 (Re ⁡ z 0 z 1 ∗) 2 + (Re ⁡ z 0 z 2 ∗) 2 + (Re ⁡ z 0 z 3 ∗) 2 + (Im ⁡ z 1 z 2 ∗) 2 + (Im ⁡ z 2 z 3 ∗) 2 + (Im ⁡ z 3 z 1 ∗) 2 {\ displaystyle {\ begin {align} \ sigma _ {\ pm} = {\ sqrt {| z_ {0} | ^ {2} + | z_ {1} | ^ {2} + | z_ {2} | ^ {2} + | z_ {3} | ^ {2} \ pm {\ sqrt {(| z_ {0} | ^ {2} + | z_ {1} | ^ {2} + | z_ {2} | ^ {2} + | z_ {3} | ^ {2}) ^ {2} - | z_ {0} ^ {2} -z_ {1} ^ {2} -z_ {2} ^ {2} -z_ {3} ^ {2} | ^ {2}}}}} \\ = {\ sqrt {| z_ {0} | ^ { 2} + | z_ {1} | ^ {2} + | z_ {2} | ^ {2} + | z_ {3} | ^ {2} \ pm 2 {\ sqrt {(\ operatorname {Re} z_ { 0} z_ {1} ^ {*}) ^ {2} + (\ operatorname {Re} z_ {0} z_ {2} ^ {*}) ^ {2} + (\ operatorname {Re} z_ {0} z_ {3} ^ {*}) ^ {2} + (\ operatorname {Im} z_ {1} z_ {2} ^ {*}) ^ {2} + (\ operatorname {Im} z_ {2} z_ { 3} ^ {*}) ^ {2} + (\ operatorname {Im} z_ {3} z_ {1} ^ {*}) ^ {2}}}}} \ end {align}}}$

В приложениях довольно необычно, чтобы полное SVD, включая полное унитарное разложение нулевого пространства матрицы, требовалось. Вместо этого часто бывает достаточно (а также быстрее и экономичнее для хранения) вычислить сокращенную версию SVD. Для матрицы M размера m × n ранга r можно выделить следующее:

Тонкий SVD

$M\; =\; U\; n\; \Sigma \; n\; V\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{U\}\; \_\; \{n\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \_\; \{n\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\}$

Вычисляются только n векторов-столбцов U, соответствующих векторам-строкам V *. Остальные векторы-столбцы U не вычисляются. Это значительно быстрее и экономичнее, чем полный SVD, если n m. Матрица U 'n, таким образом, имеет размер m × n, Σ n имеет диагональ n × n, а V имеет размер n × n.

Первым этапом вычисления тонкого SVD обычно будет QR-разложение M, которое может значительно ускорить вычисление, если n m.

Компактный SVD

$M\; =\; U\; р\; \Sigma \; r\; V\; r\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{U\}\; \_\; \{r\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \_\; \{r\}\; \backslash \; mathbf\; \{V\}\; \_\; \{r\}\; ^\; \{*\}\}$

Вычисляются только r векторов-столбцов U и r векторов-строк V *, соответствующих ненулевым сингулярным значениям Σ r. Остальные векторы U и V * не вычисляются. Это быстрее и экономичнее, чем тонкий СВД, если r ≪ n. Матрица U r, таким образом, имеет размер m × r, Σ r - диагональ r × r, а V r * - это r × n.

Усеченный SVD

$M\; ~\; =\; U\; t\; \Sigma \; t\; V\; t\; \ast \; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{\backslash \; mathbf\; \{M\}\}\}\; =\; \backslash \; mathbf\; \{U\}\; \_\; \{t\}\; \{\backslash \; boldsymbol\; \{\backslash \; Sigma\}\}\; \_\; \{t\}\; \backslash \; mathbf\; \{V\}\; \_\; \{t\}\; ^\; \{*\}\}$

Только t векторов-столбцов U и t векторов-строк V *, соответствующие t наибольшим сингулярным значениям Σ t рассчитаны. Остальная часть матрицы отбрасывается. Это может быть намного быстрее и экономичнее, чем компактный SVD, если t≪r. Матрица U t, таким образом, имеет вид m × t, Σ t - диагональ t × t, а V t * - это t × n.

Конечно, усеченный SVD больше не является точным разложением исходной матрицы M, но, как обсуждалось выше, приблизительной матрицей $M\; ~\; \{\backslash \; displaystyle\; \{\backslash \; tilde\; \{\backslash \; \backslash \; mathbf\; \{M\}\}\}\}$в очень полезном смысле является ближайшим приближением к M, которое может быть достигнуто с помощью матрицы ранга t.

Нормы Ky Fan

Сумма k наибольших сингулярных значений M представляет собой матричную норму, Ky Fan k-норма M.

Первая из норм Ky Fan, 1-норма Ky Fan, совпадает с оператором norm M как линейным оператором относительно к евклидовой норме K и K. Другими словами, 1-норма Ки Фана - это операторная норма, индуцированная стандартным ℓ евклидовым скалярным произведением. По этой причине его еще называют операторной 2-нормой. Нетрудно проверить связь между 1-нормой Ky Fan и сингулярными значениями. В общем случае это верно для ограниченного оператора M в (возможно, бесконечномерном) гильбертовом пространстве

$\Vert \; M\; \Vert \; =\; \Vert \; M\; \ast \; M\; \Vert \; 1\; 2\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; mathbf\; \{M\}\; \backslash \; |\; =\; \backslash \; |\; \backslash \; mathbf\; \{M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; |\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}$

Но в матричном случае (M * M) является нормальной матрицей, поэтому || M * M || - наибольшее собственное значение (M * M), то есть наибольшее сингулярное значение M.

Последняя из норм Ки Фана, сумма всех сингулярных значений, является нормой следа (также известная как «ядерная норма»), определяемая как || M || = Tr [(M * M)] (собственные значения M * M - это квадраты сингулярных значений).

Норма Гильберта – Шмидта

Сингулярные значения связаны с другой нормой в пространстве операторов. Рассмотрим скалярное произведение Гильберта – Шмидта на матрицах n × n, определенное как

$⟨M,\; N⟩\; =\; trace\; \; (N\; \ast \; M).\; \{\backslash \; displaystyle\; \backslash \; langle\; \backslash \; mathbf\; \{M\},\; \backslash \; mathbf\; \{N\}\; \backslash \; rangle\; =\; \backslash \; operatorname\; \{trace\}\; \backslash \; left\; (\backslash \; mathbf\; \{N\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; right).\}$

Итак индуцированная норма равна

$\Vert \; M\; \Vert \; =\; ⟨M,\; M⟩\; =\; trace\; \; (M\; \ast \; M).\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; mathbf\; \{M\}\; \backslash \; |\; =\; \{\backslash \; sqrt\; \{\backslash \; langle\; \backslash \; mathbf\; \{M\},\; \backslash \; mathbf\; \{M\}\; \backslash \; rangle\}\}\; =\; \{\backslash \; sqrt\; \{\backslash \; operatorname\; \{trace\}\; \backslash \; left\; (\backslash \; mathbf\; \{\; M\}\; ^\; \{*\}\; \backslash \; mathbf\; \{M\}\; \backslash \; right)\}\}.\}$

Поскольку след инвариантен относительно унитарной эквивалентности, это показывает

$\Vert \; M\; \Vert \; =\; \sum \; i\; \sigma \; i\; 2\; \{\backslash \; displaystyle\; \backslash \; |\; \backslash \; mathbf\; \{M\}\; \backslash \; |\; =\; \{\backslash \; sqrt\; \{\backslash \; sum\; \_\; \{i\}\; \backslash \; sigma\; \_\; \{i\}\; ^\; \{2\}\}\}\}$

где σ i - сингулярные значения М . Это называется нормой Фробениуса, 2-нормой Шаттена или нормой Гильберта – Шмидта из M . Прямой расчет показывает, что норма Фробениуса M = (m ij) совпадает с:

$\sum \; i\; j\; |\; м\; я\; j\; |\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; sqrt\; \{\backslash \; sum\; \_\; \{ij\}\; |\; m\_\; \{ij\}\; |\; ^\; \{2\}\}\}.\}$

Кроме того, норма Фробениуса и норма следа (ядерная норма) являются частными случаями Норма Шаттена.

Представление Mode-k

$M\; =\; USVT\; \{\backslash \; displaystyle\; M\; =\; USV\; ^\; \{\backslash textf\; \{T\}\}\}$может быть представлено с использованием умножения режима-k матрицы $S\; \{\backslash \; displaystyle\; S\}$с применением $\times \; 1\; U\; \{\backslash \; displaystyle\; \backslash \; times\; \_\; \{1\}\; U\}$затем $\times \; 2\; V\; \{\backslash \; displaystyle\; \backslash \; times\; \_\; \{2\}\; V\}$для результата; то есть $M\; =\; S\; \times \; 1\; U\; \times \; 2\; V\; \{\backslash \; displaystyle\; M\; =\; S\; \backslash \; times\; \_\; \{1\}\; U\; \backslash \; times\; \_\; \{2\}\; V\}$.

Tensor SVD

Два типа тензора существуют декомпозиции, которые обобщают SVD на многоходовые массивы. Один из них разбивает тензор на сумму тензоров ранга 1, что называется разложением тензорного ранга . Второй тип разложения вычисляет ортонормированные подпространства, связанные с различными факторами, появляющимися в тензорном произведении векторных пространств, в которых живет тензор. Это разложение упоминается в литературе как SVD высшего порядка (HOSVD) или Tucker3 / TuckerM. Кроме того, полилинейный анализ главных компонентов в обучении полилинейных подпространств включает в себя те же математические операции, что и разложение Таккера, и используется в другом контексте уменьшения размерности.

Масштабно-инвариантный SVD

Сингулярные значения матрицы A однозначно определены и инвариантны относительно левых и / или правых унитарных преобразований A. Другими словами, сингулярные значения UAV для унитарных U и V равны равны сингулярным значениям A. Это важное свойство для приложений, в которых необходимо сохранять евклидовы расстояния и инвариантность относительно вращений.

Масштабно-инвариантный SVD, или SI-SVD, аналогичен обычному SVD, за исключением того, что его однозначно определенные сингулярные значения инвариантны относительно диагональных преобразований A. Другими словами, сингулярные значения DAE для невырожденных диагональных матриц D и E равны сингулярным значениям A. Это важное свойство для приложений, для которых требуется инвариантность к выбору единиц измерения переменных (например, метрических единиц по сравнению с имперскими).

HOSVD функций - численная реконструкция - преобразование модели TP

преобразование модели TP численно восстанавливает HOSVD функций. Для получения дополнительной информации посетите:

• Каноническая форма функций TP и моделей qLPV на основе HOSVD
• Преобразование модели тензорного продукта
• Преобразование модели TP в теории управления

Ограниченные операторы в гильбертовых пространствах

Факторизация M= U$\Sigma \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\backslash \; Sigma\}\}$Vможет быть расширена до ограниченного оператора M в сепарабельном гильбертовом пространстве H. А именно, для любого ограниченного оператора M существует частичная изометрия U, унитарное V, пространство с мерой (X, μ) и неотрицательное измеримое f, такое что

$M\; =\; UT\; f\; V\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{U\}\; T\_\; \{f\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\}$

где $T\; f\; \{\backslash \; displaystyle\; T\_\; \{f\}\}$- умножение на f на L (X, μ).

Это можно показать, имитируя линейный алгебраический аргумент для матричного случая выше. VT f V * - это уникальный положительный квадратный корень из M * M, как указано в функциональном исчислении Бореля для самосопряженных операторов. Причина, по которой U не обязательно должен быть унитарным, заключается в том, что, в отличие от конечномерного случая, при заданной изометрии U 1 с нетривиальным ядром подходящее U 2 может не быть найдено так, что

$[U\; 1\; U\; 2]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{bmatrix\}\; U\_\; \{1\}\; \backslash \backslash \; U\_\; \{2\}\; \backslash \; end\; \{bmatrix\}\}\}$

- унитарный оператор.

Что касается матриц, факторизация по сингулярным числам эквивалентна полярному разложению для операторов: мы можем просто написать

$M\; =\; UV\; \ast \; \cdot \; VT\; f\; V\; \ast \; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; =\; \backslash \; mathbf\; \{U\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; \backslash \; cdot\; \backslash \; mathbf\; \{V\}\; T\_\; \{f\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\}$

и обратите внимание, что UV * по-прежнему частичная изометрия при положительном значении VT f V *.

Сингулярные значения и компактные операторы

Понятие сингулярных значений и левых / правых сингулярных векторов может быть расширено до компактного оператора в гильбертовом пространстве, поскольку они имеют дискретный спектр. Если T компактно, каждое ненулевое λ в его спектре является собственным значением. Более того, компактный самосопряженный оператор может быть диагонализован по его собственным векторам. Если M компактно, то MMтоже. Применяя результат диагонализации, унитарный образ его положительного квадратного корня T f имеет набор ортонормированных собственных векторов {e i }, соответствующих строго положительным собственным значениям {σ i }. Для любого ψ ∈ H

$M\; \psi \; =\; UT\; f\; V\; \ast \; \psi \; =\; \sum \; i\; ⟨UT\; f\; V\; \ast \; \psi ,\; U\; ei⟩\; U\; ei\; =\; \sum \; i\; \sigma \; i\; ⟨\psi ,\; V\; ei⟩\; U\; ei,\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{M\}\; \backslash \; psi\; =\; \backslash \; mathbf\; \{U\}\; T\_\; \{f\}\; \backslash \; mathbf\; \{V\}\; ^\; \{*\}\; \backslash \; psi\; =\; \backslash \; sum\; \_\; \{i\}\; \backslash \; left\; \backslash \; langle\; \backslash \; mathbf\; \{U\}\; T\_\; \{f\}\; \backslash \; mathbf\; \{\; V\}\; ^\; \{*\}\; \backslash \; psi,\; \backslash \; mathbf\; \{U\}\; e\_\; \{i\}\; \backslash \; right\; \backslash \; rangle\; \backslash \; mathbf\; \{U\}\; e\_\{i\}\; =\; \backslash \; sum\; \_\; \{i\}\; \backslash \; sigma\; \_\; \{i\}\; \backslash \; left\; \backslash \; langle\; \backslash \; psi,\; \backslash \; mathbf\; \{V\}\; e\_\; \{i\}\; \backslash \; right\; \backslash \; rangle\; \backslash \; mathbf\; \{U\}\; e\_\; \{i\},\}$

где ряд сходится в топологии нормы на H. Обратите внимание, как это похоже на выражение из специального кейс. σ i называются сингулярными значениями M . {Uei} (соответственно {Vei}) можно рассматривать как лево-сингулярные (соответственно право-сингулярные) топ-строение для M.

Компактные операторы в гильбертовом пространстве являются контактированием операторами конечного ранга в единой операторнойологии. Вышеупомянутое выражение ряда дает явное представление. Непосредственным следствием этого является:

Теорема. Mкомпактна тогда и только тогда, когда MMкомпактна.

Разложение по сингулярным числам было разработано различными геометрами, который хотел определить, может ли реальная билинейная форма быть сделана равной другой посредством других ортогональных преобразователей двух пространств, в которых она действует. Эухенио Бельтрами и Камилла Джордан независимо от друга в 1873 и 1874 годах разработаны, что сингулярные значения билинейных форм, представленные в виде матрицы, образуют полный набор инвариантов для билинейных форм при ортогональных подстановках. Джеймс Джозеф Сильвестр также пришел к разложению по сингулярным числам для вещественных квадратных матриц в 1889 году, по-внешнему, независимо от Бельтрами и Джордана. Сильвестр назвал сингулярные значения каноническими множителями матрицы A. Четвертым математиком, открывшим независимое разложение по сингулярным числам, является Autonne в 1915 году, который пришел к нему с помощью полярного разложения. Первое доказательство разложения по сингулярным числам для прямоугольных и комплексных матриц, по-видимому, было сделано Карлом Эккартом и Гейлом Дж. Янгом в 1936 году; они рассматривали это как обобщение преобразования главной оси для эрмитовых матриц.

В 1907 г. Эрхард Шмидт определил аналог сингулярных значений для интегральных операторов (компактные при некоторых слабых технических предположениях); похоже, он не знал о параллельной работе над сингулярными значениями конечных матриц. Эта теория была развита Эмилем Пикаром в 1910 году, который первым назвал числа $\sigma \; k\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{k\}\}$сингулярными значениями (или по-французски valeurs singulières).

Практические методы вычисления SVD восходят к Когбетлянцу в 1954, 1955 году и Хестенсу в 1958 году. Они очень похожи на алгоритм собственных значений Якоби, который использует вращения плоскости или вращения Гивенса. Однако они были заменены методом Джина Голуба и Уильяма Кахана, опубликованным в 1965 году, который использует преобразования Хаусхолдера или отражения. В 1970 году Голуб и Кристиан Райнш опубликовали вариант алгоритма Голуба / Кахана, который до сих пор остается наиболее часто используемым.

• Каноническая корреляция
• Каноническая форма
• Анализ соответствия (CA)
• Проклятие размерности
• Цифровая обработка сигналов
• Уменьшение размерности
• Собственное разложение матрицы
• Эмпирические ортогональные функции (EOF)
• Фурье-анализ
• Обобщенное разложение по сингулярным значениям
• Неравенства относительно сингулярных значений
• K-SVD
• Скрытый семантический анализ
• Скрытый семантическое индексирование
• Линейный метод наименьших квадратов
• Список преобразований, связанных с Фурье
• Хеширование с учетом местоположения
• Аппроксимация низкого ранга
• Разложение матрицы
• Многолинейный анализ главных компонентов (MPCA)
• Поиск ближайшего соседа
• Нелинейные итерационные частичные наименьшие квадраты
• Полярное разложение
• Анализ главных компонентов (PCA)
• Разложение Шмидта
• Сингулярное значение
• Временной ряд
• Двумерное разложение по сингулярным числам (2DSVD)
• Неравенство следа фон Неймана
• Вейвлет-сжатие

• Банерджи, Судипто; Рой, Аниндия (2014), Линейная алгебра и матричный анализ для статистики, Тексты в статистической науке (1-е изд.), Chapman and Hall / CRC, ISBN 978-1420095388
• Trefethen, Lloyd N. ; Бау III, Дэвид (1997). Численная линейная алгебра. Филадельфия: Общество промышленной и прикладной математики. ISBN 978-0-89871-361-9. CS1 maint: ref = harv (ссылка )
• Деммел, Джеймс ; Кахан, Уильям (1990). «Точные сингулярные значения двухдиагональных матриц». SIAM Journal on Scientific and Statistical Computing. 11 (5): 873–912. CiteSeerX 10.1.1.48.3740. doi : 10.1137 / 0911052.
• Голуб, Джин Х. ; Кахан, Уильям (1965). «Вычисление сингулярных чисел и псевдообратной матрицы». Журнал Общества промышленной и прикладной математики, серия B: численный анализ. 2 (2): 205–224. Bibcode : 1965SJNA.... 2..205G. doi : 10.1137 / 0702016. JSTOR 2949777.
• Голуб, Джин Х. ; Ван Лоан, Чарльз Ф. (1996). Matrix Computations (3-е изд.). Johns Hopkins. ISBN 978-0 -8018-5414-9.
• GSL Team (2007). «§14.4 Разложение по сингулярным значениям». Научная библиотека GNU. Справочное руководство.
• Халлдор, Бьорнссон и Венегас, Сил через А. (1997). «Руководство по анализу климатических данных EOF и SVD». Университет Макгилла, Отчет CCGCR № 97-1, Монреаль, Квебек, 52 стр.
• Hansen, P. C. (1987). «Усеченный СВД как метод регуляризации». НЕМНОГО. 27 (4): 534–553. doi : 10.1007 / BF01937276. CS1 maint: ref = harv (ссылка )
• Хорн, Роджер А.; Джонсон, Чарльз Р. (1985). «Раздел 7.3». Матричный анализ. Cambridge University Press. ISBN 978-0-521-38632-6.
• Хорн, Роджер А.; Джонсон, Чарльз Р. (1991). "Глава 3". Темы матричного анализа. Издательство Кембриджского университета. ISBN 978-0-521-46713-1.
• Самет, Х. (2006). Основы многомерных и метрических структур данных. Морган Кауфманн. ISBN 978-0-12-369446-1.
• Стренг Г. (1998). «Раздел 6.7». Линейную алгебру (3-е изд.). Wellesley-Cambridge Press. ISBN 978-0-9614088-5-5.
• Стюарт, Г. У. (1993). «О ранней истории разложения сингулярных значений». Обзор SIAM. 35 (4): 551–566. CiteSeerX 10.1.1.23.1831. DOI : 10.1137 / 1035134. HDL : 1903/566. JSTOR 2132388. CS1 maint: ref = harv (ссылка )
• Уолл, Майкл Э.; Рехтштайнер, Андреас; Роча, Луис М. (2003). «Разложение по сингулярным значениям и анализ главного компонента». В Д.П. Беррар; В. Дубицки; М. Гранцов (ред.). Практический подход к анализу данных микрочипов. Норвелл, Массачусетс: Kluwer. Стр. 91–109.
• Нажмите, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Flannery, BP (2007), «Раздел 2.6», Численные рецепты: Искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8

• Онлайн-калькулятор SVD