Законы формы

редактировать

Законы формы (далее LoF ) - книга автора Г. Книга Спенсера-Брауна, опубликованная в 1969 году, находится на границе между математикой и философией. LoF включает три различных логические системы :

«первичная арифметика» (описанная в главе 4 LoF), модели которой включают ическую арифметику ;
«первичную алгебру » (глава 6 LoF), чьи модели включают в себя двухэлементную булеву алгебру (далее сокращенно 2 ), булеву логику и классическую исчисление высказываний ;
«Уравнения второй степени» (глава 11), интерпретации которые включают конечные автоматы и ограниченный рекурсивный алгоритм Алонзо Черча Арифметика (RRA).

«Граничная алгебра» - это термин Мегуира (2011), обозначающий объединение первичной алгебры и первичной аметики. Законы формы иногда в общих чертах к «первичной алгебре», а также к LoF.

Содержание

1 Книга
2 Прием
3 Форма (Глава 1)
4 Основная арифметика (Глава 4)
- 4.1 Понятие канона
5 Основное алгебра (Глава 6)
- 5.1 Синтаксис
- 5.2 Правила логической эквивалентности
- 5.3 Инициалы
- 5.4 Теория доказательства
- 5.5 Интерпретации
  - 5.5.1 Двухэлементная булева алгебра 2
  - 5.5.2 Смысловая логика
  - 5.5. 3 Силлогизмы
- 5.6 Пример расчета
- 5.7 Отношение к магмам
6 Уравнения второй степени (Глава 11)
7 Связанные работы
8 См. также
9 Примечания
10 Ссылки
11 Внешние ссылки

Книга

В предисловии говорится, что работа была впервые исследована в 1959 году, и Спенсер Браун цитирует Бертрана Рассела как поддержку его начинанию. Он также благодарит Дж. К. П. Миллеру из Университетского колледжа Лондона за помощь с корректурой и другие рекомендации. В 1963 году Спенсер Браун был приглашен штатным преподавателем физических наук на факультете заочных исследований Лондонского университета для чтения курса математики логики.

Произошла его логическая операция в области электронной инженерии, которую он провел примерно в 1960 году, и из первых лекций по математической, которые он прочитал под эгидой Лондонского университета. программа расширения. LoF появился в нескольких выпусках. Вторая серия изданий появилась в 1972 году с «Предисловием к первому американскому изданию», в котором подчеркивалось использование парадоксов самореференции. самым последним из них был немецкий перевод 1997 года, который никогда не выходил из печати.

Математика заполняет только около 55pp и довольно элементарна. Ноическая и декламационная проза LoF и его любовь к парадоксу делают его трудным для всех. Спенс-Браун находился под областью Витгенштейна и Р. Д. Лэнг. LoF также перекликается с тем из трудов Чарльза Сандерса Пирса, Бертрана Рассела и Альфреда Норта Уайтхеда.

Вся книга написана оперативно, дать инструкции читателю вместо того, чтобы говорить ему, что «есть». В соответствии с интересом Дж. Спенсера-Брауна к парадоксам, единственное предложение, которое делает утверждение, что что-то есть, - это утверждение, в котором говорится, что такие утверждения не используются в этой книге. За исключением этого единственного предложения, книгу можно рассматривать как пример E-Prime.

Reception

Якобы работа по формальной математике и философии, LoF стала чем-то вроде культовой классики : Хайнц фон Ферстер хвалил его, когда рецензировал его для Каталога всей Земли. Те, кто согласен, указать на LoF как на воплощение загадочной «математики сознания », его алгебраический символизм, улавливающий (возможно, даже «тот») неявный корень познания : способность «различать». LoF утверждает, что первичная алгебра обнаруживает разительные связи между логикой, булевой алгеброй и арифметикой, а также философией языка и разумом.

Банашевского ( 1977) утверждает, что первичная алгебра - это не что иное, как новая запись для булевой алгебры., Двухэлементная логическая алгебра 2может рассматриваться как предполагаемая интерпретация первичной алгебры. Полностью использует двойственность, имеющую не только булевы алгебры, но и все решетки ;

. Подчеркивает, насколько синтаксически различные утверждения в логике и 2 может иметь идентичную семантику ;

Значительно упрощает вычисления булевой алгебры и доказательства в предложениях и силлогистической логике.

Кроме того, синтаксис первичной алгебры может быть расширен до формальных систем, отличных от 2 и сентенциальной логики, что приведет к граничной математике (см. связанные работы ниже).

LoF оказал влияние, среди прочего, на Хайнца фон Ферстера, Луи Кауфмана, Никласа Луманна, Умберто Матурана, Франсиско Варела и. Некоторые из этих авторов изменили первичную алгебру множеством интересных способов.

LoF утверждал, что некоторые хорошо известные математические гипотезы очень давно, такие как Теорема четырех цветов, Великая теорема Ферма и гипотеза Гольдбаха, можно доказать с помощью расширений первичной алгебры. Спенсер-Браун в конце концов распространил предполагаемое доказательство теоремы четырех цветов, но оно встретило скептицизм.

Форма (Глава 1)

Символ:

Также называемый «знаком» или «крест» - это основная черта Закона формы. В неподражаемой и загадочной манере Спенсера-Брауна Знак символизирует корень познания, то есть дуалистический Знак указывает на способность отличать «это» от «всего остального, кроме этого».

В LoF крест обозначает очертание «различия», и его можно рассматривать как означающее сразу следующее:

Акт проведения границы вокруг чего-то, таким образом отделяя его от все остальное;
То, что становится отличным от всего, проводя границу;
Переход от одной стороны границы к другой.

Все способы предполагают действие со сторонынитивная сущность (например, человек), проводящая различие. Как говорит LoF:

«Первая команда:

Нарисуйте различие

может быть выражена такими способами, как:

Пусть будет различие,
Найдите различие,
См.. Различие,
Опишите различие,
Определите различие,

Или:

Пусть будет проведено различие ". (LoF, Примечания к главе 2)

Контрапунктом помеченного состояния немаркированное Отмеченное и пустота - два примитивных значения Законов Формы.

Крест можно рассматривать как обозначение как обозначение как обозначенное состояние, которое является просто ничем, пустотой или невыразимой бесконечностью, представленной пробелом. между двумя состояниями, одним из которых является рассматриваемый нами вопрос о состоянии любопытного резонанса с некоторыми теориями и языка. LoF (исключая заднюю материю) завершается словами:

... первое различие, Знак и наблюдатель не только взаимозаменяемы, но и идентичность ны по форме.

С. С. Пирс пришел к похожему выводу в 1890-х годах; см. § Связанные работы.

Основная арифметика (Глава 4)

Синтаксис основной арифметики выглядит следующим образом. Всего два атомарных выражения :

Пустой Крест ;
Вся или часть пустой страницы («пустота»).

Есть два индуктивных правила:

Крест может быть записано поверх выражения;
Любые два выражения могут быть соединены.

семантика первичной арифметики, возможно, не что определяет, как единственное явное определение в LoF: «Различие - это совершенное воздержание ».

Пусть «немаркированное состояние» будет синонимом пустоты. Пусть пустой Крест обозначает «отмеченное состояние». Перекрестие означает переход от одного значения, неотмеченного или отмеченного состояния, к другому. Теперь мы можем указать «арифметические» аксиомы A1 и A2, на основе которых основывается первичная арифметика (и, следовательно, все законы формы):

«A1. Закон вызова ». Двойной вызов из состояния неотличим от однократного вызова. Дважды провести различие дает тот же эффект, что и один раз. Например, сказать «Да будет свет», а затем снова сказать «Да будет свет» - все равно, что сказать это один раз. Формально:

= {\ displaystyle \ =}

\ =

«A2. Закон пересечения ». После из немаркированного состояния в отмеченное, повторное пересечение («повторное пересечение»), начиная с отмеченного состояния, возвращает единицу в немаркированное состояние. Следовательно, обратное пересечение аннулируетечение. Формально:

= {\ displaystyle \ =}

\ =

И в A1, и в A2 выражение справа от '=' содержит меньше символов, чем выражение слева от '='. Это предполагает, что каждое первичное арифметическое выражение может быть упрощено повторным применением A1 и A2 до одного из двух состояний: отмеченного или немаркированного состояния. Это действительно так, и результатом является «упрощение» выражения. Две фундаментальные метатеоремы первичной арифметики утверждают, что:

Каждое конечное выражение имеет уникальное упрощение. (T3 в LoF);
Начало с начального отмеченного или немаркированного состояния, «усложнение» выражения конечным числом повторных применений A1 и A2 не может привести к выражению, упрощение которого отличается от начального состояния. (T4 в LoF).

Таким образом, отношение из логической эквивалентности разделяет все первичные арифметические выражения на два класса эквивалентности : те, которые упрощают до Креста, а те, что упрощают до пустоты.

A1 и A2 имеют свободные аналоги по свойствам последовательных и параллельных электрических цепей, а также другие способы построения диаграмм процессов, включая блок-схемы. A1 соответствует параллельному соединению, а A2 - последовательному соединению, при том, что различение соответствует изменению соединения двух точек в цепи, а не просто добавлению проводки.

Первичная арифметика соответствующим формальным языкам из математика и информатика :

A язык Дайка порядок 1 с нулевым алфавитом;
Самый простой контекстно-свободный язык в иерархии Хомского ;
A система перезаписи, которая строго нормализует и сливается.

Фраза "исчисление показаний» в LoF является синонимом «первичной арифметики».

Понятие канона

Понятие, присущее LoF, - это понятие «канон». Хотя LoF не определяет канон, следующие два отрывка из Примечательно, что к гл. 2 подходят:

Более важные структуры командования иногда называют канонами. Эти средства, направляющие правительственные предписания, группируются в созвездии, и поэтому никоим образом не являются независимыми друг от друга. т.е. указанная) строящаяся система, но команда строить (например, «провести различие»), даже если она может иметь центральное значение, не является каноном.

... основная форма математической коммуникации - не описание, а пре дписание... Музыка - это похожая форма искусства, композитор даже не пытается описать набор звуков, которые он имеет в виду, а тем более набор ощущений, вызванных ими, но записывает набор команд, которые, если исполнитель им подчиняется, могут привести к воспроизведению, слушателю, оригинального опыта композитора.

Эти отрывки к различию в металогике между объектным языком, формальным языком обсуждаемой логической системы, и метаязык, язык (часто естественный язык), отличный от объектного языка, использование для описания и обсуждения объектного языка. Первая цитата, кажется, утверждает, что каноны это часть метаязыка. Вторая цитата, кажется, утверждает, что утверждение на объектном языке, по сути, является командой, адресованным читателю. Ни то и другое утверждение не выполняется в стандартной металогике.

Первичная алгебра (Глава 6)

Синтаксис

Для любого допустимого первичного арифметического выражения вставьте в одно или несколько мест любое количество латинских букв с необязательными числовыми индексами; результатом является формула первичной алгебры . Буквы, используемые таким образом в математике и логике, называются переменными. Переменная первичной алгебры указывает место, где можно записать примитивное значение или его дополнение . Несколько экземпляров одной и той же примитивной точки обозначают несколько местоположений одного и того же примитивного значения.

Правила логической эквивалентности

Знак '=' может связывать два логически эквивалентных выражения; результатом является уравнение. Под «логически эквивалентным» понимается то, что два выражения имеют одинаковое упрощение. Логическая эквивалентность - это отношение эквивалентности над набором формул первичной алгебры, регулируемое правилом R1 и R2. Пусть «C» и «D» будут формулами, каждая из которых содержит хотя бы один экземпляр подформулы A:

R1, Замена равных. Заменить один или несколько экземпляров A в C на B, в результате получится E. Если A = B, то C = E.
R2, Равномерная замена. Замените все экземпляры A в C и D на B. C E становится, а D становится F. Если C = D, то E = F. Обратите внимание, что A = B не требуется.

R2очень часто используется в демонстрациях первичной алгебры (см. Ниже), почти всегда молча. Эти правила обычно используются в логике и большей математики, почти всегда бессознательно.

Первичная алгебра состоит из соотношений, то есть пар формул, связанных инфиксом '='. R1 и R2 позволяют преобразовывать одно уравнение в другое. Следовательно, первичная алгебра является эквациональной формальной системой, как и многие алгебраические структуры, включая булеву алгебру, которые являются разновидностями. Эквациональная логика была распространена до Principia Mathematica (например, Peirce, Johnson 1892) и имеет современных сторонников (Gries and Schneider 1993).

Обычная математическая логика состоит из тавтологических формул, сигнализируемых префиксом турникет. Чтобы обозначить, что формула первичной алгебры A является тавтологией, просто напишите «A = ». Если заменить '=' в R1 и R2 на двусмысленный, результирующие правила сохранятся в традиционной логике. Однако традиционная логика в основном полагается на правило modus ponens ; таким образом, обычная логика важна. Эквационально-поненциальная дихотомия выделяет многое из того, что отличает математическую логику от остальной математики.

Инициалы

Инициалы - это уравнение первичной алгебры, которое можно проверить с помощью процедур принятия решений , и как таковое не является аксиомой . LoF помещает инициалы:

Отсутствие чего-либо справа от "=" выше преднамеренным.

J2- это знакомый закон распределения сентенциальной логики и булевой алгебры.

Другой набор инициалов, удобнее для вычислений:

J1a:

A B

Благодаря C2 первичная алгебра является решеткой. В силу J1a это решетка с дополнениями , верхняя граница которой равна . По J0, - соответствующая нижняя граница, а элементности. J0также является алгебраической версией A2 и проясняет смысл, в котором является псевдонимом с пустой страницей.

T13 в LoF обобщает C2 следующим образом. Любую формулу первичной алгебры (или сентенциональной логики) B можно рассматривать как упорядоченное дерево с ветвями. Тогда:

T13 : A подформула A может быть по желанию на любую глубину B, большую, чем у A, при условии, что A и его копия находится в одной ветви B. того, учитывая несколько экземпляров A в одной ветви B, все экземпляры, кроме самых мелких, избыточными.

Хотя доказательство T13 потребует индукции, интуиция, лежащая в основе этого, должна быть ясной.

C2или его эквивалент назван:

«Поколение» в LoF;
«Исключение» в Джонсоне (1892 г.);

«Распространение» в работе Уильяма Бриккена. 580>Возможно, первым примером аксиомы или правил с силой C2 было «Правило (де) итерации», объединяющее T13 и AA = A, из C. В экзистенциальных графах.

С.Пирса утверждается, что конкатенация быть прочитана как коммутирующая и связывающая может по умолчанию и, следовательно, не должна явно предполагаться или демонстрироваться. (Пирс сделал аналогичное утверждение о своих экзистенциальных графах.) Пусть точка будет временной записью для группировки. Эта конкатенация коммутирует и связывает, может быть применено из:

Начального AC.D = CD.A и следствия AA = A (Byrne 1946). Этот результат верен для всех решеток, поскольку AA = A является простым следствием который элемент, выполнен для всех решеток;
Инициалы AC.D = AD.C и J0 . Поскольку J0 выполняется только для решеток с нижней границей, этот метод применим только для ограниченных решеток (которые включают первичную алгебру и 2 ). Коммутативность тривиальна; просто установите A = . Ассоциативность: AC.D = CA.D = CD.A = A.CD.

Продемонстрировав ассоциативность, точка может быть отброшена.

Инициалы в Meguire (2011): AC.D = CD.A, обозначено B1; B2, J0 выше; B3, J1a выше; и B4, C2. По дизайну эти инициалы очень похожи на аксиомы для абелевой группы, G1-G3 ниже.

Теория доказательств

Первичная алгебра содержит три вида доказанных утверждений:

Следствие - уравнение первичной алгебры, подтвержденное демонстрацией. Демонстрация состоит из последовательности шагов, каждый шаг оправдан начальным или ранее продемонстрированным следствием.
Теорема - это утверждение на метаязыке, подтвержденное доказательством, т. е. аргумент, сформулированный на метаязыке, который принимается обученными математиками и логиками.
Исходный, определенный выше. В демонстрациях и доказательствах инициал используется как аксиома.

Различие между следствием и теоремой справедливо для всех формальных систем, включая математику и логику, но обычно не делается явным. Демонстрация или процедура принятия решения может быть проведена и проверена на компьютере. доказательства теоремы быть не может.

Пусть A и B - формулы первичной алгебры . Демонстрация A = B может происходить двумя способами:

Измените A по шагам, пока не будет получено B, или наоборот;
Упростите и , и до . Это известно как «вычисление».

После демонстрации A = B можно использовать A = B для обоснования шагов в последующих демонстрациях. для демонстрации и вычислений первичной алгебры часто требуется не более J1a, J2, C2и следствия (C3в LoF), (C1) и AA = A (C5 ).

Следствие 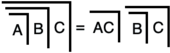, C7 'в LoF, включает алгоритм , набросанный в LoF s доказательстве T14, который преобразует произвольную формулу первичной алгебры в эквивалентную формулу, глубина которой не превышает двух. Результатом является нормальная форма, аналог первичной алгебры конъюнктивной нормальной формы. LoF (T14–15) доказывает первичный алгебраический аналог известной теоремы булевой алгебры о том, что каждая формула имеет нормальную форму.

Пусть A будет подформулой некоторой формулы B. В сочетании с C3, J1a может рассматриваться как условие закрытия для вычислений: Bявляется таутологией тогда и только тогда, когда A и (A) оба появляются в глубине 0 of B. Родственное условие появляется в версиих естественного вычета. Демонстрация вычислением часто немного больше, чем:

многократный вызов T13 для удаления избыточных подформул;
Удаление подформул, имеющей форму .

. LoF включает элегантные новые доказательства следующей стандартной метатеории :

Полнота : все следствия первичной первичной алгебры демонстрируются с инициалов (T17).
Независимость : J1не может быть установлена с помощью J2 и наоборот (T18).

Эта сентенциальная логика завершена преподается в каждом первом университетском курсе математической логики. Но в университетских курсах по булевой алгебре редко встречается полнота 2.

интерпретаций

, если отмеченные и немаркированные состояния читаются как логические значения 1 и 0 (или True и False ), первичная алгебра интерпретирует 2 (или сентенциальную логику ). LoF показывает, как первичная алгебра может интерпретировать силлогизм. Каждая из этих интерпретаций обсуждается в подразделе ниже. Расширение первичной алгебры, чтобы она могла интерпретировать стандартную логику первого порядка, еще предстоит сделать, но бета Пирса экзистенциальные графы предполагаю, что это продление возможно.

Двухэлементная булева алгебра 2

Первичная алгебра - это элегантная минималистская запись для двухэлементной булевой алгебры 2. Пусть:

Одно из логических соединение (+) или соответствует (×) интерпретировать конкатенацию ;
дополнение к A интерпретировать
0 (1) интерпретировать пустую метку, если соединение (встреча) интерпретирует конкатенацию (поскольку двоичная операция, применяемая к нулевым операндам, может рассматриваться как равная элементу идентичности операции; или другими словами, отсутствующий операнд может рассматривать как действующий по умолчанию как элемент идентичности).

Если join интерпретирует AC, то meet (join) интерпретирует $A | ¯ C | ¯ | ¯ {\ displaystyle {\ overline {{\ overline {A |}} \ \ {\ overline {C |}} {\ Big |}}}}$ ${\ displaystyle {\ overline {{\ overline {A |}} \ \ {\ overline {C |}} { \ Big |}}}}$ . Следовательно, первичная алгебра и 2 изоморфны, но для одной детали: дополнение первичной алгебры может быть нулевым, и в этом случае оно обозначает примитивное значение. По модулю этой детали 2 является моделью первичной алгебры. Первичная арифметика предлагает следующую арифметическую аксиоматизацию 2 : 1 + 1 = 1 + 0 = 0 + 1 = 1 = ~ 0 и 0 + 0 = 0 = ~ 1.

Набор $B = {{\ displaystyle \ B = \ {}$ $\ B = \ {$ $, {\ displaystyle,}$ $,$ $} {\ displaystyle \ \}}$ $\ \}$ - это логический домен или оператор связи. На языке универсальной алгебры первичной алгеброй является алгебраическая структура $⟨B, - -, - | ¯, | ¯⟩ {\ displaystyle \ langle B, - \ -, {\ overline {- \ |}}, {\ overline {\ \ |}} \ rangle}$ ${\ displaystyle \ langle B, - \ -, {\ overline {- \ |}}, {\ overline {\ \ |}} \ rangle}$ типа $⟨2, 1, 0⟩ {\ Displaystyle \ langle 2,1,0 \ rangle}$ $\ langle 2,1,0 \ rangle$ . выразительная адекватность штриха Шеффера указывает на то, что первичная алгебра также является $⟨B, - - | ¯, | ¯⟩ {\ displaystyle \ langle B, {\ overline {- \ - \ |}}, {\ overline {\ \ |}} \ rangle}$ ${\ displaystyle \ langle B, {\ overline {- \ - \ |}}, {\ overline {\ \ |}} \ rangle}$ алгебра типа $⟨2, 0⟩ { \ Displaystyle \ langle 2,0 \ rangle}$ $\ langle 2,0 \ rangle$ . В обоих случаях идентичны J1a, J0, C2 и ACD = CDA. Так как первичная алгебра и 2 изоморфны,, 2можно рассматривать как a $⟨B, +, ¬, 1⟩ {\ displaystyle \ langle B, +, \ lnot, 1 \ rangle}$ $\ langle B, +, \ lnot, 1 \ rangle$ алгебра типа $⟨2, 1, 0⟩ {\ displaystyle \ langle 2,1,0 \ rangle}$ $\ langle 2,1,0 \ rangle$ . Это описание 2 проще, чем обычное, а именно: $⟨B, +, ×, ¬, 1, 0⟩ {\ displaystyle \ langle B, +, \ times, \ lnot, 1, 0 \ rangle}$ $\ langle B, +, \ times, \ lnot, 1,0 \ rangle$ алгебра типа $⟨2, 2, 1, 0, 0⟩ {\ displaystyle \ langle 2,2,1,0,0 \ rangle}$ $\ langle 2,2,1,0,0 \ rangle$ .

две возможные интерпретации двойственны друг другу в булевом смысле. (В булевой алгебре замена AND ↔ OR и 1 ↔ 0 в уравнении дает одинаково допустимое уравнение.) Тождество сохраняется независимо от того, какая интерпретация выбрана, поэтому преобразования или режимы вычислений остаются теми же; только интерпретация каждой формы будет разной. Пример: J1a - . Интерпретируя сопоставление как ИЛИ, а как 1, это переводится в $¬ A ∨ A = 1 {\ displaystyle \ neg A \ lor A = 1}$ ${\ displaystyle \ neg A \ lor A = 1}$ , что верно. Интерпретируя сопоставление как AND и как 0, это переводится как $¬ A ∧ A = 0 {\ displaystyle \ neg A \ land A = 0}$ ${\ displaystyle \ neg A \ land A = 0}$ , что также верно (и двойное из $¬ A ∨ A = 1 {\ displaystyle \ neg A \ lor A = 1}$ ${\ displaystyle \ neg A \ lor A = 1}$ ).

Логика предложений

Пусть пустая страница обозначает Ложь, а крест читается как Не . Тогда первичная арифметика имеет следующее сентенциальное прочтение:

= Ложь

= Истина = Не Ложь

= Не Истина = Ложь

Основная алгебра интерпретирует сентенциальную логику как следует. Буква представляет любое данное предложение. Образом:

интерпретирует Не A

интерпретирует A или B

Таким образом интерпретирует Не A или B или If A Then B .

интерпретирует Не (Не A или Не B)

или Не (если A, то не B)

или A And B .

оба интерпретируют A , если и только если B или A эквивалентен B .

Таким образом, любое выражение в сентенциальной логике имеет преобразование первичной алгебры. Точно так же первичная алгебра интерпретирует сентенциальную логику. При использовании каждой модели состояния с пометкой или без пометки, этот первичный перевод алгебры сводится к первичному арифметическому выражению, которое можно упростить. Повторение этого упражнения для всех использований двух примитивных значений различных показателей, является исходное выражение тавтологическим или выполнимым. Это пример процедуры принятия решения , более или менее в духе обычных таблиц истинности. Учитывая некоторую формулу первичной алгебры, содержащую N число, эта процедура принятия решения требует упрощения двух первичных арифметических формул. О менее утомительной процедуре принятия решения, более в духе «анализа истинности» Куайна, см. Meguire (2003).

Шварц (1981) доказал, что первичная алгебра эквивалентна - синтаксически, семантически и теоретически - с классическим пропозициональное исчисление. Таким же образом можно показать, что первичная алгебра синтаксически эквивалентна выражениям, построенным обычным способом из классических значений истинности true и false, логические связки НЕ, ИЛИ, И и круглые скобки.

Интерпретация немаркированного состояния как Ложь полностью произвольна; это состояние также может быть прочитано как Истина . Все, что требуется, - это изменить интерпретацию конкатенации с ИЛИ на И. IF A THEN B теперь переводится как вместо . В более общем смысле, первичная алгебра является «само- двойным », что означает, что любая формула первичной алгебры имеет два предложения или логических значений, каждое из которых двойное другого. Еще одно следствие самодвойственности - неуместность цирка Де Моргана ; эти законы заложены в синтаксис первичной алгебры с самого начала.

Теперь проясняется истинная природа между первичной алгеброй, с одной стороны, и 2 и сентенциальной логикой, с другой. В последней формелизмах дополнение / отрицание, оперирующее «ничто», сформировано неправильно. Но пустой Крест - это хорошо сформированное выражение первичной алгебры, обозначающее состояние Отмечено, примитивное значение. Следовательно, непустой крест - это оператор , а пустой крест - это операнд , потому что он обозначает примитивное значение. Таким образом, первичная алгебра показывает, что прежде всего различные математические концепции и операнда на самом деле представляют собой просто разные грани единого фундаментального действия, различия.

Силлогизмы

Приложение 2 к LoF показывает, как перевести традиционные силлогизмы и сориты в первичную алгебру. Правильный силлогизм - это просто тот силлогизм, перевод первичной алгебры упрощенного метода до пустого Креста. Пусть A * обозначает литерал, т.е. либо A, либо $A | ¯ {\ displaystyle {\ overline {A |}}}$ ${\ displaystyle {\ overline {A |}}}$ , безразлично. Тогда каждый силлогизм, который не требует, чтобы один или несколько термов считались непустыми, является одной из 24 перестановок обобщения Барбары, чей первичный алгебраический эквивалент $A ∗ B | ¯ B | ¯ C ∗ | ¯ A * C * {\ Displaystyle {\ overline {A ^ {*} \ B |}} \ \ {\ overline {{\ overline {B |}} \ C ^ {*} {\ Big |}}} \ А ^ {*} \ C ^ {*}}$ ${\ displaystyle { \ overline {A ^ {*} \ B |}} \ \ {\ overline {{\ overline {B |}} \ C ^ {*} {\ Big | }}} \ A ^ {*} \ C ^ {*}}$ . Эти 24 агентов перестановки включают 19 силлогистических форм, признанных действующих в аристотелевской и средневековой логике. Этот первичный алгебраический перевод силлогистической логики также предполагает, что первичная алгебра может интерпретировать монадическую и логику, и что первичная алгебра имеет сходство с алгеброй Куайна (1982: Часть II).

Пример вычисления

Следующее вычисление нетривиальной теоремы Лейбница демонстрирует демонстративную мощь первичной алгебры. Пусть C1 равно $A | ¯ | ¯ {\ displaystyle {\ overline {{\ overline {A |}} {\ Big |}}}}$ ${\ displaystyle {\ overline {{\ overline {A |}} {\ Big |}}}}$ = A, C2 быть $A A B | ¯ = A B | ¯ {\ displaystyle A \ {\ overline {A \ B |}} = A \ {\ overline {B |}}}$ ${\ displaystyle A \ {\ overline {A \ B |}} = A \ {\ overline {B |}}}$ , C3 быть $| ¯ A = | ¯ {\ displaystyle {\ overline {\ \ |}} \ A = {\ overline {\ \ |}}}$ ${\ displaystyle {\ overline {\ \ |}} \ A = {\ overline {\ \ |}}}$ , J1a будет $A | ¯ A = | ¯ {\ displaystyle {\ overline {A |}} \ A = {\ overline {\ \ |}}}$ ${\ displaystyle {\ overline {A |}} \ A = {\ overline {\ \ |}}}$ , и пусть OI означает, что переменные и подформулы были переупорядочены таким образом, что коммутативность и ассоциативность разрешать.

[(P → R) ∧ (Q → S)] → [(P∧Q) → (R∧S)].

Теорема Praeclarum.

перевод первичной алгебры

C1.

О.И.

C2.

О.И.

C2.

О.И.

С2.

C1.

О.И.

J1a.

О.И.

С3.

◻ {\ displaystyle \ square}

\ square

Связь с магмами

Первичная алгебра воплощает точку, отмеченную Хантингтоном в 1933 году: Булева алгебра требует, в дополнение к одной унарной операции, одной, а не двум, двоичным операциям. Отсюда редко отмечается тот факт, что булевы алгебры - это магмы. (Магмы назывались группоидами, пока последний термин не был классмы теорией категорий.) Чтобы увидеть это, обратите внимание, что первичная алгебра - это коммутативная :

групп также требуется унарный режим, называемый инверсией, групповой аналог логического дополнения. Пусть обозначает обратное к a. Пусть обозначает элемент идентичности группы . Тогда группы и первичная алгебра имеют одинаковые сигнатуры, а именно, они обе являются $⟨- -, - | ¯, | ¯⟩ {\ displaystyle \ langle - \ -, {\ overline {- \ |}}, {\ overline {\ \ |}} \ rangle}$ ${\ displaystyle \ langle - \ -, {\ overline { - \ |}}, {\ overline {\ \ |}} \ rangle}$ алгебры типа 〈2,1,0〉. Следовательно, первичная алгебра - это граничная алгебра. Аксиомы для абелевой группы в граничных обозначениях:

G1. abc = acb (предполагая ассоциацию слева);
G2.
G3. .

Из G1 и G2, коммутативность и ассоциативность конкатенации могут быть получены, как указано выше. Обратите внимание, что G3 и J1a идентичны. G2 и J0 будут идентичны, если = заменить A2 . Это определяющее арифметическое тождество теории групп в граничных обозначениях.

Первичная алгебра отличается от абелевой группы двумя способами:

Из A2 следует, что ≠ . Если бы первичной алгеброй была группа ,, = была бы верна, и одно из a = или = a должно было бы быть следствием первичной алгебры. Обратите внимание, что и являются взаимными дополнениями первичной алгебры, как того требует теория групп, так что $| ¯ | ¯ | ¯ = | ¯ {\ Displaystyle {\ overline {\ {\ overline {\ {\ overline {\ \ |}} \ {\ Big |}}} \ {\ Bigg |}}} = {\ overline {\ \ |}}}$ ${\ displaystyle {\ overline {\ {\ overline {\ {\ overline {\ \ |}} \ {\ Big |}}} \ {\ Bigg |}}} = {\ overline {\ \ |}}}$ верно как для теории групп, так и для первичной алгебры;
C2наиболее четко отличает первичную алгебру от других магм, поскольку C2 позволяет продемонстрировать закон поглощения, который определяет решетки, и закон распределения, центральный для булевой алгебры.

Оба A2 и C2 следуют из B упорядоченный набор.

Уравнения второй степени (Глава 11)

Глава 11 LoF вводит уравнения второй степени, составленные из рекурсивных формул, которые можно увидеть как имеющий «бесконечную» глубину. Некоторые рекурсивные формулы упрощаются до отмеченного или немаркированного состояния. Другие неопределенно «колеблются» между двумя состояниями в зависимости от того, четная или нечетная заданная глубина. В частности, определенные рекурсивные формулы могут быть интерпретированы как колеблющиеся между истина и ложь в течение последовательных интервалов времени, и в этом случае считается, что формула имеет «мнимое» значение истинности. Таким образом, можно ввести течение времени в первичную алгебру.

Терни (1986) показывает, как эти рекурсивные формулы можно интерпретировать с помощью Ограниченной рекурсивной арифметики (RRA) Алонзо Черча. Черч представил RRA в 1955 году как аксиоматическую формализацию конечных автоматов. Терни (1986) представляет общий метод перевода уравнений второй степени в RRA Черча, иллюстрируя его метод с помощью формул E1, E2и E4 в главе 11 LoF. Этот перевод на RRA проливает свет на имена, которые Спенсер-Браун дал E1 и E4, а именно «память» и «счетчик». Таким образом, RRA формализует и разъясняет представление LoF о мнимой ценности истины.

Связанная работа

Готфрид Лейбниц в меморандумах, опубликованных не ранее конца 19-го и начала 20-го веков, изобрел булеву логику. Его нотация была изоморфной нотации LoF: конкатенация читалась как конъюнкция, а «не- (X)» читалась как дополнение к X. Признание новаторской роли Лейбница в предвестниками алгебраической логики стали Льюис (1918) и Решер (1954). Но полной оценки достижений Лейбница нужно было дождаться работы Вольфганга Ленцена, опубликованной в 1980-х годах и рассмотренной в Lenzen (2004).

Чарльз Сандерс Пирс (1839–1914) предвосхитил первичную алгебру в трех направлениях работы:

В двух работах, написанных им в 1886 году, предлагалась логическая алгебра, использующая только один символ, ленту, почти идентичную кресту. LoF. Семантика стримера идентична семантике Креста, за исключением того, что Пирс никогда не писал стример без ничего под ним. Отрывок из одной из этих статей был опубликован в 1976 году, но они не были опубликованы полностью до 1993 года.
В статье энциклопедии 1902 года Пирс обозначил булеву алгебру и смысловую логику в манере статьи, за исключением того, что он использовал два стиля скобок, переключаясь между '(', ')' и '[', ']' с каждым приращением в глубина формулы.
Синтаксис его альфа экзистенциальных графов представляет собой просто конкатенацию, читаемую как соединение, и вложение овалами читать как отрицание. Если конкатенация первичной алгебры читается как конъюнкция, то эти графы изоморфны первичной алгебре (Kauffman 2001).

Как ни странно, LoF цитирует т. 4 Сборника статей Пирса, источник формылизмов в (2) и (3) выше. (1) - (3) были практически неизвестны в то время (1960-е годы) и в месте написания (UK) LoF. семиотика Пирса, на основе которой LoF умалчивает, может еще пролить свет на философские аспекты LoF.

Кауфман (2001) обсуждает другую нотацию, аналогичную LoF, в статье 1917 года Жана Никода, который был учеником Бертрана Рассела.

Вышеупомянутые формылизмы, как и первичная алгебра, предоставляют собой все примеры граничной математики, то есть математики, синтаксис которой ограничен буквами и скобками (заключающими элементами). Такой минималистский синтаксис - это «граничная нотация». Обозначение границ не содержит символов операторов инфиксного, префикса постфикса. Очень известные фигурные скобки ('{', '}') теории множеств можно рассматривать как граничные обозначения.

Работа Лейбница, Пирса и Никода не связаны с метатеорией, как они писали перед знаменательной статьей Эмиля Поста 1920 года (которую цитирует LoF), доказывая, что сентенциональная логика является полным, и до Гильберт и Лукасевич показал, как доказать независимость аксиомы с помощью моделей.

Крейг (1979) утверждал, что мир и то, как люди воспринимают этот мир и взаимодействуют с ним, имеет богатую булеву структуру. Крейг был ортодоксальным логиком и авторитетом в алгебраической логике.

Второе поколение когнитивной науки появилось в 1970-х, был после того, как написан LoF. О когнитивной науке и ее значении для булевой алгебры, логики и теории множеств см. Lakoff (1987) (см. Статьи указателя в разделе «Примеры схем изображений: контейнер») и Lakoff and Núñez (2001). Ни одна из книг не цитирует LoF.

Биологи и ученые-когнитивисты Умберто Матурана и его ученик Франсиско Варела оба обсуждают LoF в своих трудах, которые определяют «различие» как фундаментальный познавательный акт. Психолог и когнитивист из Беркли Элеонора Рош много писала о связанном с этим понятии категоризации.

Другие формальные системы с возможным сродством к первичной алгебре, которая включает:

Мереологию, обычно имеет измененную решетки, очень похожую на структуру булевой алгебры. Для некоторых авторов мереология - это просто модель булевой алгебры, следовательно, и первичной алгебры.
Мереотопология, которая по своей природе богаче булевой алгебры;
Система Уайтхеда (1934), фундаментальный примитивом которой является «указание».

Первичная арифметика и алгебра - это минималистский формализм для сентенциальной логики и булевой алгебры. Другие минималистские формылизмы, обладающие силой теории множеств, включают:

лямбда-исчисление ;
Комбинаторную логику с двумя (S и K ) или даже один (X ) примитивный комбинатор;
Математическая логика, основанная всего на трех примитивных понятиях: одно связующее, И-НЕ (чей перевод первичной алгебры $AB | ¯ {\ displaystyle {\ overline {A \ \ B \ |}}}$ ${\ displaystyle {\ overline {A \ \ B \ |}}}$ или, соответственно, $A | ¯ B | ¯ {\ displaystyle {\ overline {A |}} \ \ {\ overline {B |}}}$ ${\ displaystyle {\ overline { A |}} \ \ {\ overline {B |}}}$ ), универсальная количественная оценка и одна двоичная атомарная формула, обозначающая установить членство. Это система Quine (1951).
Бета экзистенциальные графы с единственным двоичным предикатом, обозначающим членство в множестве. Это еще изучить. Альфа-графы, упомянутые выше, являются частным случаем бета-графов.

См.

Примечания

Ссылки

Издания законов о форме:
- 1969. Лондон: Аллен и Анвин, твердый переплет.
- 1972. Crown Publishers, твердый переплет: ISBN 0-517-52776-6
- 1973. Книги Bantam, мягкая обложка. ISBN 0-553-07782-1
- 1979. E.P. Даттон, мягкая обложка. ISBN 0-525-47544-3
- 1994. Портленд, штат Орегон: Cognizer Company, мягкая обложка. ISBN 0-9639899-0-1
- Немецкий перевод 1997 г., озаглавленный Gesetze der Form. Любек: Bohmeier Verlag. ISBN 3-89094-321-7
- 2008 Bohmeier Verlag, Leipzig, 5-е международное издание. ISBN 978-3-89094-580-4
Босток, Дэвид, 1997. Промежуточная логика. Oxford Univ. Press.
Бирн, Ли, 1946, «Две формулировки булевой алгебры», Бюллетень Американского математического общества: 268–71.
Крейг, Уильям (1979). «Булева логика и повседневный физический мир». Труды и адреса Американской философской ассоциации. 52 (6): 751–78. DOI : 10.2307 / 3131383. JSTOR 3131383.
Дэвид Грис и Шнайдер, Ф. Б., 1993. Логический подход к дискретной математике. Springer-Verlag.
Уильям Эрнест Джонсон, 1892, «Логическое исчисление», Mind 1 (ns): 3–30.
Луи Х. Кауфман, 2001, «Математика К.С. Пирса ", Кибернетика и человеческое знание 8: 79–110.
------, 2006," Переформулировка теоремы о цвете карты. "
--- ---, 2006a. "Законы формы - Исследование математики и основ. " Черновик книги (отсюда большой).
Ленцен, Вольфганг, 2004, "Логика Лейбница "в Габбэй, Д., и Вудс, Дж., Ред., Расцвет современной логики: от Лейбница до Фреге (Справочник по истории логики - Том 3). Амстердам: Elsevier, 1–83.
Лакофф, Джордж, 1987. Женщины, огонь и опасные предметы. University of Chicago Press.
-------- и Рафаэль Э. Нуньес, 2001. Откуда пришла математика : Как воплощенный разум воплощает математику в жизнь. Основные книги.
Мэгуайр, П.Г. (2003). «Открытие граничной алгебры: упрощенное обозначение булевой алгебры и истина» Функторы ». ional Journal of General Systems. 32 : 25–87. CiteSeerX 10.1.1.106.634. doi : 10.1080 / 0308107031000075690.
--------, 2011. Граничная алгебра: более простой подход к базовой логике и булевой алгебре. ООО «ВДМ Паблишинг» ISBN 978-3639367492. Источник большей части этой записи, включая обозначения, которые заключают в скобки то, что LoF помещает под крестиком. Избегает более спекулятивных аспектов LoF.
Уиллард Куайн, 1951. Mathematical Logic, 2-е изд. Издательство Гарвардского университета.
--------, 1982. Методы логики, 4-е изд. Издательство Гарвардского университета.
Решер, Николас (1954). «Интерпретация Лейбница его логических исчислений». Журнал символической логики. 18 (1): 1–13. DOI : 10.2307 / 2267644. JSTOR 2267644.
Шварц, Дэниел Г. (1981). "Изоморфизмы законов формы Дж. Спенсера-Брауна и исчисления Ф. Варелы для саморефлексии". Международный журнал общих систем. 6 (4): 239–55. doi : 10.1080 / 03081078108934802.
Терни, П. Д. (1986). «Законы формы и конечные автоматы». Международный журнал общих систем. 12 (4): 307–18. doi : 10.1080 / 03081078608934939.
А. Н. Уайтхед, 1934, «Указание, классы, число, подтверждение», Mind 43 (n.s.): 281–97, 543. Исправления на стр. 543 являются многочисленными и важными, и более поздние перепечатки этой статьи не включают их.
Дирк Беккер (редактор) (1993), Kalkül der Form. Зуркамп; Дирк Беккер (редактор), Probleme der Form. Suhrkamp.
Дирк Беккер (редактор) (1999), Проблемы формы, Stanford University Press.
Дирк Беккер (редактор) (2013), Математика формы, Социология Наблюдатели, Кибернетика и знание человека, т. 20, нет. 3-4.

Внешние ссылки

Законы формы, архив веб-сайта Ричарда Шупа.
Выступления Спенсера-Брауна в Эсалене, 1973 год. Самореференционные формы представлены в разделе, озаглавленном «Степень уравнений и теория типов».
Луи Х. Кауфман, «Бокс-алгебра, граничная математика, логика и законы формы. "
Киссель, Маттиас, Несистематическое, но легкое для понимания введение в Законы формы. "
Форум «Законы формы», где первичная алгебра и связанные с ней формализмы обсуждаются с 2002 года.
Встреча с GSB Моше Кляйном
Маркировка, простое введение в идеи законов формы
Исчисление BF и квадратный корень отрицания Луи Кауфмана и Артур Коллингс; он расширяет законы формы, добавляя воображаемое логическое значение. (Воображаемые логические значения представлены в главе 11 книги «Законы формы».)
Курс «Законы формы» - бесплатный онлайн-курс, знакомящий людей с основной частью текста «Законы формы» Леона Конрада, последнего ученика Спенсер-Брауна, изучавшего работу с автором.