Механика контакта

Изучение деформации тел, соприкасающихся друг с другом Напряжения в области контакта, нагруженные одновременно нормальной и касательной силой. Напряжения были сделаны видимыми с помощью фотоупругости.

Механика контакта - это исследование деформации твердого тела, которые касаются друг друга в одной или нескольких точках. Основное различие в механике контакта - между напряжением, действующими перпендикулярно поверхностям контактирующих тел (известное как нормальное направление ) и трением напряжения, действующие по касательной между поверхностями. На этой странице уделяется нормальному без внимания, то есть механике контакта трения. Механика фрикционного контакта обсуждается отдельно. Нормальные напряжения вызываются приложенными силами и адгезией, присутствующей на поверхностях в тесном контакте, если они чистые и сухие.

Контактная механика является частью механики инженерии. Физико-математическая формулировка предмета основана на механике материалов и механике сплошной среды и фокусируется на вычислениях, включающих упругость, вязкоупругость и пластмассовые корпуса в статическом или динамическом контакте. Контактная механика предоставляет информацию для безопасного и эффективного использования технических систем и для изучения трибологии, контактной жесткости, электрического сопротивления контакта и ость вдавливания. Принципы механики контактов реализованы в таких приложениях, как контакт колеса локомотива с рельсом, сцепные устройства, тормозные системы, шины, подшипники, двигатели внутреннего сгорания, механические рычаги, прокладки уплотнения, металлообработка, обработка металлов давлением, ультразвуковая сварка, электрические контакты и многие другие. анализ напряжений контактных и соединительных элементов и влияние смазки и конструкции на трение и носить. Приложения контактной механики расширяются в области микро и нанотехнологий.

Оригинальная работа по контактной механике восходит к 1881 году, когда была опубликована статья «О контакте упругих тел» («Ueber die Berührung fester elastischer Körper» ) Генрих Герц. Герц пытался понять, как оптические свойства нескольких уложенных друг на друга линз могут измениться под силы, удерживая их вместе. Контактное напряжение Герца относится к локализованным напряжениям, которые развиваются, когда две криволинейные поверхности входят в контакт и слегка деформируются под воздействием приложенных нагрузок. Эта величина деформации зависит от модуля упругости материала, находящегося в контакте. Он дает контактное напряжение как функция нормальной контактной силы, радиусов кривизны обоих тел и модуля упругости обоих тел. Контактное напряжение Герца формирует основу для определения несущей способности и усталости долговечности подшипников, шестерен и других тел, где две поверхности соприкасаются.

• 1 История
• 2 Классические решения для неклейкого эластичного контакта
  • 2.1 Контакт между сферой и полупространством
  • 2.2 Контакт между двумя сферами
  • 2.3 Контакт между двумя пересеченными цилиндры равного радиуса $R\; \{\backslash \; displaystyle\; R\}$
  • 2.4 Контакт между жестким цилиндром и упругостью полупространством
  • 2.5 Контакт между жестким коническим индором и упругим полупространством
  • 2.6 Контакт между двумя цилиндрами с параллельными осями
  • 2.7 Контакт с подшипником
  • 2.8 Метод уменьшения размерности
• 3 Теория Герца неклейкого упругого контакта
  • 3.1 Допущения теории Герца
  • 3.2 Методы аналитического решения
    • 3.2.1 Точечный контакт на (2D) полуплоскости
    • 3.2.2 Линейный контакт на (2D) полуплоскости
      • 3.2.2.1 Нормальная нагрузка в области $(a,\; b)\; \{\backslash \; displaystyle\; (a,\; b)\}$
      • 3.2.2.2 Сдвиговая нагрузка по области $(a,\; b)\; \{\backslash \; displaystyle\; (a,\; b)\}$
    • 3.2.3 Точечный контакт на a (3D) полупрос транство
  • 3.3 Техника численного решения iques
• 4 Контакт между шероховатыми поверхностями
  • 4.1 Обзор модели GW
  • 4.2 Обзор модели GT
• 5 Адгезионный контакт между упругими телами
  • 5.1 Модель жесткого контакта Брэдли
  • 5.2 Модель упругого контакта Джонсона-Кендалла-Робертса (JKR)
  • 5.3 Модель упругого контакта Дерягина-Мюллера-Топорова (DMT)
  • 5.4 Параметр Табора
  • 5.5 Модель упругого контакта Моугиса-Дагдейла
  • 5.6 Модель Carpick -Ogletree-Salmeron (COS)
  • 5.7 Влияние формы контакта
• 6 См. Также
• 7 Ссылки
• 8 Внешние ссылки

Когда сфера прижимается к упругому материалу, площадь контакта увеличивается.

Классическая механика контакта в первую очередь связана с Генрихом Герцем. В 1882 году Герц решил контакте двух упругих тел с искривленными поверхностями. Это все еще актуальное классическое решение составляет основу современных проблем контактной механики. Например, в машиностроении и трибологии контактное напряжение Герца - это описание напряжения в сопряженных деталях. Контактное напряжение Герца обычно относится к напряжению вблизи области контакта между двумя сферами разного радиуса.

Только почти почти лет спустя Джонсон, Кендалл и Робертс нашли аналогичное решение для случая контакта клея. Эту теорию отвергли Борис Дерягин и его сотрудники, предложившие другую теорию адгезии в 1970-х годах. Модель Дерягина стала известна как модель ДМТ (после Дерягина, Мюллера и Топорова), а модель Джонсона и др. Модель стала известна как модель JKR (в честь Джонсона, Кендалла и Робертса) для адгезионного эластичного контакта. Этот отказ инструментом для разработки параметров Табора и более поздних параметров Моугиса, которые количественно определяют, какая модель контакта (из моделей JKR и DMT) лучше представляет адгезивный контакт для конкретных материалов.

Дальнейшее продвижение в области контактной механики в середине двадцатого века может быть связано с такими именами, как Боуден и Табор. Боуден и Табор первыми подчеркнули важность шероховатости поверхности контактирующих тел. Путем исследования шероховатости поверхности было установлено, что истинная площадь контакта между фрикционными меньшими, чем кажущаяся площадь контакта. Такое понимание также коренным образом изменило направление работ в трибологии. Работы Боудена и Табора контакт привести к появлению несколько теорийной механики шероховатых поверхностей.

Вклад Арчарда (1957) также следует представить при обсуждении новаторских работ в этой области. Арчард пришел к выводу, что даже для шероховатых упругих поверхностей площадь контакта пропорциональна нормальная силе. Дальнейшие важные идеи в этом направлении были предоставлены Гринвудом и Уильямсоном (1966 г.), Бушем (1975 г.) и Перссоном (2002 г.). Основные результаты этих работ заключаются в том, что истинная поверхность контакта в шероховатых материалах обычно пропорциональна нормальным результатам, в то время как параметры отдельных микроконтактов (т.е. давление, размер микроконтактов) слабо зависят от нагрузки..

Теория контакта между упругими телами может установить простые контактные площадки и глубину вдавливания для геометрических фигур. Некоторые часто используются решения ниже. Теория, используемая для вычислений этих решений, обсуждается далее в статье. Решения для множества других технически важных форм, например усеченный конус, изношенный шар, шероховатые профили, полые цилиндры и т. д. можно найти в

Контакт между сферой и полупространством

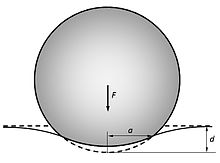
Контакт упругой сферы с упругим полупространством

Эластичная сфера с радиусом $R\; \{\backslash \; displaystyle\; R\; \}$вдавливает упругое полупространство, где общая деформация равна $d\; \{\backslash \; displaystyle\; d\}$, вызывая площадь контакта радиусом

$a\; =\; R\; d\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; sqrt\; \{Rd\}\}\}$

Приложенная сила $F\; \{\backslash \; displaystyle\; F\}$связано со смещением $d\; \{\backslash \; displaystyle\; d\}$на

$F\; =\; 4\; 3\; E\; \ast \; R\; 1\; 2\; d\; 3\; 2\; \{\backslash \; displaystyle\; F\; =\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; E\; ^\; \{*\}\; R\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; d\; ^\; \{\; \backslash \; frac\; \{3\}\; \{2\}\}\}$

где

$1\; E\; \ast \; =\; 1\; -\; \nu \; 1\; 2\; E\; 1\; +\; 1\; -\; \nu \; 2\; 2\; E\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{E\; ^\; \{*\; \}\}\}\; =\; \{\backslash \; frac\; \{1-\; \backslash \; nu\; \_\; \{1\}\; ^\; \{2\}\}\; \{E\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1-\; \backslash \; nu\; \_\; \{2\}\; ^\; \{2\}\}\; \{E\_\; \{2\; \}\}\}\}$

и $E\; 1\; \{\backslash \; displaystyle\; E\_\; \{1\}\}$,$E\; 2\; \{\backslash \; displaystyle\; E\_\; \{2\}\}$- это модули упругости и $\nu \; 1\; \{\backslash \; Displaystyle\; \backslash \; ню\; \_\; \{1\}\}$,$\nu \; 2\; \{\backslash \; Displaystyle\; \backslash \; п\; u\; \_\; \{2\}\}$коэффициенты Пуассона, связанные с каждым телом.

Распределение нормального давления в области контакта как функция расстояния от центра круга:

$p\; (r)\; =\; p\; 0\; (1\; -\; r\; 2\; a\; 2)\; 1\; 2\; \{\backslash \; displaystyle\; p\; (r)\; =\; p\_\; \{0\; \}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}$

где $p\; 0\; \{\backslash \; displaystyle\; p\_\; \{0\}\}$- максимальное контактное давление, определяемое по формуле

$p\; 0\; =\; 3\; F\; 2\; \pi \; a\; 2\; =\; 1\; \pi \; (6\; FE\; \ast \; 2\; R\; 2)\; 1\; 3\; \{\backslash \; displaystyle\; p\_\; \{\; 0\}\; =\; \{\backslash \; frac\; \{3F\}\; \{2\; \backslash \; pi\; a\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{6F\; \{E\; ^\; \{*\}\}\; ^\; \{2\; \}\}\; \{R\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\}$

Радиус круга зависит от приложенной нагрузки $F\; \{\backslash \; displaystyle\; F\}$по уравнению

$a\; 3\; =\; 3\; FR\; 4\; E\; \ast \; \{\backslash \; displaystyle\; a\; ^\; \{3\}\; =\; \{\backslash \; cfrac\; \{3FR\}\; \{4E\; ^\; \{*\}\}\}\}$

Общая деформация $d\; \{\backslash \; displaystyle\; d\}$связана с максимальным контактным давлением воздуха

$d\; =\; a\; 2\; R\; =\; (9\; F\; 2\; 16\; E\; \ast \; 2\; R)\; 1\; 3\; \{\backslash \; displaystyle\; d\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{R\; \}\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{9F\; ^\; \{2\}\}\; \{16\; \{E\; ^\; \{*\}\}\; ^\; \{2\}\; R\}\}\; \backslash \; right)\; ^\; \{\backslash \; fr\; ac\; \{1\}\; \{3\}\}\}$

Максимальное напряжение сдвига возникает внутри при $z\; \approx \; 0,49\; a\; \{\backslash \; displaystyle\; z\; \backslash \; приблизительно\; 0,49a\}$для $\nu \; =\; 0,\; 33\; \{\backslash \; displaystyle\; \backslash \; nu\; =\; 0,33\}$.

Контакт между двумя сферами

Контакт между двумя сферами. Контакт между двумя скрещенными цилиндрами равного радиуса.

Для контакта между двумя сферами радиуса $R\; 1\; \{\backslash \; displaystyle\; R\_\; \{1\}\}$и $R\; 2\; \{\backslash \; displaystyle\; R\_\; \{2\}\}$, область контакта представляет собой круг радиуса $a\; \{\backslash \; displaystyle\; a\}$. Уравнения такие же, как для сферы, контактирующей с полуплоскостью, за исключением того, что эффективный радиус $R\; \{\backslash \; displaystyle\; R\}$определяет как

$1\; R\; =\; 1\; R\; 1\; +\; 1\; R\; 2\; \{\; \backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{2\}\}\}\}$

Контакт между двумя пересеченными цилиндры равного радиуса $R\; \{\backslash \; displaystyle\; R\}$

Это эквивалентно контакту между сферой радиуса $R\; \{\backslash \; displaystyle\; R\}$и плоскостью.

Контакт между жестким цилиндром с концом концом и упругим полупространством

Контакт между жестким цилиндрическим индентором и упругим полупространством.

Если жесткий цилиндр вдавлен в упругую полупространство. пространство, он создает давление, описываемое формулой

$p\; (r)\; =\; p\; 0\; (1\; -\; r\; 2\; R\; 2)\; -\; 1\; 2\; \{\backslash \; displaystyle\; p\; (r)\; =\; p\_\; \{0\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{R\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\}$

где $R\; \{\backslash \; displaystyle\; R\}$- радиус цилиндра, а

$p\; 0\; =\; 1\; \pi \; E\; \ast \; d\; R\; \{\backslash \; displaystyle\; p\_\; \{0\}\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\}\}\; E\; ^\; \{*\}\; \{\backslash \; frac\; \{d\}\; \{\; R\}\}\}$

Связь между глубиной вдавливания и нормальной эксплуатации определяется выражением

$F\; =\; 2\; RE\; \ast \; d\; \{\backslash \; displaystyle\; F\; =\; 2RE\; ^\; \{*\}\; d\}$

Контакт между жестким коническим индентором и упругое полупространство

Контакт между жестким коническим индентором и упругим полупространством.

В случае вдавливания упругого полупространства модуля Юнга $E\; \{\backslash \; displaystyle\; E\}$с использованием жесткого конического индентора, глубины контакта $ϵ\; \{\backslash \; displaystyle\; \backslash \; epsilon\}$и радиуса контакта $a\; \{\backslash \; displaystyle\; a\}$связаны с использованием

$ϵ\; =\; загар\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; epsilon\; =\; a\; \backslash \; tan\; (\backslash \; theta)\}$

с $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$определяет угол между плоскостью и боковой поверхностью конуса. Общая глубина отступа $d\; \{\backslash \; displaystyle\; d\}$определяется как:

$d\; =\; \pi \; 2\; ϵ\; \{\backslash \; displaystyle\; d\; =\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{2\}\}\; \backslash \; epsilon\}$

Общая сила равна

$F\; =\; \pi \; E\; 2\; (1\; -\; \nu \; 2)\; a\; 2\; загар\; \; (\theta )\; =\; 2\; E\; \pi \; (1\; -\; \nu \; 2)\; d\; 2\; загар\; \; (\theta )\; \{\backslash \; displaystyle\; F\; =\; \{\backslash \; frac\; \{\backslash \; pi\; E\}\; \{2\; \backslash \; left\; (1-\; \backslash \; nu\; ^\; \{2\}\; \backslash \; right)\}\}\; a\; ^\; \{2\}\; \backslash \; tan\; (\backslash \; theta)\; =\; \{\backslash \; frac\; \{2E\}\; \{\backslash \; pi\; \backslash \; left\; (1-\; \backslash \; nu\; ^\; \{2\}\; \backslash \; right)\}\}\; \{\backslash \; frac\; \{d\; ^\; \{2\}\}\; \{\backslash \; tan\; (\backslash \; theta)\}\}\}$

Распределение давления определяется как

$p\; (r)\; =\; E\; d\; \pi \; a\; (\; 1\; -\; \nu \; 2)\; пер\; \; (ar\; +\; (ar)\; 2-1)\; =\; E\; d\; \pi \; a\; (1\; -\; \nu \; 2)\; cosh\; -\; 1\; \; (ar)\; \{\backslash \; displaystyle\; p\; \backslash \; left\; (r\; \backslash \; right)\; =\; \{\backslash \; frac\; \{Ed\}\; \{\backslash \; pi\; a\; \backslash \; left\; (1-\; \backslash \; nu\; ^\; \{2\}\; \backslash \; right)\}\}\; \backslash \; ln\; \backslash \; left\; (\{\backslash \; frac\; \{a\}\; \{r\}\}\; +\; \{\backslash \; sqrt\; \{\backslash \; left\; (\{\backslash \; frac\; \{\; a\}\; \{r\}\}\; \backslash \; right)\; ^\; \{2\}\; -1\}\}\; \backslash \; right)\; =\; \{\backslash \; frac\; \{Ed\}\; \{\backslash \; pi\; a\; \backslash \; left\; (1-\; \backslash \; nu\; ^\; \{2\}\; \backslash \; right)\}\}\; \backslash \; cosh\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{a\}\; \{r\}\}\; \backslash \; right)\}$

Напряжение имеет логарифмическую сингулярность на конце конуса.

Контакт между двумя цилиндрами с параллельными осями

Контакт между двумя цилиндрами с параллельными осями

Контакт между двумя цилиндрами с параллельными осями сила линейно пропорциональна длине цилиндров L и углублению глубина d:

$F\; \approx \; \pi \; 4\; E\; \ast \; L\; d\; \{\backslash \; displaystyle\; F\; \backslash \; приблизительно\; \{\backslash \; frac\; \{\backslash \; pi\}\; \{4\}\}\; E\; ^\; \{*\}\; Ld\}$

Радиусы кривизны полностью отсутствуют в этом отношении. Радиус контакта описывается обычным воздействием

$a\; =\; R\; d\; \{\backslash \; displaystyle\; a\; =\; \{\backslash \; sqrt\; \{Rd\}\}\}$

с

$1\; R\; =\; 1\; R\; 1\; +\; 1\; R\; 2\; \{\backslash \; displaystyle\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{2\}\}\}\}$

как при контакте двух сфер. Максимальное давление равно

$p\; 0\; =\; (E\; \ast \; F\; \pi \; LR)\; 1\; 2\; \{\backslash \; displaystyle\; p\_\; \{0\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{E\; ^\; \{*\}\; F\}\; \{\backslash \; pi\; LR\}\}\; \backslash \; справа)\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}$

Контакт подшипника

Контакт в случае подшипников часто представляет собой контакт между выпуклой поверхностью (охватываемый цилиндр или сфера) и вогнутой поверхностью (охватывающий цилиндр или сфера: отверстие или полусферическая чашка ).

Метод уменьшения размерности

Контакт между сферой и упругим полупространством и одномерная замененная модель.

Некоторые контактные задачи могут быть решены с помощью метода уменьшения размераности (MDR). В этом методе исходной трехмерной системы заменяется контактом тела с линейно-упругим или вязкоупругим основанием (см. Рис.). Свойства одномерных систем в точности совпадают со свойствами исходной трехмерной системы. MDR основан на решении осесимметричных контактных задач, впервые полученных Людвигом Фёпплом (1941) и Герхардом Шубертом (1942)

Однако требуется точных аналитических результатов, чтобы контактная задача была осесимметричной, контакты были компактным.

Классическая теория контакта фокусировалась в первую очередь на неклейком контакте, когда в зоне контакта не допускается силы натяжения, т. Е. Контактирующие тела могут отделяться без сил сцепления. Несколько аналитических и численных подходов были использованы для решения контактных задач, удовлетворяющих условию отсутствия прилипания. Сложные силы и моменты передаются между телами в местах их соприкосновения, поэтому проблемы в механике контакта могут стать довольно сложными. Кроме того, контактные напряжения обычно нелинейно зависит от деформации. Для упрощения процедур решения обычно используется система отсчета, в которой используются объекты (возможно, движущиеся относительно друг друга) статичны. Они взаимодействуют посредством поверхностного натяжения (или давления / напряжения) на их границе раздела.

В качестве примера рассмотрим два объекта, которые встречаются на некоторой поверхности $S\; \{\backslash \; displaystyle\; S\}$в ($x\; \{\backslash \; displaystyle\; x\}$,$y\; \{\backslash \; displaystyle\; y\}$) с осью $z\; \{\backslash \; displaystyle\; z\}$, перпендикулярной поверхности. Одно из тел выполняет нормально направленное давление распределение $pz\; =\; p\; (x,\; y)\; =\; qz\; (x,\; y)\; \{\backslash \; displaystyle\; p\_\; \{z\}\; =\; p\; (x,\; y)\; =\; q\_\; \{z\; \}\; (x,\; y)\}$и распределение сцепления в плоскости на поверхности $qx\; =\; qx\; (x,\; y)\; \{\backslash \; displaystyle\; q\_\; \{x\}\; =\; q\_\; \{x\}\; (\; x,\; y)\}$и $qy\; =\; qy\; (x,\; y)\; \{\backslash \; displaystyle\; q\_\; \{y\}\; =\; q\_\; \{y\}\; (x,\; y)\}$по региону $S\; \{\backslash \; Displaystyle\; S\}$. В терминах баланса ньютоновских сил, силы:

$P\; z\; =\; \int \; S\; p\; (x,\; y)\; d\; A;\; Q\; x\; =\; \int \; S\; q\; x\; (x,\; y)\; d\; A;\; Q\; Y\; знак\; равно\; \int \; S\; qy\; (x,\; y)\; d\; A\; \{\backslash \; displaystyle\; P\_\; \{z\}\; =\; \backslash \; int\; \_\; \{S\}\; p\; (x,\; y)\; ~\; \backslash \; mathrm\; \{d\}\; A\; ~;\; ~~\; Q\_\; \{x\}\; =\; \backslash \; int\; \_\; \{S\}\; q\_\; \{x\}\; (x,\; y)\; ~\; \backslash \; mathrm\; \{d\}\; A\; ~;\; ~~\; Q\_\; \{y\}\; =\; \backslash \; int\; \_\; \{S\}\; q\_\; \{y\}\; (x,\; y)\; ~\; \backslash \; mathrm\; \{d\}\; A\}$

должно быть равным и противоположным силойм, установленным в другом теле. Моменты, соответствующие этой силе:

$M\; x\; =\; \int \; S\; y\; q\; z\; (x,\; y)\; d\; A;\; M\; y\; =\; \int \; S\; -\; x\; q\; z\; (x,\; y)\; d\; A;\; Знак\; MZ\; равно\; \int \; S\; [xqy\; (x,\; y)\; -\; yqx\; (x,\; y)]\; d\; A\; \{\backslash \; displaystyle\; M\_\; \{x\}\; =\; \backslash \; int\; \_\; \{S\}\; y\; ~\; q\_\; \{z\}\; (x,\; y)\; ~\; \backslash \; mathrm\; \{d\}\; A\; ~;\; ~~\; M\_\; \{y\}\; =\; \backslash \; int\; \_\; \{S\}\; -x\; ~\; q\_\; \{z\}\; (x,\; y)\; ~\; \backslash \; mathrm\; \{d\}\; A\; ~;\; ~~\; M\_\; \{z\}\; =\; \backslash \; int\; \_\; \{S\}\; [x\; ~\; q\_\; \{y\}\; (x,\; y)\; -y\; ~\; q\_\; \{x\}\; (x,\; y)]\; ~\; \backslash \; mathrm\; \{d\}\; A\}$

также требуется для отмены между телами, чтобы они кинематически неподвижен.

Допущения теории Герца

При формировании решений контактных задач Герца делаются следующие допущения:

• образования малы и находятся в пределах упругости.
• Поверхности сплошные и не соответствуют друг другу (это означает, что площадь контакта намного меньше характерных размеров контактирующих тел).
• Каждое тело можно рассматривать как упругое полупространство.
• Поверхности не имеют трения.

Дополнительные сложности, когда некоторые или все эти проблемы допущения нарушаются, и такие проблемы с контактом обычно называют негерцевскими .

методами аналитического решения

Контакт между двумя сферами.

Аналитические методы решения проблемы неклейкого контакта можно разделить на два типа в зависимости от геометрии области контакта. Соответствующий контакт - это контакт, при котором два тела соприкасаются в нескольких точках до того, как происходит какая-либо деформация (т.е. они просто «подходят друг к другу»). несоответствующий контакт - это контакт, в котором достаточно различны, поэтому при нулевой нагрузке они касаются только в точке (или, возможно, вдоль линии). В случае несоответствия площади контакта по сравнению с размерами объектов, и напряжения сконцентрированы в этой области. Такой контакт называется концентрированным, иначе - разноплановым.

Обычный подход в линейной упругости состоит в наложении ряда решений, каждое из которых соответствует точечной нагрузке, действующей по площади контакта. Например, в случае нагружения полуплоскости решение Flamant часто используется в качестве отправной точки, а затем обобщается на различные формы области контакта. Балансы сил и моментов между двумя контактирующими телами действуют как дополнительные ограничения для решения.

Точечный контакт на (2D) полуплоскости

Схема нагружения на плоскости силой P в точке (0, 0).

Отправной точкой для решения проблем контакта является понять эффект «точечной нагрузки», приложенной к изотропной, однородной и линейной упругой полуплоскости, показанной на рисунке справа. Проблема может заключаться в плоском напряжении или плоской деформации. Это краевая задача линейной упругости с учетом тяги граничных условий :

$\sigma \; x\; z\; (x,\; 0)\; =\; 0;\; \sigma \; Z\; (Икс,\; Z)\; знак\; равно\; -\; п\; \delta \; (Икс,\; Z)\; \{\backslash \; Displaystyle\; \backslash \; sigma\; \_\; \{xz\}\; (х,\; 0)\; =\; 0\; ~;\; ~~\; \backslash \; sigma\; \_\; \{z\}\; (x,\; z)\; =\; -\; P\; \backslash \; delta\; (x,\; z)\}$

где $\delta \; (x,\; z)\; \{\backslash \; displaystyle\; \backslash \; delta\; (x,\; z)\}$- это дельта-функция Дирака. Граничные условия утверждают, что на поверхности нет касательных напряжений и дает в точке (0, 0) приложена сингулярная нормальная сила P. Применение этих условий к основным уравнениям упругости результат

$\sigma \; xx\; =\; -\; 2\; P\; \pi \; x\; 2\; z\; (x\; 2\; +\; z\; 2)\; 2\; \sigma \; zz\; знак\; равно\; -\; 2\; п\; \pi \; z\; 3\; (x\; 2\; +\; z\; 2)\; 2\; \sigma \; xz\; =\; -\; 2\; п\; \pi \; xz\; 2\; (x\; 2\; +\; z\; 2)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sigma\; \_\; \{xx\}\; =\; -\; \{\backslash \; frac\; \{2P\}\; \{\backslash \; pi\}\}\; \{\backslash \; frac\; \{x\; ^\; \{2\}\; z\}\; \{\backslash \; left\; (x\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right)\; ^\; \{2\}\; \}\}\; \backslash \backslash \backslash \; sigma\; \_\; \{zz\}\; =\; -\; \{\backslash \; frac\; \{2P\}\; \{\backslash \; pi\}\}\; \{\backslash \; frac\; \{z\; ^\; \{3\}\}\; \{\backslash \; left\; (x\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; справа)\; ^\; \{2\}\}\}\; \backslash \backslash \backslash \; sigma\; \_\; \{xz\}\; =\; -\; \{\backslash \; frac\; \{2P\}\; \{\backslash \; pi\}\}\; \{\backslash \; frac\; \{xz\; ^\; \{2\}\}\; \{\backslash \; left\; (x\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right)\; ^\; \{2\}\}\}\; \backslash \; end\; \{выравнивается\}\}\}$

для некоторой точки, $(x,\; y)\; \{\backslash \; displaystyle\; (x,\; y)\}$, в полуплоскости. Круг, показанный на рисунке, указывает на поверхность, на максимальное напряжение сдвига постоянно. Из этого поля напряжений и таким образом быть связаны компоненты деформации, с ущербом всех материальных точек.

Линейный контакт на (2D) полуплоскости

Нормальная нагрузка в области $(a,\; b)\; \{\backslash \; displaystyle\; (a,\; b)\}$

Предположим, скорее чем точечная нагрузка $P\; \{\backslash \; displaystyle\; P\}$, вместо этого к применяемой распределенной нагрузке $p\; (x)\; \{\backslash \; displaystyle\; p\; (x)\}$, в диапазоне . Принцип линейной суперпозиции может использоваться для определения результирующего поля напряжений как решения интегральных уравнений:

$\sigma \; xx\; =\; -\; 2\; z\; \pi \; \int \; abp\; (x\; \prime )\; (x\; -\; x\; \prime )\; 2\; dx\; \prime \; [(x\; -\; х\; \text{'})\; 2\; +\; z\; 2]\; 2;\; \sigma \; zz\; =\; -\; 2\; z\; 3\; \pi \; \int \; abp\; (x\; \prime )\; dx\; \prime \; [(x\; -\; x\; \prime )\; 2\; +\; z\; 2]\; 2\; \sigma \; xz\; =\; -\; 2\; z\; 2\; \pi \; \int \; abp\; (x\; \prime )\; (x\; -\; x\; \prime )\; dx\; \prime \; [(Икс\; -\; Икс)\; 2\; +\; Z\; 2]\; 2\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{Выровнено\}\; \backslash \; sigma\; \_\; \{xx\}\; =\; -\; \{\backslash \; frac\; \{2z\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{\; b\}\; \{\backslash \; frac\; \{p\; \backslash \; left\; (x\; \text{'}\backslash \; right)\; \backslash \; left\; (xx\text{'}\; \backslash \; right)\; ^\; \{2\}\; \backslash ,\; dx\; \text{'}\}\; \{\backslash \; left\; [\backslash \; left\; (xx\text{'}\; \backslash \; right)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right]\; ^\; \{2\}\}\}\; ~;\; ~~\; \backslash \; sigma\; \_\; \{zz\}\; =\; -\; \{\backslash \; frac\; \{2z\; ^\; \{3\}\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \{\backslash \; frac\; \{p\; \backslash \; left\; (x\; \text{'}\backslash \; right)\; \backslash ,\; dx\; \text{'}\}\; \{\backslash \; left\; [\backslash \; left\; (xx\text{'}\; \backslash \; right)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right]\; ^\; \{2\}\}\}\; \backslash \backslash \; [3pt]\; \backslash \; sigma\; \_\; \{xz\}\; =\; -\; \{\backslash \; frac\; \{2z\; ^\; \{2\}\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \{\backslash \; frac\; \{p\; \backslash \; left\; (x\; \text{'}\backslash \; right)\; \backslash \; left\; (xx\text{'}\; \backslash \; right)\; \backslash ,\; dx\; \text{'}\}\; \{\; \backslash \; left\; [\backslash \; left\; (xx\; \text{'}\backslash \; right)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right]\; ^\; \{2\}\}\}\; \backslash \; end\; \{align\}\}\}$

Сдвиговая нагрузка по области $(a,\; б)\; \{\backslash \; displaystyle\; (a,\; b)\}$

Тот же принцип работы для нагрузки на поверхность в плоскости поверхности. Эти виды сцепления могут возникнуть в результате трения. Решение аналогично приведенному выше (как для единичных нагрузок $Q\; \{\backslash \; displaystyle\; Q\}$, так и для распределенных нагрузок $q\; (x)\; \{\backslash \; displaystyle\; q\; (x)\}$), но с небольшими изменениями:

$\sigma \; xx\; =\; -\; 2\; \pi \; \int \; abq\; (x\; \prime )\; (x\; -\; x\; \prime )\; 3\; dx\; \prime \; [(x\; -\; x\; \prime )\; 2\; +\; z\; 2]\; 2;\; \sigma \; zz\; =\; -\; 2\; z\; 2\; \pi \; \int \; abq\; (x\; \prime )\; (x\; -\; x\; \prime )\; dx\; \prime \; [(x\; -\; x\; \prime )\; 2\; +\; z\; 2]\; 2\; \sigma \; xz\; =\; -\; 2\; z\; \pi \; \int \; abq\; (x\; \prime )\; (x\; -\; x\; \prime )\; 2\; dx\; \prime \; [(x\; -\; x\; \prime )\; 2\; +\; z\; 2]\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; sigma\; \_\; \{xx\}\; =\; -\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \{\backslash \; frac\; \{q\; \backslash \; left\; (x\; \text{'}\backslash \; right)\; \backslash \; left\; (xx\text{'}\; \backslash \; right)\; ^\; \{3\}\; \backslash ,\; dx\; \text{'}\}\; \{\backslash \; left\; [\backslash \; left\; (x-\; x\text{'})\; \backslash \; right)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right]\; ^\; \{2\}\}\}\; ~;\; ~~\; \backslash \; sigma\; \_\; \{zz\}\; =\; -\; \{\backslash \; frac\; \{2z\; ^\; \{2\}\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \{\backslash \; frac\; \{q\; \backslash \; left\; (x\; \text{'}\backslash \; right)\; \backslash \; left\; (xx\; \text{'}\backslash \; right)\; \backslash ,\; dx\text{'}\}\; \{\backslash \; left\; [\backslash \; left\; (xx\; \text{'}\backslash \; right)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right]\; ^\; \{2\}\}\}\; \backslash \backslash \; [3pt]\; \backslash \; sigma\; \_\; \{xz\}\; =\; -\; \{\backslash \; frac\; \{2z\}\; \{\backslash \; pi\}\}\; \backslash \; int\; \_\; \{a\}\; ^\; \{b\}\; \{\backslash \; frac\; \{q\; \backslash \; left\; (x\; \text{'}\backslash \; right)\; \backslash \; left\; (xx\text{'}\; \backslash \; right)\; ^\; \{\; 2\}\; \backslash ,\; dx\; \text{'}\}\; \{\backslash \; left\; [\backslash \; left\; (x-x\text{'})\; \backslash \; right)\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; \backslash \; right]\; ^\; \{2\}\}\}\; \backslash \; end\; \{align\}\}\}$

Эти результаты могут быть наложены на результаты выше, для нормальной загрузки, чтобы справиться с более сложными нагрузками.

Точечный контакт в (3D) полупространстве

Аналогично решение Flamant для 2D полуплоскости, фундаментальные решения известны и для линейно упругого 3D полупространства. Они были обнаружены Буссинеском для концентрированной нормальной нагрузки и Черрути для тангенциальной нагрузки. См. Раздел по этому вопросу в Линейная упругость.

Методы численного

При использовании схем численного решения для контактных проблем не нужно делать различия между и несоответствующим контактом. Эти методы не основаны на предположениях в процессе решения, поскольку они основаны исключительно на общих основаниях. Помимо стандартных правил, описывающих деформацию и движение тел, можно указать два дополнительных неравенства. Первый просто ограничивает движение и деформацию, предполагаемая, что проникновение. Следовательно, зазор $h\; \{\backslash \; displaystyle\; h\}$между двумя телами может быть только положительным или нулевым

$h\; \ge \; 0\; \{\backslash \; displaystyle\; h\; \backslash \; geq\; 0\}$

где $h\; =\; 0\; \{\backslash \; displaystyle\; h\; =\; 0\}$обозначает контакт. Второе допущение в механике связано с тем, что в зоне контакта не должно возникать силы натяжения (контактирующие тела можно поднимать без сил сцепления). Это приводит к неравенству. Он разработан для нормального напряжения $\sigma \; n\; =\; t\; \cdot \; n\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{n\}\; =\; \backslash \; mathbf\; \{t\}\; \backslash \; cdot\; \backslash \; mathbf\; \{n\}\}$.

в местах, где есть контакт между на поверхности зазор равенство нулю, то есть $h\; =\; 0\; \{\backslash \; displaystyle\; h\; =\; 0\}$, и там нормальное напряжение отличается от нуля, действительно, . В местах, где поверхности не соприкасаются, нормальное напряжение равно нулю; $\sigma \; N\; =\; 0\; \{\backslash \; Displaystyle\; \backslash \; sigma\; \_\; \{n\}\; =\; 0\}$, разрыв положительный; т.е. $h>0\; \{\backslash \; displaystyle\; h>0\}$. Этот тип формулировки комплементарности может быть выражен в так называемой форме Куна - Такера, а именно

$h\; \ge \; 0,\; \sigma \; n\; \le \; 0,\; \sigma \; NH\; знак\; равно\; 0,\; \{\backslash \; Displaystyle\; ч\; \backslash \; GEQ\; 0\; \backslash ,,\; \backslash \; quad\; \backslash \; sigma\; \_\; \{n\}\; \backslash \; leq\; 0\; \backslash ,,\; \backslash \; quad\; \backslash \; sigma\; \_\; \{n\}\; \backslash ,\; h\; =\; 0\; \backslash ,.\}$

Эти условия Математическая формулировка зазора зависит от кинематики лежащей в основе теории твердого тела (например, линейное или нелинейное твердое тело в двух- или трех измерениях, балка или оболочка модель). Пересчитав нормальное напряжение $\sigma \; n\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{n\}\}$с точки зрения контактного давления, $p\; \{\backslash \; displaystyle\; p\}$; т. Е. $p\; =\; -\; \sigma \; n\; \{\backslash \; displaystyle\; p\; =\; -\; \backslash \; sigma\; \_\; \{n\}\}$проблема Куна-Такера может быть переформулиро вана как в стандартной комплементарности форма, т.е.

$h\; \ge \; 0,\; p\; \ge \; 0,\; ph\; =\; 0.\; \{\backslash \; di\; splaystyle\; h\; \backslash \; geq\; 0\; \backslash ,,\; \backslash \; quad\; p\; \backslash \; geq\; 0\; \backslash ,,\; \backslash \; quad\; p\; \backslash ,\; h\; =\; 0\; \backslash ,.\}$В линейно-упругом случае зазор можно сформулировать как $h\; =\; h\; 0\; +\; g\; +\; u,\; \{\backslash \; displaystyle\; \{h\}\; =\; h\_\; \{0\}\; +\; \{g\}\; +\; u,\}$где $h\; 0\; \{\backslash \; displaystyle\; h\_\; \{0\}\}$- жесткий разделение тела, $g\; \{\backslash \; displaystyle\; g\}$- это геометрия / топография контакта (цилиндр и шероховатость), а $u\; \{\backslash \; displaystyle\; u\}$- эластичная деформация / прогиб. Если контактирующие тела аппроксимированы линейными упругими полупространствами, решение интегрального уравнения Буссинеска-Черрути может быть применено для выражения деформации ($u\; \{\backslash \; displaystyle\; u\}$) как функции контактного давления ($п\; \{\backslash \; displaystyle\; p\; \}$); т. е. $U\; знак\; равно\; \int \; \infty \; \infty \; К\; (х\; -\; s)\; п\; (s)\; ds,\; \{\backslash \; displaystyle\; u\; =\; \backslash \; int\; \_\; \{\backslash \; infty\}\; ^\; \{\backslash \; infty\}\; K\; (xs)\; p\; (s)\; ds,\}$где $K\; (x\; -\; s)\; =\; 2\; \pi \; E\; \ast \; ln\; \; |\; х\; -\; с\; |\; \{\backslash \; displaystyle\; K\; (xs)\; =\; \{\backslash \; frac\; \{2\}\; \{\backslash \; pi\; E\; ^\; \{*\}\}\}\; \backslash \; ln\; |\; xs\; |\}$для линейной загрузки эластичного полупространства и $K\; (x\; -\; s)\; Знак\; равно\; 1\; \pi \; E\; \ast \; 1\; (Икс\; 1\; -\; s\; 1)\; 2\; +\; (Икс\; 2\; -\; s\; 2)\; 2\; \{\backslash \; Displaystyle\; K\; (\; xs)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; pi\; E\; ^\; \{*\}\}\}\; \{\backslash \; гидроразрыв\; \{1\}\; \{\backslash \; sqrt\; \{\backslash \; left\; (x\_\; \{1\}\; -s\_\; \{1\}\; \backslash \; right)\; ^\; \{2\}\; +\; \backslash \; left\; (x\_\; \{2\}\; -s\_\; \{2\}\; \backslash \; right)\; ^\; \{2\}\}\}\}\}$для точечного нагружения упругого полупространства.

После дискретизации задачи линейной упругой контактной механики может быть сформулирована в стандартной форме задачи линейной дополнительности (LCP).

$час\; =\; час\; 0\; +\; g\; +\; C\; p\; час\; \cdot \; п\; знак\; равно\; 0,\; п\; \ge \; 0,\; час\; \ge \; 0,\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; \backslash \; mathbf\; \{h\}\; =\; \backslash \; mathbf\; \{h\}\; \_\; \{0\}\; +\; \backslash \; mathbf\; \{g\}\; +\; \backslash \; mathbf\; \{Cp\},\; \backslash \backslash \backslash \; mathbf\; \{h\}\; \backslash \; cdot\; \backslash \; mathbf\; \{p\}\; =\; 0,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathbf\; \{p\}\; \backslash \; geq\; 0,\; \backslash ,\; \backslash ,\; \backslash ,\; \backslash \; mathbf\; \{h\}\; \backslash \; geq\; 0,\; \backslash \backslash \backslash \; end\; \{align\}\}\}$

где $C\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{C\}\}$- матрица, элементы, которые связывают контактное давление и деформация. Представленная выше строгая формулировка задачи LCP CM позволяет напрямую применять хорошо зарекомендовавшие себя численные методы решения, такие как алгоритм поворота Лемке. Преимущество алгоритма Лемке в том, что он находит численно точное решение за конечное число итераций. Реализация MATLAB, представленная Алмквистом и др., является одним из примеров, который можно использовать для численного решения проблемы. Кроме того, пример кода для LCP-решения задачи механики линейного упругого контакта 2D также опубликован при обмене файлов MATLAB Альмквистом и др.

Когда два тела с шероховатой поверхностью прижимаются друг к другу, истинная площадь контакта, образованная между двумя телами, $A\; \{\backslash \; displaystyle\; A\}$, намного меньше, чем кажущаяся или номинальная площадь контакта $A\; 0\; \{\backslash \; displaystyle\; A\_\; \{0\}\}$. Механика контакта с шероховатыми поверхностями обсуждается с точки зрения механики контакта и статических фрикционных взаимодействий. Природные и инженерные поверхности обычно демонстрируют особенности шероховатости, известные как неровности, в широком диапазоне масштабов длины до молекулярного уровня, при этом поверхностные структуры демонстрируют само сродство, также известное как фрактальность поверхности. Признано, что самоаффинная поверхность является средством линейного масштабирования истинной площади контакта с приложенным давлением. Допуская модель сдвига сварных контактов в трибологических взаимодействий, эту повсеместно наблюдаемую линейность между площадью контакта и давлением также можно рассматривать как источник линейности зависимости между статическим трением и приложенной нормальной силой.

При контакте между «случайной шероховатой» поверхностью и упругим полупространством истинная площадь взаимодействия с нормальной силой $F\; \{\backslash \; displaystyle\; F\}$by

$A\; =\; \kappa \; E\; \ast \; h\; \prime \; F\; \{\backslash \; displaystyle\; A\; =\; \{\; \backslash \; frac\; \{\backslash \; kappa\}\; \{E\; ^\; \{*\}\; h\; \text{'}\}\}\; F\}$

с $h\; \prime \; \{\backslash \; displaystyle\; h\text{'}\}$равным среднеквадратичному (известное также как среднее квадратичное) уклона поверхности и $\kappa \; \approx \; 2\; \{\backslash \; displaystyle\; \backslash \; kappa\; \backslash \; приблизительно\; 2\}$. Среднее давление на истинной контактной поверхности

$pav\; =\; FA\; \approx \; 1\; 2\; E\; \ast \; h\; \prime \; \{\backslash \; displaystyle\; p\; \_\; \{\backslash \; mathrm\; \{av\}\}\; =\; \{\backslash \; frac\; \{F\}\; \{A\}\}\; \backslash \; приблизительно\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; E\; ^\; \{*\}\; h\; \text{'}\}$

можно разумно оценить как половину эффективного модуля упругости $E\; \ast \; \{\backslash \; displaystyle\; E\; ^\; \{*\}\}$, умнож на средний квадрат уклона поверхности $h\; \prime \; \{\backslash \; displaystyle\; h\; \text{'}\}$.

Обзор модели GW

Гринвуд и Уильямсон в 1966 г. (GW) предложили теорию механики упругого контакта грубых поверхностей, которые сегодня составляют теорий трибологии (трение, адгезия, тепловая и электрическая проводимость, износ и т. Д.). Они рассмотрели контакт между гладкой жесткой плоскостью и номинально плоской деформируемой шероховатой поверхностью, покрытой круглыми выступами на вершине того же радиуса R. Их теория предполагает, что деформация каждой выступающей части не зависит от деформации ее соседей и описывается моделью Герца.. Высота выступов распределена случайным образом. Вероятность того, что высота выступов находится между $z\; \{\backslash \; displaystyle\; z\}$и $z\; +\; dz\; \{\backslash \; displaystyle\; z\; +\; dz\}$, равна $\varphi \; (z)\; dz\; \{\backslash \; displaystyle\; \backslash \; phi\; (z)\; dz\}$. Авторы рассчитали количество пятен контакта n, общую площадь контакта $A\; r\; \{\backslash \; displaystyle\; A\_\; \{r\}\}$и общую нагрузку P в общем случае. Они представили эти формулы в двух формах: в базовой и с использованием стандартизованных переменных. Если предположить, что N выступов покрывают шероховатую поверхность, то ожидаемое количество контактов будет

$n\; =\; N\; \int \; d\; \infty \; \varphi \; (z)\; dz\; \{\backslash \; displaystyle\; n\; =\; N\; \backslash \; int\; \_\; \{d\}\; ^\; \{\backslash \; infty\}\; \backslash \; phi\; (z)\; dz\}$

Ожидаемую общую площадь контакта можно рассчитать по формуле

$A\; a\; =\; N\; \pi \; R\; \int \; d\; \infty \; (z\; -\; d)\; \varphi \; (z)\; dz\; \{\backslash \; displaystyle\; A\_\; \{a\}\; =\; N\; \backslash \; pi\; R\; \backslash \; int\; \_\; \{d\}\; ^\; \{\backslash \; infty\}\; (zd)\; \backslash \; phi\; (z)\; dz\}$

, а ожидаемая общая сила определяется как

$P\; =\; 4\; 3\; NE\; r\; R\; \int \; d\; \infty \; (z\; -\; d)\; 3\; 2\; \varphi \; (z)\; dz\; \{\backslash \; displaystyle\; P\; =\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; NE\_\; \{r\}\; \{\backslash \; sqrt\; \{R\}\}\; \backslash \; int\; \_\; \{d\}\; ^\; \{\backslash \; infty\}\; (\; zd)\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash \; phi\; (z)\; dz\}$

где:

R, радиус кривизны микровыступа,

z, высота измеренного микровыступа от линии профиля,

d, закрыть поверхность,

$E\; r\; =\; (1\; -\; \nu \; 1\; 2\; E\; 1\; +\; 1\; -\; \nu \; 2\; 2\; E\; 2)\; -\; 1\; \{\backslash \; displaystyle\; E\_\; \{r\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{1-\; \backslash \; nu\; \_\; \{1\}\; ^\; \{2\}\}\; \{E\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1-\; \backslash \; nu\; \_\; \{2\}\; ^\; \{2\}\}\; \{E\_\; \{2\})\; \}\}\; \backslash \; right)\; ^\; \{-\; 1\}\}$, модуль упругости составного Юнга,

$E\; i\; \{\backslash \; displaystyle\; E\_\; \{i\}\}$, модуль упругости поверхности лицо,

$\nu \; i\; \{\backslash \; displaystyle\; \backslash \; nu\; \_\; \{i\}\}$, поверхностные коэффициенты Пуассона.

Они ввели стандартизированное разделение $h\; =\; d\; /\; \sigma \; \{\backslash \; displaystyle\; h\; =\; d\; /\; \backslash \; sigma\}$и стандартизированное распределение высот $\varphi \; \ast \; (s)\; \{\backslash \; displaystyle\; \backslash \; phi\; ^\; \{*\}\; (s)\}$, стандартное отклонение которого равно единице. Ниже представлены формулы в стандартизованном виде.

$F\; n\; (h)\; =\; \int \; h\; \infty \; (s\; -\; h)\; n\; \varphi \; \ast \; (s)\; dsn\; =\; \eta \; A\; n\; F\; 0\; (h)\; A\; a\; =\; \pi \; \eta \; AR\; \sigma \; F\; 1\; (h)\; P\; =\; 4\; 3\; \eta \; AE\; р\; р\; \sigma \; 3\; 2\; F\; 3\; 2\; (час)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{выровнено\}\; F\_\; \{n\}\; (h)\; =\; \backslash \; int\; \_\; \{h\}\; ^\; \{\backslash \; infty\}\; (sh)\; ^\; \{n\}\; \backslash \; phi\; ^\; \{*\}\; (s)\; ds\; \backslash \backslash \; n\; =\; \backslash \; eta\; A\_\; \{n\}\; F\_\; \{0\}\; (h)\; \backslash \backslash \; A\_\; \{a\}\; =\; \backslash \; pi\; \backslash \; eta\; AR\; \backslash \; sigma\; F\_\; \{1\}\; (h)\; \backslash \backslash \; P\; =\; \{\backslash \; frac\; \{4\}\; \{3\}\}\; \backslash \; eta\; AE\_\; \{r\}\; \{\backslash \; sqrt\; \{R\}\}\; \backslash \; sigma\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; F\; \_\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; (h)\; \backslash \; end\; \{align\}\}\}$

где:

d - расстояние,

$A\; \{\backslash \; displaystyle\; A\}$- номинальная площадь контакта,

$\eta \; \{\backslash \; displaystyle\; \backslash \; eta\}$- поверхностная плотность неровностей,

$E\; \ast \; \{\backslash \; displaystyle\; E\; ^\; \{*\}\}$- эффективный модуль Юнга.

В последнее время точное приближение к $A\; r\; \{\backslash \; displaystyle\; A\_\; \{r\}\}$и $P\; \{\backslash \; displaystyle\; P\}$были опубликованы Jedynak. Они задаются следующими рациональными формулами, которые являются очень точными приближениями к интегралам $F\; n\; (h)\; \{\backslash \; displaystyle\; F\_\; \{n\}\; (h)\}$. Они рассчитаны для гауссова распределения неровностей

$F\; n\; (h)\; =\; a\; 0\; +\; a\; 1\; h\; +\; a\; 2\; h\; 2\; +\; a\; 3\; h\; 3\; 1\; +\; b\; 1\; h\; +\; b\; 2\; h\; 2\; +\; b\; 3\; h\; 3\; +\; б\; 4\; час\; 4\; +\; b\; 5\; час\; 5\; +\; b\; 6\; час\; 6\; ехр\; \; (-\; час\; 2\; 2)\; \{\backslash \; displaystyle\; F\_\; \{n\}\; (h)\; =\; \{\backslash \; frac\; \{a\_\; \{0\}\; +\; a\_\; \{1\}\; h\; +\; a\_\; \{\; 2\}\; h\; ^\; \{2\}\; +\; a\_\; \{3\}\; h\; ^\; \{3\}\}\; \{1\; +\; b\_\; \{1\}\; h\; +\; b\_\; \{2\}\; h\; ^\; \{2\}\; +\; b\_\; \{3\}\; h\; ^\; \{3\}\; +\; b\_\; \{4\; \}\; h\; ^\; \{4\}\; +\; b\_\; \{5\}\; h\; ^\; \{5\}\; +\; b\_\; \{6\}\; h\; ^\; \{6\}\}\}\; \backslash \; exp\; \backslash \; left\; (-\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; right)\}$

Для $F\; 1\; (h)\; \{\backslash \; displaystyle\; F\_\; \{1\}\; (h)\}$коэффициенты

$[a\; 0,\; a\; 1,\; a\; 2,\; a\; 3]\; =\; [0,398942280401,\; 0,159773702775,\; 0,0389687688311,\; 0,00364356495452]\; [b\; 1,\; b\; 2,\; b\; 3,\; b\; 4,\; b\; 5,\; b\; 6]\; =\; [1,653807476138,\; 1,170419428529,\; 0,448892964428,\; 0,0951971709160,\; 0,003692964428,\; 0,0951971709160,\; 0,00369389\; -\; 6,34280\; \backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; [a\_\; \{0\},\; a\_\; \{1\},\; a\_\; \{2\},\; a\_\; \{3\}]\; =\; [0.398942280401,0.159773702775,0.0389687688311,0.00364356495452]\; \backslash \backslash \; [b\_\; \{1\},\; b\_\; \{2\; \},\; b\_\; \{3\},\; b\_\; \{4\},\; b\_\; \{5\},\; b\_\; \{6\}]\; =\; \backslash \; left\; [1.653807476138,1.170419428529,0.448892964428,0.0951971709160,0.00931642803836,\; -6.383774657279\; \backslash \; times\; 10\; ^\; \{-\; 6\}\; \backslash \; right]\; \backslash \; end\; \{ali\; gned\}\}\}$

Максимальная относительная ошибка составляет $9.93\; \times \; 10-8\%\; \{\backslash \; displaystyle\; 9.93\; \backslash \; times\; 10\; ^\; \{-\; 8\}\; \backslash \%\}$.

Для $F\; 3\; 2\; (h)\; \{\; \backslash \; displaystyle\; F\; \_\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; (h)\}$коэффициенты:

$[a\; 0,\; a\; 1,\; a\; 2,\; a\; 3]\; =\; [0.430019993662,\; 0.101979509447,\; 0.0229040629580,\; 0.000688602924\; ]\; [b\; 1,\; b\; 2,\; b\; 3,\; b\; 4,\; b\; 5,\; b\; 6]\; =\; [1,671117125984,\; 1,199586555505,\; 0,46936532151,\; 0,102632881122,\; 0,010686348714,\; 0,0000517200271]\; \{\backslash \; displaystyle\; \{\; \backslash \; begin\; \{align\}\; [a\_\; \{0\},\; a\_\; \{1\},\; a\_\; \{2\},\; a\_\; \{3\}]\; =\; [0.430019993662,0.101979509447,0.0229040629580,0.000688602924]\; \backslash \backslash \; [b\_\; \{1\},\; b\_\; \{2\},\; b\_\; \{3\},\; b\_\; \{4\},\; b\_\; \{5\},\; b\_\; \{6\}]\; =\; [1.671117125984,1.199586555505,\; 0.46936532151,0.102632881122,0.010686348714,0.0000517200271]\; \backslash \; end\; \{align\}\}$

Максимальная относительная ошибка $1.91\; \times \; 10-7\%\; \{\backslash \; displaystyle\; 1.91\; \backslash \; times\; 10\; ^\; \{-\; 7\}\; \backslash \%\}$. В документе также используются точные выражения для $F\; n\; (h)\; \{\backslash \; displaystyle\; F\_\; \{n\}\; (h)\}$

$F\; 1\; (h)\; =\; 1\; 2\; \pi \; exp\; \; (-\; 1\; 2\; h\; 2)\; -\; 1\; 2\; h\; erfc\; \; (h\; 2)\; F\; 3\; 2\; (h)\; =\; 1\; 4\; \pi \; exp\; \; (-\; h\; 2\; 4)\; h\; ((h\; 2\; +\; 1)\; K\; 1\; 4\; (h\; 2\; 4)\; -\; h\; 2\; K\; 3\; 4\; (h\; 2\; 4))\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; F\_\; \{1\}\; (h)\; =\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; \backslash \; exp\; \backslash \; left\; (-\; \{\backslash \; frac\; \{1\}\; \{\; 2\}\}\; h\; ^\; \{2\}\; \backslash \; right)\; -\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; h\; \backslash ,\; \backslash \; operatorname\; \{erfc\}\; \backslash \; left\; (\{\backslash \; frac\; \{h\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; right)\; \backslash \backslash \; F\; \_\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; (h)\; =\; \{\backslash \; frac\; \{1\}\; \{4\; \{\backslash \; sqrt\; \{\backslash \; pi\}\}\}\}\; \backslash \; exp\; \backslash \; left\; (-\; \{\backslash \; frac\; \{h\; ^\; \{\; 2\}\}\; \{4\}\}\; \backslash \; right)\; \{\backslash \; sqrt\; \{h\}\}\; \backslash \; left\; (\backslash \; left\; (h\; ^\; \{2\}\; +1\; \backslash \; right)\; K\; \_\; \{\backslash \; frac\; \{1\}\; \{4\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\; -h\; ^\; \{2\}\; K\; \_\; \{\backslash \; frac\; \{3\}\; \{4\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\; \backslash \; right)\; \backslash \; end\; \{align\}\}\}$

где erfc (z) означает дополнительную функцию ошибок, а $K\; \nu \; (z)\; \{\backslash \; displaystyle\; K\; \_\; \{\backslash \; nu\}\; (z)\}$- модифицированная функция Бесселя второго рода.

Для ситуаций, когда неровности на двух поверхностях имеют распределение по высоте, а пики можно считать сферическими, средним контактным давлением достаточно, чтобы вызвать текучесть, когда $p\; av\; =\; 1,1\; \sigma \; y\; \approx \; 0,\; 39\; \sigma \; 0\; \{\backslash \; displaystyle\; p\; \_\; \{\backslash \; text\; \{av\}\}\; =\; 1.1\; \backslash \; sigma\; \_\; \{y\}\; \backslash \; приблизительно\; 0,39\; \backslash \; sigma\; \_\; \{0\}\}$где $\sigma \; y\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{y\}\}$- одноосный предел текучести и $\sigma \; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{0\}\}$- твердость при вдавливании. Гринвуд и Уильямсон определили безразмерный параметр $\Psi \; \{\backslash \; displaystyle\; \backslash \; Psi\}$, названный индексом пластичности, который можно использовать для определения того, будет ли контакт эластичным или пластичным.

Модель Гринвуда-Уильямсона требует знания двух статистически зависимых величин; стандартное отклонение шероховатости поверхности и кривизны выступов неровностей. Альтернативное определение пластичности было дано Микичем. Податливость возникает, когда давление превышает одноосный предел текучести. Предел текучести пропорционален твердости при вдании $\sigma \; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{0\}\}$, Микич определил индекс пластичности для упруго-пластического контакта как

$\Psi \; =\; E\; \ast \; h\; \prime \; \sigma \; 0>2\; 3.\; \{\backslash \; displaystyle\; \backslash \; Psi\; =\; \{\backslash \; frac\; \{E\; ^\; \{*\}\; h\; \text{'}\}\; \{\backslash \; sigma\; \_\; \{0\}\}\}>\{\backslash \; frac\; \{2\}\; \{3\}\}\; ~.\}$

В этом определении $\Psi \; \{\backslash \; displaystyle\; \backslash \; Psi\}$представляет микрошероховатость в состоянии полной пластичности, требуется только одна статистическая, из, среднеквадратичная, статистическая, среднеквадратичная. система упруго во время контакта.

в соответствии с нагрузкой на нагрузку деформированной площади. от приложенной нормальной силы.

Обзор модели GT

Модель, предложенная Гринвудом и Триппом (GT), расширила модель GW на контакт между двумя шероховатыми поверхностями. Модель GT широко используется в области эластогидродинамического анализа.

Наиболее часто цитируемые уравнения, приводимые в модели GT, относятся к области контакта неровностей

$A\; a\; =\; \pi \; 2\; (\eta \; \beta \; \sigma )\; 2\; AF\; 2\; (\lambda ),\; \{\backslash \; displaystyle\; A\_\; \{a\}\; =\; \backslash \; pi\; ^\; \{2\}\; (\backslash \; eta\; \backslash \; beta\; \backslash \; sigma)\; ^\; \{2\}\; AF\_\; \{2\}\; (\backslash \; lambda),\}$

и нагрузка на выступах

$P\; =\; 8\; 2\; 15\; \pi \; (\eta \; \beta \; \sigma )\; 2\; \sigma \; \beta \; E\; \prime \; AF\; 5\; 2\; (\lambda ),\; \{\backslash \; Displaystyle\; P\; =\; \{\backslash \; frac\; \{8\; \{\backslash \; sqrt\; \{2\}\}\}\; \{15\}\}\; \backslash \; pi\; (\backslash \; eta\; \backslash \; beta\; \backslash \; sigma)\; ^\; \{2\}\; \{\backslash \; sqrt\; \{\backslash \; frac\; \{\backslash \; sigma\}\; \{\backslash \; beta\}\}\}\; E\text{'}AF\; \_\; \{\backslash \; frac\; \{5\}\; \{2\}\}\; (\backslash \; lambda),\}$

где:

$\eta \; \beta \; \sigma \; \{\backslash \; displaystyle\; \backslash \; eta\; \backslash \; beta\; \backslash \; sigma\; \}$, параметр шероховатости,

$A\; \{\backslash \; displaystyle\; A\}$, номинальная площадь контакта,

$\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, масло Stribeck параметр фильма, впервые определенный Стрибеком \ cite {gt} как $\lambda \; =\; h\; /\; \sigma \; \{\backslash \; displaystyle\; \backslash \; lambda\; =\; h\; /\; \backslash \; sigma\}$,

$E\; \prime \; \{\backslash \; displaystyle\; E\; \text{'}\}$, эффективный модуль упругости,

$F\; 2,\; F\; 5\; 2\; (\lambda )\; \{\backslash \; displaystyle\; F\_\; \{2\},\; F\; \_\; \{\backslash \; frac\; \{5\}\; \{2\}\}\; (\backslash \; lambda)\}$, введены статистические функции для соответствия предполагаемому гауссовскому распределению неровностей.

Точное решения для $A\; a\; \{\backslash \; displaystyle\; A\_\; \{a\}\}$и $P\; \{\backslash \; displaystyle\; P\}$впервые представлены Jedynak. Они выражаются как $F\; n\; \{\backslash \; displaystyle\; F\_\; \{n\}\}$следующим образом:

$F\; 2\; =\; 1\; 2\; (h\; 2\; +\; 1)\; erfc\; \; (h\; 2)\; -\; h\; 2\; \pi \; exp\; \; (-\; h\; 2\; 2)\; F\; 5\; 2\; =\; 1\; 8\; \pi \; exp\; \; (-\; h\; 2\; 4)\; h\; 3\; 2\; ((2\; h\; 2\; +\; 3)\; K\; 3\; 4\; (h\; 2\; 4)\; -\; (2\; h\; 2\; +\; 5)\; K\; 1\; 4\; (час\; 2\; 4))\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; F\_\; \{2\}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \; left\; (h\; ^\; \{2\}\; +1\; \backslash \; right)\; \backslash \; operatorname\; \{erfc\; \}\; \backslash \; left\; (\{\backslash \; frac\; \{h\}\; \{\backslash \; sqrt\; \{2\}\}\}\; \backslash \; right)\; -\; \{\backslash \; frac\; \{h\}\; \{\backslash \; sqrt\; \{2\; \backslash \; pi\}\}\}\; \backslash \; exp\; \backslash \; left\; (-\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; right)\; \backslash \backslash \; F\; \_\; \{\backslash \; frac\; \{5\}\; \{2\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{8\; \{\backslash \; sqrt\; \{\backslash \; pi\}\}\}\}\; \backslash \; exp\; \backslash \; left\; (-\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\; h\; ^\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash \; left\; (\backslash \; left\; (2h\; ^\; \{2\}\; +3\; \backslash \; right)\; K\; \_\; \{\backslash \; frac\; \{\; 3\}\; \{4\}\}\; \backslash \; left\; (\{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\; -\; \backslash \; left\; (2h\; ^\; \{2\}\; +5\; \backslash \; right)\; K\; \_\; \{\backslash \; frac\; \{1\}\; \{4\}\; \}\; \backslash \; left\; (\{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{4\}\}\; \backslash \; right)\; \backslash \; right)\; \backslash \; end\; \{align\}\}\}$

где erfc (z) означает дополнительную функцию ошибок, а $K\; \nu \; (z)\; \{\backslash \; displaystyle\; K\; \_\; \{\backslash \; nu\}\; (z)\}$- модифицированная функция Бесселя второго рода.

В статье можно найти исчерпывающий обзор существующих приближений к $F\; 5\; 2\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; frac\; \{5\}\; \{2\}\}\}$. Новые предложения дают наиболее точные аппроксимации для $F\; 5\; 2\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; frac\; \{5\}\; \{2\}\}\}$и $F\; 2\; \{\backslash \; displaystyle\; F\_\; \{2\}\}$, о которых сообщается в литературе. Они задаются следующими рациональными формулами, которые являются очень точными приближениями к интегралам $F\; n\; (h)\; \{\backslash \; displaystyle\; F\_\; \{n\}\; (h)\}$. Они рассчитаны для гауссова распределения неровностей

$F\; n\; (h)\; =\; a\; 0\; +\; a\; 1\; h\; +\; a\; 2\; h\; 2\; +\; a\; 3\; h\; 3\; 1\; +\; b\; 1\; h\; +\; b\; 2\; h\; 2\; +\; b\; 3\; h\; 3\; +\; б\; 4\; час\; 4\; +\; b\; 5\; час\; 5\; +\; b\; 6\; час\; 6\; ехр\; \; (-\; час\; 2\; 2)\; \{\backslash \; displaystyle\; F\_\; \{n\}\; (h)\; =\; \{\backslash \; frac\; \{a\_\; \{0\}\; +\; a\_\; \{1\}\; h\; +\; a\_\; \{\; 2\}\; h\; ^\; \{2\}\; +\; a\_\; \{3\}\; h\; ^\; \{3\}\}\; \{1\; +\; b\_\; \{1\}\; h\; +\; b\_\; \{2\}\; h\; ^\; \{2\}\; +\; b\_\; \{3\}\; h\; ^\; \{3\}\; +\; b\_\; \{4\; \}\; h\; ^\; \{4\}\; +\; b\_\; \{5\}\; h\; ^\; \{5\}\; +\; b\_\; \{6\}\; h\; ^\; \{6\}\}\}\; \backslash \; exp\; \backslash \; left\; (-\; \{\backslash \; frac\; \{h\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; right)\}$

Для $F\; 2\; (h)\; \{\backslash \; displaystyle\; F\_\; \{2\}\; (h)\}$коэффициенты

$[a\; 0,\; a\; 1,\; a\; 2,\; a\; 3]\; =\; [0,5,\; 0,182536384941,\; 0,039812283118,\; 0,003684879001]\; [b\; 1,\; b\; 2,\; b\; 3,\; b\; 4,\; b\; 5,\; b\; 6]\; =\; [1,960841785003,\; 1,708677456715,\; 0,856592986083,\; 0,264996791567,\; 0,04925784389313yle]\; \backslash \; begin\; выровнено\}\; [a\_\; \{0\},\; a\_\; \{1\},\; a\_\; \{2\},\; a\_\; \{3\}]\; =\; [0.5,0.182536384941,0.039812283118,0.003684879001]\; \backslash \backslash \; [b\_\; \{1\},\; b\_\; \{2\},\; b\_\; \{3\; \},\; b\_\; \{4\},\; b\_\; \{5\},\; b\_\; \{6\}]\; =\; [1.960841785003,1.708677456715,0.856592986083,0.264996791567,0.049257843893,0.004640740133]\; \backslash \; end\; \{align\}\}\}$

Максимальная относительная ошибка: $1,68\; \times \; 10\; -\; 7\%\; \{\backslash \; displ\; aystyle\; 1,68\; \backslash \; times\; 10\; ^\; \{-\; 7\}\; \backslash \%\}$.

Для $F\; 5\; 2\; (h)\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; frac\; \{5\}\; \{2\}\}\; (h)\}$коэффициенты:

$[a\; 0,\; a\; 1,\; a\; 2,\; a\; 3]\; =\; [0,616634218997,\; 0,108855827811,\; 0,023453835635,\; 0,000449332509]\; [b\; 1,\; b\; 2,\; b\; 3,\; b\; 4,\; b\; 5,\; b\; 6]\; =\; [\; 1.919948267476,\; 1.635304362591,\; 0.799392556572,\; 0.240278859212,\; 0.043178653945,\; 0.003863334276]\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{выровнено\}\; [a\_\; \{0\},\; a\_\; \{1\},\; a\_\; \{2\},\; a\_\; \{3\}]\; =\; [0,616.10883421899738,\; 0.000449332509]\; \backslash \backslash \; [b\_\; \{1\},\; b\_\; \{2\},\; b\_\; \{3\},\; b\_\; \{4\},\; b\_\; \{5\},\; b\_\; \{6\}]\; =\; [1.919948267476,1.635304362591,0.799392556572,0.240278859212,0.043178653945276.00386\; ]\; \backslash \; end\; \{align\}\}\}$

Максимальная относительная погрешность $4,98\; \times \; 10-8\%\; \{\backslash \; displaystyle\; 4.98\; \backslash \; times\; 10\; ^\; \{-\; 8\}\; \backslash \%\}$.

Когда две твердые поверхности находятся в непосредственной близости, они испытывают притягивающие силы Ван-дер-Ваальса. Модель Ван-дер-Ваальса Брэдли позволяет рассчитать силу растяжения между двумя жесткими сферами с идеально гладкими поверхностями. Модель контакта Герца не считает адгезию возможной. Однако в конце 1960-х годов при сравнении теории Герца с экспериментами с контактом резиновых и стеклянных сфер было обнаружено несколько противоречий.

Было замечено, что, хотя теория Герца применялась при больших нагрузках, при низких нагрузках

• площадь контакта была больше, чем предсказываемая теорией Герца,
• площадь контакта имела ненулевое значение, даже когда нагрузка была снята, и
• была даже сильная адгезия, если контактирующие поверхности были чистыми и сухими.

Это указывало на то, что действуют силы сцепления. Модель Джонсона-Кендалла-Робертса (JKR) и модели Дерягина-Мюллера-Топорова (DMT) были первыми, в которых адгезия была включена в контакт Герца.

Модель жесткого контакта Брэдли

Обычно предполагается, что поверхностная сила между двумя атомными плоскостями на расстоянии $z\; \{\backslash \; displaystyle\; z\}$друг от друга может быть получено из потенциала Леннарда-Джонса. При таком предположении

$F\; (z)\; =\; 16\; \gamma \; 3\; z\; 0\; [(zz\; 0)\; -\; 9\; -\; (zz\; 0)\; -\; 3]\; \{\backslash \; displaystyle\; F\; (z)\; =\; \{\backslash \; cfrac\; \{16\; \backslash \; gamma\}\; \{3z\_\; \{\; 0\}\}\}\; \backslash \; left\; [\backslash \; left\; (\{\backslash \; cfrac\; \{z\}\; \{z\_\; \{0\}\}\}\; \backslash \; right)\; ^\; \{-\; 9\}\; -\; \backslash \; left\; (\{\backslash \; cfrac\; \{z\}\; \{z\_\; \{0\}\}\}\; \backslash \; right)\; ^\; \{-\; 3\}\; \backslash \; right]\}$

где $F\; \{\backslash \; displaystyle\; F\}$- сила (положительная при сжатии), $2\; \gamma \; \{\backslash \; displaystyle\; 2\; \backslash \; gamma\}$- общая поверхностная энергия обеих поверхностей на единицу площади, а $z\; 0\; \{\backslash \; displaystyle\; z\_\; \{0\}\}$- равновесное разделение двух атомных плоскостей.

В модели Брэдли был использован потенциал Леннарда-Джонса, чтобы найти силу сцепления между двумя жесткими сферами. Общая сила между сферами составляет

$F\; a\; (z)\; =\; 16\; \gamma \; \pi \; R\; 3\; [1\; 4\; (z\; z\; 0)\; -\; 8\; -\; (z\; z\; 0)\; -\; 2];\; 1\; р\; =\; 1\; р\; 1\; +\; 1\; р\; 2\; \{\backslash \; displaystyle\; F\_\; \{a\}\; (z)\; =\; \{\backslash \; cfrac\; \{16\; \backslash \; gamma\; \backslash \; pi\; R\}\; \{3\}\}\; \backslash \; left\; [\{\backslash \; cfrac\; \{1\}\; \{4\}\}\; \backslash \; left\; (\{\backslash \; cfrac\; \{z\}\; \{z\_\; \{0\}\}\}\; \backslash \; right)\; ^\; \{-\; 8\}\; -\; \backslash \; left\; (\{\backslash \; cfrac\; \{z\}\; \{z\_\; \{0\}\}\}\; \backslash \; right)\; ^\; \{-\; 2\}\; \backslash \; right\; ]\; ~;\; ~~\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{2\}\}\}\}$

где $R\; 1,\; R\; 2\; \{\backslash \; displaystyle\; R\_\; \{1\},\; R\_\; \{2\}\}$- радиусы двух сфер.

Две сферы полностью разделяются, когда сила отрыва достигается в $z\; =\; z\; 0\; \{\backslash \; displaystyle\; z\; =\; z\_\; \{0\}\}$в этой точке

$F\; а\; =\; F\; c\; =\; -\; 4\; \gamma \; \pi \; R.\; \{\backslash \; displaystyle\; F\_\; \{a\}\; =\; F\_\; \{c\}\; =\; -\; 4\; \backslash \; gamma\; \backslash \; pi\; R.\}$

Модель упругого контакта Джонсона-Кендалла-Робертса (JKR)

Схема площади контакта для модели JKR. Тест JKR с жестким валиком на деформируемом плоском материале: полный цикл

Чтобы учесть эффект адгезии при контакте Герца, Джонсон, Кендалл и Робертс сформулировали теорию адгезионного контакта JKR, используя баланс между накопленной упругой энергией и потерями в поверхностной энергии. Модель JKR учитывает влияние контактного давления и адгезии только внутри области контакта. Общее решение для распределения давления в зоне контакта в модели JKR:

$p\; (r)\; =\; p\; 0\; (1\; -\; r\; 2\; a\; 2)\; 1\; 2\; +\; p\; 0\; \prime \; (1\; -\; r\; 2\; a\; 2)\; -\; 1\; 2\; \{\backslash \; displaystyle\; p\; (r)\; =\; p\_\; \{0\}\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; +\; p\_\; \{0\}\; \text{'}\backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{-\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}\}$

Обратите внимание, что в первоначальной теории Герца термин, содержащий $p\; 0\; \text{'}\{\backslash \; displaystyle\; p\_\; \{0\}\text{'}\}$, не учитывался на том основании, что напряжение не могло поддерживаться в зоне контакта. Для контакта двух сфер

$p\; 0\; =\; 2\; a\; E\; \ast \; \pi \; R;\; п\; 0\; \prime \; =\; -\; (4\; \gamma \; E\; \ast \; \pi \; a)\; 1\; 2\; \{\backslash \; displaystyle\; p\_\; \{0\}\; =\; \{\backslash \; frac\; \{2aE\; ^\; \{*\}\}\; \{\backslash \; pi\; R\}\};\; \backslash \; quad\; p\_\; \{0\}\; \text{'}=\; -\; \backslash \; left\; (\{\backslash \; frac\; \{4\; \backslash \; gamma\; E\; ^\; \{*\}\}\; \{\backslash \; pi\; a\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}$

где $a\; \{\backslash \; displaystyle\; a\; \backslash ,\; \}$- радиус области контакта, $F\; \{\backslash \; displaystyle\; F\}$- приложенная сила, $2\; \gamma \; \{\backslash \; displaystyle\; 2\; \backslash \; gamma\}$- полная поверхностная энергия обеих поверхностей на единицу площади контакта, $R\; i,\; E\; i,\; \nu \; i,\; i\; =\; 1,\; 2\; \{\backslash \; displaystyle\; R\_\; \{i\},\; \backslash ,\; E\_\; \{i\},\; \backslash ,\; \backslash \; nu\; \_\; \{i\},\; ~~\; i\; =\; 1,2\}$- радиусы, модули Юнга и коэффициенты Пуассона двух сфер, а

$1\; R\; =\; 1\; р\; 1\; +\; 1\; р\; 2;\; 1\; E\; \ast \; знак\; равно\; 1\; -\; \nu \; 1\; 2\; E\; 1\; +\; 1\; -\; \nu \; 2\; 2\; E\; 2\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{R\}\}\; =\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{1\}\}\}\; +\; \{\backslash \; frac\; \{1\}\; \{R\_\; \{2\}\}\};\; \backslash \; quad\; \{\backslash \; frac\; \{1\}\; \{E\; ^\; \{*\}\}\}\; =\; \{\backslash \; frac\; \{1-\; \backslash \; nu\; \_\; \{1\}\; ^\; \{2\}\}\; \{E\_\; \{1\}\; \}\}\; +\; \{\backslash \; frac\; \{1-\; \backslash \; nu\; \_\; \{2\}\; ^\; \{2\}\}\; \{E\_\; \{2\}\}\}\}$

Расстояние приближения между двумя сферами равно

$d\; =\; \pi \; a\; 2\; E\; *\; (P\; 0\; +\; 2\; p\; 0\; \prime )\; =\; a\; 2\; R\; \{\backslash \; displaystyle\; d\; =\; \{\backslash \; frac\; \{\backslash \; pi\; a\}\; \{2E\; ^\; \{*\}\}\}\; \backslash \; left\; (p\_\; \{0\}\; +\; 2p\_\; \{0\}\; \text{'}\backslash \; right)\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{R\}\}\}$

Уравнение Герца для площади контакта между двумя сферами, модифицированное с учетом поверхностной энергии, имеет вид

$a\; 3\; =\; 3\; R\; 4\; E\; \ast \; (F\; +\; 6\; \gamma \; \pi \; R\; +\; 12\; \gamma \; \pi \; RF\; +\; (6\; \gamma \; \pi \; R)\; 2)\; \{\backslash \; displaystyle\; a\; ^\; \{3\}\; =\; \{\backslash \; frac\; \{3R\}\; \{4E\; ^\; \{*\}\}\}\; \backslash \; left\; (F\; +\; 6\; \backslash \; gamma\; \backslash \; pi\; R\; +\; \{\backslash \; sqrt\; \{12\; \backslash \; gamma\; \backslash \; pi\; RF\; +\; (6\; \backslash \; gamma\; \backslash \; pi\; R)\; ^\; \{2\}\}\}\; \backslash \; right)\}$

Когда поверхностная энергия равна нулю, $\gamma \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; gamma\; =\; 0\}$восстанавливается уравнение Герца для контакта между двумя сферами. Когда приложенная нагрузка равна нулю, радиус контакта равен

$a\; 3\; =\; 9\; R\; 2\; \gamma \; \pi \; E\; \ast \; \{\backslash \; displaystyle\; a\; ^\; \{3\}\; =\; \{\backslash \; frac\; \{9R\; ^\; \{2\}\; \backslash \; gamma\; \backslash \; pi\}\; \{E\; ^\; \{*\}\}\}\}$

Растягивающая нагрузка, при которой сферы разделяются (т. Е. $a\; =\; 0\; \{\backslash \; displaystyle\; a\; =\; 0\}$), по прогнозам, будет

$F\; c\; =\; -\; 3\; \gamma \; \pi \; R\; \{\backslash \; displaystyle\; F\; \_\; \{\backslash \; text\; \{c\}\}\; =\; -\; 3\; \backslash \; gamma\; \backslash \; pi\; R\; \backslash ,\}$

Эта сила также называется силой отрыва . Обратите внимание, что эта сила не зависит от модулей двух сфер. Однако есть другое возможное решение для значения $a\; \{\backslash \; displaystyle\; a\}$при этой нагрузке. Это критическая область контакта $ac\; \{\backslash \; displaystyle\; a\; \_\; \{\backslash \; text\; \{c\}\}\}$, задаваемая

$ac\; 3\; =\; 9\; R\; 2\; \gamma \; \pi \; 4\; E\; \ast \; \{\backslash \; displaystyle\; a\_\; \{\; \backslash \; text\; \{c\}\}\; ^\; \{3\}\; =\; \{\backslash \; frac\; \{9R\; ^\; \{2\}\; \backslash \; gamma\; \backslash \; pi\}\; \{4E\; ^\; \{*\}\}\}\}$

Если мы определим работу адгезии как

$\Delta \; \gamma \; =\; \gamma \; 1\; +\; \gamma \; 2\; -\; \gamma \; 12\; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; gamma\; =\; \backslash \; gamma\; \_\; \{1\}\; +\; \backslash \; gamma\; \_\; \{2\}\; -\; \backslash \; gamma\; \_\; \{12\}\}$

где $\gamma \; 1,\; \gamma \; 2\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{1\},\; \backslash \; gamma\; \_\; \{2\}\}$- энергии сцепления двух поверхностей, а $\gamma \; 12\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{\; 12\}\}$- член взаимодействия, мы можем записать радиус контакта JKR как

$a\; 3\; =\; 3\; R\; 4\; E\; \ast \; (F\; +\; 3\; \Delta \; \gamma \; \pi \; R\; +\; 6\; \Delta \; \gamma \; \pi \; RF\; +\; (3\; \Delta \; \gamma \; \pi \; R)\; 2)\; \{\backslash \; displaystyle\; a\; ^\; \{3\}\; =\; \{\backslash \; frac\; \{3R\}\; \{4E\; ^\; \{*\}\}\}\; \backslash \; left\; (F\; +\; 3\; \backslash \; Delta\; \backslash \; gamma\; \backslash \; pi\; R\; +\; \{\backslash \; sqrt\; \{6\; \backslash \; Delta)\; \backslash \; gamma\; \backslash \; pi\; RF\; +\; (3\; \backslash \; Delta\; \backslash \; gamma\; \backslash \; pi\; R)\; ^\; \{2\}\}\}\; \backslash \; right)\}$

Растягивающая нагрузка при отрыве

$F\; =\; -\; 3\; 2\; \Delta \; \gamma \; \pi \; R\; \{\backslash \; displaystyle\; F\; =\; -\; \{\backslash \; frac\; \{3\}\; \{2\}\}\; \backslash \; Delta\; \backslash \; gamma\; \backslash \; pi\; R\; \backslash ,\}$

, а критический радиус контакта определяется как

$ac\; 3\; =\; 9\; R\; 2\; \Delta \; \gamma \; \pi \; 8\; E\; \ast \; \{\backslash \; displaystyle\; a\; \_\; \{\backslash \; текст\; \{c\}\}\; ^\; \{3\}\; =\; \{\backslash \; frac\; \{9R\; ^\; \{2\}\; \backslash \; Delta\; \backslash \; gamma\; \backslash \; pi\}\; \{8E\; ^\; \{*\}\}\}\}$

Критическая глубина проникновения

$dc\; =\; ac\; 2\; R\; знак\; равно\; (R\; 1\; 2\; 9\; \Delta \; \gamma \; \pi \; 4\; E\; \ast )\; 2\; 3\; \{\backslash \; displaystyle\; d\; \_\; \{\backslash \; text\; \{c\}\}\; =\; \{\backslash \; frac\; \{a\_\; \{c\}\; ^\; \{2\}\}\; \{R\}\}\; =\; \backslash \; left\; (\; R\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \{\backslash \; frac\; \{9\; \backslash \; Delta\; \backslash \; gamma\; \backslash \; pi\}\; \{4E\; ^\; \{*\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\}$

Модель Дерягина-Мюллера-Топорова (DMT) упругого контакта

Модель Дерягина-Мюллера-Топорова (DMT) является альтернативной моделью для адгезионного контакта, которая предполагает, что профиль контакта остается таким же, как в контакте Герца, но с дополнительные привлекательные взаимодействия за пределами области контакта.

Радиус контакта между двумя сферами по теории ДМТ равен

$a\; 3\; =\; 3\; R\; 4\; E\; \ast \; (F\; +\; 4\; \gamma \; \pi \; R)\; \{\backslash \; displaystyle\; a\; ^\; \{3\}\; =\; \{\backslash \; cfrac\; \{3R\; \}\; \{4E\; ^\; \{*\}\}\}\; \backslash \; left\; (F\; +\; 4\; \backslash \; gamma\; \backslash \; pi\; R\; \backslash \; right)\}$

и сила отрыва равна

$F\; c\; =\; -\; 4\; \gamma \; \pi \; R\; \{\backslash \; displaystyle\; F\_\; \{\; c\}\; =\; -\; 4\; \backslash \; gamma\; \backslash \; pi\; R\; \backslash ,\}$

Когда достигается сила отрыва, площадь контакта становится равной нулю, и нет сингулярности в контактных напряжениях на краю области контакта.

С точки зрения работы адгезии $\Delta \; \gamma \; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; gamma\}$

$a\; 3\; =\; 3\; R\; 4\; E\; \ast \; (F\; +\; 2\; \Delta \; \gamma \; \pi \; R)\; \{\backslash \; displaystyle\; a\; ^\; \{3\}\; =\; \{\backslash \; cfrac\; \{3R\}\; \{4E\; ^\; \{*\}\}\}\; \backslash \; left\; (F\; +\; 2\; \backslash \; Delta\; \backslash \; gamma\; \backslash \; pi\; R\; \backslash \; right)\}$

и

$F\; c\; =\; -\; 2\; \Delta \; \gamma \; \pi \; R\; \{\backslash \; displaystyle\; F\_\; \{c\}\; =\; -\; 2\; \backslash \; Delta\; \backslash \; gamma\; \backslash \; pi\; R\; \backslash ,\}$

параметр Табора

В 1977 году Табор показал, что очевидное противоречие между теориями JKR и ДМТ может быть решено, отметив, что две теории были крайними пределами единой теории, параметризованной параметром Табора ($\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$), определенным как

$\mu \; :\; =\; dcz\; 0\; \approx \; [R\; (\Delta \; \gamma )\; 2\; E\; \ast \; 2\; z\; 0\; 3]\; 1\; 3\; \{\backslash \; displaystyle\; \backslash \; mu:\; =\; \{\backslash \; frac\; \{d\_\; \{c\}\}\; \{z\_\; \{0\}\}\}\; \backslash \; приблизительно\; \backslash \; left\; [\{\; \backslash \; frac\; \{R\; (\backslash \; Delta\; \backslash \; gamma)\; ^\; \{2\}\}\; \{\{E\; ^\; \{*\}\}\; ^\; \{2\}\; z\_\; \{0\}\; ^\; \{3\}\}\}\; \backslash \; right]\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\; \}\}$

где $z\; 0\; \{\backslash \; displaystyle\; z\_\; \{0\}\}$- равновесное расстояние между двумя контактирующими поверхностями. Теория JKR применима к большим, податливым сферам, для которых $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$является большим. Теория ДМТ применима к маленьким жестким сферам с малыми значениями $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$.

. Впоследствии Дерягин и его сотрудники, применив закон силы Брэдли к упругому полупространству, подтвердили, что параметр Табора увеличивается, сила отрыва падает от значения Брэдли $2\; \pi \; R\; \Delta \; \gamma \; \{\backslash \; displaystyle\; 2\; \backslash \; pi\; R\; \backslash \; Delta\; \backslash \; gamma\}$до значения JKR $(3/2)\; \pi \; R\; \Delta \; \gamma \; \{\backslash \; displaystyle\; (3/2)\; \backslash \; pi\; R\; \backslash \; Delta\; \backslash \; gamma\}$. Позже Гринвуд провел более подробные расчеты, показавшие S-образную кривую нагрузки / подхода, которая объясняет эффект подпрыгивания. Более эффективный метод выполнения расчетов и дополнительные результаты были даны Фэном

моделью упругого контакта Моугиса-Дагдейла

Схема зоны контакта для модели Моугиса-Дагдейла.

Дальнейшее улучшение Табора. Идея была предложена Моугисом, который представил поверхностную силу в терминах приближения Дагдейла, так что работа адгезии определяется как

$\Delta \; \gamma \; =\; \sigma \; 0\; h\; 0\; \{\backslash \; displaystyle\; \backslash \; Delta\; \backslash \; gamma\; =\; \backslash \; sigma\; \_\; \{0\}\; ~\; h\_\; \{0\}\}$

где $\sigma \; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{0\}\}$- максимальная сила, предсказанная потенциалом Леннарда-Джонса, а $h\; 0\; \{\backslash \; displaystyle\; h\_\; \{0\}\}$- максимальное разделение, полученное путем сопоставления областей под кривыми Дагдейла и Леннарда-Джонса (см. рисунок рядом). Это означает, что сила притяжения постоянна для $z\; 0\; \le \; z\; \le \; z\; 0\; +\; h\; 0\; \{\backslash \; displaystyle\; z\_\; \{0\}\; \backslash \; leq\; z\; \backslash \; leq\; z\_\; \{0\}\; +\; h\_\; \{0\}\}$. Дальнейшего проникновения при сжатии нет. Идеальный контакт происходит в области радиусом $a\; \{\backslash \; displaystyle\; a\}$и силами сцепления величиной $\sigma \; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{0\}\}$extend в область радиусом $c>a\; \{\backslash \; displaystyle\; c>a\}$. В области две поверхности разделены расстоянием $h\; (r)\; \{\backslash \; displaystyle\; h\; (r)\}$с $h\; (a)\; =\; 0\; \{\backslash \; displaystyle\; h\; (a)\; =\; 0\}$и $h\; (c)\; =\; h\; 0\; \{\backslash \; displaystyle\; h\; (c)\; =\; h\_\; \{\; 0\}\}$. Отношение $m\; \{\backslash \; displaystyle\; m\}$определяется как

$m:\; =\; ca\; \{\backslash \; displaystyle\; m:\; =\; \{\backslash \; frac\; \{c\}\; \{\; a\}\}\}$.

В теории Моугиса-Дагдейла распределение силы тяги на поверхности делится на две части: одна из-за контактного давления Герца, а другая из-за адгезионного напряжения Дагдейла. Контакт Герца предполагается в области

$p\; H\; (r)\; =\; (3\; FH\; 2\; \pi \; a\; 2)\; (1\; -\; r\; 2\; a\; 2)\; 1\; 2\; \{\backslash \; displaystyle\; p\; ^\; \{H\}\; (r)\; =\; \backslash \; left\; (\{\backslash \; frac\; \{3F\; ^\; \{H\}\}\; \{2\; \backslash \; pi\; a\; ^\; \{2\}\}\}\; \backslash \; right)\; \backslash \; left\; (1\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{2\}\}\}$

, где контактная сила Герца $FH\; \{\backslash \; displaystyle\; F\; ^\; \{H\}\}$определяется как

$FH\; =\; 4\; E\; \ast \; a\; 3\; 3\; R\; \{\backslash \; displaystyle\; F\; ^\; \{H\}\; =\; \{\backslash \; frac\; \{4E\; ^\; \{*\}\; a\; ^\; \{3\}\}\; \{3R\}\}\}$

Проникновение из-за упругого сжатия составляет

$d\; H\; =\; a\; 2\; R\; \{\; \backslash \; displaystyle\; d\; ^\; \{H\}\; =\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{R\}\}\}$

Вертикальное смещение в $r\; =\; c\; \{\backslash \; displaystyle\; r\; =\; c\}$равно

$U\; ЧАС\; (с)\; знак\; равно\; 1\; \pi \; R\; [a\; 2\; (2\; -\; м\; 2)\; грех\; -\; 1\; \; (1\; м)\; +\; a\; 2\; м\; 2\; -\; 1]\; \{\backslash \; displaystyle\; u\; ^\; \{H\}\; (c)\; =\; \{\; \backslash \; cfrac\; \{1\}\; \{\backslash \; pi\; R\}\}\; \backslash \; left\; [a\; ^\; \{2\}\; \backslash \; left\; (2-m\; ^\; \{2\}\; \backslash \; right)\; \backslash \; sin\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{m\; \}\}\; \backslash \; right)\; +\; a\; ^\; \{2\}\; \{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\; \backslash \; right]\}$

и разделение между двумя поверхностями в $r\; =\; c\; \{\backslash \; displaystyle\; r\; =\; c\}$равно

$час\; H\; (c)\; =\; c\; 2\; 2\; R\; -\; d\; H\; +\; u\; H\; (c)\; \{\backslash \; displaystyle\; h\; ^\; \{H\}\; (c)\; =\; \{\backslash \; frac\; \{c\; ^\; \{\; 2\}\}\; \{2R\}\}\; -\; d\; ^\; \{H\}\; +\; u\; ^\; \{H\}\; (c)\}$

Распределение силы сцепления на поверхности n из-за клеевого напряжения Дагдейла

$p\; D\; (r)\; =\; \{-\; \sigma \; 0\; \pi \; cos\; -\; 1\; \; [2\; -\; m\; 2\; -\; r\; 2\; a\; 2\; m\; 2\; (1\; -\; r\; 2\; m\; 2\; a\; 2)]\; для\; r\; \le \; a\; -\; \sigma \; 0\; для\; a\; \le \; r\; \le \; c\; \{\backslash \; displaystyle\; p\; ^\; \{D\}\; (r)\; =\; \{\backslash \; begin\; \{cases\}\; -\; \{\backslash \; frac\; \{\backslash \; sigma\; \_\; \{0\}\}\; \{\backslash \; pi\}\}\; \backslash \; cos\; ^\; \{-1\}\; \backslash \; left\; [\{\backslash \; frac\; \{2-m\; ^\; \{2\}\; -\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{a\; ^\; \{2\}\}\}\}\; \{m\; ^\; \{2\}\; \backslash \; left\; (1-\; \{\; \backslash \; frac\; \{r\; ^\; \{2\}\}\; \{m\; ^\; \{2\}\; a\; ^\; \{2\}\}\}\; \backslash \; right)\}\}\; \backslash \; right]\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; \backslash \; quad\; r\; \backslash \; leq\; a\; \backslash \backslash \; -\; \backslash \; sigma\; \_\; \{0\}\; \backslash \; quad\; \{\backslash \; text\; \{for\}\}\; \backslash \; quad\; a\; \backslash \; leq\; r\; \backslash \; leq\; c\; \backslash \; end\; \{cases\}\}\}$

Тогда общая сила сцепления определяется как

$FD\; =\; -\; 2\; \sigma \; 0\; м\; 2\; a\; 2\; [соз\; -\; 1\; \; (1\; м)\; +\; 1\; м\; 2\; м\; 2\; -\; 1]\; \{\backslash \; displaystyle\; F\; ^\; \{D\}\; =\; -\; 2\; \backslash \; sigma\; \_\; \{0\}\; m\; ^\; \{2\}\; a\; ^\; \{2\}\; \backslash \; left\; [\backslash \; cos\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{m\}\}\; \backslash \; right)\; +\; \{\backslash \; frac\; \{1\}\; \{m\; ^\; \{2\}\}\}\; \{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\; \backslash \; right]\}$

Сжатие из-за адгезии Дагдейла составляет

$d\; D\; =\; -\; (2\; \sigma \; 0\; a\; E\; \ast )\; m\; 2\; -\; 1\; \{\backslash \; displaystyle\; d\; ^\; \{D\}\; =\; -\; \backslash \; left\; (\; \{\backslash \; frac\; \{2\; \backslash \; sigma\; \_\; \{0\}\; a\}\; \{E\; ^\; \{*\}\}\}\; \backslash \; right)\; \{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\}$

и разрыв в $r\; =\; c\; \{\backslash \; displaystyle\; r\; =\; c\}$равно

$h\; D\; (c)\; =\; (4\; \sigma \; 0\; a\; \pi \; E\; \ast )\; [m\; 2\; -\; 1\; cos\; -\; 1\; \; (1\; m)\; +\; 1\; -\; m\; ]\; \{\backslash \; displaystyle\; h\; ^\; \{D\}\; (\; c)\; =\; \backslash \; left\; (\{\backslash \; frac\; \{4\; \backslash \; sigma\; \_\; \{0\}\; a\}\; \{\backslash \; pi\; E\; ^\; \{*\}\}\}\; \backslash \; right)\; \backslash \; left\; [\{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\; \backslash \; cos\; ^\; \{-\; 1\}\; \backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{m\}\}\; \backslash \; right)\; +\; 1-m\; \backslash \; right]\}$

Тогда чистое сцепление с поверхностью контакта определяется как $p\; (r)\; знак\; равно\; p\; H\; (r)\; +\; p\; D\; (r)\; \{\backslash \; displaystyle\; p\; (r)\; =\; p\; ^\; \{H\}\; (r)\; +\; p\; ^\; \{D\}\; (r)\}$и чистая контактная сила равна $F\; =\; FH\; +\; FD\; \{\backslash \; displaystyle\; F\; =\; F\; ^\; \{H\}\; +\; F\; ^\; \{D\}\}$. Когда $h\; (c)\; =\; h\; H\; (c)\; +\; h\; D\; (c)\; =\; h\; 0\; \{\backslash \; displaystyle\; h\; (c)\; =\; h\; ^\; \{H\}\; (c)\; +\; h\; ^\; \{D\}\; (c)\; =\; h\_\; \{0\}\}$сцепление клея падает до нуля.

Безразмерные значения $a,\; c,\; F,\; d\; \{\backslash \; displaystyle\; a,\; c,\; F,\; d\}$вводятся на этом этапе, которые определяются как

$a\; ¯\; =\; \alpha \; a;\; c\; ¯:\; =\; \alpha \; c;\; d\; ¯:\; =\; \alpha \; 2\; R\; d;\; \alpha :\; =\; (4\; E\; \ast \; 3\; \pi \; \Delta \; \gamma \; R\; 2)\; 1\; 3;\; A\; ¯:\; =\; \pi \; c\; 2;\; F\; ¯\; знак\; равно\; F\; \pi \; \Delta \; \gamma \; R\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{a\}\}\; =\; \backslash \; alpha\; a\; ~;\; ~~\; \{\backslash \; bar\; \{c\}\}:\; =\; \backslash \; alpha\; c\; ~;\; ~~\; \{\backslash \; bar\; \{d\}\}:\; =\; \backslash \; alpha\; ^\; \{2\}\; Rd\; ~;\; ~~\; \backslash \; alpha:\; =\; \backslash \; left\; (\{\backslash \; frac\; \{4E\; ^\; \{*\}\}\; \{3\; \backslash \; pi\; \backslash \; Delta\; \backslash \; gamma\; R\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; ~;\; ~~\; \{\backslash \; bar\; \{A\}\}:\; =\; \backslash \; pi\; c\; ^\; \{2\}\; ~;\; ~~\; \{\backslash \; bar\; \{F\}\}\; =\; \{\backslash \; frac\; \{F\}\; \{\backslash \; pi\; \backslash \; Delta\; \backslash \; gamma\; R\}\}\}$

Кроме того, Моугис предложил параметр $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, который эквивалентен параметру Табора $\mu \; \{\backslash \; displaystyle\; \backslash \; mu\}$. Этот параметр определяется как

$\lambda :\; =\; \sigma \; 0\; (9\; R\; 2\; \pi \; \Delta \; \gamma \; E\; \ast \; 2)\; 1\; 3\; \approx \; 1,16\; \mu \; \{\backslash \; displaystyle\; \backslash \; lambda:\; =\; \backslash \; sigma\; \_\; \{0\}\; \backslash \; left\; (\{\backslash \; frac\; \{9R\; \}\; \{2\; \backslash \; pi\; \backslash \; Delta\; \backslash \; gamma\; \{E\; ^\; \{*\}\}\; ^\; \{2\}\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; \backslash \; приблизительно\; 1,16\; \backslash \; mu\}$

где ступенчатое когезионное напряжение $\sigma \; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{0\}\}$равно теоретическому напряжению потенциала Леннарда-Джонса

$\sigma \; th\; =\; 16\; \Delta \; \gamma \; 9\; 3\; z\; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{\backslash \; text\; \{th\}\}\; =\; \{\backslash \; frac\; \{16\; \backslash \; Delta\; \backslash \; gamma\}\; \{9\; \{\backslash \; sqrt\; \{3\}\}\; z\_\; \{0\}\}\}\}$

Чжэн и Ю предложили другое значение для ступенчатого когезионного напряжения

$\sigma \; 0\; знак\; равно\; ехр\; \; (-\; 223\; 420)\; \cdot \; \Delta \; \gamma \; z\; 0\; \approx \; 0,588\; \Delta \; \gamma \; z\; 0\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{0\}\; =\; \backslash \; exp\; \backslash \; left\; (-\; \{\backslash \; frac\; \{223\}\; \{420\}\}\; \backslash \; справа)\; \backslash \; cdot\; \{\backslash \; frac\; \{\backslash \; Delta\; \backslash \; gamma\}\; \{z\_\; \{0\}\}\}\; \backslash \; приблизительно\; 0,588\; \{\backslash \; frac\; \{\backslash \; Delta\; \backslash \; gamma\}\; \{z\_\; \{0\}\}\}\}$

для соответствия потенциалу Леннарда-Джонса, что приводит к

$\lambda \; \approx \; 0,663\; \mu \; \{\backslash \; displaystyle\; \backslash \; lambda\; \backslash \; приблизительно\; 0,663\; \backslash \; mu\}$

Тогда чистая контактная сила может быть выражена как

$F\; ¯\; =\; a\; ¯\; 3\; -\; \lambda \; a\; ¯\; 2\; [m\; 2-1\; +\; м\; 2\; сек\; -\; 1\; \; м]\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{F\}\}\; =\; \{\backslash \; bar\; \{a\}\}\; ^\; \{3\; \}\; -\; \backslash \; lambda\; \{\backslash \; bar\; \{a\}\}\; ^\; \{2\}\; \backslash \; left\; [\{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\; +\; m\; ^\; \{2\}\; \backslash \; sec\; ^\; \{-\; 1\}\; m\; \backslash \; right]\}$

и упругое сжатие как

$d\; ¯\; =\; a\; ¯\; 2\; -\; 4\; 3\; \lambda \; a\; ¯\; m\; 2\; -\; 1\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{d\}\}\; =\; \{\backslash \; bar\; \{a\}\}\; ^\; \{2\}\; -\; \{\; \backslash \; frac\; \{4\}\; \{3\}\}\; ~\; \backslash \; lambda\; \{\backslash \; bar\; \{a\}\}\; \{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\}$

Уравнение когезионного зазора между двумя телами принимает вид

$\lambda \; a\; ¯\; 2\; 2\; [(m\; 2\; -\; 2)\; sec\; -\; 1\; \; m\; +\; m\; 2\; -\; 1]\; +\; 4\; \lambda \; a\; ¯\; 3\; [m\; 2\; -\; 1\; sec\; -\; 1\; \; m\; -\; m\; +\; 1]\; =\; 1\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; lambda\; \{\backslash \; bar\; \{a\}\}\; ^\; \{2\}\}\; \{2\}\}\; \backslash \; left\; [\backslash \; left\; (m\; ^\; \{2\}\; -2\; \backslash \; right)\; \backslash \; sec\; ^\; \{-\; 1\}\; m\; +\; \{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\; \backslash \; right]\; +\; \{\backslash \; frac\; \{4\; \backslash \; lambda\; \{\backslash \; bar\; \{a\}\}\}\; \{3\}\}\; \backslash \; left\; [\{\backslash \; sqrt\; \{m\; ^\; \{2\}\; -1\}\}\; \backslash \; sec\; ^\; \{-\; 1\}\; m-m\; +\; 1\; \backslash \; right]\; =\; 1\}$

Это уравнение может быть решено для получения значений $c\; \{\backslash \; displaystyle\; c\}$для различных значений $a\; \{\backslash \; displaystyle\; a\}$и $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$. Для больших значений $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$, $m\; \to \; 1\; \{\backslash \; displaystyle\; m\; \backslash \; rightarrow\; 1\}$и получается модель JKR. Для малых значений $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$извлекается модель DMT.

Модель Карпика-Оглетри-Салмерона (COS)

Модель Моугиса-Дагдейла может быть решена итеративно, только если значение $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$Не известно априори. Приближенное решение Карпика-Оглетри-Салмерона упрощает процесс за счет использования следующего соотношения для определения радиуса контакта $a\; \{\backslash \; displaystyle\; a\}$:

$a\; =\; a\; 0\; (\beta )\; (\beta \; +\; 1\; -\; F\; /\; F\; c\; (\; \beta )\; 1\; +\; \beta )\; 2\; 3\; \{\backslash \; displaystyle\; a\; =\; a\_\; \{0\}\; (\backslash \; beta)\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; beta\; +\; \{\backslash \; sqrt\; \{1-F\; /\; F\_\; \{c\}\; (\backslash \; beta)\}\}\}\}\; \{1+\; \backslash \; beta\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{2\}\; \{3\}\}\}$

где $a\; 0\; \{\backslash \; displaystyle\; a\_\; \{0\}\}$- это контактная область в нулевая нагрузка, а $\beta \; \{\backslash \; displaystyle\; \backslash \; beta\}$- параметр перехода, который связан с $\lambda \; \{\backslash \; displaystyle\; \backslash \; lambda\}$с помощью

$\lambda \; \approx \; -\; 0,924\; ln\; \; (1\; -\; 1,02\; \beta )\; \{\backslash \; displaystyle\; \backslash \; lambda\; \backslash \; приблизительно\; -0,924\; \backslash \; ln\; (1-1,02\; \backslash \; beta)\}$

Случай $\beta \; =\; 1\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; 1\}$точно соответствует теории JKR, а $\beta \; =\; 0\; \{\backslash \; displaystyle\; \backslash \; beta\; =\; 0\}$соответствует теории DMT. Для промежуточных случаев модель COS близко соответствует решению Моугиса-Дагдейла для .

Влияние формы контакта

Даже при наличии идеально гладких поверхностей геометрия может иметь значение в форма макроскопической формы области контакта. Когда жесткий пуансон с плоской, но странной формы гранью осторожно снимается с его мягкого аналога, его отделение происходит не мгновенно, а фронты отрыва начинаются с острых углов и перемещаются внутрь, пока не будет достигнута окончательная конфигурация, которая для макроскопически изотропных форм является почти круглой. Основным параметром, определяющим адгезию плоских контактов, является максимальный линейный размер контакта. Процесс отслоения можно наблюдать экспериментально на пленке.

• Клей - неметаллический материал, используемый для соединения различных материалов
• Клейкое соединение
• Адгезия железная дорога - Железная дорога, которая использует сцепную тягу для движения поезда
• Силы сцепления на поверхности
• Несущая способность - Способность грунта выдерживать нагрузки
• Динамика контакта - Движение многотельных систем
• Контактное сопротивление - физический эффект (ECR)
• Дисперсионная адгезия - Адгезия между материалами из-за межмолекулярных взаимодействий
• Электростатический генератор - Устройство, генерирующее электрический заряд на высоковольтном электроде
• Энергетически модифицированный цемент - Класс цементов, механически обработанных для преобразования реактивности
• Механика фрикционного контакта - Исследование деформации тел при наличии фрикционных эффектов
• Фрикционный привод - Механический передача мощности за счет трения между компонентами
• истирание - Форма износа, вызванная адгезией между поверхностями скольжения
• Гониометр - Инструмент, который либо измеряет угол, либо позволяет вращать объект до точного углового положения
• Негладкая механика - Подход к моделированию в механике, который больше не требует, чтобы изменения положения и скорости во времени были плавными.
• Пластиковая пленка - Тонкая пластиковая пленка, обычно используемая для герметизации пищевых продуктов
• Прокатка (обработка металлов) - Процесс обработки металла
• Удар (механика) - Внезапное неустановившееся ускорение
• Задача Синьорини - Проблема упругости при линейной упругости
• Поверхностное натяжение - Склонность поверхности жидкости к усадка для уменьшения площади поверхности
• Односторонний контакт - механическое ограничение, предотвращающее проникновение между двумя телами;
• Смачивание - способность жидкости поддерживать контакт с твердой поверхностью

• [2] : Подробнее о контактных напряжениях и эволюции подшипниковых напряжений уравнений можно найти в этой публикации исследовательского центра NASA Glenn возглавит Bearing НАСА, трансмиссии и раздел передач, Эрвин Зарецкий
• [3] :. MATLAB процедура для решения линейной упругой контактной задачи механики под названием ; «Решение LCP задачи линейной упругой контактной механики» предоставляется при обмене файлами в MATLAB Central.
• [4] : Калькулятор контактной механики.
• [5] : подробные расчеты и формулы теории JKR для двух сфер.
• [5] : код Matlab для анализа контактов Герца (включает линейные, точечные и эллиптические случаи).
• [6] : JKR, MD и DMT модели адгезии (процедуры Matlab).