| Часть серии о | |||||||
| Механика сплошной среды | |||||||
|---|---|---|---|---|---|---|---|
| Fick's laws of diffusion | |||||||
Законы
| |||||||
| Механика твердого тела | |||||||
Гидравлическая механика
| |||||||
Реология
| |||||||
| Ученые | |||||||
|
 Поток дождевой воды из навеса. Среди сил, управляющих образованием капель: поверхностное натяжение, когезия, сила Ван-дер-Ваальса, неустойчивость Плато – Рэлея.
Поток дождевой воды из навеса. Среди сил, управляющих образованием капель: поверхностное натяжение, когезия, сила Ван-дер-Ваальса, неустойчивость Плато – Рэлея.  Воспроизвести медиа Поверхностное натяжение и гидрофобность взаимодействуют в этой попытке разрезать каплю воды.
Воспроизвести медиа Поверхностное натяжение и гидрофобность взаимодействуют в этой попытке разрезать каплю воды.  Воспроизвести медиа Экспериментальная демонстрация поверхностного натяжения с мылом
Воспроизвести медиа Экспериментальная демонстрация поверхностного натяжения с мылом Поверхностное натяжение - это тенденция жидких поверхностей в состоянии покоя сжиматься до минимально возможной площади поверхности. Поверхностное натяжение - это то, что позволяет объектам с более высокой плотностью, чем вода, таким как бритвенные лезвия и насекомые (например, водомеры ), плавать по поверхности воды, даже не будучи частично погруженными в воду.
На границах раздела жидкость-воздух поверхностное натяжение возникает в результате большего притяжения молекул жидкости друг к другу (из-за когезии ), чем к молекулам в воздухе (из-за адгезии ).
Здесь задействованы два основных механизма. Один из них - внутренняя сила, действующая на молекулы поверхности, заставляющая жидкость сжиматься. Во-вторых, это касательная сила, параллельная поверхности жидкости. Эту касательную силу (на единицу длины) обычно называют поверхностным натяжением. В результате жидкость ведет себя так, как если бы ее поверхность была покрыта растянутой эластичной мембраной. Но эта аналогия не должна быть слишком далека, как напряжение в упругой мембране, зависит от степени деформации мембраны в то время как поверхностное натяжение является неотъемлемым свойством жидкости - воздуха или жидкости - интерфейс пара.
Из-за относительно высокого притяжения молекул воды друг с другом через паутину водородных связей, вода имеет более высокое поверхностное натяжение (72,8 мН (Мn) на метр при 20 ° C), чем большинство других жидкостей. Поверхностное натяжение - важный фактор в явлении капиллярности.
Поверхностное натяжение имеет размерность в силу на единицу длины, или энергии на единицу площади. Эти два понятия эквивалентны, но когда речь идет об энергии на единицу площади, обычно используется термин поверхностная энергия, который является более общим термином в том смысле, что он применим также к твердым телам.
В материаловедении поверхностное натяжение используется для определения поверхностного напряжения или поверхностной энергии.
 Схема сил сцепления на молекулах жидкости
Схема сил сцепления на молекулах жидкости Из-за сил сцепления молекула одинаково тянется во всех направлениях соседними молекулами жидкости, в результате чего результирующая сила равна нулю. Молекулы на поверхности не имеют одинаковых молекул со всех сторон и поэтому притягиваются внутрь. Это создает некоторое внутреннее давление и заставляет жидкие поверхности сжиматься до минимальной площади.
Также существует натяжение, параллельное поверхности на границе раздела жидкость-воздух, которое будет противостоять внешней силе из-за когезионной природы молекул воды.
Силы притяжения, действующие между молекулами одного типа, называются силами сцепления, а силы, действующие между молекулами разных типов, - силами сцепления. Баланс между сцеплением жидкости и ее адгезией к материалу контейнера определяет степень смачивания, угол контакта и форму мениска. Когда когезия преобладает (в частности, энергия адгезии составляет менее половины энергии сцепления), смачивание низкое и мениск выпуклый у вертикальной стенки (как для ртути в стеклянном контейнере). С другой стороны, когда адгезия преобладает (энергия адгезии превышает половину энергии сцепления), смачивание высокое и аналогичный мениск вогнутый (как в воде в стакане).
Поверхностное натяжение отвечает за форму жидких капель. Хотя капли воды легко деформируются, они имеют тенденцию принимать сферическую форму из-за дисбаланса сил сцепления поверхностного слоя. В отсутствие других сил капли практически всех жидкостей были бы приблизительно сферическими. Сферическая форма минимизирует необходимое «пристенное натяжение» поверхностного слоя в соответствии с законом Лапласа.
 Капля воды, лежащая на штофе. Поверхностное натяжение достаточно велико, чтобы не допустить плавания под тканью.
Капля воды, лежащая на штофе. Поверхностное натяжение достаточно велико, чтобы не допустить плавания под тканью. Другой способ увидеть поверхностное натяжение - это энергия. Молекула в контакте с соседом находится в более низком энергетическом состоянии, чем если бы она была одна. Внутренние молекулы имеют столько соседей, сколько они могут иметь, но граничные молекулы не имеют соседей (по сравнению с внутренними молекулами) и, следовательно, имеют более высокую энергию. Чтобы жидкость минимизировала свое энергетическое состояние, необходимо минимизировать количество граничных молекул с более высокой энергией. Минимальное количество граничных молекул приводит к минимальной площади поверхности. В результате минимизации площади поверхности поверхность примет максимально гладкую форму (математическое доказательство того, что «гладкие» формы минимизируют площадь поверхности, основано на использовании уравнения Эйлера – Лагранжа ). Поскольку любая кривизна формы поверхности приводит к увеличению площади, в результате также будет увеличиваться энергия.
С обычной водой можно увидеть несколько эффектов поверхностного натяжения:

А. Водяные бусинки на листе

Б. Вода капает из-под крана

C. Водомеры остаются наверху жидкости из-за поверхностного натяжения.

D. Лавовая лампа с взаимодействием разнородных жидкостей: воды и жидкого воска.

E. Фотография, показывающая феномен " винных слез ".
Поверхностное натяжение проявляется в других распространенных явлениях, особенно когда для его уменьшения используются поверхностно-активные вещества :
Поверхностное натяжение, обозначенное символом γ (альтернативно σ или T ), измеряется в силе на единицу длины. Его СИ единица ньютон на метр, но СГС единица дин на сантиметр также используется. Например,
 На этой диаграмме показано усилие, необходимое для увеличения площади поверхности. Эта сила пропорциональна поверхностному натяжению.
На этой диаграмме показано усилие, необходимое для увеличения площади поверхности. Эта сила пропорциональна поверхностному натяжению. Поверхностное натяжение можно определить как силу или энергию.
Поверхностное натяжение жидкости γ - это сила на единицу длины. На иллюстрации справа прямоугольная рамка состоит из трех неподвижных сторон (черные), образующих U-образную форму, и четвертой подвижной стороны (синей), которая может сдвигаться вправо. Поверхностное натяжение потянет синюю полосу влево; сила F, необходимая для удержания подвижной стороны, пропорциональна длине L неподвижной стороны. Таким образом, соотношение F/Lзависит только от внутренних свойств жидкости (состава, температуры и т. д.), а не от ее геометрии. Например, если рамка имела более сложную форму, соотношениеF/L, где L - длина подвижной стороны, а F - сила, необходимая для предотвращения скольжения, одинакова для всех форм. Поэтому мы определяем поверхностное натяжение как
Причина 1/2состоит в том, что пленка имеет две стороны (две поверхности), каждая из которых вносит равный вклад в силу; поэтому сила, вносимая одной стороной, равна γL =F/2.
Поверхностное натяжение жидкости γ - это отношение изменения энергии жидкости к изменению площади поверхности жидкости (которое привело к изменению энергии). Это можно легко связать с предыдущим определением с точки зрения силы: если F - сила, необходимая для предотвращения начала скольжения стороны, то это также сила, которая будет удерживать сторону в состоянии скольжения с постоянной скоростью ( по второму закону Ньютона). Но если сторона движется вправо (в направлении приложения силы), то площадь поверхности растянутой жидкости увеличивается, в то время как приложенная сила выполняет работу с жидкостью. Это означает, что увеличение площади поверхности увеличивает энергию пленки. Работа, совершаемая силой F при перемещении стороны на расстояние Δ x, равна W = F Δ x ; при этом общая площадь пленки увеличивается на Δ A = 2 L Δ x (коэффициент 2 здесь, потому что жидкость имеет две стороны, две поверхности). Таким образом, умножая числитель и знаменатель γ =1/2F/Lпо Δ x, получаем
Эта работа W, согласно обычным аргументам, интерпретируется как запасенная как потенциальная энергия. Следовательно, поверхностное натяжение можно также измерить в системе СИ как джоуль на квадратный метр и в системе СГС как эрг на см 2. Поскольку механические системы пытаются найти состояние минимальной потенциальной энергии, свободная капля жидкости естественным образом принимает сферическую форму, которая имеет минимальную площадь поверхности для данного объема. Эквивалентность измерения энергии на единицу площади и силы на единицу длины может быть доказана анализом размеров.
 Силы поверхностного натяжения, действующие на крошечный (дифференциальный) участок поверхности. δθ x и δθ y указывают величину изгиба по размерам заплатки. Уравновешивание сил натяжения и давления приводит к уравнению Юнга – Лапласа
Силы поверхностного натяжения, действующие на крошечный (дифференциальный) участок поверхности. δθ x и δθ y указывают величину изгиба по размерам заплатки. Уравновешивание сил натяжения и давления приводит к уравнению Юнга – Лапласа Если никакая сила не действует перпендикулярно натянутой поверхности, поверхность должна оставаться плоской. Но если давление на одной стороне поверхности отличается от давления на другой стороне, разность давлений, умноженная на площадь поверхности, дает нормальную силу. Чтобы силы поверхностного натяжения нейтрализовали силу давления, поверхность должна быть искривленной. На диаграмме показано, как кривизна поверхности крошечного участка поверхности приводит к суммарной составляющей сил поверхностного натяжения, действующих перпендикулярно центру пятна. Когда все силы уравновешены, результирующее уравнение известно как уравнение Юнга – Лапласа :
куда:
Величина в скобках справа фактически (в два раза) средняя кривизна поверхности (в зависимости от нормировки). Решения этого уравнения определяют форму водяных капель, луж, менисков, мыльных пузырей и все другие формы, определяемые поверхностным натяжением (например, форму отпечатков, которые ноги водомета оставляют на поверхности пруда). В таблице ниже показано, как внутреннее давление капли воды увеличивается с уменьшением радиуса. Для не очень маленьких капель эффект незначителен, но разница в давлении становится огромной, когда размер капель приближается к размеру молекулы. (В пределах одной молекулы концепция теряет смысл.)
| Радиус капли | 1 мм | 0,1 мм | 1 мкм | 10 нм |
|---|---|---|---|---|
| Δ p ( атм ) | 0,0014 | 0,0144 | 1,436 | 143,6 |
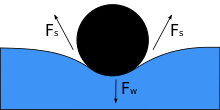 Поперечное сечение иглы, плавающей на поверхности воды. F w - вес, а F s - равнодействующие силы поверхностного натяжения.
Поперечное сечение иглы, плавающей на поверхности воды. F w - вес, а F s - равнодействующие силы поверхностного натяжения. Когда объект помещается на жидкость, его вес F w оказывает давление на поверхность, и если поверхностное натяжение и направленная вниз сила становятся равными, то это уравновешивается силами поверхностного натяжения с обеих сторон F s, каждая из которых параллельна поверхности воды в точке точки соприкосновения с объектом. Обратите внимание, что небольшое движение тела может привести к тому, что объект утонет. По мере уменьшения угла контакта поверхностное натяжение уменьшается. Горизонтальные компоненты двух стрелок F s указывают в противоположных направлениях, поэтому они компенсируют друг друга, но вертикальные компоненты указывают в одном направлении и, следовательно, складываются для баланса F w. Поверхность объекта не должна быть смачиваемой, а его вес должен быть достаточно низким, чтобы поверхностное натяжение могло его выдержать. Если m обозначает массу иглы и ускорение силы тяжести g, мы имеем
 Минимальная поверхность
Минимальная поверхность Найти форму минимальной поверхности, ограниченной рамкой произвольной формы, с помощью строго математических средств может быть непростой задачей. Тем не менее, если сделать каркас из проволоки и окунуть его в мыльный раствор, в полученной мыльной пленке в течение нескольких секунд появится локально минимальная поверхность.
Причина этого в том, что разность давлений на границе раздела жидкостей пропорциональна средней кривизне, как видно из уравнения Юнга – Лапласа. Для открытой мыльной пленки перепад давления равен нулю, следовательно, средняя кривизна равна нулю, а минимальные поверхности обладают свойством нулевой средней кривизны.
Поверхность любой жидкости - это граница между этой жидкостью и какой-либо другой средой. Например, верхняя поверхность пруда - это поверхность раздела между водой пруда и воздухом. Таким образом, поверхностное натяжение - это свойство не только жидкости, а свойство границы раздела жидкости с другой средой. Если жидкость находится в контейнере, то помимо поверхности раздела жидкость / воздух на его верхней поверхности существует также поверхность раздела между жидкостью и стенками контейнера. Поверхностное натяжение между жидкостью и воздухом обычно отличается (больше) от его поверхностного натяжения со стенками контейнера. И там, где две поверхности встречаются, их геометрия должна быть такой, чтобы все силы уравновешивались.
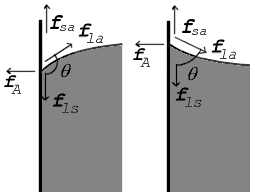 Усилия в точке контакта показаны для угла контакта более 90 ° (слева) и менее 90 ° (справа) Усилия в точке контакта показаны для угла контакта более 90 ° (слева) и менее 90 ° (справа) |
Там, где две поверхности встречаются, они образуют угол контакта, amp; thetas, который является угол касательной к поверхности образует с поверхностью твердого тела. Обратите внимание, что угол измеряется через жидкость, как показано на диаграммах выше. На диаграмме справа показаны два примера. Силы натяжения показаны для границы раздела жидкость-воздух, границы раздела жидкость-твердое тело и границы раздела твердое тело-воздух. В примере слева разность между поверхностным натяжением жидкость – твердое тело и твердое тело – воздух, γ ls - γ sa, меньше поверхностного натяжения жидкость – воздух γ la, но, тем не менее, положительна, т. Е.
На диаграмме как вертикальные, так и горизонтальные силы должны компенсироваться точно в точке контакта, известной как равновесие. Горизонтальная составляющая F ла отменяется адгезивной силой, F A.
Однако более показательный баланс сил находится в вертикальном направлении. Вертикальная составляющая f la должна точно компенсировать разность сил вдоль твердой поверхности, f ls - f sa.
| Жидкость | Твердый | Угол контакта | |||
|---|---|---|---|---|---|
| воды |
| 0 ° | |||
| спирт этиловый | |||||
| диэтиловый эфир | |||||
| четыреххлористый углерод | |||||
| глицерин | |||||
| уксусная кислота | |||||
| воды | парафиновая свеча | 107 ° | |||
| Серебряный | 90 ° | ||||
| метилиодид | натриево-известковое стекло | 29 ° | |||
| свинцовое стекло | 30 ° | ||||
| плавленый кварц | 33 ° | ||||
| Меркурий | натриево-известковое стекло | 140 ° | |||
| Некоторые краевые углы между жидкостью и твердым телом | |||||
Поскольку силы прямо пропорциональны их поверхностному натяжению, мы также имеем:
куда
Это означает, что, хотя разницу между поверхностным натяжением жидкость – твердое тело и твердое тело – воздух, γ ls - γ sa, трудно измерить напрямую, ее можно вывести из поверхностного натяжения жидкость – воздух, γ la, и равновесного краевого угла смачивания., θ, который является функцией легко измеряемых углов контакта при приближении и удалении (см. угол контакта основного изделия).
Такая же взаимосвязь существует на диаграмме справа. Но в этом случае мы видим, что, поскольку угол смачивания меньше 90 °, разница поверхностного натяжения жидкость-твердое тело / твердое тело-воздух должна быть отрицательной:
Обратите внимание, что в частном случае границы раздела вода-серебро, когда угол смачивания равен 90 °, разница поверхностного натяжения жидкость-твердое тело / твердое тело-воздух точно равна нулю.
Другой особый случай - угол контакта точно 180 °. К этому подходит вода со специально подготовленным тефлоном. Угол контакта 180 ° возникает, когда поверхностное натяжение жидкость – твердое тело в точности равно поверхностному натяжению жидкость – воздух.
 Тензиометр силы использует метод кольца Дю Нюи и метод пластины Вильгельми.
Тензиометр силы использует метод кольца Дю Нюи и метод пластины Вильгельми. Поскольку поверхностное натяжение проявляется в различных эффектах, он предлагает несколько способов его измерения. Выбор оптимального метода зависит от природы измеряемой жидкости, условий измерения ее натяжения и устойчивости ее поверхности при ее деформации. Инструмент, измеряющий поверхностное натяжение, называется тензиометром.
 Поверхностное натяжение можно измерить методом подвесной капли на гониометре.
Поверхностное натяжение можно измерить методом подвесной капли на гониометре. 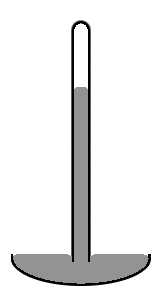 Схема ртутного барометра
Схема ртутного барометра Ртутный барометр старого образца состоит из вертикальной стеклянной трубки диаметром около 1 см, частично заполненной ртутью, и с вакуумом (так называемым вакуумом Торричелли ) в незаполненном объеме (см. Диаграмму справа). Обратите внимание, что уровень ртути в центре трубки выше, чем по краям, что делает верхнюю поверхность ртути куполообразной. Центр масс всего столбика ртути был бы немного ниже, если бы верхняя поверхность ртути была бы плоской по всему поперечному сечению трубки. Но куполообразный верх дает немного меньшую площадь поверхности всей массе ртути. Снова два эффекта объединяются, чтобы минимизировать общую потенциальную энергию. Такая форма поверхности известна как выпуклый мениск.
Мы рассматриваем площадь поверхности всей массы ртути, включая ту часть поверхности, которая контактирует со стеклом, потому что ртуть вообще не прилипает к стеклу. Таким образом, поверхностное натяжение ртути действует по всей площади ее поверхности, в том числе там, где она контактирует со стеклом. Если бы вместо стекла трубку сделали из меди, ситуация была бы совсем другой. Ртуть агрессивно прилипает к меди. Таким образом, в медной трубке уровень ртути в центре трубки будет ниже, чем на краях (то есть это будет вогнутый мениск). В ситуации, когда жидкость прилипает к стенкам своего контейнера, мы считаем, что часть площади поверхности жидкости, которая контактирует с контейнером, имеет отрицательное поверхностное натяжение. Затем жидкость работает, чтобы максимизировать площадь контактной поверхности. Таким образом, в этом случае увеличение площади контакта с контейнером скорее уменьшает, чем увеличивает потенциальную энергию. Этого уменьшения достаточно, чтобы компенсировать повышенную потенциальную энергию, связанную с подъемом жидкости возле стенок контейнера.
 Иллюстрация капиллярного подъема и падения. Красный = угол контакта менее 90 °; синий = угол контакта больше 90 °
Иллюстрация капиллярного подъема и падения. Красный = угол контакта менее 90 °; синий = угол контакта больше 90 ° Если трубка достаточно узкая и прилипание жидкости к ее стенкам достаточно сильное, поверхностное натяжение может подтягивать жидкость вверх по трубке, что называется капиллярным действием. Высота, на которую поднимается колонна, определяется законом Юрина :
куда
 Кривая профиля кромки лужи при краевом угле смачивания 180 °. Кривая задается формулой: где
Кривая профиля кромки лужи при краевом угле смачивания 180 °. Кривая задается формулой: где  Небольшие лужицы воды на гладкой чистой поверхности имеют ощутимую толщину.
Небольшие лужицы воды на гладкой чистой поверхности имеют ощутимую толщину. Если вылить ртуть на горизонтальный плоский лист стекла, образуется лужа ощутимой толщины. Лужа будет расширяться только до такой степени, что ее толщина будет чуть меньше полсантиметра, и не тоньше. Опять же, это связано с действием сильного поверхностного натяжения ртути. Жидкая масса выравнивается, потому что это приводит как можно больше ртути к максимально низкому уровню, но в то же время поверхностное натяжение сокращает общую площадь поверхности. Результатом компромисса является лужа почти фиксированной толщины.
Такую же демонстрацию поверхностного натяжения можно провести с водой, известковой водой или даже солевым раствором, но только на поверхности, сделанной из вещества, к которому вода не прилипает. Воск - такое вещество. Вода, налитая на гладкую плоскую горизонтальную восковую поверхность, скажем, на вощеный лист стекла, будет вести себя так же, как ртуть, налитая на стекло.
Толщина лужи жидкости на поверхности, угол смачивания которой составляет 180 °, определяется по формуле:
куда
На самом деле толщина луж будет немного меньше, чем предсказывается приведенной выше формулой, потому что очень немногие поверхности имеют угол контакта 180 ° с любой жидкостью. Когда угол контакта меньше 180 °, толщина определяется по формуле:
Для ртути на стекле γ Hg = 487 дин / см, ρ Hg = 13,5 г / см 3 и θ = 140 °, что дает h Hg = 0,36 см. Для воды на парафине при 25 ° C γ = 72 дин / см, ρ = 1,0 г / см 3 и θ = 107 °, что дает h H 2 O = 0,44 см.
Формула также предсказывает, что когда угол смачивания равен 0 °, жидкость будет растекаться в виде микротонкого слоя по поверхности. Такая поверхность считается полностью смачиваемой жидкостью.
 Распад вытянутой струи воды на капли из-за поверхностного натяжения. Основная статья: Неустойчивость Плато – Рэлея
Распад вытянутой струи воды на капли из-за поверхностного натяжения. Основная статья: Неустойчивость Плато – Рэлея В повседневной жизни все мы замечаем, что поток воды, выходящий из крана, распадается на капли, независимо от того, насколько плавно поток выходит из крана. Это происходит из-за явления, называемого неустойчивостью Плато – Рэлея, которое полностью является следствием эффектов поверхностного натяжения.
Объяснение этой нестабильности начинается с существования крошечных возмущений в потоке. Они всегда присутствуют, независимо от того, насколько плавный поток. Если возмущения разделить на синусоидальные компоненты, мы обнаружим, что некоторые компоненты со временем растут, а другие со временем затухают. Среди тех, которые растут со временем, одни растут быстрее, чем другие. Будет ли компонент распадаться или расти, и насколько быстро он растет, полностью зависит от его волнового числа (мера того, сколько пиков и впадин на сантиметр) и радиусов исходного цилиндрического потока.
Дж. У. Гиббс разработал термодинамическую теорию капиллярности, основанную на идее поверхностей разрыва. Гиббс рассмотрел случай, когда острая математическая поверхность помещается где-то внутри микроскопически нечеткой физической границы раздела двух однородных веществ. Понимая, что точный выбор местоположения поверхности был несколько произвольным, он оставил его гибким. Поскольку поверхность раздела находится в тепловом и химическом равновесии с веществами вокруг нее (имеющими температуру T и химические потенциалы μ i), Гиббс рассмотрел случай, когда поверхность может иметь избыточную энергию, избыточную энтропию и избыточные частицы, найдя естественную функцию свободной энергии в данном случае быть величиной, позже названной великим потенциалом и получившей символ.
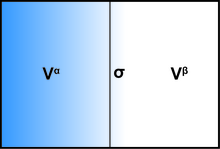 Размещение Гиббсом точной математической поверхности в нечетком физическом интерфейсе.
Размещение Гиббсом точной математической поверхности в нечетком физическом интерфейсе. Рассматривая данный подобъем, содержащий поверхность разрыва, объем делится математической поверхностью на две части A и B, с объемами и, с точно. Теперь, если эти две частей А и В были гомогенные жидкости (с давлением,) и оставался совершенно однородными вплоть до математической границы, без каких - либо поверхностных эффектов, общий грандиозный потенциал этого объема будет просто. Представляющие интерес поверхностные эффекты являются модификацией этого, и все они могут быть собраны в член поверхностной свободной энергии, так что общий великий потенциал объема становится:
Для достаточно макроскопических и слегка изогнутых поверхностей свободная энергия поверхности должна быть просто пропорциональна площади поверхности:
для поверхностного натяжения и площади поверхности.
Как указано выше, это подразумевает, что механическая работа, необходимая для увеличения площади поверхности A, равна dW = γ dA, при условии, что объемы с каждой стороны не изменяются. Термодинамика требует, чтобы для систем, поддерживаемых при постоянных химическом потенциале и температуре, все спонтанные изменения состояния сопровождались уменьшением этой свободной энергии, то есть увеличением полной энтропии с учетом возможного движения энергии и частиц с поверхности в окружающие жидкости. Отсюда легко понять, почему уменьшение площади поверхности массы жидкости всегда происходит самопроизвольно, при условии, что это не связано с какими-либо другими изменениями энергии. Отсюда следует, что для увеличения площади поверхности необходимо добавить определенное количество энергии.
Гиббс и другие ученые боролись с произволом в точном микроскопическом расположении поверхности. Для микроскопических поверхностей с очень малой кривизной неверно предполагать, что поверхностное натяжение не зависит от размера, и в игру вступают такие вопросы, как длина Толмена. Для поверхности макроскопических размеров (и плоских поверхностей) размещение поверхности не оказывает значительного влияния на γ, однако оно оказывает очень сильное влияние на значения поверхностной энтропии, поверхностной плотности избыточной массы и поверхностной внутренней энергии, которые частные производные функции поверхностного натяжения.
Гиббс подчеркнул, что для твердых тел свободная энергия поверхности может полностью отличаться от поверхностного напряжения (то, что он назвал поверхностным натяжением): свободная энергия поверхности - это работа, необходимая для формирования поверхности, а поверхностное напряжение - это работа, необходимая для растяжения поверхности. В случае границы раздела двух жидкостей нет различия между формованием и растяжением, потому что жидкости и поверхность полностью восстанавливают свою природу, когда поверхность растягивается. Для твердого тела даже упругое растяжение поверхности приводит к коренным изменениям поверхности. Кроме того, поверхностное напряжение на твердом теле является направленной величиной ( тензором напряжений ), а поверхностная энергия - скалярной.
Спустя пятнадцать лет после Гиббса Дж. Д. Ван дер Ваальс разработал теорию капиллярных эффектов, основанную на гипотезе непрерывного изменения плотности. Он добавил к плотности энергии член, где c - коэффициент капиллярности, а ρ - плотность. Для многофазных равновесий результаты подхода Ван-дер-Ваальса практически совпадают с формулами Гиббса, но для моделирования динамики фазовых переходов гораздо удобнее подход Ван-дер-Ваальса. Энергия капиллярности Ван-дер-Ваальса в настоящее время широко используется в моделях фазового поля многофазных течений. Такие члены обнаруживаются и в динамике неравновесных газов.
Давление внутри идеального сферического пузыря может быть получено из соображений термодинамики свободной энергии. Вышеуказанная свободная энергия может быть записана как:
где - разность давлений между внутренней (A) и внешней (B) стороной пузырька, а - объемом пузырька. В состоянии равновесия dΩ = 0, поэтому
Для сферического пузыря объем и площадь поверхности задаются просто как
а также
Подставляя эти соотношения в предыдущее выражение, находим
что эквивалентно уравнению Юнга – Лапласа при R x = R y.
 Температурная зависимость поверхностного натяжения между жидкой и паровой фазами чистой воды
Температурная зависимость поверхностного натяжения между жидкой и паровой фазами чистой воды 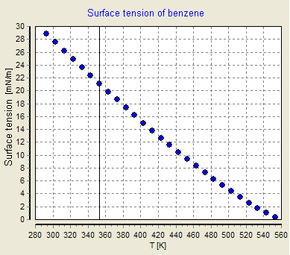 Температурная зависимость поверхностного натяжения бензола
Температурная зависимость поверхностного натяжения бензола Поверхностное натяжение зависит от температуры. По этой причине, когда указывается значение поверхностного натяжения границы раздела, температура должна быть явно указана. Общая тенденция состоит в том, что поверхностное натяжение уменьшается с повышением температуры, достигая значения 0 при критической температуре. Для получения дополнительной информации см. Правило Этвёша. Есть только эмпирические уравнения, связывающие поверхностное натяжение и температуру:
Здесь V - молярный объем вещества, T C - критическая температура, а k - постоянная величина, действующая почти для всех веществ. Типичное значение k =2,1 × 10 −7 Дж К −1 моль - 2 ⁄ 3. Для воды можно дополнительно использовать V = 18 мл / моль и T C = 647 K (374 ° C).
Вариант на Eötvös описан Рамаем и Шилдсом:
где температурный сдвиг на 6 K обеспечивает лучшее соответствие формулы с реальностью при более низких температурах.
γ ° - константа для каждой жидкости, а n - эмпирический коэффициент, значение которого11/9для органических жидкостей. Это уравнение было также предложено ван дер Ваальсом, который далее предположил, что γ ° может быть задано выражением
где K 2 - универсальная константа для всех жидкостей, а P C - критическое давление жидкости (хотя более поздние эксперименты показали, что K 2 в некоторой степени варьируется от одной жидкости к другой).
И Гуггенхайм – Катаяма, и Этвеш принимают во внимание тот факт, что поверхностное натяжение достигает 0 при критической температуре, тогда как Рамай и Шилдс не соответствуют действительности в этой конечной точке.
Растворенные вещества могут по-разному влиять на поверхностное натяжение в зависимости от природы поверхности и растворенного вещества:
Эффект усложняется тем, что растворенное вещество может существовать в другой концентрации на поверхности растворителя, чем в его объеме. Эта разница варьируется от одной комбинации растворенного вещества и растворителя к другой.
Изотерма Гиббса утверждает, что:
При ее выводе принимаются некоторые допущения, поэтому изотерма Гиббса может применяться только к идеальным (очень разбавленным) растворам с двумя компонентами.
Соотношение Клаузиуса – Клапейрона приводит к другому уравнению, также приписываемому Кельвину, как уравнение Кельвина. Это объясняет, почему из-за поверхностного натяжения давление пара для маленьких капель жидкости в суспензии больше, чем стандартное давление пара той же жидкости, когда граница раздела плоская. То есть, когда жидкость образует маленькие капли, равновесная концентрация ее пара в окружающей среде больше. Это возникает из-за того, что давление внутри капли больше, чем снаружи.
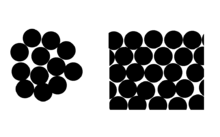 Молекулы на поверхности крошечной капли (слева) имеют в среднем меньше соседей, чем молекулы на плоской поверхности (справа). Следовательно, они более слабо связаны с каплей, чем молекулы с плоской поверхностью.
Молекулы на поверхности крошечной капли (слева) имеют в среднем меньше соседей, чем молекулы на плоской поверхности (справа). Следовательно, они более слабо связаны с каплей, чем молекулы с плоской поверхностью. Эффект объясняет перенасыщение паров. При отсутствии центров зародышеобразования крошечные капельки должны образоваться, прежде чем они смогут превратиться в более крупные капли. Для этого требуется давление пара, во много раз превышающее давление пара в точке фазового перехода.
Это уравнение также используется в химии катализаторов для оценки мезопористости твердых веществ.
Эффект можно рассматривать с точки зрения среднего числа молекулярных соседей поверхностных молекул (см. Диаграмму).
В таблице приведены некоторые расчетные значения этого эффекта для воды при разных размерах капель:
| п/P 0для капель воды разного радиуса на СТП | ||||
|---|---|---|---|---|
| Радиус капли (нм) | 1000 | 100 | 10 | 1 |
| п/P 0 | 1,001 | 1.011 | 1,114 | 2,95 |
Эффект становится очевидным для капель очень маленького размера, поскольку капля радиусом 1 нм имеет внутри около 100 молекул, что достаточно мало, чтобы потребовать анализа квантовой механики.
Два наиболее распространенных жидкостей на Земле пресные воды и морской воды. В этом разделе приведены корреляции справочных данных для поверхностного натяжения обоих.
Поверхностное натяжение чистой жидкой воды в контакте с ее паром было определено IAPWS как
где T и критическая температура T C = 647,096 K выражены в кельвинах. Область действия всей кривой парожидкостного насыщения от тройной точки (0,01 ° C) до критической точки. Он также обеспечивает разумные результаты при экстраполяции к метастабильным (переохлажденным) условиям, по крайней мере, до -25 ° C. Этот состав был первоначально принят IAPWS в 1976 году и был скорректирован в 1994 году для соответствия Международной температурной шкале 1990 года.
Неопределенность этой формулировки дана во всем диапазоне температур IAPWS. Для температур ниже 100 ° C погрешность составляет ± 0,5%.
Nayar et al. опубликованные справочные данные для поверхностного натяжения морской воды в диапазоне солености 20 ≤ S ≤ 131 г / кг и диапазоне температур 1 ≤ t ≤ 92 ° C при атмосферном давлении. Диапазон температуры и солености охватывает как океанографический диапазон, так и диапазон условий, встречающихся в технологиях термического опреснения. Погрешность измерений варьировалась от 0,18 до 0,37 мН / м при средней погрешности 0,22 мН / м.
Nayar et al. коррелировал данные со следующим уравнением
где γ sw - поверхностное натяжение морской воды в мН / м, γ w - поверхностное натяжение воды в мН / м, S - эталонная соленость в г / кг, а t - температура в градусах Цельсия. Среднее абсолютное процентное отклонение между измерениями и корреляцией составило 0,19%, а максимальное отклонение - 0,60%.
Международная ассоциация свойств воды и пара (IAPWS) приняла это соотношение в качестве международного стандарта.
| Жидкость | Температура (° C) | Поверхностное натяжение, γ |
|---|---|---|
| Уксусная кислота | 20 | 27,60 |
| Уксусная кислота (45,1%) + вода | 30 | 40,68 |
| Уксусная кислота (10,0%) + вода | 30 | 54,56 |
| Ацетон | 20 | 23,70 |
| Кровь | 22 | 55,89 |
| Диэтиловый эфир | 20 | 17.00 |
| Спирт этиловый | 20 | 22,27 |
| Этанол (40%) + вода | 25 | 29,63 |
| Этанол (11,1%) + вода | 25 | 46,03 |
| Глицерин | 20 | 63,00 |
| н- гексан | 20 | 18,40 |
| Водный раствор соляной кислоты 17,7 М | 20 | 65,95 |
| Изопропанол | 20 | 21,70 |
| Жидкий гелий II | −273 | 0,37 |
| Жидкий азот | −196 | 8,85 |
| Жидкий кислород | −182 | 13,2 |
| Меркурий | 15 | 487,00 |
| Метанол | 20 | 22,60 |
| Расплавленный хлорид серебра | 650 | 163 |
| Расплавленный хлорид натрия / хлорид кальция (47/53 мол.%) | 650 | 139 |
| н- октан | 20 | 21,80 |
| 6,0 М водный раствор натрия хлорида | 20 | 82,55 |
| Сахароза (55%) + вода | 20 | 76,45 |
| Воды | 0 | 75,64 |
| Воды | 25 | 71,97 |
| Воды | 50 | 67,91 |
| Воды | 100 | 58,85 |
| Толуол | 25 | 27,73 |

Разрушение движущегося листа воды, отскакивающего от ложки.

Фотография проточной воды, прилипшей к руке. Поверхностное натяжение создает полосу воды между потоком и рукой.

Мыльный пузырь уравновешивает силы поверхностного натяжения и внутреннее пневматическое давление.

Поверхностное натяжение предотвращает погружение монеты: монета, несомненно, плотнее воды, поэтому она должна смещать объем, превышающий ее собственный, чтобы плавучесть уравновесила массу.

Алюминиевая монета плавает на поверхности воды при температуре 10 ° C. Любой лишний вес опустит монету на дно.

Маргаритка. Цветок полностью лежит ниже уровня (ненарушенной) свободной поверхности. Вода плавно поднимается по его краю. Поверхностное натяжение предотвращает попадание воды в воздух между лепестками и, возможно, погружение цветка.

Металлическая скрепка плывет по воде. Несколько обычно можно аккуратно добавить без переливания воды.

Металлическая скрепка, плавающая на воде. Решетка перед источником света создала «контурные линии», которые показывают деформацию водной поверхности, вызванную металлической скрепкой для бумаг.