Смачивание

Способность жидкости поддерживать контакт с твердой поверхностью Водные шарики на ткани, которая не смачивается химическими веществами Рис. 1. Краевой угол смачивания капли жидкости на твердой поверхности

Смачивание - это способность жидкости поддерживать контакт с твердым телом поверхность, возникающая в результате межмолекулярных взаимодействий, когда они сводятся вместе. Степень смачивания (смачиваемость) определяется балансом сил между адгезивными и когезионными силами. Смачивание имеет дело с тремя жидкими фазами вещества: газом, мощностью и твердым телом. В настоящее время он находится в центре внимания нанотехнологии и нанонаук в связи с созданием многих наноматериалов за последние два десятилетия (например, графен, углеродная нанотрубка, нитрид бора наномеш ).

Смачивание важно для соединения или сцепления двух материалов. Смачивание и поверхностные силы, которые контролируют смачивание, также ответственны за другие эффекты, включая капиллярные эффекты.

Существует два типа смачивания: нереактивное смачивание и активное смачивание.

• 1 Пояснение
• 2 Высокоэнергетические и низкоэнергетические поверхности
  • 2.1 Смачивание на низком уровне -энергетические поверхности
• 3 Содержание Идеальные твердые поверхности
  • 3.1 Минимизация энергии, три фазы
    • 3.1.1 Упрощение до планарной геометрии, соотношение Юнга
    • 3.1.2 Упрощение до плоской геометрии, полученное из вариационных вычислений
    • 3.1.3 Неидеальные гладкие поверхности и краевой угол Юнга
    • 3.1.4 Уравнение Юнга - Дюпре и коэффициент распространение
    • 3.1.5 Уравнение Джаспера-Ананда для плоских и изогнутых поверхностей
  • 3.2 Расчетное прогнозирование смачивания
• 4 Неидеальные шероховатые твердые поверхности
  • 4.1 Модель Венцеля
  • 4.2 Модель Кэсси - Бакстера
    • 4.2. 1 Пленка-предшественник
    • 4.2.2 «Эффект лепестка» против «лотоса» эффект "
  • 4.3 Переход Кэсси-Бакстера к Венцеля
• 5 Динамика растекания
• 6 Изменение смачиваемости
  • 6.1 Поверхностно-активные вещества
  • 6.2 Поверхностны е изменения
  • 6.3 Кислородные вакансии
• 7 См. также
• 8 Ссылки
• 9 Дополнительная литература
• 10 Внешние ссылки

Адгезионные силы между жидкостью и твердым телом вызывают образование жидкости падение, чтобы растекаться по поверхности. Силы сцепления внутри жидкости заставляют каплю скатываться и избегать контакта с поверхностью.

Рис. 2	Угол смачивания	Степень. смачивания	Сила взаимодействия
			Твердое тело - жидкость	Жидкость - жидкость
S	θ = 0	Идеальное смачивание	Сильное	Слабое
C	0 < θ < 90°	Высокая смачиваемость	Сильное	Сильное
			Слабое	Слабая
B	90 ° ≤ θ < 180°	Низкая смачиваемость	Слабая	Сильная
A	θ = 180 °	Несмачиваемая	Слабое	Сильное

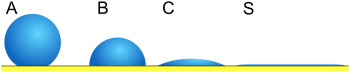Рис. 2: Смачивание разных жидкостей: A показывает жидкость с очень небольшим смачиванием, а C показывает жидкость с большим смачиванием. A имеет большой угол смачивания, а C - небольшой угол смачивания.

Угол смачивания (θ), как показано на рисунке 1, представляет собой угол, под которым граница раздела жидкость-пар встречается с твердым телом. –Жидкий интерфейс. Угол контакта определяется балансом между адгезионными и когезионными силами. По мере того, как тенденция капли растекаться по плоской твердой поверхности увеличивается, угол смачивания уменьшается. Таким образом, контактный угол обеспечивает обратную меру смачиваемости.

Контактный угол менее 90 ° (низкий контактный угол) обычно указывает на то, что смачивание поверхности очень благоприятно, и жидкость будет распространяться по большой площади. поверхности. Углы смачивания, превышающие 90 ° (высокий угол смачивания), обычно означают, что смачивание поверхности неблагоприятно, поэтому жидкость минимизирует контакт с поверхностью и образует компактную каплю жидкости.

Для воды смачиваемая поверхность также может быть названа гидрофильная, а несмачиваемая поверхность гидрофобной. Супергидрофобные поверхности имеют краевые углы более 150 °, при этом контакт между каплей жидкости и поверхности практически отсутствует. Иногда это называют «эффектом лотоса ». В таблице представлены углы смачивания и соответствующие им примеры твердого тела / жидкость и жидкость / жидкость. Для неводных жидкостей термин «лиофильный» используется для условий с низким углом смачивания, термин «лиофобный» используется для обозначения более высоких углов смачивания. Точно так же термины омнифобный и омнифильный как к полярным, так и к неполярным жидкостям.

Жидкости могут взаимодействовать с двумя типами твердых поверхностей. Традиционно твердые поверхности подразделяются на твердые тела с высокой энергией и твердые тела с низкой энергией. Относительная энергия твердого тела занимается с объемной природой самого твердого тела. Твердые вещества, такие как металлы, стекло и керамика, известны как «твердые твердые вещества», потому что химические связи, удерживающие их вместе (например, ковалентные, ионные или металлик) очень прочные. Таким образом, для разрушения этих твердых тел требуется большое количество энергии (альтернативно, требуется большое количество энергии, чтобы разрезать основную массу и образовать две поверхности), поэтому их называют высокоэнергетическими. Большинство молекулярных жидкостей полностью смачиваются высокоэнергетическими поверхностями.

Другой тип твердого вещества - это слабые молекулярные кристаллы (например, фторуглероды углеводороды и т. Д.), В молекулы удерживаются вместе в основном за счет физических сил (например, сил Ван-дер-Ваальса и водородных связей). Эти твердые твердые тела удерживаются вместе слабыми силами, для их разрушения требуется очень мало энергии, поэтому их называют «низкоэнергетическими». В зависимости от типа выбранной жидкости низкоэнергетические поверхности допускают полное или частичное смачивание.

Сообщается о динамических поверхностях, которые претерпевают изменения поверхностной энергии при приложении стимулов.. Например, показано, что поверхность, представляющая управляемые фотонами молекулярные двигатели, претерпевает изменения угла смачивания воды при изменении между бистабильными конформациями с различной поверхностной энергией.

Смачивание низкоэнергетических поверхностей

Низкое- Энергетические поверхности в первую очередь взаимодействуют с жидкостями посредством диспергирующих (ван-дер-ваальсовых ) сил. Уильям Зисман сделал несколько ключевых выводов:

Зисман заметил, что cos θ увеличивается линейно по мере уменьшения поверхностного натяжения (γLV) жидкости. Таким образом ему удалось установить линейную функцию между cos θ и поверхностным натяжением (γ LV) для различных используемых жидкостей.

Поверхность более смачиваема, когда γ LV и θ низкие. Зисман назвал пересечение этих линий, когда cos θ = 1, как (γ c) этой поверхности. Это критическое поверхностное натяжение является важным параметром, потому что оно характерно только для твердого тела.

Зная критическое поверхностное натяжение твердого тела, можно предсказать смачиваемость поверхности. Смачиваемость определяется внешними химическими группами твердого тела. Различия в смачиваемости между похожими по структуре поверхностями вызываются различиями в атомах. Например, если поверхность имеет разветвленные цепи, она будет иметь более упаковку, чем поверхность с прямыми цепями. Более низкое критическое поверхностное натяжение означает смачиваемую поверхность менее материала.

Идеальная поверхность плоской, жесткой, идеально гладкой, химически однородной и имеет нулевой гистерезис краевого угла. Нулевой гистерезис означает, что углы опережения и отступления равны. Другими словами, существует только один термодинамически стабильный контактный угол. Когда капля жидкости помещается на такую ​​поверхность, характерный угол смачивания образуется, как показано на рисунке 1. Кроме того, на идеальной поверхности капля возвращается к своей исходной форме. Следующие выводы применимы только к идеальным твердым поверхностям; они действительны только для состояния, в котором границы раздела фазны, а линия раздела фаз находится в состоянии равновесия.

Минимизация энергии, три фазы

Рисунок 3: Сосуществование трех жидких фаз во взаимном контакте; здесь каждый из α, β и θ указывает как фазу, так и ее контактный угол. 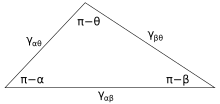Рисунок 4: Треугольник Неймана, связывающий поверхностные энергии и краевые углы трех жидких фаз, сосуществующих в статическом равновесии, как показано на рисунке 3

На рисунке 3 показывает линия контакта, где встречаются три фазы. В равновесии результирующая сила на единицу длины, действующая вдоль границы между фазами, должна быть равна нулю. Компоненты чистой оси в направлении вдоль каждой из поверхностей раздела разделов как:

$\gamma \; \alpha \; \theta \; +\; \gamma \; \theta \; \beta \; cos\; \; (\theta )\; +\; \gamma \; \alpha \; \beta \; cos\; \; (\alpha )\; =\; 0\; \gamma \; \alpha \; \theta \; cos\; \; (\theta )\; +\; \gamma \; \theta \; \beta \; +\; \gamma \; \alpha \; \beta \; соз\; \; (\beta )\; знак\; равно\; 0\; \gamma \; \alpha \; \theta \; соз\; \; (\alpha )\; +\; \gamma \; \theta \; \beta \; соз\; \; (\beta )\; +\; \gamma \; \alpha \; \beta \; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; gamma\; \_\; \{\backslash \; alpha\; \backslash \; theta\}\; +\; \backslash \; gamma\; \_\; \{\backslash \; theta\; \backslash \; beta\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \backslash \; right)\; +\; \backslash \; gamma\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; alpha\; \backslash \; right)\; =\; 0\; \backslash \backslash \backslash \; gamma\; \_\; \{\backslash \; alpha\; \backslash \; theta\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \backslash \; right)\; +\; \backslash \; gamma\; \_\; \{\backslash \; theta\; \backslash \; beta\}\; +\; \backslash \; gamma\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; beta\; \backslash \; right)\; =\; 0\; \backslash \backslash \backslash \; gamma\; \_\; \{\backslash \; alpha\; \backslash \; theta\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; alpha\; \backslash \; right)\; +\; \backslash \; gamma\; \_\; \{\backslash \; theta\; \backslash \; beta\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; beta\; \backslash \; right)\; +\; \backslash \; gamma\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; =\; 0\; \backslash \; end\; \{align\}\}\}$

где α, β и θ - показанные углы, а γ ij - поверхностная энергия между двумя указанными фазами. Эти отношения также могут быть выражены аналогом треугольника, известным как треугольник Неймана, показанного на рисунке 4. Треугольник Неймана согласуется с геометрическим ограничением: $\alpha \; +\; \beta \; +\; \theta \; =\; 2\; \pi \; \{\backslash \; displaystyle\; \backslash \; alpha\; +\; \backslash \; beta\; +\; \backslash \; theta\; =\; 2\; \backslash \; pi\}$, и применение к нему закона синусов и закона косинусов дает соотношения, которые описывают, как межфазные углы зависят от отношений поверхностных энергий.

Потому что эти три поверхностные энергии образуют стороны треугольника , они ограничены неравенствами треугольника, γ ij< γjk+ γ ik, что означает, что ни одно из поверхностных натяжений не может быть добавлено из двух других. Если три жидкости с поверхностной энергией, которые не соответствуют этим неравенствам, вступят в контакт, не будет существовать равновесная конфигурация, соответствующая рисунку 3.

Упрощение до плоской геометрии, соотношение Юнга

заменяется плоской жесткой поверхностью, как показано на рисунке 5, тогда β = π, и уравнение чистой силы упрощается до уравнение Юнга,

Рис. 5: Краевой угол смачивания капли жидкости на твердую твердую поверхность

$\gamma \; SG\; =\; \gamma \; SL\; +\; \gamma \; LG\; cos\; \; (\theta )\; \{\backslash \; displaystyle\; \backslash \; gamma\; \_\; \{SG\}\; =\; \backslash \; gamma\; \_\; \{SL\}\; +\; \backslash \; gamma\; \_\; \{LG\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \backslash \; right)\}$

, которое связывает поверхностное натяжение между тремя фазами: твердое тело, жидкость и газ. Вперед это предсказывает краевой угол смачивания жидкой капли на твердой поверхности на основе знания трех задействованных поверхностных энергий. Это уравнение также используется, если «газовая» фаза представляет собой другую, несмешивающуюся с каплей первой «жидкой» фазы.

Упрощение до плоской геометрии, соотношение Юнга, полученное из вариационных вычислений

Рассмотрим интерфейс как кривую $y\; (x)\; \{\backslash \; displaystyle\; y\; (x)\}$для $x\; \in \; I\; =\; [0,\; L]\; \{\backslash \; displaystyle\; x\; \backslash \; in\; I\; =\; [0,\; L]\}$где $L\; \{\backslash \; displaystyle\; L\}$- свободный параметр. Свободная энергия, которую необходимо минимизировать, равна

$F\; [y,\; L]\; =\; \int \; 0\; L\; (\gamma \; LG\; 1\; +\; y\; \prime \; 2\; +\; (\gamma \; SL\; -\; \gamma \; SG))\; dx\; \{\backslash \; displaystyle\; \{\backslash \; cal\; \{F\}\}\; [\; y,\; L]\; =\; \backslash \; int\; \_\; \{0\}\; ^\; \{L\}\; \backslash \; left\; (\backslash \; gamma\; \_\; \{LG\}\; \{\backslash \; sqrt\; \{1\; +\; y\; \text{'}^\; \{2\}\}\}\; +\; (\backslash \; gamma\; \_\; \{SL\}\; -\; \backslash \; gamma\; \_\; \{SG\})\; \backslash \; right)\; dx\}$

с ограничениями $y\; (0)\; =\; y\; (L)\; =\; 0\; \{\backslash \; displaystyle\; y\; (0)\; =\; y\; (L)\; =\; 0\}$которые мы можем записать как $\int \; I\; y\; \prime \; dx\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{I\}\; y\text{'}dx\; =\; 0\}$и фиксированный объем $\int \; I\; ydx\; =\; A\; \{\backslash \; displaystyle\; \backslash \; int\; \_\; \{I\}\; ydx\; =\; A\}$.

Таким образом, модифицированный лагранжиан с учетом ограничений вида

$L\; =\; \gamma \; LG\; 1\; +\; y\; \prime \; 2\; +\; (\gamma \; SL\; -\; \gamma \; SG)\; -\; \lambda \; 1\; y\; \prime \; -\; \lambda \; 2\; y\; \{\backslash \; displaystyle\; \{\backslash \; cal\; \{L\}\}\; =\; \backslash \; gamma\; \_\; \{LG\}\; \{\backslash \; sqrt\; \{1\; +\; y\; \text{'}^\; \{2\}\}\}\; +\; (\backslash \; gamma\; \_\; \{SL\}\; -\; \backslash \; gamma\; \_\; \{SG\})\; -\; \backslash \; lambda\; \_\; \{1\}\; y\; \text{'}-\; \backslash \; lambda\; \_\; \{2\}\; y\}$

где $\lambda \; i\; \{\backslash \; displaystyle\; \backslash \; lambda\; \_\; \{i\}\}$- множители Лагранжа. По определению, импульс $p\; =\; \partial \; Y\; \prime \; L\; \{\backslash \; displaystyle\; p\; =\; \backslash \; partial\; \_\; \{y\; \text{'}\}\; \{\backslash \; cal\; \{L\}\}\}$и гамильтониан $H\; =\; py\; \prime \; -\; L\; \{\backslash \; displaystyle\; \{\backslash \; cal\; \{H\}\}\; =\; py\; \text{'}-\; \{\backslash \; cal\; \{L\}\}\}$, которое вычисляется как:

$H\; =\; \gamma \; LG\; 1\; 1\; +\; y\; \prime \; 2\; -\; (\gamma \; SL\; -\; \gamma \; SG)\; +\; \lambda \; 2\; Y\; \{\backslash \; displaystyle\; \{\backslash \; cal\; \{H\}\}\; =\; \backslash \; gamma\; \_\; \{LG\}\; \{\backslash \; frac\; \{1\}\; \{\backslash \; sqrt\; \{1\; +\; y\; \text{'}^\; \{2\}\}\}\}\; -\; (\backslash \; gamma\; \_\; \{SL\}\; -\; \backslash \; gamma\; \_\; \{SG\})\; +\; \backslash \; lambda\; \_\; \{2\}\; y\}$

Теперь напомним, что граница свободна в $x\; \{\backslash \; displaystyle\; x\}$direction и $L\; \{\backslash \; displaystyle\; L\}$- свободный параметр. Следовательно, мы должны иметь:

$\partial \; F\; \partial \; L\; =\; -\; H\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{\backslash \; partial\; \{\backslash \; cal\; \{F\}\}\}\; \{\backslash \; partial\; L\}\}\; =\; -\; \{\backslash \; cal\; \{H\}\}\; =\; 0\}$

На границе $y\; (L)\; =\; 0\; \{\backslash \; displaystyle\; y\; (L)\; =\; 0\}$и $(1\; +\; y\; \prime \; 2)\; -\; 1/2\; =\; -\; cos\; \; \theta \; \{\backslash \; displaystyle\; (1\; +\; y\; \text{'}^\; \{2\})\; ^\; \{-\; 1/2\}\; =\; -\; \backslash \; cos\; \backslash \; theta\}$, поэтому мы восстанавливаем уравнение Юнга.

Неидеальные гладкие поверхности и угол смачивания Юнга

Уравнение Юнга предполагает наличие идеально плоской и жесткой поверхности, часто называемой идеальной поверхности. Во многих случаях поверхности далеки от этой жесткой ситуации здесь исследуется два случая: случай шероховатых поверхностей и случайных идеальных поверхностей, которые все еще являются действительными (конечно жесткими). Даже на идеально гладкой поверхности капля будет принимать широкий спектр углов смачивания, начиная от так называемого угла смачивания, $\theta \; A\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\backslash \; mathrm\; \{A\}\}\}$, до так называемого контактного угла, $\theta \; R\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\backslash \; mathrm\; \{R\}\}\}$. Равновесный контактный угол ($\theta \; c\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\backslash \; mathrm\; \{c\}\}\}$) можно рассчитать из $\theta \; A\; \{\backslash \; displaystyle\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{A\}\; \}\}$и $\theta \; R\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\backslash \; mathrm\; \{R\}\}\}$, как было показано Тадмором как,

$\theta \; c\; =\; arccos\; \; (\; р\; A\; соз\; \; (\theta \; A)\; +\; р\; R\; соз\; \; (\theta \; R)\; р\; A\; +\; r\; R)\; \{\backslash \; displaystyle\; \backslash \; theta\; \_\; \{\backslash \; mathrm\; \{c\}\}\; =\; \backslash \; arccos\; \backslash \; left\; (\{\backslash \; frac\; \{r\_\; \{\backslash \; mathrm\; \{A\}\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{A\}\}\; \backslash \; right)\; +\; r\; \_\; \{\backslash \; mathrm\; \{R\}\}\; \backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{R\}\}\; \backslash \; right)\; \}\; \{r\; \_\; \{\backslash \; mathrm\; \{A\}\}\; +\; r\; \_\; \{\backslash \; mathrm\; \{R\}\}\}\}\; \backslash \; right)\}$

где

$r\; A\; =\; (sin\; 3\; \; (\theta \; A)\; 2\; -\; 3\; cos\; \; (\theta \; A)\; +\; cos\; 3\; \; (\theta \; A))\; 1\; 3;\; р\; R\; знак\; равно\; (грех\; 3\; \; (\theta \; R)\; 2-3\; соз\; \; (\theta \; R)\; +\; соз\; 3\; \; (\theta \; R))\; 1\; 3\; \{\backslash \; displaystyle\; r\; \_\; \{\backslash \; mathrm\; \{A\}\}\; =\; \backslash \; left\; (\{\backslash \; гидроразрыв\; \{\backslash \; sin\; ^\; \{3\}\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{A\}\}\; \backslash \; right)\}\; \{2-3\; \backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{A\}\}\; \backslash \; right)\; +\; \backslash \; cos\; ^\; \{3\}\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{A\}\}\; \backslash \; right)\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{3\}\}\; ~;\; ~~\; r\; \_\; \{\backslash \; mathrm\; \{R\}\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{\backslash \; sin\; ^\; \{3\}\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{R\}\}\; \backslash \; right)\}\; \{2-3\; \backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{R\}\}\; \backslash \; right)\; +\; \backslash \; cos\; ^\; \{3\}\; \backslash \; left\; (\backslash \; theta\; \_\; \{\backslash \; mathrm\; \{R\}\}\; \backslash \; right)\}\}\; \backslash \; right)\; ^\; \{\backslash \; frac\; \{1\}\; \{\; 3\}\}\}$

Уравнение Юнга - Дюпре и коэффициент распространения

Уравнение Юнга - Дюпре (Thomas Young 1805; Anthanase Dupré и Paul Dupré 1869) гласит, что ни γ SG, ни γ SL не могут быть больше суммы две другие поверхностные энергии. Следствие этого ограничения является предсказанием полного смачивания при γ SG>γSL+ γ LG и нулевого смачивания при γ SL>γSG+ γ LG. Отсутствие решения уравнения Юнга - Дюпре является индикатором отсутствия равновесной конфигурации с краевым углом между 0 и 180 ° для таких ситуаций.

Полезным параметром для измерения смачивания является параметр растекания S

$S\; =\; \gamma \; SG\; -\; (\gamma \; SL\; +\; \gamma \; LG)\; \{\backslash \; Displaystyle\; S\; =\; \backslash \; gamma\; \_\; \{SG\}\; -\; \backslash \; left\; (\backslash \; gamma\; \_\; \{SL\; \}\; +\; \backslash \; gamma\; \_\; \{LG\}\; \backslash \; right)\}$

При S>0 жидкость полностью смачивает поверхность (полное смачивание). Когда S < 0, partial wetting occurs.

Объединение поисков расширения с использованием Юнга дает уравнение Юнга - Дюпре:

$S\; =\; \gamma \; LG\; (cos\; \; (\theta )\; -\; 1)\; \{\backslash \; displaystyle\; S\; =\; \backslash \; gamma\; \_\; \{LG\}\; \backslash \; left\; (\backslash \; cos\; \backslash \; left\; (\backslash \; theta\; \backslash \; right)\; -1\; \backslash \; right)\}$

который имеет физические решения для θ только при S < 0.

Уравнение Джаспера-Ананда для плоских и изогнутых поверхностей

Благодаря усовершенствованию методов измерения, таких как АСМ, конфокальная микроскопия и СЭМ, исследователи смогли получить и отображать капли во все меньших масштабах. С уменьшением размера капель появились новые экспериментальные наблюдения за смачиванием. Эти наблюдения подтвердили, что модифицированное уравнение Юнга не выполнено на микронаноуровнях.

Для сидящей капли свободная энергия трехфазной системы может быть выражена как:

$\delta \; w\; =\; \gamma \; LV\; d\; ALV\; +\; \gamma \; SL\; d\; ASL\; +\; \gamma \; SV\; d\; ASV\; -\; \kappa \; d\; L\; -\; п\; d\; V\; -\; V\; d\; P\; \{\backslash \; displaystyle\; \backslash \; delta\; w\; =\; \backslash \; gamma\; \_\; \{LV\}\; dA\_\; \{LV\}\; +\; \backslash \; gamma\; \_\; \{SL\}\; dA\_\; \{SL\}\; +\; \backslash \; gamma\; \_\; \{SV\}\; dA\_\; \{SV\}\; -\; \backslash \; kappa\; dL-\; PdV-VdP\}$

При постоянном объеме в термодинамическом равновесии это сокращено до:

$0\; =\; d\; ALV\; d\; ASL\; +\; (\gamma \; SL\; -\; \gamma \; SV)\; \gamma \; LV\; -\; \kappa \; \gamma \; LV\; d\; L\; d\; ASL\; -\; V\; \gamma \; LV\; d\; P\; d\; ASL\; \{\backslash \; displaystyle\; 0\; =\; \{\backslash \; frac\; \{dA\_\; \{LV\}\}\; \{dA\_\; \{SL\}\}\}\; +\; \{\backslash \; frac\; \{(\backslash \; gamma\; \_\; \{SL\}\; -\; \backslash \; gamma\; \_\; \{SV\})\}\; \{\backslash \; gamma\; \_\; \{LV\; \}\}\}\; -\; \{\backslash \; frac\; \{\backslash \; kappa\}\; \{\backslash \; gamma\; \_\; \{LV\}\}\}\; \{\backslash \; frac\; \{dL\}\; \{dA\_\; \{SL\}\}\}\; -\; \{\backslash \; frac\; \{V\}\; \{\backslash \; gamma\; \_\; \{LV\}\}\}\; \{\; \backslash \; frac\; \{dP\}\; \{dA\_\; \{SL\}\}\}\}$

Обычно термином VdP пренебрегают для больших капель, однако работа VdP становится существенной в малых масштабах. Изменение давления при постоянном объеме на свободной границе жидкость-пар происходит из-за давления Лапласа, пропорционально средней кривизне и не равно нулю. Решение вышеуказанного уравнения для выпуклой и вогнутых поверхностей дает:

$cos\; \; (\theta \; \mp \; \alpha )\; =\; A\; +\; B\; cos\; \; (\alpha )\; a\; \pm \; C\; sin\; \; (\theta \; \mp \; \alpha )\; (cos\; \; (\theta )\; +\; 1)\; 2\; (\; sin\; \; (\alpha )\; (cos\; \; (\alpha )\; +\; 2)\; (cos\; \; (\alpha )\; +\; 1)\; 2\; \mp \; sin\; \; (\theta )\; (cos\; \; (\theta )\; +\; 2)\; (cos\; \; (\theta )\; +\; 1)\; 2)\; \{\backslash \; displaystyle\; \backslash \; cos\; (\backslash \; theta\; \backslash \; mp\; \backslash \; alpha)\; =\; A\; +\; B\; \{\backslash \; frac\; \{\backslash \; cos\; (\backslash \; alpha)\}\; \{a\}\}\; \backslash \; pm\; C\; \backslash \; sin\; (\backslash \; theta\; \backslash \; mp\; \backslash \; alpha)\; (\backslash \; cos\; (\backslash \; тета)\; +1)\; ^\; \{2\}\; \{\backslash \; biggl\; (\}\; \{\backslash \; frac\; \{\backslash \; sin\; (\backslash \; alpha)\; (\backslash \; cos\; (\backslash \; alpha)\; +2)\}\; \{(\backslash \; cos\; (\backslash \; alpha)\; +1)\; ^\; \{2\}\; \}\}\; \backslash \; mp\; \{\backslash \; frac\; \{\backslash \; sin\; (\backslash \; theta)\; (\backslash \; cos\; (\backslash \; theta)\; +2)\}\; \{(\backslash \; cos\; (\backslash \; theta)\; +1)\; ^\; \{2\}\}\}\; \{\backslash \; biggr)\}\}$

Если постоянные параметры A, B и C определены как:

$A\; =\; (\gamma \; SV\; -\; \gamma \; SL)\; \gamma \; LV\; \{\backslash \; displaystyle\; A\; =\; \{\backslash \; frac\; \{(\backslash \; gamma\; \_\; \{SV\}\; -\; \backslash \; gamma\; \_\; \{SL\})\; \}\; \{\backslash \; gamma\; \_\; \{LV\}\}\}\}$, $B\; =\; \kappa \; \gamma \; LV\; \{\backslash \; displaystyle\; B\; =\; \{\backslash \; frac\; \{\backslash \; kappa\}\; \{\backslash \; gamma\; \_\; \{LV\}\}\}\}$и $C\; =\; \gamma \; 3\; \gamma \; LV\; \{\backslash \; displaystyle\; C\; =\; \{\backslash \; frac\; \{\backslash \; gamma\}\; \{3\; \backslash \; gamma\; \_\; \{LV\}\}\}\}$.

Это уравнение связывает контактный угол $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, геометр ическое свойство неподвижной капли в объеме термодинамика, энергия на границе трехфазного контакта $\kappa \; \{\backslash \; displaystyle\; \backslash \; kappa\}$и кривизна поверхности $\alpha \; \{\backslash \; displaystyle\; \backslash \; alpha\}$. Для особого случая неподвижной капли на плоской поверхности $(\alpha \; =\; 0)\; \{\backslash \; displaystyle\; (\backslash \; alpha\; =\; 0)\}$:

$cos\; \; (\theta )\; =\; (\gamma \; SV\; -\; \gamma \; SL)\; \gamma \; LV\; +\; \kappa \; \gamma \; LV\; 1\; a\; -\; \gamma \; 3\; \gamma \; LV\; (2влияние\; более\; длинных\; цепей\; с\; большим\; количеством\; ферроценовых\; групп\; (а\; также\; большеймолярной\; массой),\; и\; было\; обнаружено,\; что\; более\; длинные\; цепи\; вызывают\; значительно\; большее\; уменьшение\; краевого\; угла\; смачивания.$

Кислородные вакансии

Оксиды редкоземельных элементов обладают внутренней гидрофобностью и, следовательно, обозначением термически стабильных теплообменников и других приложений, связанных с высокотемпературной гидрофобностью. Наличие кислородных вакансий на поверхности оксидов церия или других оксидов играет роль в регулировании смачиваемости поверхности. Адсорбция воды на поверхностях оксидов может происходить как молекулярная адсорбция, при которой молекулы H 2 O остаются неповрежденными на конечной поверхности, или как диссоциативная адсорбция, при которой OH и H адсорбируются отдельно на твердых поверхностях. Обычно обнаруживается, что присутствие кислородных вакансий увеличивает гидрофобность и способствует диссоциативной адсорбции.

• Адсорбция - Физический феномен адгезии
• Тест Амотта
• Противотуманный - Химические вещества, которые предотвращают конденсацию воды в виде мелких капель на поверхности
• Смачивание
• Электросмачивание
• Флотация
• Метод, используя характеристики энергии твердой поверхности
• Мыльный пузырь - Тонкая пленка мыльной воды, окружающий воздух
• Подъем в сердечнике - Лабораторная техника
• Ток смачивания - Минимальный электрический ток через контакт, чтобы пробить сопротивление поверхностной пленки
• Напряжение сопротивление смачивания

• de Gennes, Pierre-Gilles; Брошар-Вяр, Франсуаза; Quéré, Дэвид (2004). Капиллярность и явления смачивания. Springer Нью-Йорк. DOI : 10.1007 / 978-0-387-21656-0. ISBN 978-1-4419-1833-8. S2CID 137894832.
• Виктор Михайлович Старов; Мануэль Г. Веларде ; Клейтон Дж. Радке (2 апреля 2007 г.). Динамика смачивания и растекания. CRC Press. ISBN 978-1-4200-1617-8.

• Что такое смачиваемость?
• СМИ, относящиеся к смачиванию на Wikimedia Commons