
Режим вибрации зажатой квадратной пластины
В механике сплошных сред, теории пластин представляют собой математические описания механики плоских пластин, основанные на теории балок. Плиты определяются как плоские конструктивные элементы с небольшой толщиной по сравнению с плоскими размерами. Типичное отношение толщины к ширине пластинчатой конструкции составляет менее 0,1. Теория пластин использует это неравенство в масштабе длины, чтобы свести полную трехмерную задачу механики твердого тела к двумерной задаче. Целью теории пластин является расчет деформации и напряжений в пластине, подверженной нагрузкам.
Из многочисленных теорий о пластинах, разработанных с конца 19 века, две широко приняты и используются в инженерии. Это
- Кирхгоф - Лав теория пластин (классическая теория пластин)
- Теория пластин Уфлянда-Миндлина (теория пластин первого порядка)
Содержание
- 1 Теория Кирхгофа – Лява для тонких пластин
- 1.1 Поле смещения
- 1.2 Соотношения деформация-смещение
- 1.3 Уравнения равновесия
- 1.4 Граничные условия
- 1.5 Соотношения напряжение – деформация
- 2 Изотропная и однородная пластина Кирхгофа
- 2.1 Чистый изгиб
- 2.2 Поперечная нагрузка
- 3 Ортотропная и однородная пластина Кирхгофа
- 4 Динамика тонких пластин Кирхгофа
- 4.1 Основные уравнения
- 4.2 Изотропные пластины
- 5 Теория Уфлянд-Миндлина для толстых пластин
- 5.1 Соотношения деформация-перемещение
- 5.2 Уравнения равновесия
- 5.3 Граничные условия
- 5.4 Определяющие соотношения
- 6 Изотропные и однородные Пластины Уфлянд-Миндлина
- 6.1 Определяющие соотношения
- 6.2 Основные уравнения
- 7 Статическая теория Рейсснера – Штейна для изотропного кантилевера p lates
- 8 Ссылки
- 9 См. также
Теория Кирхгофа – Лява для тонких пластин
- Примечание: соглашение Эйнштейна о суммировании по повторяющимся индексам используется ниже.
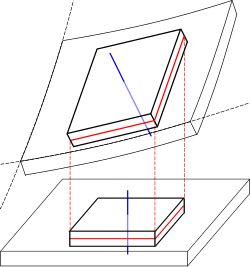
Деформация тонкой пластины, выделяющей смещение, среднюю поверхность (красный) и нормаль к средней поверхности (синий)
Теория Кирхгофа - Лава является расширением Теория пучка Эйлера – Бернулли для тонких пластин. Теория была разработана в 1888 году Лавом на основе предположений Кирхгофа. Предполагается, что плоскость средней поверхности может использоваться для представления трехмерной пластины в двухмерной форме.
Следующие кинематические допущения, сделанные в этой теории:
- прямые линии, перпендикулярные средней поверхности, остаются прямыми после деформации
- прямые линии, перпендикулярные средней поверхности, остаются нормальными к середина поверхности после деформации
- толщина пластины не изменяется во время деформации.
Поле смещения
Гипотеза Кирхгофа подразумевает, что поле смещения имеет форма

где  и
и  - декартовы координаты на средней поверхности недеформированной пластины,
- декартовы координаты на средней поверхности недеформированной пластины,  - координата направления толщины,
- координата направления толщины,  - смещения средней поверхности в плоскости, а
- смещения средней поверхности в плоскости, а  - смещение средней поверхности в направлении
- смещение средней поверхности в направлении  .
.
Если  - это углы поворота нормали к средней поверхности, тогда в теории Кирхгофа – Лява
- это углы поворота нормали к средней поверхности, тогда в теории Кирхгофа – Лява 
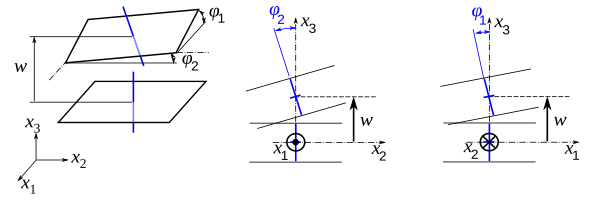 Смещение средней поверхности (слева) и нормали (справа) Смещение средней поверхности (слева) и нормали (справа) |
Деформационное смещение отношения
Для ситуации, когда деформации в пластине бесконечно малы и повороты нормалей средней поверхности меньше 10 °, отношения деформация-смещение равны

Следовательно, ненулевые деформации только в плоскостях.
Если повороты нормалей к средней поверхности находятся в диапазоне от 10 ° до 15 °, отношения деформация-смещение могут быть аппроксимированы с использованием деформаций фон Кармана. Тогда кинематические предположения теории Кирхгофа-Лява приводят к следующим соотношениям деформация-перемещение

Эта теория нелинейна из-за квадратичных членов в соотношениях деформация-перемещение.
Уравнения равновесия
Уравнения равновесия для пластины могут быть выведены из принципа виртуальной работы. Для ситуации, когда деформации и повороты пластины небольшие, уравнения равновесия для ненагруженной пластины задаются следующим образом:

где результирующие напряжения и результирующие моменты напряжения определяется как

и толщина пластины  . Величины
. Величины  представляют собой напряжения.
представляют собой напряжения.
Если плита нагружена внешней распределенной нагрузкой  , которая перпендикулярна средней поверхности и направлена положительно
, которая перпендикулярна средней поверхности и направлена положительно  направление, принцип виртуальной работы затем приводит к уравнениям равновесия
направление, принцип виртуальной работы затем приводит к уравнениям равновесия

Для умеренных вращений соотношения деформация-перемещение принимают форму фон Кармана, и уравнения равновесия могут быть выражены как
![\ begin {align} N _ {\ alpha \ beta, \ alpha} = 0 \\ M _ {\ alpha \ beta, \ alpha \ beta} + [N _ {\ alpha \ beta} ~ w ^ 0 _ {, \ beta}] _ {, \ alpha} - q = 0 \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805c3eb5885064aa33be7d31e0e054995853f47a)
Граничные условия
Граничные условия, необходимые для решения уравнения равновесия теории пластин могут быть получены из граничных членов в принципе виртуального Работа.
Для малых деформаций и малых вращений граничные условия:

Обратите внимание, что величина  - эффективная сила сдвига.
- эффективная сила сдвига.
Соотношения "напряжение-деформация"
Отношения "напряжение-деформация" для линейной упругой пластины Кирхгофа выражаются как

Поскольку  и
и  не отображаются в В уравнениях равновесия неявно предполагается, что эти величины не влияют на баланс импульса и ими пренебрегают.
не отображаются в В уравнениях равновесия неявно предполагается, что эти величины не влияют на баланс импульса и ими пренебрегают.
Удобнее работать с равнодействующими напряжений и моментов, которые входят в уравнения равновесия. Они связаны со смещениями следующим образом:

и

жесткости на растяжение - это величины

жесткость на изгиб (также называемая жесткость при изгибе ) - величины

Изотропная и однородная пластина Кирхгофа
Для изотропной и однородной пластины отношения напряжение-деформация имеют вид

Моменты, соответствующие этим напряжениям, равны

Чистый изгиб
Смещения  и
и  равны нулю в условиях чистого изгиба. Для изотропной однородной пластины при чистом изгибе основное уравнение:
равны нулю в условиях чистого изгиба. Для изотропной однородной пластины при чистом изгибе основное уравнение:

В индексной записи

В прямой тензорной нотации определяющее уравнение:

Поперечная нагрузка
Для поперечно нагруженной пластины без осевых деформаций определяющее уравнение имеет вид

где

В индексной записи,

и в прямой записи

в цилиндрических координатах  , определяющее уравнение:
, определяющее уравнение:
![\ frac {1} {r} \ cfrac {d} {dr} \ left [r \ cfrac {d} {dr} \ left \ {\ frac {1} {r} \ cfrac {d} {dr} \ left (r \ cfrac {dw} {dr} \ right) \ right \} \ right] = - \ frac {q} {D} \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8083e6e16a9118c0afe8bd3c7e1fe841e17334)
Ортотропная и однородная пластина Кирхгофа
Для ортотропной пластины

Следовательно,

и

Поперечная нагрузка
Управляющее уравнение ортотропной пластины Кирхгофа, нагруженной поперечно распределенной нагрузкой  на единицу площади равно
на единицу площади равно

где

Динамика тонких пластин Кирхгофа
Динамическая теория пластин определяет распространение волн в пластинах, а также изучение стоячих волн и режимов колебаний.
Основные уравнения
Основные уравнения динамики пластины Кирхгофа – Лява:

где для пластины с плотностью  ,
,

и

На рисунках ниже показаны некоторые колебательные режимы круглой пластины.
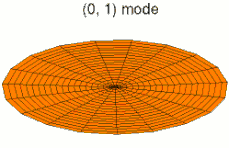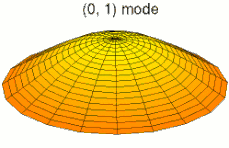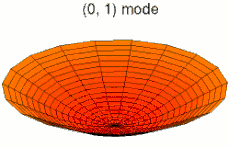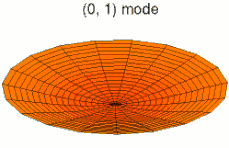
мода k = 0, p = 1
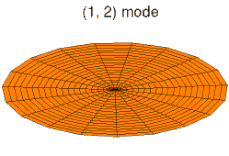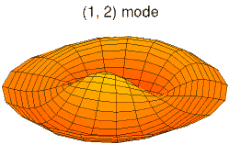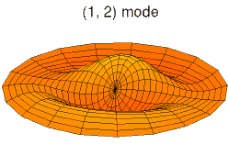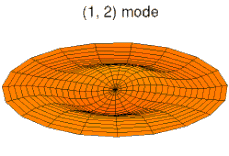
мода k = 1, p = 2
Изотропные пластины
Основные уравнения значительно упрощаются для изотропных и однородных пластин, для которых деформации в плоскости можно пренебречь и иметь вид

где  - жесткость пластины на изгиб. Для однородной пластины толщиной
- жесткость пластины на изгиб. Для однородной пластины толщиной  ,
,

В прямой записи

Теория Уфлянда-Миндлина для толстых пластин
- Примечание: соглашение Эйнштейна о суммировании суммирования повторяющихся индексов используется ниже.
В теории толстых пластин или теории Якова С. Уфлянда (подробности см. в справочнике Элишаков ), Раймонда Миндлина и Эрика Рейсснера, нормаль к средней поверхности остается прямой, но не обязательно перпендикулярно средней поверхности. Если  и
и  , обозначают углы, которые -поверхность образует с осью
, обозначают углы, которые -поверхность образует с осью  , затем
, затем

Тогда гипотеза Миндлина – Рейсснера подразумевает что

Соотношение деформация-смещение
В зависимости от величины поворота нормалей пластины два разных приближения для деформаций можно вывести из основных кинематических предположений.
Для малых деформаций и малых вращений соотношение деформация-перемещение для пластин Миндлина – Рейсснера составляет

Деформация сдвига и, следовательно, напряжение сдвига, по толщине пластины в этой теории не пренебрегается. Однако деформация сдвига постоянна по толщине пластины. Это не может быть точным, поскольку известно, что напряжение сдвига параболическое даже для пластин простой формы. Чтобы учесть неточность деформации сдвига, применяется поправочный коэффициент сдвига ( ), чтобы спрогнозировать правильное количество внутренней энергии. по теории. Тогда
), чтобы спрогнозировать правильное количество внутренней энергии. по теории. Тогда

Уравнения равновесия
Уравнения равновесия имеют несколько разные формы в зависимости от величины изгиба, ожидаемого в пластине. Для ситуации, когда деформации и повороты пластины малы, уравнения равновесия для пластины Миндлина – Рейсснера равны

Результирующие поперечные силы в приведенных выше уравнениях определяются как

Граничные условия
Граничные условия обозначаются граничными условиями в принципе виртуальной работы.
Если единственная внешняя сила - это вертикальная сила, действующая на верхнюю поверхность пластины, граничные условия следующие:

Определяющие соотношения
Соотношения между напряжением и деформацией для линейной упругой пластины Миндлина – Рейсснера определяются как

Поскольку  не появляется в равновесии Поэтому неявно предполагается, что он не влияет на баланс импульса, и им пренебрегают. Это предположение также называется предположением плоского напряжения . Остальные соотношения напряжение-деформация для ортотропного материала в матричной форме могут быть записаны как
не появляется в равновесии Поэтому неявно предполагается, что он не влияет на баланс импульса, и им пренебрегают. Это предположение также называется предположением плоского напряжения . Остальные соотношения напряжение-деформация для ортотропного материала в матричной форме могут быть записаны как

Затем,

и

Для условий сдвига

жесткости на растяжение - это величины

жесткости на изгиб - это величины

Изотропные и однородные пластины Уфлянд-Миндлина
Для равномерно толстых, однородных, и изотропных пластин соотношение напряжение – деформация в плоскости пластины составляет

где  - модуль Юнга,
- модуль Юнга,  - коэффициент Пуассона, а
- коэффициент Пуассона, а  - деформации в плоскости. Напряжения сдвига и деформации по толщине связаны соотношением
- деформации в плоскости. Напряжения сдвига и деформации по толщине связаны соотношением

, где  - модуль сдвига.
- модуль сдвига.
Определяющие соотношения
Соотношения между результирующими напряжениями и обобщенными смещениями для изотропного материала Миндлина – Рейсснера пластины:


и

Жесткость на изгиб определяется как величина

Для пластины толщиной  жесткость на изгиб имеет вид
жесткость на изгиб имеет вид

где 
Основные уравнения
Если мы проигнорируем удлинение пластины в плоскости, основные уравнения будут

В терминах обобщенных деформаций  , три основных уравнения:
, три основных уравнения:

Граница условия вдоль краев прямоугольной пластины

Статическая теория Рейсснера – Штейна для изотропных консольных пластин
В целом, точные решения для консольных пластин с использованием теории пластин довольно сложны, и в литературе можно найти несколько точных решений. Рейсснер и Штейн предлагают упрощенную теорию консольных пластин, которая является улучшением по сравнению с более ранними теориями, такими как теория пластин Сен-Венана.
Теория Рейсснера-Штейна предполагает поле поперечного смещения вида

Затем определяющие уравнения для пластины сводятся к двум связанным обыкновенным дифференциалам уравнения:

где

At  , since the beam is clamped, the boundary conditions are
, since the beam is clamped, the boundary conditions are

The boundary conditions at  are
are
![\ begin {align} bD \ cfrac {d ^ 3 w_x} {dx ^ 3} + n_1 (x) \ cfrac {d w_x} {dx} + n_2 (x) \ cfrac {d \ theta_x} {dx} + q_ {x1} = 0 \\ \ frac {b ^ 3D} {12} \ cfrac {d ^ 3 \ theta_x} {dx ^ 3} + \ left [n_3 (x) -2bD ( 1- \ nu) \ right] \ cfrac {d \ theta_x} {dx} + n_2 (x) \ cfrac {d w_x} {dx} + t = 0 \\ bD \ cfrac {d ^ 2 w_x} {dx ^ 2} + m_1 = 0 \ quad, \ quad \ frac {b ^ 3D} {12} \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} + m_2 = 0 \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaf85b9cef5f1f91c15d3c156f0e148d77c3942b)
where

| Derivation of Reissner–Stein cantilever plate equations |
|---|
The strain energy of bending of a thin rectangular plate of uniform thickness  is given by is given by ![U = \ frac {1} {2} \ int_0 ^ a \ int _ {- b / 2} ^ {b / 2} D \ left \ {\ left (\ frac {\ partial ^ 2 w} {\ partial x ^ 2} + \ frac {\ partial ^ 2 w} {\ partial y ^ 2} \ right) ^ 2 + 2 (1- \ nu) \ left [\ left (\ frac {\ partial ^ 2 w} {\ partial x \ partial y} \ right) ^ 2 - \ frac {\ partial ^ 2 w} {\ частичный x ^ 2} \ frac {\ partial ^ 2 w} {\ partial y ^ 2} \ right] \ right \} \ text {d} x \ text {d} y](https://wikimedia.org/api/rest_v1/media/math/render/svg/477d8371959f6ca933d0fa6d140e8a629fe8fd76)
where  is the transverse displacement, is the transverse displacement,  is the length, is the length,  is the width, is the width,  is the Poisson's ratio, is the Poisson's ratio,  is the Young's modulus, and is the Young's modulus, and 
The potential energy of transverse loads  (per unit length) is (per unit length) is 
The potential energy of in-plane loads  (per unit width) is (per unit width) is 
The potential energy of tip forces  (per unit width), and bending moments (per unit width), and bending moments  and and  (per unit width) is (per unit width) is 
A balance of energy requires that the total energy is 
With the Reissener–Stein assumption for the displacement, we have ![U = \ int_0 ^ a \ frac {bD} {24} \ left [12 \ left (\ cfrac {d ^ 2 w_x} {dx ^ 2} \ right) ^ 2 + b ^ 2 \ left (\ cfrac {d ^ 2 \ theta_x} {dx ^ 2} \ right) ^ 2 + 24 (1- \ nu) \ left (\ cfrac {d \ theta_x} {dx} \ right) ^ 2 \ right] \, \ text {d} x \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/e00117f97d34fd4ce59dabc4f80b249f36bd7899) ![P_q = \ int_0 ^ a \ left [\ left (\ int _ {- b / 2} ^ {b / 2} q (x, y) \, \ text {d} y \ right) w_x + \ left (\ int _ {- b / 2} ^ {b / 2} yq (x, y) \, \ text {d} y \ right) \ theta_x \ right] \, dx \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/815ee3458fe4e00affc89d024d32cdd4bed8c500) ![\ begin {align} P_n = \ frac {1} {2} \ int_0 ^ a \ left [\ left (\ int_ { -b / 2} ^ {b / 2} n_x (x, y) \, \ text {d} y \ right) \ left (\ cfrac {d w_x} {dx} \ right) ^ 2 + \ left (\ int _ {- b / 2} ^ {b / 2} y n_x (x, y) \, \ text {d} y \ right) \ cfrac {d w_x} {dx} \, \ cfrac {d \ theta_x} { dx} \ right. \\ \ left. \ qquad \ qquad + \ left (\ int _ {- b / 2} ^ {b / 2} y ^ 2 n_x (x, y) \, \ text {d} y \ right) \ left (\ cfrac {d \ theta_x} {dx} \ right) ^ 2 \ right] \ text {d} x \, \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/322eab0bf35f19a32f8d170b85f0399b09d03d5d)
и ![\ begin {align} P_t = \ left (\ int _ {- b / 2} ^ {b / 2} q_x (y) \, \ text {d} y \ right) w_x - \ left (\ int _ {- b / 2} ^ {b / 2} m_x (y) \, \ text {d} y \ right) \ cfrac {d w_x} {dx} + \ left [\ int _ {- b / 2 } ^ {b / 2} \ left (y q_x (y) + m_ {xy} (y) \ right) \, \ text {d} y \ right] \ theta_x \\ \ qquad \ qquad - \ left ( \ int _ {- b / 2} ^ {b / 2} y m_x (y) \, \ text {d} y \ right) \ cfrac {d \ theta_x} {dx} \,. \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2774040f1d5cedf7724fba946ed7f259b19acef6)
Взяв первый вариант  относительно относительно  и установка его на ноль дает нам уравнения Эйлера и установка его на ноль дает нам уравнения Эйлера 
и 
где 
Поскольку балка зафиксирована в точке  , мы имеем , мы имеем 
Граничные условия в  можно найти путем интегрирования по частям: можно найти путем интегрирования по частям: ![\ begin {align} bD \ cfrac {d ^ 3 w_x} {dx ^ 3} + n_1 (x) \ cfrac {d w_x} {dx} + n_2 (x) \ cfrac {d \ theta_x} {dx} + q_ {x1} = 0 \\ \ frac {b ^ 3D} {12} \ cfrac {d ^ 3 \ theta_x} {dx ^ 3} + \ left [n_3 (x) -2bD ( 1- \ nu) \ right] \ cfrac {d \ theta_x} {dx} + n_2 (x) \ cfrac {d w_x} {dx} + t = 0 \\ bD \ cfrac {d ^ 2 w_x} {dx ^ 2} + m_1 = 0 \ quad, \ quad \ frac {b ^ 3D} {12} \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} + m_2 = 0 \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaf85b9cef5f1f91c15d3c156f0e148d77c3942b)
где 
|
Литература
- ^Тимошенко С., Войновски-Кригер С. "Теория пластин и оболочек". Макгроу-Хилл, Нью-Йорк, 1959.
- ^А. Е. Х. Лав, О малых свободных колебаниях и деформациях упругих оболочек, Философский пер. Королевского общества (Лондон), 1888 г., Vol. серия A, № 17 стр. 491–549.
- ^Редди, Дж. Н., 2007, Теория и анализ упругих пластин и оболочек, CRC Press, Тейлор и Фрэнсис.
- ^Уфлянд, Я. С., 1948, Распространение волн при поперечных колебаниях балок и пластин, ПММ: Журнал прикладной математики и механики, т. 12, 287-300 (на русском языке)
- ^Елишаков, И., 2020, Справочник по теориям луча Тимошенко-Эренфеста и пластины Уфлянд-Миндлина, World Scientific, Сингапур, ISBN 978-981-3236-51-6
- ^Р. Д. Миндлин, Влияние вращательной инерции и сдвига на изгибные движения изотропных упругих пластин, Журнал прикладной механики, 1951, т. 18 п. 31–38.
- ^Э. Рейсснер и М. Штейн. Кручение и поперечный изгиб консольных пластин. Техническая нота 2369, Национальный консультативный комитет по аэронавтике, Вашингтон, 1951.
См. Также
 Режим вибрации зажатой квадратной пластины
Режим вибрации зажатой квадратной пластины  Деформация тонкой пластины, выделяющей смещение, среднюю поверхность (красный) и нормаль к средней поверхности (синий)
Деформация тонкой пластины, выделяющей смещение, среднюю поверхность (красный) и нормаль к средней поверхности (синий) 







 Смещение средней поверхности (слева) и нормали (справа)
Смещение средней поверхности (слева) и нормали (справа)







![\ begin {align} N _ {\ alpha \ beta, \ alpha} = 0 \\ M _ {\ alpha \ beta, \ alpha \ beta} + [N _ {\ alpha \ beta} ~ w ^ 0 _ {, \ beta}] _ {, \ alpha} - q = 0 \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/805c3eb5885064aa33be7d31e0e054995853f47a)




















![\ frac {1} {r} \ cfrac {d} {dr} \ left [r \ cfrac {d} {dr} \ left \ {\ frac {1} {r} \ cfrac {d} {dr} \ left (r \ cfrac {dw} {dr} \ right) \ right \} \ right] = - \ frac {q} {D} \,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8083e6e16a9118c0afe8bd3c7e1fe841e17334)


























































![\ begin {align} bD \ cfrac {d ^ 3 w_x} {dx ^ 3} + n_1 (x) \ cfrac {d w_x} {dx} + n_2 (x) \ cfrac {d \ theta_x} {dx} + q_ {x1} = 0 \\ \ frac {b ^ 3D} {12} \ cfrac {d ^ 3 \ theta_x} {dx ^ 3} + \ left [n_3 (x) -2bD ( 1- \ nu) \ right] \ cfrac {d \ theta_x} {dx} + n_2 (x) \ cfrac {d w_x} {dx} + t = 0 \\ bD \ cfrac {d ^ 2 w_x} {dx ^ 2} + m_1 = 0 \ quad, \ quad \ frac {b ^ 3D} {12} \ cfrac {d ^ 2 \ theta_x} {dx ^ 2} + m_2 = 0 \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaf85b9cef5f1f91c15d3c156f0e148d77c3942b)

 is given by
is given by