Гибка

Гибка двутавровой балки

В прикладной механике, гибка (также известная как изгиб ) характеризует поведение тонкого структурного элемента, подверженного внешней нагрузке, приложенной перпендикулярно продольной оси элемента.

Предполагается, что структурный элемент такой, что по крайней мере один из его размеров составляет небольшую долю, обычно 1/10 или меньше, двух других. Когда длина значительно больше ширины и толщины, элемент называется балкой. Например, шкаф стержень провисает под весом одежды на вешалках, является примером изгиба балки. С другой стороны, оболочка представляет собой конструкцию любой геометрической формы, длина и ширина которой имеют одинаковый порядок величины, но толщина конструкции (известной как «стена») значительно меньше.. Тонкостенная короткая трубка большого диаметра, поддерживаемая на концах и нагруженная с боков, является примером изгиба оболочки.

При отсутствии квалификатора термин «изгиб» неоднозначен, поскольку изгиб может происходить локально во всех объектах. Следовательно, чтобы сделать использование этого термина более точным, инженеры ссылаются на конкретный объект, такой как; изгиб стержней, изгиб балок, изгиб пластин, изгиб оболочек и так далее.

• 1 Квазистатический изгиб балок
  • 1.1 Теория изгиба Эйлера – Бернулли
  • 1.2 Расширения теории изгиба балок Эйлера-Бернулли
    • 1.2.1 Пластический изгиб
    • 1.2.2 Комплекс или асимметричный изгиб
    • 1.2.3 Большая деформация изгиба
  • 1.3 Теория изгиба Тимошенко
• 2 Динамический изгиб балок
  • 2.1 Теория Эйлера – Бернулли
    • 2.1.1 Свободные колебания
  • 2.2 Тимошенко – Рэлея Теория
    • 2.2.1 Свободные колебания
• 3 Квазистатическое изгибание пластин
  • 3.1 Теория пластин Кирхгофа – Лява
  • 3.2 Теория пластин Миндлина – Рейсснера
• 4 Динамическое изгибание пластин
  • 4.1 Динамика тонких пластин Кирхгофа
• 5 См. также
• 6 Ссылки
• 7 Внешние ссылки

Балка деформируется, и внутри нее возникают напряжения при приложении поперечной нагрузки в теме. В квазистатическом случае предполагается, что величина изгиба прогиб и возникающие напряжения не изменяются со временем. В горизонтальной балке, поддерживаемой на концах и нагруженной вниз посередине, материал на внешней стороне балки сжимается, а материал на нижней стороне растягивается. Существуют две формы внутренних напряжений, вызванных боковыми нагрузками:

• напряжение сдвига, параллельное боковой нагрузке, плюс дополнительное напряжение сдвига в плоскостях, перпендикулярных направлению нагрузки;
• прямое сжимающее напряжение в верхней части балки и прямое растягивающее напряжение в нижней части балки.

Эти последние две силы образуют пару или момент, поскольку они равны по величине и противоположны по направлению. Этот изгибающий момент препятствует деформации провисания, характерной для балки, испытывающей изгиб. Распределение напряжений в балке можно предсказать довольно точно, если использовать некоторые упрощающие предположения.

Теория изгиба Эйлера – Бернулли

Элемент изогнутой балки: волокна образуют концентрические дуги, верхние волокна сжаты и нижние волокна растянуты. Изгибающие моменты в балке

В теории Эйлера – Бернулли тонких балок, основное допущение состоит в том, что «плоские секции остаются плоскими». Другими словами, никакая деформация из-за сдвига по сечению не учитывается (деформация сдвига отсутствует). Кроме того, это линейное распределение применимо только в том случае, если максимальное напряжение меньше предела текучести материала. Для напряжений, превышающих предел текучести, см. Статью пластический изгиб. При текучести максимальное напряжение, испытываемое в сечении (в наиболее удаленных точках от нейтральной оси балки), определяется как прочность на изгиб.

Рассмотрим балки, если выполняются следующие условия:

• Балка изначально прямая и тонкая, а любой конус небольшой
• Материал изотропный (или ортотропный ), линейно-упругий и однородный по любому поперечному сечению (но не обязательно по его длине)
• Учитываются только небольшие прогибы

В этом случае уравнение, описывающее прогиб балки ($w\; \{\backslash \; displaystyle\; w\}$) можно приблизительно представить как:

$d\; 2\; w\; (x)\; dx\; 2\; =\; M\; (x)\; E\; (x)\; I\; (x)\; \{\backslash \; displaystyle\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{2\}\; w\; (x)\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{M\; (x)\}\; \{E\; (x)\; I\; (x)\}\}\}$

где вторая производная его отклонена форма относительно $x\; \{\backslash \; displaystyle\; x\}$интерпретируется как его кривизна, $E\; \{\backslash \; displaystyle\; E\}$- это модуль Юнга, $I\; \{\backslash \; отображает\; tyle\; I\}$- это момент инерции площади поперечного сечения, а $M\; \{\backslash \; displaystyle\; M\}$- внутренний изгибающий момент в луч.

Если, кроме того, балка однородна и по своей длине, а не сужается (т.е. с постоянным поперечным сечением) и прогибается под действием приложенной поперечной нагрузки $q\; (x)\; \{\backslash \; displaystyle\; q\; (x)\}$, можно показать, что:

$EI\; d\; 4\; w\; (x)\; dx\; 4\; =\; q\; (x)\; \{\backslash \; displaystyle\; EI\; ~\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{4\}\; w\; (x)\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{4\}\}\}\; =\; q\; (x)\}$

Это уравнение Эйлера – Бернулли для изгиба балки.

После получения решения для смещения балки изгибающий момент ($M\; \{\backslash \; displaystyle\; M\}$) и поперечная сила ($Q\; \{\backslash \; displaystyle\; Q\}$) в балке можно рассчитать с использованием соотношений

$M\; (x)\; =\; -\; EI\; d\; 2\; wdx\; 2;\; Q\; (х)\; =\; d\; M\; d\; x.\; \{\backslash \; Displaystyle\; M\; (x)\; =\; -\; EI\; ~\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{2\}\; w\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{2\}\}\}\; ~;\; ~~\; Q\; (x)\; =\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; M\}\; \{\backslash \; mathrm\; \{d\}\; x\}\}.\}$

Простой изгиб балки часто анализируется с помощью уравнения Эйлера – Бернулли. Условия использования простой теории изгиба:

1. Балка подлежит чистому изгибу. Это означает, что поперечная сила равна нулю, и что отсутствуют скручивающие или осевые нагрузки.
2. Материал изотропный (или ортотропный ) и однородный.
3. Материал подчиняется закону Гука (он линейно упруг и не деформируется пластически).
4. Изначально балка прямая с постоянным поперечным сечением. по всей длине балки.
5. Балка имеет ось симметрии в плоскости изгиба.
6. Пропорции балки таковы, что она может выйти из строя из-за изгиба, а не из-за раздавливания, сморщивания или вбок изгиб.
7. Поперечные сечения балки во время изгиба остаются плоскими.

Прогиб балки, отклоненной симметрично, и принцип наложения

Сжимающие и растягивающие силы развиваются в направлении оси балки под действием изгибающих нагрузок. Эти силы вызывают напряжения в балке. Максимальное сжимающее напряжение находится на самом верхнем крае балки, а максимальное растягивающее напряжение - на нижнем крае балки. Поскольку напряжения между этими двумя противоположными максимумами изменяются линейно, следовательно, существует точка на линейной траектории между ними, где нет напряжения изгиба. Геометрическое место этих точек является нейтральной осью. Из-за этой области без напряжения и прилегающих областей с низким напряжением использование балок с равномерным поперечным сечением при изгибе не является особенно эффективным средством поддержки нагрузки, поскольку оно не использует полную мощность балки, пока она не окажется на грани коллапс. Широкополочные балки (двутавровые балки ) и балки балки эффективно устраняют эту неэффективность, поскольку они минимизируют количество материала в этой недонагруженной области.

Классическая формула для определения напряжения изгиба в балке при простом изгибе:

$\sigma \; x\; =\; M\; zy\; I\; z\; =\; M\; z\; W\; z\; \{\backslash \; displaystyle\; \backslash \; sigma\; \_\; \{x\}\; =\; \{\backslash \; frac\; \{M\_\; \{z\}\; y\}\; \{I\_\; \{z\}\}\}\; =\; \{\backslash \; frac\; \{M\_\; \{z\}\}\; \{W\_\; \{z\}\}\}\}$

где

• $\sigma \; x\; \{\backslash \; displaystyle\; \{\backslash \; sigma\; \_\; \{x\; \}\}\}$- напряжение изгиба
• $M\; z\; \{\backslash \; displaystyle\; M\_\; \{z\}\}$- момент относительно нейтральной оси
• $y\; \{\backslash \; displaystyle\; y\}$- перпендикулярное расстояние к нейтральной оси
• $I\; z\; \{\backslash \; displaystyle\; I\_\; \{z\}\}$- второй момент области относительно нейтральной оси z.
• $W\; z\; \{\backslash \; displaystyle\; W\_\; \{z\}\}$- Момент сопротивления относительно нейтральной оси z. $W\; z\; =\; I\; z\; /\; y\; \{\backslash \; displaystyle\; W\_\; \{z\}\; =\; I\_\; \{z\}\; /\; y\}$

Расширения теории изгиба балок Эйлера-Бернулли

Пластический изгиб

Уравнение $\sigma \; =\; M\; y\; I\; x\; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; \{\backslash \; tfrac\; \{My\}\; \{I\_\; \{x\}\}\}\}$действительно только тогда, когда напряжение на крайнем волокне (т. Е. часть балки, наиболее удаленная от нейтральной оси) находится ниже предела текучести материала, из которого она изготовлена. При более высоких нагрузках распределение напряжений становится нелинейным, и пластичные материалы в конечном итоге переходят в состояние пластического шарнира, в котором величина напряжения равна пределу текучести повсюду в балке, с разрывом на нейтральной оси, где напряжение изменяется от растяжение к сжатию. Это состояние пластического шарнира обычно используется в качестве предельного состояния при проектировании стальных конструкций.

Сложный или асимметричный изгиб

Приведенное выше уравнение действительно только в том случае, если поперечное сечение симметрично. Для однородных балок с асимметричным сечением максимальное изгибающее напряжение в балке определяется как

$\sigma \; x\; (y,\; z)\; =\; -\; M\; z\; I\; y\; +\; M\; y\; I\; yz\; I\; y\; I\; z\; -\; I\; yz\; 2\; y\; +\; M\; y\; I\; Z\; +\; M\; Z\; I\; YZ\; I\; Y\; I\; Z\; -\; I\; YZ\; 2\; Z\; \{\backslash \; Displaystyle\; \backslash \; sigma\; \_\; \{x\}\; (y,\; z)\; =\; -\; \{\backslash \; frac\; \{M\_\; \{z\}\; ~\; I\_\; \{y\}\; +\; M\_\; \{y\}\; ~\; I\_\; \{yz\}\}\; \{I\_\; \{y\}\; ~\; I\_\; \{z\}\; -I\_\; \{yz\}\; ^\; \{2\}\}\}\; y\; +\; \{\backslash \; frac\; \{M\_\; \{y\}\; ~\; I\_\; \{z\}\; +\; M\_\; \{z\}\; ~\; I\_\; \{yz\; \}\}\; \{I\_\; \{y\}\; ~\; I\_\; \{z\}\; -I\_\; \{yz\}\; ^\; \{2\}\}\}\; z\}$

где $y,\; z\; \{\backslash \; displaystyle\; y,\; z\}$- координаты точки на поперечном сечении, в которой необходимо определить напряжение, как показано справа: $M\; y\; \{\backslash \; displaystyle\; M\_\; \{y\}\}$и $M\; z\; \{\backslash \; displaystyle\; M\_\; \{z\}\}$- изгибающие моменты относительно осей y и z центроида, $I\; y\; \{\backslash \; displaystyle\; I\_\; \{y\}\}$и $I\; z\; \{\backslash \; displaystyle\; I\_\; \{z\}\}$- вторые моменты площади (отличные от моментов инерции) относительно осей y и z, а $I\; yz\; \{\backslash \; displaystyle\; I\_\; \{yz\; \}\}$- это произведение моментов площади. Используя это уравнение, можно рассчитать изгибающее напряжение в любой точке поперечного сечения балки, независимо от ориентации момента или формы поперечного сечения. Обратите внимание, что $M\; y,\; M\; z,\; I\; y,\; I\; z,\; I\; yz\; \{\backslash \; displaystyle\; M\_\; \{y\},\; M\_\; \{z\},\; I\_\; \{y\},\; I\_\; \{z\},\; I\_\; \{yz\}\}$не меняются от одной точки к другой на поперечном сечении.

Большая деформация изгиба

Для больших деформаций тела напряжение в поперечном сечении рассчитывается с использованием расширенной версии этой формулы. Сначала должны быть сделаны следующие допущения:

1. Допущение плоских сечений - до и после деформации рассматриваемое сечение тела остается плоским (т.е. не закручено).
2. Сдвиговые и нормальные напряжения в этом сечении, которые имеют перпендикулярно вектору нормали поперечного сечения не влияет на нормальные напряжения, параллельные этому сечению.

Следует учитывать большие изгибы, когда радиус изгиба $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$меньше десяти высот сечения h:

С такими допущениями напряжение при большом изгибе рассчитывается как:

$\sigma \; =\; FA\; +\; M\; \rho \; A\; +\; MI\; x\; \prime \; y\; \rho \; \rho \; +\; y\; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; \{\backslash \; frac\; \{F\}\; \{A\}\}\; +\; \{\backslash \; frac\; \{M\}\; \{\backslash \; rho\; A\}\}\; +\; \{\backslash \; frac\; \{M\}\; \{\{I\_\; \{x\}\}\; \text{'}\}\}\; y\; \{\backslash \; frac\; \{\backslash \; rho\}\; \{\backslash \; rho\; +\; y\}\}\}$

где

$F\; \{\backslash \; displaystyle\; F\}$- нормальная сила

$A\; \{\backslash \; displaystyle\; A\}$- сечение area

$M\; \{\backslash \; displaystyle\; M\}$- изгибающий момент;

$\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$- локальный радиус изгиба (радиус s изгиба в текущем сечении)

$I\; x\; \prime \; \{\backslash \; displaystyle\; \{\{I\_\; \{x\}\}\; \text{'}\}\}$- момент инерции площади вдоль оси x, в месте $y\; \{\backslash \; displaystyle\; y\}$(см. теорема Штейнера )

$y\; \{\backslash \; displaystyle\; y\}$- это положение вдоль оси y на площадь сечения, в которой вычисляется напряжение $\sigma \; \{\backslash \; displaystyle\; \backslash \; sigma\}$.

Когда радиус изгиба $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$приближается к бесконечности и $y\; \ll \; \rho \; \{\backslash \; displaystyle\; y\; \backslash \; ll\; \backslash \; rho\}$, вернулась исходная формула:

$\sigma \; =\; FA\; \pm \; M\; y\; I\; \{\backslash \; displaystyle\; \backslash \; sigma\; =\; \{F\; \backslash \; over\; A\}\; \backslash \; pm\; \{\backslash \; frac\; \{My\}\; \{I\}\}\}$.

Теория изгиба Тимошенко

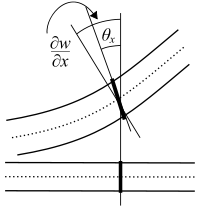
Деформация балки Тимошенко. Нормаль поворачивается на величину $\theta \; \{\backslash \; displaystyle\; \backslash \; theta\}$, которая не равна $dw\; /\; dx\; \{\backslash \; displaystyle\; dw\; /\; dx\}$.

В 1921 году Тимошенко усовершенствовал теорию балок Эйлера – Бернулли, добавив эффект сдвига в уравнение балки. Кинематические допущения теории Тимошенко следующие:

• нормали к оси балки остаются прямыми после деформации
• нет изменения толщины балки после деформации

Однако нормали к оси не требуются после деформации оставаться перпендикулярно оси.

Уравнение квазистатического изгиба линейной упругой изотропной однородной балки с постоянным поперечным сечением при этих предположениях имеет вид

$EI\; d\; 4\; wdx\; 4\; =\; q\; (x)\; -\; EI\; k\; AG\; d\; 2\; qdx\; 2\; \{\backslash \; displaystyle\; EI\; ~\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{4\}\; w\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{4\}\}\}\; =\; q\; (x)\; -\; \{\backslash \; cfrac\; \{EI\}\; \{kAG\}\; \}\; ~\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{2\}\; q\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{2\}\}\}\}$

где $I\; \{\backslash \; displaystyle\; I\}$- момент инерции площади поперечного сечения, $A\; \{\backslash \; displaystyle\; A\}$- площадь поперечного сечения, $G\; \{\backslash \; displaystyle\; G\}$- модуль сдвига, $k\; \{\backslash \; displaystyle\; k\}$- поправочный коэффициент сдвига, а $q\; (x)\; \{\backslash \; displaystyle\; q\; (x)\}$- приложенная поперечная нагрузка. Для материалов с коэффициентом Пуассона ($\nu \; \{\backslash \; displaystyle\; \backslash \; nu\}$), близким к 0,3, коэффициент поправки на сдвиг для прямоугольного поперечного сечения составляет приблизительно

$k\; =\; 5\; +\; 5\; \nu \; 6\; +\; 5\; \nu \; \{\backslash \; displaystyle\; k\; =\; \{\backslash \; cfrac\; \{5\; +\; 5\; \backslash \; nu\}\; \{6\; +\; 5\; \backslash \; nu\}\}\}$

Вращение ($\phi \; (x)\; \{\backslash \; displaystyle\; \backslash \; varphi\; (x)\}$) нормали описывается уравнением

$d\; \phi \; dx\; =\; -\; d\; 2\; wdx\; 2\; -\; q\; (x)\; k\; AG\; \{\backslash \; displaystyle\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; varphi\}\; \{\backslash \; mathrm\; \{d\}\; x\}\}\; =\; -\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{2\}\; w\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{2\}\}\}\; -\; \{\backslash \; cfrac\; \{q\; (x)\}\; \{kAG\}\}\}$

Изгибающий момент ($M\; \{\backslash \; displaystyle\; M\}$) и поперечная сила ($Q\; \{\backslash \; displaystyle\; Q\}$) равны

$M\; (x)\; =\; -\; EI\; d\; \phi \; dx;\; Q\; (Икс)\; знак\; равно\; К\; AG\; (dwdx\; -\; \phi )\; =\; -\; EI\; d\; 2\; \phi \; dx\; 2\; =\; d\; M\; dx\; \{\backslash \; displaystyle\; M\; (x)\; =\; -\; EI\; ~\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; \backslash \; varphi\}\; \{\backslash \; mathrm\; \{d\}\; x\}\}\; ~;\; ~~\; Q\; (x)\; =\; kAG\; \backslash \; left\; (\{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; w\}\; \{\backslash \; mathrm\; \{d\}\; x\}\}\; -\; \backslash \; varphi\; \backslash \; right)\; =\; -\; EI\; ~\; \{\; \backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{2\}\; \backslash \; varphi\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{2\}\}\}\; =\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; M\}\; \{\backslash \; mathrm\; \{d\}\; x\}\}\}$

Динамический изгиб балок, также известный как балки, впервые исследовал Даниэль Бернулли в конце 18 века. Уравнение Бернулли движения вибрирующей балки имело тенденцию к завышению собственных частот балок и было незначительно улучшено Рэлеем в 1877 году путем добавления вращения средней плоскости. В 1921 году Стивен Тимошенко усовершенствовал теорию, добавив влияние сдвига на динамический отклик изгибающихся балок. Это позволило использовать теорию для задач, связанных с высокими частотами вибрации, где динамическая теория Эйлера – Бернулли неадекватна. Теории Эйлера-Бернулли и Тимошенко для динамического изгиба балок по-прежнему широко используются инженерами.

Теория Эйлера – Бернулли

Уравнение Эйлера – Бернулли для динамического изгиба тонких, изотропных, однородных балок постоянного поперечного сечения под действием приложенной поперечной нагрузки $q\; (x,\; t)\; \{\backslash \; displaystyle\; q\; (x,\; t)\}$is

$EI\; \partial \; 4\; w\; \partial \; x\; 4\; +\; m\; \partial \; 2\; w\; \partial \; t\; 2\; =\; q\; (x,\; t)\; \{\backslash \; displaystyle\; EI\; ~\; \{\backslash \; cfrac\; \{\backslash \; partial\; ^\; \{4\; \}\; w\}\; \{\backslash \; partial\; x\; ^\; \{4\}\}\}\; +\; m\; ~\; \{\backslash \; cfrac\; \{\backslash \; partial\; ^\; \{2\}\; w\}\; \{\backslash \; partial\; t\; ^\; \{2\}\}\}\; =\; q\; (x,\; t)\}$

где $E\; \{\backslash \; displaystyle\; E\}$- модуль Юнга, $I\; \{\backslash \; displaystyle\; I\}$- момент инерции площади поперечного сечения, $w\; (x,\; t)\; \{\backslash \; displaystyle\; w\; (x,\; t)\}$- отклонение нейтральной оси балки, а $m\; \{\backslash \; displaystyle\; m\}$- масса на единицу длины балки.

Свободные колебания

Для ситуации, когда на балку нет поперечной нагрузки, уравнение изгиба принимает вид

$EI\; \partial \; 4\; w\; \partial \; x\; 4\; +\; m\; \partial \; 2\; w\; \partial \; t\; 2\; знак\; равно\; 0\; \{\backslash \; Displaystyle\; EI\; ~\; \{\backslash \; cfrac\; \{\backslash \; partial\; ^\; \{4\}\; w\}\; \{\backslash \; partial\; x\; ^\; \{4\}\}\}\; +\; m\; ~\; \{\backslash \; cfrac\; \{\backslash \; partial\; ^\; \{2\}\; w\}\; \{\backslash \; partial\; t\; ^\; \{2\}\}\}\; =\; 0\}$

Свободные гармонические колебания балки могут быть выражены как

$w\; (x,\; t)\; =\; Re\; [w\; ^\; (x)\; e\; -\; i\; \omega \; t]\; ⟹\; \partial \; 2\; w\; \partial \; T\; 2\; знак\; равно\; -\; \omega \; 2\; вес\; (Икс,\; T)\; \{\backslash \; Displaystyle\; ш\; (х,\; т)\; =\; \{\backslash \; текст\; \{Re\}\}\; [\{\backslash \; Hat\; \{w\}\}\; (х)\; ~\; е\; ^\; \{-\; я\; \backslash \; омега\; т\; \}]\; \backslash \; quad\; \backslash \; подразумевает\; \backslash \; quad\; \{\backslash \; cfrac\; \{\backslash \; partial\; ^\; \{2\}\; w\}\; \{\backslash \; partial\; t\; ^\; \{2\}\}\}\; =\; -\; \backslash \; omega\; ^\; \{2\}\; ~\; w\; (x,\; t)\}$

и уравнение изгиба можно записать как

$EI\; d\; 4\; w\; ^\; dx\; 4\; -\; m\; \omega \; 2\; w\; ^\; =\; 0\; \{\backslash \; displaystyle\; EI\; ~\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{4\}\; \{\backslash \; hat\; \{w\}\}\; \}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{4\}\}\}\; -\; m\; \backslash \; omega\; ^\; \{2\}\; \{\backslash \; hat\; \{w\}\}\; =\; 0\}$

Общее решение приведенного выше уравнения:

$w\; ^\; =\; A\; 1\; сш\; \; (\beta \; Икс)\; +\; A\; 2\; зп\; \; (\beta \; Икс)\; +\; A\; 3\; соз\; \; (\beta \; Икс)\; +\; A\; 4\; грех\; \; (\beta \; Икс)\; \{\backslash \; Displaystyle\; \{\backslash \; Hat\; \{w\}\}\; =\; A\_\; \{1\}\; \backslash \; cosh\; (\backslash \; beta\; x)\; +\; A\_\; \{2\}\; \backslash \; sinh\; (\backslash \; beta\; x)\; +\; A\_\; \{3\}\; \backslash \; cos\; (\backslash \; beta\; x)\; +\; A\_\; \{4\}\; \backslash \; sin\; (\backslash \; beta\; x)\}$

где $A\; 1,\; A\; 2,\; A\; 3,\; A\; 4\; \{\backslash \; displaystyle\; A\_\; \{1\},\; A\_\; \{2\},\; A\_\; \{3\},\; A\_\; \{4\}\}$- константы, а $\beta :\; =\; (m\; EI\; \omega \; 2)\; 1/4\; \{\backslash \; displaystyle\; \backslash \; beta:\; =\; \backslash \; left\; (\{\backslash \; cfrac\; \{m\}\; \{EI\}\}\; ~\; \backslash \; omega\; ^\; \{2\}\; \backslash \; справа)\; ^\; \{1/4\}\}$

Формы колебаний консольной двутавровой балки
1-й поперечный изгиб	1-й крутильный	1-й вертикальный изгиб
2-й поперечный изгиб	2-й крутильный	2-й вертикальный изгиб

Теория Тимошенко – Рэлея

В 1877 году Рэлей предложил усовершенствование динамической теории пучка Эйлера – Бернулли, включив в него эффект инерции вращения поперечного сечения балки. Тимошенко усовершенствовал эту теорию в 1922 году, добавив эффект сдвига в уравнение балки. Сдвиговые деформации нормали к средней поверхности балки допускаются в теории Тимошенко – Рэлея.

Уравнение изгиба линейно-упругой, изотропной, однородной балки постоянного поперечного сечения при этих предположениях имеет вид

$EI\; \partial \; 4\; w\; \partial \; x\; 4\; +\; m\; \partial \; 2\; w\; \partial \; t\; 2\; -\; (J\; +\; EI\; mk\; AG)\; \partial \; 4\; w\; \partial \; x\; 2\; \partial \; t\; 2\; +\; J\; mk\; AG\; \partial \; 4\; w\; \partial \; t\; 4\; =\; q\; (x,\; t)\; +\; J\; k\; AG\; \partial \; 2\; q\; \partial \; t\; 2\; -\; EI\; k\; AG\; \partial \; 2\; q\; \partial \; x\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; EI\; ~\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{4\}\; w\}\; \{\backslash \; partial\; x\; ^\; \{4\}\}\}\; +\; m\; ~\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; w\}\; \{\; \backslash \; partial\; t\; ^\; \{2\}\}\}\; -\; \backslash \; left\; (J\; +\; \{\backslash \; frac\; \{EIm\}\; \{kAG\}\}\; \backslash \; right)\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{4\}\; w\}\; \{\backslash \; partial\; x\; ^\; \{2\}\; ~\; \backslash \; partial\; t\; ^\; \{2\}\}\}\; +\; \{\backslash \; frac\; \{Jm\}\; \{kAG\}\}\; ~\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{4\}\; w\}\; \{\backslash \; partial\; t\; ^\; \{4\}\}\}\; \backslash \backslash \; [6pt]\; =\; \{\}\; q\; (x,\; t)\; +\; \{\backslash \; frac\; \{J\}\; \{kAG\}\}\; ~\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; q\}\; \{\backslash \; partial\; t\; ^\; \{2\}\}\}\; -\; \{\backslash \; frac\; \{EI\}\; \{kAG\}\}\; ~\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; q\}\; \{\backslash \; partial\; x\; ^\; \{2\}\}\}\; \backslash \; end\; \{align\}\}\}$

где $J\; =\; m\; IA\; \{\backslash \; displaystyle\; J\; =\; \{\backslash \; tfrac\; \{\; mI\}\; \{A\}\}\}$- полярный момент инерции поперечного сечения, $m\; =\; \rho \; A\; \{\backslash \; displaystyle\; m\; =\; \backslash \; rho\; A\}$- масса единицы длины балки, $\rho \; \{\backslash \; displaystyle\; \backslash \; rho\}$- плотность am, $A\; \{\backslash \; displaystyle\; A\}$- площадь поперечного сечения, $G\; \{\backslash \; displaystyle\; G\}$- модуль сдвига, и $k\; \{\; \backslash \; displaystyle\; k\}$- коэффициент поправки на сдвиг . Для материалов с коэффициентом Пуассона ($\nu \; \{\backslash \; displaystyle\; \backslash \; nu\}$), близким к 0,3, коэффициент поправки на сдвиг составляет приблизительно

$k\; =\; 5\; +\; 5\; \nu \; 6\; +\; 5\; \nu \; прямоугольного\; поперечного\; сечения.\; Знак\; равно\; 6\; +\; 12\; \nu \; +\; 6\; \nu \; 2\; 7\; +\; 12\; \nu \; +\; 4\; \nu \; 2\; круговое\; поперечное\; сечение\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; k\; =\; \{\backslash \; frac\; \{5\; +\; 5\; \backslash \; nu\}\; \{6\; +\; 5\; \backslash \; nu\}\}\; \backslash \; quad\; \{\backslash \; text\; \{прямоугольное\; сечение\}\}\; \backslash \backslash \; [6pt]\; =\; \{\backslash \; frac\; \{6\; +\; 12\; \backslash \; nu\; +6\; \backslash \; nu\; ^\; \{2\}\}\; \{7\; +\; 12\; \backslash \; nu\; +4\; \backslash \; nu\; ^\; \{2\; \}\}\}\; \backslash \; quad\; \{\backslash \; text\; \{круговое\; поперечное\; сечение\}\}\; \backslash \; end\; \{align\}\}\}$

Свободные колебания

Для свободных гармонических колебаний уравнения Тимошенко – Рэлея принимают вид

$EI\; d\; 4\; вес\; ^\; dx\; 4\; +\; м\; \omega \; 2\; (J\; m\; +\; EI\; k\; AG)\; d\; 2\; w\; ^\; dx\; 2\; +\; m\; \omega \; 2\; (\omega \; 2\; J\; k\; AG\; -\; 1)\; w\; ^\; =\; 0\; \{\backslash \; displaystyle\; EI\; ~\; \{\backslash \; cfrac\; \{\; \backslash \; mathrm\; \{d\}\; ^\; \{4\}\; \{\backslash \; hat\; \{w\}\}\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{4\}\}\}\; +\; m\; \backslash \; omega\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; cfrac\; \{J\}\; \{m\}\; \}\; +\; \{\backslash \; cfrac\; \{EI\}\; \{kAG\}\}\; \backslash \; right)\; \{\backslash \; cfrac\; \{\backslash \; mathrm\; \{d\}\; ^\; \{2\}\; \{\backslash \; hat\; \{w\}\}\}\; \{\backslash \; mathrm\; \{d\}\; x\; ^\; \{2\}\}\}\; +\; m\; \backslash \; omega\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; cfrac\; \{\backslash \; omega\; ^\; \{2\}\; J\}\; \{kAG\}\}\; -\; 1\; \backslash \; right)\; ~\; \{\backslash \; hat\; \{w\}\}\; =\; 0\}$

Это уравнение можно решить отмечая, что все производные от $w\; \{\backslash \; displaystyle\; w\}$должен иметь ту же форму для компенсации и, следовательно, в качестве решения формы $ekx\; \{\backslash \; displaystyle\; e\; ^\; \{kx\}\}$может быть ожидается. Это наблюдение приводит к характеристическому уравнению

$\alpha \; k\; 4\; +\; \beta \; k\; 2\; +\; \gamma \; =\; 0;\; \alpha :\; знак\; равно\; EI,\; \beta :\; знак\; равно\; м\; \omega \; 2\; (J\; м\; +\; EI\; k\; AG),\; \gamma :\; знак\; равно\; m\; \omega \; 2\; (\omega \; 2\; J\; k\; AG\; -\; 1)\; \{\backslash \; Displaystyle\; \backslash \; альфа\; ~\; к\; ^\; \{4\}\; +\; \backslash \; бета\; ~\; k\; ^\; \{2\}\; +\; \backslash \; gamma\; =\; 0\; ~;\; ~~\; \backslash \; alpha:\; =\; EI\; ~,\; ~~\; \backslash \; beta:\; =\; m\; \backslash \; omega\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; cfrac\; \{J\}\; \{m\}\}\; +\; \{\backslash \; cfrac\; \{EI\}\; \{kAG\}\}\; \backslash \; right)\; ~,\; ~~\; \backslash \; gamma:\; =\; m\; \backslash \; omega\; ^\; \{2\}\; \backslash \; left\; (\{\backslash \; cfrac\; \{\backslash \; omega\; ^\; \{2\}\; J\}\; \{kAG\}\}\; -\; 1\; \backslash \; right)\; \}$

Решения этого уравнения четвертой степени следующие:

$k\; 1\; =\; +\; z\; +,\; k\; 2\; =\; -\; z\; +,\; k\; 3\; =\; +\; z\; -,\; k\; 4\; =\; -\; z\; -\; \{\backslash \; displaystyle\; k\_\; \{1\}\; =\; +\; \{\backslash \; sqrt\; \{z\; \_\; \{+\}\}\}\; ~,\; ~~\; k\_\; \{2\}\; =\; -\; \{\backslash \; sqrt\; \{z\; \_\; \{+\}\}\}\; ~,\; ~~\; k\_\; \{3\}\; =\; +\; \{\backslash \; sqrt\; \{\; z\; \_\; \{-\}\}\}\; ~,\; ~~\; k\_\; \{4\}\; =\; -\; \{\backslash \; sqrt\; \{z\; \_\; \{-\}\}\}\}$

где

$z\; +:\; =\; -\; \beta \; +\; \beta \; 2\; -\; 4\; \alpha \; \gamma \; 2\; \alpha ,\; z\; -:\; =\; -\; \beta \; -\; \beta \; 2\; -\; 4\; \alpha \; \gamma \; 2\; \alpha \; \{\backslash \; displaystyle\; z\; \_\; \{+\}:\; =\; \{\backslash \; cfrac\; \{-\; \backslash \; beta\; +\; \{\backslash \; sqrt\; \{\backslash \; beta\; ^\; \{2\}\; -4\; \backslash \; alpha\; \backslash \; gamma\}\}\; \}\; \{2\; \backslash \; alpha\}\}\; ~,\; ~~\; z\; \_\; \{-\}:\; =\; \{\backslash \; cfrac\; \{-\; \backslash \; beta\; -\; \{\backslash \; sqrt\; \{\backslash \; beta\; ^\; \{2\}\; -4\; \backslash \; alpha\; \backslash \; gamma\}\}\}\; \{2\; \backslash \; alpha\}\}\; \}$

Общее решение уравнения Тимошенко-Рэлея для свободных колебаний может быть записано как

$w\; ^\; =\; A\; 1\; ek\; 1\; x\; +\; A\; 2\; e\; -\; k\; 1\; x\; +\; A\; 3\; ek\; 3\; x\; +\; A\; 4\; е\; -\; К\; 3\; Икс\; \{\backslash \; Displaystyle\; \{\backslash \; Шляпа\; \{w\}\}\; =\; A\_\; \{1\}\; ~\; e\; ^\; \{k\_\; \{1\}\; x\}\; +\; A\_\; \{2\}\; ~\; e\; ^\; \{-\; k\_\; \{1\}\; x\}\; +\; A\_\; \{3\; \}\; ~\; e\; ^\; \{k\_\; \{3\}\; x\}\; +\; A\_\; \{4\}\; ~\; e\; ^\; \{-\; k\_\; \{3\}\; x\}\}$

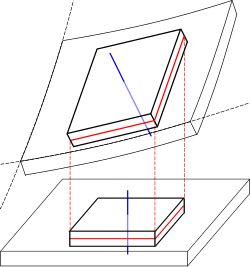
Деформация тонкой пластины с выделением смещения, середина поверхность (красный) и нормаль к средней поверхности (синий)

Определяющей особенностью балок является то, что один из размеров намного больше двух других. Конструкция называется пластиной, если она плоская, и один из ее размеров намного меньше двух других. Существует несколько теорий, которые пытаются описать деформацию и напряжение в пластине под действием приложенных нагрузок, две из которых широко используются. Это

• теория пластин Кирхгофа – Лява (также называемая классической теорией пластин)
• теория пластин Миндлина – Рейсснера (также называемая теорией пластин первого порядка сдвига)

теория Кирхгофа – Лява пластин

Согласно предположениям теории Кирхгофа – Лява,

• прямые линии, нормальные к средней поверхности, остаются прямыми после деформации
• прямые линии, нормальные к средней поверхности, остаются нормальными к середине -поверхность после деформации
• толщина пластины не меняется во время деформации.

Из этих предположений следует, что

$u\; \alpha \; (x)\; =\; -\; x\; 3\; \partial \; w\; 0\; \partial \; x\; \alpha \; =\; -\; x\; 3\; Вт,\; \alpha \; 0;\; \alpha \; знак\; равно\; 1,\; 2\; U\; 3\; (Икс)\; знак\; равно\; вес\; 0\; (Икс\; 1,\; Икс\; 2)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; u\; \_\; \{\backslash \; alpha\}\; (\backslash \; mathbf\; \{x\})\; =\; -\; x\_\; \{3\}\; ~\; \{\; \backslash \; frac\; \{\backslash \; partial\; w\; ^\; \{0\}\}\; \{\backslash \; partial\; x\; \_\; \{\backslash \; alpha\}\}\}\; =\; -\; x\_\; \{3\}\; ~\; w\; \_\; \{,\; \backslash \; alpha\}\; ^\; \{0\}\; ~;\; ~~\; \backslash \; alpha\; =\; 1,2\; \backslash \backslash \; u\_\; \{3\}\; (\backslash \; mathbf\; \{x\})\; =\; w\; ^\; \{0\}\; (x\_\; \{1\},\; x\_\; \{2\})\; \backslash \; end\; \{align\}\}\}$

где $u\; \{\backslash \; displaystyle\; \backslash \; mathbf\; \{\; u\}\}$- это смещение точки на пластине, а $w\; 0\; \{\backslash \; displaystyle\; w\; ^\; \{0\}\}$- смещение средней поверхности.

Соотношение деформация-смещение:

$\epsilon \; \alpha \; \beta \; =\; -\; x\; 3\; w,\; \alpha \; \beta \; 0\; \epsilon \; \alpha \; 3\; =\; 0\; \epsilon \; 33\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; varepsilon\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; =\; -\; x\_\; \{3\}\; ~\; w\; \_\; \{,\; \backslash \; alpha\; \backslash \; beta\}\; ^\; \{0\}\; \backslash \backslash \backslash \; varepsilon\; \_\; \{\backslash \; alpha\; 3\}\; =\; 0\; \backslash \backslash \backslash \; varepsilon\; \_\; \{33\}\; =\; 0\; \backslash \; end\; \{выровнено\}\}\}$

Уравнения равновесия:

$M\; \alpha \; \beta ,\; \alpha \; \beta \; +\; q\; (x)\; =\; 0;\; M\; \alpha \; \beta :\; знак\; равно\; \int \; -\; hhx\; 3\; \sigma \; \alpha \; \beta \; dx\; 3\; \{\backslash \; Displaystyle\; M\; \_\; \{\backslash \; alpha\; \backslash \; beta,\; \backslash \; alpha\; \backslash \; beta\}\; +\; q\; (x)\; =\; 0\; ~;\; ~~\; M\; \_\; \{\backslash \; alpha\; \backslash \; beta\}:\; =\; \backslash \; int\; \_\; \{-\; h\}\; ^\; \{h\}\; x\_\; \{3\}\; ~\; \backslash \; sigma\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; ~\; dx\_\; \{3\}\}$

где $q\; (x)\; \{\backslash \; displaystyle\; q\; (x)\}$- приложенная нагрузка, нормальная к поверхности пластины.

В терминах перемещений уравнения равновесия изотропной линейно-упругой пластины в отсутствие внешней нагрузки могут быть записаны как

$w,\; 1111\; 0\; +\; 2\; w,\; 1212\; 0\; +\; w,\; 2222\; 0\; =\; 0\; \{\backslash \; displaystyle\; w\; \_\; \{,\; 1111\}\; ^\; \{0\}\; +\; 2\; ~\; w\; \_\; \{,\; 1212\}\; ^\; \{0\}\; +\; w\; \_\; \{,\; 2222\}\; ^\; \{0\}\; =\; 0\}$

В прямой тензорной записи

$\nabla \; 2\; \nabla \; 2\; вес\; =\; 0\; \{\backslash \; displaystyle\; \backslash \; nabla\; ^\; \{2\}\; \backslash \; nabla\; ^\; \{2\}\; w\; =\; 0\}$

Теория пластин Миндлина – Рейсснера

Специальное предположение этой теории состоит в том, что нормали к средняя поверхность остается прямой и нерастяжимой, но не обязательно перпендикулярно средней поверхности после деформации. Смещения пластины определяются как

$u\; \alpha \; (x)\; =\; -\; x\; 3\; \phi \; \alpha ;\; \alpha \; знак\; равно\; 1,\; 2\; U\; 3\; (Икс)\; знак\; равно\; вес\; 0\; (Икс\; 1,\; Икс\; 2)\; \{\backslash \; Displaystyle\; \{\backslash \; begin\; \{align\}\; u\; \_\; \{\backslash \; alpha\}\; (\backslash \; mathbf\; \{x\})\; =\; -\; x\_\; \{3\}\; ~\; \backslash \; varphi\; \_\; \{\backslash \; alpha\}\; ~;\; ~~\; \backslash \; alpha\; =\; 1,2\; \backslash \backslash \; u\_\; \{3\}\; (\backslash \; mathbf\; \{x\})\; =\; w\; ^\; \{0\}\; (x\_\; \{1\},\; x\_\; \{2\})\; \backslash \; end\; \{\; выровнен\}\}\}$

где $\phi \; \alpha \; \{\backslash \; displaystyle\; \backslash \; varphi\; \_\; \{\backslash \; alpha\}\}$- это вращения нормали.

Соотношения деформация-смещение, возникающие из этих предположений, следующие:

$\epsilon \; \alpha \; \beta \; =\; -\; x\; 3\; \phi \; \alpha ,\; \beta \; \epsilon \; \alpha \; 3\; =\; 1\; 2\; \kappa \; (w,\; \alpha \; 0\; -\; \phi \; \alpha )\; \epsilon \; 33\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; \backslash \; varepsilon\; \_\; \{\backslash \; alpha\; \backslash \; beta\}\; =\; -\; x\_\; \{3\}\; ~\; \backslash \; varphi\; \_\; \{\backslash \; alpha,\; \backslash \; beta\}\; \backslash \backslash \backslash \; varepsilon\; \_\; \{\backslash \; alpha\; 3\}\; =\; \{\; \backslash \; cfrac\; \{1\}\; \{2\}\}\; ~\; \backslash \; kappa\; \backslash \; left\; (w\; \_\; \{,\; \backslash \; alpha\}\; ^\; \{0\}\; -\; \backslash \; varphi\; \_\; \{\backslash \; alpha\}\; \backslash \; right)\; \backslash \backslash \backslash \; varepsilon\; \_\; \{33\}\; =\; 0\; \backslash \; end\; \{\; выровнено\}\}\}$

где $\kappa \; \{\backslash \; displaystyle\; \backslash \; kappa\}$- коэффициент поправки на сдвиг.

Уравнения равновесия:

$M\; \alpha \; \beta ,\; \beta \; -\; Q\; \alpha \; =\; 0\; Q\; \alpha ,\; \alpha \; +\; q\; =\; 0\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; M\; \_\; \{\backslash \; alpha\; \backslash \; beta,\; \backslash \; beta\}\; -Q\; \_\; \{\backslash \; alpha\}\; =\; 0\; \backslash \backslash \; Q\; \_\; \{\backslash \; alpha,\; \backslash \; alpha\}\; +\; q\; =\; 0\; \backslash \; end\; \{align\}\}\}$

где

$Q\; \alpha :\; =\; \kappa \; \int \; -\; hh\; \sigma \; \alpha \; 3\; dx\; 3\; \{\; \backslash \; displaystyle\; Q\; \_\; \{\backslash \; alpha\}:\; =\; \backslash \; kappa\; ~\; \backslash \; int\; \_\; \{-\; h\}\; ^\; \{h\}\; \backslash \; sigma\; \_\; \{\backslash \; alpha\; 3\}\; ~\; dx\_\; \{3\}\}$

Динамика тонких пластин Кирхгофа

Динамическая теория пластин определяет распространение волн в пластинах, а также изучение стоячих волн и режимов колебаний. Уравнения, управляющие динамическим изгибом пластин Кирхгофа, следующие:

$M\; \alpha \; \beta ,\; \alpha \; \beta \; -\; q\; (x,\; t)\; =\; J\; 1\; w\; ¨\; 0\; -\; J\; 3\; w\; ¨,\; \alpha \; \alpha \; 0\; \{\backslash \; displaystyle\; M\; \_\; \{\backslash \; alpha\; \backslash \; бета,\; \backslash \; alpha\; \backslash \; beta\}\; -q\; (x,\; t)\; =\; J\_\; \{1\}\; ~\; \{\backslash \; ddot\; \{w\}\}\; ^\; \{0\}\; -J\_\; \{3\}\; ~\; \{\backslash \; ddot\; \{w\}\}\; \_\; \{,\; \backslash \; alpha\; \backslash \; альфа\}\; ^\; \{0\}\}$

где для пластины с плотностью $\rho \; =\; \rho \; (x)\; \{\backslash \; displaystyle\; \backslash \; rho\; =\; \backslash \; rho\; (x)\}$,

$J\; 1:\; =\; \int \; -\; hh\; \rho \; dx\; 3;\; J\; 3:\; =\; \int \; -\; hhx\; 3\; 2\; \rho \; dx\; 3\; \{\backslash \; displaystyle\; J\_\; \{1\}:\; =\; \backslash \; int\; \_\; \{-\; h\}\; ^\; \{h\}\; \backslash \; rho\; ~\; dx\_\; \{3\}\; ~;\; ~~\; J\_\; \{3\}:\; =\; \backslash \; int\; \_\; \{-\; h\}\; ^\; \{h\}\; x\_\; \{3\}\; ^\; \{2\}\; ~\; \backslash \; rho\; ~\; dx\_\; \{3\}\}$

и

$w\; ¨\; 0\; =\; \partial \; 2\; w\; 0\; \partial \; t\; 2;\; вес\; ¨,\; \alpha \; \beta \; 0\; знак\; равно\; \partial \; 2\; вес\; ¨\; 0\; \partial \; Икс\; \alpha \; \partial \; Икс\; \beta \; \{\backslash \; Displaystyle\; \{\backslash \; ddot\; \{w\}\}\; ^\; \{0\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; w\; ^\; \{0\}\}\; \{\; \backslash \; partial\; t\; ^\; \{2\}\}\}\; ~;\; ~~\; \{\backslash \; ddot\; \{w\}\}\; \_\; \{,\; \backslash \; alpha\; \backslash \; beta\}\; ^\; \{0\}\; =\; \{\backslash \; frac\; \{\backslash \; partial\; ^\; \{2\}\; \{\backslash \; ddot\; \{w\}\}\; ^\; \{0\}\}\; \{\backslash \; partial\; x\; \_\; \{\backslash \; alpha\}\; \backslash ,\; \backslash \; partial\; x\; \_\; \{\backslash \; beta\}\}\}\}$

На рисунках ниже показаны некоторые колебательные режимы круглой пластины.

• 

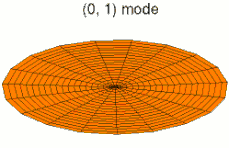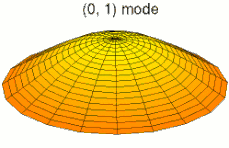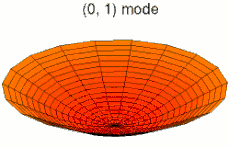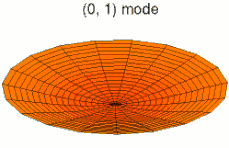
  режим k = 0, p = 1

• 

  режим k = 0, p = 2

• 

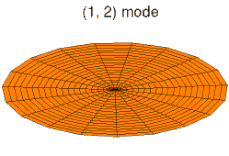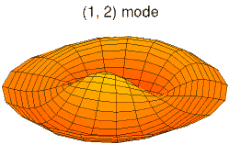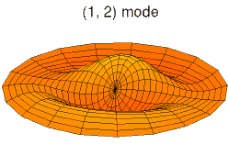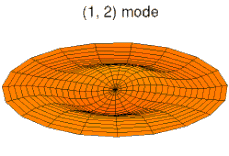
  режим k = 1, p = 2

• Изгибающий момент
• Гибочный станок (плоский гибка металла)
• Тормоз (гибка листового металла)
• Эффект жаровни
• Гибка пластин
• Гибка (металлообработка)
• Механика сплошной среды
• Contraflexure
• Прогиб (инженерия)
• Гибкость подшипник
• Список моментов инерции области
• Диаграмма сдвига и момента
• Прочность на сдвиг
• Сэндвич-теория
• Вибрация
• Вибрация пластин

• Формулы изгиба
• Напряжение и прогиб балки, таблицы прогиба балки