Инверсивная геометрия

В геометрии, обратная геометрия - это изучение тех свойств фигур, которые сохраняется путем обобщения типа преобразования евклидовой плоскости, называемого инверсией. Эти преобразования сохраняют углы и отображают обобщенные окружности в обобщенные окружности, где обобщенный круг означает либо круг, либо линию (грубо говоря, круг с бесконечный радиус ). Многие сложные геометрические задачи становятся более решаемыми, когда применяется инверсия.

Концепция инверсии может быть обобщена на многомерные пространства.

• 1 Инверсия по кругу
  • 1.1 Инверсия точки
    • 1.1.1 Компас и линейка конструкция
  • 1.2 Конструкция Датты
  • 1.3 Свойства
  • 1.4 Примеры в двух измерениях
  • 1.5 Применение
    • 1.5.1 Полюса и полярность
• 2 В трех измерениях
  • 2.1 Примеры в трех измерениях
    • 2.1.1 Сфера
    • 2.1.2 Цилиндр, конус, тор
    • 2.1.3 Сфероид
    • 2.1.4 Гиперболоид одного листа
  • 2.2 Стереографическая проекция как инверсия сферы
  • 2.3 6-сферические координаты
• 3 Аксиоматика и обобщение
• 4 Инвариант
• 5 Связь с программой Erlangen
  • 5.1 Расширение
  • 5.2 Взаимное движение
  • 5.3 Преобразование кругов в круги
  • 5.4 Высшая геометрия
• 6 В высших измерениях
• 7 Свойство антиконформного сопоставления
• 8 Инверсная геометрия и гиперболическая геометрия
• 9 См. Также
• 10 Примечания
• 11 Ссылки
• 12 Внешние ссылки

Инверс e точки

P 'является обратным P по отношению к окружности.

Инвертировать число в арифметике обычно означает принимать его обратным. Тесно связанная с этим идея в геометрии - это «переворачивание» точки. В плоскости, то обратная точки Р по отношению к опорной окружности (O) с центром О и радиусом г является точка Р», лежащей на луче из O через P такое, что

$OP\; \cdot \; OP\; \prime \; =\; r\; 2.\; \{\backslash \; displaystyle\; OP\; \backslash \; cdot\; OP\; ^\; \{\backslash \; prime\}\; =\; r\; ^\; \{2\}.\}$

Это называется инверсией окружности или инверсией плоскости . Инверсия, переводящая любую точку P (кроме O) в ее образ P ', также возвращает P' обратно в P, поэтому результатом двойного применения одной и той же инверсии является тождественное преобразование во всех точках плоскости, кроме O (самоинверсия ). Чтобы сделать инверсию инволюцией, необходимо ввести точку на бесконечности, единственную точку, размещенную на всех линиях, и расширить инверсию, по определению, чтобы поменять местами центр O и эта точка на бесконечности.

Из определения следует, что инверсия любой точки внутри контрольной окружности должна лежать за ее пределами, и наоборот, при этом центр и точка на бесконечности меняют положение, в то время как любая точка на окружности не изменяется (инвариантно относительно инверсии). Таким образом, чем ближе точка к центру, тем дальше происходит ее преобразование, и наоборот.

Конструкция циркуля и линейки

Точка вне окружности

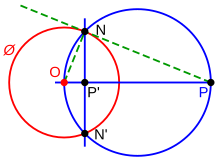Чтобы построить точку P, обратную P 'вне окружности Ø: Пусть r будет радиусом Ø. Правые треугольники OPN и ONP 'похожи. OP - это r, как r - OP '.

Чтобы построить обратную P' точки P за пределами круга Ø:

• Проведите отрезок от O (центр круга Ø) до P.
• Пусть M будет средней точкой OP.
• Нарисуйте окружность c с центром M, проходящим через P.
• Пусть N и N 'будут точками, где Ø и c пересекается.
• Нарисуйте сегмент NN '.
• P' - это место пересечения OP и NN '.

Точка внутри круга

Для построения обратной точки P точки P' внутри Ø круга:

• Нарисуйте луч r от O (центр круга Ø) через P '.
• Проведите линию s через P' перпендикулярно r.
• Пусть N будет одним из точки пересечения Ø и s.
• Нарисуйте сегмент ON.
• Проведите линию t через N перпендикулярно ON.
• P - место пересечения луча r и линии t.

Построение Датты

Существует конструкция точки, обратной к A относительно окружности P, которая не зависит от того, находится ли A внутри или снаружи P.

Рассмотрим окружность P с центром O и точка A, которая может лежать внутри или вне окружности P.

• Возьмем точку пересечения C луча OA с окружностью P.
• Соедините точку C с произвольной точкой B на окружности P (отличной от C)
• Отразите луч BA по линии BC, и пусть h будет отражением, которое пересекает луч OC в точке A '. A '- точка, обратная A относительно окружности P.

Свойства

• 

  Обратной по отношению к красному кругу окружности, проходящей через O (синий), является линия, не проходящая через O (зеленый), наоборот.

• 

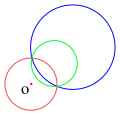
  Обратной по отношению к красному кругу круга, не проходящего через O (синий), является круг, не проходящий через O (зеленый), и наоборот.

• 

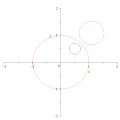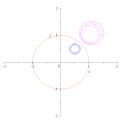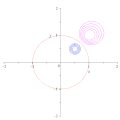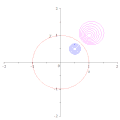
  Инверсия по отношению к окружности не отображает центр окружности в центр ее изображения.

Инверсия набора точек на плоскости относительно окружности - это набор инверсий этих точек. Следующие свойства делают инверсию окружности полезной.

• Окружность, проходящая через центр O контрольной окружности, превращается в прямую, проходящую не через O, а параллельную касательной к исходной окружности в точке O, и наоборот; тогда как прямая, проходящая через O, инвертирована сама в себя (но не поточечно инвариантна).
• Окружность, не проходящая через O, инвертируется в окружность, не проходящую через O. пересечения также находятся на обратной окружности. Окружность (или линия) не изменяется при инверсии тогда и только тогда, когда она ортогональна контрольной окружности в точках пересечения.

Дополнительные свойства включают:

• Если окружность q проходит через два различных точек A и A ', которые являются обратными относительно окружности k, то окружности k и q ортогональны.
• Если окружности k и q ортогональны, то прямая линия, проходящая через центр O окружности k и пересекая q, делает это в точках, обратных к k.
• Дан треугольник OAB, в котором O является центром круга k, а точки A 'и B' противоположны A и B относительно к k, то

$\angle \; OAB\; =\; \angle \; OB\; \prime \; A\; \prime \; и\; \angle \; OBA\; =\; \angle \; OA\; \prime \; B\; \prime .\; \{\backslash \; displaystyle\; \backslash \; angle\; OAB\; =\; \backslash \; angle\; OB\text{'}A\; \text{'}\backslash \; \{\backslash \; text\; \{and\}\}\; \backslash \; \backslash \; angle\; OBA\; =\; \backslash \; angle\; OA\text{'}B\text{'}.\}$

• Точки пересечения двух окружностей p и q, ортогональных окружности k, являются обратными по отношению к k.
• Если M и M 'являются обратными точками по отношению к окружности k на двух кривых m и m', также обратных относительно k, то касательные к m и m 'в точках M и M' либо перпендикулярны прямой MM ', либо образуют с этой линией равнобедренный треугольник с основанием MM'.
• Инверсия оставляет неизменной меру углов, но меняет ориентацию ориентированных углов.

Примеры в двух измерениях

Примеры инверсии окружностей от A до J относительно красного круга в точке O. Круги от A до F, которые проходят через точку O, отображаются в прямые линии. Круги от G до J, которые не отображаются в другие круги. Контрольный круг и линия L сопоставляются сами с собой. Круги пересекают свои обратные точки, если таковые имеются, на контрольной окружности. В файле SVG щелкните или наведите указатель мыши на кружок, чтобы выделить его.

• Инверсия линии - это окружность, содержащая центр инверсии; или это сама линия, если она содержит центр
• Инверсия круга - это другой круг; или это линия, если исходный круг содержит центр
• Инверсия параболы - это кардиоида
• Инверсия гиперболы - это лемниската Бернулли

Приложение

Для круга, не проходящего через центр инверсии, центр инвертируемого круга и центр его изображения при инверсии коллинеарны с центром эталонной окружности. Этот факт может использоваться для доказательства того, что линия Эйлера сенсорного треугольника треугольника совпадает с его линией OI. Доказательство примерно выглядит следующим образом:

Инвертировать относительно вписанной окружности треугольника ABC. средний треугольник внутрисенсорного треугольника инвертирован в треугольник ABC, что означает центр описанной окружности среднего треугольника, то есть центр из девяти точек внутри сенсорного треугольника, центр окружности и центр описанной окружности треугольника ABC коллинеарно.

Любые две непересекающиеся окружности можно инвертировать в концентрические окружности. Затем обратное расстояние (обычно обозначаемое δ) определяется как натуральный логарифм отношения радиусов двух концентрических окружностей.

Кроме того, любые две непересекающиеся окружности могут быть инвертированы в конгруэнтные окружности, используя круг инверсии с центром в точке на круге антиподобия.

Связка Поселье – Липкина - это механическое воплощение инверсии по кругу. Он обеспечивает точное решение важной проблемы преобразования между линейным и круговым движением.

Полюс и полярность

Полярная линия q, ведущая к точке Q относительно окружности радиуса r с центром в точке O . Точка P является точкой инверсии из Q ; полярная линия - это линия, проходящая через P, которая перпендикулярна линии, содержащей O, Pи Q.

. Если точка R является обратной точкой P, то прямые перпендикулярны линии PR через одну из точек проходит полярный другой точки (полюс ).

Полюса и поляры обладают несколькими полезными свойствами:

• Если точка P лежит на прямой l, то полюс L прямой l лежит на полярный p точки P.
• Если точка P движется вдоль прямой l, ее полярный p вращается вокруг полюса L прямой l.
• Если два касательные могут быть проведены от полюса к окружности, тогда его полярная точка проходит через обе точки касания.
• Если точка лежит на окружности, ее полярность является касательной через эту точку.
• Если точка P лежит на своей полярной линии, то P находится на окружности.
• Каждая линия имеет ровно один полюс.

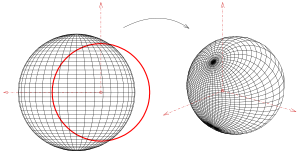Инверсия сферы в красной сфере Инверсия сфероида (в красной сфере) Инверсия гиперболоида одного листа

Инверсия круга обобщается на инверсию сферы в три измерения. Инверсия точки P в 3D относительно эталонной сферы с центром в точке O радиуса R - это точка P 'такая, что $OP\; \times \; OP\text{'}\; =\; R\; 2\; \{\backslash \; displaystyle\; OP\; \backslash \; times\; OP\; ^\; \{\backslash \; prime\; \}\; =\; R\; ^\; \{2\}\}$и точки P и P 'находятся на одном луче, начиная с O. Как и в 2D-версии, сфера инвертируется в сферу, за исключением того, что если сфера проходит через центр O эталонной сферы, затем он переворачивается в плоскость. Любая плоскость, не проходящая через O, превращается в сферу, касающуюся точки O. Окружность, то есть пересечение сферы с секущей плоскостью, превращается в круг, за исключением того, что если круг проходит через O, он превращается в линию. Это сводится к двухмерному случаю, когда секущая плоскость проходит через точку O, но это настоящее трехмерное явление, если секущая плоскость не проходит через точку O.

Примеры в трех измерениях

Сфера

Самая простая поверхность (помимо плоскости) - сфера. На первом рисунке показана нетривиальная инверсия (центр сферы не является центром инверсии) сферы вместе с двумя ортогональными пересекающимися пучками окружностей.

Цилиндр, конус, тор

Инверсия цилиндра, конуса или тора приводит к циклиду Дюпена.

Сфероиду

Сфероид - это поверхность вращения и содержит пучок окружностей, который отображается на пучок окружностей (см. рисунок). Прообраз сфероида - это поверхность степени 4.

Гиперболоид одного листа

Гиперболоид одного листа, который представляет собой поверхность вращения, содержит пучок окружностей, который отображается на карандаш кругов. Гиперболоид на одном листе содержит еще два пучка прямых, которые отображаются на пучки окружностей. На картинке изображена одна такая линия (синяя) и ее инверсия.

Стереографическая проекция как инверсия сферы

Стереографическая проекция как инверсия сферы

A стереографическая проекция обычно проецирует сферу из точки $N\; \{\backslash \; displaystyle\; N\}$(северный полюс) сферы на касательную плоскость в противоположной точке $S\; \{\backslash \; displaystyle\; S\}$(южный полюс). Это отображение может быть выполнено путем инверсии сферы на ее касательную плоскость. Если сфера (которая будет проецироваться) имеет уравнение $x\; 2\; +\; y\; 2\; +\; z\; 2\; =\; -\; z\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; z\; ^\; \{2\}\; =\; -\; z\}$(альтернативно записывается $x\; 2\; +\; y\; 2\; +\; (z\; +\; 1\; 2)\; 2\; =\; 1\; 4\; \{\backslash \; displaystyle\; x\; ^\; \{2\}\; +\; y\; ^\; \{2\}\; +\; (z\; +\; \{\backslash \; tfrac\; \{1\})\; \{2\}\})\; ^\; \{2\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{4\}\}\}$; центр $(0,\; 0,\; -\; 0,5)\; \{\backslash \; displaystyle\; (0,0,\; -0,5)\}$, радиус $0.5\; \{\backslash \; displaystyle\; 0.5\}$, на картинке зеленый), то он будет отображен инверсией на единичной сфере (красный) на касательную плоскость в точке $S\; =\; (0,\; 0,\; -\; 1)\; \{\backslash \; displaystyle\; S\; =\; (0,0,\; -1)\}$. Линии, проходящие через центр инверсии (точка $N\; \{\backslash \; displaystyle\; N\}$), отображаются сами на себя. Это проекционные линии стереографической проекции.

6-сферические координаты

6-сферические координаты представляют собой систему координат для трехмерного пространства, полученную путем инвертирования декартовых координат.

Одним из первых, кто рассмотрел основы инверсивной геометрии, был Марио Пиери в 1911 и 1912 годах. Эдвард Каснер написал диссертацию на тему «Теория инвариантов инверсионной группы. ".

Совсем недавно математическая структура инверсной геометрии была интерпретирована как структура инцидентности, где обобщенные окружности называются" блоками ": In incidence geometry, любая аффинная плоскость вместе с единственной точкой на бесконечности образует плоскость Мебиуса, также известную как инверсионная плоскость. Ко всем линиям добавляется бесконечно удаленная точка. Эти плоскости Мебиуса могут быть описаны аксиоматически и существуют как в конечной, так и в бесконечной версиях.

A модель для плоскости Мебиуса, которая исходит из евклидовой плоскости, - это сфера Римана.

перекрестное отношение между 4 точками $x,\; y,\; z,\; w\; \{\backslash \; displaystyle\; x,\; y,\; z,\; w\}$инвариантно относительно инверсии. В частности, если O является центром инверсии и $r\; 1\; \{\backslash \; displaystyle\; r\_\; \{1\}\}$и $r\; 2\; \{\backslash \; displaystyle\; r\_\; \{2\}\}$- это расстояния до концов линии L, тогда длина линии $d\; \{\backslash \; displaystyle\; d\}$станет $d\; /\; (r\; 1\; r\; 2)\; \{\backslash \; displaystyle\; d\; /\; (r\_\; \{1\}\; r\_\; \{2\})\}$при инверсии с центром O. Инвариант:

$I\; =\; |\; х\; -\; у\; |\; |\; w\; -\; z\; |\; |\; х\; -\; ш\; |\; |\; у\; -\; г\; |\; \{\backslash \; displaystyle\; I\; =\; \{\backslash \; frac\; \{|\; xy\; ||\; wz\; |\}\; \{|\; xw\; ||\; yz\; |\}\}\}$

Согласно Кокстеру, преобразование инверсией по кругу было изобретен Л. И. Магнус в 1831 году. С тех пор это отображение стало путем к высшей математике. Пройдя несколько этапов применения карты инверсии круга, изучающий геометрию преобразований вскоре осознает значение программы Феликса Кляйна Erlangen, являющейся результатом определенного модели гиперболической геометрии

Расширение

Комбинация двух инверсий в концентрических окружностях приводит к подобию, гомотетическому преобразованию или расширению, характеризующемуся отношение радиусов окружности.

$x\; \mapsto \; R\; 2\; x\; |\; х\; |\; 2\; =\; y\; \mapsto \; T\; 2\; y\; |\; y\; |\; 2\; =\; (Т\; R)\; 2\; х.\; \{\backslash \; displaystyle\; x\; \backslash \; mapsto\; R\; ^\; \{2\}\; \{\backslash \; frac\; \{x\}\; \{|\; x\; |\; ^\; \{2\}\}\}\; =\; y\; \backslash \; mapsto\; T\; ^\; \{2\}\; \{\backslash \; frac\; \{y\}\; \{|\; y\; |\; ^\; \{2\}\; \}\}\; =\; \backslash \; left\; (\{\backslash \; frac\; \{T\}\; \{R\}\}\; \backslash \; right)\; ^\; \{2\}\; x.\}$

Взаимное движение

Когда точка на плоскости интерпретируется как комплекс число $z\; =\; x\; +\; iy,\; \{\backslash \; displaystyle\; z\; =\; x\; +\; iy,\}$с комплексно-сопряженным $z\; ¯\; =\; x\; -\; iy,\; \{\backslash \; displaystyle\; \{\backslash \; bar\; \{z\}\}\; =\; x-iy,\}$, тогда обратное z равно

$1\; z\; =\; z\; ¯\; |\; z\; |\; 2.\; \{\backslash \; displaystyle\; \{\backslash \; frac\; \{1\}\; \{z\}\}\; =\; \{\backslash \; frac\; \{\backslash \; bar\; \{z\}\}\; \{|\; z\; |\; ^\; \{2\}\}\}.\}$

Следовательно, алгебраическая форма обращения в единице круг задается формулой $z\; \mapsto \; w\; \{\backslash \; displaystyle\; z\; \backslash \; mapsto\; w\}$где:

$w\; =\; 1\; z\; ¯\; =\; (1\; z)\; ¯\; \{\backslash \; displaystyle\; w\; =\; \{\backslash \; frac\; \{1\; \}\; \{\backslash \; bar\; \{z\}\}\}\; =\; \{\backslash \; overline\; \{\backslash \; left\; (\{\backslash \; frac\; \{1\}\; \{z\}\}\; \backslash \; right)\}\}\}$.

Возврат является ключевым в теории преобразований как генератор из группы Мебиуса. Другие генераторы - это перенос и вращение, оба знакомые по физическим манипуляциям в окружающем 3-м пространстве. Введение возвратно-поступательного движения (зависящего от инверсии окружности) - вот что порождает особую природу геометрии Мёбиуса, которую иногда отождествляют с инверсивной геометрией (евклидовой плоскости). Однако инверсивная геометрия является более обширным исследованием, поскольку она включает в себя грубую инверсию круга (еще не сделанную с сопряжением в возвратно-поступательное движение). Инверсивная геометрия также включает отображение сопряжения. Ни сопряжение, ни инверсия в круге не входят в группу Мёбиуса, поскольку они неконформны (см. Ниже). Элементы группы Мёбиуса являются аналитическими функциями всей плоскости и поэтому обязательно конформными.

Преобразование окружностей в окружности

Рассмотрим в комплексной плоскости окружность радиуса $r\; \{\backslash \; displaystyle\; r\}$вокруг точки $a\; \{\backslash \; displaystyle\; a\}$

$(z\; -\; a)\; (z\; -\; a)\; \ast \; =\; r\; 2\; \{\backslash \; displaystyle\; (za)\; (za)\; ^\; \{*\}\; =\; r\; ^\; \{2\}\}$

где без ограничения общности $a\; \in \; R.\; \{\backslash \; displaystyle\; a\; \backslash \; in\; \backslash \; mathbb\; \{R\}.\}$Использование определения инверсии

$w\; =\; 1\; z\; \ast \; \{\backslash \; displaystyle\; w\; =\; \{\backslash \; frac\; \{1\}\; \{z\; ^\; \{*\}\}\; \}\}$

легко показать, что $w\; \{\backslash \; displaystyle\; w\}$подчиняется уравнению

$ww\; \ast \; -\; a\; (a\; 2\; -\; r\; 2)\; (w\; +\; w\; \ast )\; +\; a\; 2\; (a\; 2\; -\; r\; 2)\; 2\; =\; r\; 2\; (a\; 2\; -\; r\; 2)\; 2\; \{\backslash \; displaystyle\; ww\; ^\; \{*\}\; -\; \{\backslash \; frac\; \{a\}\; \{(a\; ^\; \{2\}\; -r\; ^\; \{2\})\; \}\}\; (w\; +\; w\; ^\; \{*\})\; +\; \{\backslash \; frac\; \{a\; ^\; \{2\}\}\; \{(a\; ^\; \{2\}\; -r\; ^\; \{2\})\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{r\; ^\; \{\; 2\}\}\; \{(a\; ^\; \{2\}\; -r\; ^\; \{2\})\; ^\; \{2\}\}\}\}$

и, следовательно, $w\; \{\backslash \; displaystyle\; w\}$описывает круг с центром $aa\; 2\; -\; r\; 2\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{a\}\; \{a\; ^\; \{2\}\; -r\; ^\; \{2\}\}\}\}$и радиус $r\; |\; a\; 2\; -\; r\; 2\; |.\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{r\}\; \{|\; a\; ^\; \{2\}\; -r\; ^\; \{2\}\; |\}\}.\}$

Когда $a\; \to \; r,\; \{\backslash \; displaystyle\; a\; \backslash \; to\; r,\}$круг трансформируется в прямую, параллельную мнимой оси $w\; +\; w\; \ast \; =\; 1\; a.\; \{\backslash \; displaystyle\; w\; +\; w\; ^\; \{*\}\; =\; \{\backslash \; tfrac\; \{1\}\; \{a\}\}.\}$

Для $a\; \notin \; R\; \{\backslash \; displaystyle\; a\; \backslash \; not\; \backslash \; in\; \backslash \; mathbb\; \{R\}\}$и $aa\; \ast \; \ne \; r\; 2\; \{\backslash \; displaystyle\; aa\; ^\; \{*\}\; \backslash \; neq\; r\; ^\; \{2\}\}$результат для $w\; \{\backslash \; displaystyle\; w\}$равно

$ww\; \ast \; -\; aw\; +\; a\; \ast \; w\; \ast \; (a\; \ast \; a\; -\; r\; 2)\; +\; aa\; \ast \; (aa\; \ast \; -\; r\; 2)\; 2\; =\; r\; 2\; (aa\; \ast \; -\; r\; 2)\; 2\; ⟺\; (w\; -\; a\; \ast \; aa\; \ast \; -\; r\; 2)\; (w\; \ast \; -\; aa\; \ast \; a\; -\; r\; 2)\; =\; (r\; |\; aa\; \ast \; -\; r\; 2\; |)\; 2\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; ww\; ^\; \{*\}\; -\; \{\backslash \; frac\; \{aw\; +\; a\; ^\; \{*\}\; w\; ^\; \{*\}\}\; \{(a\; ^\; \{*\}\; ar\; ^\; \{2\})\}\}\; +\; \{\backslash \; frac\; \{aa\; ^\; \{*\}\}\; \{(aa\; ^\; \{*\}\; -\; r\; ^\; \{2\; \})\; ^\; \{2\}\}\}\; =\; \{\backslash \; frac\; \{r\; ^\; \{2\}\}\; \{(aa\; ^\; \{*\}\; -\; r\; ^\; \{2\})\; ^\; \{2\}\}\}\; \backslash \backslash \; [4pt]\; \backslash \; Longleftrightarrow\; \{\}\; \backslash \; left\; (w\; -\; \{\backslash \; frac\; \{a\; ^\; \{*\}\}\; \{aa\; ^\; \{*\}\; -\; r\; ^\; \{2\}\}\}\; \backslash \; right)\; \backslash \; left\; (w\; ^\; \{*\}\; -\; \{\backslash \; frac\; \{a\}\; \{a\; ^\; \{\; *\}\; ar\; ^\; \{2\}\}\}\; \backslash \; right)\; =\; \backslash \; left\; (\{\backslash \; frac\; \{r\}\; \{\backslash \; left\; |\; aa\; ^\; \{*\}\; -\; r\; ^\; \{2\}\; \backslash \; right\; |\}\}\; \backslash \; right)\; ^\; \{2\}\; \backslash \; конец\; \{выравнивается\}\}\}$

показывает, что $w\; \{\backslash \; displaystyle\; w\}$описывает круг с центром $a\; \ast \; (aa\; \ast \; -\; r\; 2)\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{a\; ^\; \{*\}\}\; \{(aa\; ^\; \{*\}\; -\; r\; ^\; \{2\})\}\}\}$и радиус $r\; |\; a\; \ast \; a\; -\; r\; 2\; |\; \{\backslash \; textstyle\; \{\backslash \; frac\; \{r\}\; \{\backslash \; left\; |\; a\; ^\; \{*\}\; ar\; ^\; \{2\}\; \backslash \; right\; |\}\}\}$.

Когда $a\; \ast \; a\; \to \; r\; 2,\; \{\backslash \; displaystyle\; a\; ^\; \{*\; \}\; a\; \backslash \; to\; r\; ^\; \{2\},\}$уравнение для $w\; \{\backslash \; displaystyle\; w\}$принимает вид

$aw\; +\; a\; \ast \; w\; \ast \; =\; 1\; ⟺\; 2\; Re\; \; \{aw\}\; =\; 1\; ⟺\; Re\; \; \{a\}\; Re\; \; \{w\}\; -\; Im\; \; \{a\}\; Im\; \; \{w\}\; =\; 1\; 2\; ⟺\; Im\; \; \{w\}\; =\; Re\; \; \{a\}\; Im\; \; \{a\}\; \cdot \; Re\; \; \{w\}\; -\; 1\; 2\; \cdot \; Im\; \; \{a\}.\; \{\backslash \; displaystyle\; \{\backslash \; begin\; \{align\}\; aw\; +\; a\; ^\; \{*\}\; w\; ^\; \{*\}\; =\; 1\; \backslash \; Longleftrightarrow\; 2\; \backslash \; operatorname\; \{Re\}\; \backslash \; \{aw\; \backslash \}\; =\; 1\; \backslash \; Longleftrightarrow\; \backslash \; operatorname\; \{Re\}\; \backslash \; \{a\; \backslash \}\; \backslash \; operatorname\; \{Re\}\; \backslash \; \{w\; \backslash \}\; -\; \backslash \; operatorname\; \{Im\}\; \backslash \; \{a\; \backslash \}\; \backslash \; operatorname\; \{Im\}\; \backslash \; \{w\; \backslash \}\; =\; \{\backslash \; frac\; \{1\}\; \{2\}\}\; \backslash \backslash \; [4pt]\; \backslash \; Longleftrightarrow\; \{\; \}\; \backslash \; operatorname\; \{Im\}\; \backslash \; \{w\; \backslash \}\; =\; \{\backslash \; frac\; \{\backslash \; operatorname\; \{Re\}\; \backslash \; \{a\; \backslash \}\}\; \{\backslash \; operatorname\; \{Im\}\; \backslash \; \{a\; \backslash \}\}\}\; \backslash \; cdot\; \backslash \; operatorname\; \{Re\}\; \backslash \; \{\; w\; \backslash \}\; -\; \{\backslash \; frac\; \{1\}\; \{2\; \backslash \; cdot\; \backslash \; operatorname\; \{Im\}\; \backslash \; \{a\; \backslash \}\}\}.\; \backslash \; end\; \{align\}\}\}$

Высшая геометрия

Как упоминалось выше, ноль, начало координат, требует специального рассмотрения при отображении инверсии окружности. Подход состоит в том, чтобы присоединиться к бесконечно удаленной точке, обозначенной как ∞ или 1/0. В подходе комплексных чисел, где взаимное действие является очевидной операцией, эта процедура приводит к сложной проективной линии, часто называемой сферой Римана. Именно подпространства и подгруппы этого пространства и группы отображений были применены для создания ранних моделей гиперболической геометрии Белтрами, Кэли и Клейном. Таким образом, инверсивная геометрия включает идеи, исходящие от Лобачевского и Бойяи в их плоской геометрии. Более того, Феликс Кляйн был настолько увлечен этой возможностью отображений для идентификации геометрических явлений, что в 1872 году он выступил с манифестом, программой Эрлангена. С тех пор многие математики оставляют термин геометрия для пробел вместе с группой отображений этого пространства. Существенными свойствами фигур в геометрии являются те, которые инвариантны по отношению к этой группе.

Например, Смогоржевский разработал несколько теорем инверсивной геометрии до начала геометрии Лобачевского.

В n-мерном пространстве, где есть сфера радиуса r, инверсия в сфере задается как

$xi\; \mapsto \; r\; 2\; xi\; \sum \; jxj\; 2\; \{\backslash \; displaystyle\; x\_\; \{i\}\; \backslash \; mapsto\; \{\backslash \; frac\; \{r\; ^\; \{2\}\; x\_\; \{i\}\}\; \{\backslash \; sum\; \_\; \{j\}\; x\_\; \{j\}\; ^\; \{2\}\}\}\}$

Преобразование по инверсия в гиперплоскостях или гиперсферах в E может использоваться для генерации растяжений, перемещений или вращений. Действительно, две концентрические гиперсферы, используемые для создания последовательных инверсий, приводят к расширению или сжатию в центре гиперсфер. Такое отображение называется подобием.

. Когда две параллельные гиперплоскости используются для создания последовательных отражений, результатом является перевод. Когда две гиперплоскости пересекаются в плоскости (n – 2) - , последовательные отражения создают поворот, где каждая точка (n – 2) -плоскости является фиксированной точкой . каждого отражения и, следовательно, композиции.

Все это конформные отображения, и фактически, если пространство имеет три или более измерений, отображения, генерируемые инверсией, являются единственными конформными отображениями. Теорема Лиувилля является классической теоремой конформной геометрии.

. Добавление точки на бесконечности в пространство устраняет различие между гиперплоскостью и гиперсферой; инверсивная геометрия более высоких измерений часто изучается в предполагаемом контексте n-сферы как базового пространства. Преобразования инверсивной геометрии часто называют преобразованиями Мёбиуса. Инверсивная геометрия была применена к изучению раскраски или разбиения n-сферы.

Карта инверсии круга антиконформна, что означает, что в каждой точке она сохраняет углов и меняет ориентацию (карта называется конформной, если она сохраняет ориентированные углы). Алгебраически карта является антиконформной, если в каждой точке якобиан является скаляром, умноженным на ортогональную матрицу с отрицательным определителем: в двух измерениях якобиан должен быть скалярным, умноженным на отражение в каждой точке.. Это означает, что если J - якобиан, то $J\; \cdot \; JT\; =\; k\; I\; \{\backslash \; displaystyle\; J\; \backslash \; cdot\; J\; ^\; \{T\}\; =\; kI\}$и $det\; (J)\; =\; -\; k.\; \{\backslash \; displaystyle\; \backslash \; det\; (J)\; =\; -\; \{\backslash \; sqrt\; \{k\}\}.\}$Вычисление якобиана в случае z i = x i / | | x ||, где || x || = x 1 +... + x n дает JJ = kI, где k = 1 / || x ||, и дополнительно det (J) отрицательный; следовательно, обратное отображение антиконформно.

В комплексной плоскости наиболее очевидное отображение инверсии круга (т. Е. Использование единичного круга с центром в начале координат) - это комплексное сопряжение комплексного обратного отображения, переводящего z в 1 / z. Комплексное аналитическое обратное отображение конформно, а сопряженное с ним - обращение окружности - антиконформно. В этом случае гомография конформна, а антигомография антиконформна.

(n - 1) -сфера с уравнением

$x\; 1\; 2\; +\; \cdots \; +\; xn\; 2\; +\; 2\; a\; 1\; x\; 1\; +\; \cdots \; +\; 2\; тревога\; +\; c\; =\; 0\; \{\backslash \; displaystyle\; x\_\; \{1\}\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; ^\; \{2\}\; +\; 2a\_\; \{1\}\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; 2a\_\; \{n\}\; x\_\; \{n\}\; +\; c\; =\; 0\}$

будет иметь положительный радиус, если a 1 +... + a n больше, чем c, и при инверсии дает сферу

$Икс\; 1\; 2\; +\; \cdots \; +\; xn\; 2\; +\; 2\; a\; 1\; cx\; 1\; +\; \cdots \; +\; 2\; ancxn\; +\; 1\; c\; =\; 0.\; \{\backslash \; displaystyle\; x\_\; \{1\}\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; ^\; \{2\}\; +2\; \{\backslash \; frac\; \{a\_\; \{1\}\}\; \{c\}\}\; x\_\; \{1\}\; +\; \backslash \; cdots\; +2\; \{\backslash \; frac\; \{a\_\; \{n\}\}\; \{c\}\}\; x\_\; \{n\}\; +\; \{\backslash \; frac\; \{1\}\; \{c\; \}\}\; =\; 0.\}$

Следовательно, он будет инвариантным относительно инверсии тогда и только тогда, когда c = 1. Но это условие ортогональности единичной сфере. Следовательно, мы вынуждены рассматривать (n - 1) -сферы с уравнением

$x\; 1\; 2\; +\; \cdots \; +\; xn\; 2\; +\; 2\; a\; 1\; x\; 1\; +\; \cdots \; +\; 2\; travelling\; +\; 1\; =\; 0,\; \{\backslash \; displaystyle\; x\_\; \{1\}\; ^\; \{2\}\; +\; \backslash \; cdots\; +\; x\_\; \{n\}\; ^\; \{2\}\; +\; 2a\_\; \{1\}\; x\_\; \{1\}\; +\; \backslash \; cdots\; +\; 2a\_\; \{n\}\; x\_\; \{n\}\; +\; 1\; =\; 0,\}$

, которые инвариантны относительно инверсия, ортогональная единичной сфере и имеющая центры вне сферы. Они вместе с гиперплоскостями подпространства, разделяющими полусферы, являются гиперповерхностями модели диска Пуанкаре гиперболической геометрии.

Поскольку инверсия в единичной сфере оставляет сферы, ортогональные ей, инвариантными, инверсия отображает точки внутри единичной сферы наружу и наоборот. Следовательно, это верно в целом для ортогональных сфер, и, в частности, инверсия в одной из сфер, ортогональных единичной сфере, отображает единичную сферу в себя. Он также отображает внутреннюю часть единичной сферы на себя, с точками вне ортогональной сферы, отображающей внутри, и наоборот; это определяет отражения модели диска Пуанкаре, если мы также включим в него отражения через диаметры, разделяющие полусферы единичной сферы. Эти отражения создают группу изометрий модели, которая говорит нам, что изометрии конформны. Следовательно, угол между двумя кривыми в модели такой же, как угол между двумя кривыми в гиперболическом пространстве.

• Круг антиподобия
• Двойственность (проективная геометрия)
• Обратная кривая
• Предельная точка (геометрия)
• преобразование Мёбиуса
• Проективная геометрия
• гекслет Содди
• Инверсия кривых и поверхностей (немецкий)

• Альтшиллер-Корт, Натан (1952), Геометрия колледжа: введение в современную геометрию треугольника и круга ( 2-е изд.), Нью-Йорк: Barnes Noble, LCCN 52-13504
• Блэр, Дэвид Э. (2000), Inversion Theory and Conformal Mapping, American Математическое общество, ISBN 0-8218-2636-0
• Brannan, David A.; Эсплен, Мэтью Ф.; Грей, Джереми Дж. (1998), «Глава 5: Инверсивная геометрия», Геометрия, Кембридж: Cambridge University Press, стр. 199–260, ISBN 0-521-59787-0
• Coxeter, HSM (1969) [1961], Введение в геометрию (2-е изд.), John Wiley Sons, ISBN 0-471-18283- 4
• Хартшорн, Робин (2000), «Глава 7: Неевклидова геометрия, Раздел 37: Круговая инверсия», Геометрия: Евклид и не только, Спрингер, ISBN 0-387-98650-2
• Кей, Дэвид К. (1969), College Geometry, Нью-Йорк: Холт, Райнхарт и Уинстон, LCCN 69-12075

• Инверсия: Отражение в круге в разрезании узла
• страница инверсивной геометрии Уилсона Стотера
• Учебные материалы IMO Compendium практические задачи о том, как использовать инверсию для математических олимпиад
• Вайсштейн, Эрик У. «Инверсия». MathWorld.
• Визуальный словарь специальных плоских кривых Xah Lee