Гиперупругий материал

Часть серии по
Механика сплошной среды
Законы Сохранение Масса Импульс Энергия Неравенства Клаузиус-Дюгем (энтропия)
Механика твердого тела Деформация Эластичность линейный Пластичность Закон Гука Стресс Конечная деформация Бесконечно малая деформация Совместимость Гибка Контактная механика фрикционный Теория разрушения материала Механика разрушения
Гидравлическая механика Жидкости Статика   Динамика Принцип Архимеда   Принцип Бернулли Уравнения Навье – Стокса Уравнение Пуазейля   Закон Паскаля Вязкость ( Ньютоновский   неньютоновский ) Плавучесть   Смешивание   Давление Жидкости Поверхностное натяжение Капиллярное действие Газы Атмосфера Закон Бойля Закон Чарльза Закон Гей-Люссака Закон о комбинированном газе Плазма
Реология Вязкоупругость Реометрия Реометр Умные жидкости Электрореологический Магнитореологический Феррожидкости
Ученые Бернулли Бойл Коши Чарльз Эйлер Гей-Люссак Гук Ньютон Навье Нолл Паскаль Стокса Truesdell
v т е

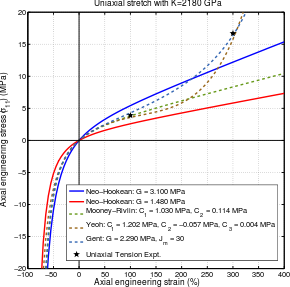
Кривые напряжение – деформация для различных моделей гиперупругих материалов.

Гиперупругая или зеленый упругая материал представляет собой тип конститутивной модели для идеально упругого материала, для которого напряжения-деформация отношений происходят от функции плотности энергии деформации. Гиперупругий материал - это частный случай эластичного материала Коши.

Для многих материалов линейные упругие модели неточно описывают наблюдаемое поведение материала. Наиболее распространенным примером такого рода материала резины, чье напряжение - деформация отношения могут быть определены как нелинейно упругой, изотропной, несжимаемой и вообще не зависит от скорости деформации. Гиперупругость позволяет моделировать поведение таких материалов при напряжении и деформации. Поведение ненаполненных вулканизированных эластомеров часто близко соответствует идеалу гиперупругости. Заполненные эластомеры и биологические ткани также часто моделируются с помощью гиперупругой идеализации.

Рональд Ривлин и Мелвин Муни разработали первые гиперупругие модели, твердые тела Неогука и Муни – Ривлина. С тех пор было разработано множество других гиперупругих моделей. Другие широко используемые модели гиперупругого материала включают модель Огдена и модель Арруда – Бойса.

• 1 Модели гиперупругих материалов
  • 1.1 Модель Сен-Венана – Кирхгофа
  • 1.2 Классификация моделей гиперупругих материалов
• 2 Отношения напряжения и деформации
  • 2.1 Сжимаемые гиперупругие материалы
    • 2.1.1 Первое напряжение Пиолы – Кирхгофа
    • 2.1.2 Второе напряжение Пиолы – Кирхгофа
    • 2.1.3 Напряжение Коши
  • 2.2 Несжимаемые гиперупругие материалы
• 3 Выражения для напряжения Коши
  • 3.1 Сжимаемые изотропные гиперупругие материалы
  • 3.2 Несжимаемые изотропные гиперупругие материалы
• 4 Постоянство с линейной эластичностью
  • 4.1 Условия согласованности изотропных гиперупругих моделей
  • 4.2 Условия консистенции резиновых материалов на несжимаемой основе${\ displaystyle I_ {1}}$
• 5 ссылки
• 6 См. Также

Модель Сен-Венана – Кирхгофа

Простейшей моделью гиперупругого материала является модель Сен-Венана – Кирхгофа, которая является просто расширением геометрически линейной модели упругого материала до геометрически нелинейного режима. Эта модель имеет общий вид и изотропный вид соответственно.

${\ displaystyle {\ boldsymbol {S}} = {\ boldsymbol {C}}: {\ boldsymbol {E}}}$

${\ displaystyle {\ boldsymbol {S}} = \ lambda ~ {\ text {tr}} ({\ boldsymbol {E}}) {\ boldsymbol {\ mathit {I}}} + 2 \ mu {\ boldsymbol {E }}{\текст{.}}}$

где - второе напряжение Пиолы – Кирхгофа, - тензор жесткости четвертого порядка и - лагранжева деформация Грина, определяемая формулой ${\ displaystyle {\ boldsymbol {S}}}$${\ displaystyle {\ boldsymbol {C}}: {\ rm {I \! R}} ^ {3 \ times 3} \ rightarrow {\ rm {I \! R}} ^ {3 \ times 3}}$ ${\ displaystyle {\ boldsymbol {E}}}$

${\ displaystyle \ mathbf {E} = {\ frac {1} {2}} \ left [(\ nabla _ {\ mathbf {X}} \ mathbf {u}) ^ {T} + \ nabla _ {\ mathbf {X}} \ mathbf {u} + (\ nabla _ {\ mathbf {X}} \ mathbf {u}) ^ {T} \ cdot \ nabla _ {\ mathbf {X}} \ mathbf {u} \ right ] \, \!}$

${\ displaystyle \ lambda}$и - константы Ламе, - единичный тензор второго порядка. ${\ displaystyle \ mu}$ ${\ displaystyle {\ boldsymbol {\ mathit {I}}}}$

Функция плотности энергии деформации для модели Сен-Венана – Кирхгофа имеет вид

${\ displaystyle W ({\ boldsymbol {E}}) = {\ frac {\ lambda} {2}} [{\ text {tr}} ({\ boldsymbol {E}})] ^ {2} + \ mu {\ text {tr}} ({\ boldsymbol {E}} ^ {2})}$

а второе напряжение Пиолы – Кирхгофа может быть получено из соотношения

${\ displaystyle {\ boldsymbol {S}} = {\ cfrac {\ partial W} {\ partial {\ boldsymbol {E}}}} ~.}$

Классификация моделей гиперупругих материалов

Модели гиперупругих материалов можно разделить на:

1) феноменологические описания наблюдаемого поведения

• Гриб
• Муни – Ривлин
• Огден
• Полиномиальный
• Сен-Венан-Кирхгоф
• Ага
• Марлоу

2) механистические модели, основанные на аргументах о базовой структуре материала.

• Модель Арруда – Бойса
• Нео-гуковская модель
• Модель Буше – Зильберштейна.

3) гибриды феноменологической и механистической моделей

• Гент
• Ван дер Ваальс

Как правило, гиперупругая модель должна удовлетворять критерию устойчивости Друкера. Некоторые гиперупругие модели удовлетворяют гипотезе Валаниса-Ландела, согласно которой функция энергии деформации может быть разделена на сумму отдельных функций главных участков : ${\ displaystyle (\ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3})}$

${\ Displaystyle W = е (\ lambda _ {1}) + f (\ lambda _ {2}) + f (\ lambda _ {3}) \,.}$

Сжимаемые гиперупругие материалы

Первое напряжение Пиолы – Кирхгофа

Если - функция плотности энергии деформации, 1-й тензор напряжений Пиолы – Кирхгофа может быть рассчитан для гиперупругого материала как ${\ displaystyle W ({\ boldsymbol {F}})}$

${\ displaystyle {\ boldsymbol {P}} = {\ frac {\ partial W} {\ partial {\ boldsymbol {F}}}} \ qquad {\ text {или}} \ qquad P_ {iK} = {\ frac {\ partial W} {\ partial F_ {iK}}}.}$

где - градиент деформации. В терминах лагранжевой деформации Грина () ${\ displaystyle {\ boldsymbol {F}}}$ ${\ displaystyle {\ boldsymbol {E}}}$

${\ displaystyle {\ boldsymbol {P}} = {\ boldsymbol {F}} \ cdot {\ frac {\ partial W} {\ partial {\ boldsymbol {E}}}} \ qquad {\ text {или}} \ qquad P_ {iK} = F_ {iL} ~ {\ frac {\ partial W} {\ partial E_ {LK}}} ~.}$

В терминах правого тензора деформации Коши – Грина () ${\ displaystyle {\ boldsymbol {C}}}$

${\ displaystyle {\ boldsymbol {P}} = 2 ~ {\ boldsymbol {F}} \ cdot {\ frac {\ partial W} {\ partial {\ boldsymbol {C}}}} \ qquad {\ text {или} } \ qquad P_ {iK} = 2 ~ F_ {iL} ~ {\ frac {\ partial W} {\ partial C_ {LK}}} ~.}$

Второе напряжение Пиолы – Кирхгофа

Если - второй тензор напряжений Пиолы – Кирхгофа, то ${\ displaystyle {\ boldsymbol {S}}}$

${\ displaystyle {\ boldsymbol {S}} = {\ boldsymbol {F}} ^ {- 1} \ cdot {\ frac {\ partial W} {\ partial {\ boldsymbol {F}}}} \ qquad {\ text {или}} \ qquad S_ {IJ} = F_ {Ik} ^ {- 1} {\ frac {\ partial W} {\ partial F_ {кДж}}} ~.}$

В терминах лагранжевой деформации Грина

${\ displaystyle {\ boldsymbol {S}} = {\ frac {\ partial W} {\ partial {\ boldsymbol {E}}}} \ qquad {\ text {или}} \ qquad S_ {IJ} = {\ frac {\ partial W} {\ partial E_ {IJ}}} ~.}$

В терминах правого тензора деформации Коши – Грина

${\ displaystyle {\ boldsymbol {S}} = 2 ~ {\ frac {\ partial W} {\ partial {\ boldsymbol {C}}}} \ qquad {\ text {или}} \ qquad S_ {IJ} = 2 ~ {\ frac {\ partial W} {\ partial C_ {IJ}}} ~.}$

Вышеупомянутое соотношение также известно как формула Дойля-Эриксена в конфигурации материала.

Напряжение Коши

Точно так же напряжение Коши определяется выражением

${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {1} {J}} ~ {\ cfrac {\ partial W} {\ partial {\ boldsymbol {F}}}} \ cdot {\ boldsymbol {F }} ^ {T} ~; ~~ J: = \ det {\ boldsymbol {F}} \ qquad {\ text {или}} \ qquad \ sigma _ {ij} = {\ cfrac {1} {J}} ~ {\ cfrac {\ partial W} {\ partial F_ {iK}}} ~ F_ {jK} ~.}$

В терминах лагранжевой деформации Грина

${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {1} {J}} ~ {\ boldsymbol {F}} \ cdot {\ cfrac {\ partial W} {\ partial {\ boldsymbol {E}} }} \ cdot {\ boldsymbol {F}} ^ {T} \ qquad {\ text {or}} \ qquad \ sigma _ {ij} = {\ cfrac {1} {J}} ~ F_ {iK} ~ { \ cfrac {\ partial W} {\ partial E_ {KL}}} ~ F_ {jL} ~.}$

В терминах правого тензора деформации Коши – Грина

${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {J}} ~ {\ boldsymbol {F}} \ cdot {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}} }} \ cdot {\ boldsymbol {F}} ^ {T} \ qquad {\ text {or}} \ qquad \ sigma _ {ij} = {\ cfrac {2} {J}} ~ F_ {iK} ~ { \ cfrac {\ partial W} {\ partial C_ {KL}}} ~ F_ {jL} ~.}$

Приведенные выше выражения действительны даже для анизотропных сред (в этом случае подразумевается, что потенциальная функция неявно зависит от эталонных направленных величин, таких как начальная ориентация волокон). В частном случае изотропии напряжение Коши может быть выражено через левый тензор деформации Коши-Грина следующим образом:

${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {J}} ~ {\ boldsymbol {B}} \ cdot {\ cfrac {\ partial W} {\ partial {\ boldsymbol {B}} }} \ qquad {\ text {или}} \ qquad \ sigma _ {ij} = {\ cfrac {2} {J}} ~ B_ {ik} ~ {\ cfrac {\ partial W} {\ partial B_ {kj }}} ~.}$

Несжимаемые гиперупругие материалы

Для несжимаемого материала. Таким образом, ограничение несжимаемости равно. Для обеспечения несжимаемости гиперупругого материала функцию энергии деформации можно записать в виде: ${\ Displaystyle J: = \ det {\ boldsymbol {F}} = 1}$${\ displaystyle J-1 = 0}$

${\ Displaystyle W = W ({\ boldsymbol {F}}) - п ~ (J-1)}$

где гидростатическое давление действует как множитель Лагранжа для обеспечения ограничения несжимаемости. Первое напряжение Пиолы-Кирхгофа теперь становится ${\ displaystyle p}$

${\ displaystyle {\ boldsymbol {P}} = - p ~ J {\ boldsymbol {F}} ^ {- T} + {\ frac {\ partial W} {\ partial {\ boldsymbol {F}}}} = - p ~ {\ boldsymbol {F}} ^ {- T} + {\ boldsymbol {F}} \ cdot {\ frac {\ partial W} {\ partial {\ boldsymbol {E}}}} = - p ~ {\ boldsymbol {F}} ^ {- T} + 2 ~ {\ boldsymbol {F}} \ cdot {\ frac {\ partial W} {\ partial {\ boldsymbol {C}}}} ~.}$

Этот тензор напряжений впоследствии может быть преобразован в любой из других традиционных тензоров напряжений, таких как тензор напряжений Коши, который определяется выражением

${\ displaystyle {\ boldsymbol {\ sigma}} = {\ boldsymbol {P}} \ cdot {\ boldsymbol {F}} ^ {T} = - p ~ {\ boldsymbol {\ mathit {1}}} + {\ frac {\ partial W} {\ partial {\ boldsymbol {F}}}} \ cdot {\ boldsymbol {F}} ^ {T} = - p ~ {\ boldsymbol {\ mathit {1}}} + {\ boldsymbol {F}} \ cdot {\ frac {\ partial W} {\ partial {\ boldsymbol {E}}}} \ cdot {\ boldsymbol {F}} ^ {T} = - p ~ {\ boldsymbol {\ mathit { 1}}} + 2 ~ {\ boldsymbol {F}} \ cdot {\ frac {\ partial W} {\ partial {\ boldsymbol {C}}}} \ cdot {\ boldsymbol {F}} ^ {T} ~.}$

Сжимаемые изотропные гиперупругие материалы

Для изотропных гиперупругих материалов напряжение Коши может быть выражено через инварианты левого тензора деформации Коши – Грина (или правого тензора деформации Коши – Грина ). Если функция плотности энергии деформации равна, то ${\ displaystyle W ({\ boldsymbol {F}}) = {\ hat {W}} (I_ {1}, I_ {2}, I_ {3}) = {\ bar {W}} ({\ bar { I}} _ {1}, {\ bar {I}} _ {2}, J) = {\ tilde {W}} (\ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3 })}$

${\ displaystyle {\ begin {align} {\ boldsymbol {\ sigma}} amp; = {\ cfrac {2} {\ sqrt {I_ {3}}}} \ left [\ left ({\ cfrac {\ partial {\ hat {W}}} {\ partial I_ {1}}} + I_ {1} ~ {\ cfrac {\ partial {\ hat {W}}} {\ partial I_ {2}}} \ right) {\ boldsymbol {B}} - {\ cfrac {\ partial {\ hat {W}}} {\ partial I_ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] +2 {\ sqrt {I_ {3}}} ~ {\ cfrac {\ partial {\ hat {W}}} {\ partial I_ {3}}} ~ {\ boldsymbol {\ mathit {1}}} \\ amp; = {\ cfrac {2} {J}} \ left [{\ cfrac {1} {J ^ {2/3}}}} \ left ({\ cfrac {\ partial {\ bar {W}}} {\ partial { \ bar {I}} _ {1}}} + {\ bar {I}} _ {1} ~ {\ cfrac {\ partial {\ bar {W}}} {\ partial {\ bar {I}} _ {2}}} \ right) {\ boldsymbol {B}} - {\ cfrac {1} {J ^ {4/3}}} ~ {\ cfrac {\ partial {\ bar {W}}} {\ partial {\ bar {I}} _ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] \\ amp; \ qquad \ qquad + \ left [{\ cfrac {\ partial {\ bar {W}}} {\ partial J}} - {\ cfrac {2} {3J}} \ left ({\ bar {I}} _ {1} ~ {\ cfrac {\ partial {\ bar { W}}} {\ partial {\ bar {I}} _ {1}}} + 2 ~ {\ bar {I}} _ {2} ~ {\ cfrac {\ partial {\ bar {W}}} { \ partial {\ bar {I}} _ {2}}} \ right) \ right] ~ {\ boldsymbol {\ mathi t {1}}} \\ amp; = {\ cfrac {2} {J}} \ left [\ left ({\ cfrac {\ partial {\ bar {W}}}} {\ partial {\ bar {I}} _ {1}}} + {\ bar {I}} _ {1} ~ {\ cfrac {\ partial {\ bar {W}}} {\ partial {\ bar {I}} _ {2}}} \ справа) {\ bar {\ boldsymbol {B}}} - {\ cfrac {\ partial {\ bar {W}}} {\ partial {\ bar {I}} _ {2}}} ~ {\ bar {\ boldsymbol {B}}} \ cdot {\ bar {\ boldsymbol {B}}} \ right] + \ left [{\ cfrac {\ partial {\ bar {W}}} {\ partial J}} - {\ cfrac {2} {3J}} \ left ({\ bar {I}} _ {1} ~ {\ cfrac {\ partial {\ bar {W}}} {\ partial {\ bar {I}} _ {1} }} + 2 ~ {\ bar {I}} _ {2} ~ {\ cfrac {\ partial {\ bar {W}}} {\ partial {\ bar {I}} _ {2}}} \ right) \ right] ~ {\ boldsymbol {\ mathit {1}}} \\ amp; = {\ cfrac {\ lambda _ {1}} {\ lambda _ {1} \ lambda _ {2} \ lambda _ {3}} } ~ {\ cfrac {\ partial {\ tilde {W}}} {\ partial \ lambda _ {1}}} ~ \ mathbf {n} _ {1} \ otimes \ mathbf {n} _ {1} + { \ cfrac {\ lambda _ {2}} {\ lambda _ {1} \ lambda _ {2} \ lambda _ {3}}} ~ {\ cfrac {\ partial {\ tilde {W}}} {\ partial \ лямбда _ {2}}} ~ \ mathbf {n} _ {2} \ otimes \ mathbf {n} _ {2} + {\ cfrac {\ lambda _ {3}} {\ lambda _ {1} \ lambda _ {2} \ lambda _ {3}}} ~ {\ cfrac {\ partial {\ tilde {W}}} {\ partial \ lamb да _ {3}}} ~ \ mathbf {n} _ {3} \ otimes \ mathbf {n} _ {3} \ конец {выровнено}}}$

( Определения этих символов см. На странице слева тензор деформации Коши – Грина ).

Доказательство 1:

Второго тензора напряжений Пиола-Кирхгофа для гиперупругого материала задается ${\ displaystyle {\ boldsymbol {S}} = 2 ~ {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}}}$ где это верно Коши-Грина тензор деформации и является градиент деформации. Напряжений Коши задается ${\ displaystyle {\ boldsymbol {C}} = {\ boldsymbol {F}} ^ {T} \ cdot {\ boldsymbol {F}}}$ ${\ displaystyle {\ boldsymbol {F}}}$ ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {1} {J}} ~ {\ boldsymbol {F}} \ cdot {\ boldsymbol {S}} \ cdot {\ boldsymbol {F}} ^ { T} = {\ cfrac {2} {J}} ~ {\ boldsymbol {F}} \ cdot {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}} \ cdot {\ boldsymbol {F }} ^ {T}}$ где. Позвольте быть три основных инварианта. потом ${\ Displaystyle J = \ det {\ boldsymbol {F}}}$${\ displaystyle I_ {1}, I_ {2}, I_ {3}}$${\ displaystyle {\ boldsymbol {C}}}$ ${\ displaystyle {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}} = {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ cfrac {\ partial I_ { 1}} {\ partial {\ boldsymbol {C}}}} + {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ {\ cfrac {\ partial I_ {2}} {\ partial {\ boldsymbol {C}}}} + {\ cfrac {\ partial W} {\ partial I_ {3}}} ~ {\ cfrac {\ partial I_ {3}} {\ partial {\ boldsymbol {C}}}} ~.}$ В производные инвариантов симметричного тензора являются ${\ displaystyle {\ boldsymbol {C}}}$ ${\ displaystyle {\ frac {\ partial I_ {1}} {\ partial {\ boldsymbol {C}}}} = {\ boldsymbol {\ mathit {1}}} ~; ~~ {\ frac {\ partial I_ { 2}} {\ partial {\ boldsymbol {C}}}} = I_ {1} ~ {\ boldsymbol {\ mathit {1}}} - {\ boldsymbol {C}} ~; ~~ {\ frac {\ partial I_ {3}} {\ partial {\ boldsymbol {C}}}} = \ det ({\ boldsymbol {C}}) ~ {\ boldsymbol {C}} ^ {- 1}}$ Следовательно, мы можем написать ${\ displaystyle {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}} = {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ boldsymbol {\ mathit {1 }}} + {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ (I_ {1} ~ {\ boldsymbol {\ mathit {1}}} - {\ boldsymbol {F}} ^ {T } \ cdot {\ boldsymbol {F}}) + {\ cfrac {\ partial W} {\ partial I_ {3}}} ~ I_ {3} ~ {\ boldsymbol {F}} ^ {- 1} \ cdot { \ boldsymbol {F}} ^ {- T} ~.}$ Подстановка выражения для напряжения Коши дает ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {J}} ~ \ left [{\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ boldsymbol {F} } \ cdot {\ boldsymbol {F}} ^ {T} + {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ (I_ {1} ~ {\ boldsymbol {F}} \ cdot {\ boldsymbol {F}} ^ {T} - {\ boldsymbol {F}} \ cdot {\ boldsymbol {F}} ^ {T} \ cdot {\ boldsymbol {F}} \ cdot {\ boldsymbol {F}} ^ { T}) + {\ cfrac {\ partial W} {\ partial I_ {3}}} ~ I_ {3} ~ {\ boldsymbol {\ mathit {1}}} \ right]}$ Используя левый тензор деформации Коши – Грина и отмечая, что мы можем записать ${\ displaystyle {\ boldsymbol {B}} = {\ boldsymbol {F}} \ cdot {\ boldsymbol {F}} ^ {T}}$${\ displaystyle I_ {3} = J ^ {2}}$ ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {\ sqrt {I_ {3}}}} ~ \ left [\ left ({\ cfrac {\ partial W} {\ partial I_ {1) }}} + I_ {1} ~ {\ cfrac {\ partial W} {\ partial I_ {2}}} \ right) ~ {\ boldsymbol {B}} - {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] + 2 ~ {\ sqrt {I_ {3}}} ~ {\ cfrac {\ partial W} {\ partial I_ {3}}} ~ {\ boldsymbol {\ mathit {1}}} ~.}$ Для несжимаемого материала и, следовательно,. ${\ displaystyle I_ {3} = 1}$${\ Displaystyle W = W (I_ {1}, I_ {2})}$ ${\ displaystyle {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}} = {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ cfrac {\ partial I_ { 1}} {\ partial {\ boldsymbol {C}}}} + {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ {\ cfrac {\ partial I_ {2}} {\ partial {\ boldsymbol {C}}}} = {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ boldsymbol {\ mathit {1}}} + {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ (I_ {1} ~ {\ boldsymbol {\ mathit {1}}} - {\ boldsymbol {F}} ^ {T} \ cdot {\ boldsymbol {F}})}$ Следовательно, напряжение Коши определяется выражением ${\ displaystyle {\ boldsymbol {\ sigma}} = 2 \ left [\ left ({\ cfrac {\ partial W} {\ partial I_ {1}}} + I_ {1} ~ {\ cfrac {\ partial W}) {\ partial I_ {2}}} \ right) ~ {\ boldsymbol {B}} - {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] -p ~ {\ boldsymbol {\ mathit {1}}} ~.}$ где - неопределенное давление, которое действует как множитель Лагранжа для обеспечения ограничения несжимаемости. ${\ displaystyle p}$ Если, кроме того, имеем и, следовательно, ${\ displaystyle I_ {1} = I_ {2}}$${\ Displaystyle W = W (I_ {1})}$ ${\ displaystyle {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}} = {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ cfrac {\ partial I_ { 1}} {\ partial {\ boldsymbol {C}}}} = {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ boldsymbol {\ mathit {1}}}}$ В этом случае напряжение Коши можно выразить как ${\ displaystyle {\ boldsymbol {\ sigma}} = 2 {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ boldsymbol {B}} - p ~ {\ boldsymbol {\ mathit {1} }} ~.}$

Доказательство 2:

Изохорная градиент деформации определяется как, в результате изохорной градиента деформации, имеющей определитель 1, другими словами, это объем простирания бесплатно. Используя это, впоследствии можно определить изохорный левый тензор деформации Коши – Грина. ${\ displaystyle {\ bar {\ boldsymbol {F}}}: = J ^ {- 1/3} {\ boldsymbol {F}}}$${\ displaystyle {\ bar {\ boldsymbol {B}}}: = {\ bar {\ boldsymbol {F}}} \ cdot {\ bar {\ boldsymbol {F}}} ^ {T} = J ^ {- 2 / 3} {\ boldsymbol {B}}}$ Инварианты: Набор инвариантов, которые используются для определения искажающего поведения, представляют собой первые два инварианта изохорного левого тензора деформации Коши – Грина (которые идентичны тем, которые используются для правого тензора растяжения Коши Грина), и добавляют в бой, чтобы описать объемное поведение. ${\ displaystyle {\ bar {\ boldsymbol {B}}}}$${\ displaystyle {\ begin {align} {\ bar {I}} _ {1} amp; = {\ text {tr}} ({\ bar {\ boldsymbol {B}}}) = J ^ {- 2/3 } {\ text {tr}} ({\ boldsymbol {B}}) = J ^ {- 2/3} I_ {1} \\ {\ bar {I}} _ {2} amp; = {\ frac {1 } {2}} \ left ({\ text {tr}} ({\ bar {\ boldsymbol {B}}}) ^ {2} - {\ text {tr}} ({\ bar {\ boldsymbol {B} }} ^ {2}) \ right) = {\ frac {1} {2}} \ left (\ left (J ^ {- 2/3} {\ text {tr}} ({\ boldsymbol {B}}) \ right) ^ {2} - {\ text {tr}} (J ^ {- 4/3} {\ boldsymbol {B}} ^ {2}) \ right) = J ^ {- 4/3} I_ {2} \\ {\ bar {I}} _ {3} amp; = \ det ({\ bar {\ boldsymbol {B}}}) = J ^ {- 6/3} \ det ({\ boldsymbol {B }}) = J ^ {- 2} I_ {3} = J ^ {- 2} J ^ {2} = 1 \ end {выровнено}}}$${\ displaystyle J}$ Чтобы выразить напряжение Коши через инварианты, напомним, что ${\ displaystyle {\ bar {I}} _ {1}, {\ bar {I}} _ {2}, J}$ ${\ displaystyle {\ bar {I}} _ {1} = J ^ {- 2/3} ~ I_ {1} = I_ {3} ^ {- 1/3} ~ I_ {1} ~; ~~ { \ bar {I}} _ {2} = J ^ {- 4/3} ~ I_ {2} = I_ {3} ^ {- 2/3} ~ I_ {2} ~; ~~ J = I_ {3 } ^ {1/2} ~.}$ Цепное правило дифференциации дает нам ${\ displaystyle {\ begin {align} {\ cfrac {\ partial W} {\ partial I_ {1}}} amp; = {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1} }} ~ {\ cfrac {\ partial {\ bar {I}} _ {1}} {\ partial I_ {1}}} + {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} ~ {\ cfrac {\ partial {\ bar {I}} _ {2}} {\ partial I_ {1}}} + {\ cfrac {\ partial W} {\ partial J}} ~ { \ cfrac {\ partial J} {\ partial I_ {1}}} \\ amp; = I_ {3} ^ {- 1/3} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} = J ^ {- 2/3} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} \\ {\ cfrac {\ partial W} {\ partial I_ {2}}} amp; = {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} ~ {\ cfrac {\ partial {\ bar {I}} _ {1}} {\ partial I_ {2}}} + {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} ~ {\ cfrac {\ partial {\ bar {I }} _ {2}} {\ partial I_ {2}}} + {\ cfrac {\ partial W} {\ partial J}} ~ {\ cfrac {\ partial J} {\ partial I_ {2}}} \ \ amp; = I_ {3} ^ {- 2/3} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} = J ^ {- 4/3} ~ { \ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \\ {\ cfrac {\ partial W} {\ partial I_ {3}}} amp; = {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} ~ {\ cfrac {\ partial {\ bar {I}} _ {1}} {\ partial I_ {3}}} + {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} ~ {\ cfrac {\ partial {\ bar {I }} _ {2}} {\ partial I_ {3}}} + {\ cfrac {\ partial W} {\ partial J}} ~ {\ cfrac {\ partial J} {\ partial I_ {3}}} \ \ amp; = - {\ cfrac {1} {3}} ~ I_ {3} ^ {- 4/3} ~ I_ {1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} - {\ cfrac {2} {3}} ~ I_ {3} ^ {- 5/3} ~ I_ {2} ~ {\ cfrac {\ partial W} {\ partial {\ bar { I}} _ {2}}} + {\ cfrac {1} {2}} ~ I_ {3} ^ {- 1/2} ~ {\ cfrac {\ partial W} {\ partial J}} \\ amp; = - {\ cfrac {1} {3}} ~ J ^ {- 8/3} ~ J ^ {2/3} ~ {\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} - {\ cfrac {2} {3}} ~ J ^ {- 10/3} ~ J ^ {4/3} ~ {\ bar {I }} _ {2} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} + {\ cfrac {1} {2}} ~ J ^ {- 1} ~ {\ cfrac {\ partial W} {\ partial J}} \\ amp; = - {\ cfrac {1} {3}} ~ J ^ {- 2} ~ \ left ({\ bar {I}} _ {1 } ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} + 2 ~ {\ bar {I}} _ {2} ~ {\ cfrac {\ partial W} { \ partial {\ bar {I}} _ {2}}} \ right) + {\ cfrac {1} {2}} ~ J ^ {- 1} ~ {\ cfrac {\ partial W} {\ partial J} } \ конец {выровнено}}}$ Напомним, что напряжение Коши определяется выражением ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {\ sqrt {I_ {3}}}} ~ \ left [\ left ({\ cfrac {\ partial W} {\ partial I_ {1) }}} + I_ {1} ~ {\ cfrac {\ partial W} {\ partial I_ {2}}} \ right) ~ {\ boldsymbol {B}} - {\ cfrac {\ partial W} {\ partial I_ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] + 2 ~ {\ sqrt {I_ {3}}} ~ {\ cfrac {\ partial W} {\ partial I_ {3}}} ~ {\ boldsymbol {\ mathit {1}}} ~.}$ В терминах инвариантов имеем ${\ displaystyle {\ bar {I}} _ {1}, {\ bar {I}} _ {2}, J}$ ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {J}} ~ \ left [\ left ({\ cfrac {\ partial W} {\ partial I_ {1}}} + J ^ { 2/3} ~ {\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} {\ partial I_ {2}}} \ right) ~ {\ boldsymbol {B}} - {\ cfrac { \ partial W} {\ partial I_ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] + 2 ~ J ~ {\ cfrac {\ partial W} {\ partial I_ {3}}} ~ {\ boldsymbol {\ mathit {1}}} ~.}$ Подставляя выражения для производных от по, мы имеем ${\ displaystyle W}$${\ displaystyle {\ bar {I}} _ {1}, {\ bar {I}} _ {2}, J}$ ${\ displaystyle {\ begin {align} {\ boldsymbol {\ sigma}} amp; = {\ cfrac {2} {J}} ~ \ left [\ left (J ^ {- 2/3} ~ {\ cfrac {\ частичный W} {\ partial {\ bar {I}} _ {1}}} + J ^ {- 2/3} ~ {\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} { \ partial {\ bar {I}} _ {2}}} \ right) ~ {\ boldsymbol {B}} - J ^ {- 4/3} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] + \\ amp; \ qquad 2 ~ J ~ \ left [- {\ cfrac {1} {3}} ~ J ^ {- 2} ~ \ left ({\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}} } + 2 ~ {\ bar {I}} _ {2} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \ right) + {\ cfrac {1} {2}} ~ J ^ {- 1} ~ {\ cfrac {\ partial W} {\ partial J}} \ right] ~ {\ boldsymbol {\ mathit {1}}} \ end {align}}}$ или же, ${\ displaystyle {\ begin {align} {\ boldsymbol {\ sigma}} amp; = {\ cfrac {2} {J}} ~ \ left [{\ cfrac {1} {J ^ {2/3}}} ~ \ left ({\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} + {\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \ right) ~ {\ boldsymbol {B}} - {\ cfrac {1} {J ^ {4/3}}} ~ {\ cfrac {\ partial W } {\ partial {\ bar {I}} _ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] \\ amp; \ qquad + \ left [{\ cfrac { \ partial W} {\ partial J}} - {\ cfrac {2} {3J}} \ left ({\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} + 2 ~ {\ bar {I}} _ {2} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \ right) \ right] {\ boldsymbol {\ mathit {1}}} \ end {выравнивается}}}$ В терминах девиаторной части мы можем написать ${\ displaystyle {\ boldsymbol {B}}}$ ${\ displaystyle {\ begin {align} {\ boldsymbol {\ sigma}} amp; = {\ cfrac {2} {J}} ~ \ left [\ left ({\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} + {\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \ right) ~ {\ bar {\ boldsymbol {B}}} - {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} ~ {\ bar {\ boldsymbol {B}}} \ cdot {\ bar {\ boldsymbol {B}}} \ right] \\ amp; \ qquad + \ left [{\ cfrac {\ partial W} {\ partial J}} - {\ cfrac {2} {3J}} \ left ({\ bar {I}} _ {1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} + 2 ~ {\ bar {I}} _ { 2} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \ right) \ right] {\ boldsymbol {\ mathit {1}}} \ end {выровнено}} }$ Для несжимаемого материала и, следовательно, напряжение Коши определяется выражением ${\ displaystyle J = 1}$${\ displaystyle W = W ({\ bar {I}} _ {1}, {\ bar {I}} _ {2})}$ ${\ displaystyle {\ boldsymbol {\ sigma}} = 2 \ left [\ left ({\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} + I_ {1} ~ { \ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \ right) ~ {\ bar {\ boldsymbol {B}}} - {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} ~ {\ bar {\ boldsymbol {B}}} \ cdot {\ bar {\ boldsymbol {B}}} \ right] -p ~ {\ boldsymbol {\ mathit {1}}} ~.}$ где - неопределенный член множителя Лагранжа, подобный давлению. Кроме того, если, у нас есть и, следовательно, напряжение Коши может быть выражено как ${\ displaystyle p}$${\ displaystyle {\ bar {I}} _ {1} = {\ bar {I}} _ {2}}$${\ Displaystyle W = W ({\ bar {I}} _ {1})}$ ${\ displaystyle {\ boldsymbol {\ sigma}} = 2 {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} ~ {\ bar {\ boldsymbol {B}}} - п ~ {\ boldsymbol {\ mathit {1}}} ~.}$

Доказательство 3:

Чтобы выразить напряжение Коши через отрезки, напомним, что ${\ displaystyle \ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3}}$ ${\ displaystyle {\ cfrac {\ partial \ lambda _ {i}} {\ partial {\ boldsymbol {C}}}} = {\ cfrac {1} {2 \ lambda _ {i}}} ~ {\ boldsymbol { R}} ^ {T} \ cdot (\ mathbf {n} _ {i} \ otimes \ mathbf {n} _ {i}) \ cdot {\ boldsymbol {R}} ~; ~~ i = 1,2, 3 ~.}$ Цепное правило дает ${\ displaystyle {\ begin {align} {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}} amp; = {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} ~ {\ cfrac {\ partial \ lambda _ {1}} {\ partial {\ boldsymbol {C}}}} + {\ cfrac {\ partial W} {\ partial \ lambda _ {2}}} ~ {\ cfrac {\ partial \ lambda _ {2}} {\ partial {\ boldsymbol {C}}}} + {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}} ~ {\ cfrac {\ partial \ лямбда _ {3}} {\ partial {\ boldsymbol {C}}}} \\ amp; = {\ boldsymbol {R}} ^ {T} \ cdot \ left [{\ cfrac {1} {2 \ lambda _ { 1}}} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} ~ \ mathbf {n} _ {1} \ otimes \ mathbf {n} _ {1} + {\ cfrac { 1} {2 \ lambda _ {2}}} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {2}}} ~ \ mathbf {n} _ {2} \ otimes \ mathbf {n} _ {2} + {\ cfrac {1} {2 \ lambda _ {3}}} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}} ~ \ mathbf {n} _ {3} \ otimes \ mathbf {n} _ {3} \ right] \ cdot {\ boldsymbol {R}} \ end {align}}}$ Напряжение Коши определяется выражением ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {J}} ~ {\ boldsymbol {F}} \ cdot {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}} }} \ cdot {\ boldsymbol {F}} ^ {T} = {\ cfrac {2} {J}} ~ ({\ boldsymbol {V}} \ cdot {\ boldsymbol {R}}) \ cdot {\ cfrac {\ partial W} {\ partial {\ boldsymbol {C}}}} \ cdot ({\ boldsymbol {R}} ^ {T} \ cdot {\ boldsymbol {V}})}$ Подстановка выражения для производной от приводит к ${\ displaystyle W}$ ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {2} {J}} ~ {\ boldsymbol {V}} \ cdot \ left [{\ cfrac {1} {2 \ lambda _ {1}} } ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} ~ \ mathbf {n} _ {1} \ otimes \ mathbf {n} _ {1} + {\ cfrac {1} { 2 \ lambda _ {2}}} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {2}}} ~ \ mathbf {n} _ {2} \ otimes \ mathbf {n} _ {2} + {\ cfrac {1} {2 \ lambda _ {3}}} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}} ~ \ mathbf {n} _ {3} \ otimes \ mathbf {n} _ {3} \ right] \ cdot {\ boldsymbol {V}}}$ Используя спектральное разложение из нас ${\ displaystyle {\ boldsymbol {V}}}$ ${\ displaystyle {\ boldsymbol {V}} \ cdot (\ mathbf {n} _ {i} \ otimes \ mathbf {n} _ {i}) \ cdot {\ boldsymbol {V}} = \ lambda _ {i} ^ {2} ~ \ mathbf {n} _ {i} \ otimes \ mathbf {n} _ {i} ~; ~~ i = 1,2,3.}$ Также обратите внимание, что ${\ Displaystyle J = \ det ({\ boldsymbol {F}}) = \ det ({\ boldsymbol {V}}) \ det ({\ boldsymbol {R}}) = \ det ({\ boldsymbol {V}}) = \ lambda _ {1} \ lambda _ {2} \ lambda _ {3} ~.}$ Следовательно, выражение для напряжения Коши можно записать как ${\ displaystyle {\ boldsymbol {\ sigma}} = {\ cfrac {1} {\ lambda _ {1} \ lambda _ {2} \ lambda _ {3}}} ~ \ left [\ lambda _ {1} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} ~ \ mathbf {n} _ {1} \ otimes \ mathbf {n} _ {1} + \ lambda _ {2} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {2}}} ~ \ mathbf {n} _ {2} \ otimes \ mathbf {n} _ {2} + \ lambda _ {3} ~ {\ cfrac { \ partial W} {\ partial \ lambda _ {3}}} ~ \ mathbf {n} _ {3} \ otimes \ mathbf {n} _ {3} \ right]}$ Для несжимаемого материала а значит. Следуя Огдену П. 485, можно написать ${\ displaystyle \ lambda _ {1} \ lambda _ {2} \ lambda _ {3} = 1}$${\ Displaystyle W = W (\ lambda _ {1}, \ lambda _ {2})}$ ${\ displaystyle {\ boldsymbol {\ sigma}} = \ lambda _ {1} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} ~ \ mathbf {n} _ {1} \ otimes \ mathbf {n} _ {1} + \ lambda _ {2} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {2}}} ~ \ mathbf {n} _ {2} \ otimes \ mathbf {n} _ {2} + \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}} ~ \ mathbf {n} _ {3} \ otimes \ mathbf {n } _ {3} -p ~ {\ boldsymbol {\ mathit {1}}} ~}$ На этом этапе требуется некоторая осторожность, потому что, когда собственное значение повторяется, оно, как правило, дифференцируемо только по Гато, но не по Фреше. Строгую тензорную производную можно найти только путем решения другой задачи на собственные значения. Если выразить напряжение в терминах различий между компонентами, ${\ displaystyle \ sigma _ {11} - \ sigma _ {33} = \ lambda _ {1} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} - \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}} ~; ~~ \ sigma _ {22} - \ sigma _ {33} = \ lambda _ {2} ~ {\ cfrac {\ частичный W} {\ partial \ lambda _ {2}}} - \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}}}$ Если в дополнение к несжимаемости у нас есть то возможное решение проблемы требует, и мы можем записать разницу напряжений в виде ${\ displaystyle \ lambda _ {1} = \ lambda _ {2}}$${\ displaystyle \ sigma _ {11} = \ sigma _ {22}}$ ${\ displaystyle \ sigma _ {11} - \ sigma _ {33} = \ sigma _ {22} - \ sigma _ {33} = \ lambda _ {1} ~ {\ cfrac {\ partial W} {\ partial \ лямбда _ {1}}} - \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}}}$

Несжимаемые изотропные гиперупругие материалы

Для несжимаемых изотропных гиперупругих материалов функция плотности энергии деформации равна. Напряжение Коши тогда определяется выражением ${\ displaystyle W ({\ boldsymbol {F}}) = {\ hat {W}} (I_ {1}, I_ {2})}$

${\ displaystyle {\ begin {align} {\ boldsymbol {\ sigma}} amp; = - p ~ {\ boldsymbol {\ mathit {1}}} + 2 \ left [\ left ({\ cfrac {\ partial {\ hat {W}}} {\ partial I_ {1}}} + I_ {1} ~ {\ cfrac {\ partial {\ hat {W}}} {\ partial I_ {2}}} \ right) {\ boldsymbol { B}} - {\ cfrac {\ partial {\ hat {W}}} {\ partial I_ {2}}} ~ {\ boldsymbol {B}} \ cdot {\ boldsymbol {B}} \ right] \\ amp; = -p ~ {\ boldsymbol {\ mathit {1}}} + 2 \ left [\ left ({\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {1}}} + I_ { 1} ~ {\ cfrac {\ partial W} {\ partial {\ bar {I}} _ {2}}} \ right) ~ {\ bar {\ boldsymbol {B}}} - {\ cfrac {\ partial W } {\ partial {\ bar {I}} _ {2}}} ~ {\ bar {\ boldsymbol {B}}} \ cdot {\ bar {\ boldsymbol {B}}} \ right] \\ amp; = - p ~ {\ boldsymbol {\ mathit {1}}} + \ lambda _ {1} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} ~ \ mathbf {n} _ {1} \ otimes \ mathbf {n} _ {1} + \ lambda _ {2} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {2}}} ~ \ mathbf {n} _ {2} \ otimes \ mathbf {n} _ {2} + \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}} ~ \ mathbf {n} _ {3} \ otimes \ mathbf {п} _ {3} \ end {выровнено}}}$

где - неопределенное давление. Что касается различий в стрессе ${\ displaystyle p}$

${\ displaystyle \ sigma _ {11} - \ sigma _ {33} = \ lambda _ {1} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {1}}} - \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}} ~; ~~ \ sigma _ {22} - \ sigma _ {33} = \ lambda _ {2} ~ {\ cfrac {\ частичный W} {\ partial \ lambda _ {2}}} - \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}}}$

Если вдобавок, то ${\ displaystyle I_ {1} = I_ {2}}$

${\ displaystyle {\ boldsymbol {\ sigma}} = 2 {\ cfrac {\ partial W} {\ partial I_ {1}}} ~ {\ boldsymbol {B}} - p ~ {\ boldsymbol {\ mathit {1} }} ~.}$

Если, то ${\ displaystyle \ lambda _ {1} = \ lambda _ {2}}$

${\ displaystyle \ sigma _ {11} - \ sigma _ {33} = \ sigma _ {22} - \ sigma _ {33} = \ lambda _ {1} ~ {\ cfrac {\ partial W} {\ partial \ лямбда _ {1}}} - \ lambda _ {3} ~ {\ cfrac {\ partial W} {\ partial \ lambda _ {3}}}}$

Согласованность с линейной упругостью часто используется для определения некоторых параметров моделей гиперупругих материалов. Эти условия согласованности можно найти, сравнив закон Гука с линеаризованной гиперупругостью при малых деформациях.

Условия согласованности изотропных гиперупругих моделей

Чтобы изотропные гиперупругие материалы согласовывались с изотропной линейной упругостью, соотношение напряжение-деформация должно иметь следующую форму в пределе бесконечно малой деформации :

${\ displaystyle {\ boldsymbol {\ sigma}} = \ lambda ~ \ mathrm {tr} ({\ boldsymbol {\ varepsilon}}) ~ {\ boldsymbol {\ mathit {1}}} + 2 \ mu {\ boldsymbol { \ varepsilon}}}$

где - постоянные Ламе. Функция плотности энергии деформации, соответствующая приведенному выше соотношению, имеет вид ${\ displaystyle \ lambda, \ mu}$

${\ displaystyle W = {\ tfrac {1} {2}} \ lambda ~ [\ mathrm {tr} ({\ boldsymbol {\ varepsilon}})] ^ {2} + \ mu ~ \ mathrm {tr} ({ \ boldsymbol {\ varepsilon}} ^ {2})}$

Для несжимаемого материала и мы имеем ${\ Displaystyle \ mathrm {tr} ({\ boldsymbol {\ varepsilon}}) = 0}$

${\ displaystyle W = \ mu ~ \ mathrm {tr} ({\ boldsymbol {\ varepsilon}} ^ {2})}$

Чтобы любая функция плотности энергии деформации сводилась к указанным выше формам для малых деформаций, должны быть выполнены следующие условия: ${\ Displaystyle W (\ lambda _ {1}, \ lambda _ {2}, \ lambda _ {3})}$

${\ displaystyle {\ begin {align} amp; W (1,1,1) = 0 ~; ~~ {\ cfrac {\ partial W} {\ partial \ lambda _ {i}}} (1,1,1) = 0 \\ amp; {\ cfrac {\ partial ^ {2} W} {\ partial \ lambda _ {i} \ partial \ lambda _ {j}}} (1,1,1) = \ lambda +2 \ mu \ дельта _ {ij} \ конец {выровнено}}}$

Если материал несжимаемый, то вышеуказанные условия могут быть выражены в следующей форме.

${\ displaystyle {\ begin {align} amp; W (1,1,1) = 0 \\ amp; {\ cfrac {\ partial W} {\ partial \ lambda _ {i}}} (1,1,1) = { \ cfrac {\ partial W} {\ partial \ lambda _ {j}}} (1,1,1) ~; ~~ {\ cfrac {\ partial ^ {2} W} {\ partial \ lambda _ {i} ^ {2}}} (1,1,1) = {\ cfrac {\ partial ^ {2} W} {\ partial \ lambda _ {j} ^ {2}}} (1,1,1) \\ amp; {\ cfrac {\ partial ^ {2} W} {\ partial \ lambda _ {i} \ partial \ lambda _ {j}}} (1,1,1) = \ mathrm {independentof} ~ i, j \ neq i \\ amp; {\ cfrac {\ partial ^ {2} W} {\ partial \ lambda _ {i} ^ {2}}} (1,1,1) - {\ cfrac {\ partial ^ {2} W} {\ partial \ lambda _ {i} \ partial \ lambda _ {j}}} (1,1,1) + {\ cfrac {\ partial W} {\ partial \ lambda _ {i}}} (1, 1,1) = 2 \ mu ~~ (i \ neq j) \ end {align}}}$

Эти условия могут быть использованы для нахождения соотношений между параметрами данной гиперупругой модели и модулями сдвига и объемного сжатия.

Условия консистенции для резиновых материалов на несжимаемой основе${\ displaystyle I_ {1}}$

Многие эластомеры адекватно моделируются функцией плотности энергии деформации, которая зависит только от. Таких материалов у нас есть. Условия консистенции для несжимаемых материалов в этом случае могут быть выражены как ${\ displaystyle I_ {1}}$${\ Displaystyle W = W (I_ {1})}$${\ displaystyle I_ {1} = 3, \ lambda _ {i} = \ lambda _ {j} = 1}$

${\ Displaystyle W (I_ {1}) {\ biggr |} _ {I_ {1} = 3} = 0 \ quad {\ text {и}} \ quad {\ cfrac {\ partial W} {\ partial I_ { 1}}} {\ biggr |} _ {I_ {1} = 3} = {\ frac {\ mu} {2}} \,.}$

Второе условие согласованности выше можно вывести, отметив, что

${\ displaystyle {\ cfrac {\ partial W} {\ partial \ lambda _ {i}}} = {\ cfrac {\ partial W} {\ partial I_ {1}}} {\ cfrac {\ partial I_ {1} } {\ partial \ lambda _ {i}}} = 2 \ lambda _ {i} {\ cfrac {\ partial W} {\ partial I_ {1}}} \ quad {\ text {and}} \ quad {\ cfrac {\ partial ^ {2} W} {\ partial \ lambda _ {i} \ partial \ lambda _ {j}}} = 2 \ delta _ {ij} {\ cfrac {\ partial W} {\ partial I_ { 1}}} + 4 \ lambda _ {i} \ lambda _ {j} {\ cfrac {\ partial ^ {2} W} {\ partial I_ {1} ^ {2}}} \,.}$

Эти соотношения затем можно подставить в условие согласованности для изотропных несжимаемых гиперупругих материалов.

• Эластичный материал Коши
• Механика сплошной среды
• Деформация (механика)
• Теория конечных деформаций
• Модель Огдена – Роксбурга
• Эластичность резины
• Стрессовые меры
• Стресс (механика)